1. Introduction
It is well known that the geostrophic state is a two-dimensional basic state for large-scale atmospheric motion [
1,
2,
3]. In the geostrophic state, the motion is nondivergent, and thus, there is no vertical motion [
4,
5]. However, in reality, the atmospheric motions are three-dimensional, and the motion is certainly upward or downward as a result of various reasons. Spiral structures of vortices in the atmosphere in different scales form in these cases [
6]. A typical three-dimensional basic state is cyclonic vorticity with rising motion due to surface convergence and anticyclonic vorticity as well as sinking motion due to surface divergence. Exact solutions of the Navier–Stokes equations for a three-dimensional vortex have been discovered [
7,
8,
9,
10,
11]; of particular interest is Sullivan’s two-cell vortex solution, because the flow not only spirals in toward the axis and out along it, but it also has a region of reverse flow near the axis.
It should be noted that there are a large number of works dedicated to the theoretical study of atmospheric vortices. However, most of these are concerned with the numerical solution of the atmospheric motion equations. Analytical models of steady-state vortexes in the atmosphere have been examined in fewer studies (e.g., [
12,
13]). In [
14,
15,
16], three-dimensional atmospheric vortex motion is analyzed by considering the primitive dynamic and thermodynamic equations, including the Coriolis, pressure gradient and viscous forces. It should be noted that nondivergent motion has been studied in [
14,
15,
16]. Furthermore, a strong assumption of the model in [
14,
15,
16] is that the viscous friction force linearly depends on the velocity. In this paper, we further develop the theoretical model of the vortex motion state of the atmosphere. The main goal of the study is to refine the model by taking into account the nonzero velocity divergence term in the equations of motion. In addition, we use a more general expression for the friction force in the form of proportionality to the velocity Laplacian.
2. Main Equations
In the local coordinate system, the atmospheric state is described by the set of Equations (1)–(5):
Here, ; and are the air temperatures of the disturbed and undisturbed atmosphere correspondingly; are the projections of the air velocity on the axes; is the air density; is the air pressure; are the projections of the earth’s angular velocity on the axes; is the air kinematic viscosity; is the air temperature conductivity coefficient; is the air thermal expansion coefficient, where ; is the temperature vertical gradient; is the “autoconvective vertical gradient”; is the acceleration of gravity; is the dry-air specific gas constant. The x-axis is tangential to the parallel line in the direction of the earth’s rotation, the y-axis is tangential to the meridian in the direction from the equator to the North Pole, and the z-axis is perpendicular to the earth’s surface. Thus, . Here we neglect the geoidal shape of the earth and assume it to be spherical. The air density has the form ; the static density decreases with height by the exponential law. Equation (5) has been obtained by substitution of the density expression into the continuity equation.
The basic state of the atmosphere is assumed to be in hydrostatic balance:
We let the atmospheric parameters have the form of perturbation of the static state:
Here, is the dry-air adiabatic temperature gradient.
It is convenient to convert the equations into dimensionless form. The length scales for horizontal and vertical directions are taken as
L and
H, the velocity scale in horizontal directions is
U, the time scale is
L/
U, the vertical velocity scale is
HU/
L, the scale for pressure is
, and the temperature
scale is
. At the same time, we set
,
(Reynolds number),
(Richardson number),
N (Brunt–Väisälä frequency,
),
(Prandtl number),
(Rossby number), and
. If we drop the advective terms in Equations (1)–(5) and assume
(i.e.,
L =
H), then the set of equations can be written as
Differentiating with respect to
y and
x and subtracting Equation (1) from Equation (2), we obtain
Here
are the vertical vorticity and horizontal divergence, correspondingly.
Analogously, differentiating and summing Equations (6) and (7), we obtain
We assume that the three-dimensional atmospheric state is time independent and stationary. Neglecting the advective terms, Equations (11)–(15) can be transformed:
Excluding
,
,
and
, we obtain the required partial differential equation:
where
Ra is the Rayleigh number, and Ta is the Taylor number.
3. Solution of the Main Equations
Following the previous studies [
7,
8,
9,
10,
11,
14,
15,
16], we assume that
has the form
where
k is the wave number;
is the initial phase determining the initial value of the air vertical velocity component at
;
n is the mode number equal to the number of wave lengths within the characteristic length scale
L. In fact,
n is the number of the vortex cell on the vertical axis; hereafter we assume that
n = 1.
Substituting Equation (23) into Equation (21), we obtain
The functional form of the zonal velocity components differs from the corresponding expressions in the previous studies [
7,
8,
9,
10,
11,
14,
15,
16] because of the fact that the velocity divergence is nonzero. Thus, we seek the expression of
u in the form:
Assuming
and
, we obtain, for the Brunt–Väisälä frequency,
or
From here it follows that the critical value of the vertical temperature gradient is close to the value of the dry-air adiabatic gradient.
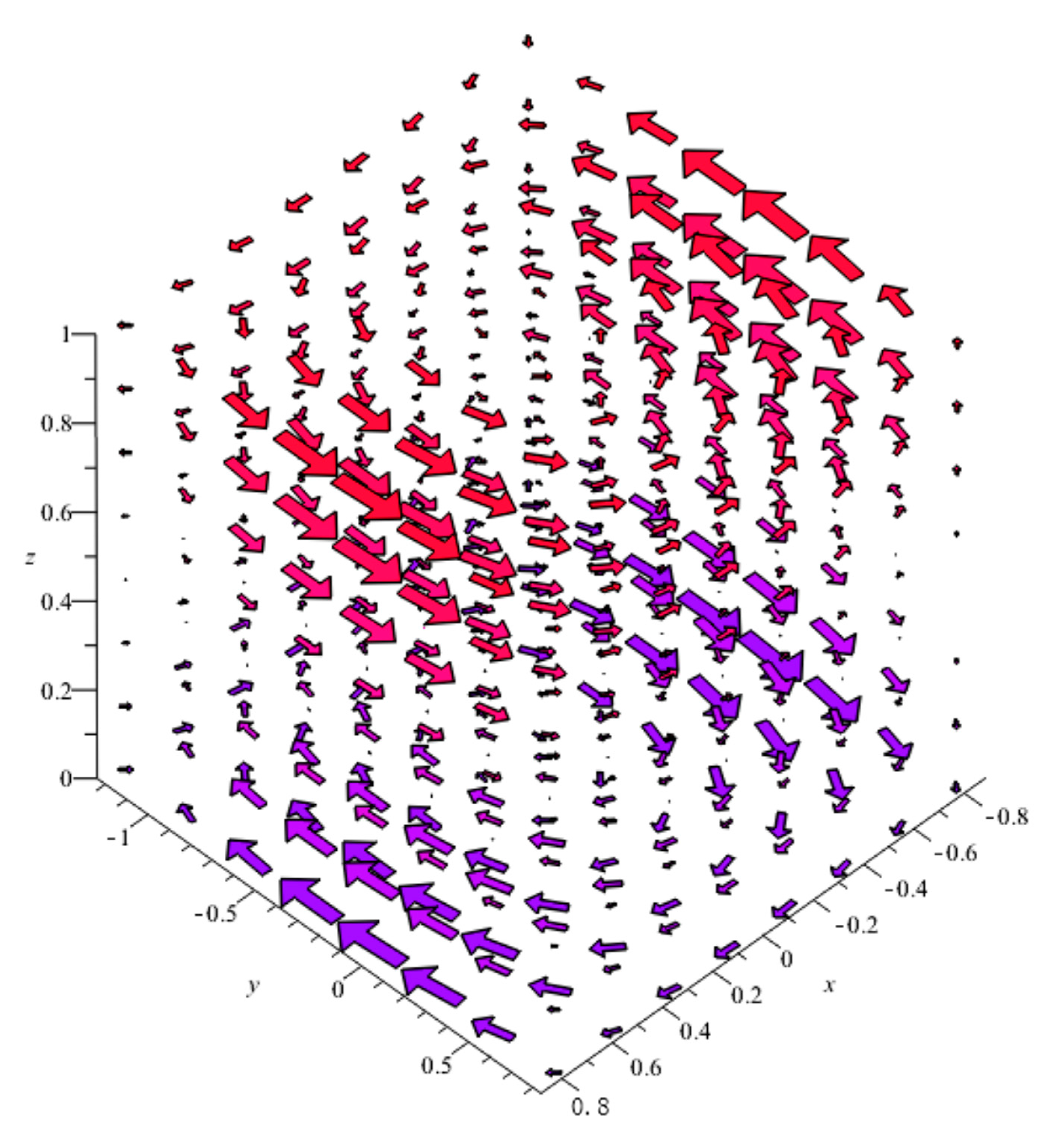
Figure 1 shows the velocity field in accordance with Equations (24)–(26). In all calculations, we assume that
. It is seen that the air parcel motion has a three-dimensional vortex structure.
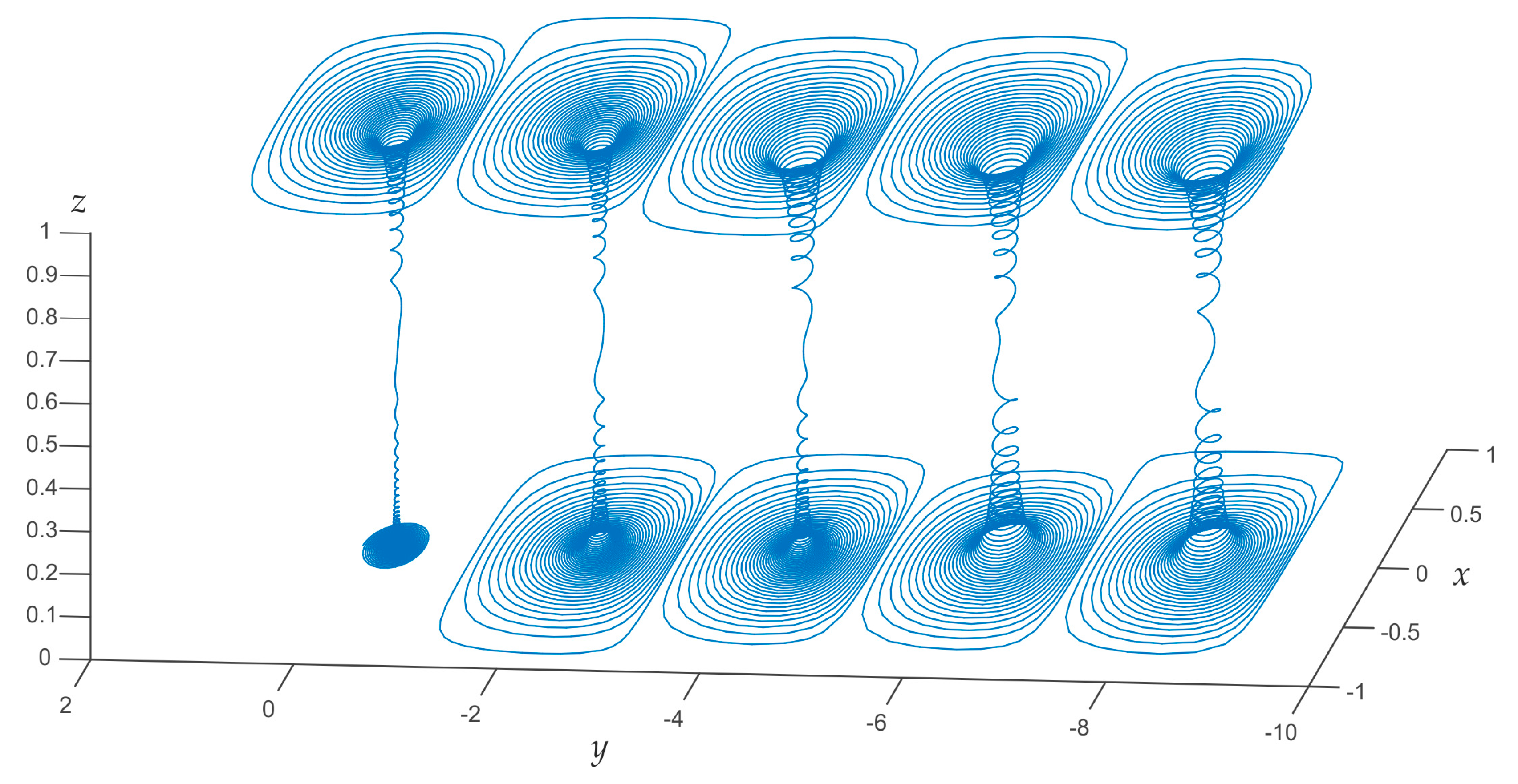
Figure 2 shows the air parcel trajectory numerically calculated in accordance with Equations (24)–(26). As is seen from
Figure 2, the air parcel trajectory is an unclosed curve. In other words, the parcel passes from one vortex cell to another. It is also seen that while the air parcel in the lower level is spirally converged towards the center, the air is lifted up. After the air parcel arrives at high level, the air parcel is spirally diverged outwards. In the same way, if the air parcel is spirally converged towards the center at the upper level, then it moves downwards to the lower level and diverges. Thus, one can see that the basic state of the atmosphere in the case of nonzero divergence is a sequence of connected vortex cells. On the other hand, at zero divergence, the air parcel trajectory is a closed curve and the atmospheric state is a pair of connected vortices, as has been shown in previous studies.
It can be seen from Equation (20) that if the velocity divergence is equal to zero, then the vertical velocity component has the following height dependence:
where
is the initial value of velocity at the earth’s surface at
. From here it follows that at zero initial velocity and zero divergence, the upward air movement is absent. Letting the velocity divergence be nonzero and constant, then from Equation (20), we have
One can see that the upward air movement in the lower atmosphere is only possible at negative divergence (D < 0).
Equation (11) represents a vortex transport (diffusion) equation with a source of the form . It follows that if and (convergent horizontal air motion in the lower atmosphere, D < 0), then and . This means that the vortex has a cyclonic vorticity in the lower atmosphere. In analogy, Equation (12) represents a divergence transport (diffusion) equation with a source of the form . It follows from Equation (17) that if the velocity divergence is constant and negative (D < 0), then . From here it follows that if . This means that the pressure is low at the center of the cyclonic vortex.
Equations (18) and (19) relate the three-dimensional flow pattern and the temperature field. At positive vertical velocity, it follows from Equation (19) that . This means that the cyclonic vortex center is heated, that is, the temperature maximum is at the cyclonic vortex center.
The obtained solution describes the basic state of the atmosphere, which is the vortex motion state. It can be demonstrated that the traditional geostrophic state is a limiting case of the vortex motion state. Indeed, at
, that is, when the viscosity is negligible, and
, from Equation (16), one can obtain that
. From Equation (18) it follows that
For the stationary state, from Equations (6)–(10), one can obtain the components of the geostrophic velocity:
These expressions coincide with the expressions for the geostrophic state of the atmosphere [
1,
2,
3].
We return to the system of Equations (16)–(20). The expression for the velocity divergence can be obtained from Equation (20):
From here it follows that the horizontal divergence reverses sign at a height of
If within a layer the horizontal divergence is negative and the convergence takes place, then within the layer , the horizontal divergence will be positive, and vice versa. This is a manifestation of Dines’s compensation principle. Thus, one can see that this principle takes place not only at zero total velocity divergence but also at nonzero total divergence.
The expression for the temperature disturbance can be obtained from Equation (19):
The expression for the pressure disturbance can be obtained from Equation (18):
The expression for the vorticity can be obtained from Equation (17):
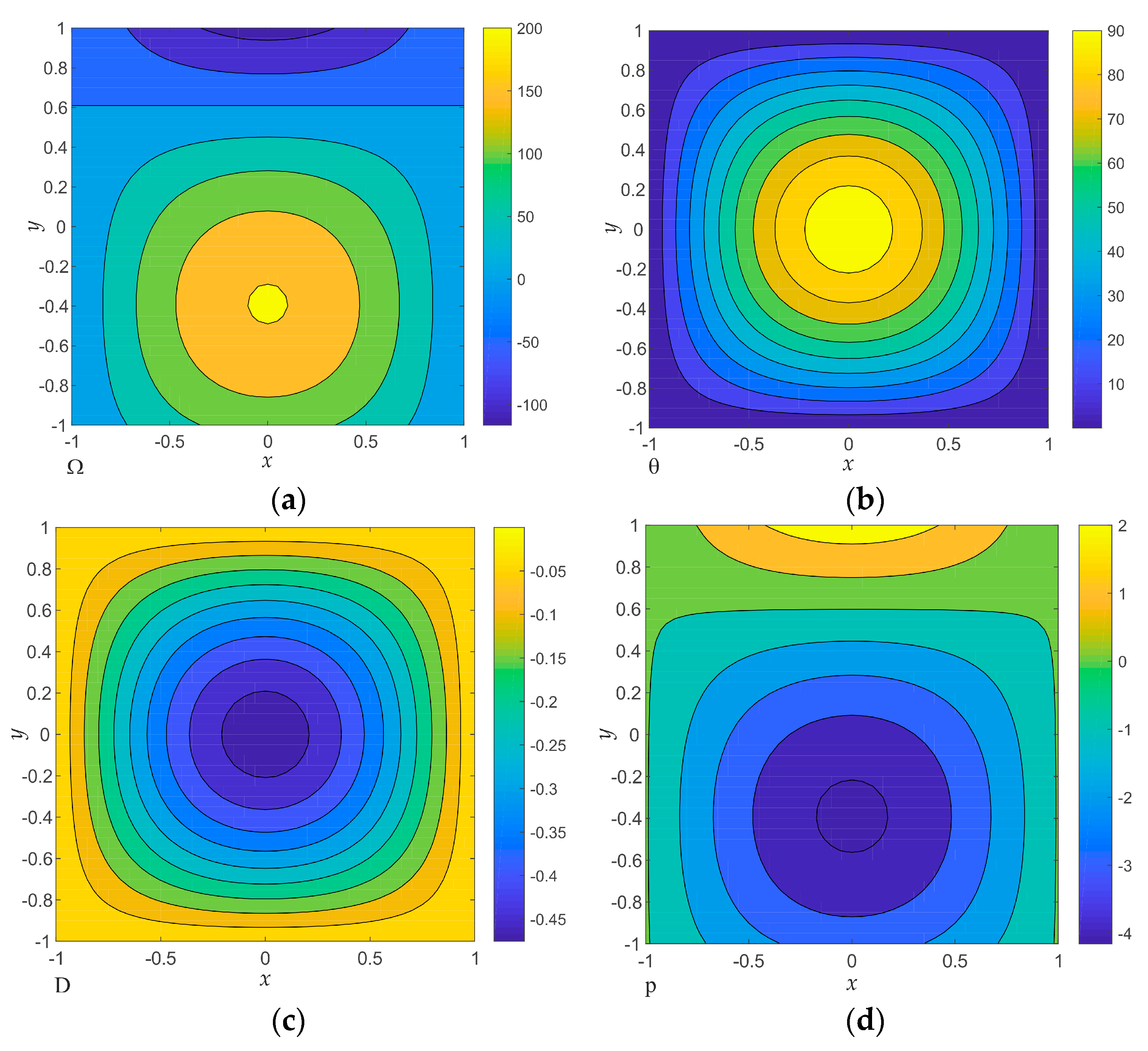
Figure 3 and
Figure 4 show the fields of vorticity, temperature, divergence, and pressure at the altitudes
(lower part of the vortex cell) and
(upper part of the vortex cell), correspondingly. As is seen, if the motion field in the lower part of the cell has a cyclonic vorticity, then in the upper part, it has an anticyclonic vorticity, and vice versa. The divergence changes in sign at the transition from one part to another. The pressure field is in antiphase with the vorticity field; that is, if the pressure field in the lower part is of cyclonic character, then the vorticity field is of anticyclonic character. In the upper part, the situation is the opposite.