Medium-Range Probabilistic Forecasts of Wind Power Generation and Ramps in Japan Based on a Hybrid Ensemble
Abstract
1. Introduction
2. Data and Method
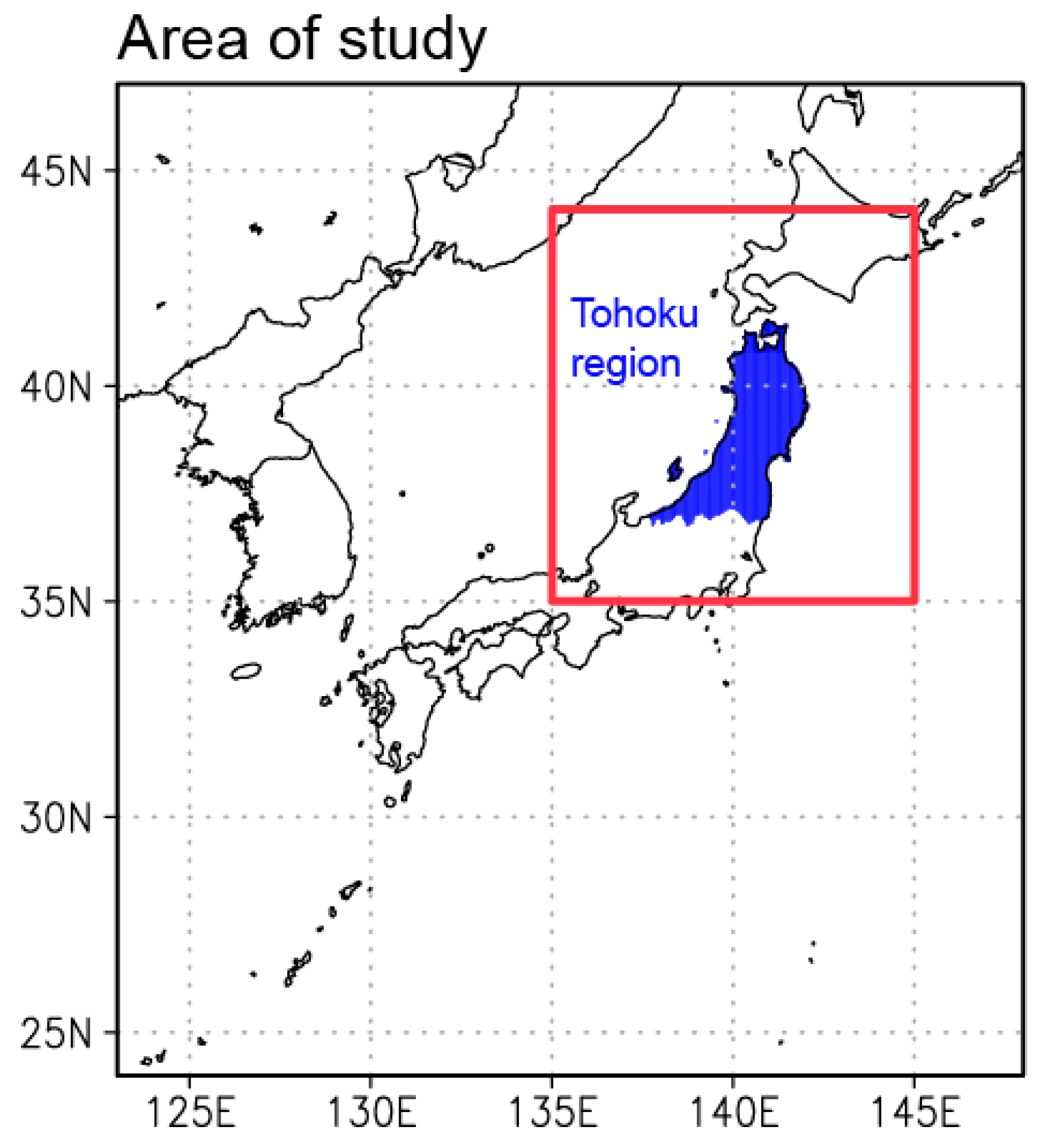
2.1. Data
2.2. Ensemble Forecasts
2.3. SOM Technique
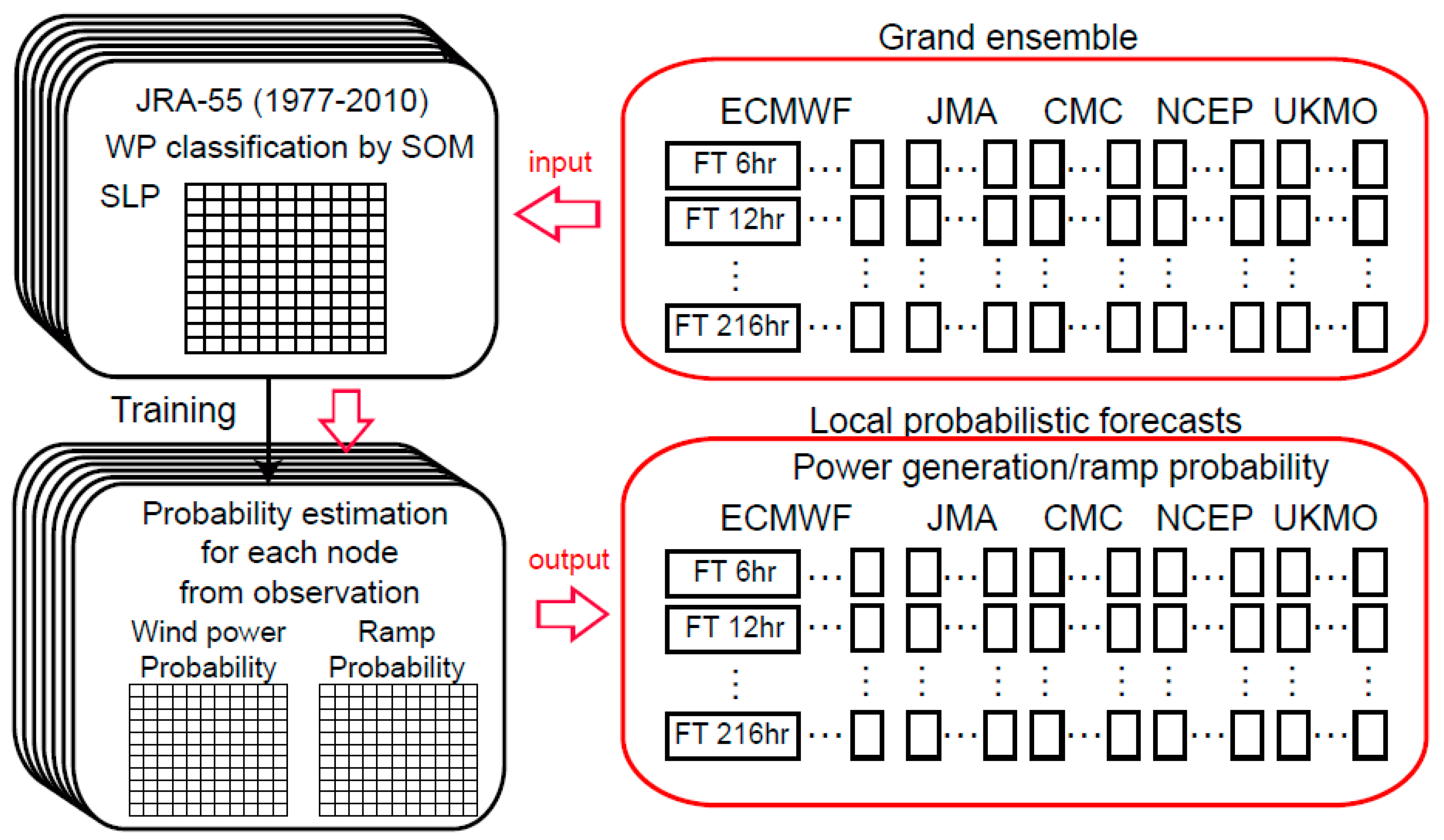
2.4. SOM-Based Analog Ensemble
- (1)
- Nine SOMs are applied to the atmospheric variables (top-left panel). 50 × 50, 80 × 80, and 100 × 100 SOMs are used. Each SOM is trained separately with absolute wind speed, wind vector, and SLP, i.e., a total of nine SOMs was used (as shown in Table 1).
- (2)
- PDFs of wind power generation and ramp probability are estimated (obtained from observational data; bottom-left panel) for each node of nine SOM in Table 1. To develop a PDF for each SOM node, in addition to the targeted node, samplings are also obtained from eight neighboring nodes that are assigned lower (half) weights compared with the center node.
- (3)
- Using the SOMs obtained in (1), the node that best matches the output of the multi-model ensemble forecasts (top-right panel) is selected from the SOM maps, respectively.
- (4)
- Wind power PDFs are derived by compositing the individual results of ensemble forecasts obtained in (3) (bottom-right panel).
- (5)
- The ensemble composited PDF of wind power generation for the targeted region is obtained from (4).
3. Wind Ramp Prediction Based on Multi-Model Ensemble Forecast
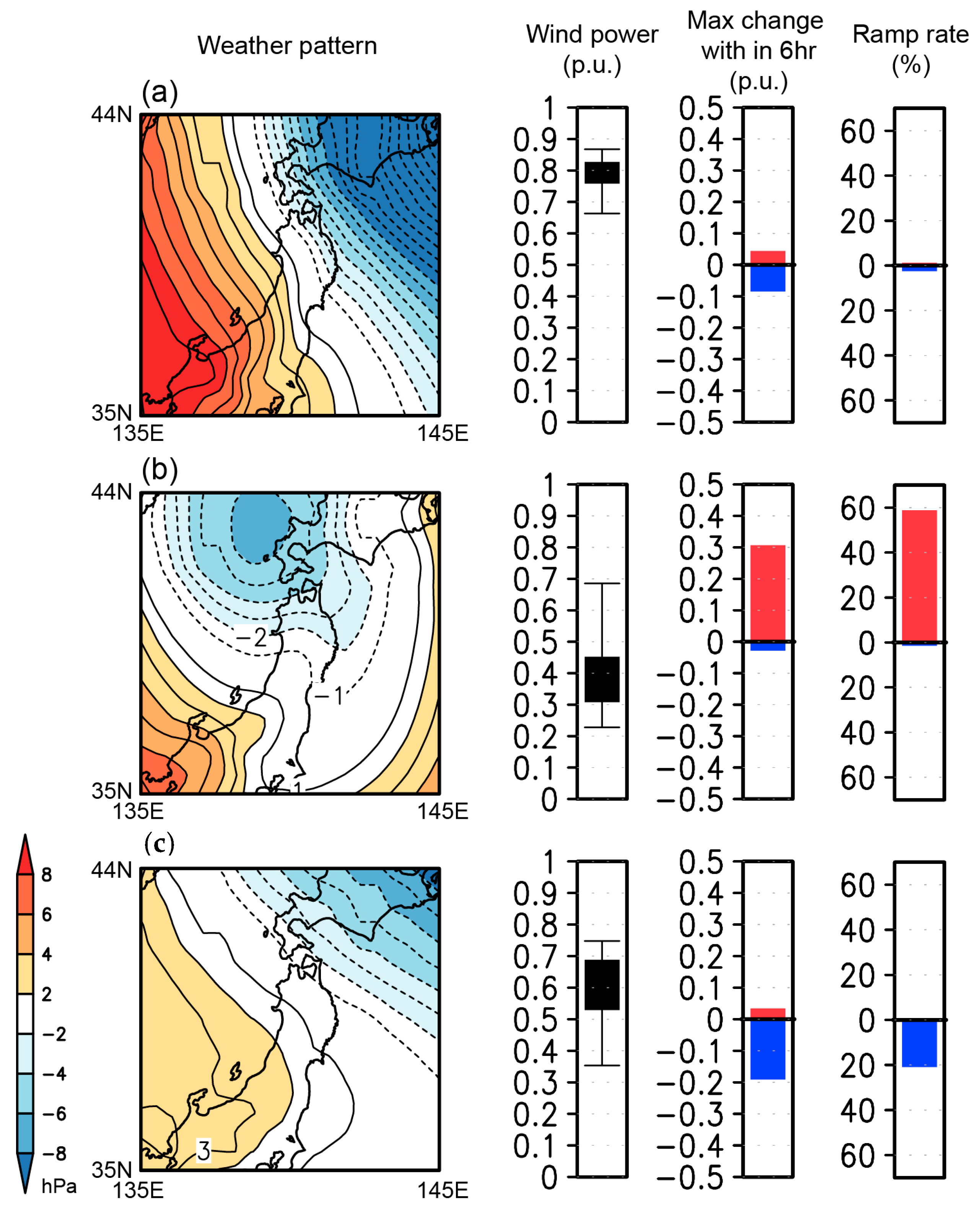
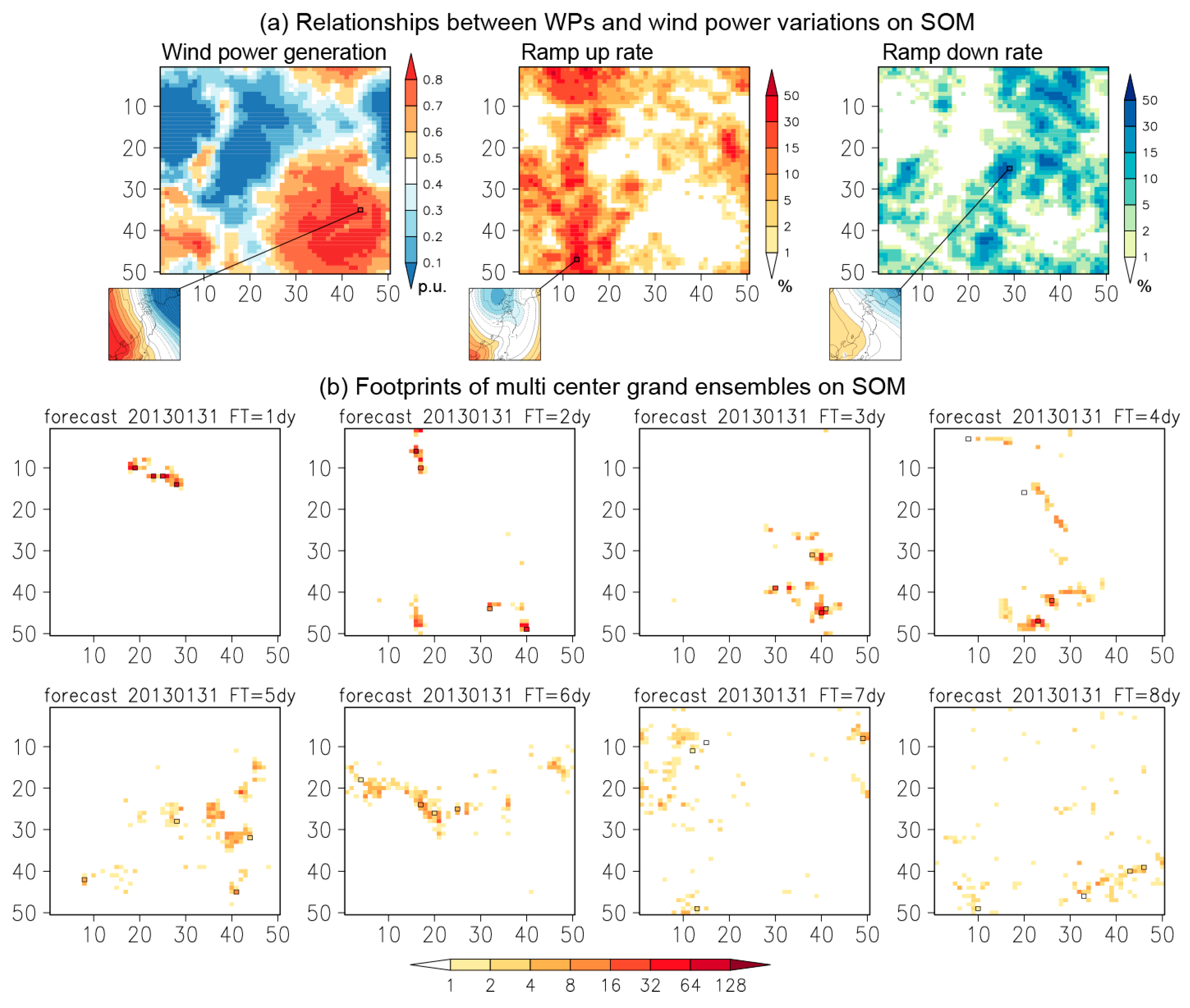
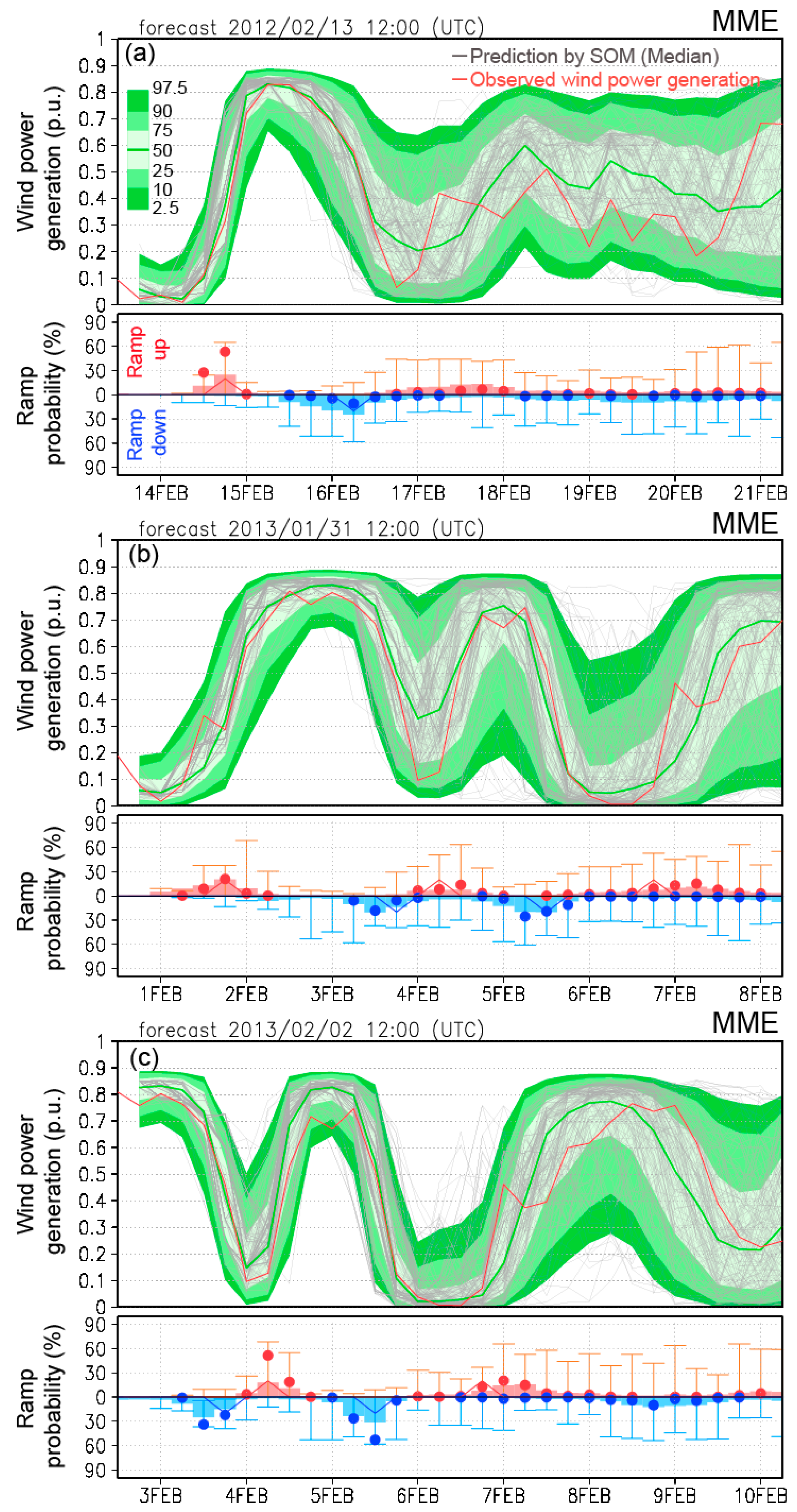
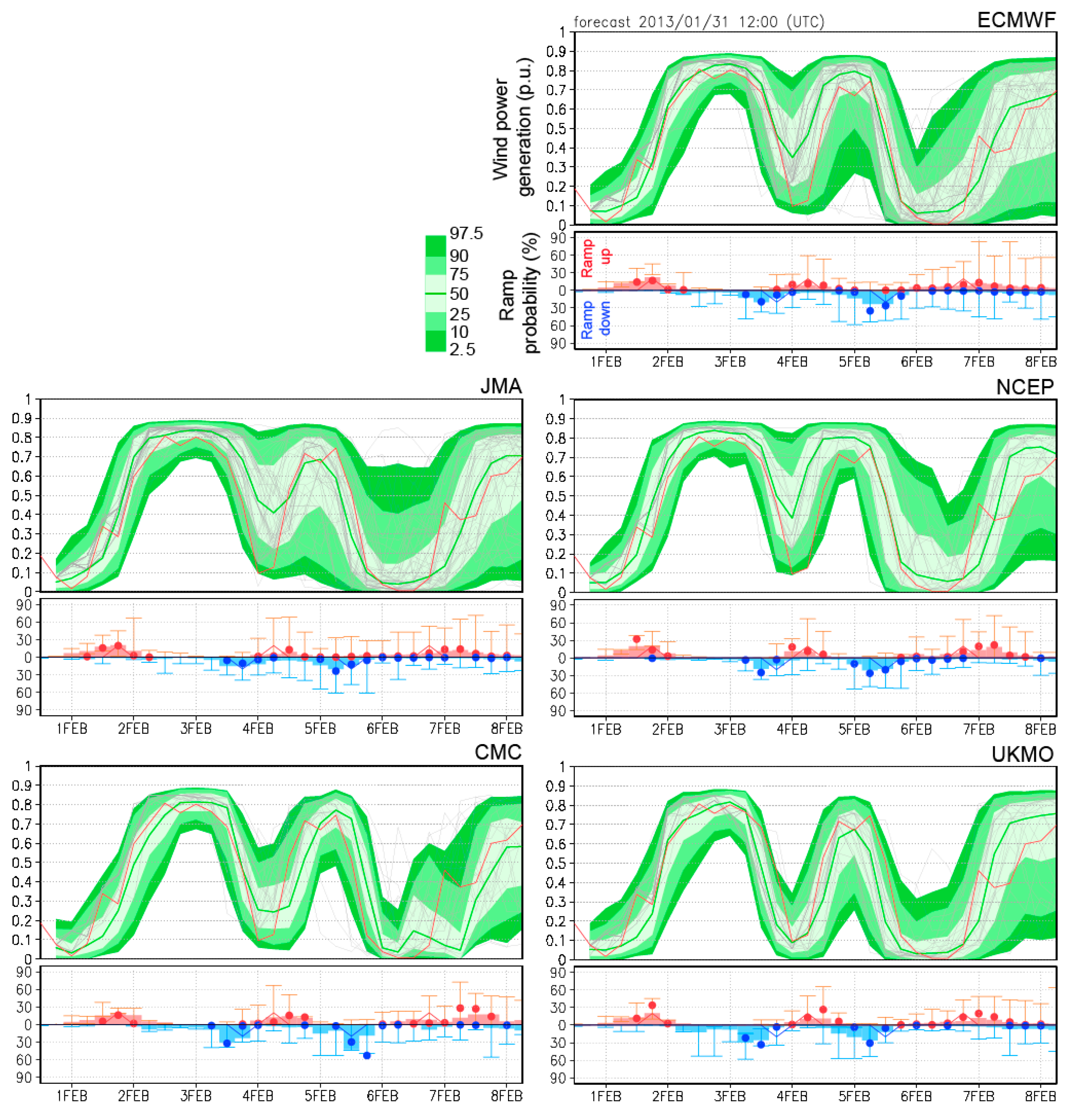
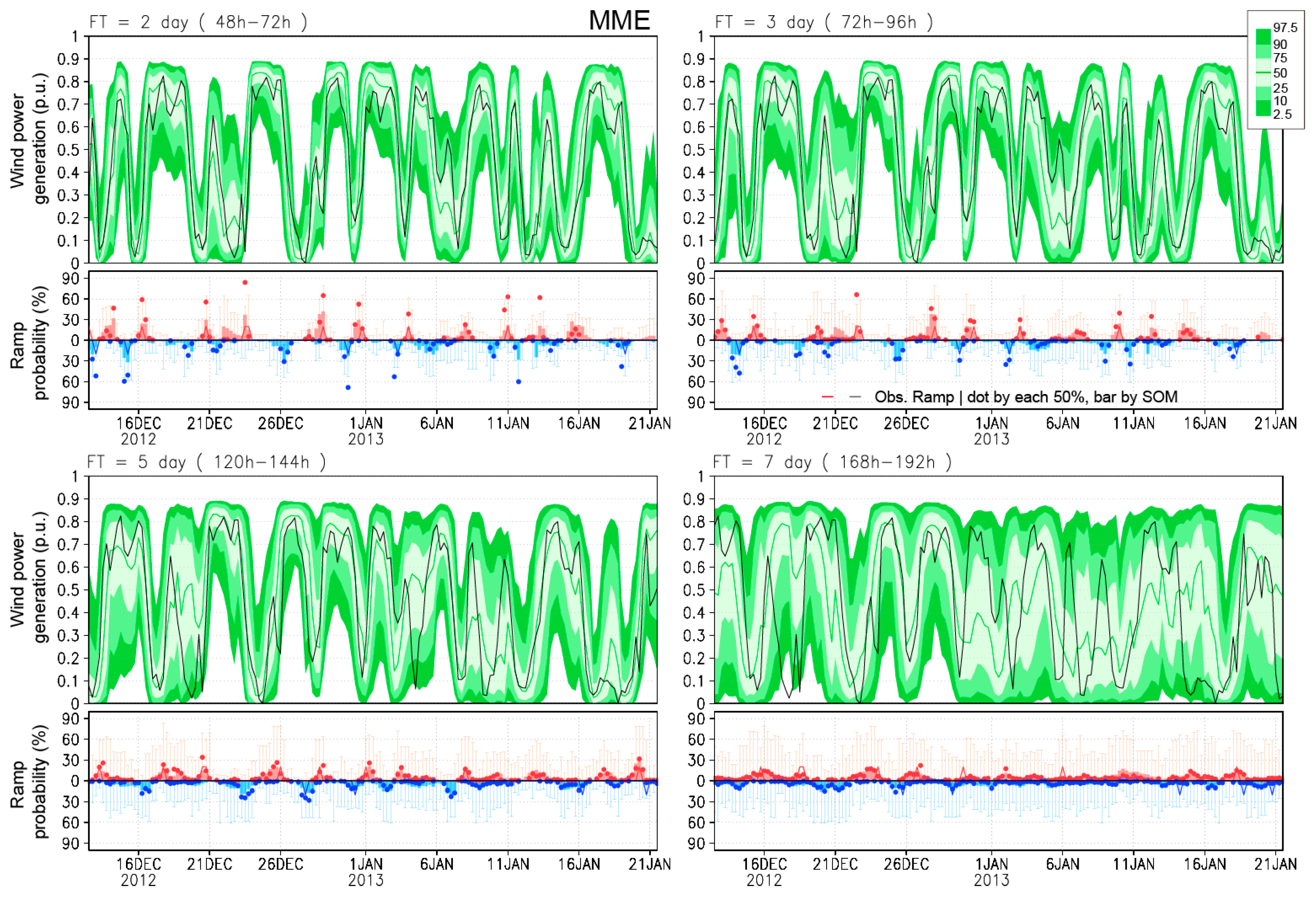
3.1. Estimated Wind Power and Ramp
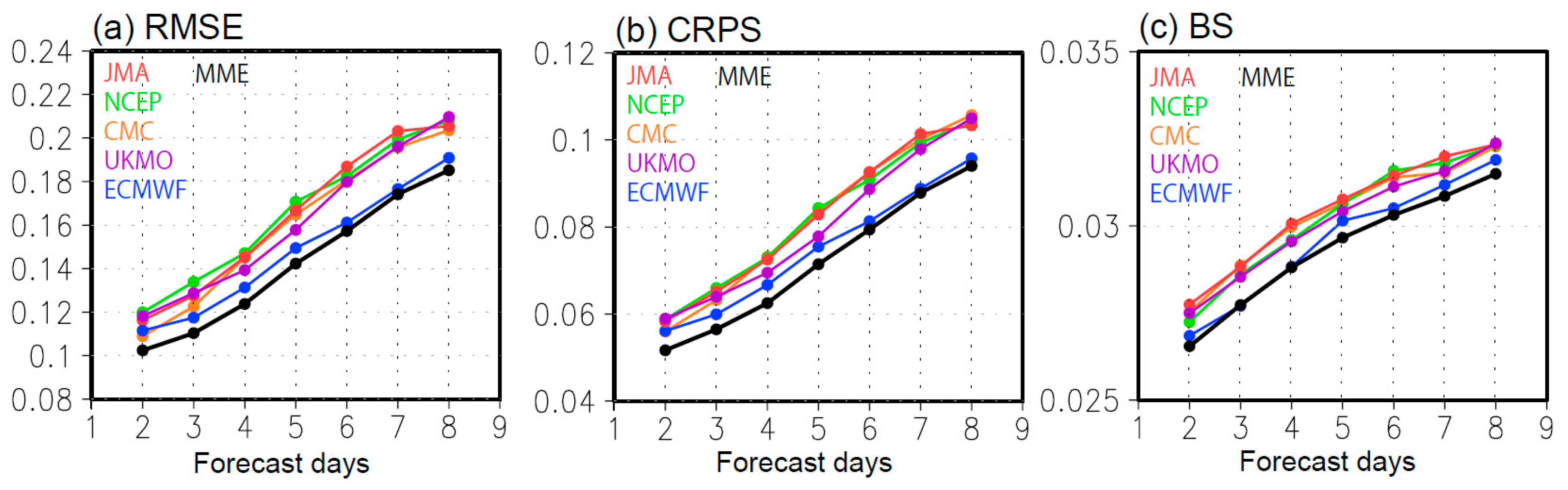
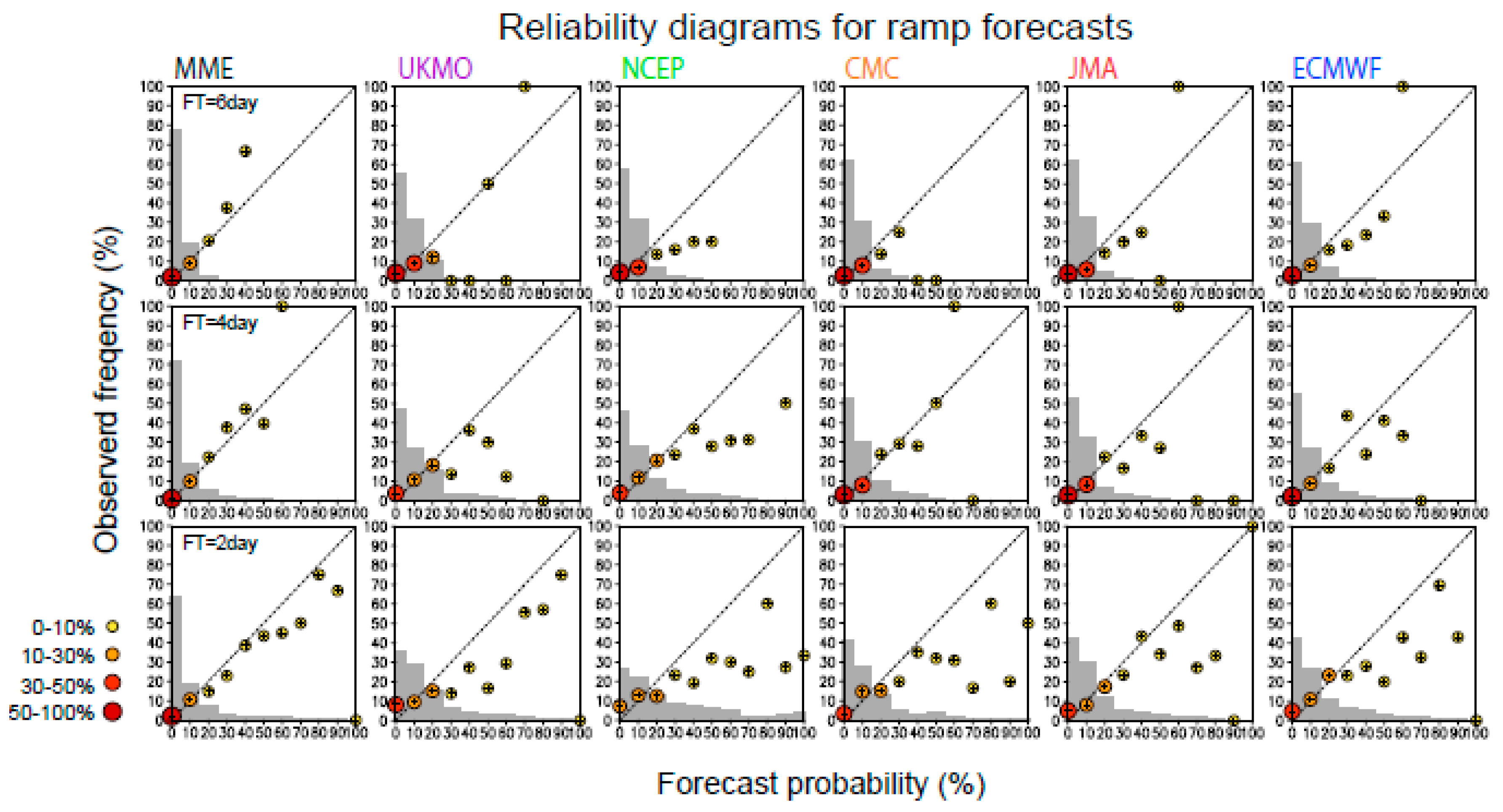
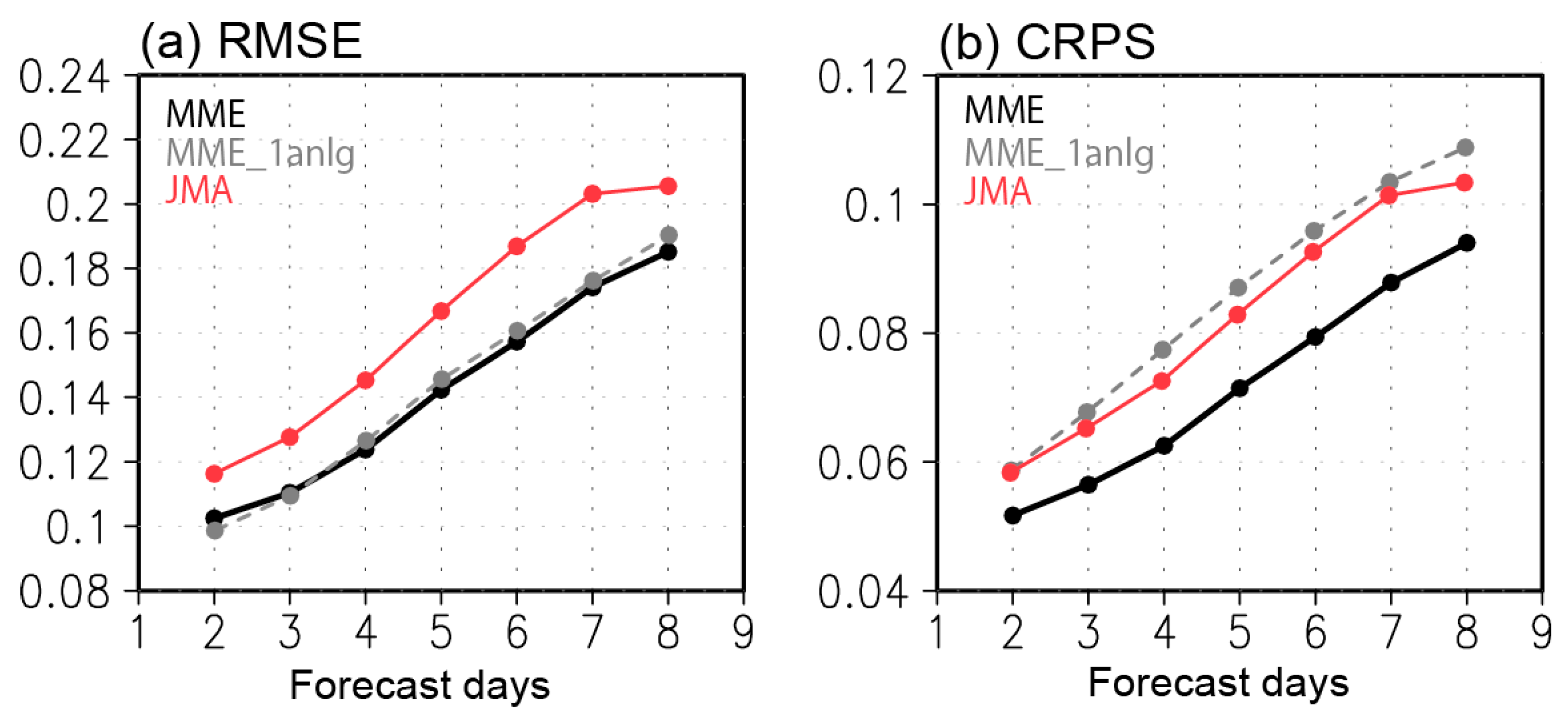
3.2. Forecast Skill of Wind Power Variations
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Energy Outlook: 2016. International Energy Agency. OECD/IEA: 2016. p. 684. Available online: https://www.iea.org/media/publications/weo/WEO2016Chapter1.pdf (accessed on 20 September 2018).
- Marquis, M.; Wilczak, J.; Ahlstrom, M.; Sharp, J.; Stern, A.; Smith, J.C.; Calvert, S. Forecasting the wind to reach significant penetration levels of wind energy. Bull. Am. Meteorol. Soc. 2011, 92, 1159–1171. [Google Scholar] [CrossRef]
- Park, Y.Y.; Buizza, R.; Leutbecher, M. TIGGE: Preliminary results on comparing and combining ensembles. Q. J. R. Meteorol. Soc. 2008, 134, 2051–2066. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogs. J. Atmos. Sci. 1969, 26, 639–646. [Google Scholar] [CrossRef]
- Zorita, E.; von Storch, H. The analog method as a simple statistical downscaling technique: Comparison with more complicated methods. J. Clim. 1999, 12, 2474–2489. [Google Scholar] [CrossRef]
- Timbal, B.; McAvaney, B.J. An analogue-based method to downscale surface air temperature: Application for Australia. Clim. Dyn. 2001, 17, 947–963. [Google Scholar] [CrossRef]
- Gutierrez, J.M.; Cofino, A.S.; Cano, R.; Sordo, C. Analysis and downscaling multi-model seasonal forecasts in Peru using self-organizing maps. Tellus A 2005, 57, 435–447. [Google Scholar] [CrossRef]
- Garcia-Morales, M.B.; Dubus, L. Forecasting precipitation for hydroelectric power management: How to exploit GCM’s seasonal ensemble forecasts. Int. J. Climatol. 2007, 27, 1691–1705. [Google Scholar] [CrossRef]
- Delle Monache, L.; Eckel, T.; Rife, D.; Nagarajan, B. Probabilistic weather prediction with an analog ensemble. Mon. Weather Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef]
- Junk, C.; Delle Monache, L.; Alessandrini, S.; von Bremen, L.; Cervone, G. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z. 2015, 24, 361–379. [Google Scholar] [CrossRef]
- Davò, F.; Alessandrini, S.; Sperati, S.; Delle Monache, L.; Airoldi, D.; Vespucci, M.T. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Hewitson, B.C.; Crane, R.G. Consensus between GCM climate change projections with empirical downscaling: Precipitation downscaling over South Africa. Int. J. Climatol. 2006, 26, 1315–1337. [Google Scholar] [CrossRef]
- Borah, N.; Sahai, A.K.; Chattopadhyay, R.; Joseph, S.; Abhilash, S.; Goswami, B.N. Self-organizing map-based ensemble forecast system for extended range prediction of active/break cycles of Indian summer monsoon. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Ohba, M.; Nohara, D.; Kadokura, S.; Toyoda, Y. Rainfall Downscaling of Weekly Ensemble Forecasts using Self-Organizing Maps. Tellus A 2016, 68, 29293. [Google Scholar] [CrossRef]
- Eckel, F.A.; Delle Monache, L. A hybrid NWP-analog ensemble. Mon. Weather Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Harada, Y.; Kamahori, H.; Kobayashi, C.; Endo, H.; Kobayashi, S.; Ota, Y.; Onoda, H.; Onogi, K.; Miyaoka, K.; Takahashi, K. The JRA-55 Reanalysis: Representation of atmospheric circulation and climate variability. J. Meteorol. Soc. Jpn. 2016, 94, 269–302. [Google Scholar] [CrossRef]
- Ohba, M.; Nohara, D.; Kadokura, S. Impacts of Synoptic Circulation Patterns on Wind Power Ramp Events in East Japan. Renew. Energy 2016, 96, 591–602. [Google Scholar] [CrossRef]
- Ohba, M.; Kadokura, S.; Nohara, D.; Toyoda, Y. Anomalous Weather Patterns in Relation to Heavy Precipitation Events in Japan during the Baiu Season. J. Hydrometeorol. 2015, 16, 688–701. [Google Scholar] [CrossRef]
- Reusch, D.B.; Alley, R.B.; Hewitson, B.C. North Atlantic climate variability from a self-organizing map perspective. J. Geophys. Res. 2007, 112, D02104. [Google Scholar] [CrossRef]
- Ito, M.; Miyoshi, T.; Masuyama, H. The characteristics of the torus self-organizing map. In Proceedings of the 16th Fuzzy System Symposium Akita Japan Society for Fuzzy and Systems, Akita, Japan, 6–8 September 2000; pp. 373–374. [Google Scholar]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Nissen, J. Short-term wind power forecasting with an analog ensemble. Renew. Energy 2015, 76, 768–781. [Google Scholar] [CrossRef]
- Vanvyve, E.; Delle Monache, L.; Monaghan, A.J.; Pinto, J. Wind resource estimates with an analog ensemble approach. Renew. Energy 2015, 74, 761–773. [Google Scholar] [CrossRef]
- Klink, K. Atmospheric circulation effects on wind speed variability at turbine height. J. Appl. Meteorol. Climatol. 2007, 46, 445–456. [Google Scholar] [CrossRef]
- Cutler, N.J.; Outhred, H.R.; MacGill, I.F.; Kepert, J.D. Predicting and presenting plausible future scenarios of wind power production from numerical weather prediction systems: A qualitative ex ante evaluation for decision making. Wind Energy 2012, 15, 473–488. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Hamlington, P.E.; Collins, S.G.; Alexander, S.R.; Kim, K.Y. Effects of climate oscillations on wind resource variability in the United States. Geophys. Res. Lett. 2015, 42, 145–152. [Google Scholar] [CrossRef]
- Gibson, P.B.; Cullen, N.J. Synoptic and sub-synoptic circulation effects on wind resource variability—A case study from a coastal terrain setting in New Zealand. Renew. Energy 2015, 78, 253–263. [Google Scholar] [CrossRef]
- Pryor, S.C.; Schoof, J.; Barthelmie, R.J. The impact of non-stationarities in the climate system on the definition of a ‘normal wind year’: A case study from the Baltic. Int. J. Climatol. 2005, 25, 735–752. [Google Scholar] [CrossRef]
- Davy, R.; Milton, J.; Russel, C.; Coppin, P. Statistical downscaling of wind variability from meteorological fields. Bound Layer Meteorol. 2010, 135, 165–175. [Google Scholar] [CrossRef]
- Peña, J.C.; Aran, M.; Cunillera, J.; Amaro, J. Atmospheric circulation patterns associated with strong wind events in Catalonia. Nat. Hazards Earth Syst. Sci. 2011, 11, 145–155. [Google Scholar] [CrossRef]
- Brayshaw, D.J.; Troccoli, A.; Fordham, R.; Methven, J. The impact of large scale atmospheric circulation patterns on wind power generation and its potential predictability: A case study over the UK. Renew. Energy 2011, 36, 2087–2096. [Google Scholar] [CrossRef]
- Ely, C.R.; Brayshaw, D.J.; Methven, J.; Cox, J.; Pearce, P. Implications of the North Atlantic Oscillation for a UK-Norway renewable power system. Energy Policy 2013, 62, 1420–1427. [Google Scholar] [CrossRef]
- Gibson, P.B.; Cullen, N.J. Regional variability in New Zealand’s wind resource linked to synoptic-scale circulation: Implications for generation reliability. J. Appl. Meteorol. Climatol. 2015, 54, 944–958. [Google Scholar] [CrossRef]
- Deppe, A.J.; Gallus, W.A.; Takle, E.S. A WRF ensemble for improved wind speed forecasts at turbine height. Weaher Forecast. 2013, 28, 212–228. [Google Scholar] [CrossRef]
- Matsumoto, J. The seasonal changes in Asian and Australian monsoon regions. J. Meteorol. Soc. Jpn. 1992, 70, 257–273. [Google Scholar] [CrossRef]
- Marshall, A.G.; Hudson, D.; Hendon, H.H.; Pook, M.J.; Alves, O.; Wheeler, M.C. Simulation and prediction of blocking in the Australian region and its influence on intra-seasonal rainfall in POAMA-2. Clim. Dyn. 2014, 42, 3271–3288. [Google Scholar] [CrossRef]
- Hudson, D.; Alves, O.; Hendon, H.H.; Marshall, A.G. Bridging the Gap between Weather and Seasonal Forecasting: Intraseasonal Forecasting for Australia. Q. J. R. Meteorol. Soc. 2011, 137, 673–689. [Google Scholar] [CrossRef]
- White, C.J.; Hudson, D.; Alves, O. ENSO, the IOD and the intraseasonal prediction of heat extremes across Australia using POAMA-2. Clim. Dyn. 2014, 43, 1791–1810. [Google Scholar] [CrossRef]
- Johnson, N.C.; Collins, D.C.; Feldstein, S.B.; L’Heureux, M.L.; Riddle, E.E. Skillful wintertime North American temperature forecasts out to four weeks based on the state of ENSO and the MJO. Weather Forecast. 2014, 29, 23–38. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Evaluation of global wind power. J. Geophys. Res. Atmos. 2005, 110, D12110. [Google Scholar] [CrossRef]
- Matsueda, M.; Tanaka, H.L. Can MCGE outperform the ECMWF ensemble? SOLA 2008, 4, 77–80. [Google Scholar] [CrossRef]
- Johnson, C.; Swinbank, R. Medium-range multimodel ensemble combination and calibration. Q. J. R. Meteorol. Soc. 2009, 135, 777–794. [Google Scholar] [CrossRef]
| Atmospheric Variables | SOM Size | |
|---|---|---|
| 1. | Sea Level Pressure | 50 × 50 |
| 2. | Sea Level Pressure | 80 × 80 |
| 3. | Sea Level Pressure | 100 × 100 |
| 4. | Sfc. wind vector | 50 × 50 |
| 5. | Sfc. wind vector | 80 × 80 |
| 6. | Sfc. wind vector | 100 × 100 |
| 7. | Absolute wind speed | 50 × 50 |
| 8. | Absolute wind speed | 80 × 80 |
| 9. | Absolute wind speed | 100 × 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohba, M.; Kadokura, S.; Nohara, D. Medium-Range Probabilistic Forecasts of Wind Power Generation and Ramps in Japan Based on a Hybrid Ensemble. Atmosphere 2018, 9, 423. https://doi.org/10.3390/atmos9110423
Ohba M, Kadokura S, Nohara D. Medium-Range Probabilistic Forecasts of Wind Power Generation and Ramps in Japan Based on a Hybrid Ensemble. Atmosphere. 2018; 9(11):423. https://doi.org/10.3390/atmos9110423
Chicago/Turabian StyleOhba, Masamichi, Shinji Kadokura, and Daisuke Nohara. 2018. "Medium-Range Probabilistic Forecasts of Wind Power Generation and Ramps in Japan Based on a Hybrid Ensemble" Atmosphere 9, no. 11: 423. https://doi.org/10.3390/atmos9110423
APA StyleOhba, M., Kadokura, S., & Nohara, D. (2018). Medium-Range Probabilistic Forecasts of Wind Power Generation and Ramps in Japan Based on a Hybrid Ensemble. Atmosphere, 9(11), 423. https://doi.org/10.3390/atmos9110423





