1. Introduction
In most countries, Gaussian models are the reference tool recommended for atmospheric regulatory modeling applications. The most widely used of such Gaussian models is AERMOD, developed and distributed by the US-EPA [
1]. The success of Gaussian models is due to several important factors, such as the simplicity of the algorithm, the direct physical interpretation of the parameters involved, and the limited number of input parameters required. Moreover, practical applications for regulatory purposes typically require the calculation of statistical parameters based on multi-year hourly values of concentration of pollutants emitted by several sources. Gaussian models are particularly fit for such simulations because of their fast execution, even on desktop computers.
However, Gaussian models show various limitations. For example, the stationarity of the solution over one hour implies constant meteorology and does not allow the simulation of accumulation and recirculation effects. In addition, the horizontal homogeneity of the meteorological conditions for any fixed height above terrain does not allow the treatment of variable land-use and orographic effects and limits the extent of the modeling domain where meteorological conditions are representative. The Gaussian solution to the dispersion equation is valid only for non-zero wind speed. For this reason, calm or very low wind conditions cannot be accounted for. Turbulence is assumed to be Gaussian via the dispersion coefficients, and this poses a limit in modeling convective conditions that are known to be characterized by updrafts and downdrafts that make the distribution of vertical wind velocity fluctuations non-Gaussian and non-homogeneous. Another limitation is the assumption of an infinite extent of the plume, up to distances that can be inconsistent with the wind velocity (i.e., impacts several kilometers downwind in low-wind conditions).
Most of these limitations are overcome by Lagrangian models. A popular model is the Lagrangian puff model CALPUFF [
2]. This model implements a hybrid approach, because the mass of emitted pollutant is divided into puffs that are transported by the average local wind and expand in size with a Gaussian distribution.
In addition to Lagrangian puff models, Lagrangian particle dispersion models (LPDMs) have become more and more appealing as a modeling tool to simulate atmospheric dispersion of pollutants. Their main feature is the ability to reproduce the stochastic nature of turbulence under all conditions (e.g., [
3]).
Lagrangian particle models simulate the released pollutants by following several independent computational particles—each one representing a fraction of the released mass—in a sequence of finite time intervals. The motion of each particle is driven by a time-varying velocity field, which can be divided into an average component, the average wind, plus a fluctuation velocity describing the effects of atmospheric turbulence and those wind variations not included in the mean component. The fluctuation velocity can be described by a nonlinear form of the Langevin stochastic differential equation.
While particles in Lagrangian particle models are generally considered computational markers of the atmospheric fluid that allow the simulation of the concentration field of the pollutant, the description of released matter in terms of particles allows easy incorporation of some physical processes, such as radioactive decay and deposition. Since computational particles represent the pollutants as gas or particulate, deposition and gravitational settling can also be taken into account.
Lagrangian particle models often require: (1) a large number of particles to obtain satisfactory resolution and statistically-sound results; and (2) a short time interval to numerically integrate the equation of motion of the particles. The computational resources commonly available nowadays make these models suitable for implementations oriented both to real time applications (e.g., 24-h forecasting), and to simulate long periods (e.g., months or years of emission from a source).
One of the available, peer-reviewed Lagrangian particle models is LAPMOD [
4]. LAPMOD is a freely-available open-source model that is interfaced to the CALMET meteorological preprocessor [
5] of the CALPUFF modeling system [
2]. LAPMOD is also capable of using the AERMOD meteorological input files via its LAPMET preprocessor. The theoretical formulation of the LAPMOD model and its validation in rural environment against the Kincaid SF
6 and SO
2 datasets [
6,
7] have been described in a previous paper [
4].
A correct description of the plume rise is fundamental in atmospheric dispersion models. Once a plume is emitted by a stack into the atmosphere, three different phases may be individuated while it rises in the atmosphere (e.g., [
8]). The initial phase is composed of three sub-phases. Initially, a vertical jet may form until effluents are deflected after release. The successive steps are the bent-over sub-phase, where the plume starts to bend due to the entrainment with the air, and the thermal sub-phase, where the plume grows due to its internal turbulence. During the transition phase, the plume has lost much of its internal turbulence, but it continues to grow, vertically and horizontally, due to the increasing role of atmospheric turbulence. Finally, in the diffusion phase, the plume has lost all its energy and the pollutant is advected and dispersed only due to the average wind speed and atmospheric turbulence. The first two phases are typically summarized with the term “plume rise”. They happen due to the thermal buoyancy of the effluent (i.e., its temperature is greater than the temperature of the surrounding air), and to the momentum of the effluent (i.e., its exit speed).
Different algorithms have been proposed in the past, and may be grouped into three classes: semi-empirical, analytical, and numerical. Independent of the type of algorithm, the most important variables to describe the plume rise are the stack diameter, the exit temperature, the exit speed, the ambient temperature, and the temperature vertical gradient in the atmosphere. For the particular cases of dense plumes, densities must be considered too. There are two parameters that may be defined to characterize the plume when it is released: the buoyancy flux and the momentum flux. The buoyancy flux is directly proportional to the difference between the effluent temperature and the atmospheric temperature, the exit speed, and the exit area of the stack. The momentum flux is directly proportional to the square of the exit speed and to the exit area of the stack.
Analytical algorithms [
9,
10] allow the determination of the final plume rise, or the plume rise at a given downwind distance from the stack, with different expressions based on the above-mentioned variables and depending on the atmospheric stability. The semi-empirical algorithms assume constant values of the variables (e.g., wind speed, temperature) and express the plume rise height at a given downwind distance from the source as proportional to the product by the heat emission rate, the wind speed, and the distance itself, each one elevated at a specific power (e.g., [
11]). These algorithms, similar to the analytical ones, assume constant values of the input variables.
The plume rise numerical algorithms are models within the models that solve different equations describing the emissions, e.g., the conservation of mass, energy, and momentum. They do not require simplification assumptions but need more computational resources than the analytical and semi-empirical solutions. These algorithms do not require constant meteorological variables; both wind and temperature may vary.
This paper describes the incorporation of two numerical plume rise algorithms [
12,
13] in the Lagrangian particle model LAPMOD [
4]. The plume rise algorithms are validated against the Indianapolis field experiment carried out in an urban environment [
14]. Once a set of input variables giving satisfactory results for Indianapolis is determined, we use the same model configuration to evaluate LAPMOD against the Kincaid dataset [
15], both for SF
6 and SO
2. The purpose of this second validation is to determine a default model configuration that may be used for future studies both in rural and in urban environments.
3. Results and Discussion
The following paragraphs describe the effects of plume rise algorithms on ground level concentrations and evaluate the LAPMOD model against the results of field experiments.
3.1. Indianapolis SF6
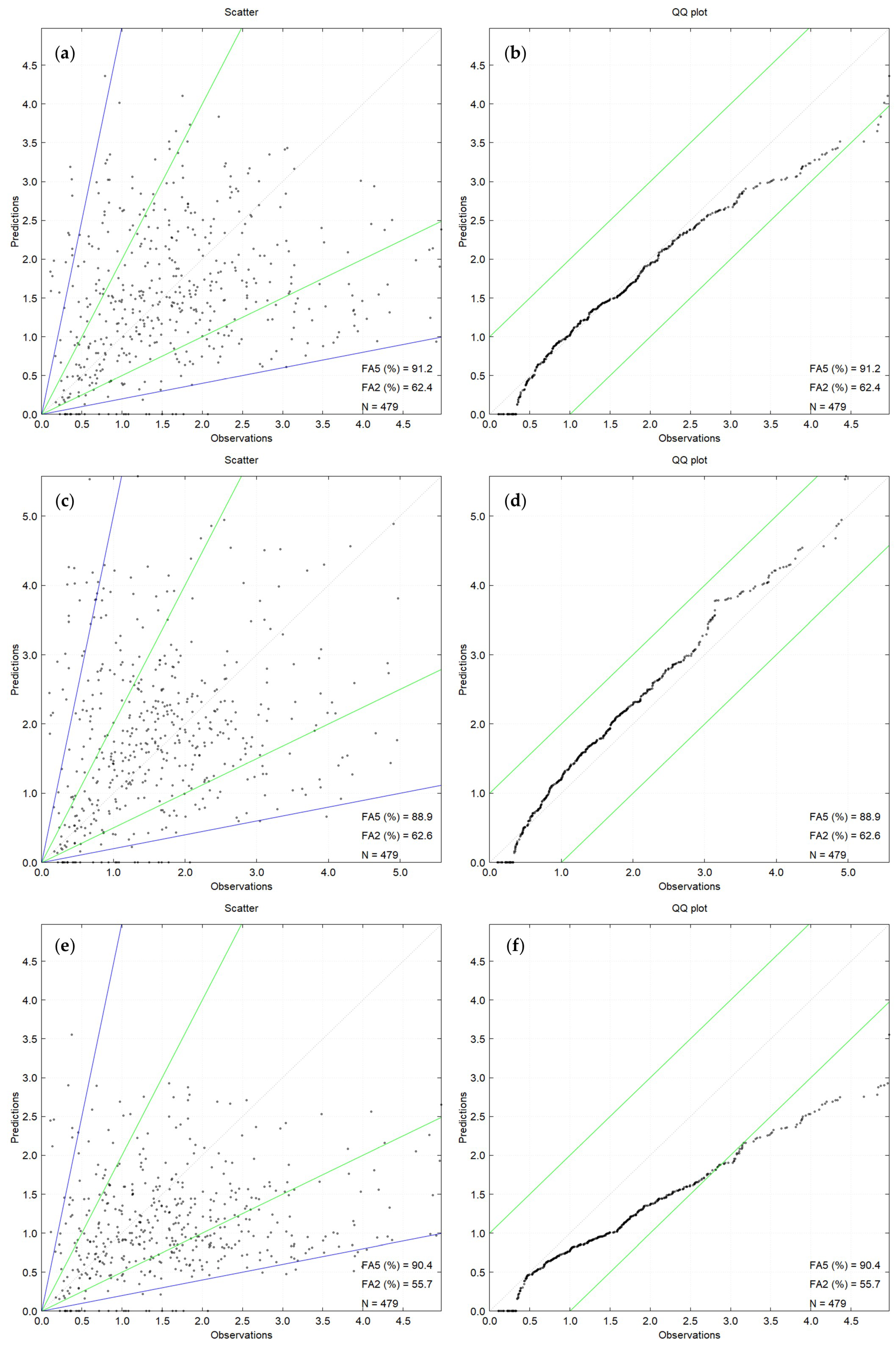
The scatter plots of predictions against observations are shown in
Figure 1a for the three plume rise algorithms considered; they also report the FA2 and FA5 statistics. The predicted one-hour concentrations reported in the following figures have been obtained by calculating the concentrations three times during each hour (i.e., every 20 min) and then taking the arithmetic mean. The QQ plots are reported on the right panels of
Figure 1.
It is observed that the regions of FA2 and FA5, delimited by the green and the blue lines of the scatter plots, respectively, are quite similar for the three plume rise algorithms: FA2 ranges from 55.7% (JJ + JJ) to 62.6% (JJ + RS), while FA5 ranges from 88.9% (JJ + RS) to 91.2% (WT). The QQ plots show three different behaviors depending on the plume rise algorithm. When the WT algorithm is used, LAPMOD has a tendency to underpredict for values of concentrations up to about 0.5 μg m−3, the distributions are in agreement for values in the range 0.5–2.3 μg m−3, then the model underpredicts for values greater than 2.3 μg m−3. When the JJ + RS algorithm is used, LAPMOD underpredicts for values smaller than 0.5 μg m−3 and overpredicts above such a value. Finally, when the JJ + JJ algorithm is used, the model always underpredicts the observed values. The QQ plot of the WT algorithm suggests proportionality between the distributions over the approximate range 1 to 3 μg m−3 (i.e., predictions and observations have similar mean and variance over this range). A similar proportionality over about the same range is observed for the JJ + RS algorithm, but shifted by about 0.2 μg m−3. It seems that, over this range, LAPMOD always overestimates the observations by about 0.2 μg m−3 when the JJ + RS algorithm is used.
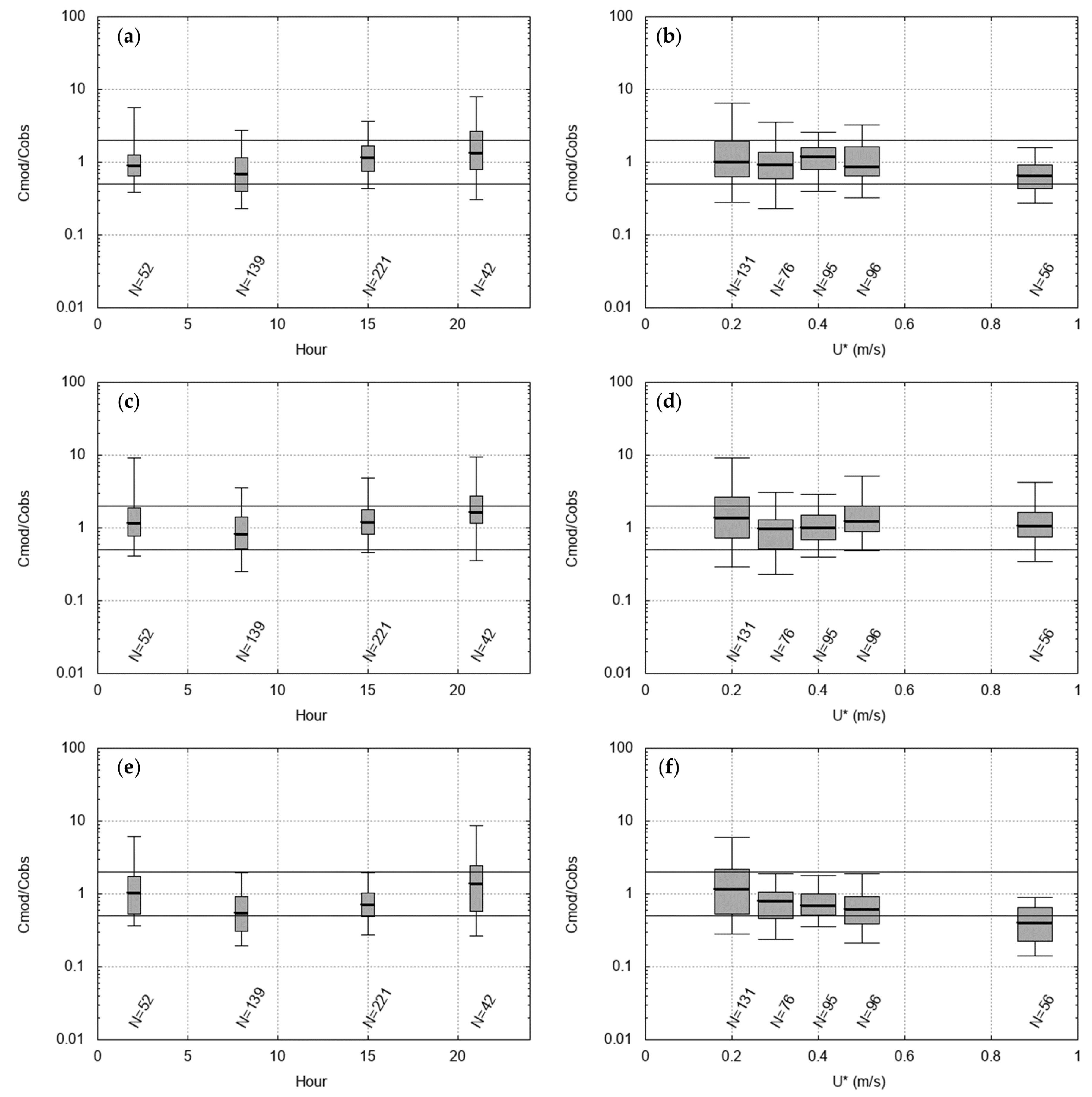
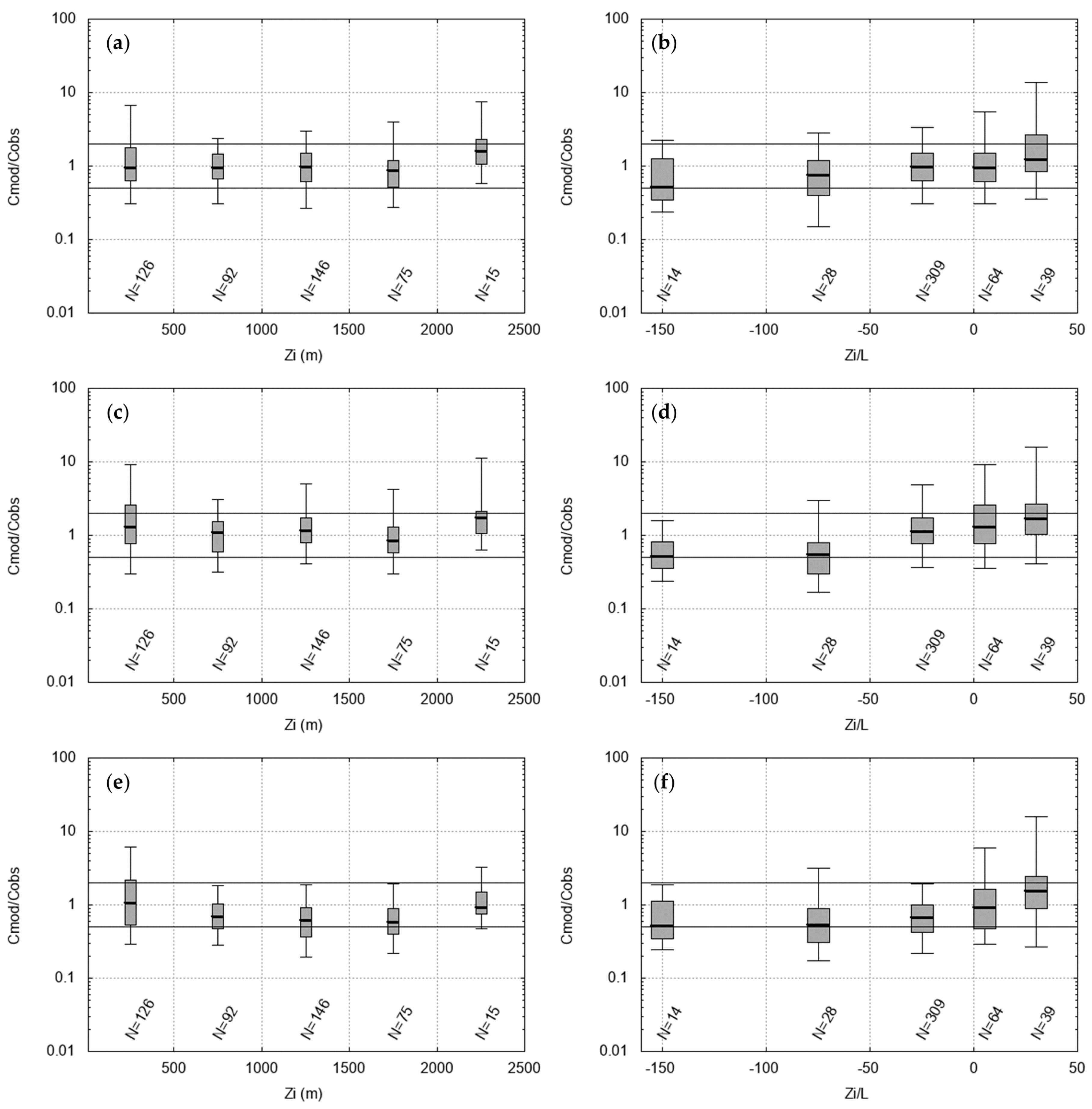
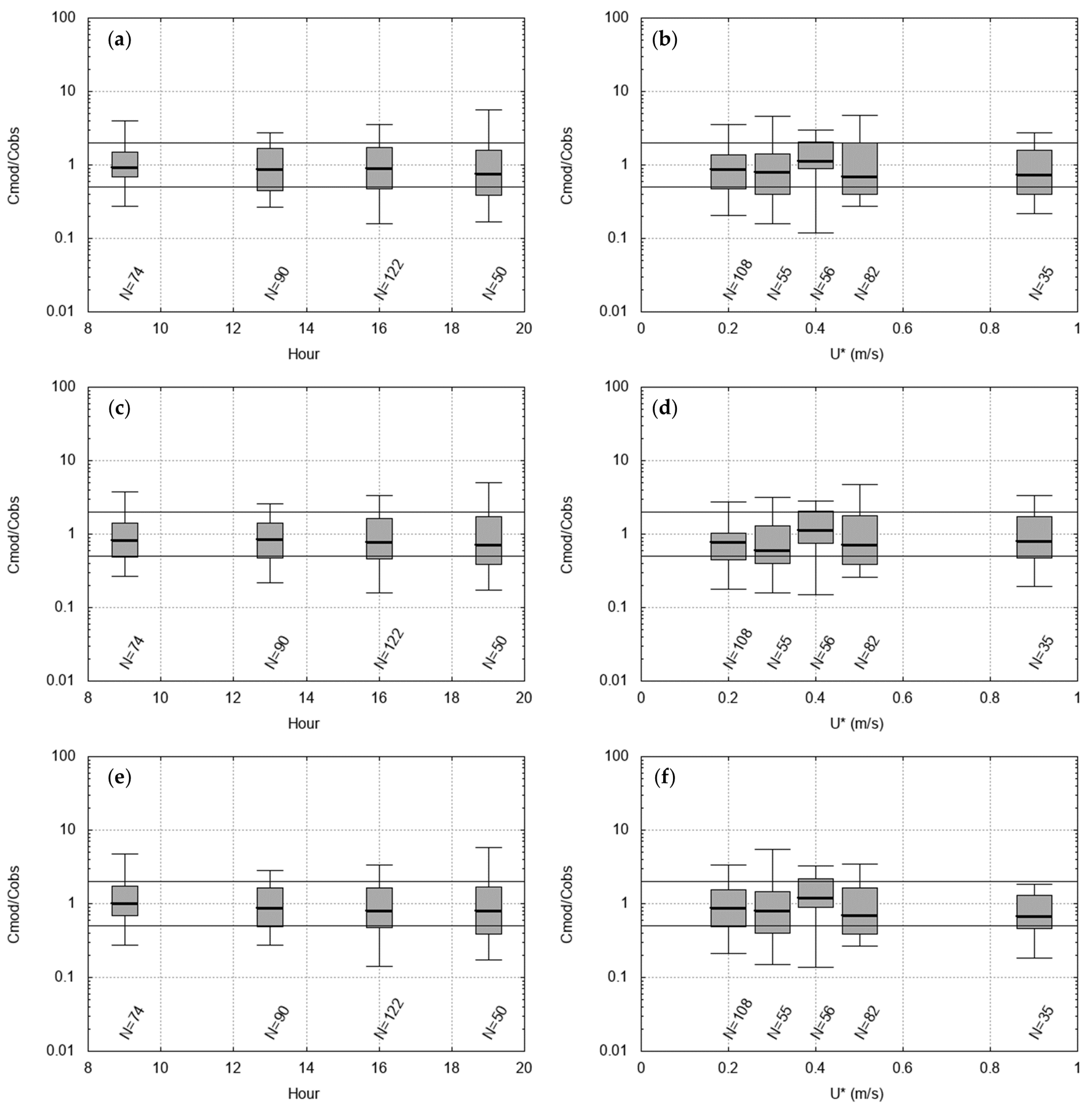
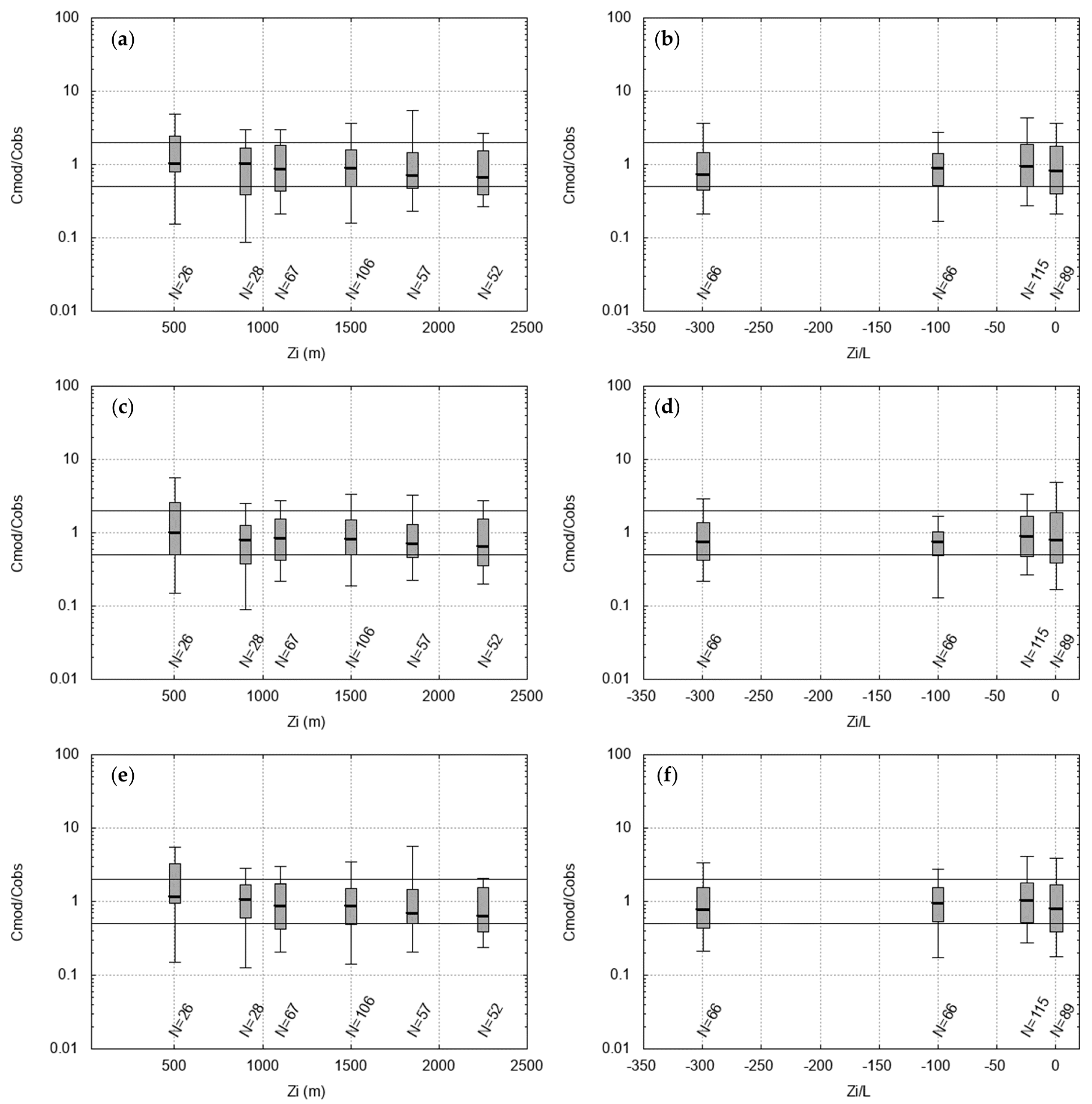
The residual box plots for Indianapolis best-quality data are reported in
Figure 2 and
Figure 3.
Remembering that the ratio between predictions and observations for a perfect model should always be 1, it is noticed that the LAPMOD results show that the medians of the ratios are almost always close to 1, and a significant proportion of the residuals falls within a factor of 2. The notable exception is the case with high friction velocity (>0.8 m s−1) when the JJ + JJ plume rise algorithm is used. In these situations, all in the early afternoon, the observed wind speed is above 6 m s−1, indicating slightly unstable to neutral stability conditions.
In
Figure 2 and
Figure 3, the data do not sum to 479 because there are situations where LAPMOD does not predict any concentration even though non-zero concentrations are measured. These situations are well visible on the X axis of the scatterplots (
Figure 1a); specifically, for all three plume rise algorithms, there are always 25 combinations of hours and arcs in which this happens. This behavior is usually associated with strong stability conditions. For example, on 12 October 1985 (nocturnal release from 24:00 to 04:00), there are five situations where LAPMOD does not predict any concentration at ground level, while observations are in the range 0.72 μg m
−3 to 1.77 μg m
−3. In addition, on 11 October 1985, there are four situations where LAPMOD does not predict ground concentrations (all at 01:00), while observations range from 0.29 μg m
−3 to 0.37 μg m
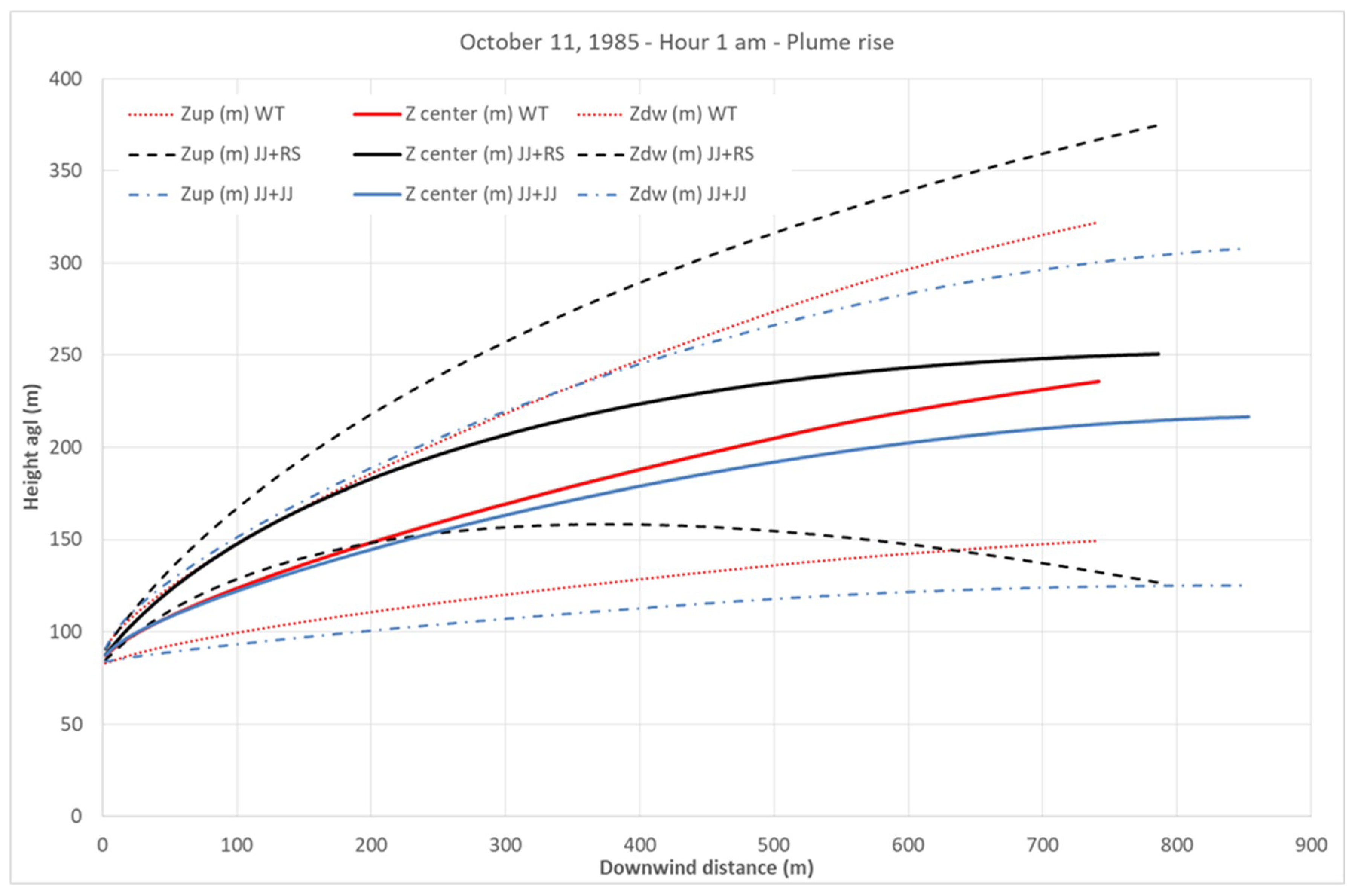
−3. Similar situations are observed at 3 arcs at 01:00 on 1 October 1985, and three other times from 01:00 to 02:00 of 27 September 1985. The reason for this lack of modeling performance in cases of strong stability might be because the plume is too narrow aloft, and particles do not contribute to the ground level concentration. As an example,
Figure 4 shows the plume shapes calculated by the three algorithms at 01:00 on 11 October 1985. At that hour the mixing height is 47 m and the concentrations observed at arcs from 1 km to 3 km are in the interval 0.29 μg m
−3 to 0.37 μg m
−3. Wind blows from the north with a speed of about 1.3 m s
−1, and the Monin–Obukhov length is 11.2 m, thus indicating stability. The thick solid lines in
Figure 4 show the plume’s centerlines, while the thin lines represent the plume boundary calculated by adding and subtracting the plume radius to the plume centerline.
The three algorithms in this specific hour behave very similarly: the final rise distance is in the interval 740–850 m, and the plume centerline is in the range from 217 m (JJ + JJ) to 251 m (JJ + RS). This is the case of a plume directly emitted above the mixing layer (stack height 83.8 m, mixing height 47 m), with a plume induced turbulence that is strong close to the emission point and reduces to the weak turbulence level of a stable layer as the distance from the stack increases. Therefore, at least theoretically, the model behavior seems to be correct. However, the measurements indicate that the tracer concentrations were observed at ground level. For ground level tracer concentrations to be measured in this situation, it is likely that the stable plume aloft is affected by intermittent effects caused by mechanical turbulence. In other words, the wind speed fluctuates and, during occasional and very brief time periods, it can be much higher than the average wind speed. During these short time intervals, the higher wind speed creates mechanical turbulence and mixing that grabs some fraction of the plume and fumigates below. Similar behavior has also been observed by other authors. For example, Luhar and Hurley [
24] reported that “in TAPM occasionally the plume does not mix down to the ground under nighttime stable conditions, while the observations show otherwise”. Additional investigation is needed in both the model algorithms and the meteorological data to reconcile these inconsistencies.
The LAPMOD results for Indianapolis have been compared against observations using the MVK [
7] too.
Table 1 and
Table 2 show the performances of LAPMOD with different plume rise configurations against the measurements carried out at Indianapolis. Both observations and model predictions have been normalized by dividing the concentrations for the emission rate and multiplying by 1000.
The values of the robust higher concentration, RHC
R [
23], are shown in
Table 3. For comparison purposes, another evaluation ([
1], in their
Table 2), reports for AERMOD 16216 with different input options values ranging from 4 to 5. Additionally, other authors [
25] reported a ratio between modeled and observed RHC
R, with R = 26, equal to 1.18 for AERMOD and 1.30 for ISCST3. We observe in
Table 3 that the same ratios for LAPMOD are within the interval from 0.63 (worst result when JJ + JJ is used) to 1.02 (best results when JJ + RS is used).
3.2. Kincaid SF6
For the Kincaid SF
6 field experiment, LAPMOD was used with the same input variable configuration as the Indianapolis model run. A previous version of LAPMOD has already been validated against the Kincaid SF
6 data [
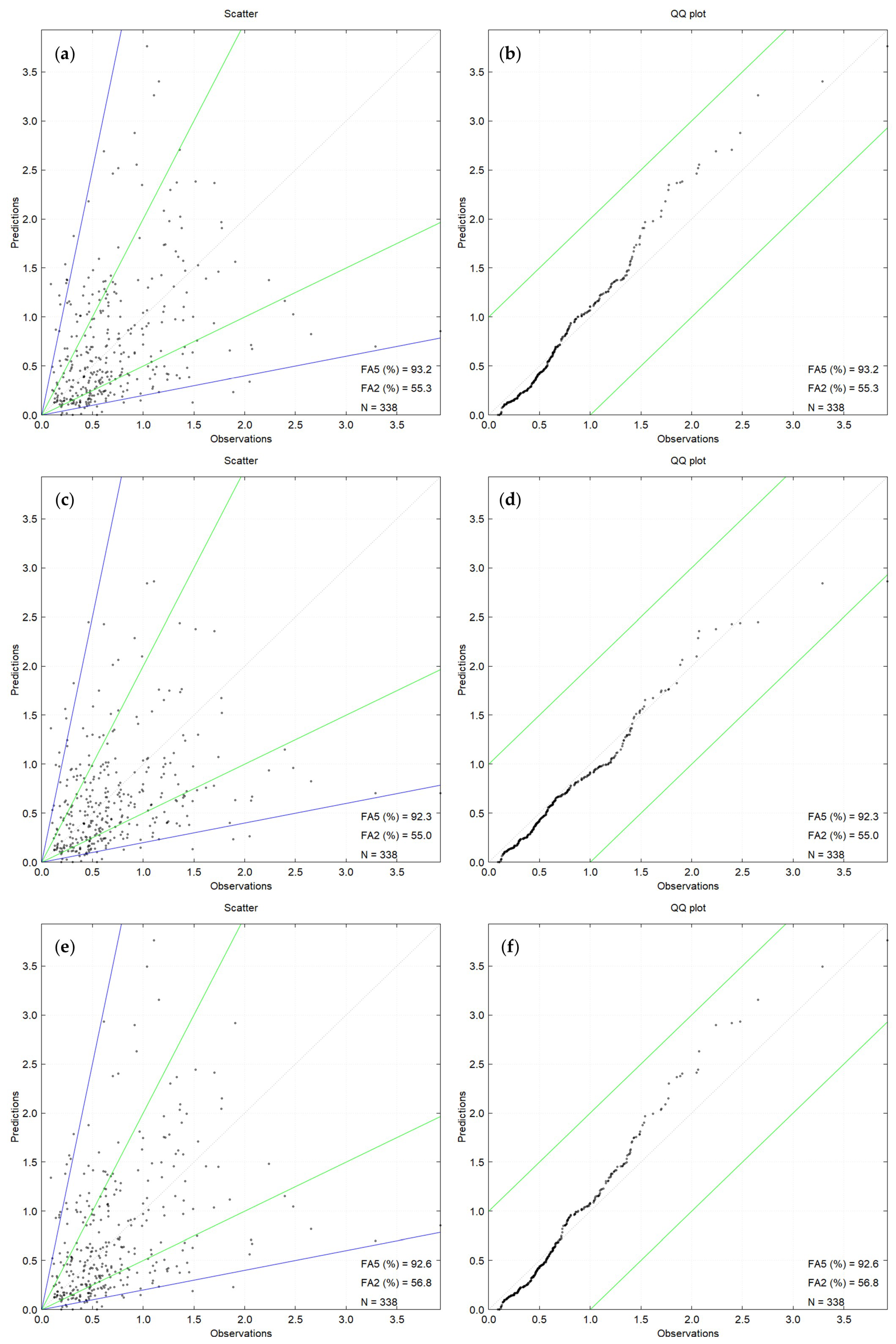
4]; the validation is repeated here with a new version of the model and with the same input setting used for Indianapolis. As done for the Indianapolis dataset, only observations of best quality (338 values) were used for comparison with the model predictions. The scatter plots of predictions against observations are shown in the left panel of
Figure 5 for the three plume rise algorithm considered, while the QQ plots are shown in the right panel of the same figure. The residual box plots for Kincaid best-quality data are reported in
Figure 6 and
Figure 7; these plots have been created as described for the Indianapolis SF
6 data.
FA2 and FA5 are quite similar for the three plume rise algorithms: FA2 ranges from 55.0% (JJ + RS) to 56.8% (JJ + JJ), while FA5 ranges from 92.3% (JJ + RS) to 93.2% (WT). Concerning the QQ plot, it is observed that for the Kincaid SF6 data the LAPMOD results are almost parallel to the x = y line up to about 1.5 μg m−3, 2 μg m−3 and 1.2 μg m−3, respectively, for algorithms WT, JJ + RS and JJ + JJ. A closer look to the curves shows that LAPMOD has a slight tendency to underpredict for values of concentrations up to about 0.7 μg m−3 when the WT and JJ + JJ algorithms are used, while above this value it overpredicts. When the JJ + RS plume rise algorithm is used, the overpredictions start at about 1.4 μg m−3. The residual box plots are always very similar, independently from the plume rise algorithm selected. The medians of the ratios are almost always close to 1, and a significant proportion of the residuals falls between a factor of 2.
The Kincaid observations of best quality and the LAPMOD predictions have been normalized by dividing them by the emission rate and multiplying by 1000. The MVK applied to the normalized data gives the results shown in
Table 4. Additional LAPMOD statistics are reported in
Table 5.
The statistics of extreme values for Kincaid SF
6, including the values of RHC
R with R = 11 and R = 26, are given in
Table 6. The statistics are reported for the observations, for LAPMOD with different plume rise algorithms, and, for comparison purposes, for the NAME model [
13]. The maximum concentration is perfectly matched by NAME, while it overestimates RHC
11, as done by LAPMOD WT, which adopts the same plume rise algorithm. Other authors [
25] reported a ratio between modeled and observed RHC
R equal to 0.77 for AERMOD and 0.68 for ISCST3 (with R = 26). We observe in
Table 6 that the same ratios for LAPMOD are within the interval 0.95 (when JJ + RS is used) to 1.19 (when WT is used).
3.3. Kincaid SO2
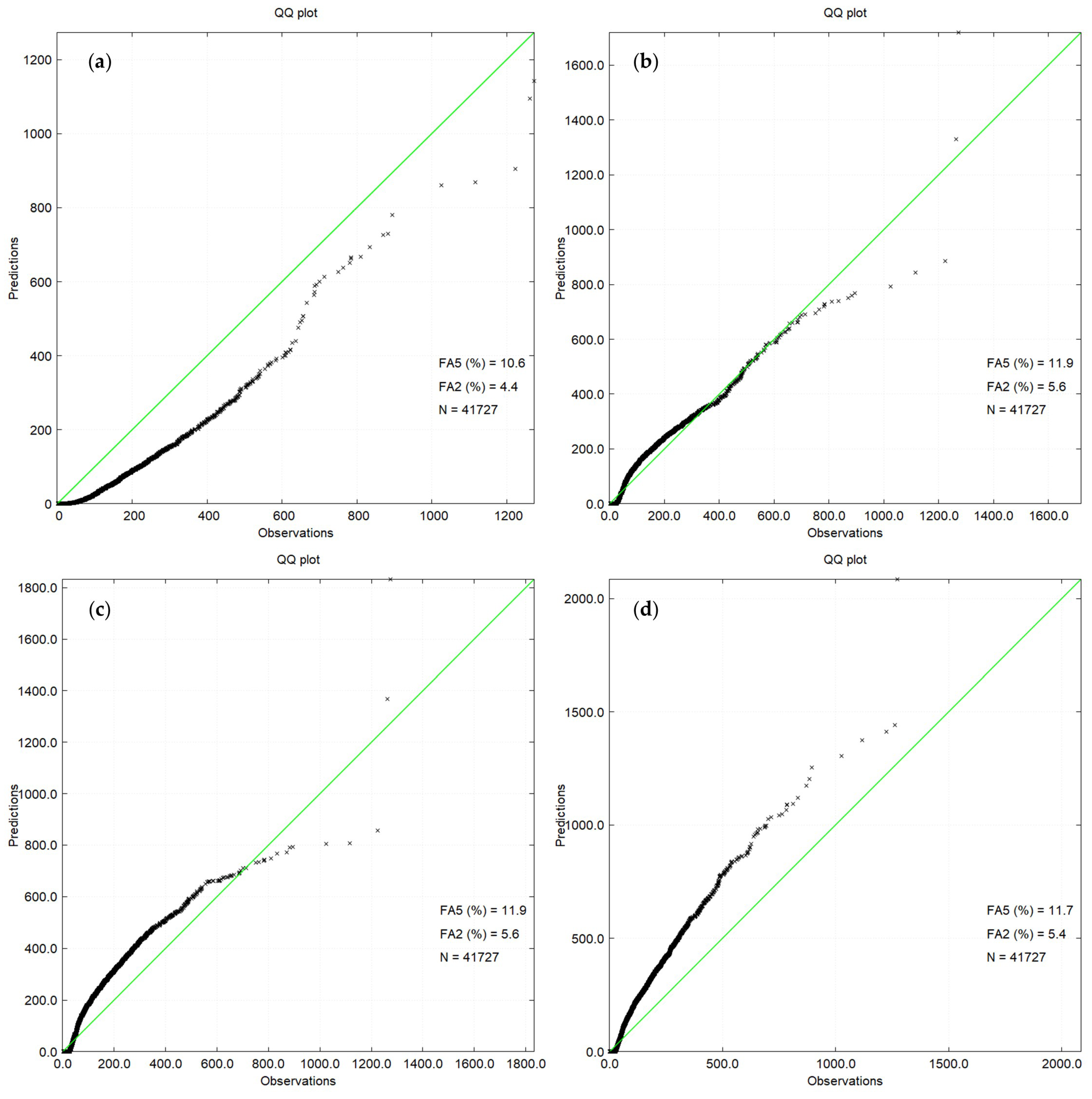
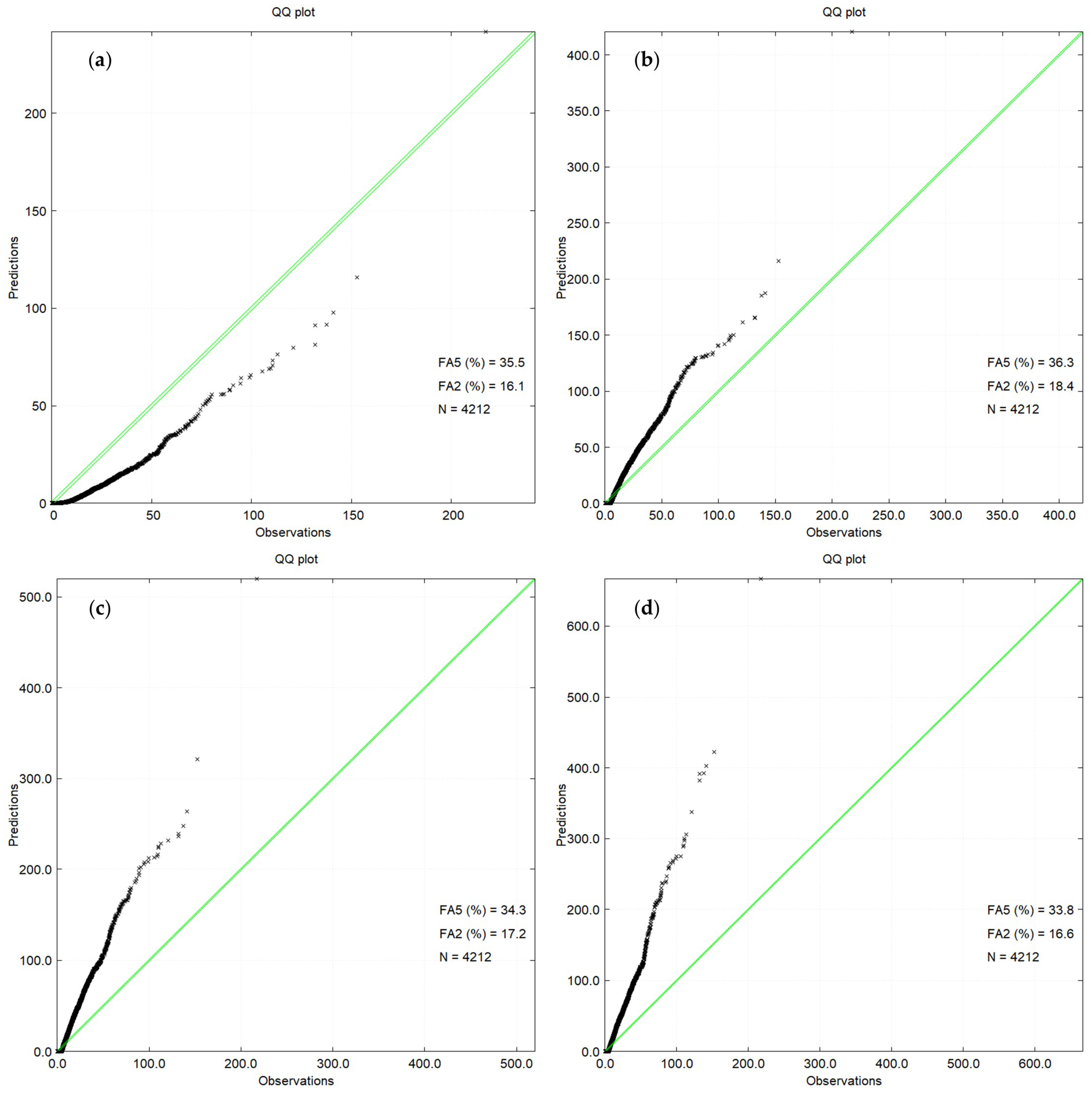
The QQ plot obtained for the one-hour average SO
2 concentration is shown in
Figure 8 for AERMOD (upper left), LAPMOD WT (upper right), LAPMOD JJ + RS (bottom left) and LAPMOD JJ + JJ (bottom right). The AERMOD plots reported in this section have been created with the predictions distributed with the EPA’s model evaluation databases [
20], which were obtained with a previous version of AERMOD (02222). AERMOD underestimates the one-hour concentrations while LAPMOD always overestimates them when the JJ + JJ plume rise algorithm is used. LAPMOD overestimates the observed concentration values up to about 700 μg m
−3 and underestimates greater values when the JJ + RS algorithm is used, and it is in good agreement with the observations up to about 700 μg m
−3 when the WT algorithm is used, while it underestimates for greater concentrations. The FA2 and FA5 values reported in
Figure 8 are lower than those found for the SF
6 release because, as anticipated, the SO
2 release predictions and observations at each receptor have been paired in time. The values of these two statistics are similar for AERMOD and LAPMOD with different plume rise configurations.
The values of RHC and other statistics are reported in
Table 7. The RHC
26 of AERMOD and LAPMOD WT are very close to the RHC
26 of the observations, confirming the ability to describe peak concentrations. On the contrary, LAPMOD JJ + RS and LAPMOD JJ + JJ tend to overestimate the observations.
The QQ plots obtained for the 24-h average SO
2 concentration are shown in
Figure 9 for AERMOD (top left), LAPMOD WT (top right), LAPMOD JJ + RS (bottom left) and LAPMOD JJ + JJ (bottom right). AERMOD still underestimates the observations, while LAPMOD overestimates them with all the plume rise algorithms tested.
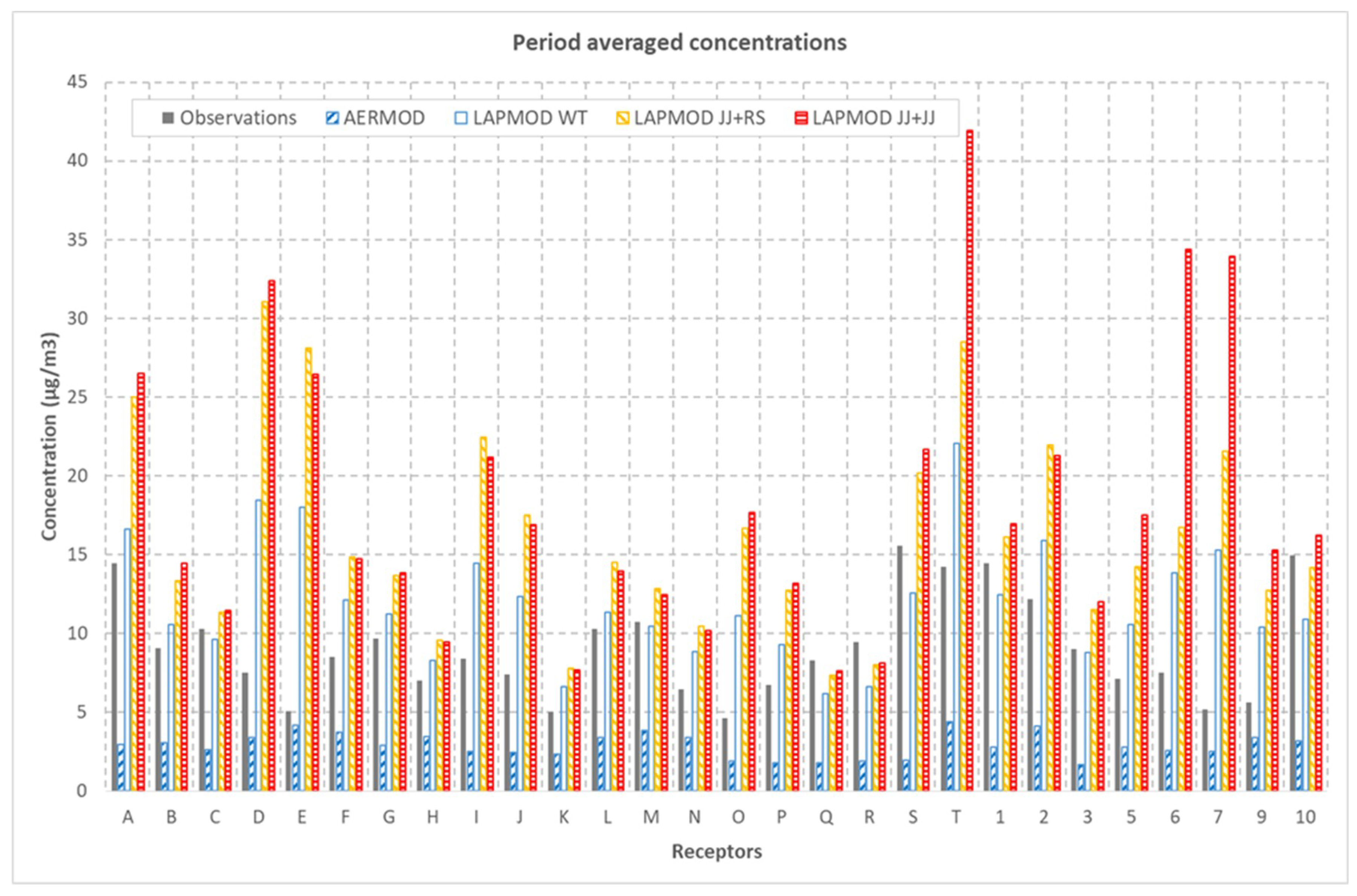
Figure 10 shows the period averaged concentrations at each receptor. After removing the values corresponding to zero SO
2 emission from the stack, the period-average at each receptor involve from 3023 to 4812 data. Generally, the LAPMOD average concentrations are in good agreement with the observations, with FA2 values ranging from 64.3% (JJ + JJ plume rise algorithm) to 85.7% (WT plume rise algorithm), and 10.7% for AERMOD. There are receptors at which LAPMOD greatly overestimates the observed concentrations, particularly at three receptors: T (the closest to the source at north), 6 (the closest to the source at south), and 7 (the closest to the source at south east). Considering also the behavior at other receptors, LAPMOD tends to overestimate average values close to the source.
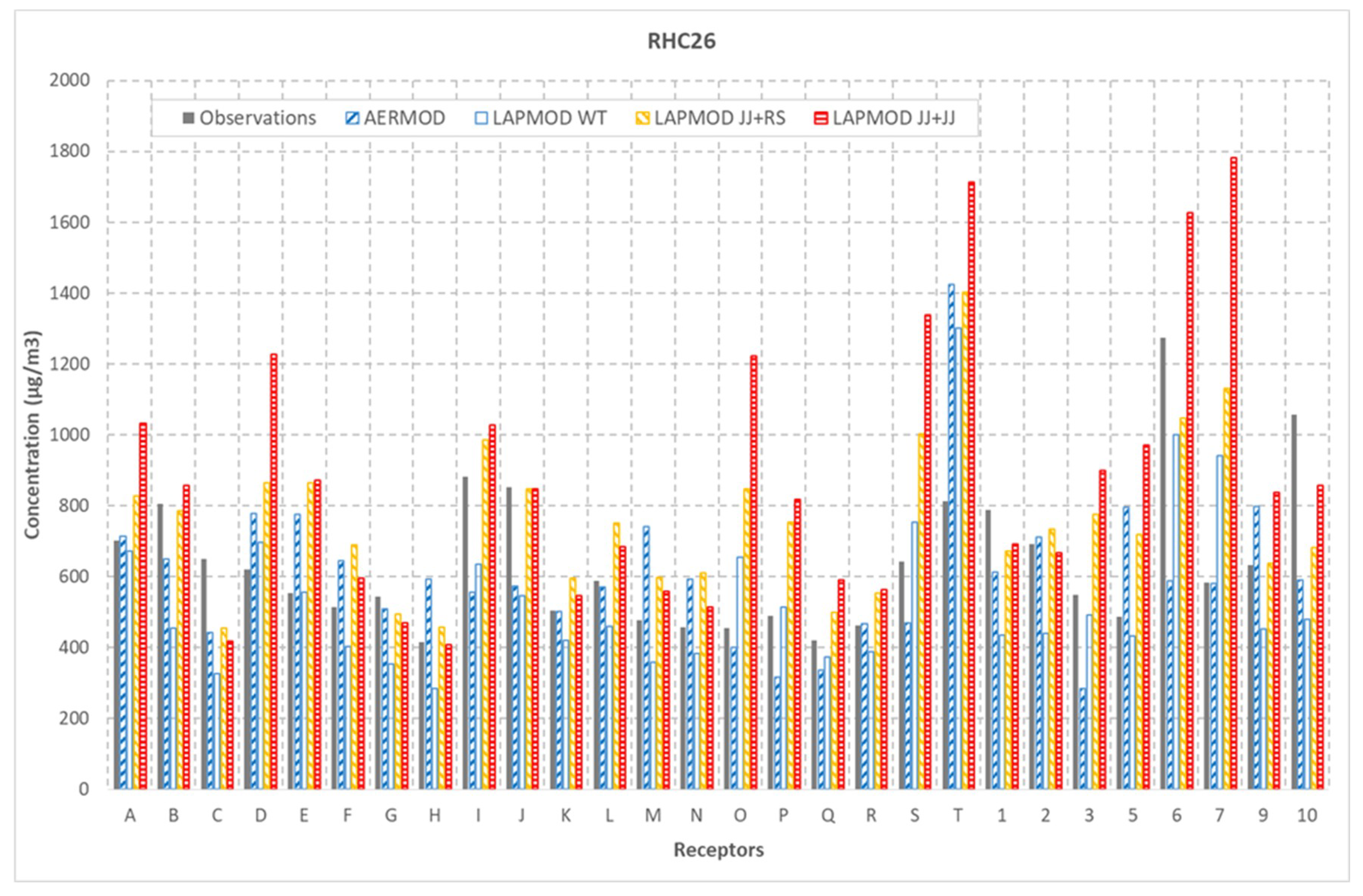
Figure 11 shows the RHC
26 values at each receptor. It is observed that considering the single receptors, instead of the whole one-hour concentration distribution independently from the position, the ability of LAPMOD to reproduce the peak concentrations improves. The maximum AERMOD RHC
26 (1424 μg m
−3) is predicted at receptor T (the closest to the source at north), where observations give a value of 811 μg m
−3 and LAPMOD WT a value of 1300 μg m
−3. The maximum observed RHC
26 (1275 μg m
−3) is at receptor 6 (the closest to the source at south), where AERMOD predicts 587 μg m
−3, and LAPMOD WT 1000 μg m
−3. For the other two plume rise algorithms, LAPMOD JJ + RS and JJ + JJ, the maximum observed RHC
26 values are 1046 μg m
−3 and 1626 μg m
−3, respectively. Receptors with a good agreement between observations and AERMOD are for example 7 and K.
4. Conclusions
This paper describes the numerical plume rise algorithms incorporated in the Lagrangian particle model LAPMOD [
4] and their validation against experimental datasets. The LAPMOD model and its pre- and post-processors are freely distributed through the Enviroware’s website (
https://www.enviroware.com/lapmod). The LAPMOD input files used to carry out the validations described in this paper are also available at:
https://www.enviroware.com/lapmod/validations.html. The meteorological field input to LAPMOD can be prepared with the CALMET diagnostic meteorological model [
5]. Thanks to its preprocessor LAPMET, the meteorological input can also be prepared starting from the AERMET output files. The LAPOST postprocessor allows the extraction of air quality statistics, concentration and deposition maps, and particle trajectories from the output binary files of LAPMOD.
Two plume rise algorithms have been incorporated in LAPMOD: Webster and Thomson [
13] and Janicke and Janicke [
12]. In this paper, we tested the WT algorithm and the JJ algorithm with two different entrainment mechanisms described in [
12,
16]. Therefore, we considered three different plume rise algorithms in total.
The WT and JJ plume rise formulations are comparable if the plume water content is not considered. The JJ algorithm has in its formulation the possibility to consider the effects of water, but in the datasets of Kincaid and Indianapolis, as in many others, the plume water content is unknown. Anyway, even for a dry plume, the JJ algorithm includes the effects of ambient humidity.
Apart from the plume rise algorithms, we defined the remaining LAPMOD input variables using the Indianapolis dataset, which was carried out in an urban environment. Then, we used the same input configuration for comparing the LAPMOD results against the Kincaid SF6 and SO2 datasets. Our goal was to verify that the model setting used for the Indianapolis data was also satisfactory for the Kincaid data to define a sort of default model configuration for future studies.
The results of LAPMOD with the different plume rise algorithms show that the Indianapolis data are best predicted when the JJ + RS plume rise algorithm is used. In such a case, FA2 is 62.6%, the QQ plot shows a good agreement between the observed and predicted data distributions, and good values for RHCN are obtained, indicating a satisfactory capability to reproduce the highest concentration values as well. The results obtained with the WT algorithm are also good, while those relative to the JJ + JJ algorithm are characterized by a high value of FB (0.382). When the Kincaid SF6 dataset is considered, the LAPMOD performances using the three plume rise algorithms are very similar. For example, the FA2 values are all within a narrow range (55.0–56.8%). Finally, the best LAPMOD results for Kincaid SO2 have been obtained with the WT plume rise algorithm, both in terms of RHC26 (1333 predicted versus 1327 observed) and in terms of period average concentration at each receptor.
Some performance evaluation criteria have been proposed [
26,
27] to define a “good” model. They require that at the same time the following three rules be observed:
the fraction of predictions within a factor of two of observations is about 50% or greater (i.e., FA2 > 50%);
the mean bias is within ±30% of the mean (i.e., roughly |FB| < 0.3 or 0.7 < geometric mean bias < 1.3); and
the random scatter is about a factor of two to three of the mean (i.e., roughly NMSE < 1.5 or geometric variance < 4).
The above rules are not firm guidelines and it is necessary to consider all performance measures in making a decision concerning model acceptance. According to these criteria and to the results presented for Indianapolis and Kincaid SF6, LAPMOD is a “good” model with all the three plume rise algorithms tested.
The above criteria do not hold for data paired in time and space, such as in the Kincaid SO2 dataset where the performance statistics are lower.
Starting from the results obtained in this work, it seems that the model configuration used, with WT or JJ + RS plume rise algorithm, may be considered a good default for LAPMOD.
The LAPMOD computer running times are comparable with those of CALPUFF, and therefore LAPMOD is a cost-effective choice for air quality studies. Moreover, the structure of Lagrangian particle models is such that they can highly benefit from parallelization, for example distributing the particles’ movements to different processors.