Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study
Abstract
1. Introduction
2. Methods
2.1. The SIRANE Model
2.2. Modelling Chemical Reactions
2.3. Source Apportionment Module
2.3.1. Inert Pollutant Species
2.3.2. Reactive Pollutant Species
Model SA-NO
Model SA-NOX
2.4. Data Assimilation Using Source Apportionment Results
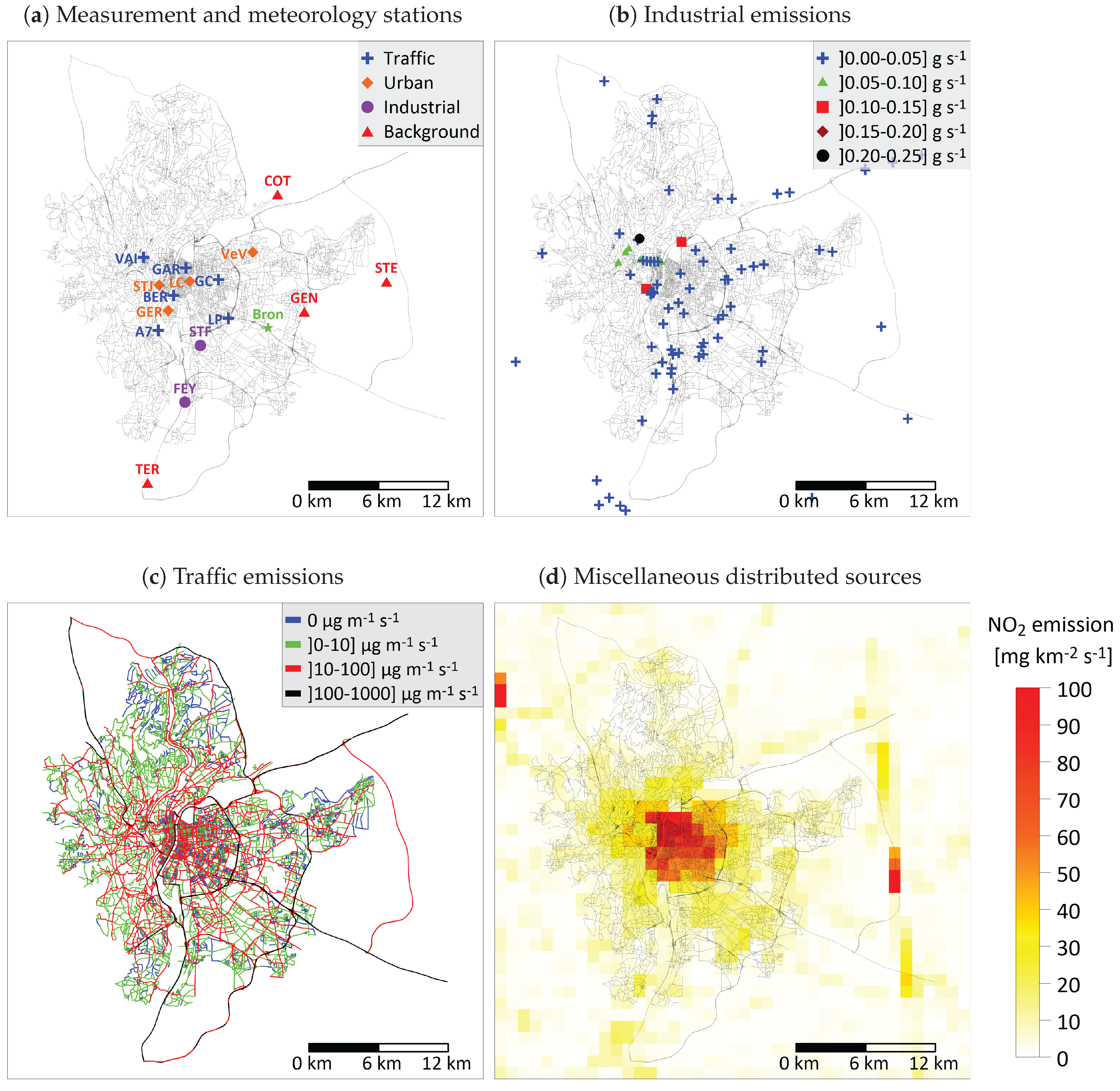
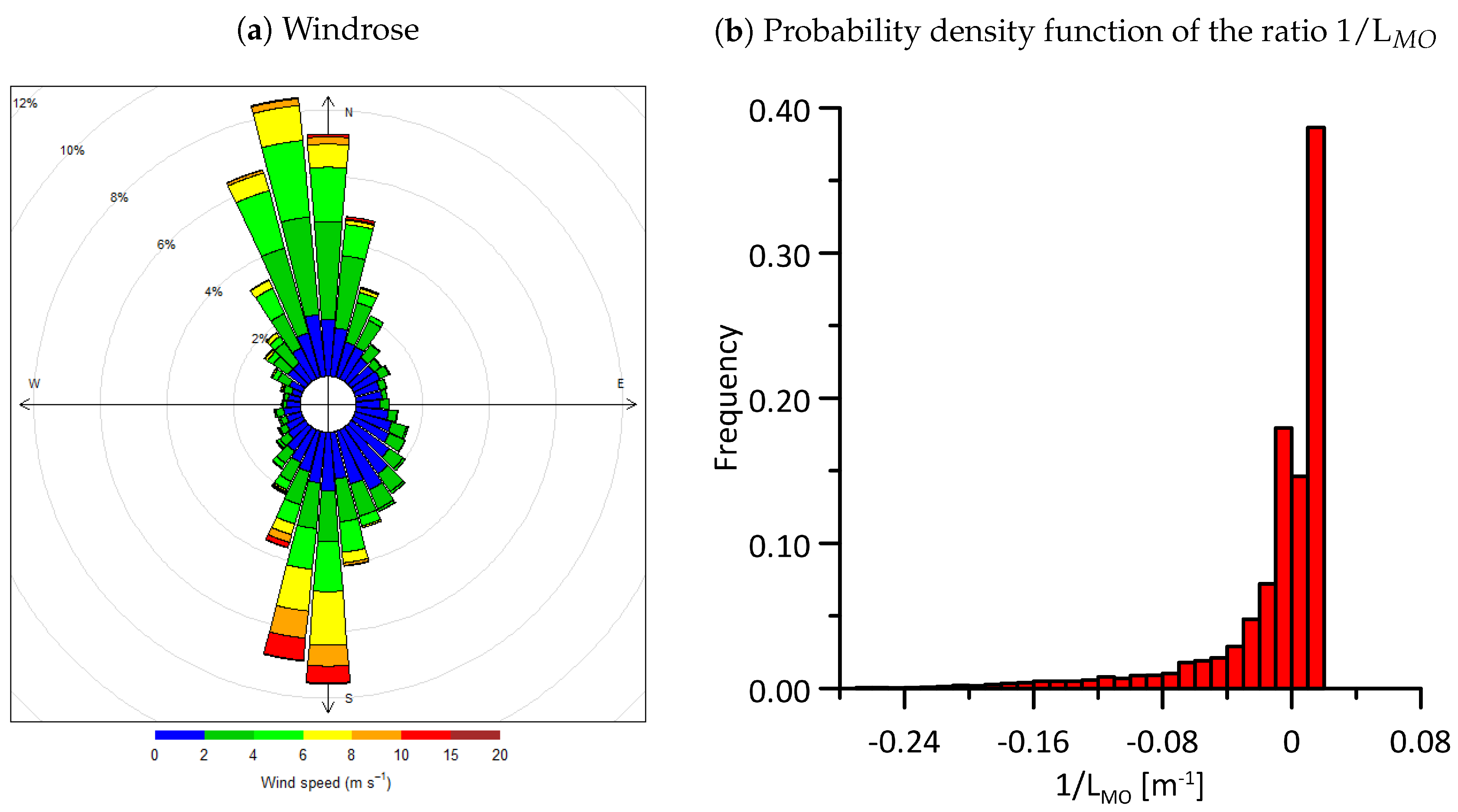
3. Case Study—The Lyon Urban Agglomeration
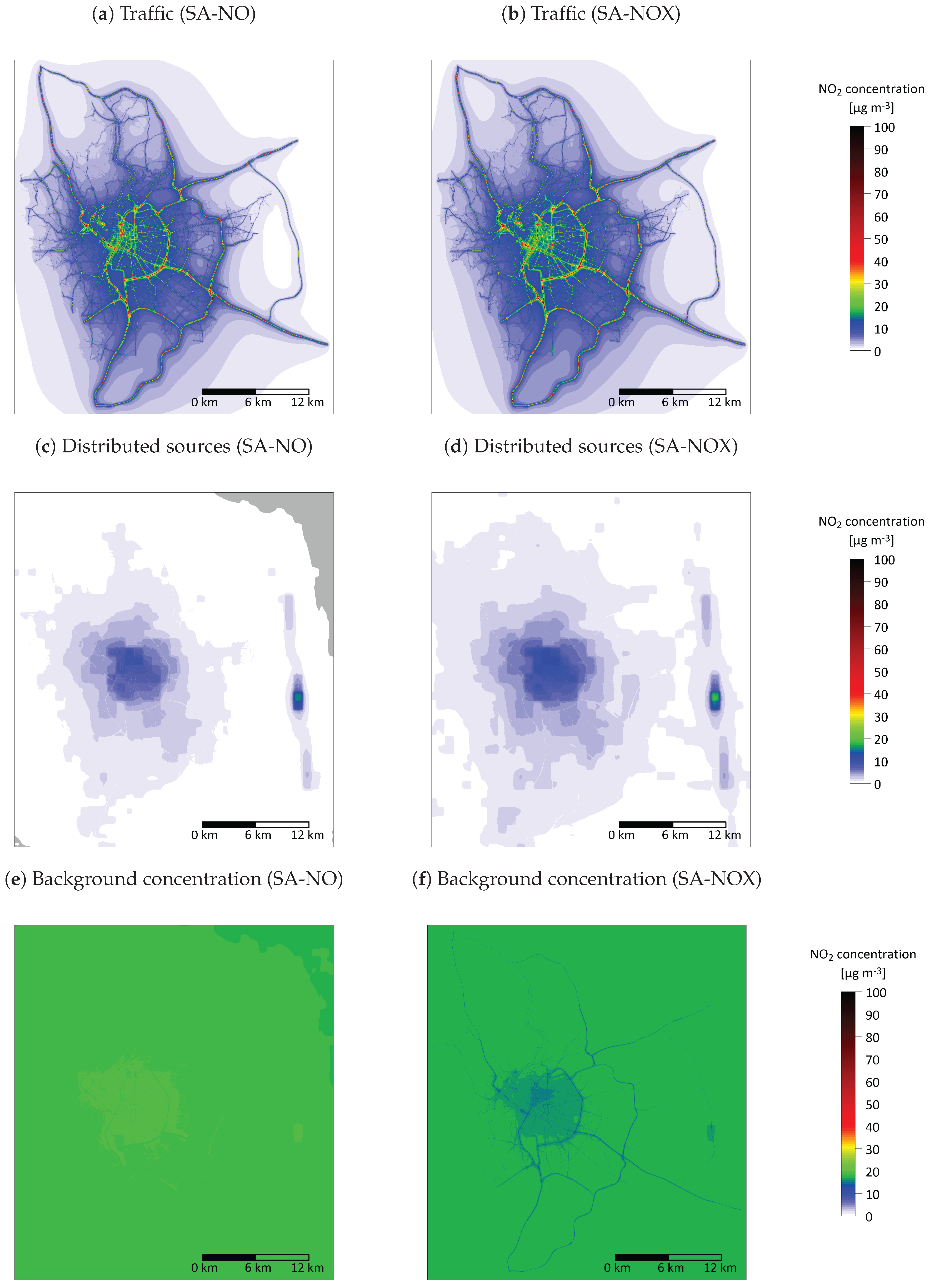
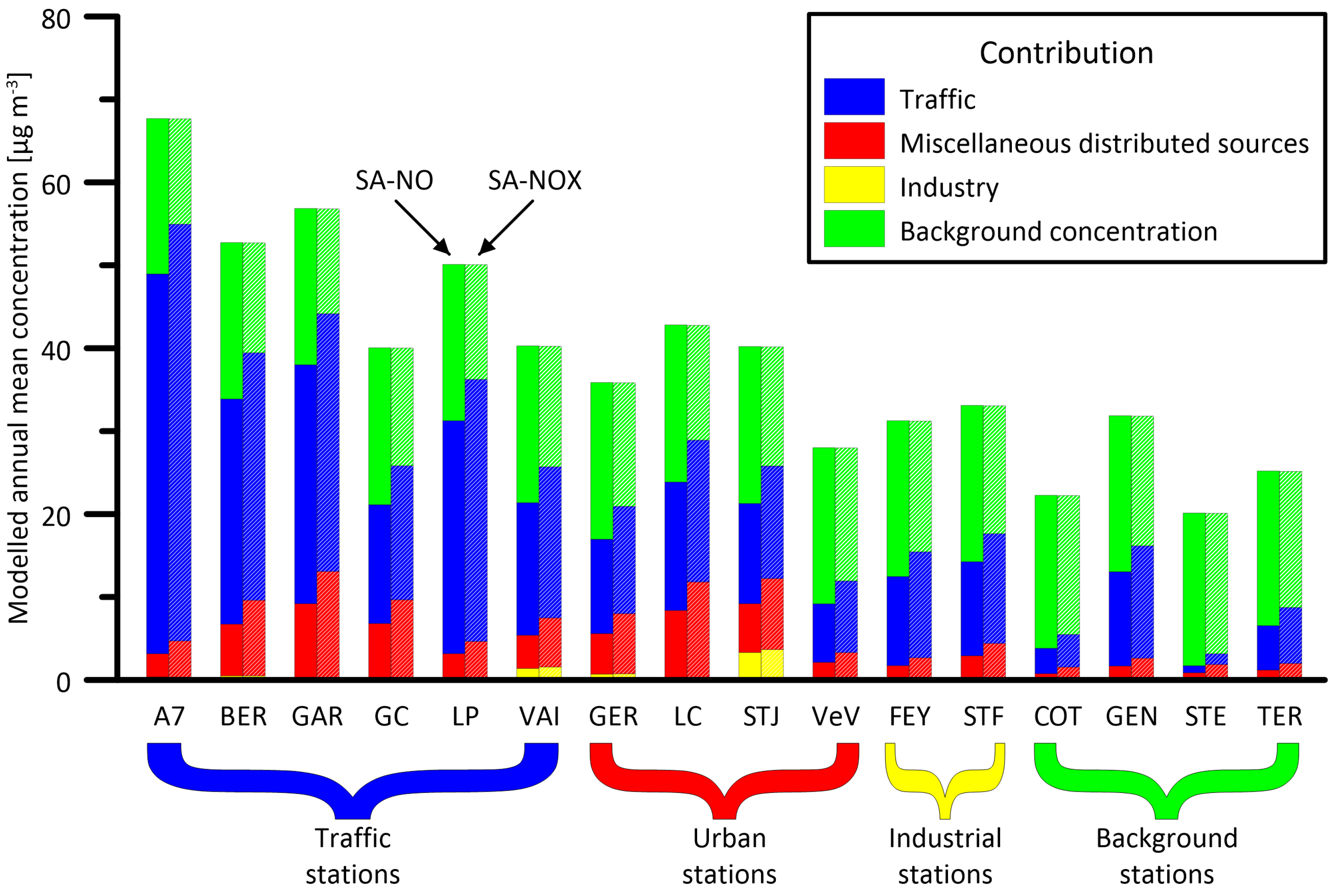
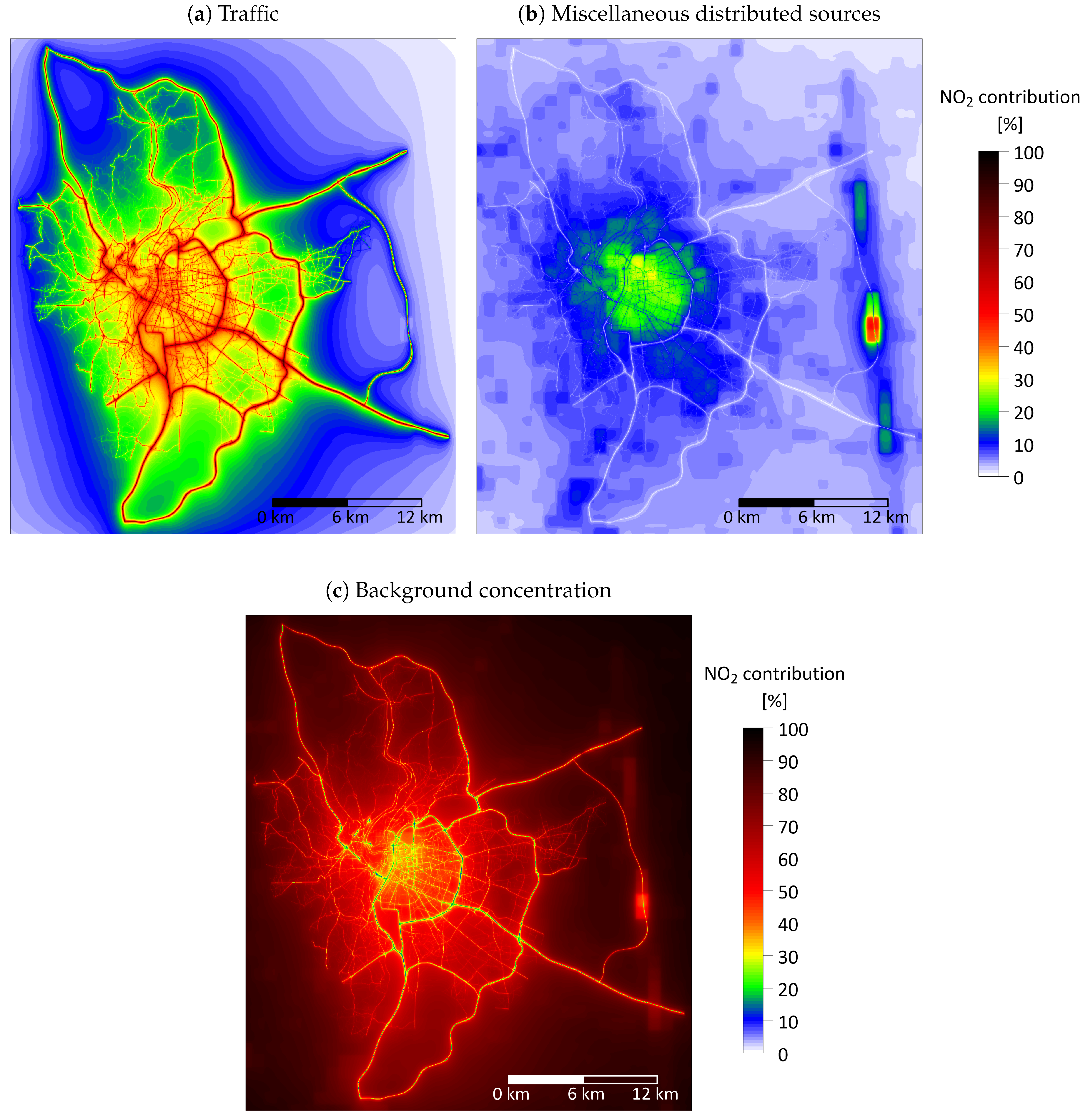
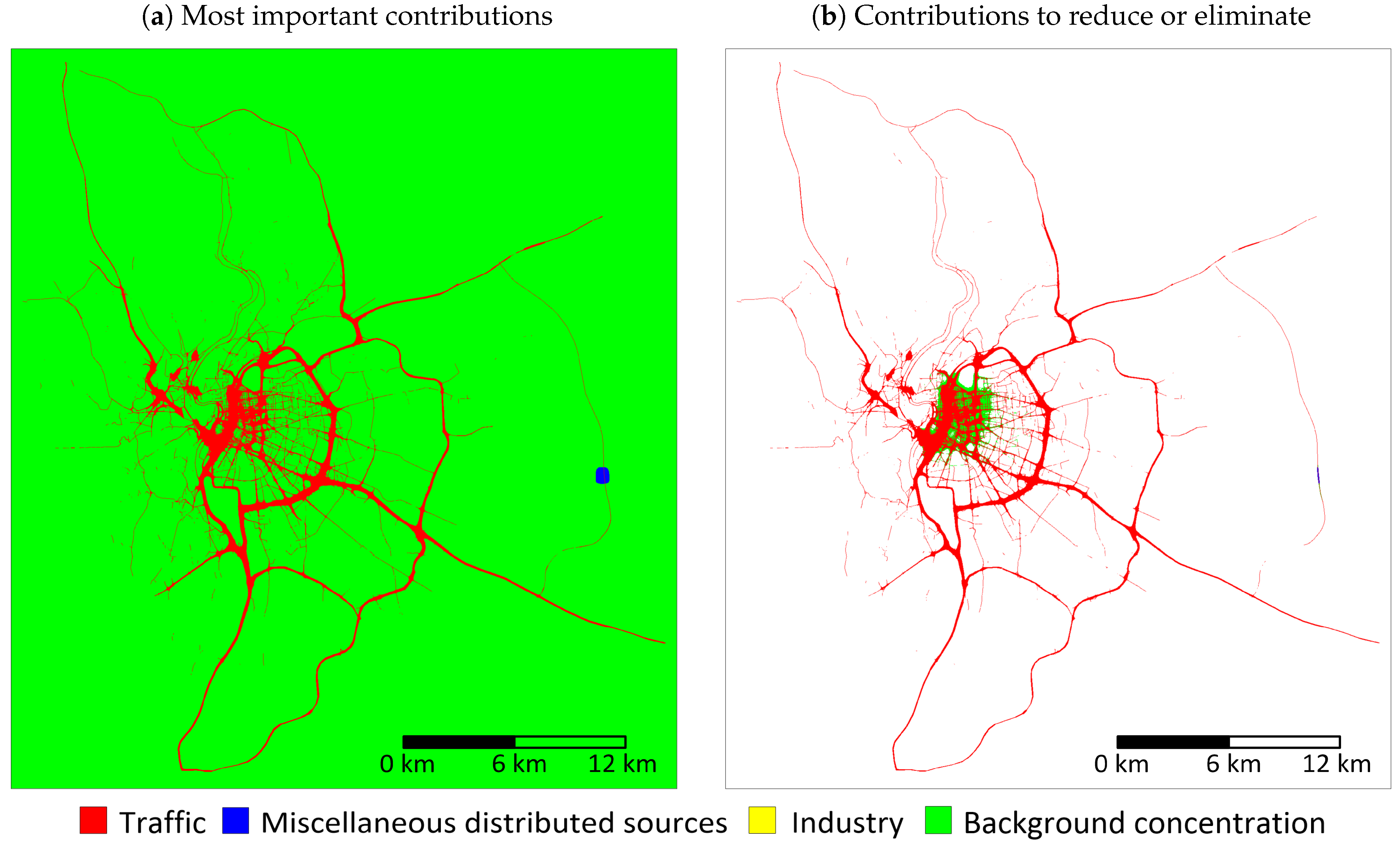
3.1. Source Apportionment Results
3.1.1. Comparison of the Results Obtained with the SA-NO and SA-NOX Models
3.1.2. Estimates of Sources’ Contributions
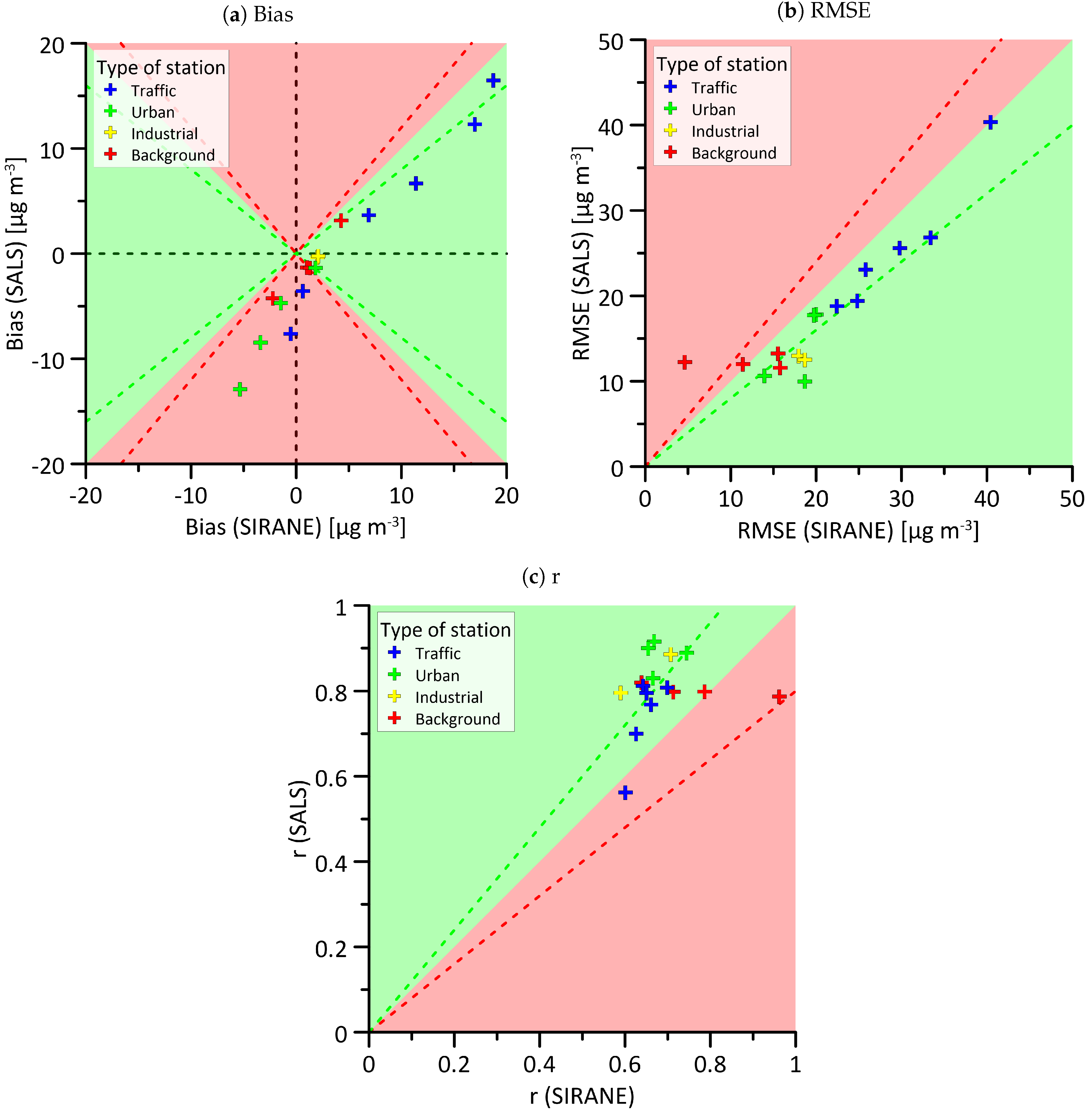
3.2. Data Assimilation Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BFM | Brut Force Method |
| CMB | Chemical Mass Balance |
| PM | Particulate Matter |
| SALS | Source Apportionment Least Square |
References
- Wagstrom, K.M.; Pandis, S.N.; Yarwood, G.; Wilson, G.M.; Morris, R.E. Development and application of a computationally efficient particulate matter apportionment algorithm in a three-dimensional chemical transport model. Atmos. Environ. 2008, 42, 5650–5659. [Google Scholar] [CrossRef]
- Yim, S.H.; Fung, J.C.; Lau, A.K. Use of high-resolution MM5/CALMET/CALPUFF system: SO2 apportionment to air quality in Hong Kong. Atmos. Environ. 2010, 44, 4850–4858. [Google Scholar] [CrossRef]
- Cho, S.; Morris, R.; McEachern, P.; Shah, T.; Johnson, J.; Nopmongcol, U. Emission sources sensitivity study for ground-level ozone and PM2.5 due to oil sands development using air quality modelling system: Part II—Source apportionment modelling. Atmos. Environ. 2012, 55, 542–556. [Google Scholar] [CrossRef]
- Grewe, V.; Dahlmann, K.; Matthes, S.; Steinbrecht, W. Attributing ozone to NOx emissions: Implications for climate mitigation measures. Atmos. Environ. 2012, 59, 102–107. [Google Scholar] [CrossRef]
- Kwok, R.; Napelenok, S.; Baker, K. Implementation and evaluation of PM2.5 source contribution analysis in a photochemical model. Atmos. Environ. 2013, 80, 398–407. [Google Scholar] [CrossRef]
- Ying, Q.; Kleeman, M.J. Source contributions to the regional distribution of secondary particulate matter in California. Atmos. Environ. 2006, 40, 736–752. [Google Scholar] [CrossRef]
- Yarwood, G.; Morris, R.E.; Wilson, G.M. Particulate matter source apportionment technology (PSAT) in the CAMx photochemical grid model. In Air Pollution Modeling and Its Application XVII; Springer: Boston, MA, USA, 2007; pp. 478–492. [Google Scholar]
- Wang, Z.S.; Chien, C.J.; Tonnesen, G.S. Development of a tagged species source apportionment algorithm to characterize three-dimensional transport and transformation of precursors and secondary pollutants. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Pio, C.A.; Alves, C.A.; Duarte, A.C. Identification, abundance and origin of atmospheric organic particulate matter in a Portuguese rural area. Atmos. Environ. 2001, 35, 1365–1375. [Google Scholar] [CrossRef]
- Querol, X.; Alastuey, A.; Rodríguez, S.; Plana, F.; Ruiz, C.R.; Cots, N.; Massagué, G.; Puig, O. PM10 and PM2.5 source apportionment in the Barcelona Metropolitan area, Catalonia, Spain. Atmos. Environ. 2001, 35, 6407–6419. [Google Scholar] [CrossRef]
- Putaud, J.P.; Raes, F.; Van Dingenen, R.; Brüggemann, E.; Facchini, M.C.; Decesari, S.; Fuzzi, S.; Gehrig, R.; Hüglin, C.; Laj, P.; et al. A European aerosol phenomenology—2: Chemical characteristics of particulate matter at kerbside, urban, rural and background sites in Europe. Atmos. Environ. 2004, 38, 2579–2595. [Google Scholar] [CrossRef]
- Gijzen, M.; Lewinsohn, E.; Savage, T.J.; Croteau, R.B. Conifer monoterpenes: Biochemistry and bark beetle chemical ecology. ACS Symp. Ser. 1993, 525, 8–22. [Google Scholar]
- Watson, J.G. Overview of receptor model principles. J. Air Pollut. Control Assoc. 1984, 34, 619–623. [Google Scholar] [CrossRef]
- Viana, M.; Kuhlbusch, T.; Querol, X.; Alastuey, A.; Harrison, R.; Hopke, P.; Winiwarter, W.; Vallius, M.; Szidat, S.; Prévôt, A.; et al. Source apportionment of particulate matter in Europe: A review of methods and results. J. Aerosol Sci. 2008, 39, 827–849. [Google Scholar] [CrossRef]
- Held, T.; Ying, Q.; Kleeman, M.J.; Schauer, J.J.; Fraser, M.P. A comparison of the UCD/CIT air quality model and the CMB source–receptor model for primary airborne particulate matter. Atmos. Environ. 2005, 39, 2281–2297. [Google Scholar] [CrossRef]
- Subramanian, R.; Donahue, N.M.; Bernardo-Bricker, A.; Rogge, W.F.; Robinson, A.L. Contribution of motor vehicle emissions to organic carbon and fine particle mass in Pittsburgh, Pennsylvania: Effects of varying source profiles and seasonal trends in ambient marker concentrations. Atmos. Environ. 2006, 40, 8002–8019. [Google Scholar] [CrossRef]
- Rizzo, M.J.; Scheff, P.A. Fine particulate source apportionment using data from the USEPA speciation trends network in Chicago, Illinois: Comparison of two source apportionment models. Atmos. Environ. 2007, 41, 6276–6288. [Google Scholar] [CrossRef]
- Subramanian, R.; Donahue, N.M.; Bernardo-Bricker, A.; Rogge, W.F.; Robinson, A.L. Insights into the primary–secondary and regional–local contributions to organic aerosol and PM2.5 mass in Pittsburgh, Pennsylvania. Atmos. Environ. 2007, 41, 7414–7433. [Google Scholar] [CrossRef]
- Duvall, R.M.; Norris, G.A.; Burke, J.M.; Olson, D.A.; Vedantham, R.; Williams, R. Determining spatial variability in PM2.5 source impacts across Detroit, MI. Atmos. Environ. 2012, 47, 491–498. [Google Scholar] [CrossRef]
- Guo, H.; Wang, T.; Louie, P. Source apportionment of ambient non-methane hydrocarbons in Hong Kong: Application of a principal component analysis/absolute principal component scores (PCA/APCS) receptor model. Environ. Pollut. 2004, 129, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Almeida, S.M.; Pio, C.A.; Freitas, M.C.; Reis, M.A.; Trancoso, M.A. Approaching PM2.5 and PM2.5–10 source apportionment by mass balance analysis, principal component analysis and particle size distribution. Sci. Total Environ. 2006, 368, 663–674. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Xie, S.; Zhang, Y.; Zeng, L.; Salmon, L.G.; Zheng, M. Source apportionment of PM2.5 in Beijing using principal component analysis/absolute principal component scores and UNMIX. Sci. Total Environ. 2006, 372, 278–286. [Google Scholar] [CrossRef] [PubMed]
- Shi, G.L.; Li, X.; Feng, Y.C.; Wang, Y.Q.; Wu, J.H.; Li, J.; Zhu, T. Combined source apportionment, using positive matrix factorization–chemical mass balance and principal component analysis/multiple linear regression–chemical mass balance models. Atmos. Environ. 2009, 43, 2929–2937. [Google Scholar] [CrossRef]
- Escrig, A.; Monfort, E.; Celades, I.; Querol, X.; Amato, F.; Minguillón, M.C.; Hopke, P.K. Application of Optimally Scaled Target Factor Analysis for Assessing Source Contribution of Ambient PM10. J. Air Waste Manag. Assoc. 2009, 59, 1296–1307. [Google Scholar] [CrossRef] [PubMed]
- Minguillón, M.C.; Schembari, A.; Triguero-Mas, M.; de Nazelle, A.; Dadvand, P.; Figueras, F.; Salvado, J.A.; Grimalt, J.O.; Nieuwenhuijsen, M.; Querol, X. Source apportionment of indoor, outdoor and personal PM2.5 exposure of pregnant women in Barcelona, Spain. Atmos. Environ. 2012, 59, 426–436. [Google Scholar] [CrossRef]
- Alier, M.; Felipe-Sotelo, M.; Hernàndez, I.; Tauler, R. Variation patterns of nitric oxide in Catalonia during the period from 2001 to 2006 using multivariate data analysis methods. Anal. Chim. Acta 2009, 642, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Alier, M.; Felipe, M.; Hernández, I.; Tauler, R. Trilinearity and component interaction constraints in the multivariate curve resolution investigation of NO and O3 pollution in Barcelona. Anal. Bioanal. Chem. 2011, 399, 2015–2029. [Google Scholar] [CrossRef] [PubMed]
- Koo, B.; Wilson, G.M.; Morris, R.E.; Dunker, A.M.; Yarwood, G. Comparison of source apportionment and sensitivity analysis in a particulate matter air quality model. Environ. Sci. Technol. 2009, 43, 6669–6675. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, C.; Kranenburg, R.; Kuenen, J.; van Gijlswijk, R.; Kruit, R.W.; Segers, A.; van der Gon, H.D.; Schaap, M. The origin of ambient particulate matter concentrations in the Netherlands. Atmos. Environ. 2013, 69, 289–303. [Google Scholar] [CrossRef]
- Grewe, V. A diagnostic for ozone contributions of various NOx emissions in multi-decadal chemistry-climate model simulations. Atmos. Chem. Phys. 2004, 4, 729–736. [Google Scholar] [CrossRef]
- Held, T.; Ying, Q.; Kaduwela, A.; Kleeman, M. Modeling particulate matter in the San Joaquin Valley with a source-oriented externally mixed three-dimensional photochemical grid model. Atmos. Environ. 2004, 38, 3689–3711. [Google Scholar] [CrossRef]
- Grewe, V.; Tsati, E.; Hoor, P. On the attribution of contributions of atmospheric trace gases to emissions in atmospheric model applications. Geosci. Model Dev. 2010, 3, 487. [Google Scholar] [CrossRef]
- Butler, T.; Lawrence, M.; Taraborrelli, D.; Lelieveld, J. Multi-day ozone production potential of volatile organic compounds calculated with a tagging approach. Atmos. Environ. 2011, 45, 4082–4090. [Google Scholar] [CrossRef]
- Emmons, L.; Hess, P.; Lamarque, J.F.; Pfister, G. Tagged ozone mechanism for MOZART-4, CAM-chem and other chemical transport models. Geosci. Model Dev. 2012, 5, 1531. [Google Scholar] [CrossRef]
- Kranenburg, R.; Segers, A.; Hendriks, C.; Schaap, M. Source apportionment using LOTOS-EUROS: Module description and evaluation. Geosci. Model Dev. 2013, 6, 721–733. [Google Scholar] [CrossRef]
- Granier, C.; Mueller, J.; Pétron, G.; Brasseur, G. A three-dimensional study of the global CO budget. Chemosphere-Glob. Chang. Sci. 1999, 1, 255–261. [Google Scholar] [CrossRef]
- Granier, C.; Pétron, G.; Müller, J.F.; Brasseur, G. The impact of natural and anthropogenic hydrocarbons on the tropospheric budget of carbon monoxide. Atmos. Environ. 2000, 34, 5255–5270. [Google Scholar] [CrossRef]
- Lamarque, J.F.; Hess, P. Model analysis of the temporal and geographical origin of the CO distribution during the TOPSE campaign. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Pfister, G.; Petron, G.; Emmons, L.; Gille, J.; Edwards, D.; Lamarque, J.F.; Attie, J.L.; Granier, C.; Novelli, P. Evaluation of CO simulations and the analysis of the CO budget for Europe. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Huang, Q.; Cheng, S.; Perozzi, R.E.; Perozzi, E.F. Use of a MM5–CAMx–PSAT modeling system to study SO2 source apportionment in the Beijing Metropolitan Region. Environ. Model. Assess. 2012, 17, 527–538. [Google Scholar] [CrossRef]
- Talagrand, O. Assimilation of observations, an introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar] [CrossRef]
- Rabier, F. Assimilation variationnelle de données météorologiques en présence d’instabilité barocline. La Météorologie 1993, 8, 57–72. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Swinbank, R.; Shutyaev, V.; Lahoz, W.A. Data Assimilation for the Earth System; Springer Science & Business Media: Berlin, Germany, 2003. [Google Scholar]
- Denby, B.; Horálek, J.; Walker, S.E.; Eben, K.; Fiala, J. Interpolation and assimilation methods for European scale air quality assessment and mapping. In Part I: Review and Recommendations; European Topic Centre on Air and Climate Change (ETC/ACC): Copenhagen, Denmark, 2005; Volume 7. [Google Scholar]
- Morel, P.; Talagrand, O. Dynamic approach to meteorological data assimilation. Tellus 1974, 26, 334–344. [Google Scholar] [CrossRef]
- McPherson, R.D. Progress, problems, and prospects in meteorological data assimilation. Bull. Am. Meteorol. Soc. 1975, 56, 1154–1166. [Google Scholar] [CrossRef]
- Miyakoda, K.; Umscheid, L.; Lee, D.; Sirutis, J.; Lusen, R.; Pratte, F. The near-real-time, global, four-dimensional analysis experiment during the GATE period, Part I. J. Atmos. Sci. 1976, 33, 561–591. [Google Scholar] [CrossRef]
- Miyakoda, K.; Strickler, R.; Chludzinski, J. Initialization with the data assimilation method. Tellus 1978, 30, 32–54. [Google Scholar] [CrossRef]
- McPherson, R.; Bergman, K.; Kistler, R.; Rasch, G.; Gordon, D. The NMC operational global data assimilation system. Mon. Weather Rev. 1979, 107, 1445–1461. [Google Scholar] [CrossRef]
- Elbern, H.; Schmidt, H.; Ebel, A. Variational data assimilation for tropospheric chemistry modeling. J. Geophys. Res. Atmos. 1997, 102, 15967–15985. [Google Scholar] [CrossRef]
- Elbern, H.; Schmidt, H. A four-dimensional variational chemistry data assimilation scheme for Eulerian chemistry transport modeling. J. Geophys. Res. Atmos. 1999, 104, 18583–18598. [Google Scholar] [CrossRef]
- Elbern, H.; Schmidt, H.; Talagrand, O.; Ebel, A. 4D-variational data assimilation with an adjoint air quality model for emission analysis. Environ. Model. Softw. 2000, 15, 539–548. [Google Scholar] [CrossRef]
- Segers, A.J.; Heemink, A.W.; Verlaan, M.; van Loon, M. A modified rrsqrt-filter for assimilating data in atmospheric chemistry models. Environ. Model. Softw. 2000, 15, 663–671. [Google Scholar] [CrossRef]
- Van Loon, M.; Builtjes, P.J.H.; Segers, A.J. Data assimilation of ozone in the atmospheric transport chemistry model LOTOS. Environ. Model. Softw. 2000, 15, 603–609. [Google Scholar] [CrossRef]
- Brown, D.; Comrie, A. Spatial modeling of winter temperature and precipitation in Arizona and New Mexico, USA. Clim. Res. 2002, 22, 115–128. [Google Scholar] [CrossRef]
- Hooyberghs, J.; Mensink, C.; Dumont, G.; Fierens, F. Spatial interpolation of ambient ozone concentrations from sparse monitoring points in Belgium. J. Environ. Monit. 2006, 8, 1129–1135. [Google Scholar] [CrossRef] [PubMed]
- ETC/ACC. Spatial Mapping of Air Quality for European Scale Assessment; ETC/ACC: Copenhagen, Denmark, 2007. [Google Scholar]
- Lü, C.; Tian, H. Spatial and temporal patterns of nitrogen deposition in China: Synthesis of observational data. J. Geophys. Res. D Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Denby, B.; Schaap, M.; Segers, A.; Builtjes, P.; Horálek, J. Comparison of two data assimilation methods for assessing PM10 exceedances on the European scale. Atmos. Environ. 2008, 42, 7122–7134. [Google Scholar] [CrossRef]
- EEA. Spatial Assessment of PM10 and Ozone Concentrations in Europe (2005); European Environment Agency (EEA): Copenhagen, Denmark, 2009. [Google Scholar]
- Joseph, J.; Sharif, H.O.; Sunil, T.; Alamgir, H. Application of validation data for assessing spatial interpolation methods for 8-h ozone or other sparsely monitored constituents. Environ. Pollut. 2013, 178, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, C.L.; Tanenbaum, S.; Hidy, G.M. Spatial and temporal variability of air pollution in Birmingham, Alabama. Atmos. Environ. 2014, 89, 382–391. [Google Scholar] [CrossRef]
- Candiani, G.; Carnevale, C.; Pisoni, E.; Volta, M. Assimilation of Chemical Ground Measurements in Air Quality Modeling. In Large-Scale Scientific Computing; Lirkov, I., Margenov, S., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 157–164. [Google Scholar]
- Wang, X.; Mallet, V.; Berroir, J.P.; Herlin, I. Assimilation of OMI NO2 retrievals into a regional chemistry-transport model for improving air quality forecasts over Europe. Atmos. Environ. 2011, 45, 485–492. [Google Scholar] [CrossRef]
- Kumar, U.; De Ridder, K.; Lefebvre, W.; Janssen, S. Data assimilation of surface air pollutants (O3 and NO2) in the regional-scale air quality model AURORA. Atmos. Environ. 2012, 60, 99–108. [Google Scholar] [CrossRef]
- Candiani, G.; Carnevale, C.; Finzi, G.; Pisoni, E.; Volta, M. A comparison of reanalysis techniques: Applying optimal interpolation and Ensemble Kalman Filtering to improve air quality monitoring at mesoscale. Sci. Total Environ. 2013, 458–460, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Tilloy, A.; Mallet, V.; Poulet, D.; Pesin, C.; Brocheton, F. BLUE-based NO2 data assimilation at urban scale. J. Geophys. Res. Atmos. 2013, 118, 2031–2040. [Google Scholar] [CrossRef]
- Soulhac, L.; Salizzoni, P.; Cierco, F.X.; Perkins, R. The model SIRANE for atmospheric urban pollutant dispersion; part I, presentation of the model. Atmos. Environ. 2011, 45, 7379–7395. [Google Scholar] [CrossRef]
- Soulhac, L.; Salizzoni, P.; Mejean, P.; Didier, D.; Rios, I. The model SIRANE for atmospheric urban pollutant dispersion; PART II, validation of the model on a real case study. Atmos. Environ. 2012, 49, 320–337. [Google Scholar] [CrossRef]
- Soulhac, L. ModéLisation de la Dispersion Atmosphérique à L’intérieur de la Canopée Urbaine. Ph.D. Thesis, Ecole centrale de Lyon, Ecully, France, 2000. [Google Scholar]
- Soulhac, L.; Nguyen, C.V.; Volta, P.; Salizzoni, P. The model SIRANE for atmospheric urban pollutant dispersion. PART III: Validation against NO2 yearly concentration measurements in a large urban agglomeration. Atmos. Environ. 2017, 167, 377–388. [Google Scholar] [CrossRef]
- Seinfeld, J.H. Atmospheric Chemistry and Physics of Air Pollution, 1st ed.; Wiley-Interscience: New York, NY, USA, 1986. [Google Scholar]
- Bloss, W. Atmospheric chemical processes of importance in cities. Issues Environ. Sci. Technol. 2009, 28, 42. [Google Scholar]
- Zhong, J.; Cai, X.M.; Bloss, W.J. Modelling the dispersion and transport of reactive pollutants in a deep urban street canyon: Using large-eddy simulation. Environ. Pollut. 2015, 200, 42–52. [Google Scholar] [CrossRef] [PubMed]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Vardoulakis, S.; Fisher, B.E.; Pericleous, K.; Gonzalez-Flesca, N. Modelling air quality in street canyons: A review. Atmos. Environ. 2003, 37, 155–182. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R. Linear least squares with linear inequality constraints. Chap 1974, 23, 158–173. [Google Scholar]
- Hanna, S.; Chang, J. Acceptance criteria for urban dispersion model evaluation. Meteorol. Atmos. Phys. 2012, 116, 133–146. [Google Scholar] [CrossRef]
| Bias | RMSE | r | |
| Definition | |||
| Criteria | |||
| FB | NMSE | FAC2 | |
| Definition | Fraction of data that satisfy | ||
| Criteria |
| Type | Station | Bias | FB | RMSE | NMSE | r | FAC2 | ||
|---|---|---|---|---|---|---|---|---|---|
| (g m) | (g m) | (g m) | (g m) | ||||||
| Traffic | A7 | 79.05 | 72.39 | 6.66 | 0.09 | 40.33 | 0.28 | 0.56 | 0.79 |
| BER | 52.50 | 60.14 | 18.77 | 0.11 | 0.81 | 0.92 | |||
| GAR | 74.06 | 61.78 | 12.28 | 0.18 | 26.80 | 0.16 | 0.81 | 0.95 | |
| GC | 47.06 | 43.41 | 3.65 | 0.08 | 19.39 | 0.18 | 0.79 | 0.90 | |
| LP | 50.67 | 54.26 | 23.04 | 0.19 | 0.70 | 0.87 | |||
| VAI | 59.10 | 42.63 | 16.47 | 0.32 | 25.60 | 0.26 | 0.77 | 0.82 | |
| Urban | GER | 38.08 | 39.47 | 9.95 | 0.07 | 0.91 | 0.96 | ||
| LC | 37.95 | 50.87 | −12.92 | 17.82 | 0.16 | 0.90 | 0.87 | ||
| STJ | 36.78 | 45.27 | 17.88 | 0.19 | 0.83 | 0.89 | |||
| VeV | 26.67 | 31.39 | 10.61 | 0.13 | 0.89 | 0.82 | |||
| Industrial | FEY | 33.84 | 34.23 | 12.94 | 0.14 | 0.80 | 0.89 | ||
| STF | 35.35 | 35.59 | 12.50 | 0.12 | 0.88 | 0.93 | |||
| Background | COT | 23.26 | 24.59 | 11.98 | 0.25 | 0.80 | 0.73 | ||
| GEN | 33.36 | 34.73 | 13.22 | 0.15 | 0.80 | 0.86 | |||
| STE | 17.78 | 22.04 | 12.21 | 0.38 | 0.79 | 0.64 | |||
| TER | 29.41 | 26.27 | 3.14 | 0.11 | 11.57 | 0.17 | 0.82 | 0.83 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, C.V.; Soulhac, L.; Salizzoni, P. Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study. Atmosphere 2018, 9, 8. https://doi.org/10.3390/atmos9010008
Nguyen CV, Soulhac L, Salizzoni P. Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study. Atmosphere. 2018; 9(1):8. https://doi.org/10.3390/atmos9010008
Chicago/Turabian StyleNguyen, Chi Vuong, Lionel Soulhac, and Pietro Salizzoni. 2018. "Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study" Atmosphere 9, no. 1: 8. https://doi.org/10.3390/atmos9010008
APA StyleNguyen, C. V., Soulhac, L., & Salizzoni, P. (2018). Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study. Atmosphere, 9(1), 8. https://doi.org/10.3390/atmos9010008






