Estimating the Biogenic Non-Methane Hydrocarbon Emissions over Greece
Abstract
:1. Introduction
2. Methodology
2.1. The Mathematical Model
2.2. The Computational Model
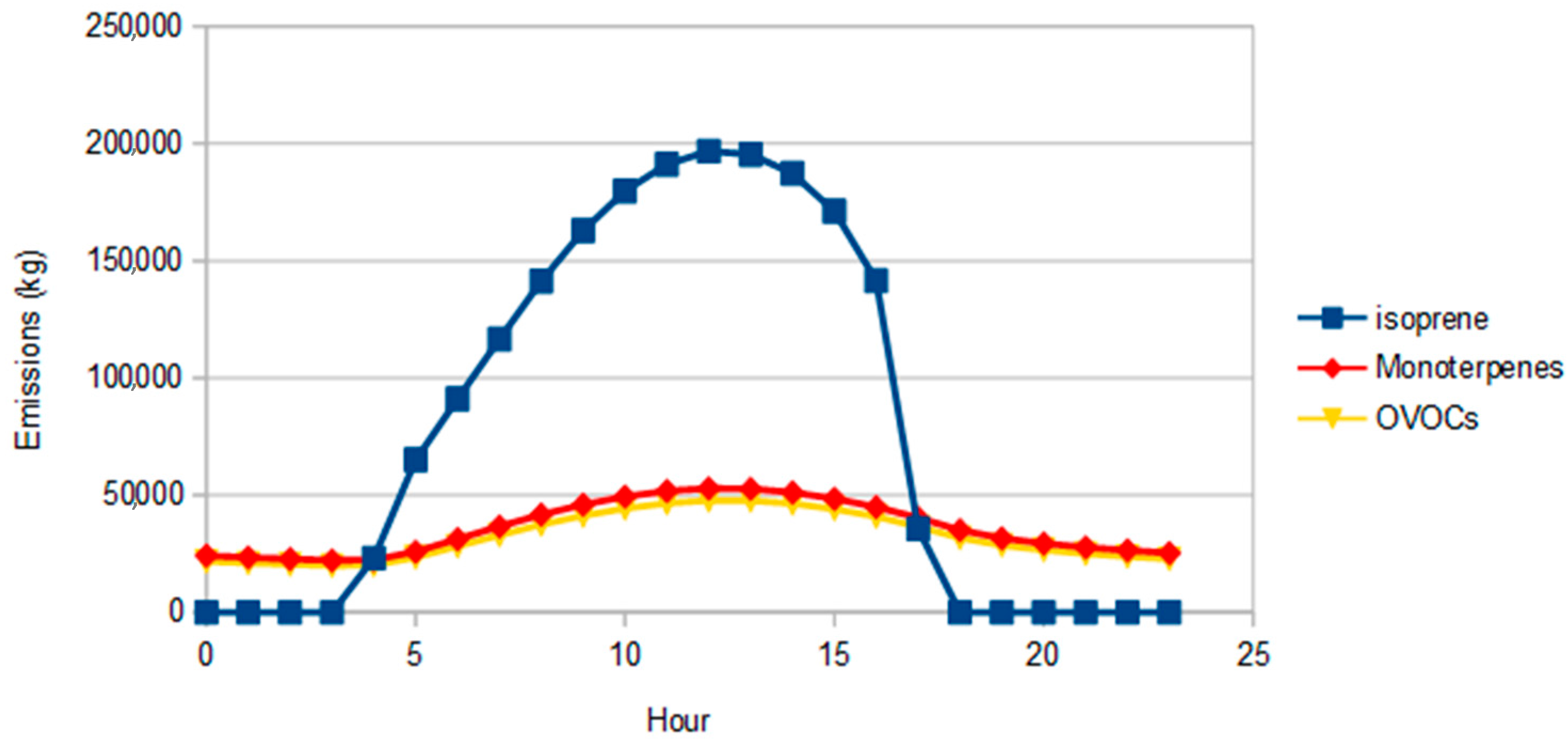
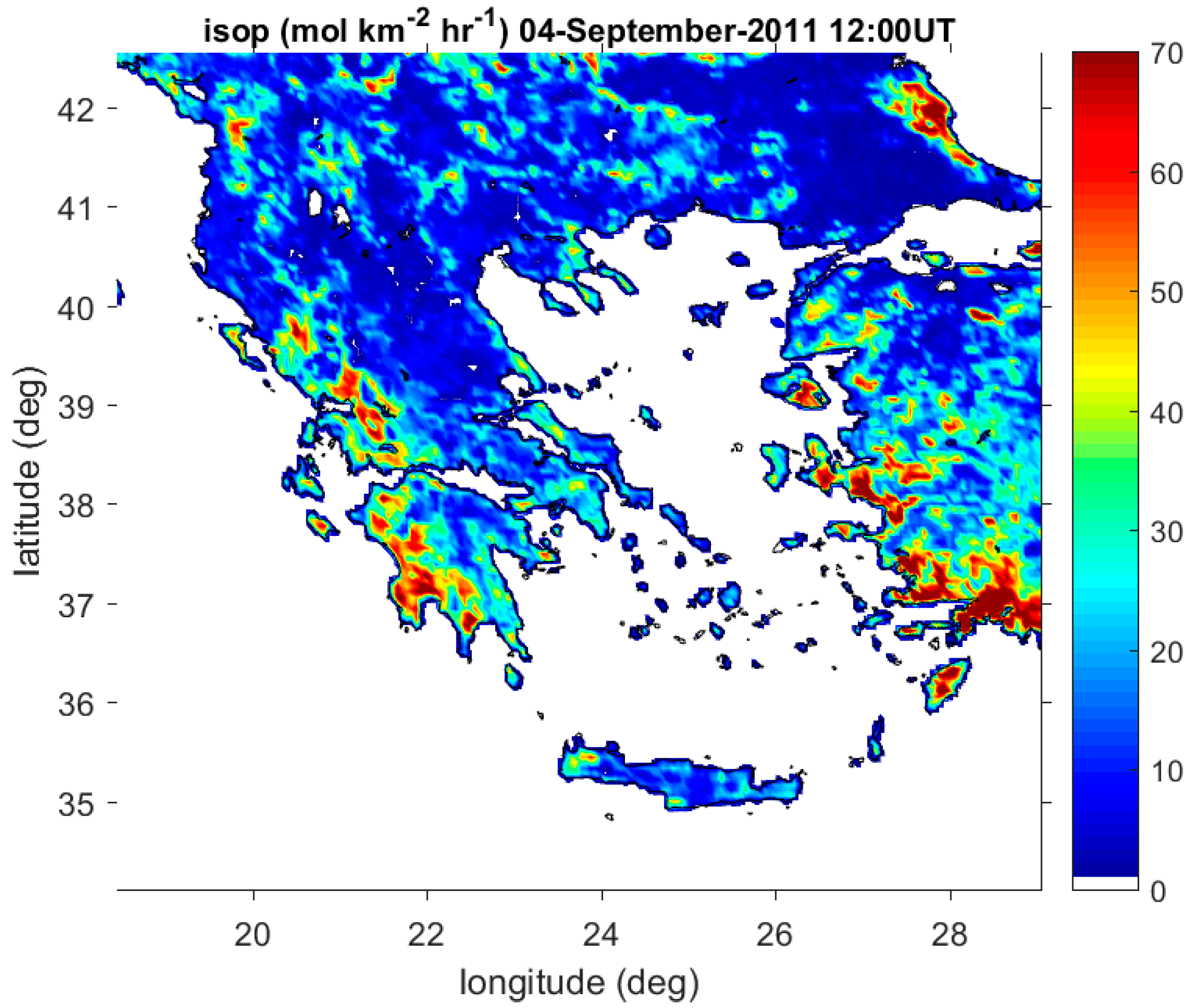
3. Results
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guenther, A.; Hewitt, C.N.; Erickson, D.; Fall, R.; Geron, C.; Graedel, T.; Harley, P.; Klinger, L.; Lerdau, M.; McKay, W. A global model of natural volatile organic compound emissions. J. Geophys. Res. Atmos. 1995, 100, 8873–8892. [Google Scholar] [CrossRef]
- Poupkou, A.; Giannaros, T.; Markakis, K.; Kioutsioukis, I.; Curci, G.; Melas, D.; Zerefos, C. A model for European Biogenic Volatile Organic Compound emissions: Software development and first validation. Environ. Model. Softw. 2010, 31, 45–56. [Google Scholar] [CrossRef]
- Piccot, S.D.; Watson, J.J.; Jones, J.W. A global inventory of volatile organic compound emissions from anthropogenic sources. J. Geophys. Res. Atmos. 1992, 97, 9897–9912. [Google Scholar] [CrossRef]
- Curci, G.; Beekmann, M.; Vautard, R.; Smiatek, G.; Steinbrecher, R.; Theloke, J.; Friedrich, R. Modelling study of the impact of isoprene and terpene biogenic emissions on European ozone levels. Atmos. Environ. 2009, 43, 1444–1455. [Google Scholar] [CrossRef]
- Fameli, K.-M.; Assimakopoulos, V.D. The new open flexible emission inventory for greece and the greater athens area (fei-gregaa): Account of pollutant sources and their importance from 2006 to 2012. Atmos.Environ. 2016, 137, 17–37. [Google Scholar] [CrossRef]
- Geron, C.D.; Guenther, A.B.; Pierce, T.E. An improved model for estimating emissions of volatile organic compounds from forests in the eastern united states. J. Geophys. Res. Atmos. 1994, 99, 12773–12791. [Google Scholar] [CrossRef]
- Naik, V.; Delire, C.; Wuebbles, D.J. Sensitivity of global biogenic isoprenoid emissions to climate variability and atmospheric co2. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Staudt, M.; Seufert, G. Light-dependent emission of monoterpenes by holm oak (Quercus ilex L.). Naturwissenschaften 1995, 82, 89–92. [Google Scholar] [CrossRef]
- Symeonidis, P.; Poupkou, A.; Gkantou, A.; Melas, D.; Yay, O.D.; Pouspourika, E.; Balis, D. Development of a computational system for estimating biogenic nmvocs emissions based on gis technology. Atmos. Environ. 2008, 42, 1777–1789. [Google Scholar] [CrossRef]
- Guenther, A.; Greenberg, J.; Harley, P.; Helmig, D.; Klinger, L.; Vierling, L.; Zimmerman, P.; Geron, C. Leaf, branch, stand and landscape scale measurements of volatile organic compound fluxes from us woodlands. Tree Physiol. 1996, 16, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Bossioli, E.; Tombrou, M.; Karali, A.; Dandou, A.; Paronis, D.; Sofiev, M. Ozone production from the interaction of wildfire and biogenic emissions: A case study in Russia during spring 2006. Atmos. Chem. Phys. 2012, 12, 7931. [Google Scholar] [CrossRef]
- Liakakou, E.; Vrekoussis, M.; Bonsang, B.; Donousis, C.; Kanakidou, M.; Mihalopoulos, N. Isoprene above the Eastern Mediterranean: Seasonal variation and contribution to the oxidation capacity of the atmosphere. Atmos. Environ. 2007, 41, 1002–1010. [Google Scholar] [CrossRef]
- Kaltsonoudis, C.; Kostenidou, E.; Florou, K.; Psichoudaki, M.; Pandis, S.N. Temporal variability and sources of VOCs in urban areas of the eastern Mediterranean. Atmos. Chem. Phys. 2016, 16, 14825. [Google Scholar] [CrossRef]
- Guenther, A.B.; Monson, R.K.; Fall, R. Isoprene and monoterpene emission rate variability: Observations with eucalyptus and emission rate algorithm development. J. Geophys. Res. Atmos. 1991, 96, 10799–10808. [Google Scholar] [CrossRef]
- Guenther, A.; Zimmerman, P.; Wildermuth, M. Natural volatile organic compound emission rate estimates for us woodland landscapes. Atmos. Environ. 1994, 28, 1197–1210. [Google Scholar] [CrossRef]
- Fameli, K.-M.; Assimakopoulos, V.D.; Kotroni, V. A Modelling Study of the Photochemical and Particulate Pollution Characteristics above a Typical Southeast Mediterranean Urban Area; Institute for Environmental Research and Sustainable Development: Thessaloniki, Greece, 2015; p. 36. [Google Scholar]
- Steinbrecher, R.; Smiatek, G.; Köble, R.; Seufert, G.; Theloke, J.; Hauff, K.; Ciccioli, P.; Vautard, R.; Curci, G. Intra-and inter-annual variability of voc emissions from natural and semi-natural vegetation in europe and neighbouring countries. Atmos. Environ. 2009, 43, 1380–1391. [Google Scholar] [CrossRef]
- Taylor, M.; Kosmopoulos, P.; Kazadzis, S.; Keramitsoglou, I.; Kiranoudis, C. Neural network radiative transfer solvers for the generation of high resolution solar irradiance spectra parameterized by cloud and aerosol parameters. J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 176–192. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Raptis, P.I.; Keramitsoglou, I.; Kiranoudis, C.; Bais, A.F. Assessment of surface solar irradiance derived from real-time modelling techniques and verification with ground-based measurements. Atmos. Meas. Tech. Discuss. 2017. [Google Scholar] [CrossRef]
- Simpson, D.; Winiwarter, W.; Börjesson, G.; Cinderby, S.; Ferreiro, A.; Guenther, A.; Hewitt, C.N.; Janson, R.; Khalil, M.A.K.; Owen, S. Inventorying emissions from nature in europe. J. Geophys. Res. Atmos. 1999, 104, 8113–8152. [Google Scholar] [CrossRef]
- Bossioli, E.; Tombrou, M.; Kalogiros, J.; Allan, J.; Bacak, A.; Bezantakos, S.; Mihalopoulos, N. Atmospheric composition in the Eastern Mediterranean: Influence of biomass burning during summertime using the WRF-Chem model. Atmos. Environ. 2016, 132, 317–331. [Google Scholar] [CrossRef]
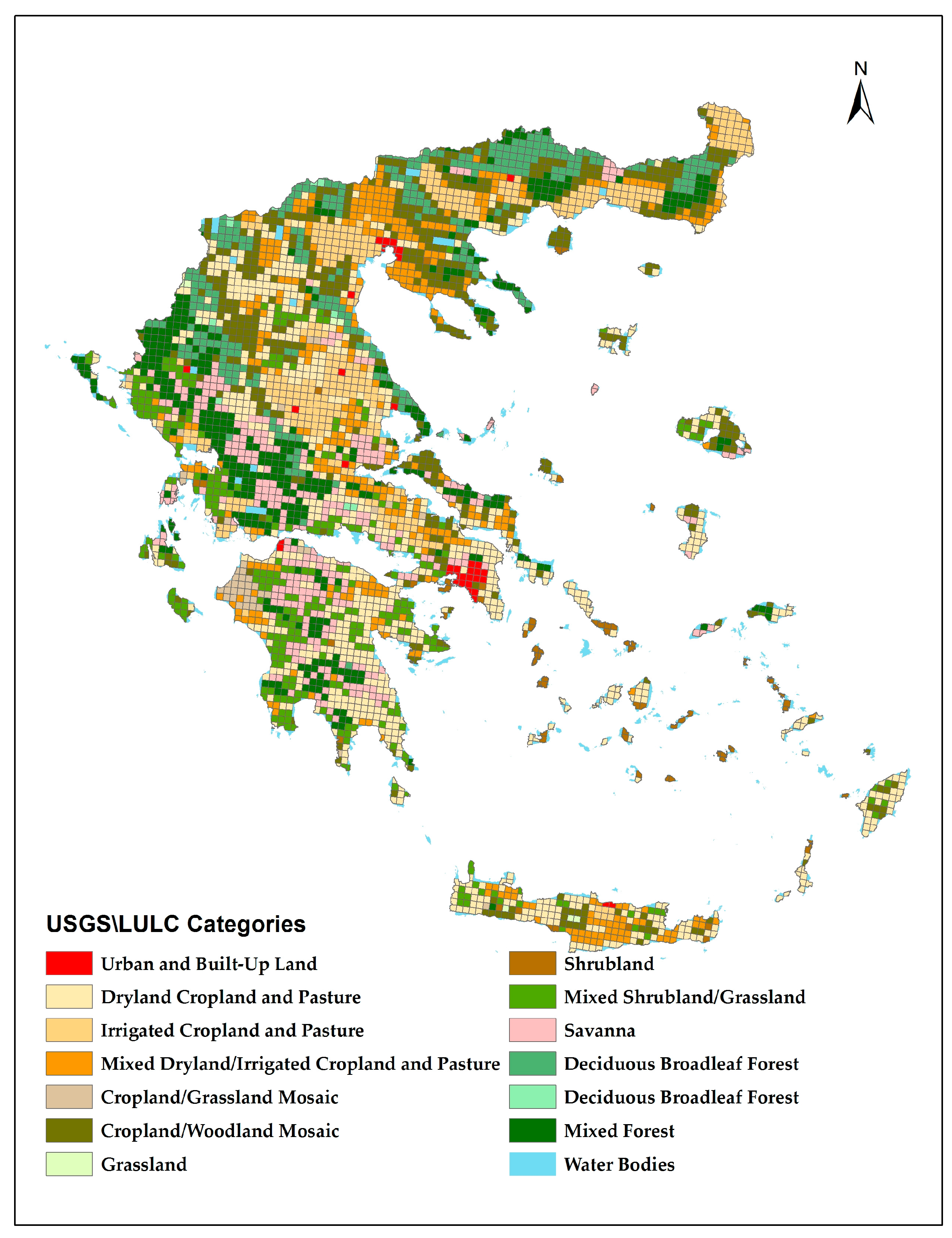
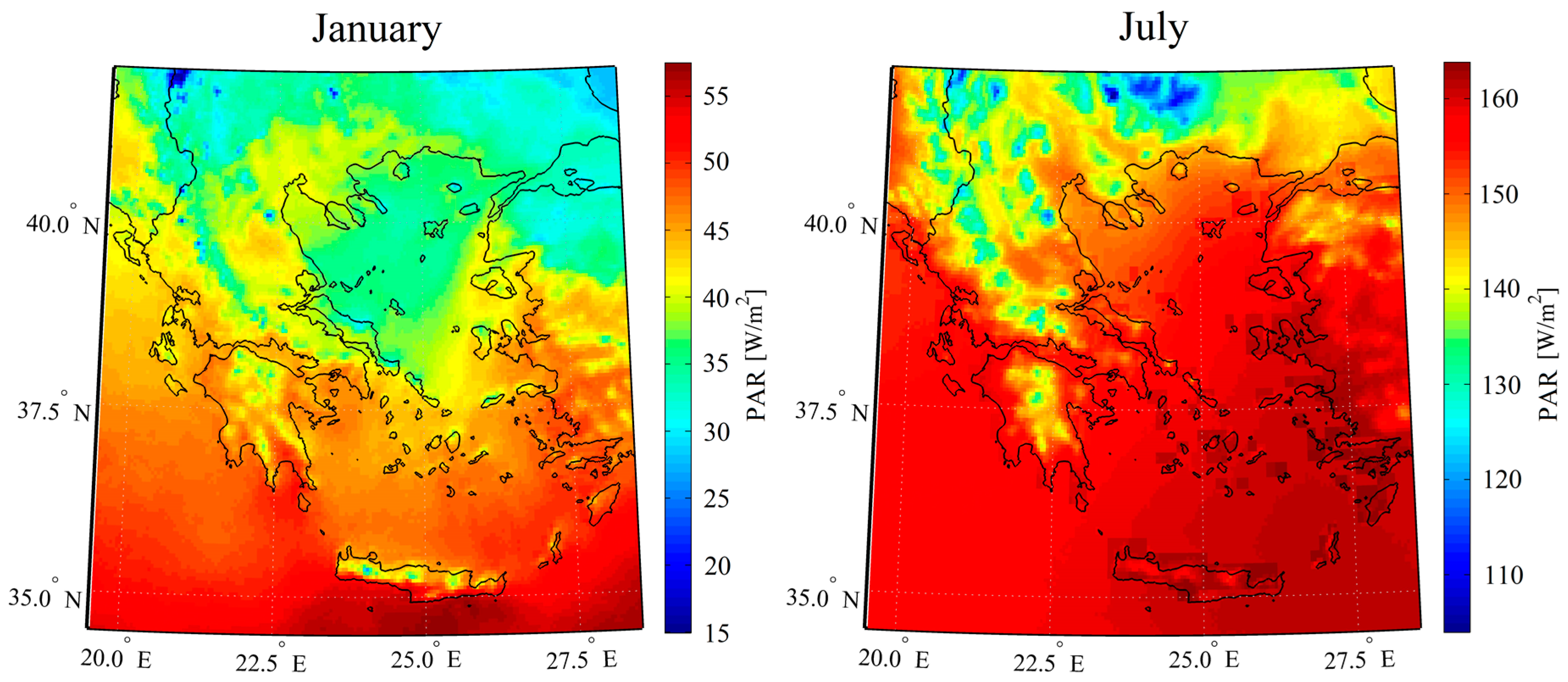
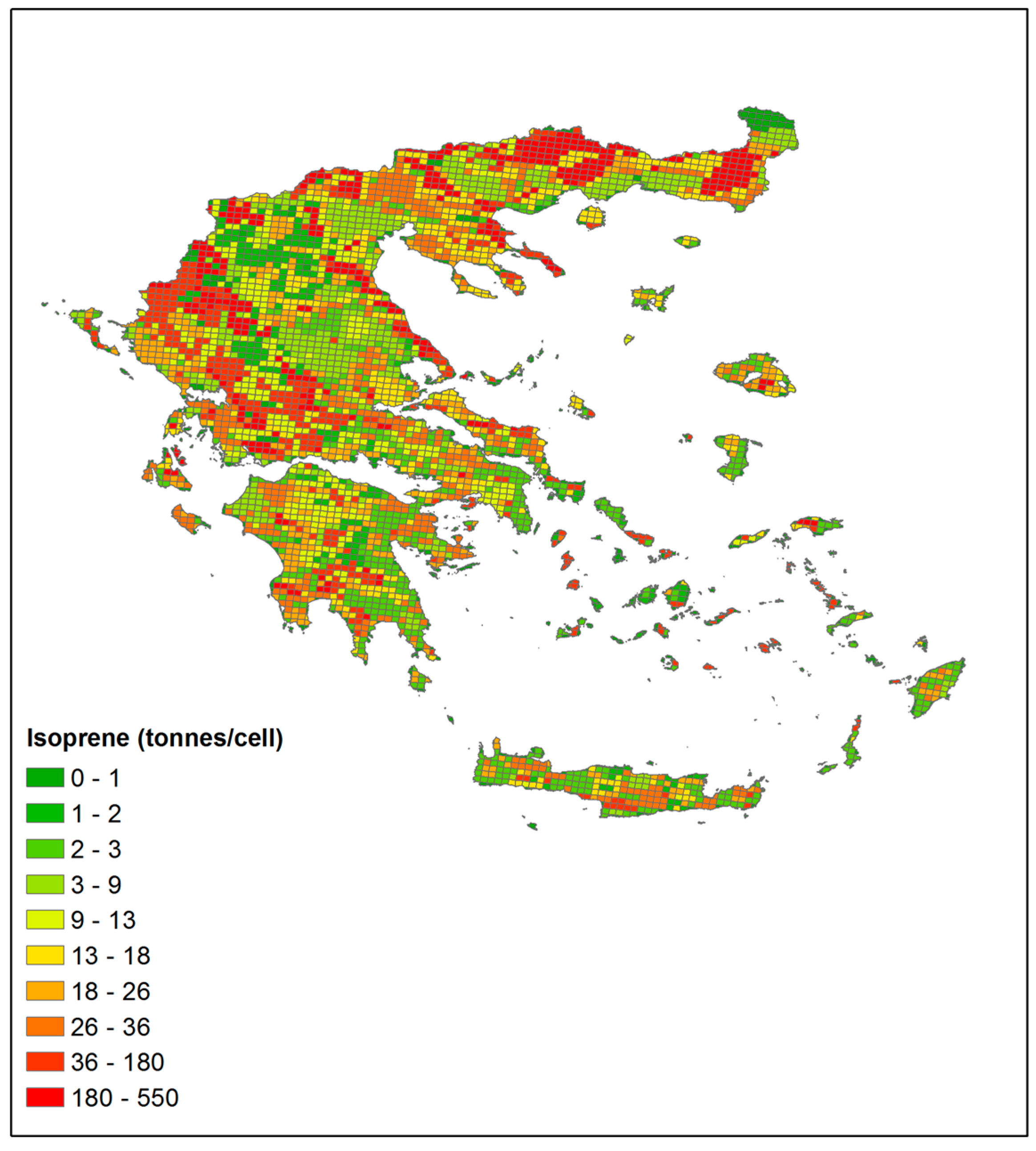
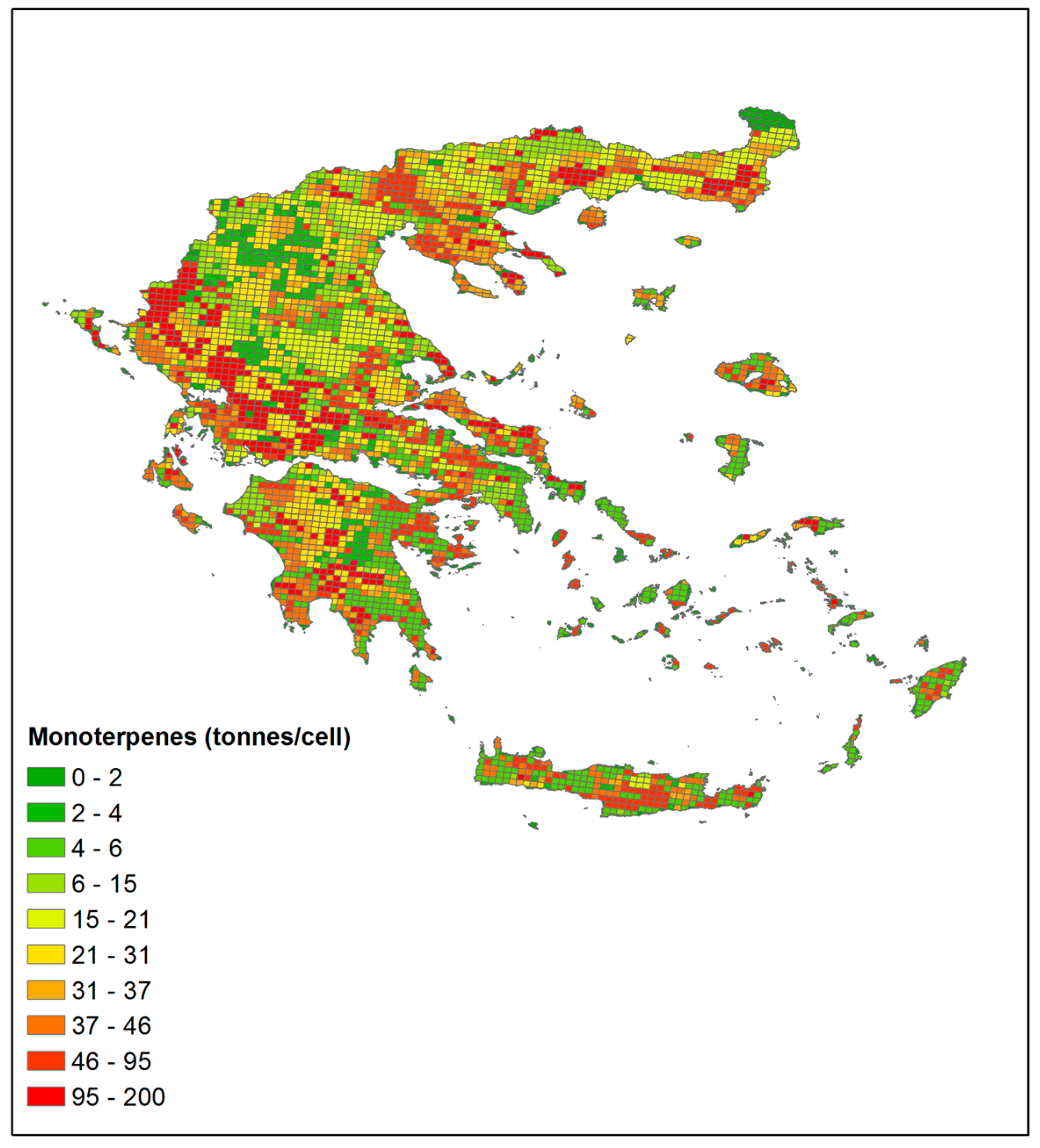
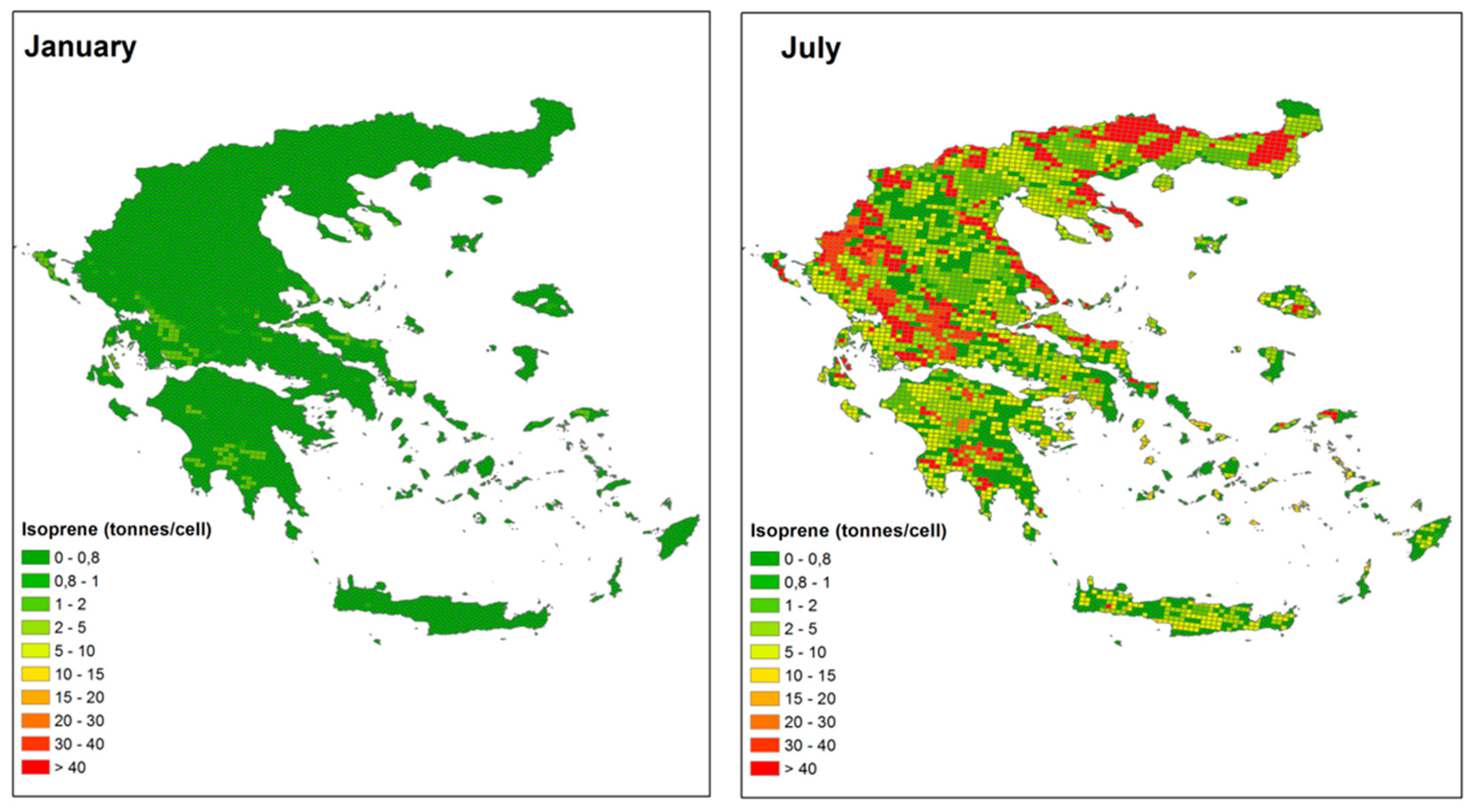
| Land-Use Category | January | July | ||||
|---|---|---|---|---|---|---|
| Foliar Biomass Density | Isoprene Emission Potential | Monoterpene Emission Potential | Foliar Biomass Density | Isoprene Emission Potential | Monoterpene Emission Potential | |
| Urban and Built-Up Land | 50 | 2 | 1 | 100 | 2 | 1 |
| Dryland Cropland and Pasture | 25 | 0.5 | 0.5 | 100 | 0.5 | 0.5 |
| Irrigated Cropland and Pasture | 300 | 0.5 | 0.5 | 300 | 0.5 | 0.5 |
| Mixed Dryland–Irrigated Cropland and Pasture | 194 | 1.1 | 0.95 | 325 | 1.85 | 1.56 |
| Cropland–Grassland Mosaic | 156 | 0.5 | 0.5 | 175 | 0.5 | 0.5 |
| Cropland/Woodland Mosaic | 200 | 1.6 | 1.6 | 200 | 1.63 | 1.63 |
| Grassland | 12.5 | 0.5 | 0.5 | 50 | 0.5 | 0.5 |
| Shrubland | 87.5 | 3 | 2.5 | 350 | 3 | 2.5 |
| Mixed Shrubland–Grassland | 50 | 2.69 | 2.25 | 200 | 2.69 | 2.25 |
| Savanna | 56.3 | 4.5 | 4.5 | 75 | 3.5 | 3.5 |
| Deciduous Broadleaf Forest | 0 | 30 | 0.5 | 340 | 30 | 0.5 |
| Evergreen Needleleaf Forest | 700 | 1 | 2.5 | 700 | 1 | 2.5 |
| Mixed Forest | 250 | 7 | 3 | 500 | 7 | 3 |
| Water Bodies | 0 | 0 | 0 | 0 | 0 | 0 |
| Month | Isoprene | Monoterpene | OVOCs |
|---|---|---|---|
| January | 10.5 | 46.8 | 42.7 |
| February | 14.4 | 44.5 | 41.1 |
| March | 24.8 | 39.1 | 36.1 |
| April | 38.0 | 32.4 | 29.6 |
| May | 44.2 | 29.3 | 26.5 |
| June | 52.0 | 25.1 | 22.9 |
| July | 53.6 | 24.4 | 22.0 |
| August | 52.3 | 25.1 | 22.6 |
| September | 44.7 | 29.1 | 26.2 |
| October | 30.7 | 36.5 | 32.8 |
| November | 22.0 | 41.2 | 36.8 |
| December | 10.3 | 47.0 | 42.7 |
| Time (UT) | Mitilene Island | Mount Parnitha | Kalamata | |||
|---|---|---|---|---|---|---|
| MEGAN | This Work | MEGAN | This Work | MEGAN | This Work | |
| 5:00 | 0.4517 | 2.9428 | 0.1052 | 1.6083 | 0.2400 | 1.7286 |
| 6:00 | 1.1784 | 4.4107 | 0.3770 | 2.6558 | 0.8125 | 2.8487 |
| 7:00 | 1.9918 | 5.7848 | 0.6786 | 3.3429 | 1.3987 | 3.6122 |
| 8:00 | 2.9012 | 6.8139 | 0.9886 | 3.8856 | 2.0378 | 4.2774 |
| 9:00 | 3.7761 | 7.7954 | 1.2923 | 4.3828 | 2.5964 | 4.8008 |
| 10:00 | 4.4177 | 8.6426 | 1.4921 | 4.7437 | 2.9047 | 5.1691 |
| 11:00 | 4.7303 | 9.2528 | 1.5702 | 4.9988 | 2.9818 | 5.2909 |
| 12:00 | 4.5271 | 9.3756 | 1.4915 | 4.8454 | 2.6724 | 5.2071 |
| 13:00 | 3.9158 | 9.3631 | 1.3166 | 4.7316 | 2.0577 | 5.0542 |
| 14:00 | 2.8421 | 8.6822 | 0.9882 | 4.3925 | 1.5332 | 4.5949 |
| 15:00 | 1.4652 | 6.7755 | 0.5508 | 3.4415 | 0.9130 | 3.6578 |
| 16:00 | 0.3887 | 0.6073 | 0.1916 | 0.5165 | 0.3537 | 0.5730 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitropoulou, E.; Assimakopoulos, V.D.; Fameli, K.M.; Flocas, H.A.; Kosmopoulos, P.; Kazadzis, S.; Lagouvardos, K.; Bossioli, E. Estimating the Biogenic Non-Methane Hydrocarbon Emissions over Greece. Atmosphere 2018, 9, 14. https://doi.org/10.3390/atmos9010014
Dimitropoulou E, Assimakopoulos VD, Fameli KM, Flocas HA, Kosmopoulos P, Kazadzis S, Lagouvardos K, Bossioli E. Estimating the Biogenic Non-Methane Hydrocarbon Emissions over Greece. Atmosphere. 2018; 9(1):14. https://doi.org/10.3390/atmos9010014
Chicago/Turabian StyleDimitropoulou, Ermioni, Vasiliki D. Assimakopoulos, Kyriaki M. Fameli, Helena A. Flocas, Panagiotis Kosmopoulos, Stelios Kazadzis, Kostas Lagouvardos, and Elizabeth Bossioli. 2018. "Estimating the Biogenic Non-Methane Hydrocarbon Emissions over Greece" Atmosphere 9, no. 1: 14. https://doi.org/10.3390/atmos9010014
APA StyleDimitropoulou, E., Assimakopoulos, V. D., Fameli, K. M., Flocas, H. A., Kosmopoulos, P., Kazadzis, S., Lagouvardos, K., & Bossioli, E. (2018). Estimating the Biogenic Non-Methane Hydrocarbon Emissions over Greece. Atmosphere, 9(1), 14. https://doi.org/10.3390/atmos9010014










