Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method
Abstract
1. Introduction
2. Methodology
2.1. Turbulence Models for Urban Airflow Modeling
2.2. Model Description in the CFD Validation Case
2.3. Model Description in All CFD Test Cases
2.4. ACH Indexes and Age of Air by Concentration Decay Method
2.4.1. Volumetric Flow Rates and the Corresponding ACH [23,37,38,39,40,41,42]
2.4.2. Actual or Net ACH and Urban Age of Air by the Concentration Decay Method
3. Results and Discussion
3.1. Evaluation of CFD Simulations Using Wind Tunnel Data
3.2. Flow and Concentration Decay in an Example Case [5-5, 0°] (θ = 0°)
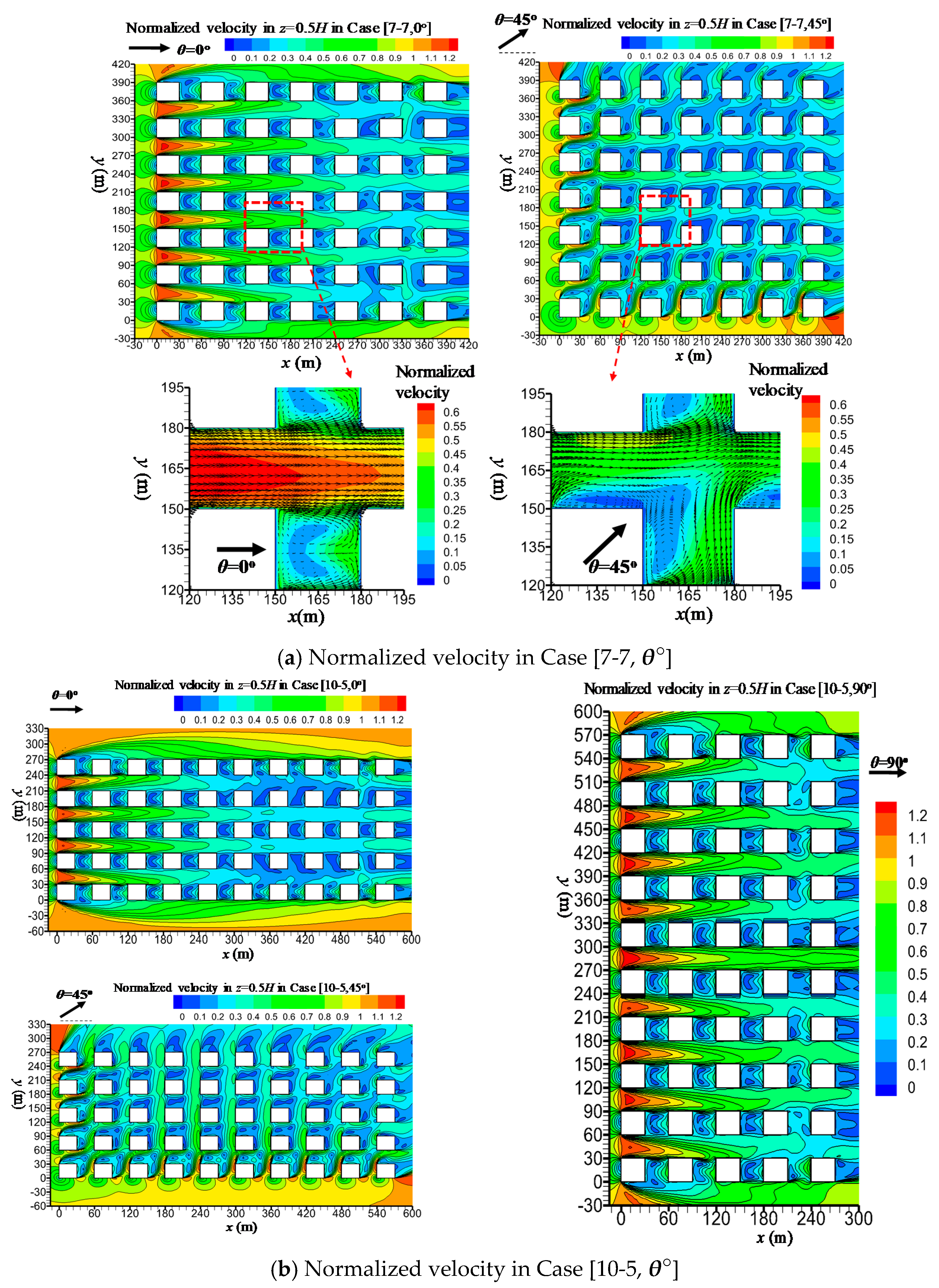
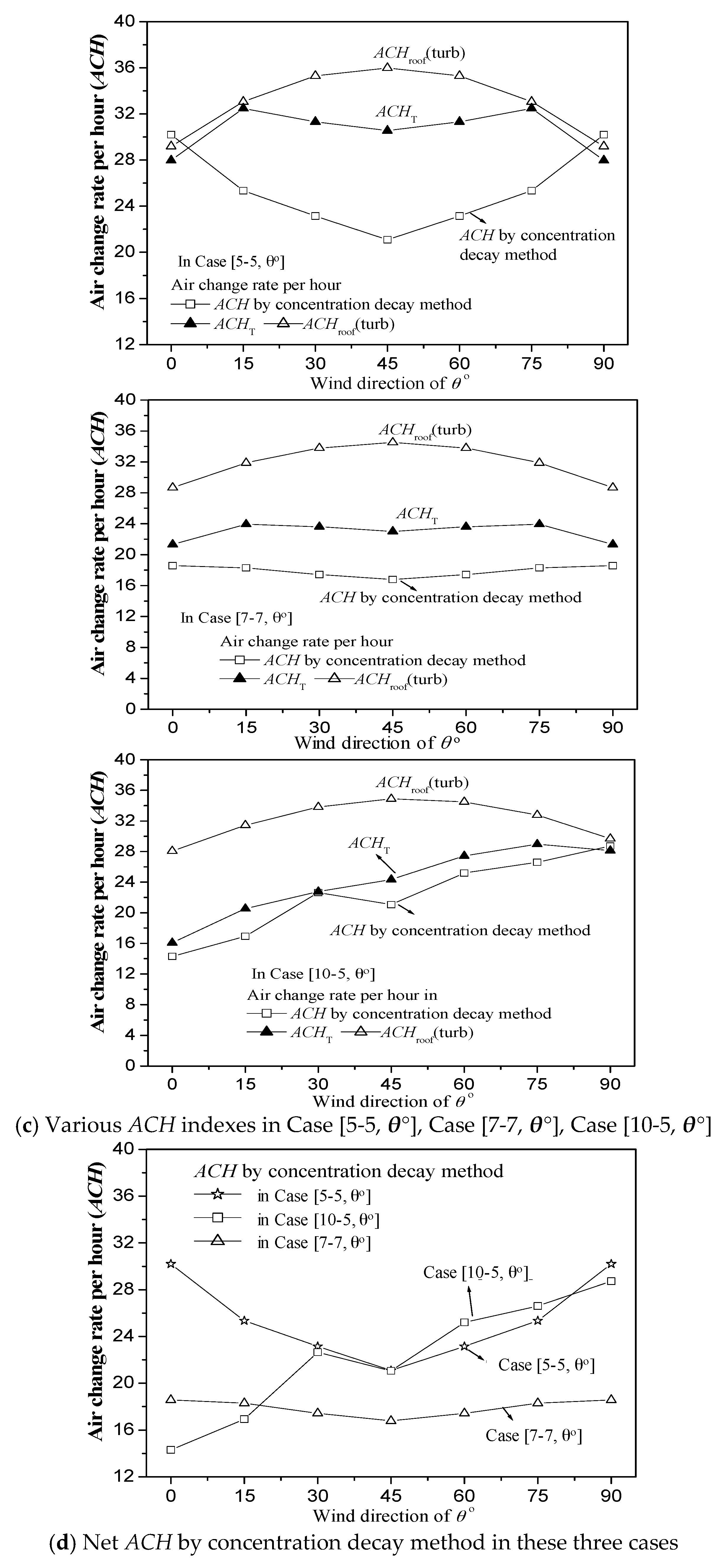
3.3. Effect of Overall Urban Form and Ambient Wind Direction on UCL Ventilation
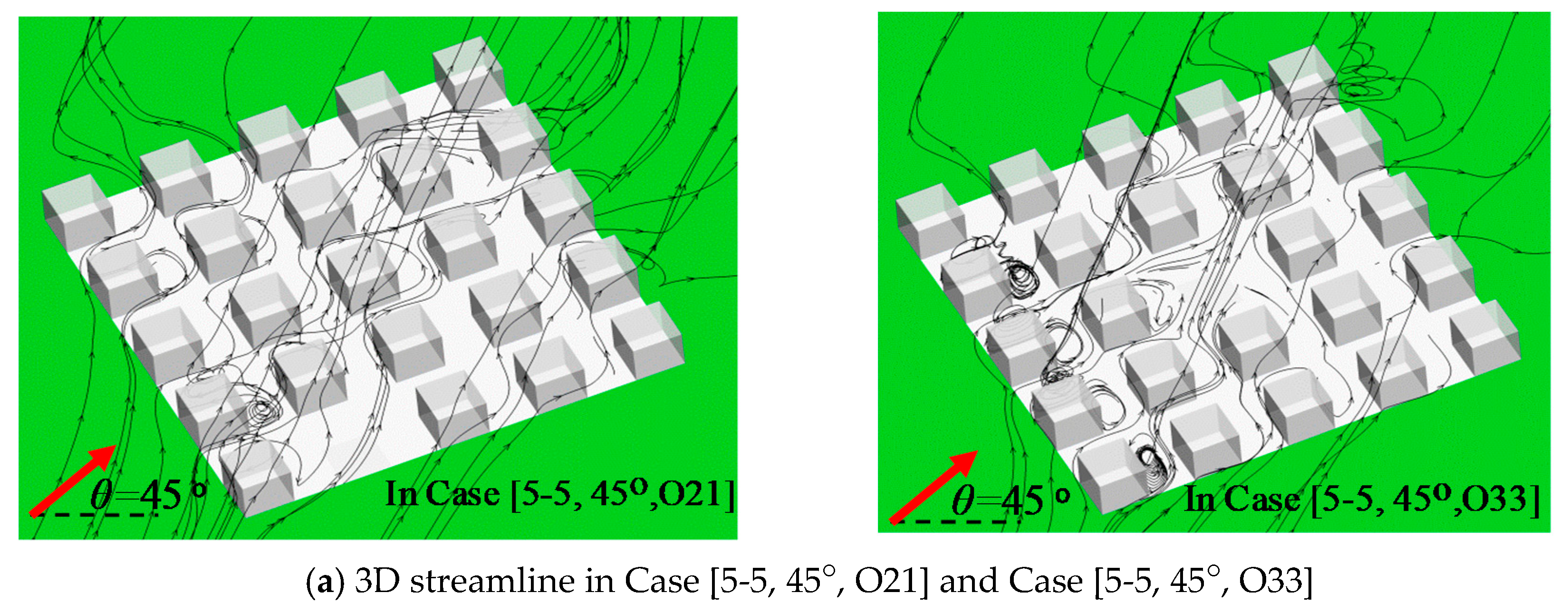
3.4. Effect of Open Space Arrangements and Ambient Wind Direction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | area of a surface (m2) |
| ACH | air change rate per hour by concentration decay method |
| ACHT | ACH calculated by QT for entire UCL volume |
| ACHturb | ACH calculated by Qroof(turb) for entire UCL volume |
| B, H, L, W | building width, building height, total length, street width |
| C, <C> | time-averaged pollutant concentration and its spatial mean value |
| , | turbulent eddy diffusivity of pollutant and momentum |
| λp | building area density (or plan area index) |
| λf | frontal area density (or frontal area index) |
| k, ε | turbulent kinetic energy and its dissipation rate |
| normal direction of street openings or canopy roofs | |
| Q | flow rate through street openings or street roofs |
| Qin, Qout | total inflow and outflow rate by mean flows across UCL boundaries |
| QT | total ventilation flow rate by mean flows |
| Qroof(turb) | effective flow rate across street roofs by turbulence |
| Sct | turbulent Schmidt number |
| fluctuation velocity on street roofs | |
| age of air (s) | |
| U0(z) | velocity profiles used at CFD domain inlet for ventilation cases |
| Uref | reference velocity at z = H at the domain inlet |
| , | velocity and coordinate components |
| velocity vector | |
| Vol | control volume |
| x, y, z | stream-wise, span-wise, vertical directions |
| , , | stream-wise, lateral, vertical velocity components |
| u′, v′, w′ | stream-wise, lateral, vertical velocity fluctuations |
References
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Methuen Publishing: London, UK, 1987; p. 289. [Google Scholar]
- Bady, M.; Kato, S.; Huang, H. Towards the application of indoor ventilation efficiency indices to evaluate the air quality of urban areas. Build. Environ. 2008, 43, 1991–2004. [Google Scholar] [CrossRef]
- Hang, J.; Sandberg, M.; Li, Y.G. Age of air and air exchange efficiency in idealized city models. Build. Environ. 2009, 44, 1714–1723. [Google Scholar] [CrossRef]
- Buccolieri, R.; Sandberg, M.; Di Sabatino, S. City breathability and its link to pollutant concentration distribution within urban-like geometries. Atmos. Environ. 2010, 44, 1894–1903. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.G. Age of air and air exchange efficiency in high-rise urban areas. Atmos. Environ. 2011, 45, 5572–5585. [Google Scholar] [CrossRef]
- Ramponi, R.; Blocken, B.; Laura, B.; Janssen, W.D. CFD simulation of outdoor ventilation of generic urban configurations with different urban densities and equal and unequal street widths. Build. Environ. 2015, 92, 152–166. [Google Scholar] [CrossRef]
- Hang, J.; Luo, Z.W.; Sandberg, M.; Gong, J. Natural ventilation assessment in typical open and semi-open urban environments under various wind directions. Build. Environ. 2013, 70, 318–333. [Google Scholar] [CrossRef]
- Kim, J.J. Assessment of observation environment for surface wind in urban areas using a CFD model. Atmosphere 2015, 25, 449–459. (In Korean) [Google Scholar]
- Ashie, Y.; Kono, T. Urban-scale CFD analysis in support of a climate-sensitive design for the Tokyo Bay area. Int. J. Climatol. 2011, 31, 174–188. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.G. The impact of building density and building height heterogeneity on average urban albedo and street surface temperature. Build. Environ. 2015, 90, 146–156. [Google Scholar] [CrossRef]
- Hang, J.; Luo, Z.; Wang, X.; He, L.; Wang, B.; Zhu, W. The influence of street layouts and viaduct settings on daily CO exposure and intake fraction in idealized urban canyons. Environ. Pollut. 2017, 220, 72–86. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Li, Y.G.; Nazaroff, W.W. Intake fraction of nonreactive motor vehicle exhaust in Hong Kong. Atmos. Environ. 2010, 44, 1913–1918. [Google Scholar] [CrossRef]
- Ng, W.; Chau, C. A modeling investigation of the impact of street and building configurations on personal air pollutant exposure in isolated deep urban canyons. Sci. Total Environ. 2014, 468, 429–448. [Google Scholar] [CrossRef] [PubMed]
- Meroney, R.N.; Pavegeau, M.; Rafailidis, S.; Schatzmann, M. Study of line source characteristics for 2-D physical modelling of pollutant dispersion in street canyons. J. Wind Eng. Ind. Aerodyn. 1996, 62, 37–56. [Google Scholar] [CrossRef]
- Li, X.X.; Liu, C.H.; Leung, D.Y.C.; Lam, K.M. Recent progress in CFD modelling of wind field and pollutant transport in street canyons. Atmos. Environ. 2006, 40, 5640–5658. [Google Scholar] [CrossRef]
- Li, X.X.; Liu, C.H.; Leung, D.Y.C. Numerical investigation of pollutant transport characteristics inside deep urban street canyons. Atmos. Environ. 2009, 43, 2410–2418. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Gu, Z.; Lee, S.C.; Fu, T.M.; Ho, K.F. Numerical simulation and in situ investigation of fine particle dispersion in an actual deep street canyon in Hong Kong. Indoor Built Environ. 2011, 20, 206–216. [Google Scholar] [CrossRef]
- Lin, L.; Hang, J.; Wang, X.X.; Wang, X.M.; Fan, S.J.; Fan, Q.; Liu, Y.H. Integrated effects of street layouts and wall heating on vehicular pollutant dispersion and their reentry into downstream canyons. Aerosol Air Qual. Res. 2016, 16, 3142–3163. [Google Scholar] [CrossRef]
- Dong, J.L.; Tan, Z.J.; Xiao, X.M.; Tu, J.Y. Seasonal changing effect on airflow and pollutant dispersion characteristics in urban street canyons. Atmosphere 2017, 8, 43. [Google Scholar] [CrossRef]
- Gu, Z.; Zhang, Y.; Cheng, Y.; Lee, S.C. Effect of uneven building layout on air flow and pollutant dispersion in non-uniform street canyons. Build. Environ. 2011, 46, 2657–2665. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.; Sandberg, M.; Buccolieri, R.; Di Sabatino, S. The influence of building height variability on pollutant dispersion and pedestrian ventilation in idealized high-rise urban areas. Build. Environ. 2012, 56, 346–360. [Google Scholar] [CrossRef]
- Panagiotou, I.; Neophytou, M.K.A.; Hamlyn, D.; Britter, R.E. City breathability as quantified by the exchange velocity and its spatial variation in real inhomogeneous urban geometries: An example from central London urban area. Sci. Total Environ. 2013, 442, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Hang, J.; Li, Y.G.; Luo, Z.W.; Sandberg, M. Quantitative ventilation assessments of idealized urban canopy layers with various urban layouts and the same building packing density. Build. Environ. 2014, 79, 152–167. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.J. A study on the characteristics of flow and reactive pollutants’ dispersion in step-up street canyons using a CFD model. Atmosphere 2015, 25, 473–482. (In Korean) [Google Scholar] [CrossRef]
- Chen, L.; Hang, J.; Sandberg, M.; Claesson, L.; Di Sabatino, S.; Wigo, H. The impacts of building height variations and building packing densities on flow adjustment and city breathability in idealized urban models. Build. Environ. 2017, 118, 344–361. [Google Scholar] [CrossRef]
- Li, X.X.; Britter, R.E.; Norford, L.K. Transport processes in and above two-dimensional urban street canyons under different stratification conditions: results from numerical simulation. Environ. Fluid Mech. 2015, 15, 399–417. [Google Scholar] [CrossRef]
- Nazarian, N.; Kleissl, J. Realistic solar heating in urban areas: Air exchange and street-canyon ventilation. Build. Environ. 2016, 95, 75–93. [Google Scholar] [CrossRef]
- Cui, P.Y.; Li, Z.; Tao, W.Q. Wind-tunnel measurements for thermal effects on the air flow and pollutant dispersion through different scale urban areas. Build. Environ. 2016, 97, 137–151. [Google Scholar] [CrossRef]
- Wang, X.X.; Li, Y.G. Predicting urban heat island circulation using CFD. Build. Environ. 2016, 99, 82–97. [Google Scholar] [CrossRef]
- Fan, Y.F.; Hunt, J.C.R.; Li, Y.G. Buoyancy and turbulence-driven atmospheric circulation over urban areas. J. Environ. Sci. 2017. [Google Scholar] [CrossRef]
- Hang, J.; Wang, Q.; Chen, X.Y.; Sandberg, M.; Zhu, W.; Buccolieri, R.; Di Sabatino, S. City breathability in medium density urban-like geometries evaluated through the pollutant transport rate and the net escape velocity. Build. Environ. 2015, 94, 166–182. [Google Scholar] [CrossRef]
- Etheridge, D.; Sandberg, M. Building Ventilation: Theory and Measurement; John Wiley & Sons: New York, NY, USA, 1996; pp. 573–633. [Google Scholar]
- Lim, E.S.; Ito, K.; Sandberg, M. New ventilation index for evaluating imperfect mixing conditions—Analysis of Net Escape Velocity based on RANS approach. Build. Environ. 2013, 61, 45–56. [Google Scholar] [CrossRef]
- Li, J.Q.; Ward, I.C. Developing computational fluid dynamics conditions for urban natural ventilation study. In Proceedings of the Building Simulation, Beijing, China, 3–6 September 2007. [Google Scholar]
- Zaki, S.A.; Hagishima, A.; Tanimoto, J. Experimental study of wind-induced ventilation in urban building of cube arrays with various layouts. J. Wind Eng. Ind. Aerodyn. 2012, 103, 31–40. [Google Scholar] [CrossRef]
- Padilla-Marcos, M.Á.; Meiss, A.; Feijó-Muñoz, J. Proposal for a simplified CFD procedure for obtaining patterns of the age of air in outdoor spaces for the natural ventilation of buildings. Energies 2017, 10, 1252. [Google Scholar] [CrossRef]
- Li, X.X.; Liu, C.H.; Leung, D.Y.C. Development of a k-ε model for the determination of air exchange rates for street canyons. Atmos. Environ. 2005, 39, 7285–7296. [Google Scholar] [CrossRef]
- Liu, C.H.; Leung, D.Y.C.; Barth, M.C. On the prediction of air and pollutant exchange rates in street canyons of different aspect ratio using large-eddy simulation. Atmos. Environ. 2005, 39, 1567–1574. [Google Scholar] [CrossRef]
- Moonen, P.; Dorer, D.; Carmeliet, J. Evaluation of the ventilation potential of courtyards and urban street canyons using RANS and LES. J. Wind Eng. Ind. Aerodyn. 2011, 99, 414–423. [Google Scholar] [CrossRef]
- Hang, J.; Sandberg, M.; Li, Y. Effect of urban morphology on wind condition in idealized city models. Atmos. Environ. 2009, 43, 869–878. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.G. Ventilation strategy and air change rates in idealized high-rise compact urban areas. Build. Environ. 2010, 45, 2754–2767. [Google Scholar] [CrossRef]
- Liu, J.; Luo, Z.; Zhao, J.; Shui, T. Ventilation in a street canyon under diurnal heating conditions. Int. J. Vent. 2012, 11, 141–154. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.G. City ventilation of Hong Kong at no-wind conditions. Atmos. Environ. 2009, 43, 3111–3121. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.G. Thermal conditions and ventilation in an ideal city model of Hong Kong. Energy Build. 2011, 43, 1139–1148. [Google Scholar] [CrossRef]
- Gao, N.P.; Niu, J.L.; Perino, M.; Heiselberg, P. The airborne transmission of infection between flats in high-rise residential buildings: Tracer gas simulation. Build. Environ. 2008, 43, 1805–1817. [Google Scholar] [CrossRef]
- Hooff, V.T.; Blocken, B. CFD evaluation of natural ventilation of indoor environments by the concentration decay method: CO2 gas dispersion from a semi-enclosed stadium. Build. Environ. 2013, 61, 1–17. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Zajic, D.; Di Sabatino, S.; Dimitrova, R.; Hedquist, B.; Dallman, A. Flow, turbulence, and pollutant dispersion in urban atmospheres. Phys. Fluids 2010, 22, 051301. [Google Scholar] [CrossRef]
- Di Sabatino, S.; Buccolieri, R.; Salizzoni, P. Recent advancements in numerical modelling of flow and dispersion in urban areas: a short review. Int. J. Environ. Pollut. 2013, 52, 172–191. [Google Scholar] [CrossRef]
- Blocken, B. Computational fluid dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Brown, M.J.; Lawson, R.E.; DeCroix, D.S.; Lee, R.L. Comparison of Centerline Velocity Measurements Obtained Around 2D and 3D Buildings Arrays in a Wind Tunnel; Report LA-UR-01–4138; Los Alamos National Laboratory: Los Alamos, NM, USA, 2001; p. 7.
- Lien, F.S.; Yee, E. Numerical modelling of the turbulent flow developing within and over a 3-D building array, part I: A high-resolution Reynolds-averaged Navier-Stokes approach. Bound. Layer Meteorol. 2004, 112, 427–466. [Google Scholar] [CrossRef]
- Santiago, J.L.; Martilli, A.; Martin, F. CFD simulation of airflow over a regular array of cubes Part I: Three-dimensional simulation of the flow and validation with wind-tunnel measurements. Bound. Layer Meteorol. 2007, 122, 609–634. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.G. Wind conditions in idealized building clusters: Macroscopic simulations by a porous turbulence model. Bound. Layer Meteorol. 2010, 136, 129–159. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, H.; Carissimo, B. The COST732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Inter. J. Environ. Pollut. 2011, 44, 419–427. [Google Scholar] [CrossRef]
- FLUENT V6.3. User’s Manual. Available online: http://www.fluent.com (accessed on 20 August 2017).
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Kim, J.J.; Baik, J.J. A numerical study of the effects of ambient wind direction on flow and dispersion in urban street canyons using the RNG k-ε turbulence model. Atmos. Environ. 2004, 38, 3039–3048. [Google Scholar] [CrossRef]
- Kanda, M. Large-eddy simulations on the effects of surface geometry of building arrays on turbulent organized structures. Bound. Layer Meteorol. 2006, 18, 151–168. [Google Scholar] [CrossRef]
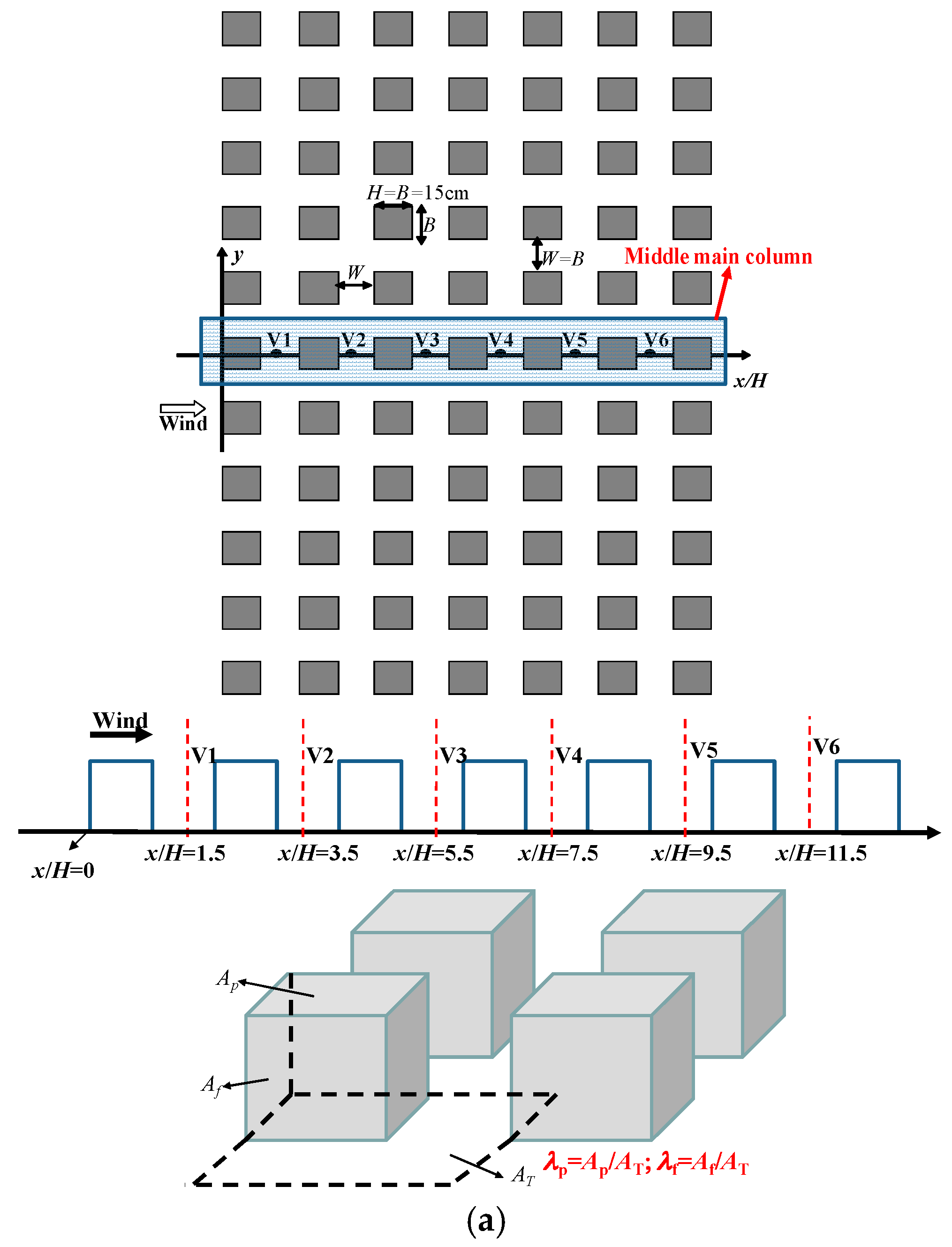
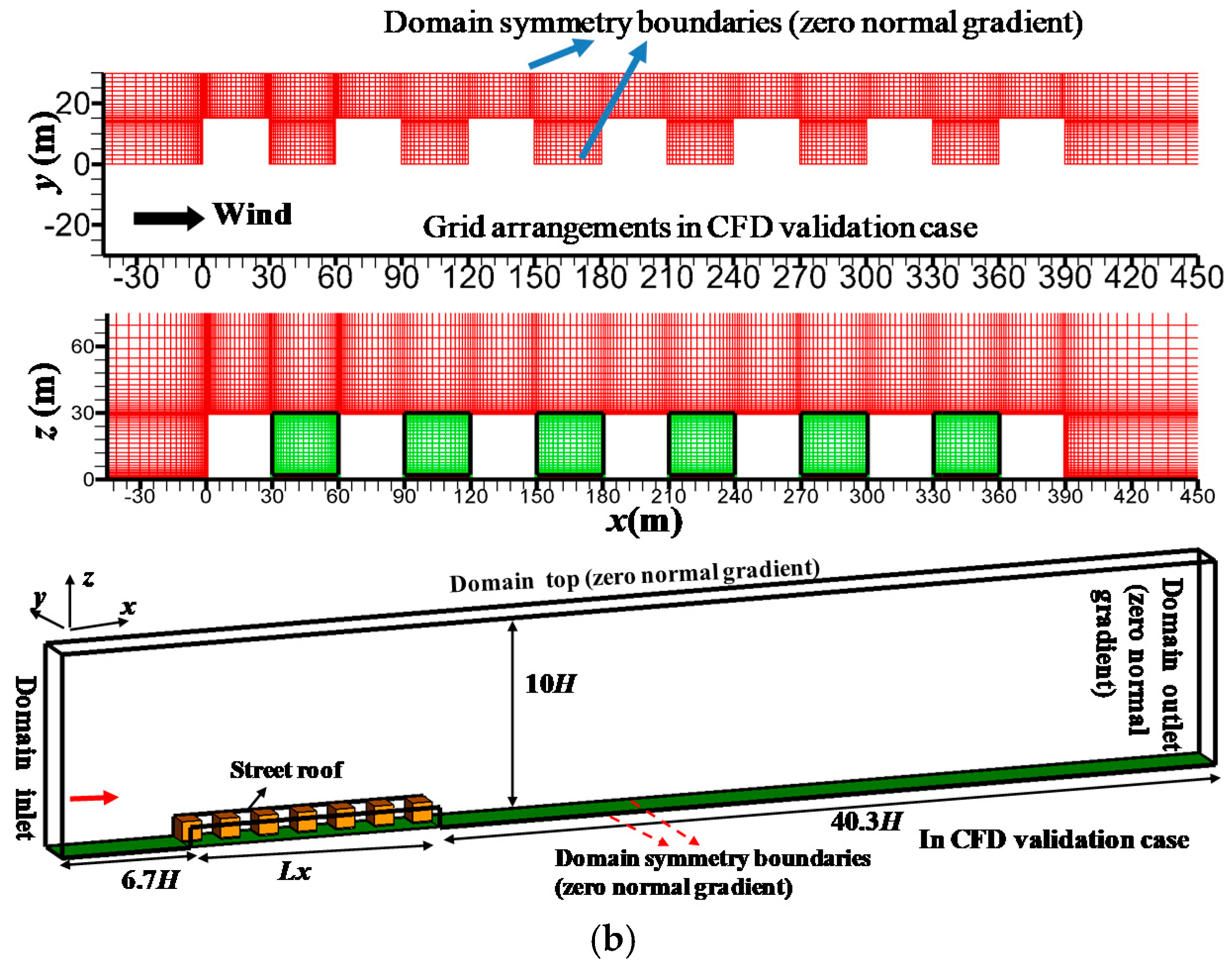
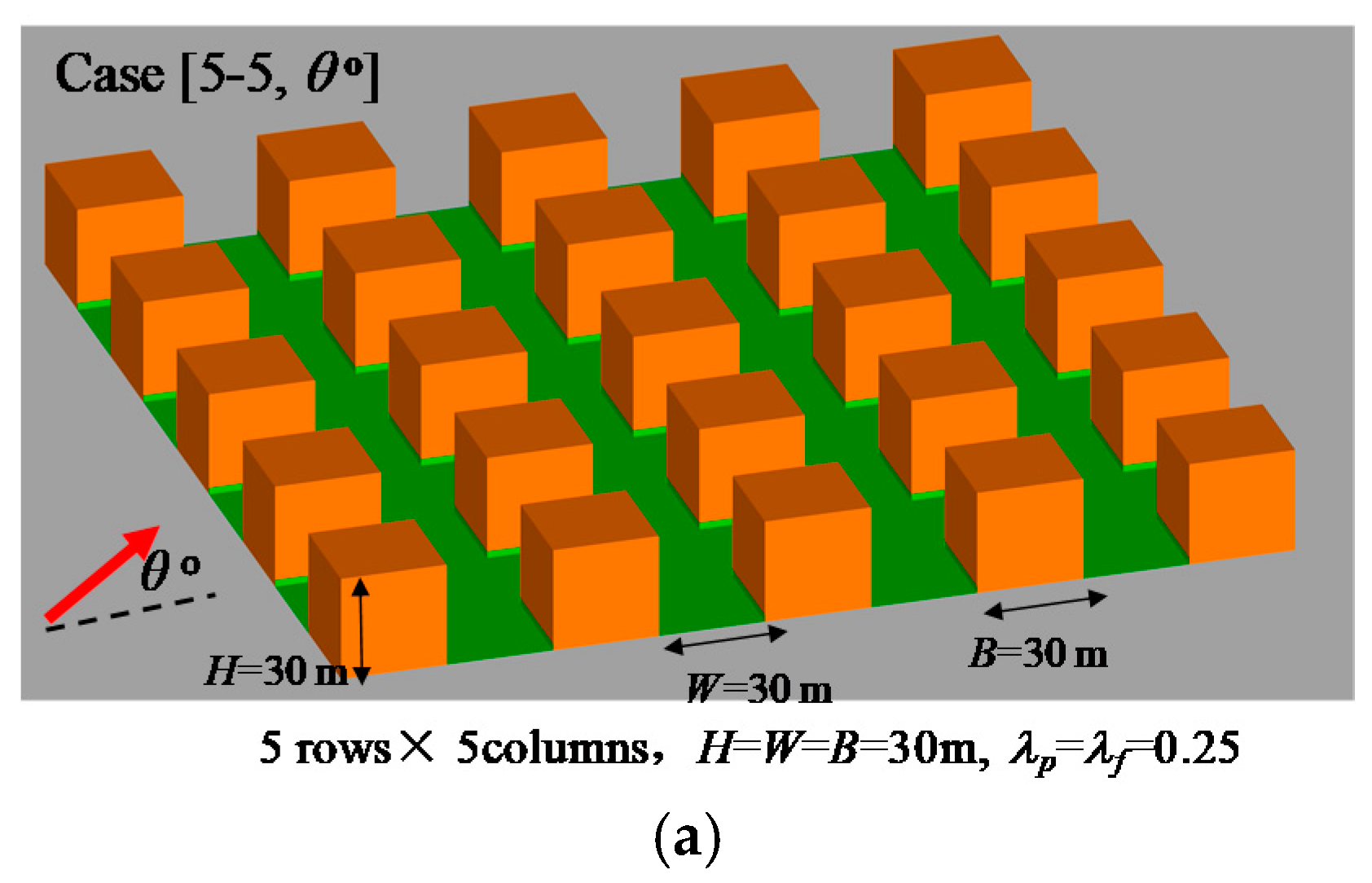
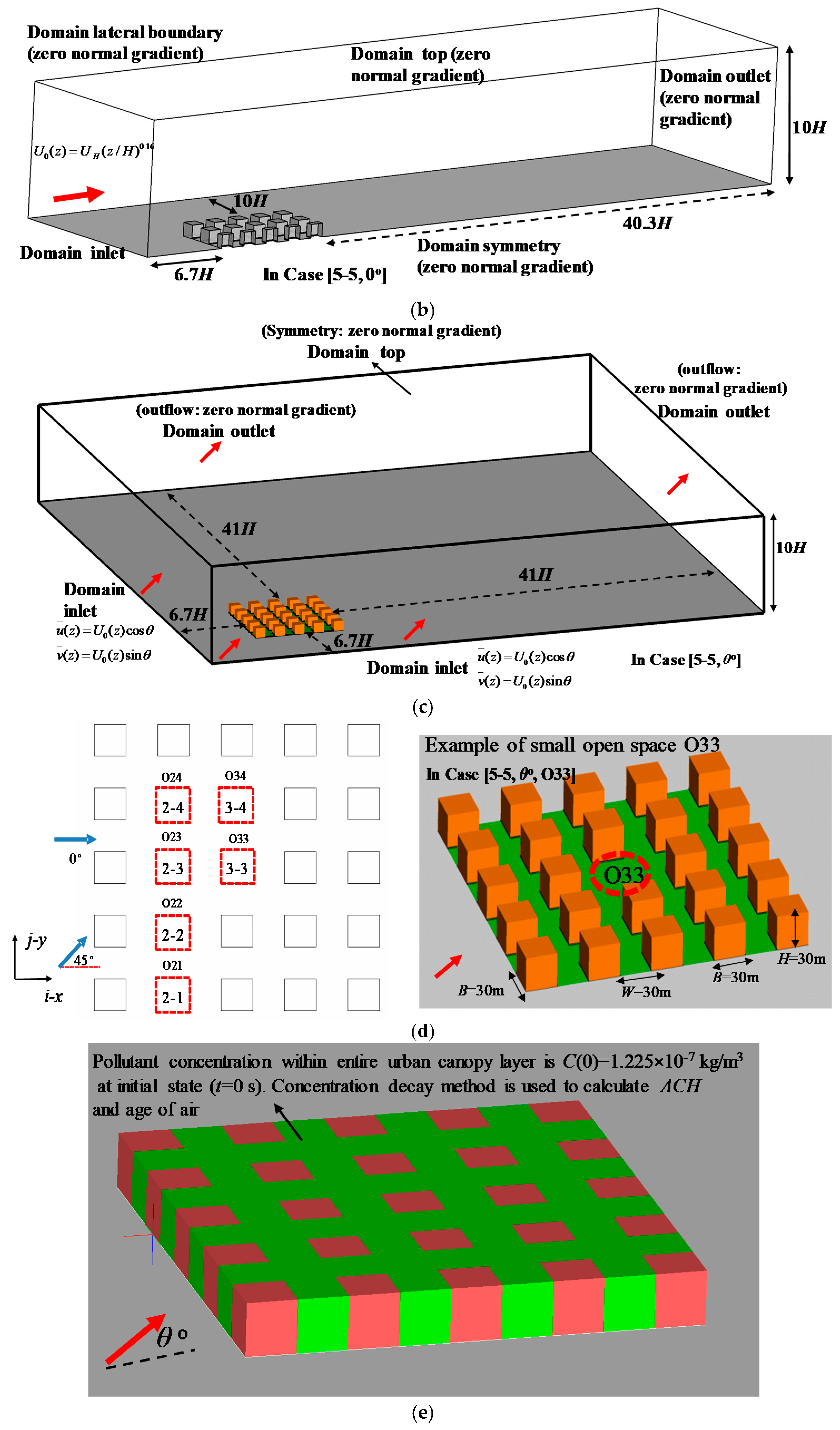
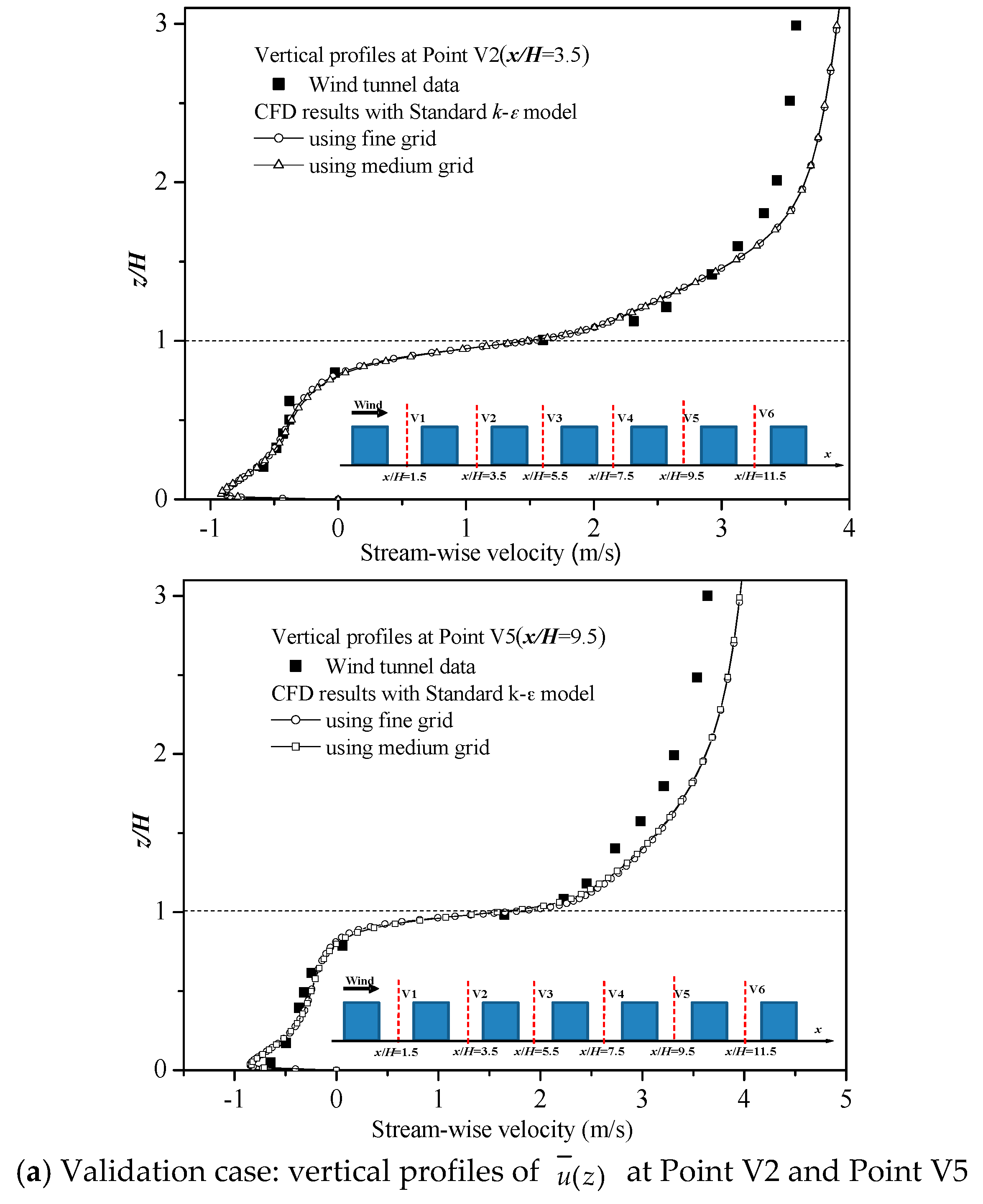
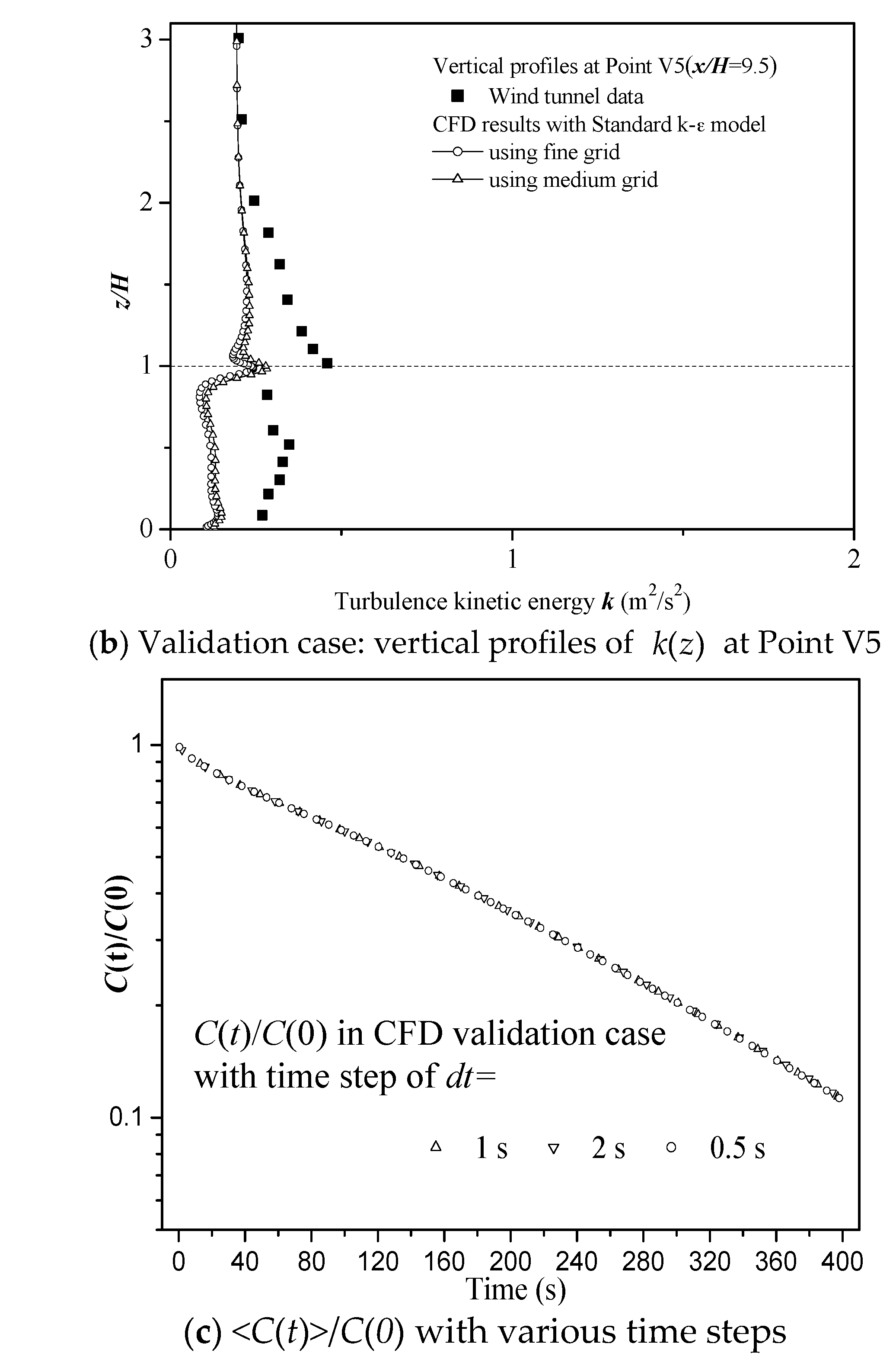
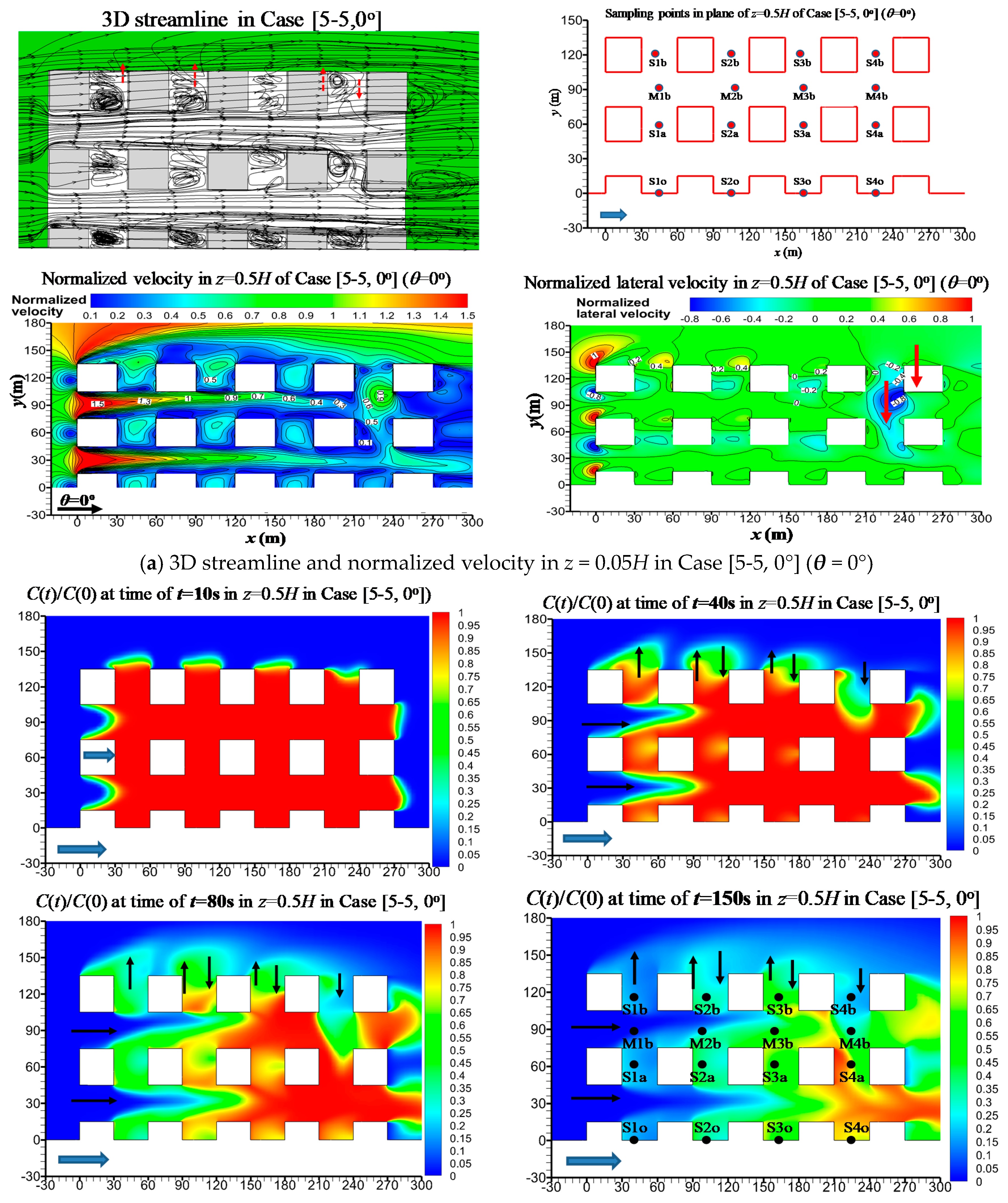
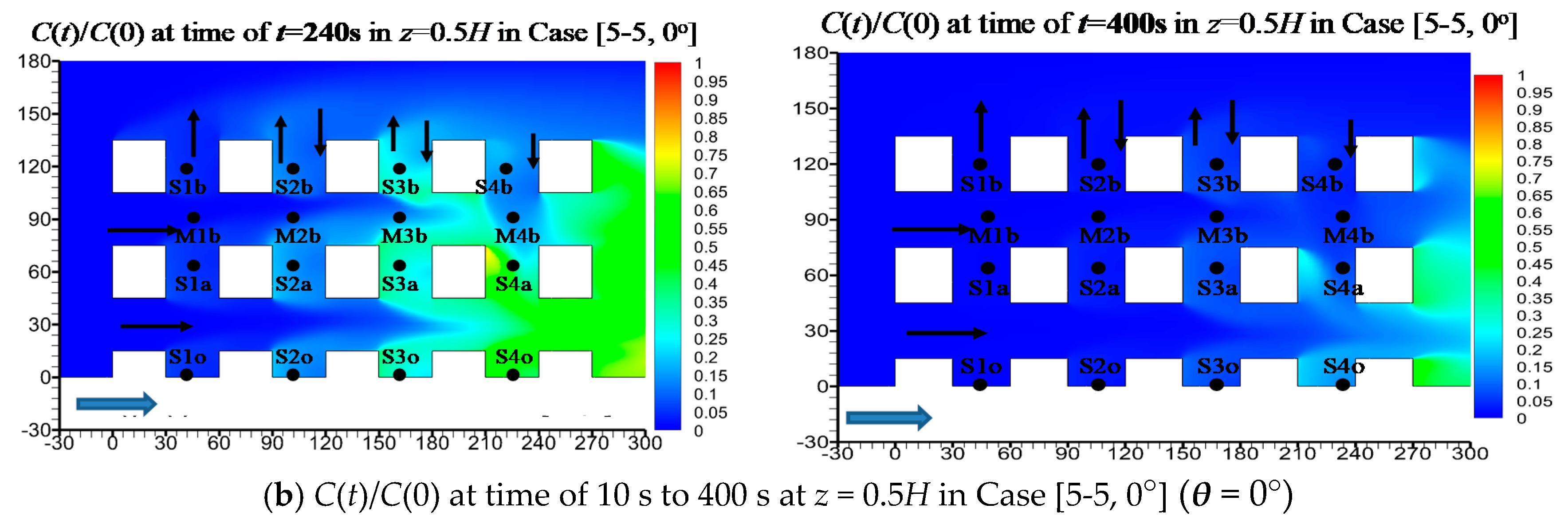
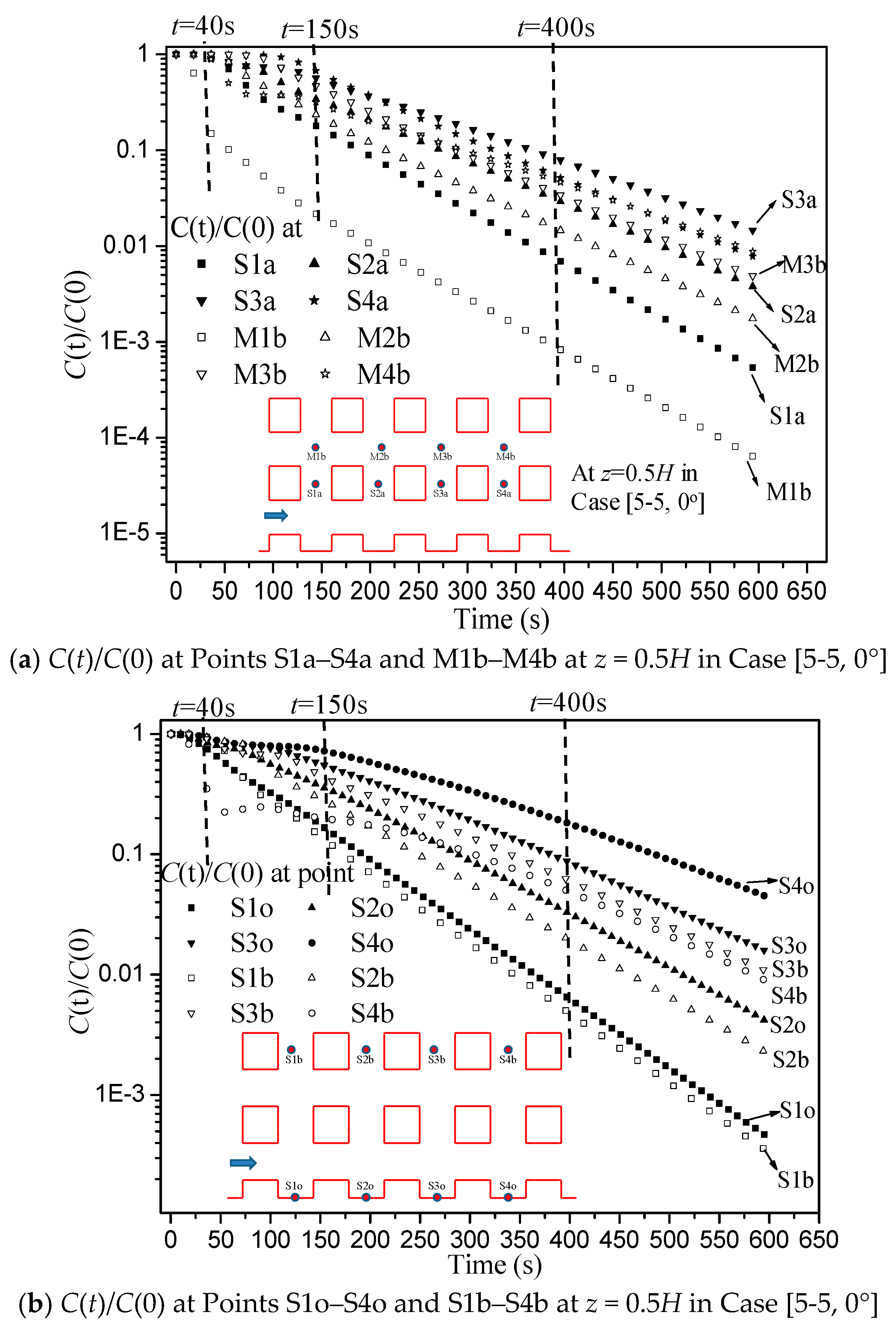
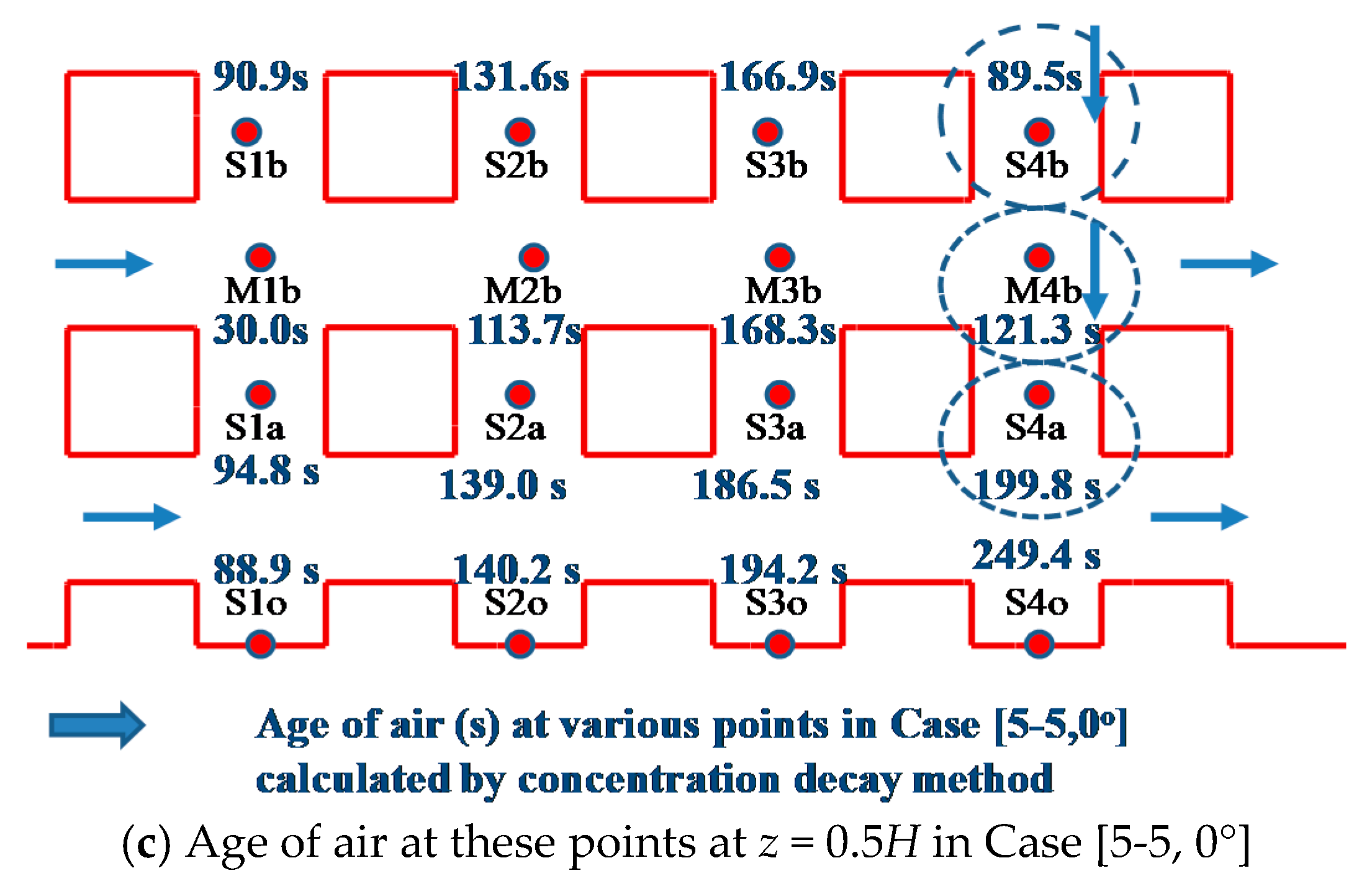
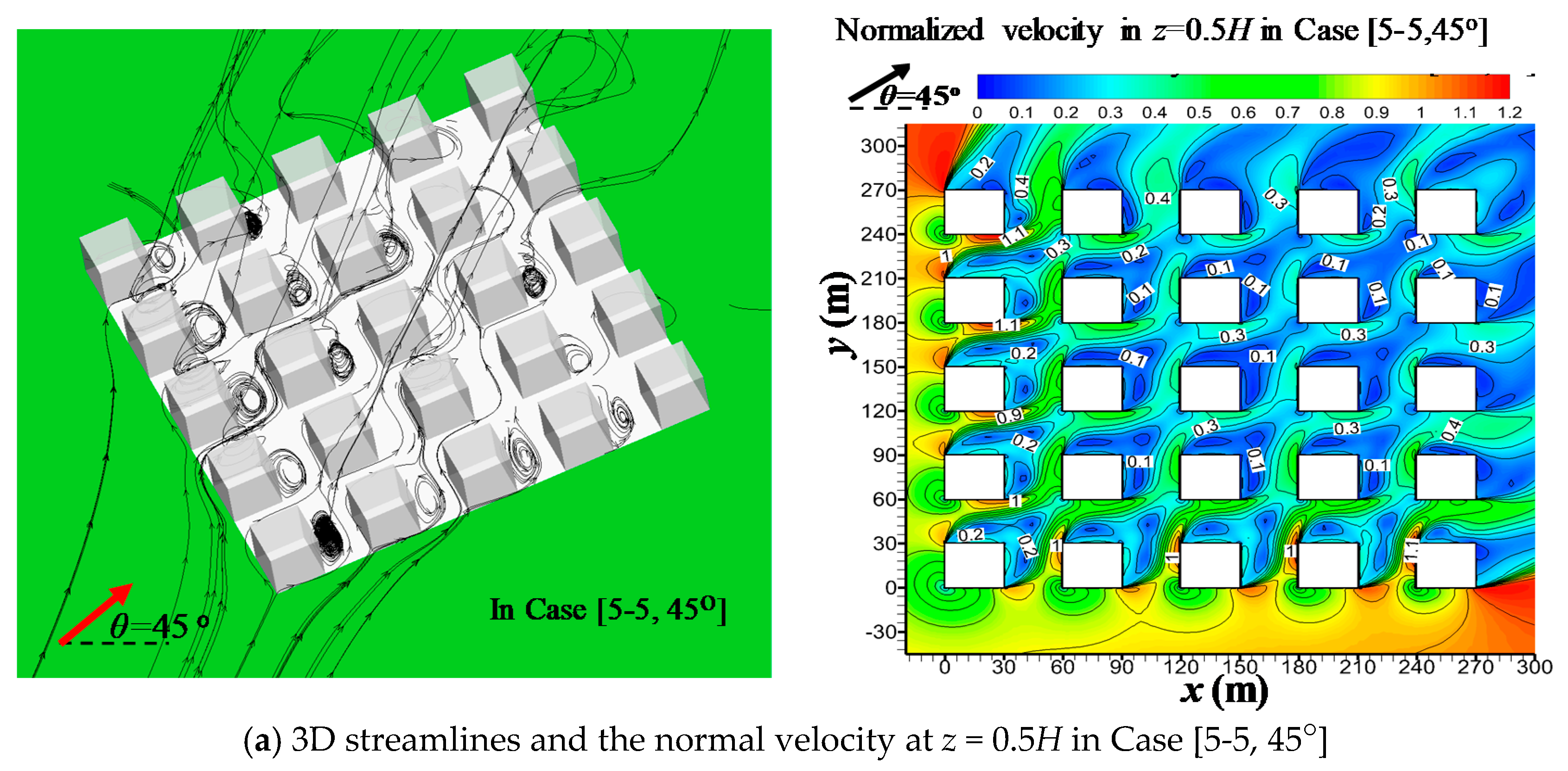
| Case Name | Number of Rows/Columns, Urban Sizes Lx and Ly | Wind Direction(θ°) |
|---|---|---|
| Group I | ||
| [5-5, θ°] | 5 rows, 5 columns, Lx = Ly = 270 m | 0°, 15°, 30°, 45° |
| [7-7, θ°] | 7 rows, 7 columns, Lx = Ly = 390 m | |
| [10-5, θ°] | 10 rows, 5 columns, Lx = 570 m, Ly = 270 m | 0°, 15°, 30°, 45°, 60°, 75°, 90° |
| Group II | ||
| [5-5, θ°, Oij] | 5 rows, 5 columns, Lx = Ly = 270 m, Oij = O21, O22, O23, O24, O33, O34 | 0°, 15°, 30°, 45° |
| Variable (Position) | Cases | (V5) | (V2) | (V5) |
|---|---|---|---|---|
| Average | ||||
| Wind tunnel | 0.31 | 1.61 | 1.58 | |
| CFD | 0.17 | 1.66 | 1.69 | |
| Standard deviation | ||||
| Wind tunnel | 0.07 | 1.76 | 1.70 | |
| CFD | 0.05 | 1.83 | 1.85 | |
| FAC2 | 0.50 | 0.93 | 0.93 | |
| NMSE | 0.52 | 0.01 | 0.02 | |
| FB | 0.61 | –0.03 | –0.07 | |
| R | 0.13 | 0.93 | 0.93 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Sandberg, M.; Lin, Y.; Yin, S.; Hang, J. Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method. Atmosphere 2017, 8, 169. https://doi.org/10.3390/atmos8090169
Wang Q, Sandberg M, Lin Y, Yin S, Hang J. Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method. Atmosphere. 2017; 8(9):169. https://doi.org/10.3390/atmos8090169
Chicago/Turabian StyleWang, Qun, Mats Sandberg, Yuanyuan Lin, Shi Yin, and Jian Hang. 2017. "Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method" Atmosphere 8, no. 9: 169. https://doi.org/10.3390/atmos8090169
APA StyleWang, Q., Sandberg, M., Lin, Y., Yin, S., & Hang, J. (2017). Impacts of Urban Layouts and Open Space on Urban Ventilation Evaluated by Concentration Decay Method. Atmosphere, 8(9), 169. https://doi.org/10.3390/atmos8090169






