Decadal Spatial-Temporal Variations in the Spatial Pattern of Anomalies of Extreme Precipitation Thresholds (Case Study: Northwest Iran)
Abstract
:1. Introduction
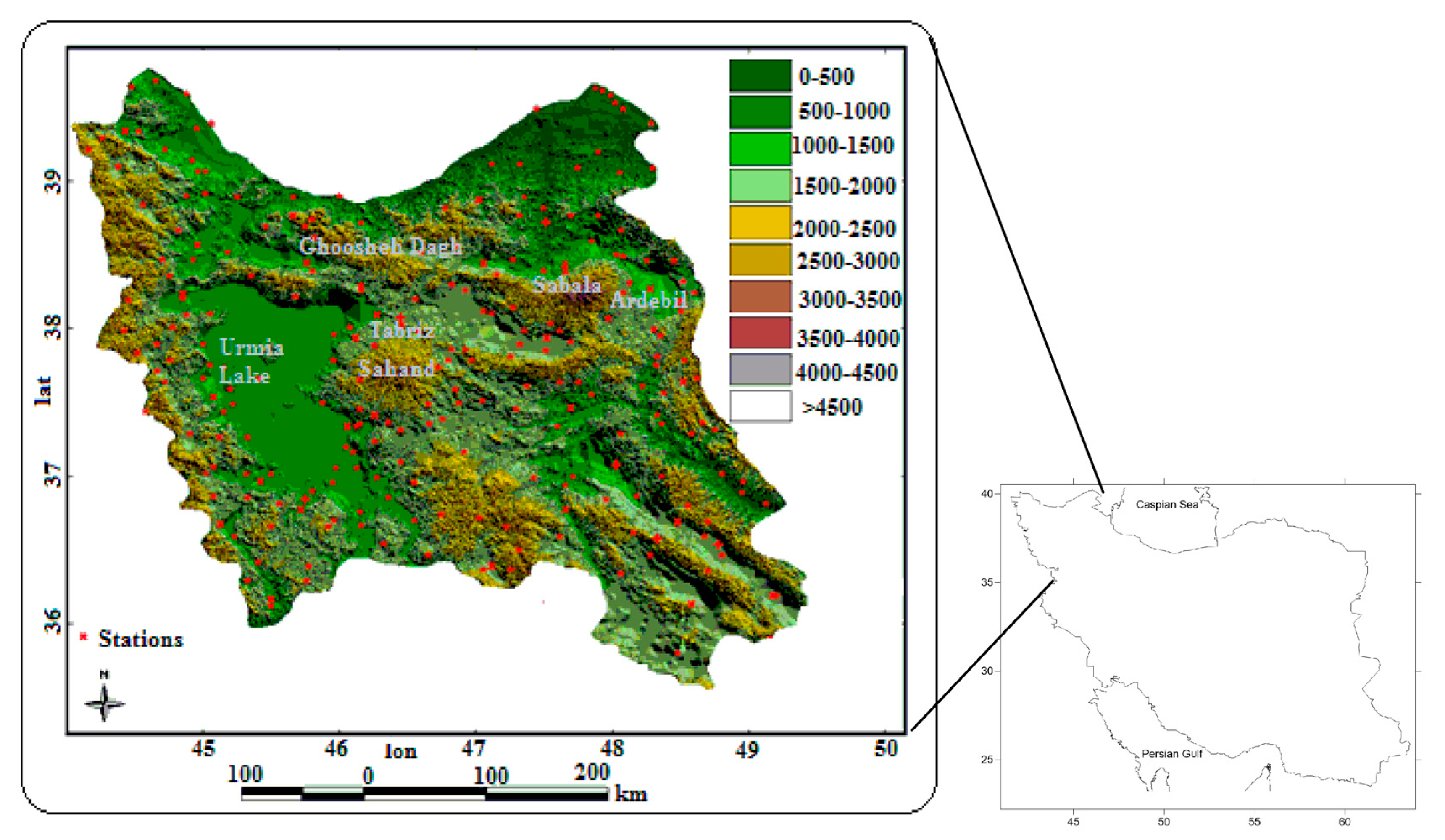
2. Materials and Method
3. Results and Discussion
3.1. General Features of Extreme Precipitation
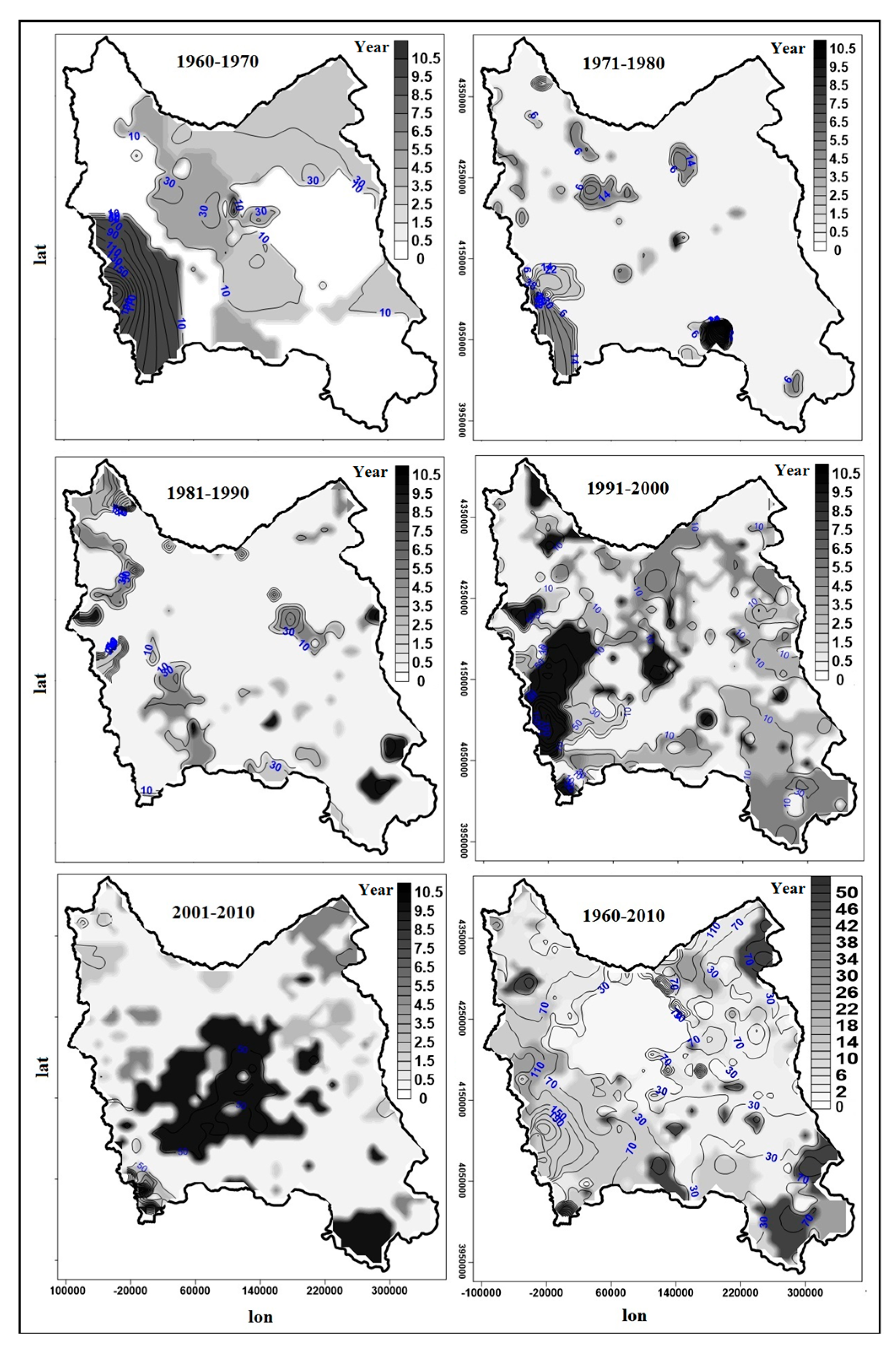
3.2. Analysis of Threshold Spatial Autocorrelation Pattern
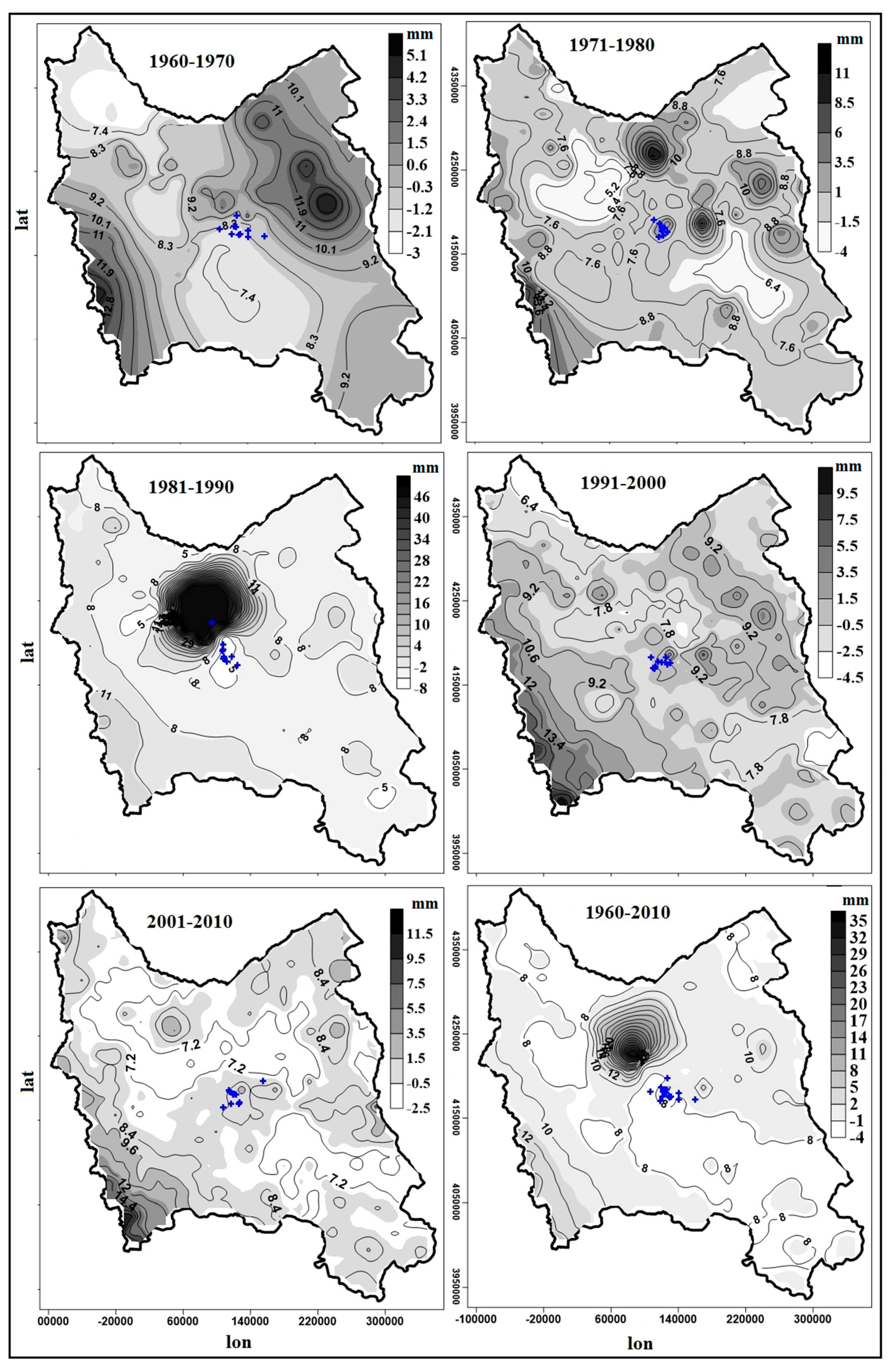
3.3. Analysis of Extreme Precipitation Threshold Patterns in the Northwest of Iran
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Data, C. Guidelines on Analysis of Extremes in A Changing Climate in Support of Informed Decisions for Adaptation. Available online: http://www.wmo.int/pages/prog/wcp/wcdmp/wcdmp_series/documents/WCDMP_72_TD_1500_en__1.pdf (accessed on 4 June 2017).
- Rousta, I.; Doostkamian, M.; Haghighi, E.; Mirzakhani, B. Statistical-synoptic analysis of the atmosphere thickness pattern of iran’s pervasive frosts. Climate 2016, 4, 41. [Google Scholar] [CrossRef]
- Alijani, B.; Doostkamyan, M.; Bayat, A.; Balyani, Y.; Javanmard, A. Analysis of precipitation in iran. In The Second International Conference on Environmental Hazards; Khuarazmi University Press: Tehran, Iran, 2013; Volume 2, p. 220. [Google Scholar]
- Rousta, I.; Khosh Akhlagh, F.; Soltani, M.; Modir Taheri Sh, S. Assessment of blocking effects on rainfall in northwestern iran. In Comecap 2014; COMECAP: Heraklion, Grecce, 2014; Volume 1, pp. 127–132. [Google Scholar]
- Masoudian, S.A.; Kaviani, M.R. Climatology of Iran; Isfahan University Press: Isfahan, Iran, 2007; Volume 1. [Google Scholar]
- Martin, G.; Ringer, M.; Pope, V.; Jones, A.; Dearden, C.; Hinton, T. The physical properties of the atmosphere in the new hadley centre global environmental model (Hadgem1). Part I: Model description and global climatology. J. Clim. 2006, 19, 1274–1301. [Google Scholar] [CrossRef]
- Lohmann, U.; Rotstayn, L.; Storelvmo, T.; Jones, A.; Menon, S.; Quaas, J.; Ekman, A.M.; Koch, D.; Ruedy, R. Total aerosol effect: Radiative forcing or radiative flux perturbation? Atmos. Chem. Phys. 2010, 10, 3235–3246. [Google Scholar] [CrossRef]
- Asakereh, H. Frequency distribution change of extreme precipitation in zanjan city. Geogr. Environ. Plan. 2012, 23, 51–66. [Google Scholar]
- Andrews, T.; Forster, P.M.; Gregory, J.M. A surface energy perspective on climate change. J. Clim. 2009, 22, 2557–2570. [Google Scholar] [CrossRef]
- Andrews, T.; Forster, P.M.; Boucher, O.; Bellouin, N.; Jones, A. Precipitation, radiative forcing and global temperature change. Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar] [CrossRef]
- Eriyagama, N.; Smakhtin, V.; Chandrapala, L.; Fernando, K. Impacts of Climate Change on Water Resources and Agriculture in Sri Lanka: A Review and Preliminary Vulnerability Mapping; IWMI: Colombo, Sri Lanka, 2010; Volume 135. [Google Scholar]
- Verner, D.; Lee, D.; Ashwill, M. Increasing Resilience to Climate Change in the Agricultural Sector of the Middle East: The Cases of Jordan and Lebanon; World Bank Publications: Washington, DC, USA, 2013. [Google Scholar]
- Knapp, A.K.; Beier, C.; Briske, D.D.; Classen, A.T.; Luo, Y.; Reichstein, M.; Smith, M.D.; Smith, S.D.; Bell, J.E.; Fay, P.A.; et al. Consequences of more extreme precipitation regimes for terrestrial ecosystems. BioScience 2008, 58, 811–821. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Easterling, D.R.; Karl, T.R.; Hegerl, G.C.; Razuvaev, V.N. Trends in intense precipitation in the climate record. J. Clim. 2005, 18, 1326–1350. [Google Scholar] [CrossRef]
- New, M.; Todd, M.; Hulme, M.; Jones, P. Precipitation measurements and trends in the twentieth century. Int. J. Climatol. 2001, 21, 1889–1922. [Google Scholar] [CrossRef]
- Zahran, M.A. Afro-asian mediterranean coastal lands. In Climate—Vegetation: Afro-Asian Mediterranean and Red Sea Coastal Lands; Gilbert, F., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 1–103. [Google Scholar]
- Alexander, L.; Zhang, X.; Peterson, T.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Bordi, I.; Fraedrich, K.; Petitta, M.; Sutera, A. Extreme value analysis of wet and dry periods in sicily. Theor. Appl. Climatol. 2007, 87, 61–71. [Google Scholar] [CrossRef]
- Sen Roy, S. A spatial analysis of extreme hourly precipitation patterns in india. Int. J. Climatol. 2009, 29, 345–355. [Google Scholar] [CrossRef]
- Sugahara, S.; Da Rocha, R.P.; Silveira, R. Non-stationary frequency analysis of extreme daily rainfall in sao paulo, brazil. Int. J. Climatol. 2009, 29, 1339–1349. [Google Scholar] [CrossRef]
- Łupikasza, E.B.; Hänsel, S.; Matschullat, J. Regional and seasonal variability of extreme precipitation trends in southern poland and central-eastern germany 1951–2006. Int. J. Climatol. 2011, 31, 2249–2271. [Google Scholar] [CrossRef]
- Wüest, M.; Frei, C.; Altenhoff, A.; Hagen, M.; Litschi, M.; Schär, C. A gridded hourly precipitation dataset for switzerland using rain-gauge analysis and radar-based disaggregation. Int. J. Climatol. 2010, 30, 1764–1775. [Google Scholar] [CrossRef] [Green Version]
- Hand, W.H.; Fox, N.I.; Collier, C.G. A study of twentieth-century extreme rainfall events in the United Kingdom with implications for forecasting. Meteorol. Appl. 2004, 11, 15–31. [Google Scholar] [CrossRef]
- Unkašević, M. Statistical analysis of daily maximum and monthly precipitation at Belgrade. Theor. Appl. Climatol. 2000, 66, 241–249. [Google Scholar] [CrossRef]
- Seibert, P.; Frank, A.; Formayer, H. Synoptic and regional patterns of heavy precipitation in Austria. Theor. Appl. Climatol. 2007, 87, 139–153. [Google Scholar] [CrossRef]
- Mätlik, O.; Post, P. Synoptic weather types that have caused heavy precipitation in Estonia in the period 1961–2005. Estonian J. Eng. 2008, 14, 195–208. [Google Scholar]
- Soltani, M.; Laux, P.; Kunstmann, H.; Stan, K.; Sohrabi, M.; Molanejad, M.; Sabziparvar, A.; SaadatAbadi, A.R.; Ranjbar, F.; Rousta, I. Assessment of climate variations in temperature and precipitation extreme events over Iran. Theor. Appl. Climatol. 2016, 126, 775–795. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Asgari, A.; Fattahi, E. Variability of extreme temperature and precipitation in Iran during recent decades. Int. J. Climatol. 2009, 29, 329–343. [Google Scholar] [CrossRef]
- Rousta, I.; Soltani, M.; Zhou, W.; Cheung, H.H. Analysis of extreme precipitation events over central plateau of Iran. Am. J. Clim. Chang. 2016, 5, 297. [Google Scholar] [CrossRef]
- Zolfagari, H.; Hashemi, R.; Fashi, M. The proportion of daily maximum precipitation to annual precipitation in Iran. Geogr. Res. Q. 2010, 92, 165–188. [Google Scholar]
- Rousta, I.; Doostkamian, M.; Haghighi, E.; Ghafarian Malamiri, H.R.; Yarahmadi, P. Analysis of spatial autocorrelation patterns of heavy and super-heavy rainfall in Iran. Adv. Atmos. Sci. 2017, 34, 1069–1081. [Google Scholar]
- Soltani, M.; Rousta, I.; Khosh Akhlagh, F.; Modir Taheri Sh, S. Statistical synoptic analysis of summertime extreme precipitation events over Kerman Province, Iran. In COMECAP 2014; COMECAP: Heraklion, Grecce, 2014; Volume 1, pp. 164–169. [Google Scholar]
- Soltani, M.; Rousta, I.; Taheri, S.S.M. Using mann-kendall and time series techniques for statistical analysis of long-term precipitation in gorgan weather station. World Appl. Sci. J. 2013, 28, 902–908. [Google Scholar]
- Alijani, B. Spatial analysis of critical temperatures and daily precipitation in Iran. J. Geogr. Sci. Appl. Res. 2011, 20, 9–30. [Google Scholar]
- Razmi, R.; Asakereh, H.; Asakereh, H. Analysis of annual precipitation changes in northwest of Iran. Geogr. Environ. Plan. 2012, 23, 147–162. [Google Scholar]
- Asakereh, H.; Doostkamian, M.; Sadrafshary, S. Anomalies and cycles of precipitable water over Iran in recent decades. Arab. J. Geosci. 2015, 11, 9569–9576. [Google Scholar] [CrossRef]
- Asakereh, H. Trends in monthly precipitation over the northwest of Iran (Nwi). Theor. Appl. Climatol. 2016. [Google Scholar] [CrossRef]
- Mohammadi, H.; Azizi, G.; khoshahklagh, F.; Ranjbar, F. Analysis of daily precipitation extreme indices trend in Iran. Phys. Geogr. Res. Q. 2017, 49, 21–37. [Google Scholar]
- Jahahnbakhsh Asl, S.; Mirhashemi, H.; Tadayyon, M. Synoptic and thermodynamic analysis, the heavy in north west of Iran (East Azarbaijan Province). Geogr. Plan. 2015, 19, 107–125. [Google Scholar]
- Mehdinasab, M.; Tavousi, T.; Mirzaei, R. Prediction probable flood and maximum precipitation using poldukhtar basin suffered partial series. Iran’s Nat. Ecosyst. 2014, 5, 97–109. [Google Scholar]
- Moghbel, M.; Davodi, M.; Naistani, A.; Taghavi, F. Identify changes in iran’s precipitation regime in recent decades. NIVAR 2011, 35, 55–66. [Google Scholar]
- Javari, M. Spatial variability of rainfall trends in Iran. Arab. J. Geosci. 2017, 10, 78. [Google Scholar] [CrossRef]
- George, R. A new approach to time series with mixed spectra. Available online: https://statistics.stanford.edu/sites/default/files/PAR%20NSF%2014.pdf (accessed on 4 June 2017).
- Lee, J.; Wong, D.W.S. Statistical Analysis with Arcview Gis; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Masoodian, S.; Mohammadi, B. The analysis of frontogenesis frequency at time of super heavy rainfall in Iran. Geogr. Res. 2012, 27, 1–23. [Google Scholar]
- Alijani, B. The Climate of Iran; Payam Noor University Press: Tehran, Iran, 1995; p. 230. [Google Scholar]
- Kalayci, S.; Karabörk, M.; Kahya, E. Analysis of El Nino signals on Turkish streamflow and precipitation patterns using spectral analysis. Fresenius Environ. Bull. 2004, 13, 719–725. [Google Scholar]
- Hartmann, H.; Becker, S.; King, L. Quasi-periodicities in Chinese precipitation time series. Theor. Appl. Climatol. 2008, 92, 155–163. [Google Scholar] [CrossRef]
- García, J.; Serrano, A.; De la Cruz Gallego, M. A spectral analysis of Iberian Peninsula monthly rainfall. Theor. Appl. Climatol. 2002, 71, 77–95. [Google Scholar] [CrossRef]
- Jo, Y.-J.; Lee, J.-Y. Time series analysis of hydrologic data obtained from a man-made undersea Lpg cavern. Eng. Geol. 2010, 113, 70–80. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal changes in the enso–monsoon system. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Azad, S.; Vignesh, T.; Narasimha, R. Periodicities in Indian monsoon rainfall over spectrally homogeneous regions. Int. J. Climatol. 2010, 30, 2289–2298. [Google Scholar] [CrossRef]
- Selvam, A.M.; Joshi, R. Universal spectrum for interannual variability in Coads global air and sea-surface temperatures. Int. J. Climatol. 1995, 15, 613–623. [Google Scholar] [CrossRef]
- Jahanbakhsh, S.; Edalat, D.M. Study of climate change in Iran (case study: North atlantic oscillation as an indicator of the impact of solar activity on changes in precipitation of Azerbaijan region). In Third International Conference on Iran’s Water Resources Management Iran; School of Civil Engineering: Tabriz, Iran, 2009; Volume 1, p. 325. [Google Scholar]
- Lana, X.; Martínez, M.; Serra, C.; Burgueño, A. Periodicities and irregularities of indices describing the daily pluviometric regime of the Fabra Observatory (Ne Spain) for the years 1917–1999. Theor. Appl. Climatol. 2005, 82, 183–198. [Google Scholar] [CrossRef]
- Kane, R.P.; Teixeira, N.R. Power spectrum analysis of the annual rainfall series for Massachusetts (Ne, USA). Clim. Chang. 1991, 18, 89–94. [Google Scholar] [CrossRef]
| Index | 1961–1970 | 1971–1980 | 1981–1990 | 1991–2000 | 2001–2010 | 1961–2010 |
|---|---|---|---|---|---|---|
| mean | 9.2 | 8.4 | 11.2 | 9.1 | 8.1 | 9.2 |
| median | 8.9 | 7.9 | 7.5 | 8.7 | 8.0 | 8.2 |
| mode | 5.8 | 6.3 | 7.3 | 6.1 | 7.0 | 4.7 |
| var | 8.9 | 8.1 | 2363.2 | 7.7 | 10.7 | 480.8 |
| std | 3.0 | 2.8 | 48.6 | 2.8 | 3.3 | 21.9 |
| cv | 32.3 | 33.9 | 433.8 | 30.4 | 40.2 | 237.8 |
| Skewness | 1.1 | 2.8 | 20.2 | 1.5 | 0.6 | 44.4 |
| kurtosis | 6.0 | 25.0 | 491.9 | 7.0 | 7.0 | 239.1 |
| max | 29.5 | 51.0 | 165.5 | 28.5 | 33.7 | 165.5 |
| Q1 | 7.2 | 6.6 | 6.1 | 7.3 | 6.8 | 6.8 |
| Q2 | 8.9 | 7.9 | 7.5 | 8.7 | 8.0 | 8.2 |
| Q3 | 10.9 | 9.6 | 9.4 | 10.4 | 9.6 | 10.1 |
| Cycle | 1961–1970 | 1971–1980 | 1981–1990 | 1991–2000 | 2001–2010 | 1961–2010 |
|---|---|---|---|---|---|---|
| 6–8 | 23.9 | 42.4 | 59.7 | 57.3 | 59.7 | 34.5 |
| 8–10 | 50 | 45.5 | 20 | 28.8 | 3.23 | 50.5 |
| 10–12 | 21.3 | 8.5 | 13.6 | 8.9 | 5.6 | 9.7 |
| 12–14 | 4.3 | 2.7 | 4.4 | 3.8 | 1.4 | 3.8 |
| >14 | 0.4 | 0.9 | 2.3 | 1.2 | 0.9 | 1.5 |
| Anomaly% | ||||||
| negative | 52.6 | 56.6 | 82.4 | 61.5 | 65.5 | 73.98 |
| Positive | 47.4 | 43.4 | 17.6 | 38.5 | 34.5 | 26.11 |
| 1961–1970 | 1971–1980 | 1981–1990 | 1991–2000 | 2001–2010 | 1961–2010 | |
|---|---|---|---|---|---|---|
| <−2.58 Std-Dev. | 25.90521 | 12.00632 | 0 | 10.34755 | 4.344392 | 0 |
| −2.58–−1.96 Std-Dev. | 6.872038 | 6.240126 | 0 | 5.845182 | 10.11058 | 0.473934 |
| −1.96–−1.65 Std-Dev. | 3.080569 | 3.554502 | 0 | 3.00158 | 6.082148 | 4.186414 |
| −1.65–1.65 Std-Dev. | 39.17852 | 60.29384 | 91.46603 | 70.00316 | 68.60979 | 86.4613 |
| 1.65–1.96 Std-Dev. | 0.157978 | 0.394945 | 0.078989 | 0.078989 | 0.157978 | 0.078989 |
| 1.96–2.58 Std-Dev. | 3.974724 | 2.685624 | 0.157978 | 1.342812 | 0.947867 | 0.552923 |
| >2.58 Std-Dev. | 20.06319 | 15.08689 | 7.633491 | 9.636651 | 8.503949 | 8.766193 |
| Cycle | 1961–1970 | 1971–1980 | 1981–1990 | 1991–2000 | 2001–2010 | 1961–2010 |
|---|---|---|---|---|---|---|
| 0–2 | 42.7 | 86.9 | 81.1 | 44.5 | 60.7 | 46.1 |
| 2–4 | 28.4 | 4.1 | 8 | 23.9 | 10.9 | 18.7 |
| 4–6 | 12.6 | 8.2 | 8.4 | 18.6 | 6.7 | 1.7 |
| 6–8 | 0 | 0 | 0 | 0 | 0 | 24.4 |
| >8 | 11.7 | 0.9 | 2.7 | 13 | 21.6 | 9.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rousta, I.; Nasserzadeh, M.H.; Jalali, M.; Haghighi, E.; Ólafsson, H.; Ashrafi, S.; Doostkamian, M.; Ghasemi, A. Decadal Spatial-Temporal Variations in the Spatial Pattern of Anomalies of Extreme Precipitation Thresholds (Case Study: Northwest Iran). Atmosphere 2017, 8, 135. https://doi.org/10.3390/atmos8080135
Rousta I, Nasserzadeh MH, Jalali M, Haghighi E, Ólafsson H, Ashrafi S, Doostkamian M, Ghasemi A. Decadal Spatial-Temporal Variations in the Spatial Pattern of Anomalies of Extreme Precipitation Thresholds (Case Study: Northwest Iran). Atmosphere. 2017; 8(8):135. https://doi.org/10.3390/atmos8080135
Chicago/Turabian StyleRousta, Iman, Mohammad Hossain Nasserzadeh, Masoud Jalali, Esmaeil Haghighi, Haraldur Ólafsson, Saeide Ashrafi, Mehdi Doostkamian, and Ali Ghasemi. 2017. "Decadal Spatial-Temporal Variations in the Spatial Pattern of Anomalies of Extreme Precipitation Thresholds (Case Study: Northwest Iran)" Atmosphere 8, no. 8: 135. https://doi.org/10.3390/atmos8080135






