The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Instrumentation
2.2. Fog Events and Synoptic Weather
2.3. Data Processing
3. Results
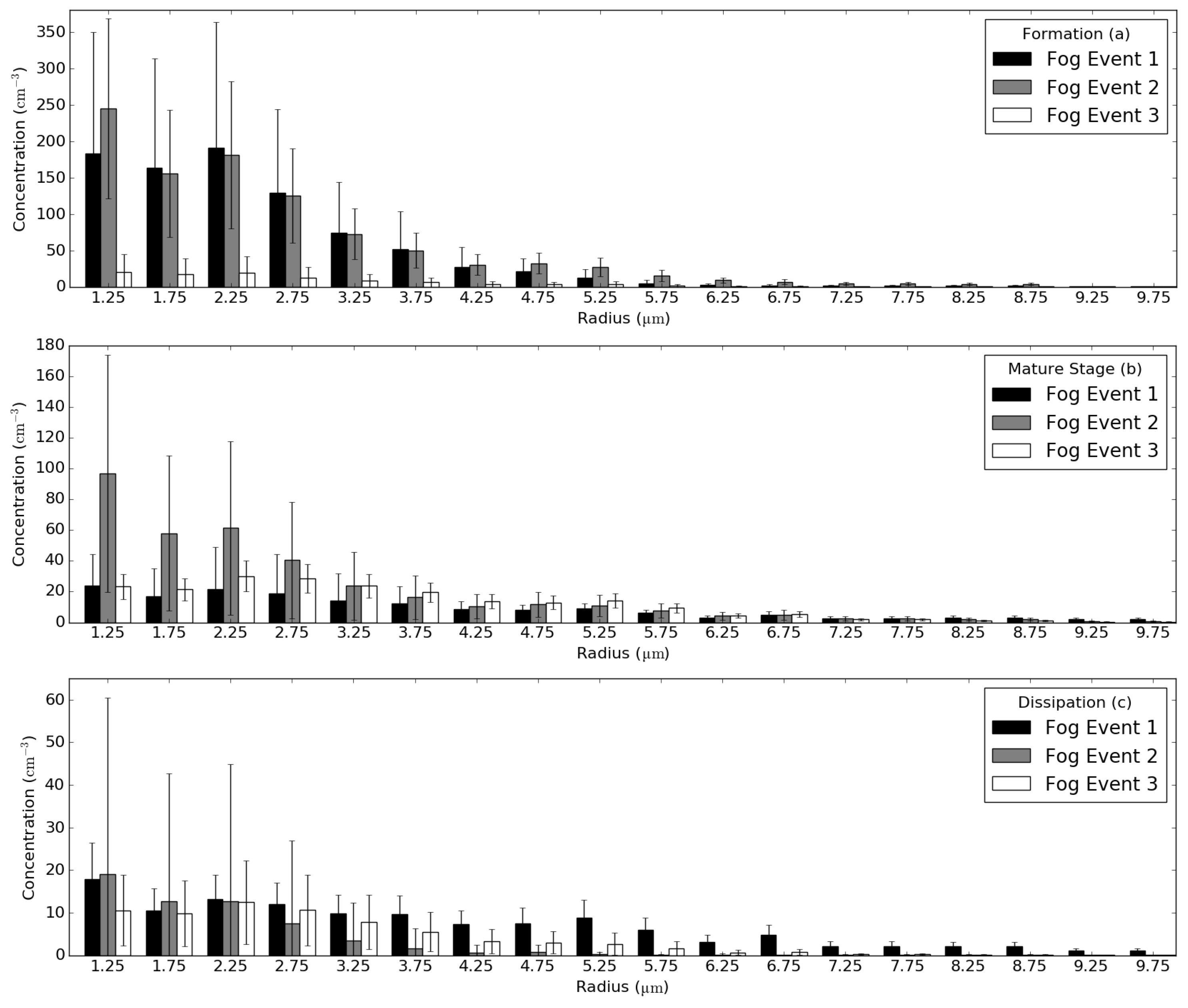
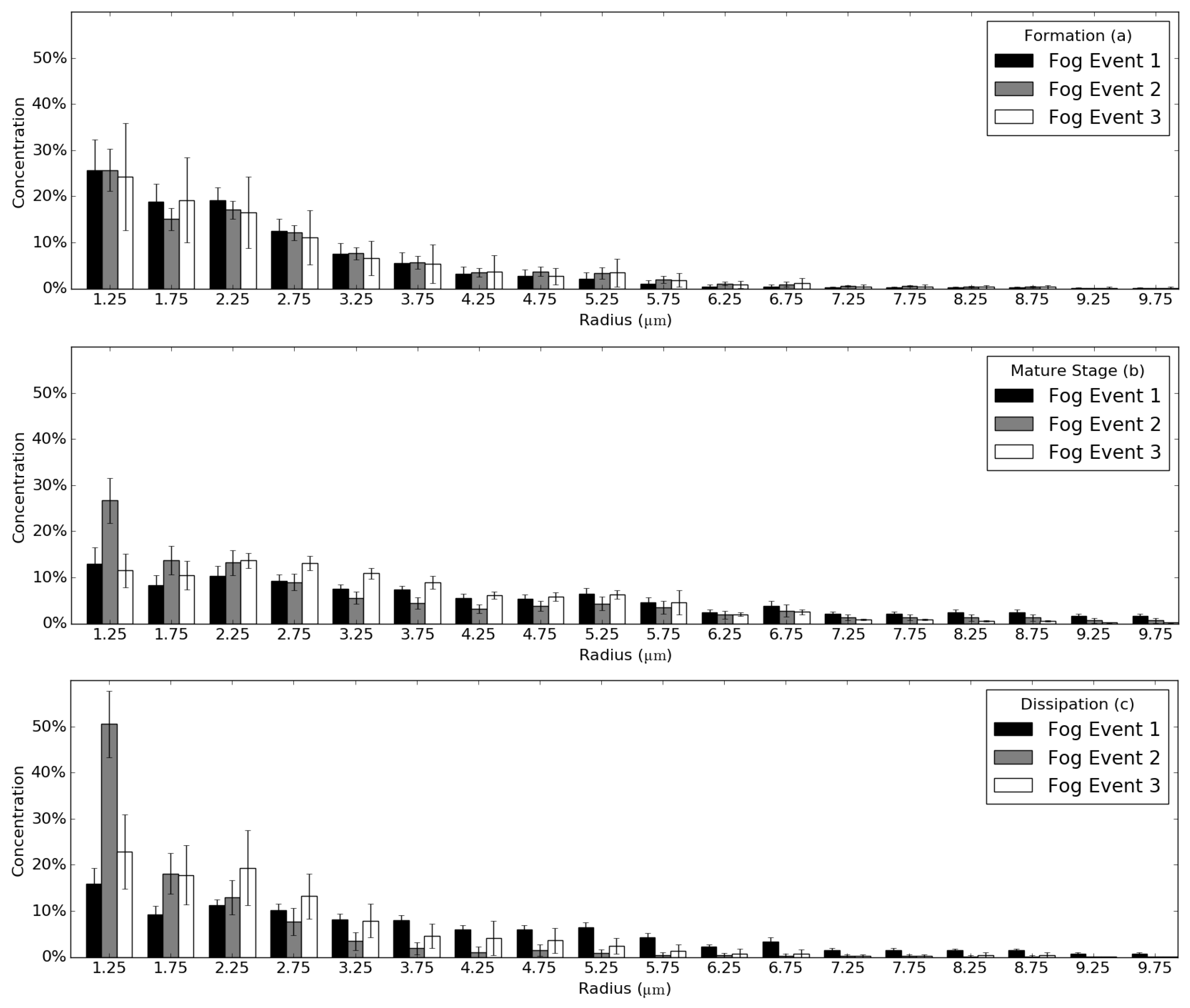
3.1. Visual Analysis of DSD Differences for Different Fog Life Cycle Stages
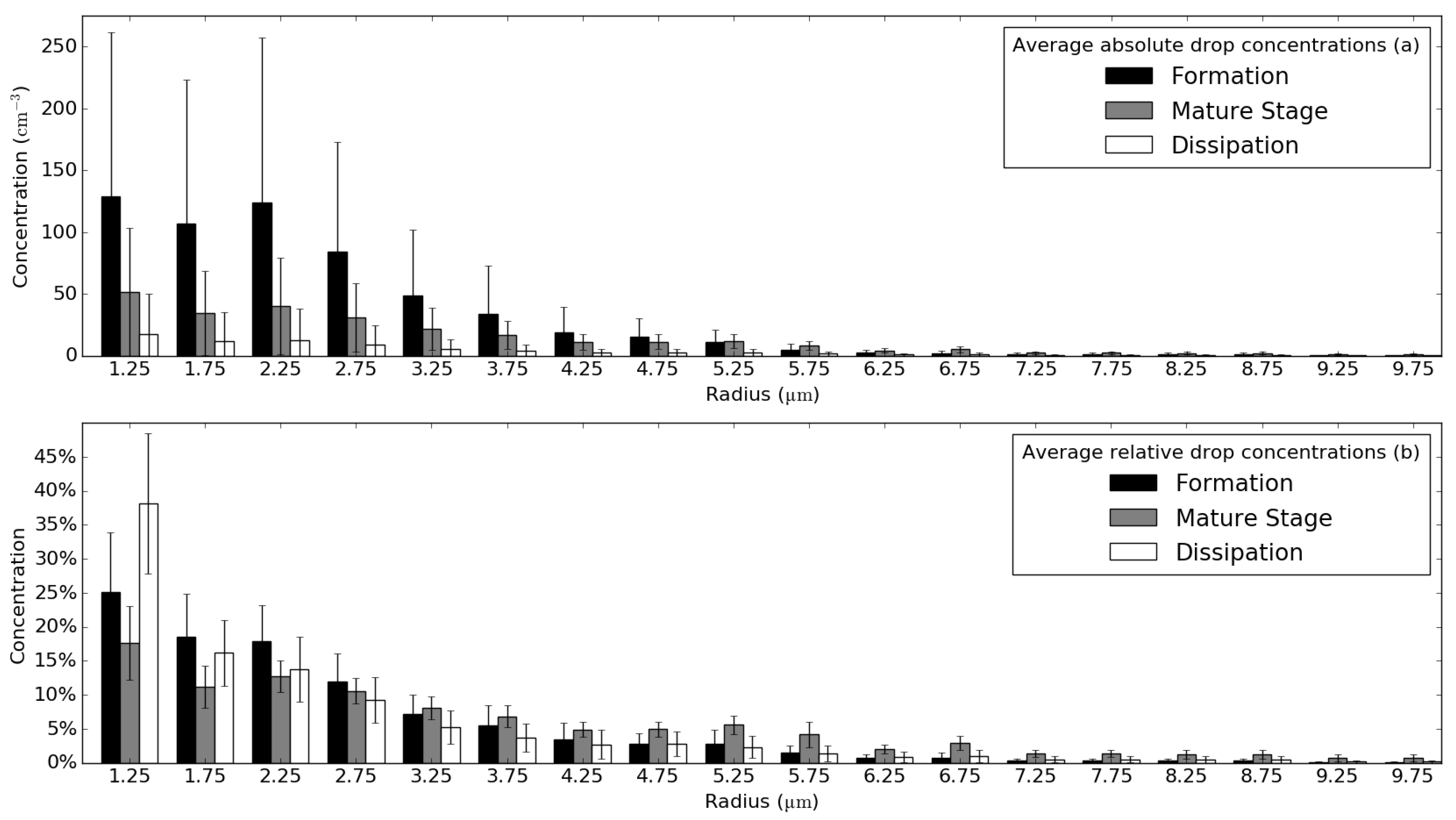
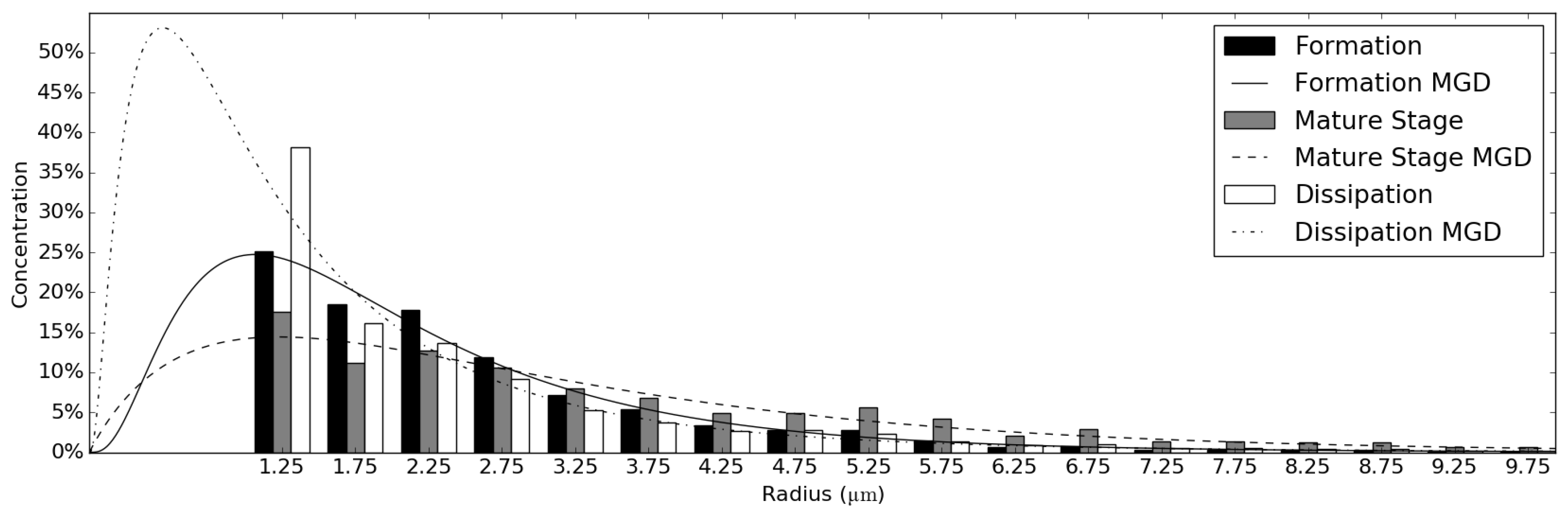
3.2. Representativity of Average DSDs for Different Fog Life Cycle Stages
3.3. The Z-LWC Relationship
3.3.1. Derived Parameters of the Modified Gamma Distribution
3.3.2. The Proportionality Factor Ω
3.3.3. Derivation of Reliable Z-LWC Relationships by Means of Stage-Dependent Characteristic DSDs
4. Discussion
4.1. Differences in DSDs between Fog Life Cycle Stages
4.2. Representativity of Stage-Averaged Spectra
4.3. Feasibility of the Z-LWC Approach
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BM | Weather classification: zonal ridge across Central Europe |
| CDP | Cloud Droplet Probe |
| DSD | Drop size distribution |
| FMCW | Frequency-modulated continuous wave technique |
| HNA | Weather classification: high pressure ridge over Central Europe |
| LWC | Liquid water content |
| MGD | Modified gamma distribution |
| SA | Weather classification: anticyclonic southerly |
| SEZ | Weather classification: cyclonic south-easterly |
| Z | Radar reflectivity |
Appendix A
References
- Nemery, B.; Hoet, P.H.M.; Nemmar, A. The Meuse Valley fog of 1930: An air pollution disaster. Lancet 2001, 357, 704–708. [Google Scholar] [CrossRef]
- Pinto, R.; Larrain, H.; Cereceda, P.; Lázaro, P.; Osses, P.; Schemenauer, R.S. Monitoring fog-vegetation communities at a fog-site in Alto Patache, South of Iquique, Northern Chile, during “El Niño” and “La Niña” events (1997–2000). In Proceedings of the Second International Conference on Fog and Fog Collection, International Development Research Center, Ottawa, ON, Canada, 15–20 July 2001; pp. 293–296. [Google Scholar]
- Sampurno Bruijnzeel, L.; Eugster, W.; Burkard, R. Fog as a Hydrologic Input. In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Chichester, UK, 2005; pp. 559–582. [Google Scholar]
- Maier, F.; Bendix, J.; Thies, B. Simulating Z-LWC relations in natural fogs with radiative transfer calculations for future application to a cloud radar profiler. Pure Appl. Geophys. 2012, 169, 793–807. [Google Scholar] [CrossRef]
- Schulze-Neuhoff, H. Nebelfeinanalyse mittels zusätzlicher 420 Klimastationen—Taktische Analyse 1:2 statt 1:5 Mill. Meteorol. Rundsch. 1976, 29, 75–84. [Google Scholar]
- Gultepe, I.; Tardif, R.; Michaelides, S.C.; Cermak, J.; Bott, A.; Bendix, J.; Müller, M.D.; Pagowski, M.; Hansen, B.; Ellrod, G.; et al. Fog Research: A Review of Past Achievements and Future Perspectives. Pure Appl. Geophys. 2007, 164, 1121–1159. [Google Scholar] [CrossRef]
- Terradellas, E.; Bergot, T. Comparison between two-single-column models designed for short-terms fog and low-clouds forecasting. Física de la Tierra 2007, 19, 189–203. [Google Scholar]
- Cermak, J.; Bendix, J. A novel approach to fog/low stratus detection using Meteosat 8 data. Atmos. Res. 2008, 87, 279–292. [Google Scholar] [CrossRef]
- Bendix, J.; Thies, B.; Cermak, J.; Nauß, T. Ground Fog Detection from Space Based on MODIS Daytime Data—A Feasibility Study. Weather Forecast. 2005, 20, 989–1005. [Google Scholar] [CrossRef]
- Cermak, J.; Bendix, J. Detecting ground fog from space—A microphysics-based approach. Int. J. Remote Sens. 2011, 32, 3345–3371. [Google Scholar] [CrossRef]
- Kollias, P.; Clothiaux, E.E.; Miller, M.A.; Albrecht, B.A.; Stephens, G.L.; Ackerman, T.P. Millimeter-wavelength radars: New frontier in atmospheric cloud and precipitation research. Bull. Am. Meteorol. Soc. 2007, 88, 1608–1624. [Google Scholar] [CrossRef]
- Nowak, D.; Ruffieux, D.; Agnew, J.L.; Vuilleumier, L. Detection of fog and low cloud boundaries with ground-based remote sensing systems. J. Atmos. Ocean. Technol. 2008, 25, 1357–1368. [Google Scholar] [CrossRef]
- Sauvageot, H.; Omar, J. Radar Reflectivity of Cumulus Clouds. J. Atmos. Ocean. Technol. 1987, 4, 264–272. [Google Scholar] [CrossRef]
- Liao, L.; Sassen, K. Investigation of relationships between Ka-band radar reflectivity and ice and liquid water contents. Atmos. Res. 1994, 34, 231–248. [Google Scholar] [CrossRef]
- Sassen, K.; Liao, L. Estimation of Cloud Content by W-Band Radar. J. Appl. Meteorol. 1996, 35, 932–938. [Google Scholar] [CrossRef]
- Fox, N.I.; Illingworth, A.J. The Retrieval of Stratocumulus Cloud Properties by Ground-Based Cloud Radar. J. Appl. Meteorol. 1997, 36, 485–492. [Google Scholar] [CrossRef]
- Donovan, D.P.; van Lammeren, A.C.A.P. Cloud effective particle size and water content profile retrievals using combined lidar and radar observations: 1. Theory and examples. J. Geophys. Res. 2001, 106, 27425. [Google Scholar] [CrossRef]
- Löhnert, U.; Crewel, S.; Simmer, C.; Macke, A. Profiling cloud liquid water by combining active and passive microwave measurements with cloud model statistics. J. Atmos. Ocean. Technol. 2001, 18, 1354–1366. [Google Scholar] [CrossRef]
- Frisch, A.S.; Fairall, C.W.; Snider, J.B. Measurement of Stratus Cloud and Drizzle Parameters in ASTEX with a Kα–Band Doppler Radar and a Microwave Radiometer. J. Atmos. Sci. 1995, 52, 2788–2799. [Google Scholar] [CrossRef]
- Khain, A.; Pinsky, M.; Magaritz, L.; Krasnov, O.; Russchenberg, H.W.J. Combined observational and model investigations of the Z-LWC relationship in stratocumulus clouds. J. Appl. Meteorol. Climatol. 2008, 47, 591–606. [Google Scholar] [CrossRef]
- Pilié, R.J.; Mack, E.J.; Kocmond, W.C.; Eadie, W.J.; Rogers, C.W. The Life Cycle of Valley Fog. Part II: Fog Microphysics. J. Appl. Meteorol. 1975, 14, 364–374. [Google Scholar] [CrossRef]
- Meyer, M.B.; Lala, G.G.; Jiusto, J.E. Fog-82: A Cooperative Field Study of Radiation Fog. Bull. Am. Meteorol. Soc. 1986, 67, 825–832. [Google Scholar] [CrossRef]
- Welch, R.M.; Ravichandran, M.G.; Cox, S.K. Prediction of Quasi-Periodic Oscillations in Radiation Fogs. Part I: Comparison of Simple Similarity Approaches. J. Atmos. Sci. 1986, 43, 633–651. [Google Scholar] [CrossRef]
- Wendisch, M.; Mertes, S.; Heintzenberg, J.; Wiedensohler, A.; Schell, D.; Wobrock, W.; Frank, G.; Martinsson, B.G.; Fuzzi, S.; Orsi, G.; et al. Drop size distribution and LWC in Po Valley fog. Contrib. Atmos. Phys. 1998, 71, 87–100. [Google Scholar]
- Guyot, G.; Gourbeyre, C.; Febvre, G.; Shcherbakov, V.; Burnet, F.; Dupont, J.C.; Sellegri, K.; Jourdan, O. Quantitative evaluation of seven optical sensors for cloud microphysical measurements at the Puy-de-Dôme Observatory, France. Atmos. Meas. Tech. 2015, 8, 4347–4367. [Google Scholar] [CrossRef]
- Egli, S.; Maier, F.; Bendix, J.; Thies, B. Vertical distribution of microphysical properties in radiation fogs—A case study. Atmos. Res. 2015, 151, 130–145. [Google Scholar] [CrossRef]
- Droplet Measurement Technologies (DMT). Data Analysis User’s Guide Chapter I : Single Particle Light Scattering; Droplet Measurement Technologies: Boulder, CO, USA, 2009; p. 44. [Google Scholar]
- Lance, S.; Brock, C.A.; Rogers, D.; Gordon, J.A. Water droplet calibration of the Cloud Droplet Probe (CDP) and in-flight performance in liquid, ice and mixed-phase clouds during ARCPAC. Atmos. Meas. Tech. 2010, 3, 1683–1706. [Google Scholar] [CrossRef]
- Bristol Industrial & Research Associates Ltd (Biral). HSS VPF-730 Combined Visibility & Present Weather Sensor; Bristol Industrial and Research Associates Limited: Portishead, Bristol, UK, 2012; p. 2. [Google Scholar]
- Maier, F.; Bendix, J.; Thies, B. Development and application of a method for the objective differentiation of fog life cycle phases. Tellus Ser. B 2013, 65, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods, 4th ed.; Hodder Arnold: London, UK, 1976; p. 210. [Google Scholar]
- Fisher, R. Statistical Methods for Research Workers, 5th ed.; Oliver & Boyd: Edinburgh, UK, 1925; p. 336. [Google Scholar]
- Hess, P.; Brezowsky, H. Katalog der Grosswetterlagen Europas 1881–1976, 3. verbesserte und ergänzte Aufl.; Deutscher Wetterdienst: Offenbach am Main, Germany, 1977; p. 68. [Google Scholar]
- James, P.M. An objective classification method for Hess and Brezowsky Grosswetterlagen over Europe. Theor. Appl. Climatol. 2007, 88, 17–42. [Google Scholar] [CrossRef]
- Garbow, B.S.; Hillstrom, K.E.; More, J.J. Documentation for MINPACK subroutine LMDIF; Argonne National Laboratory: Argonne, IL, USA, 1980. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Adirosi, E.; Volpi, E.; Lombardo, F.; Baldini, L. Raindrop size distribution: Fitting performance of common theoretical models. Adv. Water Resour. 2016, 96, 290–305. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583. [Google Scholar] [CrossRef]
- Harris, D. The attenuation of electromagnetic waves due to atmospheric fog. Int. J. Infrared Millim. Waves 1995, 16, 1091–1108. [Google Scholar] [CrossRef]
- Arnulf, A.; Bricard, J.; Curé, E.; Véret, C. Transmission by Haze and Fog in the Spectral Region 0.35 to 10 Microns. J. Opt. Soc. Am. 1957, 47, 491–497. [Google Scholar] [CrossRef]
- Best, A.C. Drop-size distribution in cloud and fog. Q. J. R. Meteorol. Soc. 1951, 77, 418–426. [Google Scholar] [CrossRef]
- Eldridge, R.G. Haze and Fog Aerosol Distributions. J. Atmos. Sci. 1966, 23, 605–613. [Google Scholar] [CrossRef]
- Garland, J.A. Some fog droplet size distributions obtained by an impaction method. Q. J. R. Meteorol. Soc. 1971, 97, 483–494. [Google Scholar] [CrossRef]
- Pilié, R.; Eddie, W.; Mack, E.; Rogers, C.; Kocmond, W. Project Fog Drops Part I: Investigations of Warm Fog Properties; Technical Report August; Cornell Aeronautical Laboratory, Inc.: Buffalo, NY, USA, 1972. [Google Scholar]
- Garland, J.A.; Branson, J.R.; Cox, L.C. A study of the contribution of pollution to visibility in a radiation fog. Atmos. Environ. 1973, 7, 1079–1092. [Google Scholar] [CrossRef]
- Reudenbach, C.; Bendix, J. Experiments with a straightforward model for the spatial forecast of fog/low stratus clearance based on multi-source data. Meteorol. Appl. 1998, 5, 205–216. [Google Scholar] [CrossRef]
- Tampieri, F.; Tomasi, C. Size distribution models of stratospheric particles in terms of the modified gamma function. Arch. Meteorol. Geophys. Bioklimatol. Ser. A 1976, 25, 47–54. [Google Scholar] [CrossRef]
- Tomasi, C.; Tampieri, F. Features of the proportionality coefficient in the relationship between visibility and liquid water content in haze and fog. Atmosphere 1976, 14, 61–76. [Google Scholar]
- Joss, J.; Gori, E.G. Shapes of Raindrop Size Distributions. J. Appl. Meteorol. 1978, 17, 1054–1061. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Flatau, P.J.; Tripoli, G.J.; Verlinde, J.; Cotton, W.R. The CSU-RAMS Cloud Microphysics Module: General Theory and Code Documentation; Colorado State University, Deptartment of Atmospheric Science: Fort Collins, CO, USA, 1989; p. 90. [Google Scholar]
- Deirmendjian, D. Electromagnetic Scattering on Spherical Polydispersions; American Elsevier Publishing Company: New York, NY, USA, 1969; p. 318. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Sums, Series, and Products, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Danne, O. Messungen physikalischer Eigenschaften stratiformer Bewölkung mit einem 94 GHz—Wolkenradar. Ph.D Thesis, University of Hannover, Hannover, Germany, 1996. [Google Scholar]
- Rinehart, R.E. Radar for Meteorologists, 4th ed.; Rinehart Publications: Columbia, SC, USA, 1997; p. 428. [Google Scholar]
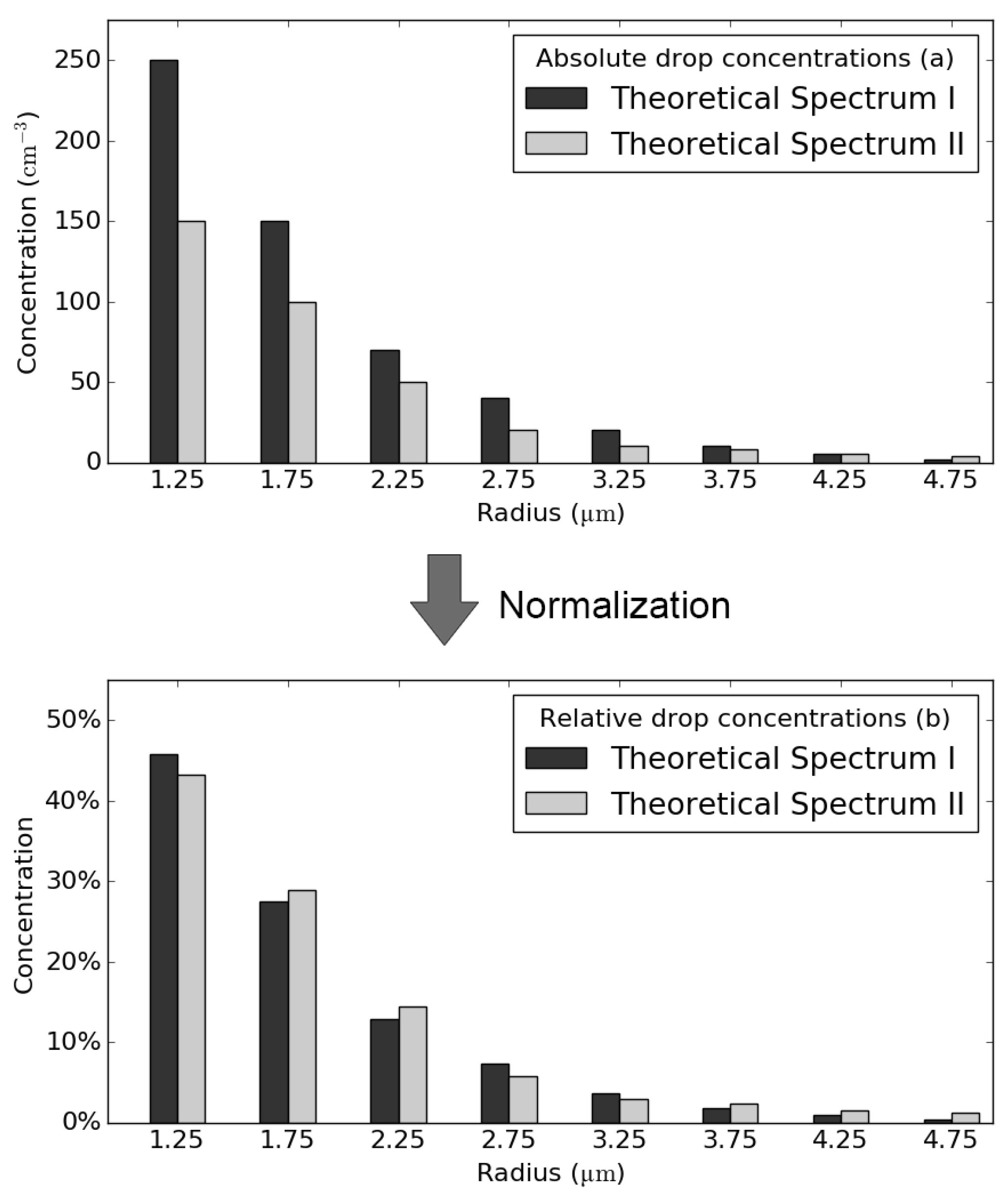
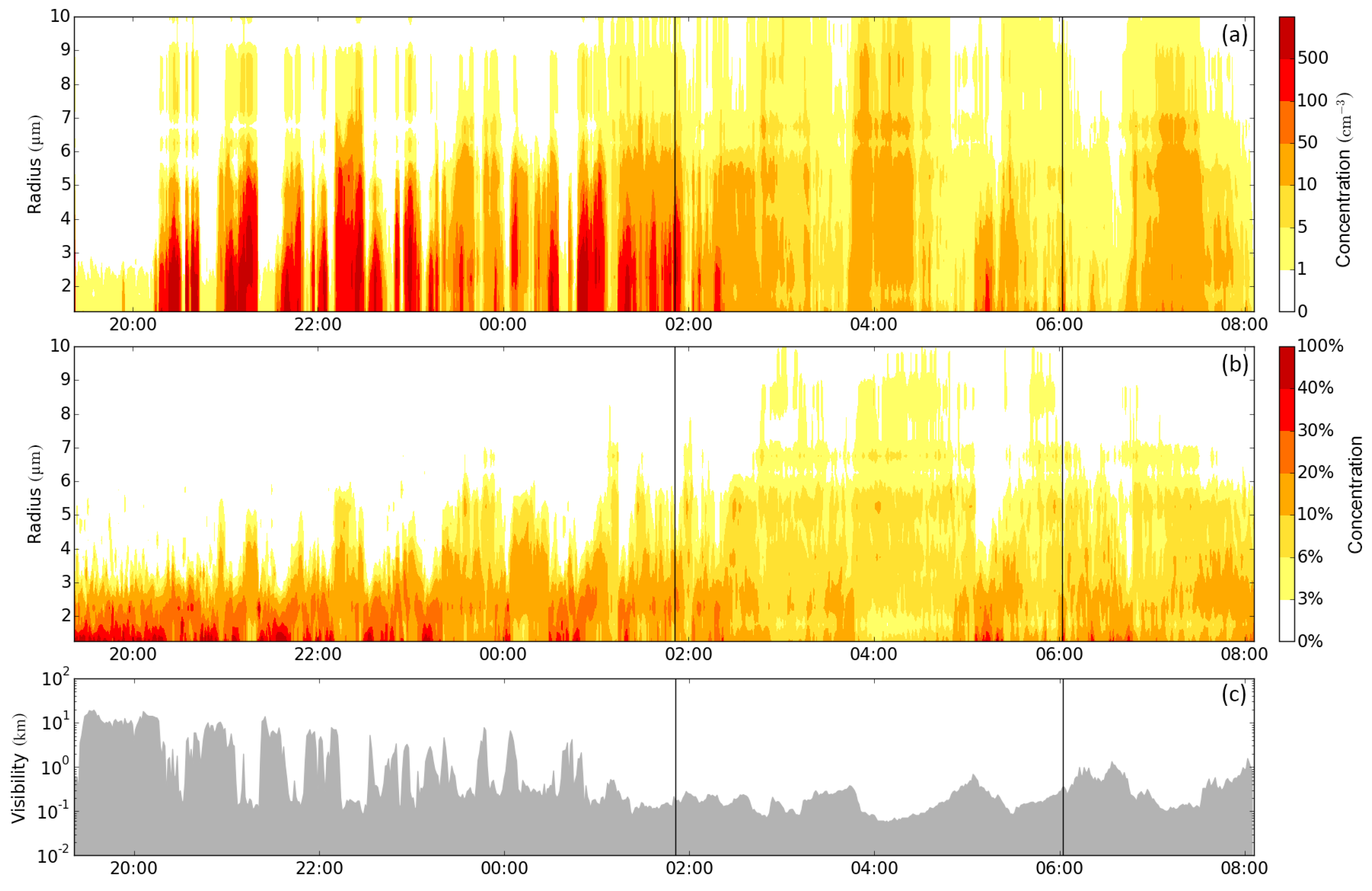
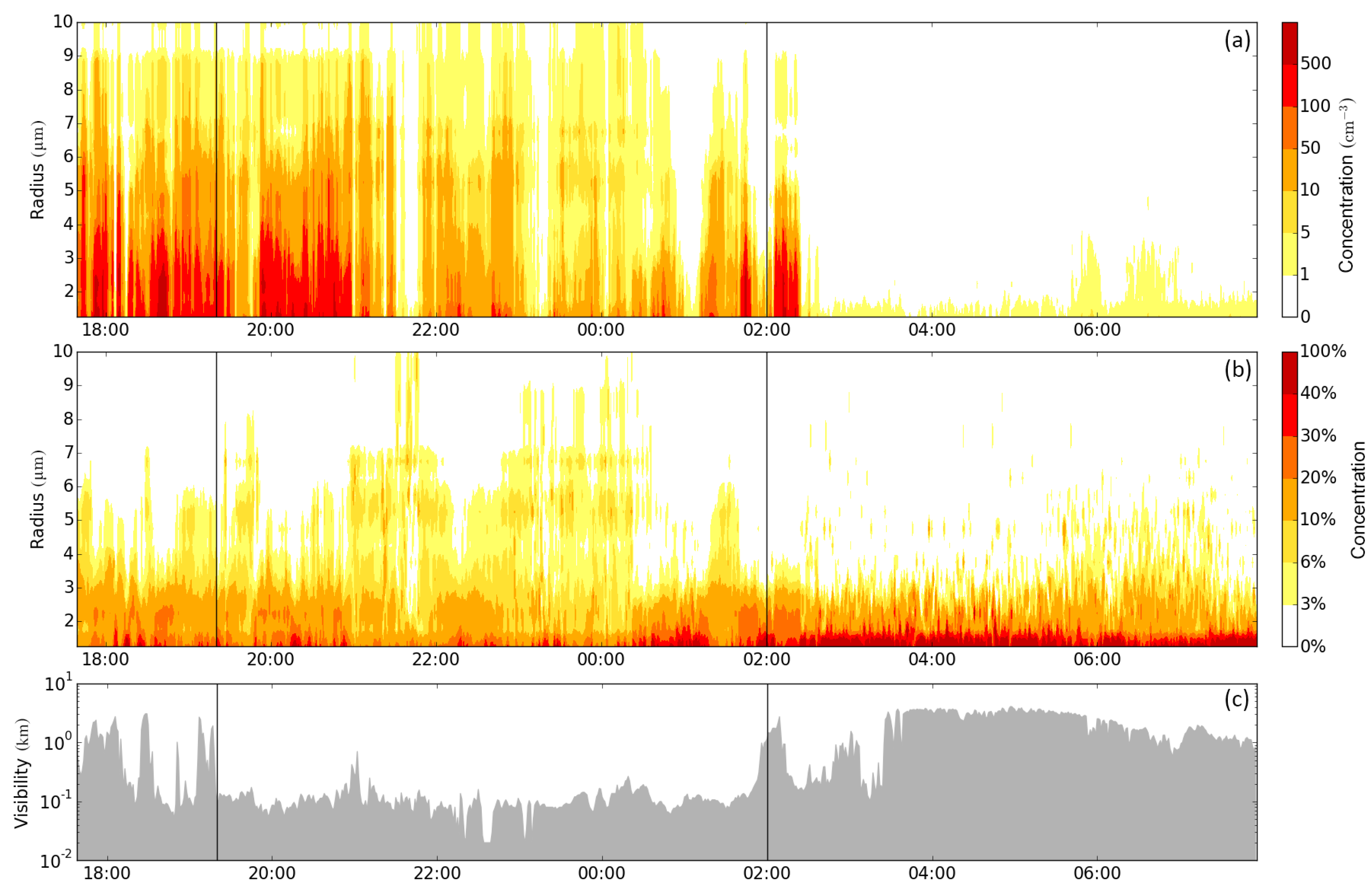
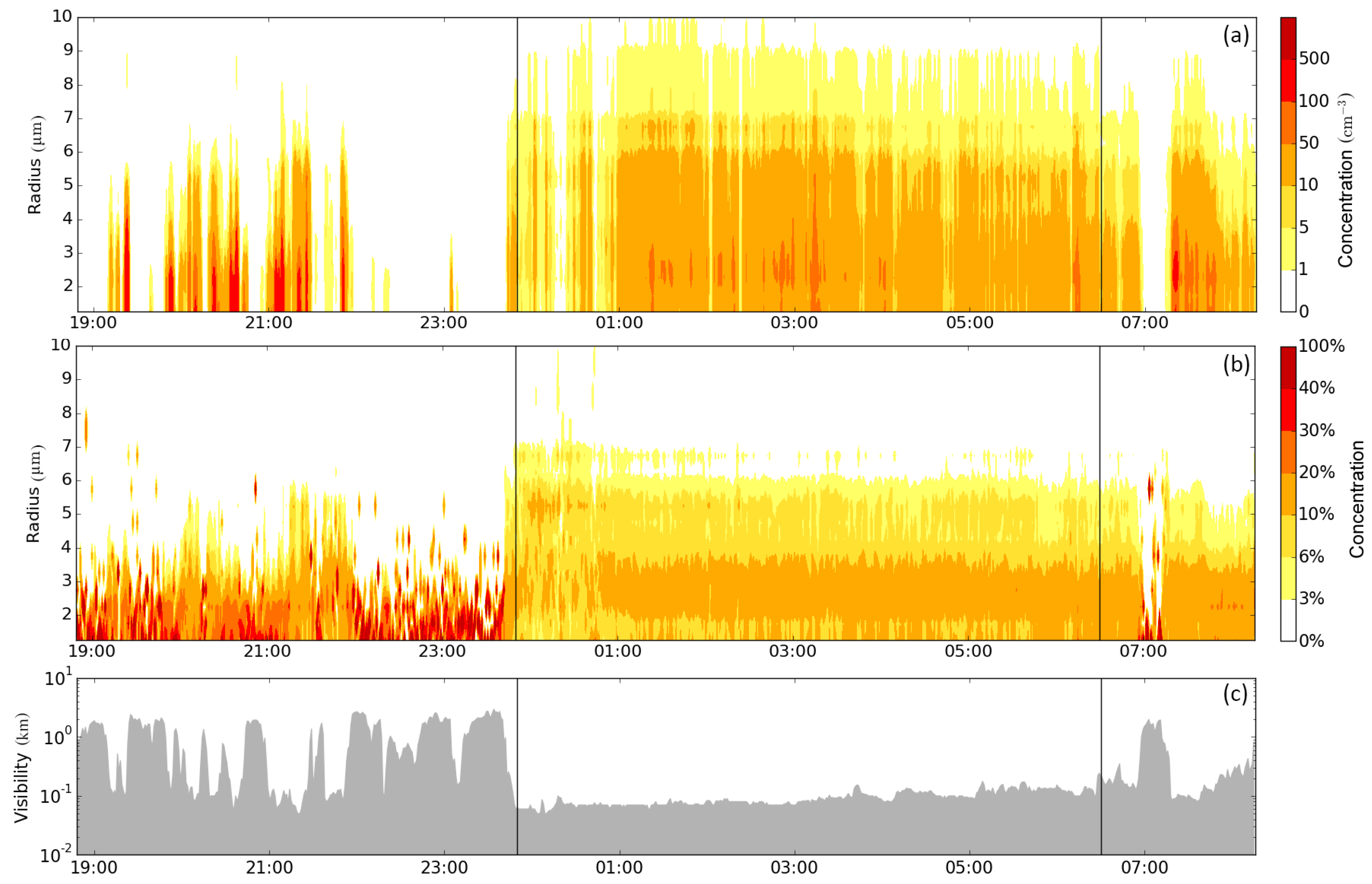
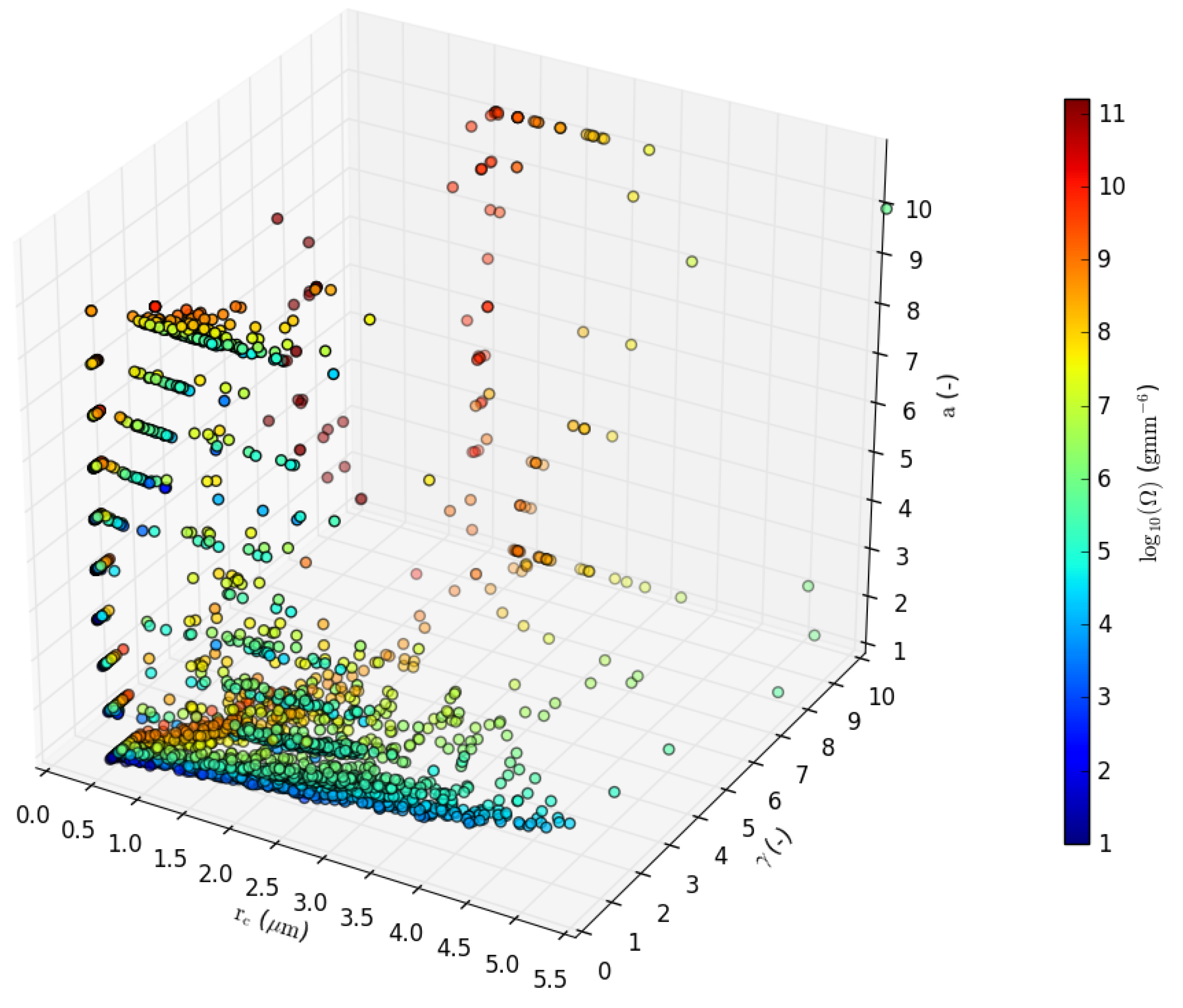

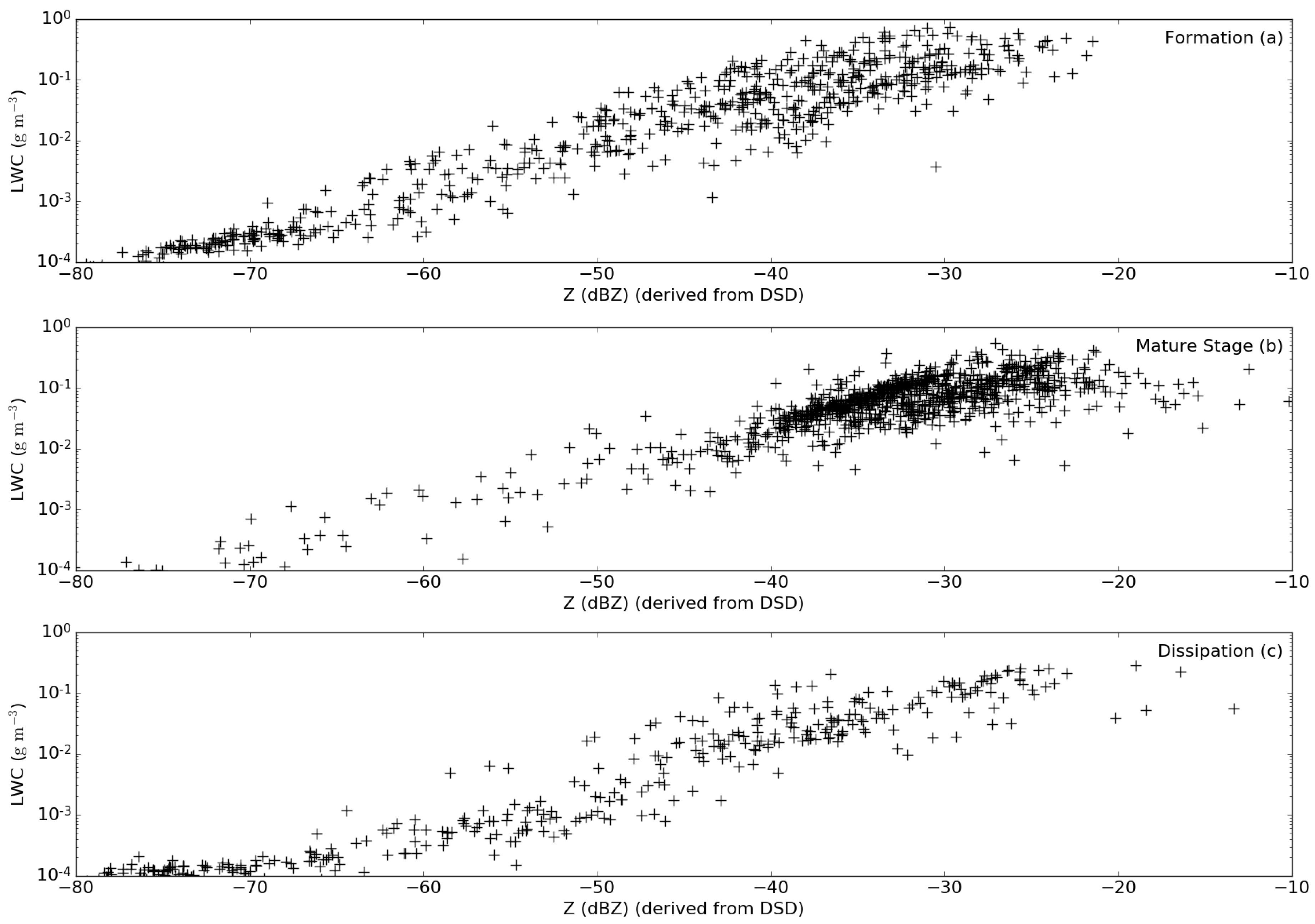
| No. | Start and End Date (UTC) | Stage Duration (min) | Weather Regime | ||
|---|---|---|---|---|---|
| Formation | Mature Stage | Dissipation | |||
| 1 | 26 Oct. 2011 19:21 to 27 Oct. 2011 08:05 | 390 | 250 | 125 | SEZ |
| 2 | 31 Oct. 2011 17:38 to 01 Nov. 2011 07:55 | 100 | 400 | 358 | BM to SA |
| 3 | 13 Nov. 2011 18:48 to 14 Nov. 2011 08:15 | 300 | 400 | 108 | HNA |
| No. | Absolute Average Spectra | Relative Average Spectra | ||||
|---|---|---|---|---|---|---|
| Formation | Mature Stage | Dissipation | Formation | Mature Stage | Dissipation | |
| 1 | 1.03 × 103 | 1.30 × 102 | 8.90 × 102 | 0.46 | 0.34 | 0.29 |
| 2 | 7.41 × 102 | 3.75 × 102 | 1.02 × 102 | 0.30 | 0.43 | 0.43 |
| 3 | 1.32 × 102 | 1.10 × 102 | 8.70 × 102 | 0.79 | 0.19 | 0.65 |
| 1,2,3 | 7.41 × 102 | 2.27 × 102 | 1.05 × 102 | 0.57 | 0.41 | 0.60 |
| Life Cycle Stage | b | |||
|---|---|---|---|---|
| Formation | 5 | 0.36 | 13.37 | 1.13 |
| Mature stage | 1 | 0.84 | 0.96 | 1.29 |
| Dissipation | 5 | 0.21 | 27.10 | 0.50 |
| No. | Stage | Min. | Mean | Max. | Range | STD | 5% PCTL | 95% PCTL |
|---|---|---|---|---|---|---|---|---|
| 1 | F | 2.76 × 101 | 1.67 × 103 | 8.29 × 103 | 8.26 × 103 | 1.53 × 103 | 1.13 × 103 | 4.86 × 103 |
| 1 | M | 5.00 × 10−1 | 8.28 × 101 | 8.03 × 102 | 8.02 × 102 | 7.68 × 101 | 6.74 × 101 | 1.78 × 102 |
| 1 | D | 3.50 × 10−1 | 1.06 × 102 | 3.56 × 102 | 3.56 × 102 | 6.34 × 101 | 1.00 × 102 | 2.26 × 102 |
| 2 | F | 2.34 × 101 | 4.09 × 102 | 4.87 × 103 | 4.85 × 103 | 8.07 × 102 | 1.92 × 102 | 1.61 × 103 |
| 2 | M | 3.00 × 10−2 | 3.76 × 102 | 1.12 × 104 | 1.12 × 104 | 1.04 × 103 | 8.13 × 101 | 1.91 × 103 |
| 2 | D | 3.19 × 101 | 5.12 × 103 | 6.37 × 104 | 6.37 × 104 | 7.52 × 103 | 3.42 × 103 | 1.69 × 104 |
| 3 | F | 4.20 | 6.57 × 103 | 7.32 × 104 | 7.32 × 104 | 1.44 × 104 | 1.48 × 103 | 2.04 × 104 |
| 3 | M | 8.80 × 101 | 1.16 × 103 | 7.19 × 104 | 7.19 × 104 | 7.35 × 103 | 2.02 × 102 | 4.22 × 102 |
| 3 | D | 4.35 × 101 | 5.37 × 103 | 7.25 × 104 | 7.25 × 104 | 1.23 × 104 | 9.74 × 102 | 1.82 × 104 |
| 1,2,3 | F | 4.20 | 3.38 × 103 | 7.32 × 104 | 7.32 × 104 | 9.31 × 103 | 9.67 × 102 | 1.06 × 104 |
| 1,2,3 | M | 3.00 × 10−2 | 6.03 × 102 | 7.19 × 104 | 7.19 × 104 | 4.60 × 103 | 1.43 × 102 | 7.27 × 102 |
| 1,2,3 | D | 3.50 × 10−1 | 4.10 × 103 | 7.25 × 104 | 7.25 × 104 | 8.10 × 103 | 1.29 × 103 | 1.59 × 104 |
| 1 | F,M,D | 3.50 × 10−1 | 8.95 × 102 | 8.29 × 103 | 8.29 × 103 | 1.35 × 103 | 1.84 × 102 | 3.80 × 103 |
| 2 | F,M,D | 3.00 × 10−2 | 2.36 × 103 | 6.37 × 104 | 6.37 × 104 | 5.44 × 103 | 2.56 × 102 | 9.87 × 103 |
| 3 | F,M,D | 4.20 | 3.73 × 103 | 7.32 × 104 | 7.32 × 104 | 1.14 × 104 | 2.48 × 102 | 1.77 × 104 |
| 1,2,3 | F,M,D | 3.00 × 10−2 | 2.36 × 103 | 7.32 × 104 | 7.32 × 104 | 7.46 × 103 | 2.43 × 102 | 8.74 × 103 |
| Life Cycle Stage | ZLWC5% | ZLWCmed | ZLWC95% | LWCZ5% | LWCZmed% | LWCZ95% |
|---|---|---|---|---|---|---|
| Formation stage | −74.9 | −42.1 | −29.5 | 1.45 × 10−7 | 6.82 × 10−3 | 4.03 × 10−1 |
| Mature stage | −45.5 | −30.6 | −25.2 | 2.48 × 10−4 | 3.95 × 10−2 | 4.64 × 10−1 |
| Dissipation stage | −64.2 | −56.3 | −26.8 | 1.32 × 10−7 | 8.65 × 10−6 | 1.15 × 10−1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thies, B.; Egli, S.; Bendix, J. The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs. Atmosphere 2017, 8, 142. https://doi.org/10.3390/atmos8080142
Thies B, Egli S, Bendix J. The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs. Atmosphere. 2017; 8(8):142. https://doi.org/10.3390/atmos8080142
Chicago/Turabian StyleThies, Boris, Sebastian Egli, and Jörg Bendix. 2017. "The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs" Atmosphere 8, no. 8: 142. https://doi.org/10.3390/atmos8080142
APA StyleThies, B., Egli, S., & Bendix, J. (2017). The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs. Atmosphere, 8(8), 142. https://doi.org/10.3390/atmos8080142





