4.1. Control Simulations
To first have a broad picture of the difference in the initial environmental conditions in the CTL experiments between the two basins,
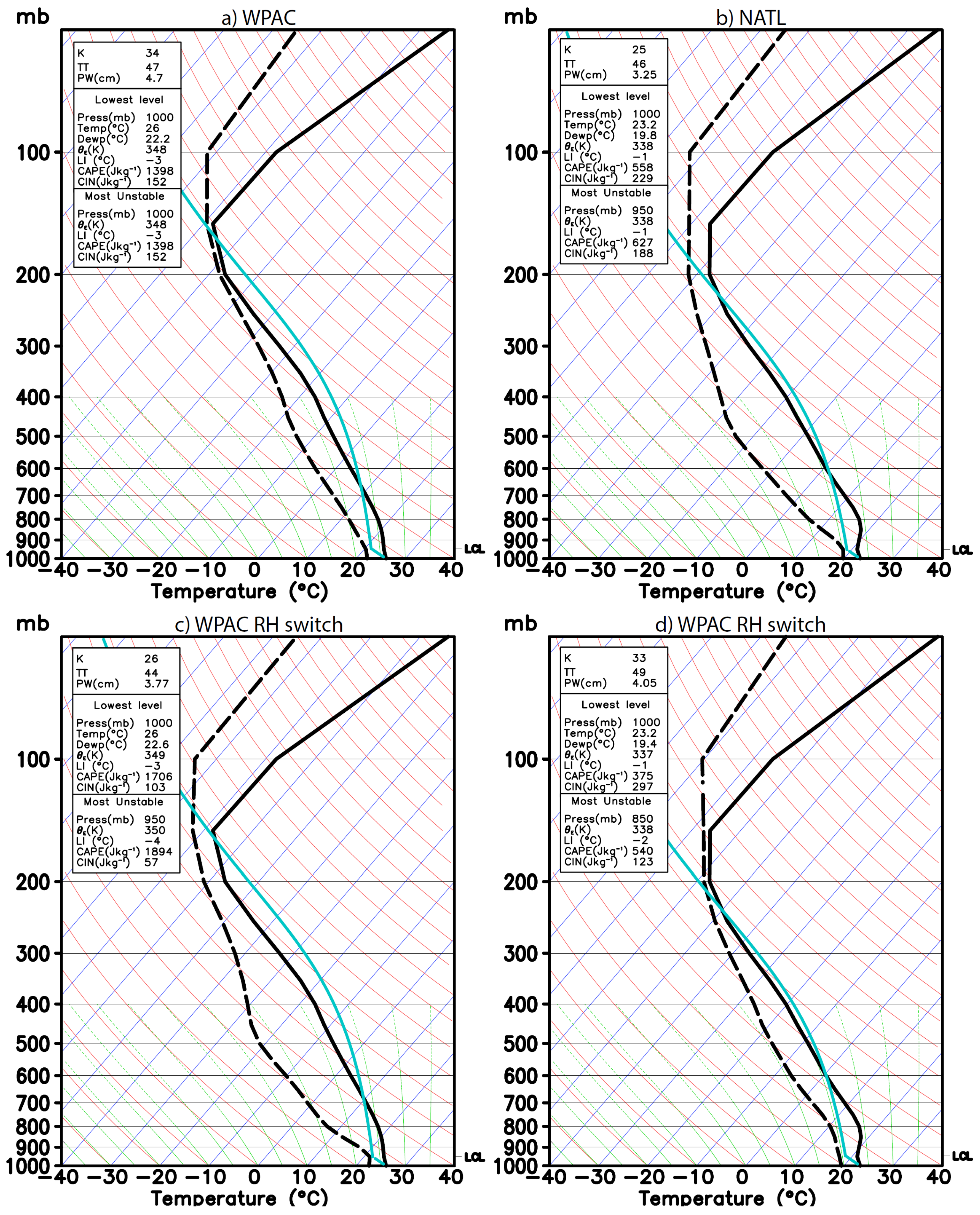
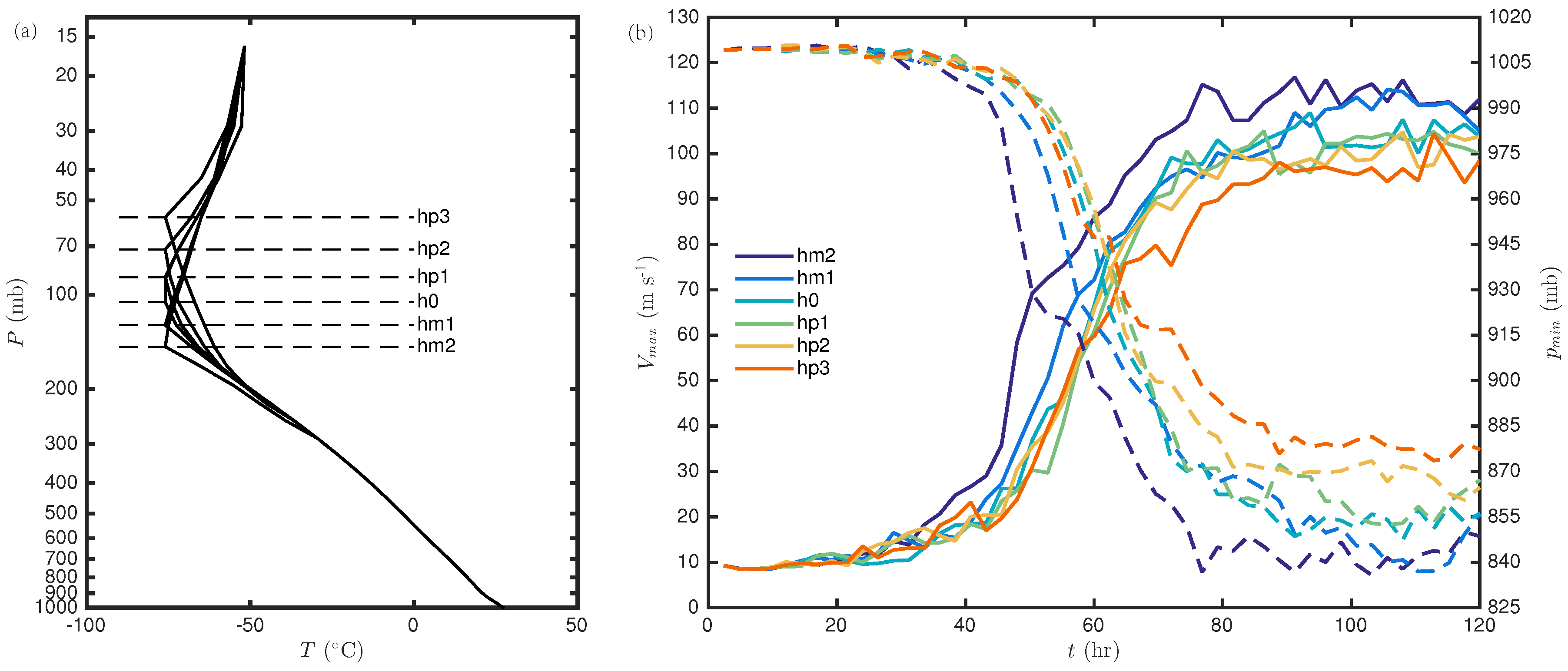
Figure 3 shows the initial soundings used to initialize the HWRF model in the NATL and WPAC basins. Consistent with the large-scale characteristics of the troposphere, the WPAC profile has a generally higher tropopause and more tropospheric moisture compared to the NATL sounding. A simple evaluation of the tropopause height, using the tropopause definition as a layer in which the temperature is minimum and the temperature gradient is less than 1 K km
−1, indicates that the tropopause in the WPAC basin is located around the 120–130 hPa level (
Figure 3a), while it is roughly at 140–150 hPa in the NATL basin (
Figure 3b). Likewise, the difference in the relative humidity is as large as 25% for much of the troposphere, indicating substantially more tropospheric moisture in the WPAC basin.
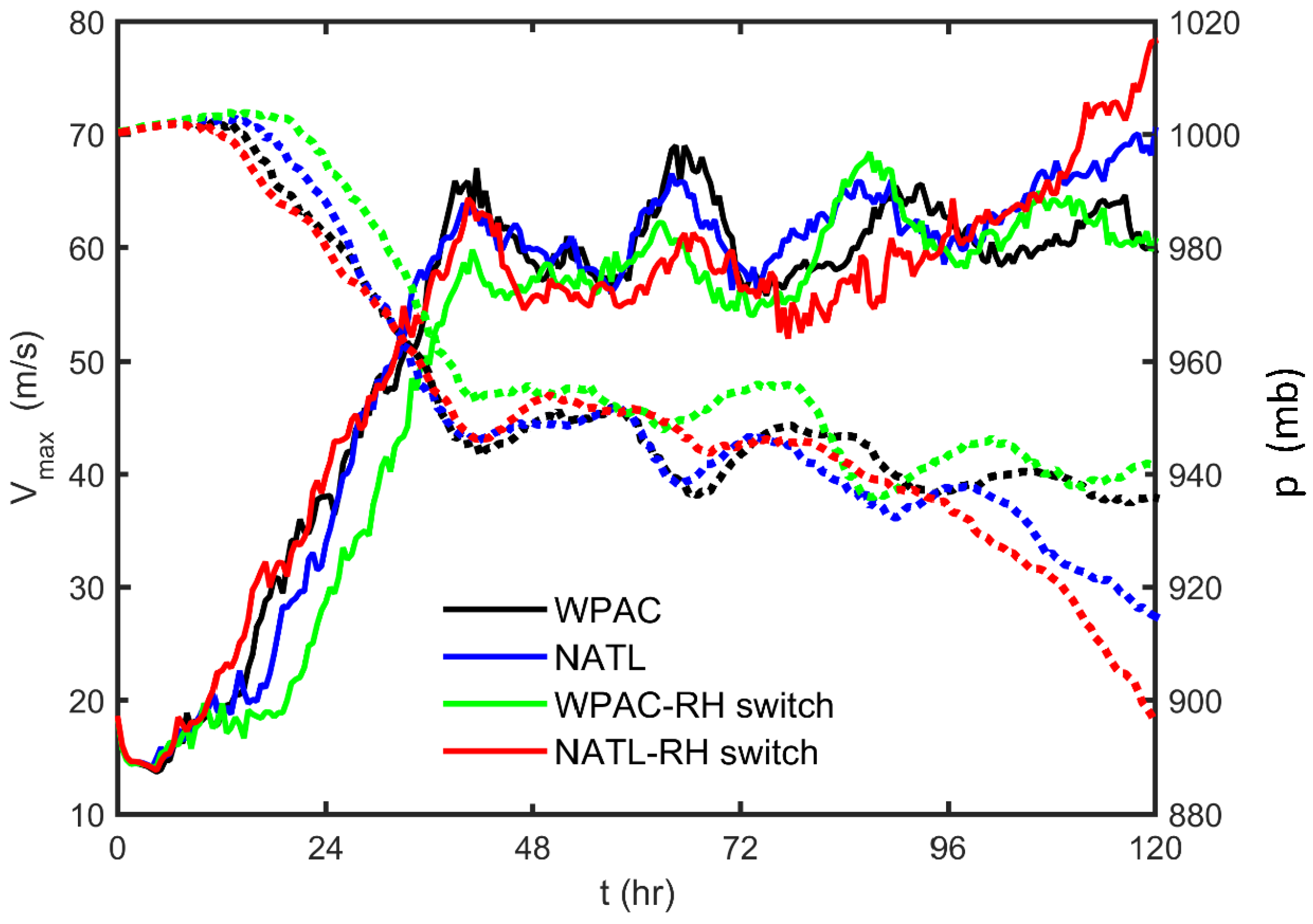
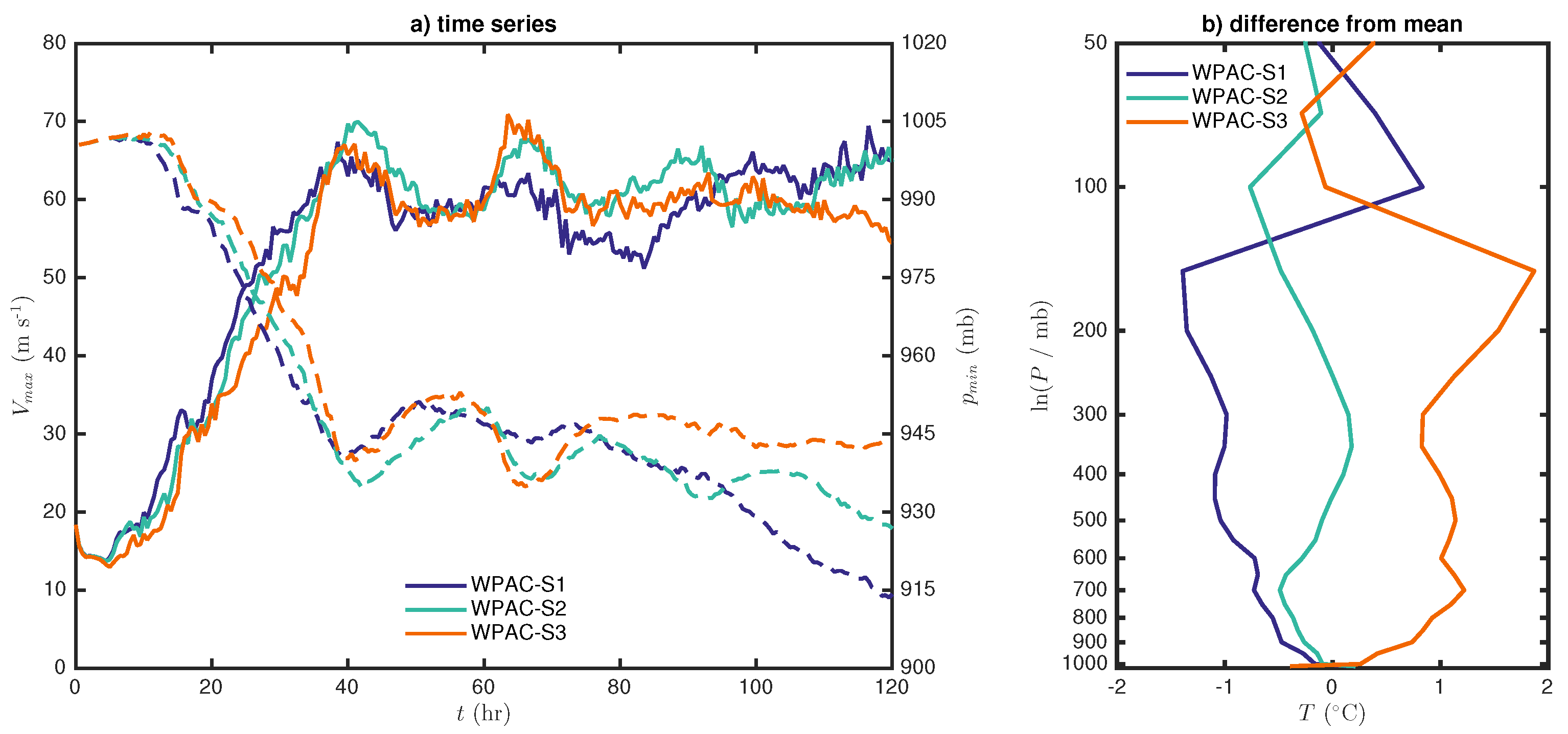
Figure 4 displays the time series of the maximum 10-m tangential wind (
) and the minimum central pressure (
) for the CTL experiments in both the WPAC and NATL basins, along with the two additional experiments in which the moisture profiles are switched. Unlike the expectation of a stronger storm in the WPAC basin from the climatological perspective, it is of interest to notice that both idealized TCs developing in the NATL basin attain significantly higher
and lower
after five days of simulation than those in the WPAC basin under the same SST condition. The strongest storm by a large margin appears to be that initialized with the temperature profile from NATL but with a more moist RH profile from the WPAC. Similarly, the WPAC storm using the NATL moisture profile is slightly less intense than the WPAC-CTL storm at 5 days into integration.
That the NATL temperature sounding results in stronger storms regardless of the moisture profiles indicates the overall more important role of the temperature structure in determining the maximum intensity limit. On the other hand, the similar role of the moisture profiles in changing the storm intensity between the CTL experiments and the RH-switching experiments in both the WPAC and the NATL basins suggests that the theoretical MPI limit may not fully explain the model-simulated maximum intensity limit. Specifically, the less mid-tropospheric moisture profile tends to delay the intensification as seen from both the RH-switched experiments in
Figure 4. One can readily verify the relative role of the temperature and moisture profile to TC intensity within the MPI framework by using the theoretical MPI calculation based on the expression in [
31] for four different soundings. While the theoretical MPI limits tend to overestimate the actual maximum intensity obtained from the HWRF model as shown in
Table 3, it is apparent that the NATL’s temperature profile is more conducive to TC development than that in the WPAC, similar to the HWRF simulations (cf.
Figure 4).
It is somewhat intriguing to see from
Figure 4 and
Table 3 that the NATL storms are consistently stronger than those in the WPAC basin in all the CTL experiments. This may appear difficult to understand at first, because it is well-known from the climatological standpoint that the WPAC basin tends to possess more intense TCs on average [
27]. Such contradictory behaviors of the model storm in the CTL experiments are, nevertheless, understandable if one recalls that the SST is fixed at 302 K in all experiments. In practice, the SST in the NATL basin is on average 2–3 K cooler than that in the WPAC basin, which translates to significantly smaller enthalpy fluxes and results in a climatology of overall less counts of intense TCs in the NATL basin. Our sensitivity experiments with both the HWRF model and the theoretical MPI calculations confirm that the MPI limit depends crucially on the SST values (not shown). With a fixed SST value of 302 K, the above CTL experiments reveal however an interesting consequence that the tropospheric structure in the NATL basin during August 2013 turns out to be more conducive to the development of intense TCs, thus resulting in a stronger storm as seen in
Figure 4.
It should be mentioned that the more favorable structure for TC development in the NATL basin contrasts with the fact that the 2012–2014 seasons were relatively less active in the NATL basin with very few major hurricanes, particularly in the 2014 season. This inactive season in the NATL basin reflects the fact that the TC development depends on other large-scale conditions such as dry air intrusion, vertical wind shear, SST variation, or the Sahara dust intrusion that the idealized configuration in this study could not capture.
Given the importance of the DWC structure in the development of intense TCs as discussed in [
11], it is anticipated that the lower tropopause height in the NATL basin could be a factor determining its higher storm intensity through the enhanced DWC development. To examine how the DWC development is related to the more favorable tropopause condition with the NATL sounding,
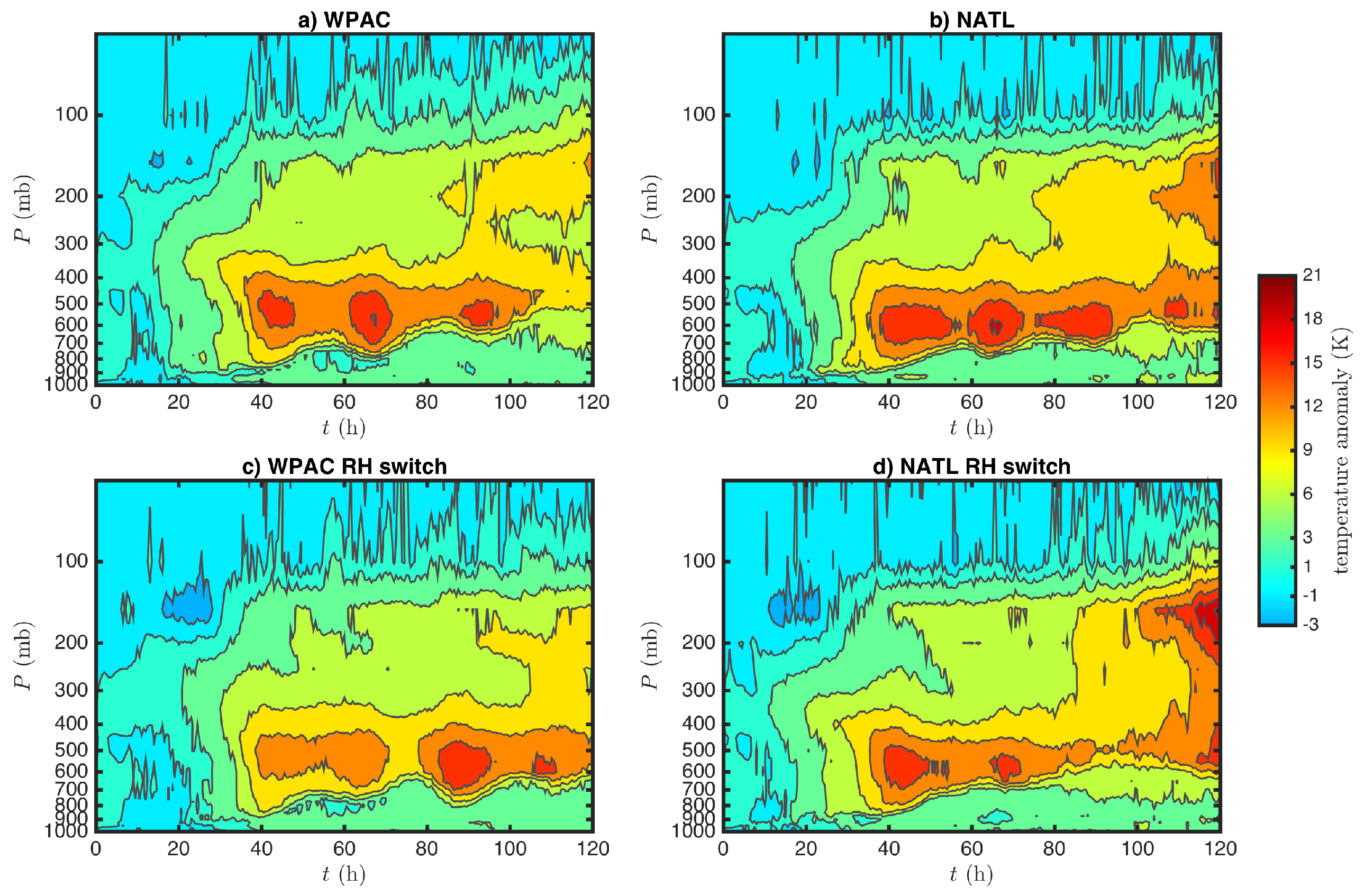
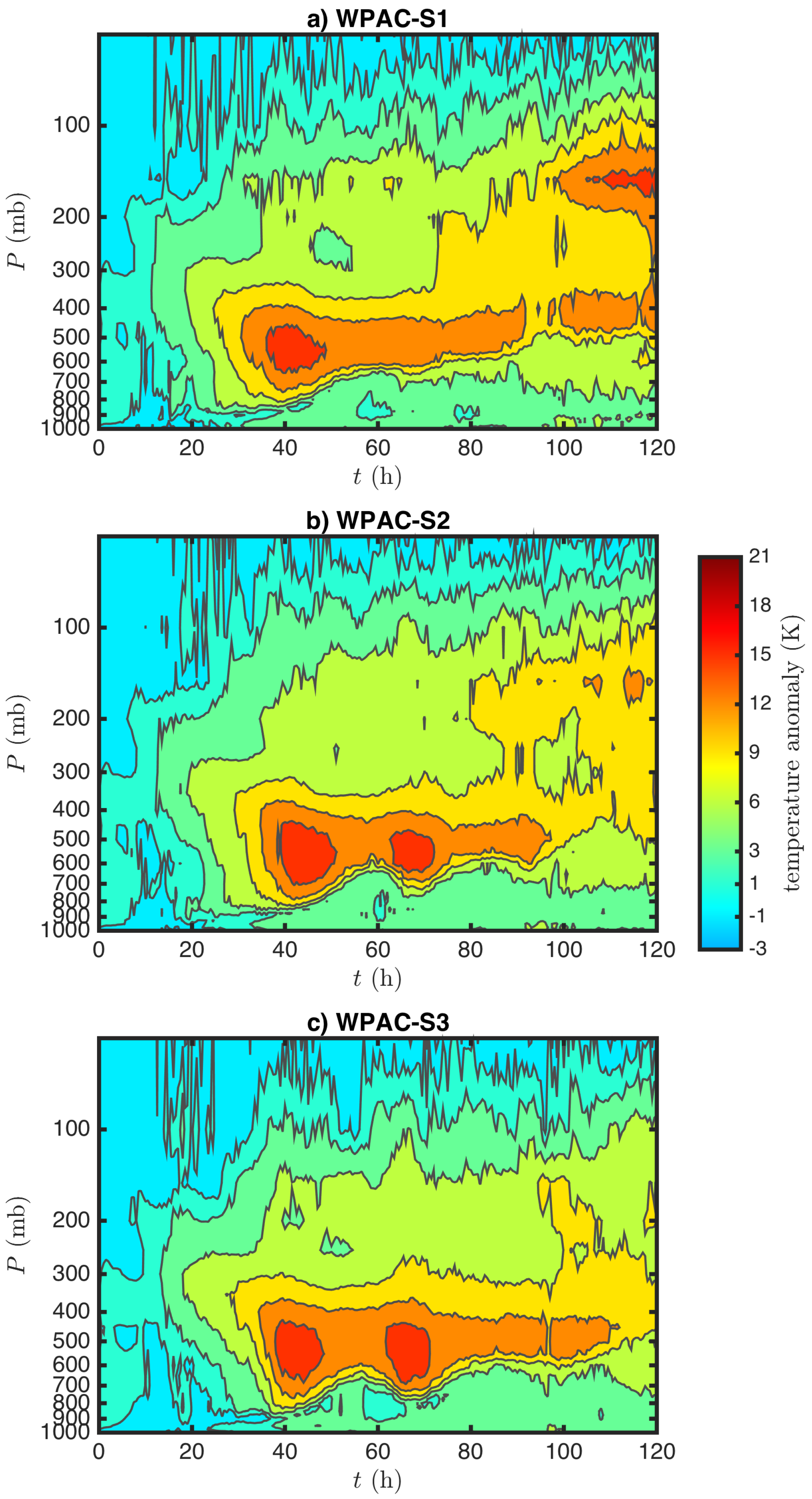
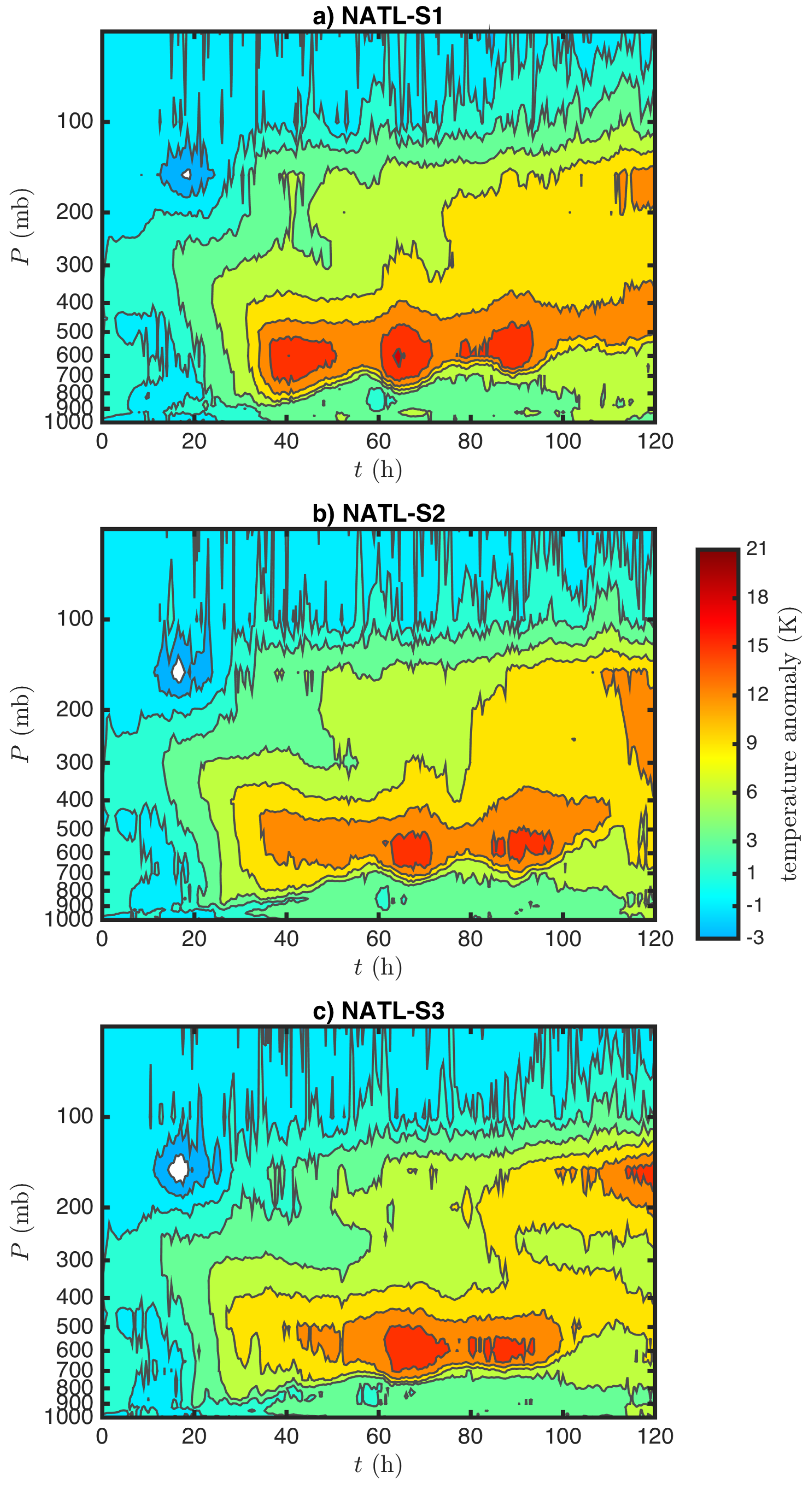
Figure 5 shows the Hovmöller diagram of the temperature anomaly at the storm center in the CTL experiments during the course of the 5-day integration. Here, the temperature anomaly is defined as the temperature difference between the vortex center and the far-field ambient environment similar to the definition used in [
11]. The far-field ambient temperature in this study is defined as the area-averaged temperature within an annulus of 1000–2000 km radii.
As seen in
Figure 5, the most prominent feature in the CTL experiments is the development of a DWC structure towards the end of the 5-day simulation, regardless of the moisture profile. Consistent with its strongest intensity, the NATL-CTL experiment with the WPAC moisture possesses a larger positive temperature anomaly at the end of the simulation, with the HWC temperature anomaly as large as 18 K (
Figure 5b) as compared to 12 K in the WPAC-CTL experiment (
Figure 5a). Use of the WPAC moisture profile produces even a larger impact in the NATL basin in terms of the magnitude of the upper warm anomaly, resulting in an HWC with a temperature anomaly ∼21 K (
Figure 5d). In the WPAC, the moisture profile switch experiment appears to have less of an impact, and its influence is not apparent in the first 48 h. The DWC development seen in
Figure 5 is consistent with the time series of the
in
Figure 4, suggesting that the later phase of intensification of the model storm from
h to
h is related to the interaction of the LSL with the TC inner core, at least in our CTL idealized configurations with a constant SST.
It is important to note that while the formation of an mid-level warm core is natural and persists in the 500–400 hPa layer throughout all stages of the TC development, the formation of an HWC is intermittent during the early phase of the storm development in all experiments. Similar to [
11], the HWC in all four CTL experiments becomes most apparent only after the vortex intensity reaches 61 m s
−1 with a well-defined eye. Additionally, the emergence of the HWC is separate from the mid-level warm core, and its formation precedes a second phase of intensification from
h to
h (cf.
Figure 4) in all experiments. Such independent development of the HWC and the lower warm core around 5–6 km is not specific to the HWRF model or any experiments, but can be seen also in recent analyses of temperature anomalies by [
14,
15], suggesting that the HWC development is strongly associated with the late intensification of an already intense storm.
To further see the differences in the entire DWC structure among different experiments,
Figure 6 shows a radius-height cross section of the temperature anomaly at the storm center valid at
h at which the DWC is most distinct. In accordance with the interpretation of the Hovmöller diagrams, the HWC is well-defined and situated near the tropopause in all CTL experiments. Compared to the NATL experiments with a more dominant HWC (
Figure 6b,d) and temperature anomalies reaching ∼14 K, the WPAC experiments capture a weaker HWC with the largest temperature anomaly of only ∼9 K. Except for the WPAC experiment with the NATL moisture profile that has the least signal of the HWC, the location of the HWC is always near the tropopause in all experiments, which is very similar to the recent observation of the warm core structure in Hurricane Patricia (2015) during the Office of Naval Research (ONR) Tropical Cyclone Intensity (TCI) field experiment reported by [
8].
That the HWC is always located right below the tropopause indicates that its formation must have some connection with the lower stratosphere aloft. A recent study by [
11] suggested that the development of the HWC could be connected to the existence of an upper-level inflow in the lower stratosphere layer. As discussed in [
11], an upper-level inflow may emerge if there exits a sufficiently strong inward pressure gradient in the 100–70 hPa layer. Two possible mechanisms for the development of such an inward pressure gradient are radiative cooling at the cloud top in the outer-core region, and the returning inflow associated with overshooting convective rings in the eyewall region as disccused in [
19].
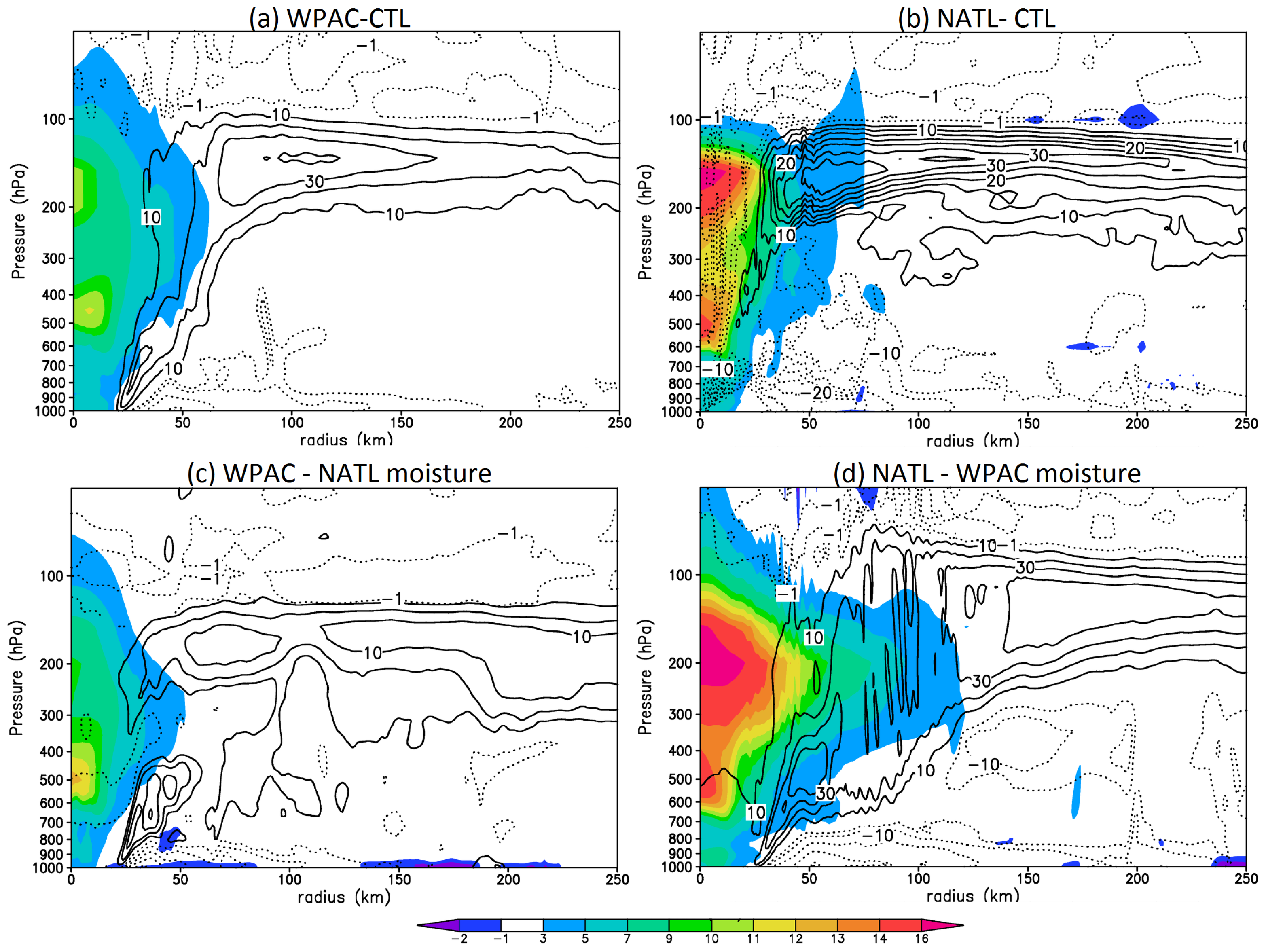
To verify the existence of such an upper-level inflow in the CTL experiments,
Figure 7 shows streamlines averaged in the lower stratosphere layer (i.e., 100–70 hPa), along with streamlines representing the outflow within 150–100 hPa layer valid at
h. As seen in
Figure 3, the 100–70 hPa layer is well within the lower stratosphere layer and can therefore represent well the upper-level inflow above the outflow level in both of the NATL and WPAC basins. One notices in
Figure 3 a clear signal of a cold outer-core annulus from 200 km to 800 km (blue shaded area) along with the existence of the inflow in the LSL very similar to the results in [
11]. The NATL experiment with the WPAC moisture profile (
Figure 7d) most clearly exhibits the upper-level inflow in the lower stratosphere, showing streamlines in the LSL strongly converging toward the vortex center. Our analyses of the temperature budget show that such an upper-level inflow is responsible for a warm advection towards the storm center, thus related to the formation of the HWC as discussed in [
11] (not shown).
The existence of an upper-level inflow above the outflow level as seen in
Figure 6 and
Figure 7 is noteworthy, because it indicates that the LSL is not a simple lid but could strongly interact and modify the structure of intense TCs. Our preliminary analysis of the HDSS dropsondes data for Hurricane Patricia (2015) during the Tropical-Cyclone Intensity field program appears to capture a similar reverse of the flow from outflow around 16.5 km to inflow near the 18-km level. That the HWRF model could capture this upper-level inflow along with the DWC structure consistently in all experiments thus provides strong evidence to support the dynamical role of the lower stratosphere in the development of TCs that is still elusive at present.
4.2. Sensitivity Experiments: WPAC Subdomains
While the CTL experiments could demonstrate the relative importance of the temperature profile as compared to the RH profile in determining the maximum intensity limit and the different inner-core structure between the NATL and the WPAC basins, a remaining question is how the influences of the LSL variations on the DWC development are realized in each basin. An implication obtained from the above CTL experiments in the WPAC and NATL basins is that the lower tropopause height in the NATL basin tends to be more favorable for the DWC development and results in a stronger storm than that in the WPAC basin under the same SST condition.
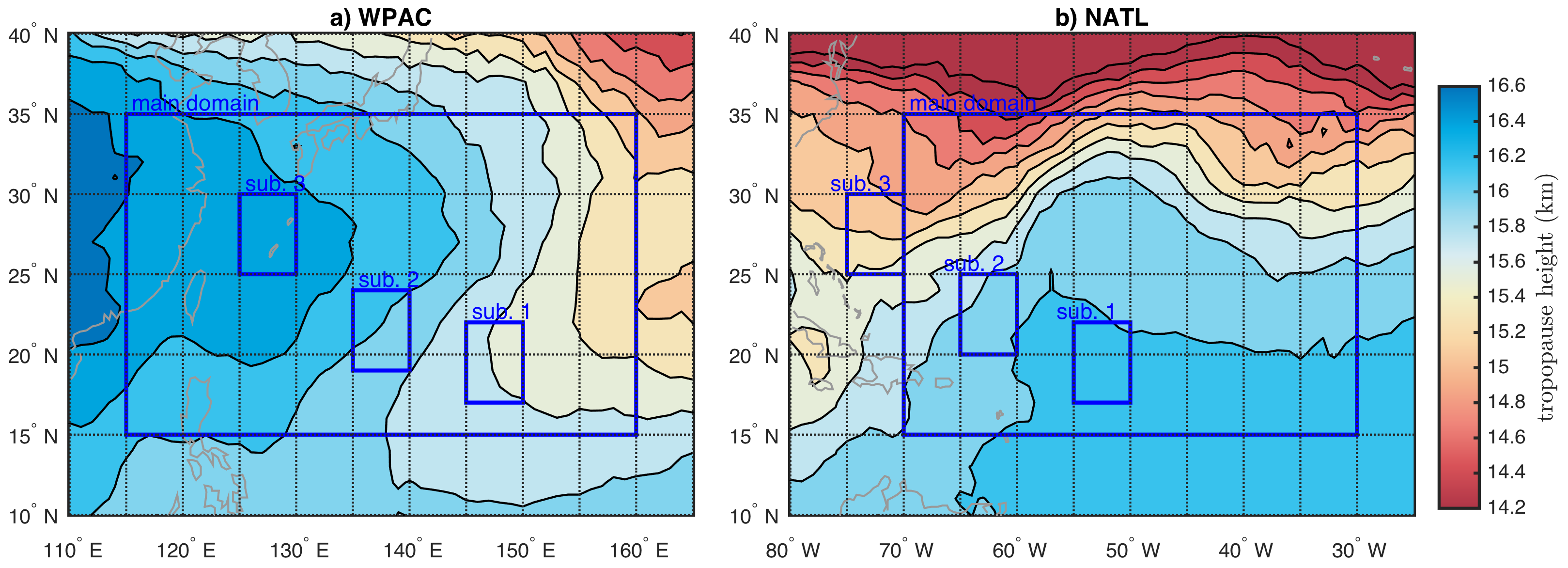
To examine the impacts of tropopause level on the TC inner-core structure in each basin, three subdomains are chosen along the climatological TC tracks in the WPAC basin such that subdomain 1 has the lowest tropopause and subdomain 3 the highest tropopause level as discussed in
Section 3.2 (cf.
Figure 1). With a fixed RH profile in all of these subdomain experiments, it is expected from the CTL experiments that the lower tropopause height would be more favorable for strong storms, i.e., a model vortex developed in subdomain 1 (hereinafter WS1) will be stronger at its peak intensity as compared to those in the subdomain 2 (WS2) and subdomain 3 (WS3) experiments.
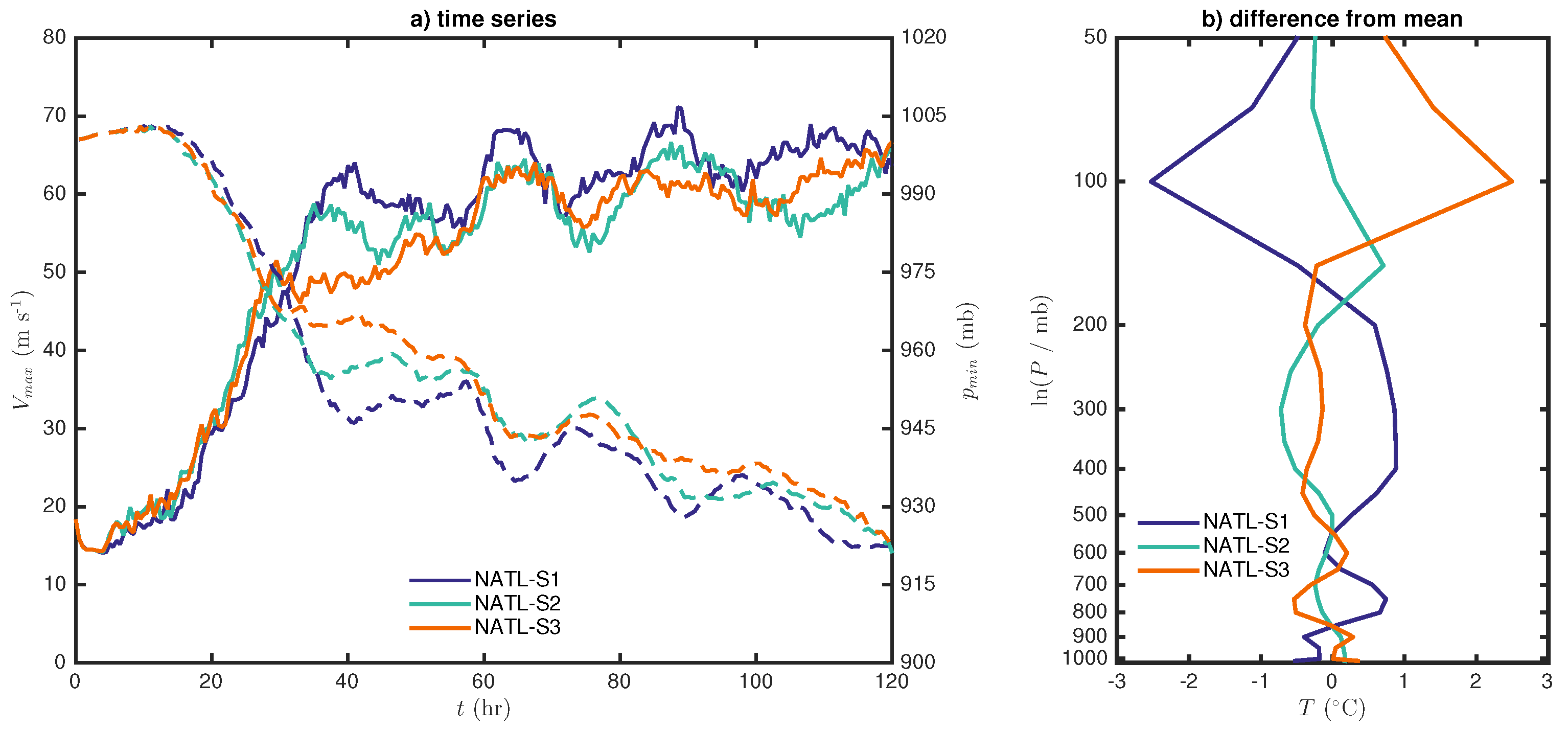
Figure 8 shows the resulting time series for the three WPAC subdomain experiments, along with the comparison of the three initial temperature profiles in the subdomains 1–3. Similar to the results obtained from the CTL experiments, it is of significance to notice a correspondence between the increase in the tropopause height and a general decrease in storm intensity among the three subdomains. The difference in
is generally insignificant during the intensification stage, but more apparent at the end of the simulations during which the interaction between the model vortex and the lower stratosphere appears to be most effective. Specifically, the
in the WS1 experiment reaches as high as 68 m s
−1 at
days, whereas the WS3 storm reaches about 61 m s
−1. The difference in storm intensity is realized even more in terms of
, which shows a clear separation among the three experiments after 5 days into integration, with WS1 having the lowest minimum central pressure and WS3 the highest, and WS2 in between. Although
does not show as a clear signal as
, these sensitivity experiments reiterate the impacts of the tropopause height on the TC development similar to those obtained from the CTL experiments.
Consistent with the time series of the
and
, the Hovmöller diagrams of the temperature anomaly at the storm center confirm the corresponding DWC structure at the later stage of the development of the TCs (
Figure 9). Similar to the CTL experiments seen in
Figure 5, all three subdomain experiments share similar development for the first 12 h. Looking at the 9 K temperature anomaly contour, WS1 seems to show first evidence of formation of a HWC around ∼75 h, followed by WS2 at
h and WS3 at
h. Subsequently, the WS1 storm develops a prominent DWC structure after 5 days into integration, while WS3 has only a vague suggestion of an HWC (cf.
Figure 1 and
Figure 8). Although these idealized experiments are insufficient to make a compelling case for causation of increased intensity due to the lower tropopause, these results do suggest again that the TCs developing in regions of relatively lower tropopause height develop a more distinct DWC structure and consequently attain a greater intensity, at least in the WPAC basin.
That the lower tropopause level in these WPAC subdomain experiment produces a stronger storm may look at first contradictory to RE’s idealized experiments in which they demonstrated that a lower tropopause would lead to weaker storms rather than stronger storms as shown in
Figure 8 (see their experiments A, F, G, H, I). Detailed examination of RE’s tropopause experiments shows, however, that their design of lowering the tropopause implicitly assumed a fixed lapse rate in the upper troposphere such that lowering the tropopause must correspond to a warmer tropopause temperature (see RE’s
Figure 6 and
Figure 7 and their discussion therein). In our WPAC subdomain experiments, note particularly that the tropopause level and temperature in the subdomain experiments S1–S3 do not follow RE’s design (the tropopause temperature of experiments WS1, WS2, WS3 experiments are −74.7 °C, −76.0 °C, and −75.1 °C, respectively). In addition to the variations of tropopause temperature in our WPAC subdomain experiments, we note also that the WPAC subdomain soundings change within the troposphere as seen in
Figure 8b, whereas RE’s experiments maintain the same lapse rate throughout the troposphere. In this regard, the change of the tropopause level in the real environment affects not only the way the model vortex interacts with the LSL aloft, but also the stratification of the troposphere that RE’s experiments could not fully capture. This different design thus accounts for the discrepancy between our WPAC sensitivity experiments and RE’s tropopause experiments.
4.3. Sensitivity Experiments: NATL Subdomains
Unlike the WPAC basin where the tropopause level increases along the climatological storm tracks, the tropopause level in the NATL basin actually decreases as TCs get closer to the coastline. This characteristic of the tropopause level in the NATL basin allows for an opposite way to verify the important role of the TC–lower stratosphere interaction in the DWC development. Note that because of this tropopause height distribution (cf.
Figure 1), subdomain 1 in the NATL basin (NS1), which represents a region where most storms are in earlier developmental stages, has the highest tropopause level, while subdomain 3 (NS3) has the lowest tropopause height, and subdomain 2 (NS2) in the middle but closer to NS1. Given the inverse relationship between the tropopause height and the peaked intensity obtained from the CTL experiments and the subdomain experiments in the WPAC basin, it is expected that the NS3 storm will be most intense, while the NS1 storm is the weakest of the three in the NATL subdomain experiments.
Figure 10a displays time series of intensity for three subdomain experiments in the NATL basin. Unlike the WPAC subdomain experiments, it is intriguing to notice that the three subdomain experiments in the NATL basin are not significantly different from each other at the end of simulations in terms of both the
and the
metric. In fact, NS1 appears to possess slightly higher intensity on average during the entire simulation, while NS2 and NS3 storms are comparable towards the end of the 5-day simulation. Likewise, the indistinguishable
values in
Figure 10 do not allow any justifiable distinction in the storm intensity among all three NATL subdomain experiments.
Analyses of the warm core structure in all NATL subdomain experiments reveal that these experiments in fact possess a similar warm core structure after 5 days into integration instead of very contrasting warm core features as in the WPAC subdomain experiments (see
Figure 9,
Figure 10 and
Figure 11). Corresponding to the insignificant difference in the storm intensity is clear evidence of an HWC in all NATL subdomain experiments (
Figure 11) , although the magnitudes of these HWCs are not exactly equal. Careful examination of the temperature anomaly at
days shows that NS3 has in fact a more prominent HWC as expected from its lowest tropopause height, which exhibits an upper warm core anomaly as large as 15 K at
days, as compared to only 11 K in the NS1 experiment (
Figure 11a,c). However, the NS3 storm eventually approaches a weaker intensity consistent with its weaker lower-level warm core. The dominance of the HWC relative to the mid-level warm core in the NS3 experiment is somewhat difficult to understand, and may be related to the unfavorable tropospheric stratification associated with the lower tropopause that offsets the benefits of the enhanced LSL interaction aloft. While our current model diagnostics is insufficient to confirm this heuristic speculation, the development of a strong HWC with the relatively lower tropopause height in the NS3 experiment could at least indicate that the interaction between TCs and the lower stratosphere is sensitive to the height of the tropopause.
The contrasting outcomes from the above subdomain experiments in the WPAC and the NATL basins can be justified if we recall that the influences of the tropopause height on the TC development and structure are two-fold. On the one hand, the lowering or raising of the tropopause with fixed SST and outflow implies a modification of the entire tropospheric stratification, thus affecting deep convection and the stability of the troposphere. On the other hand, any change to the tropopause height can also alter the LSL stratification, and therefore change how effectively the LSL interacts with the TCs. Depending on the relative roles of these changes in the troposphere and the LSL, the net impact could strengthen or weaken TCs. In our CTL and the WPAC subdomain experiments, a lower tropopause appears to help enhance the TC development by forming a more distinct DWC structure, which indicates the important role of the LSL stratification. However, that the tropopause height tends to have minimal effects in the NATL basin suggests that changes in the troposphere and the LSL associated with the tropopause height variation may cancel out, thus explaining why there is no clear distinction in the storm intensity in the NATL subdomain experiments.
We should mention that the above sensitivity of the TC development to the tropopause height variation is realized not only for the mean soundings in August 2013, but is in fact observed in all of our sensitivity experiments for other months in 2013 including September and October (not shown). In this regard, the contrasting net impact of the tropopause height on the TC development in different basins highlights the hidden role of the LSL that is potentially essential for understanding of the long-term behaviors of intense TCs in different basins. Of course, our results concerning the role of the tropopause height in modulating the TC-LSL interaction are entirely confined within an idealized framework with constant SST and no vertical wind shear nor other large-scale external factors such as the monsoon troughs, topography, or random convective-scale forcings. In practice, variabilities of SST and environmental vertical wind shear have been shown to be also important in determining the long-term variabilities of TC intensity (see, e.g., [
35,
36]). Given its average of 2–3 K warmer SST than the NATL basin, it is expected that the WPAC basin should produce more intense TCs as well as higher TC frequency in this area, As a result, TCs in the WPAC basin are potentially subject to stronger interaction with the lower stratosphere and higher sensitivity to the tropopause height variations.