Estimation of the Elemental to Organic Carbon Ratio in Biomass Burning Aerosol Using AERONET Retrievals
Abstract
:1. Introduction
2. Data and Method
2.1. Measurement and Model Data
2.1.1. Measurements
2.1.2. Simulations
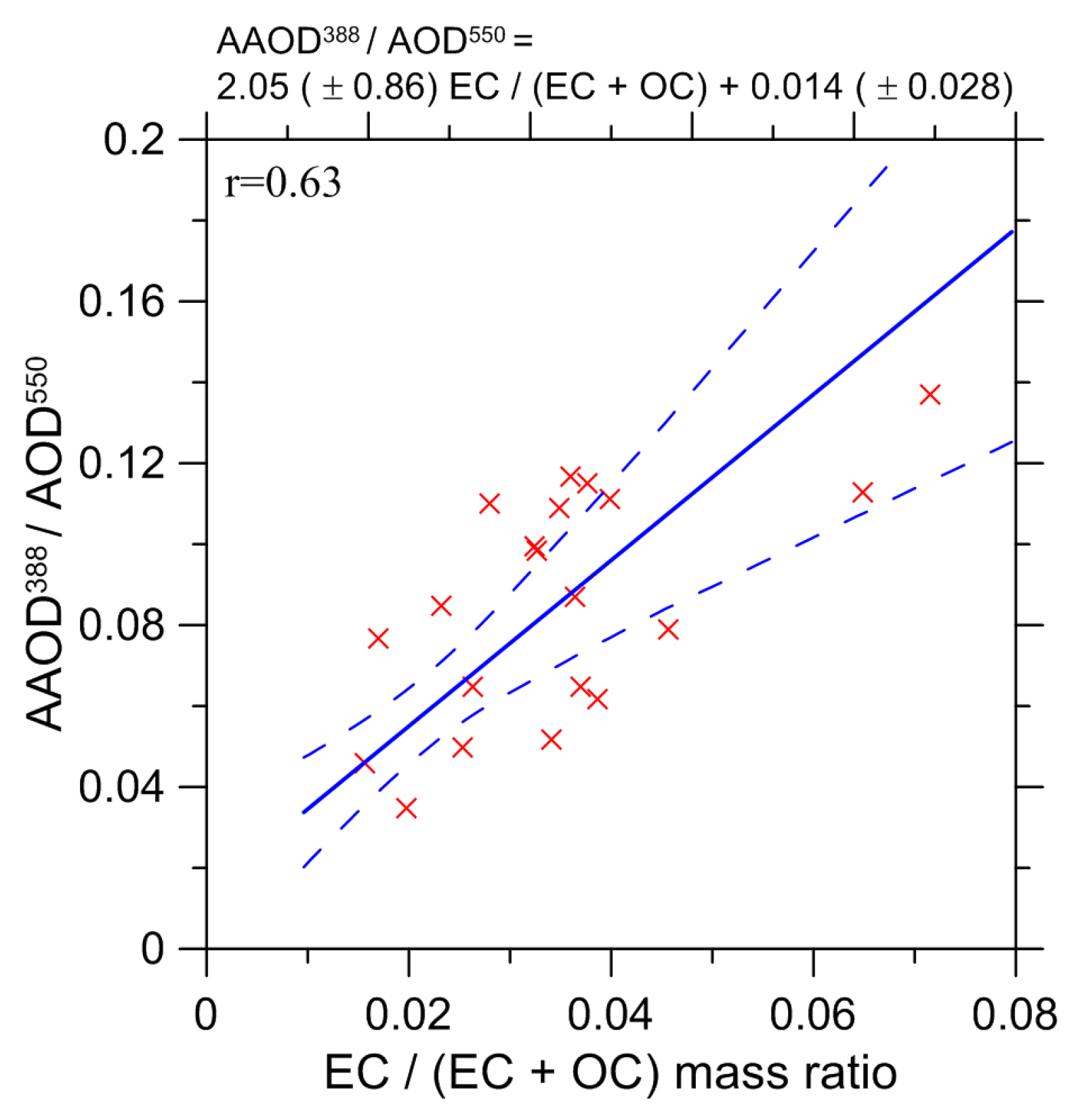
2.2. Method for Estimation of the EC/OC Ratio
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovermental Panel on Climate Change. Climate Change 2013: The Physical Science Basis; Summary for Policymakers; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ten Hoeve, J.E.; Jacobson, M.Z.; Remer, L. Comparing results from a physical model with satellite and in situ observations to determine whether biomass burning aerosols over the Amazon brighten or burn off clouds. J. Geophys. Res. 2012, 117, D08203. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Effects of biomass burning on climate, accounting for heat and moisture fluxes, black and brown carbon, and cloud absorption effects. J. Geophys. Res. Atmos. 2014, 119, 980–9002. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Kuznetsova, I.N.; Yurova, A.; Zvyagintsev, A.M. Atmospheric impacts of the 2010 Russian wildfires: Integrating modelling and measurements of an extreme air pollution episode in the Moscow region. Atmos. Chem. Phys. 2011, 11, 10031–10056. [Google Scholar] [CrossRef]
- Strand, T.M.; Larkin, N.; Craig, K.J.; Raffuse, S.; Sullivan, D.; Solomon, R.; Rorig, M.; Wheeler, N.; Pryden, D. Analyses of BlueSky Gateway PM2.5 predictions during the 2007 southern and 2008 northern California fires. J. Geophys. Res. 2012, 117, D17301. [Google Scholar] [CrossRef]
- Navarro, K.M.; Cisneros, R.; O’Neill, S.M.; Schweizer, D.; Larkin, N.K.; Balmes, J.R. Air-Quality Impacts and Intake Fraction of PM2.5 during the 2013 Rim Megafire. Environ. Sci. Technol. 2016, 50, 11965–11973. [Google Scholar] [CrossRef] [PubMed]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Myhre, G.; Samset, B.H.; Schulz, M.; Balkanski, Y.; Bauer, S.; Berntsen, T.K.; Bian, H.; Bellouin, N.; Chin, T.; Diehl, T.; et al. Radiative forcing of the direct aerosol effect from AeroCom Phase II simulations. Atmos. Chem. Phys. 2013, 13, 1853–1877. [Google Scholar] [CrossRef]
- Saleh, R.; Robinson, E.S.; Tkacik, D.S.; Ahern, A.T.; Liu, S.; Aiken, A.C.; Sullivan, R.C.; Presto, A.A.; Dubey, M.K.; Yokelson, R.J.; et al. Brownness of organics in aerosols from biomass burning linked to their black carbon content. Nature Geosci. 2014, 7, 647–650. [Google Scholar] [CrossRef]
- Lu, Z.; Streets, D.G.; Winijkul, E.; Yan, F.; Chen, Y.; Bond, T.C.; Feng, Y.; Dubey, M.K.; Liu, S.; Pinto, J.P.; et al. Light absorption properties and radiative effects of primary organic aerosol emissions. Environ. Sci. Technol. 2015, 49, 4868–4877. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Heald, C.L.; Sedlacek, A.J.; de Sá, S.S.; Martin, S.T.; Alexander, M.L.; Watson, T.B.; Aiken, A.C.; Springston, S.R.; Artaxo, P. Deriving brown carbon from multiwavelength absorption measurements: Method and application to AERONET and Aethalometer observations. Atmos. Chem. Phys. 2016, 16, 12733–12752. [Google Scholar] [CrossRef]
- Pokhrel, R.P.; Beamesderfer, E.R.; Wagner, N.L.; Langridge, J.M.; Lack, D.A.; Jayarathne, T.; Stone, E.A.; Stockwell, C.E.; Yokelson, R.J.; Murphy, S.M. Relative importance of black carbon, brown carbon, and absorption enhancement from clear coatings in biomass burning emissions. Atmos. Chem. Phys. 2017, 17, 5063–5078. [Google Scholar] [CrossRef]
- Chung, C.E.; Ramanathan, V.; Decremer, D. Observationally constrained estimates of carbonaceous aerosol radiative forcing. Proc. Natl. Acad. Sci. USA 2012, 109, 11624–11629. [Google Scholar] [CrossRef] [PubMed]
- Kirchstetter, T.W.; Thatcher, T.L. Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation. Atmos. Chem. Phys. 2012, 12, 6067–6072. [Google Scholar] [CrossRef]
- Bahadur, R.; Praveen, P.S.; Xu, Y.; Ramanathan, V. Solar absorption by elemental and brown carbon determined from spectral observations. Proc. Natl. Acad. Sci. USA 2012, 109, 17366–17371. [Google Scholar] [CrossRef] [PubMed]
- Forrister, H.; Liu, J.; Scheuer, E.; Dibb, J.; Ziemba, L.; Thornhill, K.L.; Anderson, B.; Diskin, G.; Perring, A.E.; Schwarz, J.P.; et al. Evolution of brown carbon in wildfire plumes. Geophys. Res. Lett. 2015, 42, 4623–4630. [Google Scholar] [CrossRef]
- Akagi, S.K.; Craven, J.S.; Taylor, J.W.; McMeeking, G.R.; Yokelson, R.J.; Burling, I.R.; Urbanski, S.P.; Wold, C.E.; Seinfeld, J.H.; Coe, H.; et al. Evolution of trace gases and particles emitted by a chaparral fire in California. Atmos. Chem. Phys. 2012, 12, 1397–1421. [Google Scholar] [CrossRef]
- Vakkari, V.; Kerminen, V.M.; Beukes, J.P.; Tiitta, P.; van Zyl, P.G.; Josipovic, M.; Venter, A.D.; Jaars, K.; Worsnop, D.R.; Kulmala, M.; et al. Rapid Changes in biomass burning aerosols by atmospheric oxidation. Geophys. Res. Lett. 2014, 41, 2644–2651. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Berezin, E.V.; Petetin, H.; Mielonen, T.; Kuznetsova, I.N.; Andreae, M.O. The role of semi-volatile organic compounds in the mesoscale evolution of biomass burning aerosol: A modeling case study of the 2010 mega-fire event in Russia. Atmos. Chem. Phys. 2015, 15, 13269–13297. [Google Scholar] [CrossRef]
- Konovalov, I.B.; Beekmann, M.; Berezin, E.V.; Formenti, P.; Andreae, M.O. Probing into the aging dynamics of biomass burning aerosol by using satellite measurements of aerosol optical depth and carbon monoxide. Atmos. Chem. Phys. 2017, 17, 4513–4537. [Google Scholar] [CrossRef]
- Andreae, M.O.; Gelencsér, A. Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols. Atmos. Chem. Phys. 2006, 6, 3131–3148. [Google Scholar] [CrossRef]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Collatz, G.J.; Mu, M.; Kasibhatla, P.S.; Morton, D.C.; DeFries, R.S.; Jin, Y.; van Leeuwen, T.T. Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997–2009). Atmos. Chem. Phys. 2010, 10, 11707–11735. [Google Scholar] [CrossRef]
- Wiedinmyer, C.; Akagi, S.K.; Yokelson, R.J.; Emmons, L.K.; Al-Saadi, J.A.; Orlando, J.J.; Soja, A.J. The Fire INventory from NCAR (FINN): A high resolution global model to estimate the emissions from open burning. Geosci. Model Dev. 2011, 4, 625–641. [Google Scholar] [CrossRef]
- Kaiser, J.W.; Flemming, J.; Schultz, M.G.; Suttie, M.; Wooster, M.J. The MACC global fire assimilation system: first emission products (GFASv0). ECMWF Tech. Memo. 2009, 596, 1–16. [Google Scholar]
- Akagi, S.K.; Yokelson, R.J.; Wiedinmyer, C.; Alvarado, M.J.; Reid, J.S.; Karl, T.; Crounse, J.D.; Wennberg, P.O. Emission factors for open and domestic biomass burning for use in atmospheric models. Atmos. Chem. Phys. 2011, 11, 4039–4072. [Google Scholar] [CrossRef]
- Andreae, M.O.; Merlet, P. Emission of trace gases and aerosols from biomass burning. Glob. Biogeochem. Cycles 2001, 15, 955–966. [Google Scholar] [CrossRef]
- Andreae, M.O.; (Max Planck Institute for Chemistry, Mainz, Germany). Biomass burning emission factors. Personal communication, 2015. [Google Scholar]
- Schmidt, T.L.; Raile, G.K. Sustainability of Siberia and Far East Russia’s Forest Resource. J. Sustain. For. 2000, 11, 1–21. [Google Scholar] [CrossRef]
- Sutton, W. Siberia has a very large forest resource but…. N. Z. J. For. 2013, 58, 16–19. [Google Scholar]
- Konovalov, I.B.; Berezin, E.V.; Ciais, P.; Broquet, G.; Beekmann, M.; Hadji-Lazaro, J.; Clerbaux, C.; Andreae, M.O.; Kaiser, J.W.; Schulze, E.-D. Constraining CO2 emissions from open biomass burning by satellite observations of co-emitted species: A method and its application to wildfires in Siberia. Atmos. Chem. Phys. 2014, 14, 10383–10410. [Google Scholar] [CrossRef]
- Ikeda, K.; Tanimoto, H. Exceedances of air quality standard level of PM2.5 in Japan caused by Siberian wildfires. Environ. Res. Lett. 2015, 10, 105001. [Google Scholar] [CrossRef]
- Jung, J.; Lyu, Y.; Lee, M.; Hwang, T.; Lee, S.; Oh, S. Impact of Siberian forest fires on the atmosphere over the Korean Peninsula during summer 2014. Atmos. Chem. Phys. 2016, 16, 6757–6770. [Google Scholar] [CrossRef]
- Laing, J.R.; Jaffe, D.A.; Hee, J.R. Physical and optical properties of aged biomass burning aerosol from wildfires in Siberia and the Western USA at the Mt. Bachelor Observatory. Atmos. Chem. Phys. 2016, 16, 15185–15197. [Google Scholar] [CrossRef]
- Evangeliou, N.; Balkanski, Y.; Hao, W.M.; Petkov, A.; Silverstein, R.P.; Corley, R.; Nordgren, B.L.; Urbanski, S.P.; Eckhardt, S.; Stohl, A.; et al. Wildfires in northern Eurasia affect the budget of black carbon in the Arctic—A 12-year retrospective synopsis (2002–2013). Atmos. Chem. Phys. 2016, 16, 7587–7604. [Google Scholar] [CrossRef]
- Arctic Report Card. Richter-Menge, J.; Overland, E.; Mathis, J.T. (Eds.) 2016. Available online: http://www.arctic.noaa.gov/Report-Card (accessed on 15 May 2017).
- Soja, A.J.; Cofer, W.R.; Shugart, H.H.; Sukhinin, A.I.; Stackhouse, P.W., Jr.; McRae, D.J.; Conard, S.G. Estimating fire emissions and disparities in boreal Siberia (1998–2002). J. Geophys. Res. 2004, 109, D14S06. [Google Scholar] [CrossRef]
- Randerson, J.T.; Liu, H.; Flanner, M.G.; Chambers, S.D.; Jin, Y.; Hess, P.G.; Pfister, G.; Mack, M.C.; Treseder, K.K.; Welp, L.R.; et al. The impact of boreal forest fire on climate warming. Science 2006, 314, 1130–1132. [Google Scholar] [CrossRef] [PubMed]
- Balzter, H.; Gerard, F.; Weedon, G.; Grey, W.; Combal, B.; Bartholome, E.; Bartalev, S.; Los, S. Coupling of vegetation growing season anomalies with hemispheric and regional scale climate patterns in Central and East Siberia. J. Clim. 2007, 20, 3713–3729. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Sato, M.; Hansen, J.; Kock, D.; Lacis, A.; Ruedy, R.; Dubovik, O.; Holben, B.; Chin, M.; Novakov, T. Global atmospheric black carbon inferred from AERONET. Proc. Natl. Acad. Sci. USA 2003, 100, 6319–6324. [Google Scholar] [CrossRef] [PubMed]
- Koch, D.; Schulz, M.; Kinne, S.; McNaughton, C.; Spackman, J.R.; Balkanski, Y.; Bauer, S.; Berntsen, T.; Bond, T.C.; Boucher, O.; et al. Evaluation of black carbon estimations in global aerosol models. Atmos. Chem. Phys. 2009, 9, 9001–9026. [Google Scholar] [CrossRef]
- Huang, K.; Fu, J.S.; Prikhodko, V.Y.; Storey, J.M.; Romanov, A.; Hodson, E.L.; Cresko, J.; Morozova, I.; Ignatieva, Y.; Cabaniss, J. Russian anthropogenic black carbon: Emission reconstruction and Arctic black carbon simulation. J. Geophys. Res. Atmos. 2015, 120, 11306–11333. [Google Scholar] [CrossRef]
- Pan, X.; Chin, M.; Gautam, R.; Bian, H.; Kim, D.; Colarco, P.R.; Diehl, T.L.; Takemura, T.; Pozzoli, L.; Tsigaridis, K.; et al. A multi-model evaluation of aerosols over South Asia: common problems and possible causes. Atmos. Chem. Phys. 2015, 15, 5903–5928. [Google Scholar] [CrossRef]
- Ocko, I.B.; Ginoux, P.A. Comparing multiple model-derived aerosol optical properties to spatially collocated ground-based and satellite measurements. Atmos. Chem. Phys. 2017, 17, 4451–4475. [Google Scholar] [CrossRef]
- Torres, O.; Tanskanen, A.; Veihelmann, B.; Ahn, C.; Braak, R.; Bhartia, P.K.; Veefkind, P.; Levelt, P. Aerosols and surface UV products from Ozone Monitoring Instrument observations: An overview. J. Geophys. Res. 2007, 112, D24S47. [Google Scholar] [CrossRef]
- Zhang, L.; Henze, D.K.; Grell, G.A.; Carmichael, G.R.; Bousserez, N.; Zhang, Q.; Torres, O.; Ahn, C.; Lu, Z.; Cao, J.; et al. Constraining black carbon aerosol over Asia using OMI aerosol absorption optical depth and the adjoint of GEOS-Chem. Atmos. Chem. Phys. 2015, 15, 10281–10308. [Google Scholar] [CrossRef]
- Curci, G.; Hogrefe, C.; Bianconi, R.U.; Balzarini, A.; Baró, R.; Brunner, D.; Forkel, R.; Giordano, L.; Hirtl, M.; Honzak, L.; et al. Uncertainties of simulated aerosol optical properties induced by assumptions on aerosol physical and chemical properties: An AQMEII-2 perspective. Atmos. Environ. 2015, 115, 541–542. [Google Scholar] [CrossRef]
- Clarke, A.; McNaughton, C.; Kapustin, V.; Shinozuka, Y.; Howell, S.; Dibb, J.; Zhou, J.; Anderson, B.; Brekhovskikh, V.; Turner, H.; et al. Biomass Burning and Pollution Aerosol over North America: Organic Components and Their Influence on Spectral Optical Properties and Humidification Response. J. Geophys. Res. 2007, 112, D12S18. [Google Scholar] [CrossRef]
- Liu, J.; Scheuer, E.; Dibb, J.; Diskin, G.S.; Ziemba, L.D.; Thornhill, K.L.; Anderson, B.E.; Wisthaler, A.; Mikoviny, T.; Devi, J.J.; et al. Brown carbon aerosol in the North American continental troposphere: Sources, abundance, and radiative forcing. Atmos. Chem. Phys. 2015, 15, 7841–7858. [Google Scholar] [CrossRef]
- Olson, M.R.; Victoria Garcia, M.; Robinson, M.A.; Van Rooy, P.; Dietenberger, M.A.; Bergin, M.; Schauer, J.J. Investigation of black and brown carbon multiplewavelength-dependent light absorption from biomass and fossil fuel combustion source emissions. J. Geophys. Res. Atmos. 2015, 120, 6682–6697. [Google Scholar] [CrossRef]
- Pokhrel, R.P.; Wagner, N.L.; Langridge, J.M.; Lack, D.A.; Jayarathne, T.; Stone, E.A.; Stockwell, C.E.; Yokelson, R.J.; Murphy, S.M. Parameterization of single-scattering albedo (SSA) and absorption Ångström exponent (AAE) with EC/OC for aerosol emissions from biomass burning. Atmos. Chem. Phys. 2016, 16, 9549–9561. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Mattoo, S.; Vermote, E.F.; Kaufman, Y.J. Second-generation operational algorithm: Retrieval of aerosol properties over land from inversion of Moderate Resolution Imaging Spectroradiometer spectral reflectance. J. Geophys. Res. 2007, 112, 13211. [Google Scholar] [CrossRef]
- AERONET (Aerosol Robotic Network). Available online: https://aeronet.gsfc.nasa.gov (accessed on 17 April 2017).
- Hand, J.L.; Day, D.E.; McMeeking, G.M.; Levin, E.J.T.; Carrico, C.M.; Kreidenweis, S.M.; Malm, W.C.; Laskin, A.; Desyaterik, Y. Measured and modeled humidification factors of fresh smoke particles from biomass burning: role of inorganic constituents. Atmos. Chem. Phys. 2010, 10, 6179–6194. [Google Scholar] [CrossRef]
- Mikhailov, E.F.; Mironov, G.N.; Pöhlker, C.; Chi, X.; Krüger, M.L.; Shiraiwa, M.; Förster, J.-D.; Pöschl, U.; Vlasenko, S.S.; Ryshkevich, T.I.; et al. Chemical composition, microstructure, and hygroscopic properties of aerosol particles at the Zotino Tall Tower Observatory (ZOTTO), Siberia, during a summer campaign. Atmos. Chem. Phys. 2015, 15, 8847–8869. [Google Scholar] [CrossRef]
- Dahlkötter, F.; Gysel, M.; Sauer, D.; Minikin, A.; Baumann, R.; Seifert, P.; Ansmann, A.; Fromm, M.; Voigt, C.; Weinzierl, B. The Pagami Creek smoke plume after long-range transport to the upper troposphere over Europe—Aerosol properties and black carbon mixing state. Atmos. Chem. Phys. 2014, 14, 6111–6137. [Google Scholar] [CrossRef]
- Boreddy, S.K.R.; Kawamura, K.; Mkoma, S.; Fu, P. Hygroscopic behavior of water-soluble matter extracted from biomass burning aerosols collected at a rural site in Tanzania, East Africa. J. Geophys. Res. Atmos. 2014, 119, 12233–12245. [Google Scholar] [CrossRef]
- Dubovik, O.; Smirnov, A.; Holben, B.N.; King, M.D.; Kaufman, Y.J.; Eck, T.F.; Slutsker, I. Accuracy assessments of aerosol optical properties retrieved from Aerosol Robotic Network (AERONET) Sun and sky radiance measurements. J. Geophys. Res. 2000, 105, 9791–9806. [Google Scholar] [CrossRef]
- Andrews, E.; Ogren, J.A.; Kinne, S.; Samset, B. Comparison of AOD, AAOD and column single scattering albedo from AERONET retrievals and in situ profiling measurements. Atmos. Chem. Phys. 2017, 17, 6041–6072. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Reverb: The Next Generation Earth Science Discovery Tool. Available online: https://reverb.echo.nasa.gov (accessed on 26 April 2017).
- Menut, L.; Bessagnet, B.; Khvorostyanov, D.; Beekmann, M.; Blond, N.; Colette, A.; Coll, I.; Curci, G.; Foret, G.; Hodzic, A.; et al. CHIMERE-2013: A model for regional atmospheric composition modeling. Geosci. Model Dev. 2013, 6, 981–1028. [Google Scholar] [CrossRef]
- Mailler, S.; Menut, L.; Khvorostyanov, D.; Valari, M.; Couvidat, F.; Siour, G.; Turquety, S.; Briant, R.; Tuccella, P.; Bessagnet, B.; et al. CHIMERE-2016: From urban to hemispheric chemistry-transport modeling. Geosci. Model Dev. Discuss. 2016. [Google Scholar] [CrossRef]
- Documentation of the Chemistry-Transport Model CHIMERE. Version CHIMERE 2016a. Available online: http://www.lmd.polytechnique.fr/chimere/docs/CHIMEREdoc2016a.pdf (accessed on 3 July 2017).
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Dentener, F.; Muntean, M.; Pouliot, G.; Keating, T.; Zhang, Q.; Kurokawa, J.; Wankmüller, R.; et al. HTAP_v2.2: A mosaic of regional and global emission grid maps for 2008 and 2010 to study hemispheric transport of air pollution. Atmos. Chem. Phys. 2015, 15, 11411–11432. [Google Scholar] [CrossRef]
- Berezin, E.V.; Konovalov, I.B.; Romanova, Y.Y. Inverse Modeling of Nitrogen Oxides Emissions from the 2010 Russian Wildfires by Using Satellite Measurements of Nitrogen Dioxide. Atmosphere 2016, 7, 132. [Google Scholar] [CrossRef]
- Global Fire Emissions Database. Available online: http://www.globalfiredata.org (accessed on 17 April 2017).
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF; NCAR Tech. Notes–475CSTR; National Center for Atmospheric Research: Boulder, CO, USA, 2008; p. 113. [Google Scholar]
- Yokelson, R.J.; Crounse, J.D.; DeCarlo, P.F.; Karl, T.; Urbanski, S.; Atlas, E.; Campos, T.; Shinozuka, Y.; Kapustin, V.; Clarke, A.D.; et al. Emissions from biomass burning in the Yucatan. Atmos. Chem. Phys. 2009, 9, 5785–5812. [Google Scholar] [CrossRef]
- Chubarova, N.; Nezval’, Ye.; Sviridenkov, I.; Smirnov, A.; Slutsker, I. Smoke aerosol and its radiative effects during extreme fire event over Central Russia in summer 2010. Atmos. Meas. Tech. 2012, 5, 557–568. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: New York, NY, USA, 1993. [Google Scholar]
- Liu, J.; Lin, P.; Laskin, A.; Laskin, J.; Kathmann, S.M.; Wise, M.; Caylor, R.; Imholt, F.; Selimovic, V.; Shilling, J.E. Optical properties and aging of light-absorbing secondary organic aerosol. Atmos. Chem. Phys. 2016, 16, 12815–12827. [Google Scholar] [CrossRef]
- Mikhailov, E.; Mironova, S.; Mironov, G.; Vlasenko, S.; Panov, A.; Chi, X.; Walter, D.; Carbone, S.; Artaxo, P.; Pöschl, U.; et al. Long-term measurements (2010–2014) of carbonaceous aerosol and carbon monoxide at the Zotino Tall Tower Observatory (ZOTTO) in central Siberia. Atmos. Chem. Phys. Discuss. 2017. under review. [Google Scholar] [CrossRef]
- Shrivastava, M.; Easter, R.; Liu, X.; Zelenyuk, A.; Singh, B.; Zhang, K.; Ma, P.-L.; Chand, D.; Ghan, S.; Jimenez, J.L.; et al. Global transformation and fate of SOA: Implications of low volatility SOA and gas phase fragmentation reactions. J. Geophys. Res. Atmos. 2015, 120, 4169–4195. [Google Scholar] [CrossRef]
- Jolleys, M.D.; Coe, H.; McFiggans, G.; Capes, G.; Allan, J.D.; Crosier, J.; Williams, P.I.; Allen, G.; Bower, K.N.; Jimenez, J.L.; et al. Characterizing the aging of biomass burning organic aerosol by use of mixing ratios: A meta-analysis of four regions. Environ. Sci. Tech. 2012, 46, 13093–13102. [Google Scholar] [CrossRef] [PubMed]
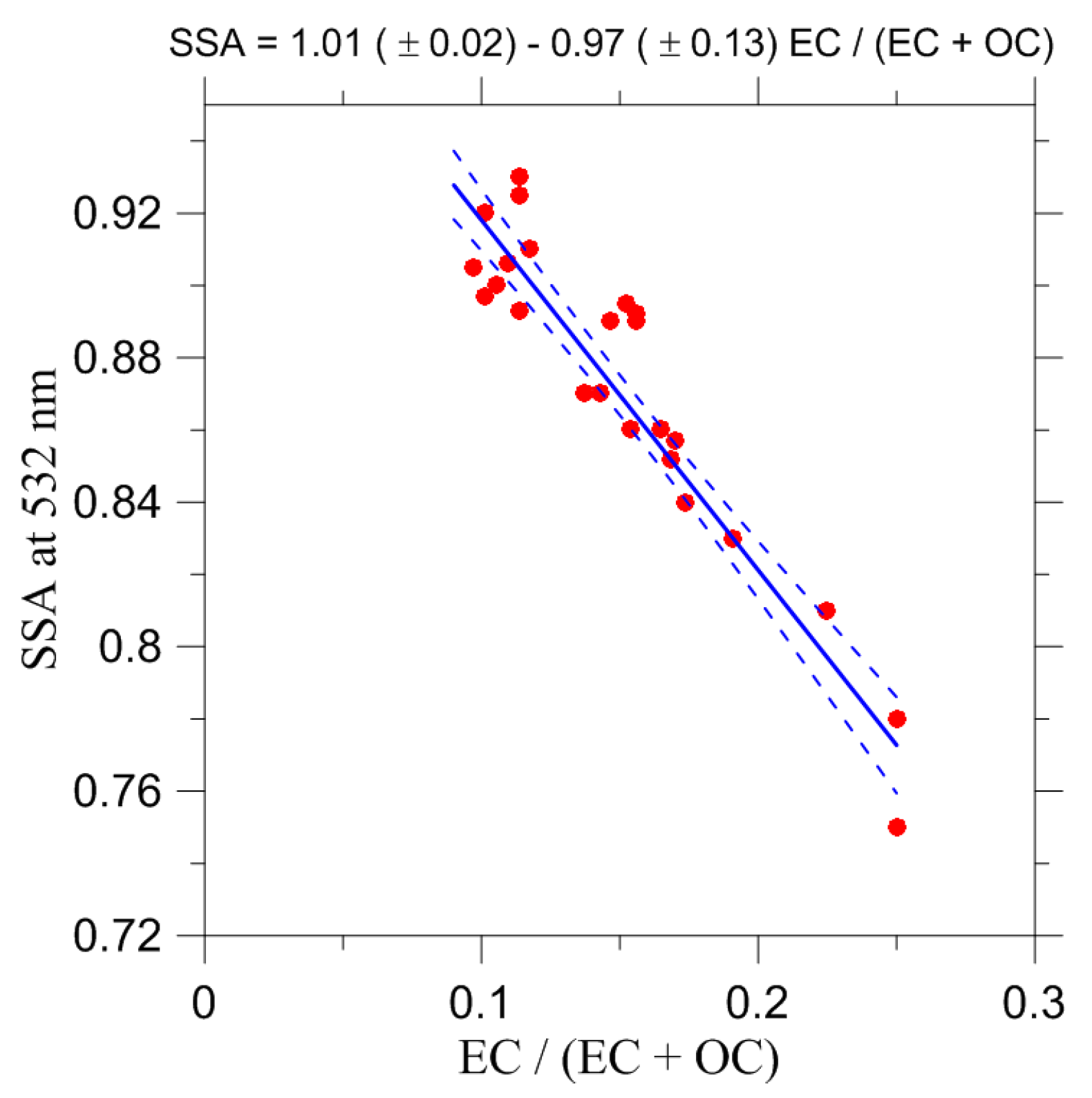
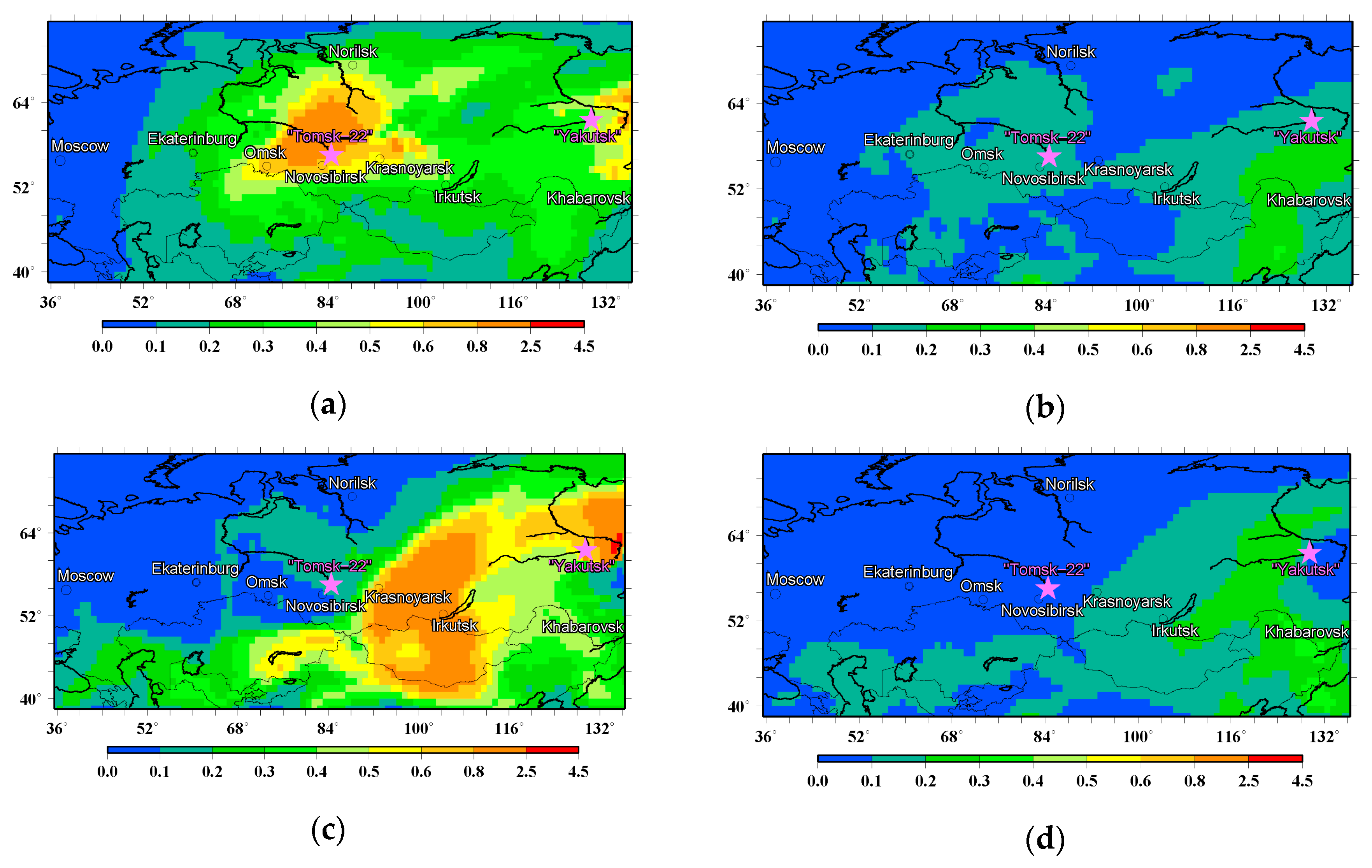
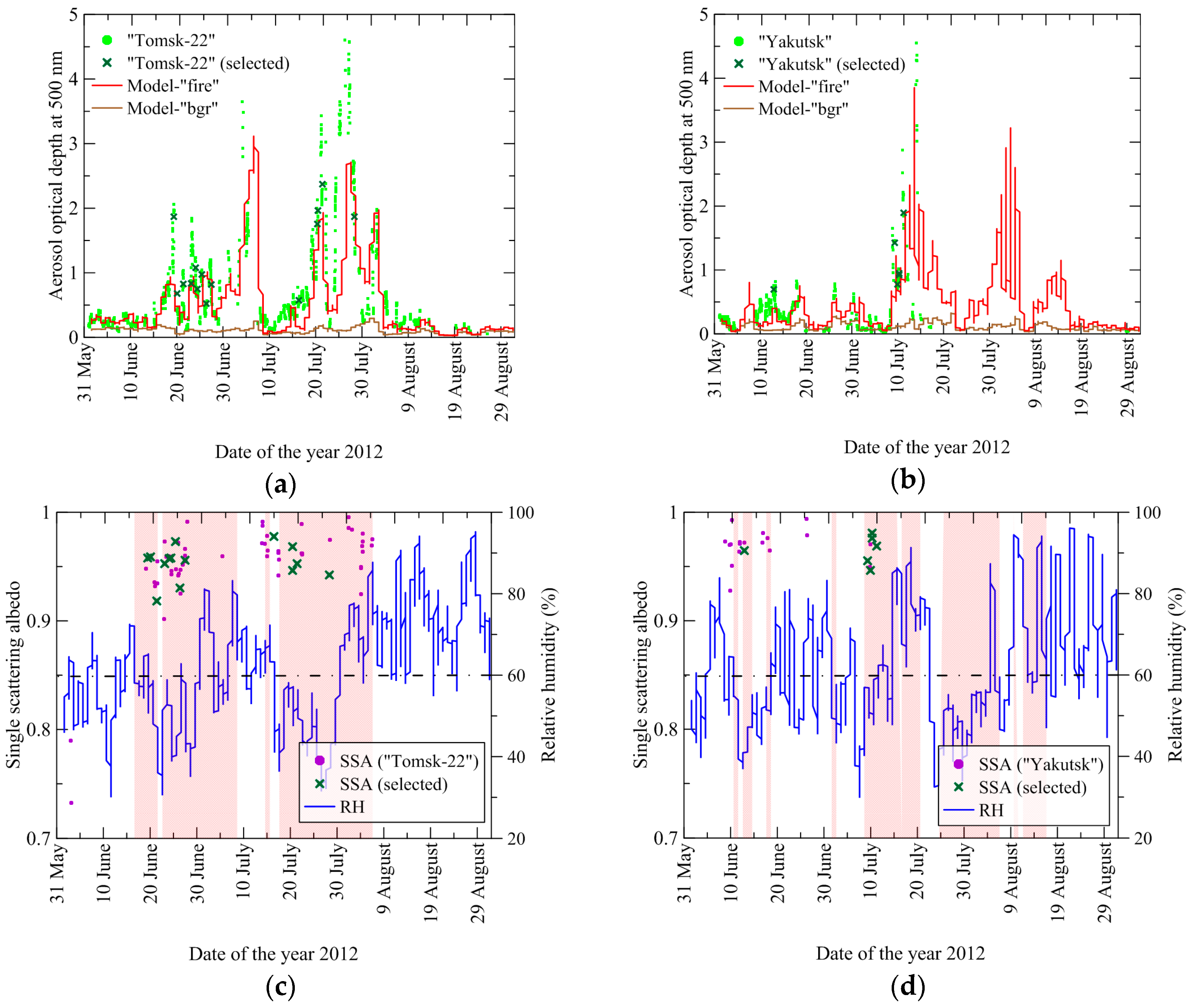
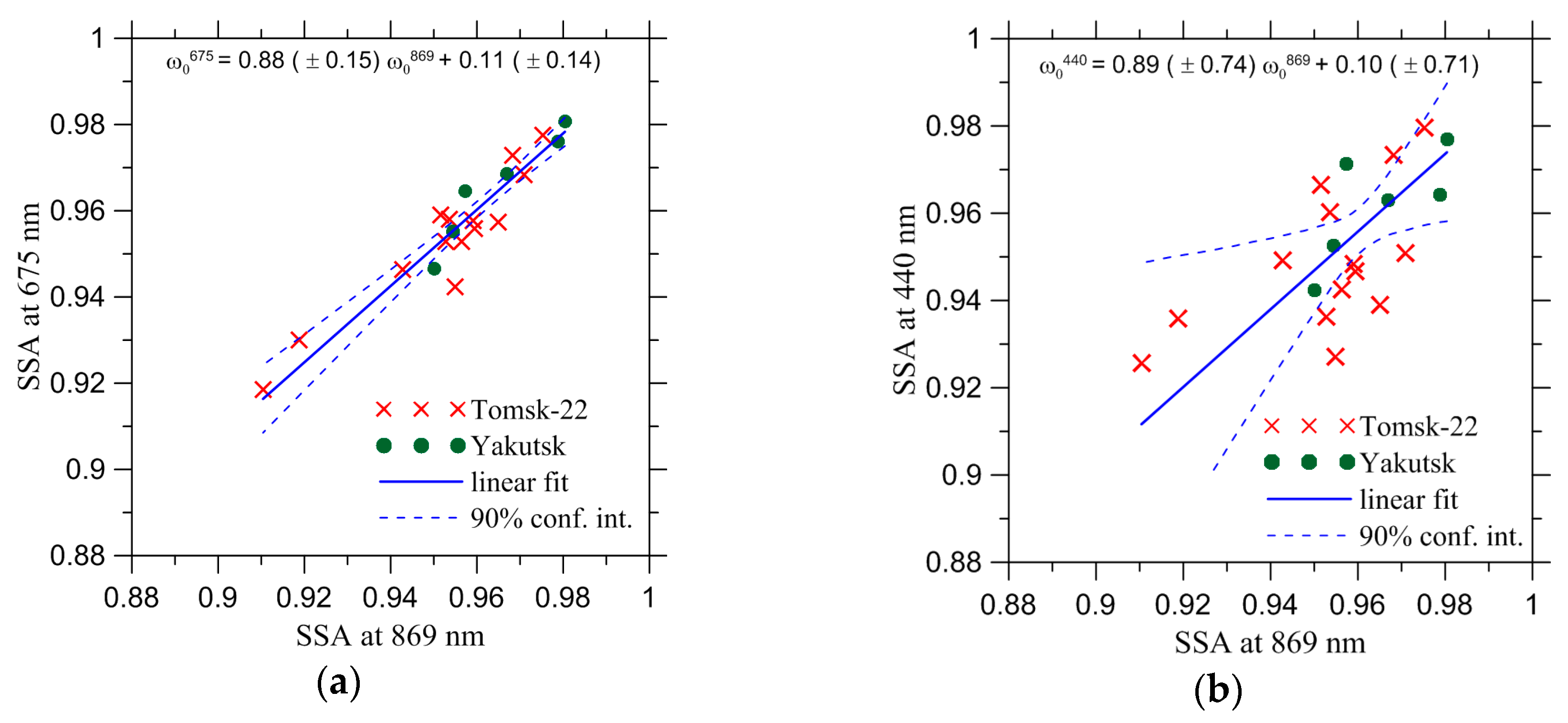
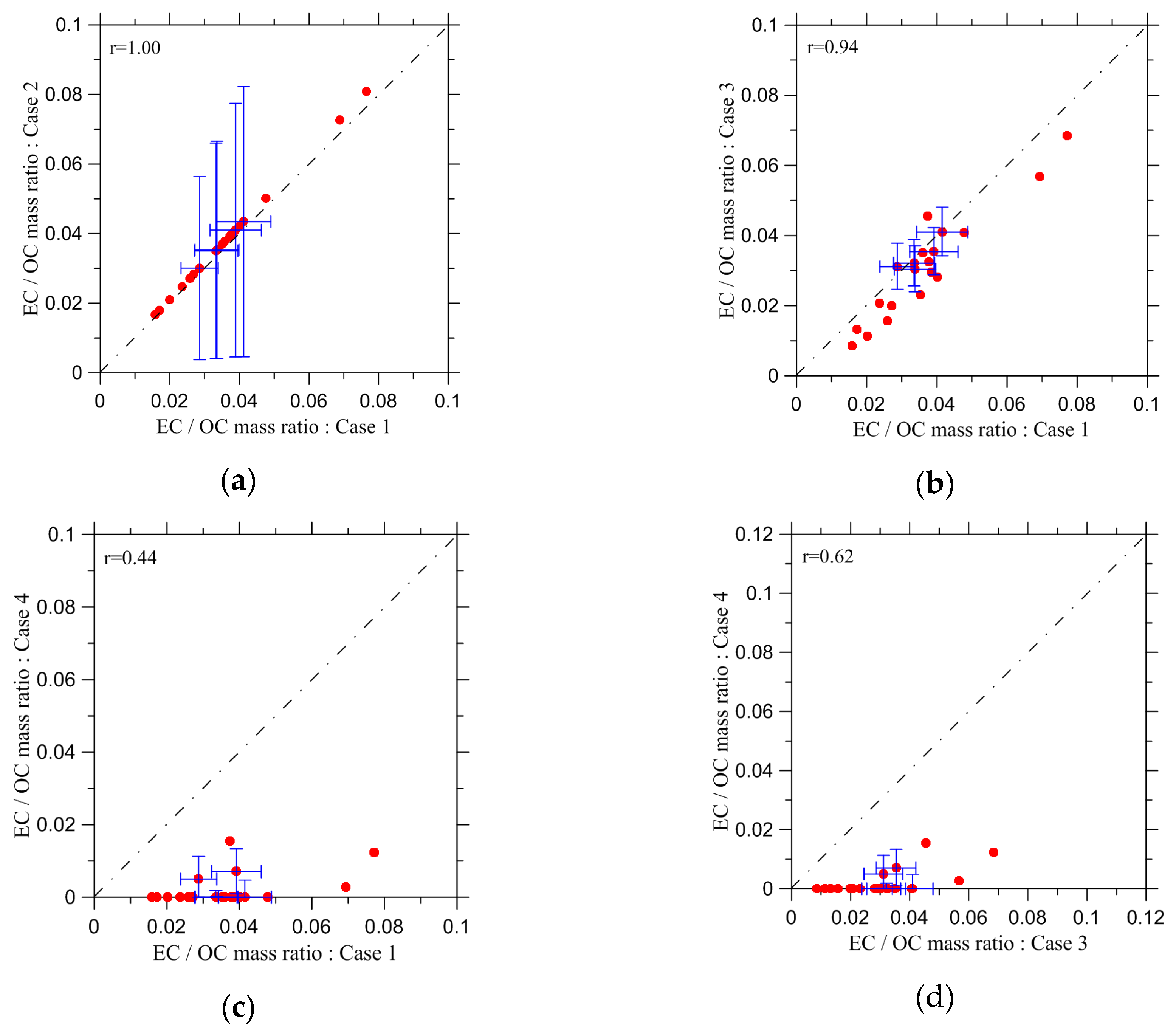
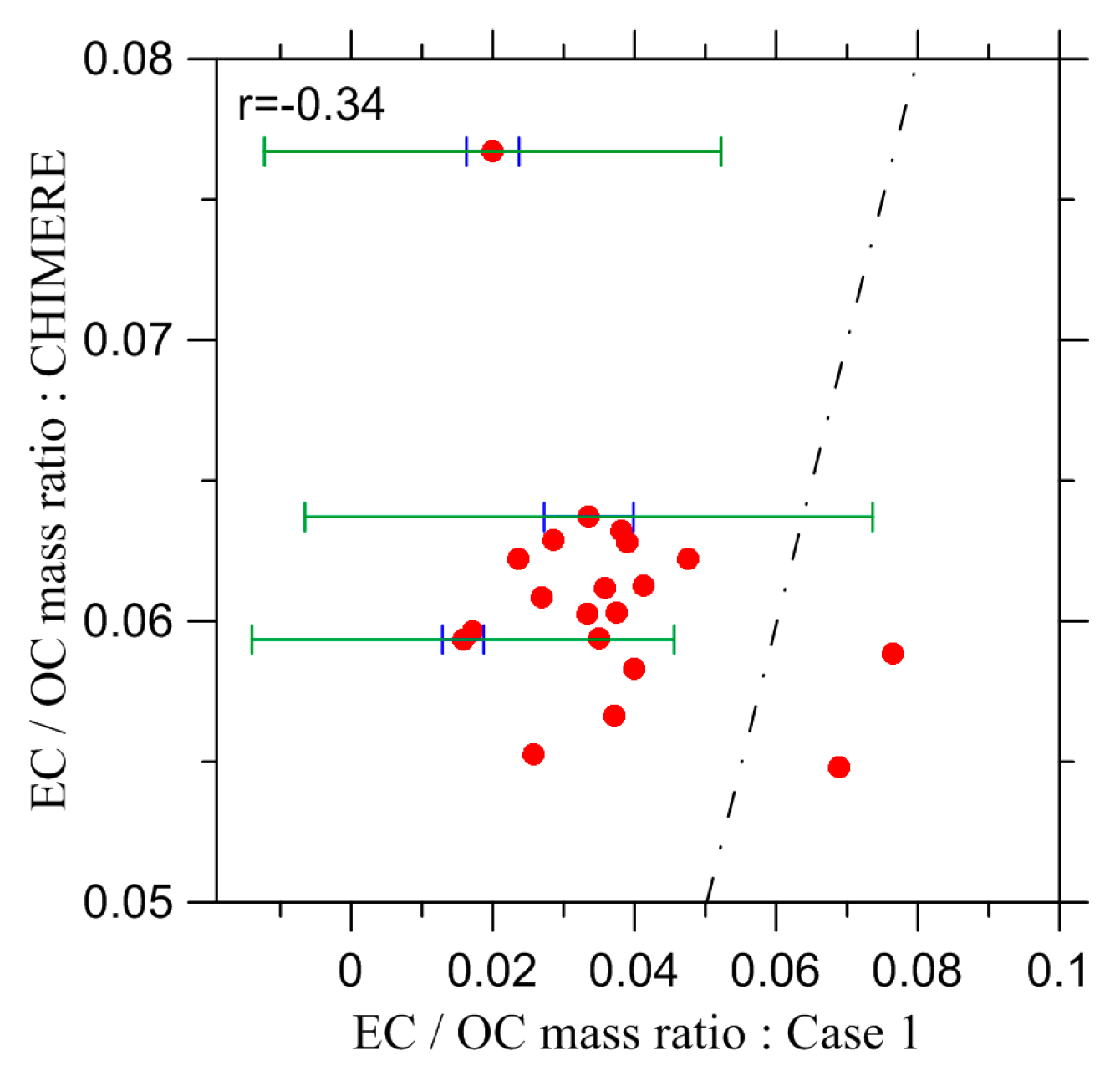
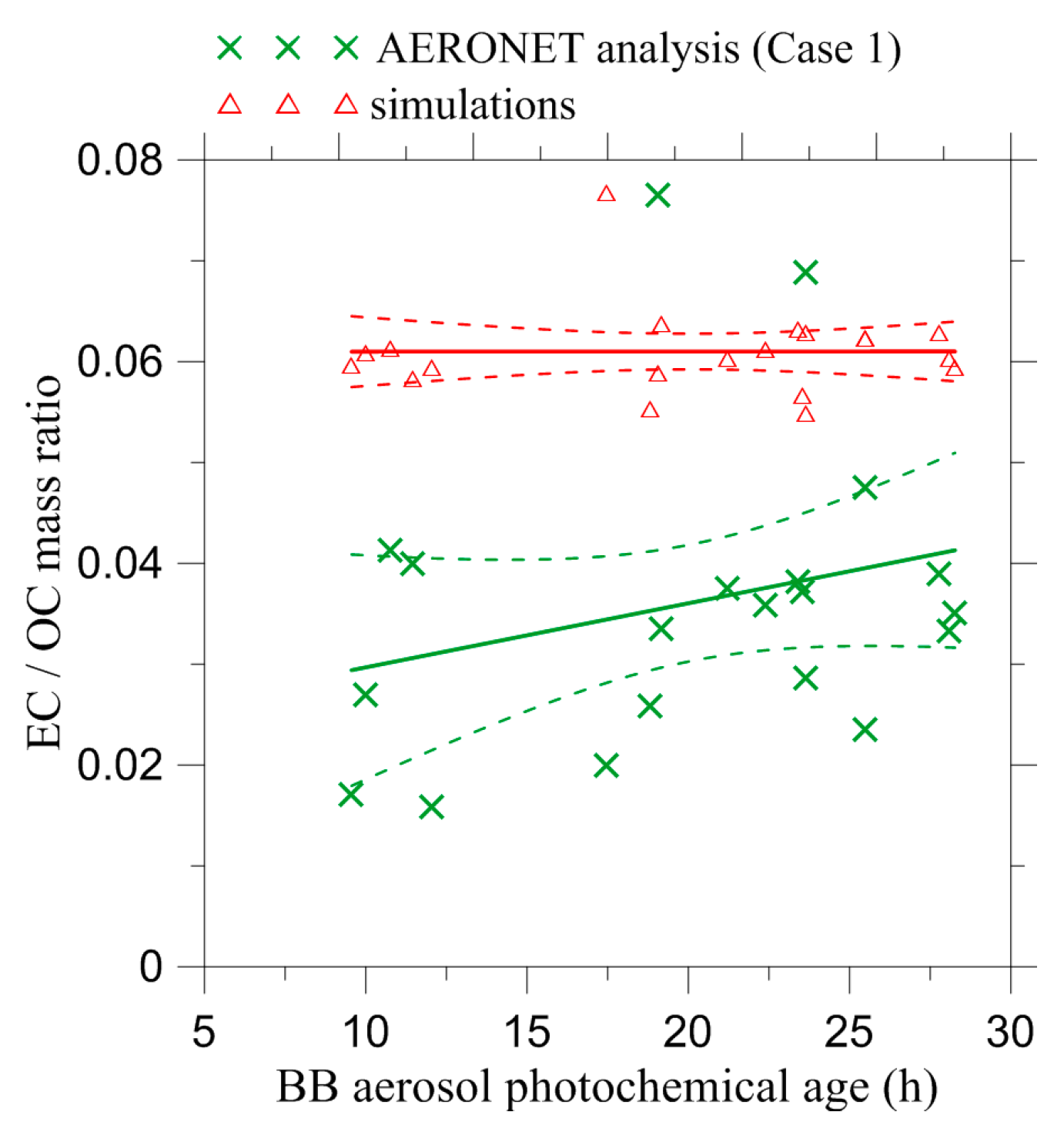
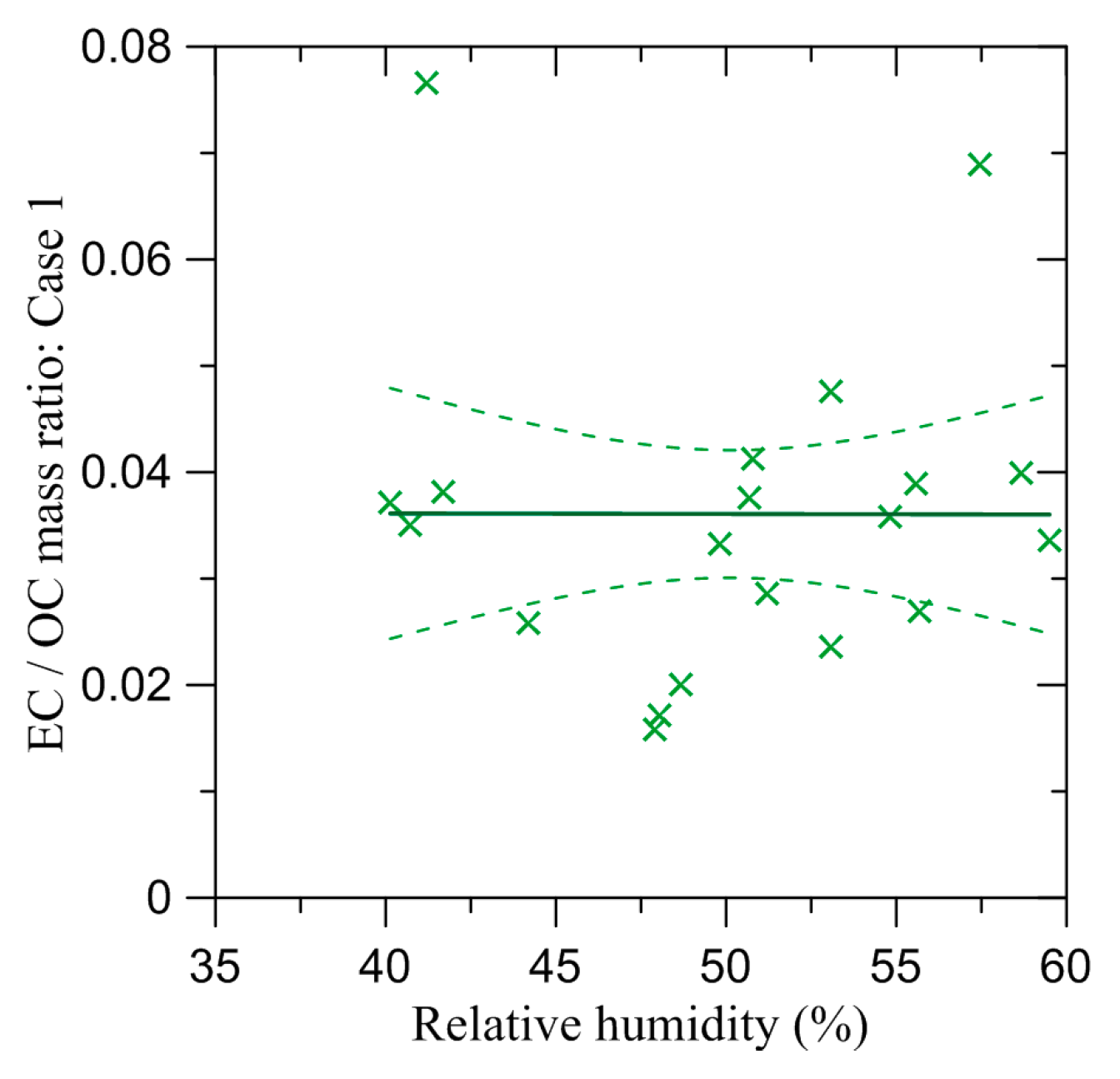
| Criterion No. | Selection Parameter | Threshold Value |
|---|---|---|
| 1 | Aerosol optical depth 1 at 500 nm | 0.5 |
| 2 | Relative humidity 2 in the BB aerosol column | 60% |
| 3 | BB aerosol photochemical age 2 | 30 h |
| Wavelength (nm) | Slope (a) | Intercept (b) |
|---|---|---|
| 405 | −1.07 (±0.08) | 0.94 (±0.007) |
| 532 | −1.06 (±0.04) | 0.99 (±0.004) |
| 660 | −1.11 (±0.04) | 0.99 (±0.004) |
| Estimation Cases | Distinctive Features of Estimation Procedures |
|---|---|
| Case 1 | The estimates are obtained using Equation (8) and SSA observations at 675 nm |
| Case 2 | The same as Case 1, but using SSA observations at 440 nm |
| Case 3 | The estimates are obtained using the available parameterization [52] for SSA at 660 nm (see Equation (1) and Table 2) |
| Case 4 | The same as Case 3, but using the similar parameterization for SSA at 405 nm |
| Estimation Case | Average Value of the EC/OC Ratio |
|---|---|
| Case 1 | 0.036 (±0.009) |
| Case 2 | 0.038 (±0.035) |
| Case 3 | 0.031 (±0.009) |
| Case 4 | 0.002 (±0.011) |
| CHIMERE | 0.061 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalov, I.B.; Lvova, D.A.; Beekmann, M. Estimation of the Elemental to Organic Carbon Ratio in Biomass Burning Aerosol Using AERONET Retrievals. Atmosphere 2017, 8, 122. https://doi.org/10.3390/atmos8070122
Konovalov IB, Lvova DA, Beekmann M. Estimation of the Elemental to Organic Carbon Ratio in Biomass Burning Aerosol Using AERONET Retrievals. Atmosphere. 2017; 8(7):122. https://doi.org/10.3390/atmos8070122
Chicago/Turabian StyleKonovalov, Igor B., Daria A. Lvova, and Matthias Beekmann. 2017. "Estimation of the Elemental to Organic Carbon Ratio in Biomass Burning Aerosol Using AERONET Retrievals" Atmosphere 8, no. 7: 122. https://doi.org/10.3390/atmos8070122
APA StyleKonovalov, I. B., Lvova, D. A., & Beekmann, M. (2017). Estimation of the Elemental to Organic Carbon Ratio in Biomass Burning Aerosol Using AERONET Retrievals. Atmosphere, 8(7), 122. https://doi.org/10.3390/atmos8070122





