1. Introduction
The occurrence of repeated eruptions of the Soufrière Hills Volcano on the island of Montserrat over the past 20 years have stimulated many observational programmes and theoretical studies. One aspect of some interest is the observation that the eruption of this volcano generates internal gravity waves in the atmosphere that are observable with microbarographs. These clearly give information about the eruption, if one can interpret the signal. For significant volcanos in remote locations, it is possible that an array of suitably placed instruments could provide important immediate information about eruptions that is not available by other means.
The first attempt at modelling atmospheric internal wave generation by eruptions was by Kanamori et al. [
1], who used a model that had been developed to describe the internal and acoustic waves generated by nuclear explosions in the atmosphere. This model consisted of a source of heat and mass at a particular point in the atmosphere, for a given short period of time. A subsequent model of a similar nature but with a vertical distribution of the sources was presented by Baines & Sacks [
2], which provides more details of the motivation and the background to the observations made on Montserrat. The Kanamori–type point-source model has also been employed by Ripepe et al. [
3] for comparison with recent observations. All of these studies involve the representation of the eruption by the injection of heat and/or mass into the atmosphere at appropriate elevated locations.
Here, a different approach is taken, in which the dynamics of the volcanic eruption are used to describe its effect on the generation of internal gravity waves—in particular, the eruption is modelled as a turbulent plume, specified by a source of buoyancy at ground level. Volcanic eruptions can be quite complex, but the main properties can be explored by assuming that the structure is simple, and adding additional features and complex time dependence as required. Here, the plume representing the eruption is assumed to have constant form and height, which grows linearly in time for a specified period, lasts at constant strength for another period (here, mostly zero), and then rapidly decays. This behaviour reproduces most of the observed features of surface pressure fluctuations, and these are described and displayed in the following sections.
The parameters used in this analysis are chosen to suit the environment of Montserrat, but the model can be applied to most locations on the planet. The atmospheric structure varies with location, but for present purposes the main feature is the height of the tropopause (separating the troposphere and stratosphere) and the difference in the buoyancy frequency above and below it. These properties vary with latitude, but the present model may be applied by simply changing the values of the relevant parameters.
The plan of the paper is as follows. The plume model of the eruptions and its properties are described in
Section 2. Relevant properties of internal waves and the effect of atmospheric density structure are presented in
Section 3. The equations governing internal waves in an atmosphere where the tropopause is an important feature, and the methodology for solving them, are described in
Section 4, and the results are described in
Section 5. Comparisons with some observations are shown in
Section 6, and the conclusions are summarized in
Section 7. Some technical features of the analysis are presented in two appendices, particularly with regard to how forcing in the stratosphere can affect the surface pressure signal.
2. A Representative Model of Volcanic Eruptions
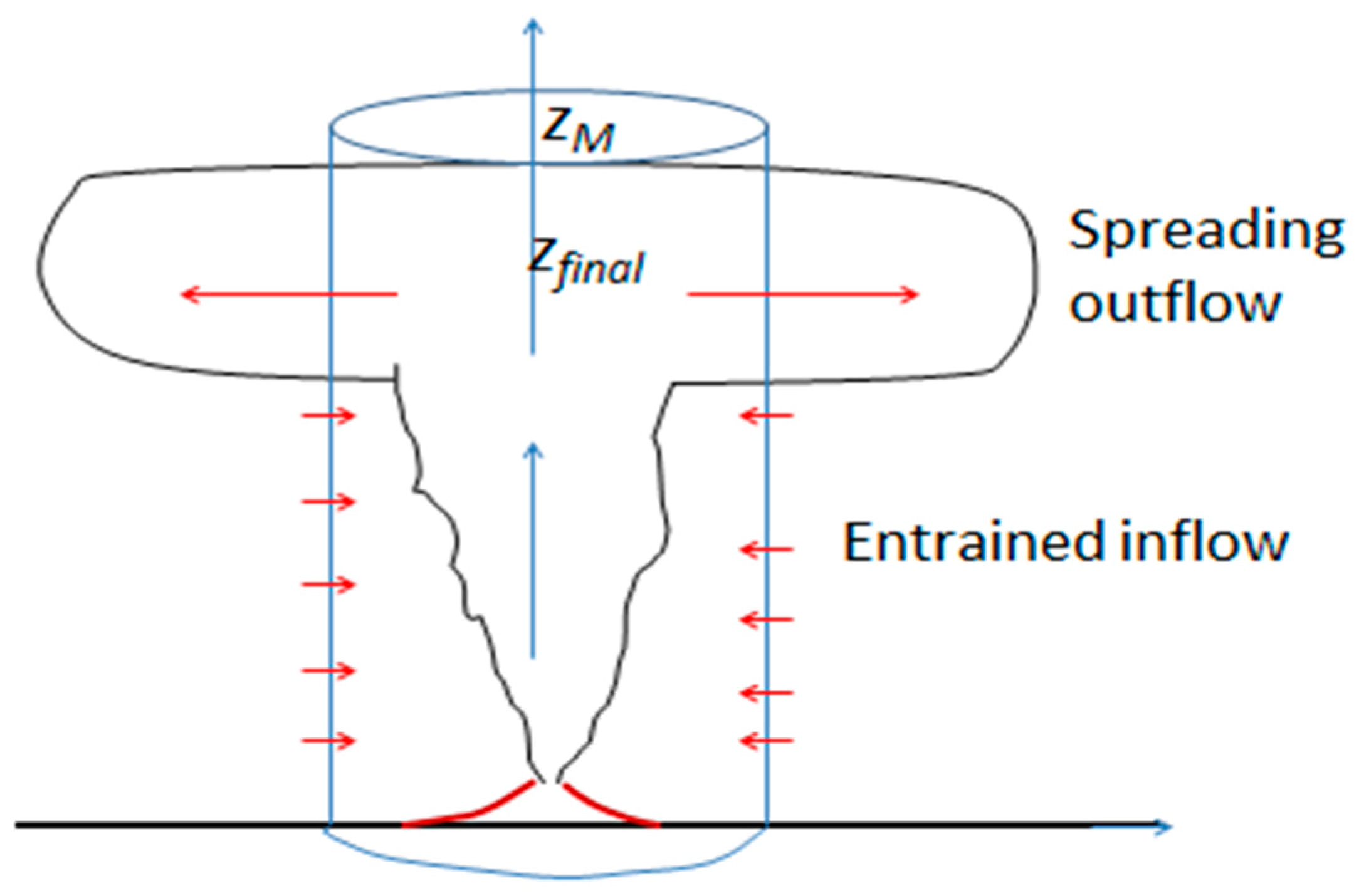
The simplest forms of volcanic eruptions can be described as turbulent plumes. In a stably stratified environment such as the atmosphere, a turbulent plume in steady state consists of a source of buoyancy at ground level that causes rising motion that entrains environmental air as it rises. Because of the stratification, the fluid in this column reaches a maximum height and then falls back to spread laterally. This behaviour is depicted schematically in
Figure 1. A mathematical model (known as Morton-Taylor-Turner) by Morton et al. [
4] provided a quantitative description of this behaviour, and subsequent literature has presented variations of it in differing and more complex situations.
This model has been applied to volcanic eruptions by Woods [
5], in which the source produces particular hot solid material in addition to hot gases. This introduces additional features to the flow. In particular, if the starting plume does not entrain enough air, and consequent buoyancy, it may fall back to ground, and the eruption is thereby constrained to near-ground level. On the other hand, if the entrainment process is efficient, the plume may arise slowly at first, but then increase in upward velocity as heat from the heavy particles is passed to the entrained surrounding air, and the eruption plume may then rise to very great heights as a result.
In volcanic eruptions (and models of them), there is a variety of variables: the temperature and gas mass fraction of the emitted material, the ejected velocity and radius of the source, the ambient atmospheric stratification, and the heat capacity of the emitted solids. However, the emitted heavy material (hot rocks, boulders, etc.) that falls out close to the source have negligible effect on flow at higher levels, and if these are omitted, and if the heat of the remaining solids is communicated to the entrained air, the main properties of the eruption are well-described by plume theory.
One conclusion from these plume models is that the principal properties of the plume may be described by two parameters: the buoyancy flux at the source, and the buoyancy frequency of the atmosphere. In particular, the equilibrium height
zeq, the maximum height
zM and the final height around which the fluid spreads
zfinal are given by (e.g., Rooney and Devenish [
6])
where the “
c”s are constants,
F0 is the buoyancy flux at the source, and
N the atmospheric buoyancy frequency, defined by
Here,
ρ denotes potential density,
g gravity,
b plume radius and
w the mean vertical velocity, with subscript “0” denoting conditions at the source. Morton et al. [
4] made the assumption that the turbulent plume entrained environmental fluid as it rises, at a rate proportional to the mean vertical velocity
w, so that
where
ue is the entrainment inflow velocity, and α is a coefficient whose value is not precisely known, but is here taken to be 0.09, following Woods [
5,
7]. With these values, the coefficients of Equation (1) have the values (Rooney and Devenish [
6])
Further, the total spreading volume flux at the top of the plume has the value
The nett effect of the eruption plume on the motion of the local environmental air is, therefore, an extended region of entrainment of environmental fluid over most of its vertical extent, surmounted by a narrower region of strong outflow. This may be used to determine boundary conditions of horizontal velocity on a bounding cylinder (of radius a) that encloses the main part of the eruption column. There is some variability in the profile of this, but a reasonable representative profile has been adopted for present purposes, as follows.
The (vertical) width of the upper outflow region is taken to be 0.3
zM, centred on
zeq, and the profile of this outflow is assumed to have a parabolic form. Below the level 0.7
zM, the fluid is entrained at a rate which is 0.09
w at the edge of the rising plume. In general,
w decreases with height and the mean radius of the plume (where the entrainment condition is applied) increases. These two factors tend to cancel, so that the net inflow velocity at a fixed radius (enclosing the plume) may be regarded as approximately constant, and this is assumed to be the case here. Hence, the boundary conditions on a steady-state plume on the surface of a cylinder of radius
a that encloses it are here taken as follows:
This form has been chosen so that the total outflow in the region z > 0.7zM is equal to the entrained inflow below this level. The volume of the original outflow from the source of the eruption has not been included in this profile, partly because it can have a wide range of values independent of F0, depending on the initial radius and velocity at the source. Further, unless the eruption is constrained to reach very low heights (which are of little interest), it is a small fraction of the total volume of fluid reaching the upper level outflow. From Equation (6) we see that once the maximum height is determined, the main effects of the eruption on the environment (from the viewpoint of generating internal waves) are determined also.
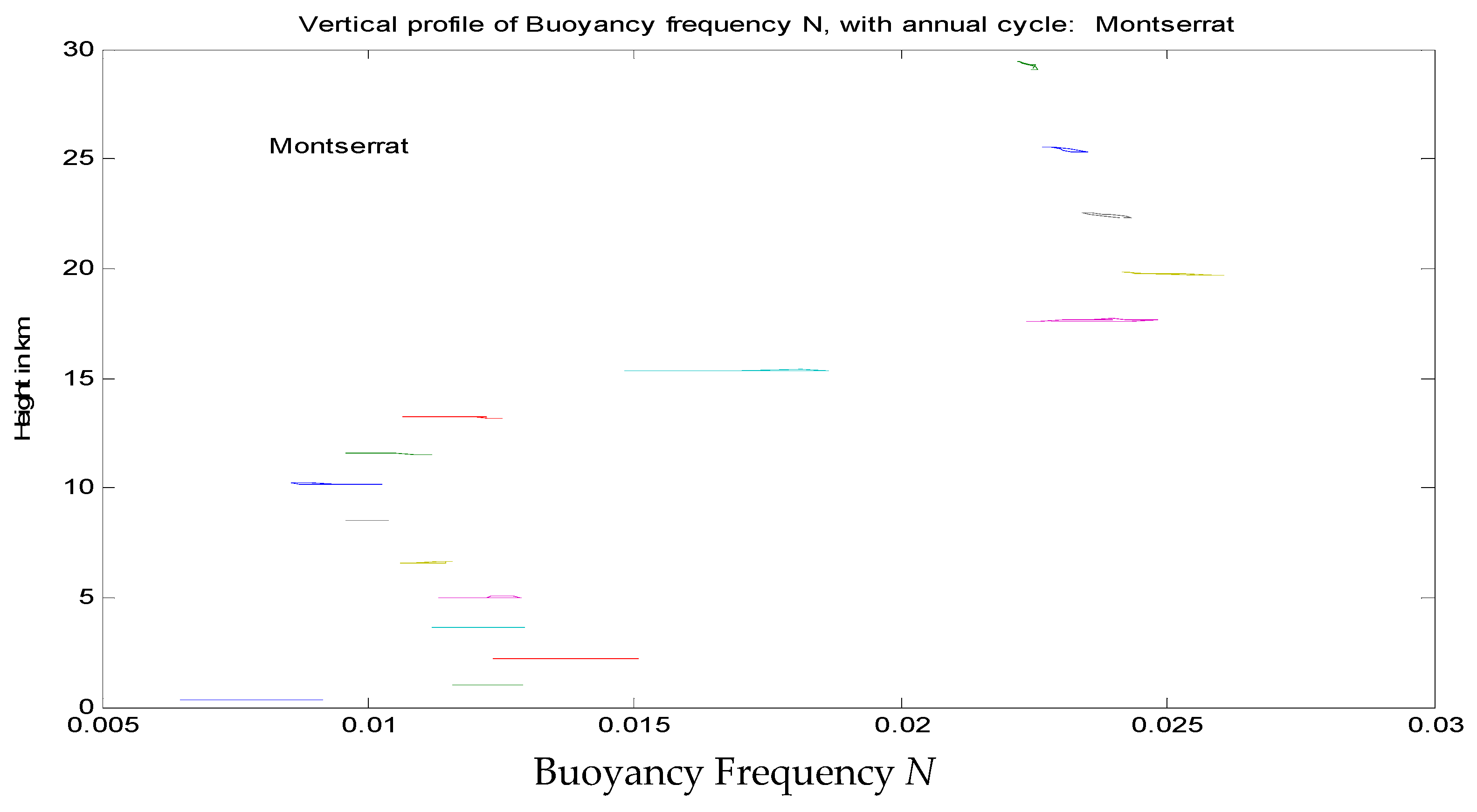
The site for which most observations of internal wave generation by eruptions has been made is the island of Montserrat in the Caribbean. Here, the height of the source is approximately 900 m above sea level. The seasonal variation of the buoyancy frequency is shown in
Figure 2. For present purposes the atmospheric profile of this buoyancy frequency may be assumed to be constant within the troposphere and separately within the stratosphere, with a discontinuity at the tropopause).
The assumed form of an eruption in this model is to take the fixed form Equation (6), multiplied by a function of time. In a real eruption the vertical structure varies with time, as the column initially grows in height, reaching its maximum height in the time scale 1/
N. This introduces complexity to the calculations, which are avoided here, and the simpler form of separated spatial and temporal dependence is expected to capture the main features of internal wave generation, for present purposes. Hence, the horizontal velocity at radius
a is here assumed to have the form
where
u(
a,
z) is given by Equation (6), and
f(
t) has the form
where
t1,
t2 and
t3 are constants. In other words, the form of the velocity field of Equation (6) is assumed to grow linearly for time
t1, remain constant for time
t2–
t1, and then decay exponentially in time scale
t3.
3. Atmospheric Structure and Internal Waves
Internal waves in the atmosphere may have frequencies ranging from near zero (actually, the Coriolis frequency, f) to N, the local buoyancy (or Brunt–Väisällä) frequency (as defined in Equation (2)). The oscillatory fluid motion associated with them tends to be nearly horizontal at near-zero frequency, and nearly vertical near frequency N, varying continuously from one to the other for frequencies in between, but constrained by features such as the ground and the tropopause.
If volcanic eruptions reach significant heights in the atmosphere, the internal waves generated by them occupy the full depth of the troposphere, and their propagation is influenced by the overall atmospheric density profile. The principal quantity is the buoyancy frequency, and a vertical profile for the vicinity of Montserrat is shown in
Figure 2. The short horizontal curves at different heights show the annual cycle in
N-values, with the tropopause at 14–15 km being the principal feature. In general, the annual cycle is not large, and the constant profile of Equation (7) gives a reasonable approximation throughout the year. In other latitudes, the pattern is similar, but the height of the tropopause decreases with increasing latitude.
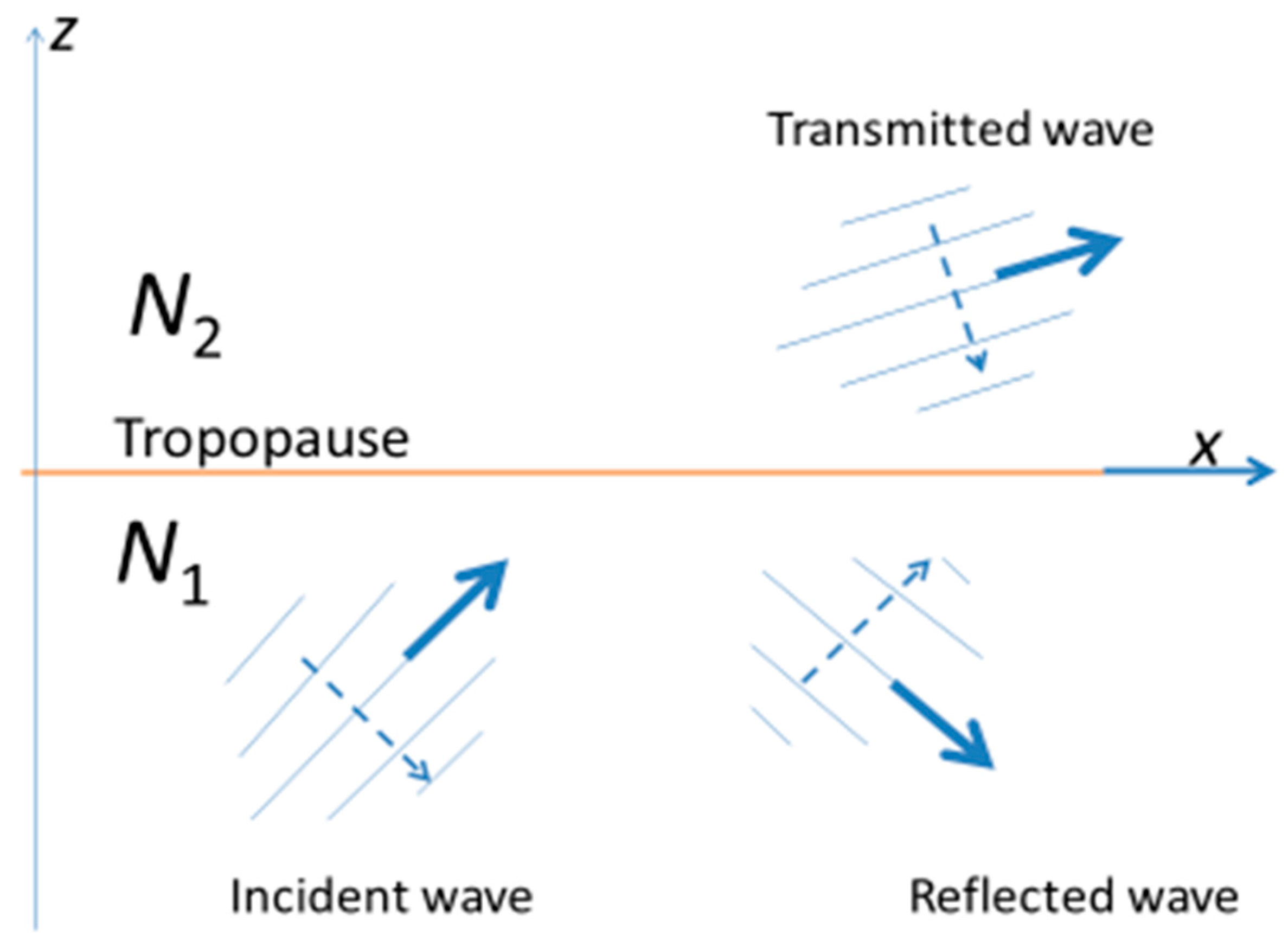
Internal waves generated by the eruption within the troposphere are affected by the tropopause. Part of the incident energy passes through it into the stratosphere, and part is reflected back, as indicated in
Figure 3, which shows a wave packet with dominant frequency
ω of the form
(where
p’ denotes pressure, but could also represent vertical displacement or a velocity component), incident on the tropopause from below. The wave packet moves in the direction of the solid arrow, which is the direction of the group velocity for waves of frequency
ω. The dashed arrow shows the direction of phase propagation within the packet, which is perpendicular to the group velocity, so that the vertical components of the phase and group velocities are in opposite directions.
Boundary conditions of continuity of pressure and vertical displacement across the tropopause determine the amplitudes of the transmitted and reflected waves, which are dependent on the wave frequency. In particular, for the pressure variable, the amplitude of the reflected wave relative to the incident is
Similar behaviour applies for waves generated in the stratosphere that are incident on the tropopause from above, except that waves generated in the stratosphere with frequency ω in the range N1 < ω < N2 are totally reflected. These details need to be incorporated into the governing equations, as described below.
4. Equations for Internal Wave Generation by Eruptions
This section describes the mathematical methodology for computing internal waves generated by an eruption. The mean vertical density profile of the atmosphere at rest is taken to be
where
zt is the height of the tropopause,
Hst the scale height in the troposphere and
Hss the scale height in the stratosphere, in a mean state of hydrostatic balance with pressure
p0(
z). Writing
the governing equations for linearised wave propagation in a stratified compressible atmosphere have the form (Gill [
8], Kanamori et al. [
1])
where
r denotes position,
p’ and
ρ’ the perturbation pressure and density,
u = (
u,
v,
w) with
w the vertical velocity component, and
cs the speed of sound.
For present purposes, we focus on the variables
w and
p’. If we define
where (
u,
v) denote radial and azimuthal velocities in plane polar coordinates (
r,
θ), the above equations may be expressed in terms of
P and
W in the form
where
denotes the horizontal Laplacian, and the buoyancy frequency
N and parameter Γ are defined by Gill [
8]
These equations contain solutions that consist of acoustic waves with frequencies greater than the acoustic cut-off
ωa given by
and internal waves with frequencies ranging from zero to
N. If
W is eliminated between Equations (17) and (18) in favour of
P, one obtains the equation
where
is the Laplacian. At this point we make the further approximation of assuming that the wave motions considered are effectively of low frequency (≤
N) and are incompressible, so that terms involving 1/
cs2 and
Γ are omitted. In fact, the term
Ptttt/
cs2 is smaller by two orders of magnitude, for these motions; the term
is smaller by about 1/20, but can be retained. It is omitted here for convenience, and its effect is expected to be very small. The change of density with height, however, is significant and must be retained. Equation (21) then simplifies to
with the boundary conditions
where
u(
a,
z,
t) is the horizontal velocity at
r = a, forced by the volcanic eruption. It is assumed that
for
z > zM for some value of
zM. For an eruption having the structure and time dependence as described in
Section 2, this boundary condition becomes
where
and
f(
t) are given by Equations (6) and (9), respectively.
We solve Equation (22) for the waves forced by boundary condition Equation (25), subject to the initial conditions that
P(
r,
z, 0) = 0 for
r > a. We first take the Laplace transform of Equation (22), defining
obtaining
with
We assume that the buoyancy frequency has two-layer structure, where
N(
z)
= N1 in the troposphere, and
N2 in the stratosphere, as given by Equation (7). Having obtained the appropriate solution for
, the solution for
P(
r,
z,
t) is then given by the inverted Laplace transform, which gives
where
s =
iω,
c.c. denotes complex conjugate and
δ is a small positive constant that may here be taken as zero. Writing
, Equation (27) becomes
where
in the troposphere, and
in the stratosphere, with
.
Appropriate solutions of Equation (29) in the troposphere have the forms
where
k is a real number and the
H denote Hankel functions, and one may make appropriate combinations of these forms to generate solutions that are consistent with internal wave dynamics and propagation.
We consider forcing in the troposphere and stratosphere separately. For eruptions where
zM <
zT, where
zT denotes the height of the tropopause, we may represent the forcing by a cosine series in
z, so that
where
(In the present context, the n = 0 term is inconsequential, and is not included in the following calculations.)
Hence, for
we have
and the solution may be expressed in the form
where, near
r = a, since
, with
time dependence, outward phase and energy propagation is given by
Substituting Equations (35) and (36) into Equation (34), and since
, we obtain
Hence, from Equation (28), the solution for the atmospheric pressure
is given by
where “Re” denotes that the real part of the integral is taken, and the integration is taken over the range 0 <
ω <
N1. The functions
and
are given by Equation (35) close to the forcing at
r = a. However for
r >
a, two factors must be taken into account. The first concerns the time taken for the constituent waves to reach a given distance
r, and second is the partial reflection at the tropopause. Both of these depend on the properties of internal wave propagation, as follows.
The constituent waves have the form
, with the dispersion relation
The horizontal phase velocity is given by
ω/
k and the group velocity by
Since the leading part of each wave component travels at the group velocity, at distance
r from the source (
r = a) there can be no wave component of mode number
n unless
r <
a +
cgt. This implies that for the terms
and
, the signal must be zero unless
A corresponding relation applies in the stratosphere. For the second factor, if the tropopause were a rigid surface, the form Equation (36) would apply for all values of
r, but because of its transmissive/reflective nature, this must be allowed for in computing the results based on Equation (37). This has been done by embedding the reflection condition described in
Section 3 into the code used to calculate the solution, starting with Equations (35) and (37) near
r = a. For the remaining factor in Equation (38), if
f(
t) is given by Equation (9), the function
has the form
If the volcanic eruption reaches heights greater than the tropopause height
zT, forcing in the troposphere still occurs and is calculated in the same manner as just described. However, here, forcing also occurs in the overlying stratosphere, which will add to the tropospheric forcing. The details for stratospheric forcing have some differences from those for the troposphere, and these are described in the
Appendix A. For the pressure signal at ground level, the results from forcing in both regions are additive.
5. Wave Generation by the Representative Eruption Model
Volcanic eruptions with different properties give different signals in atmospheric surface pressure. Here we describe properties of surface pressure variation in the neighbourhood of erupting volcanoes for a range of eruption types.
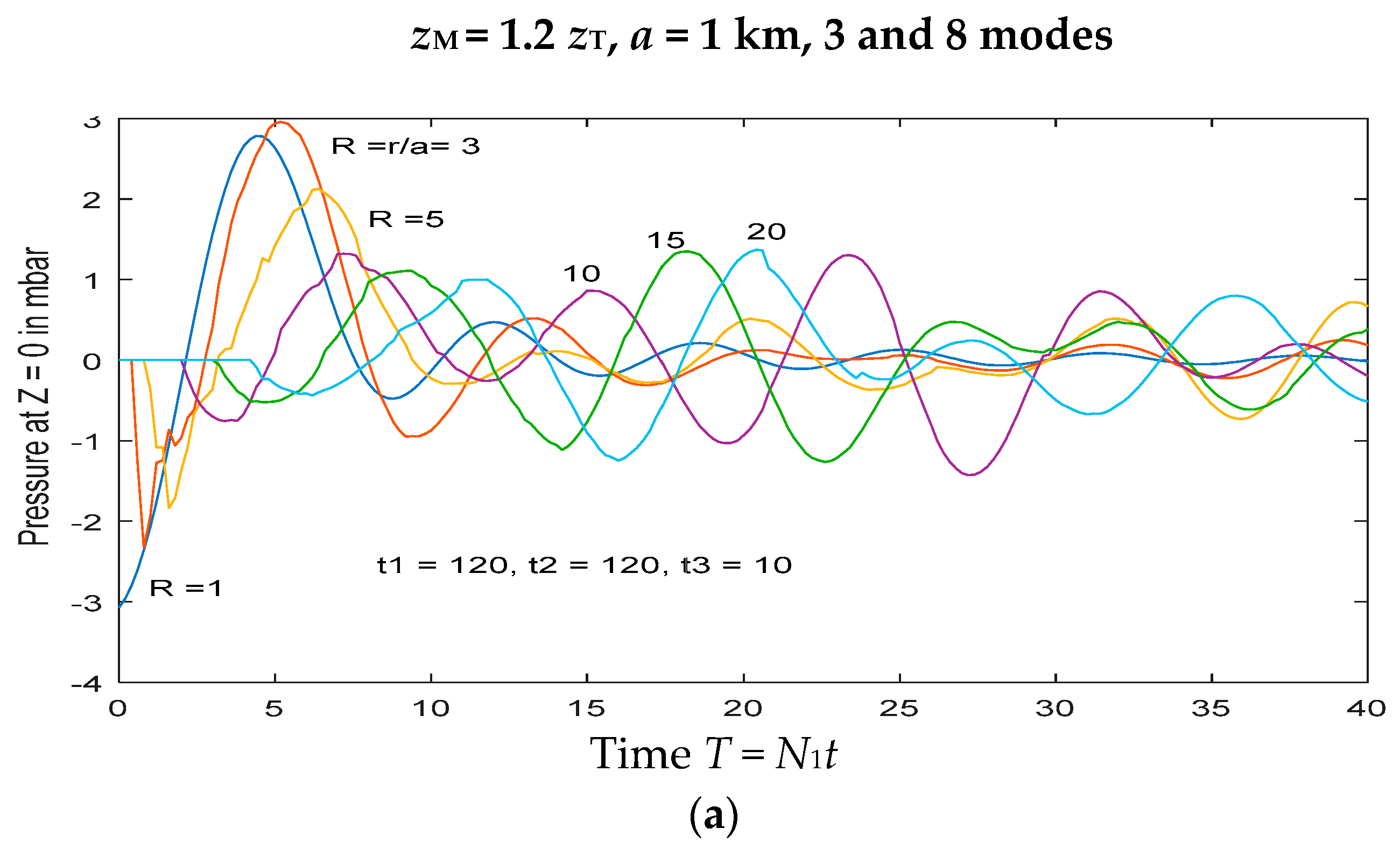
We first consider eruptions that are confined to the troposphere, and with explosive eruptions in mind, we take as a “base case” an eruption that builds for two minutes and then abruptly ceases. With temporal behaviour as described by Equation (9), this base case has t1 = 120 s, t2 = 120 s, and t3 = 1 s. Comparisons with eruptions with longer and shorter duration are described below.
The choice of the radius a of the cylinder that encloses the eruption, and where the boundary condition is applied, is taken to be 1 km for small to medium-sized eruptions, but could be up to 3 km for large eruptions. This requires the assumptions that the main part of the eruption (excluding perhaps part of the upper level spreading cloud) is contained within the cylinder, and that there is no significant wave development where r < a. For the internal wave model, comparisons show that the differences resulting from these choices are small (for r > 3 km). It should be noted that the radial distance r is scaled with a and the results are plotted with variable R = r/a, and a = 1 km is used in all results presented.
(i) Tropospheric eruptions.
Eruptions that are confined to the troposphere are those where
zM ≤
zT, which from Equation (6) implies that the initial buoyancy flux
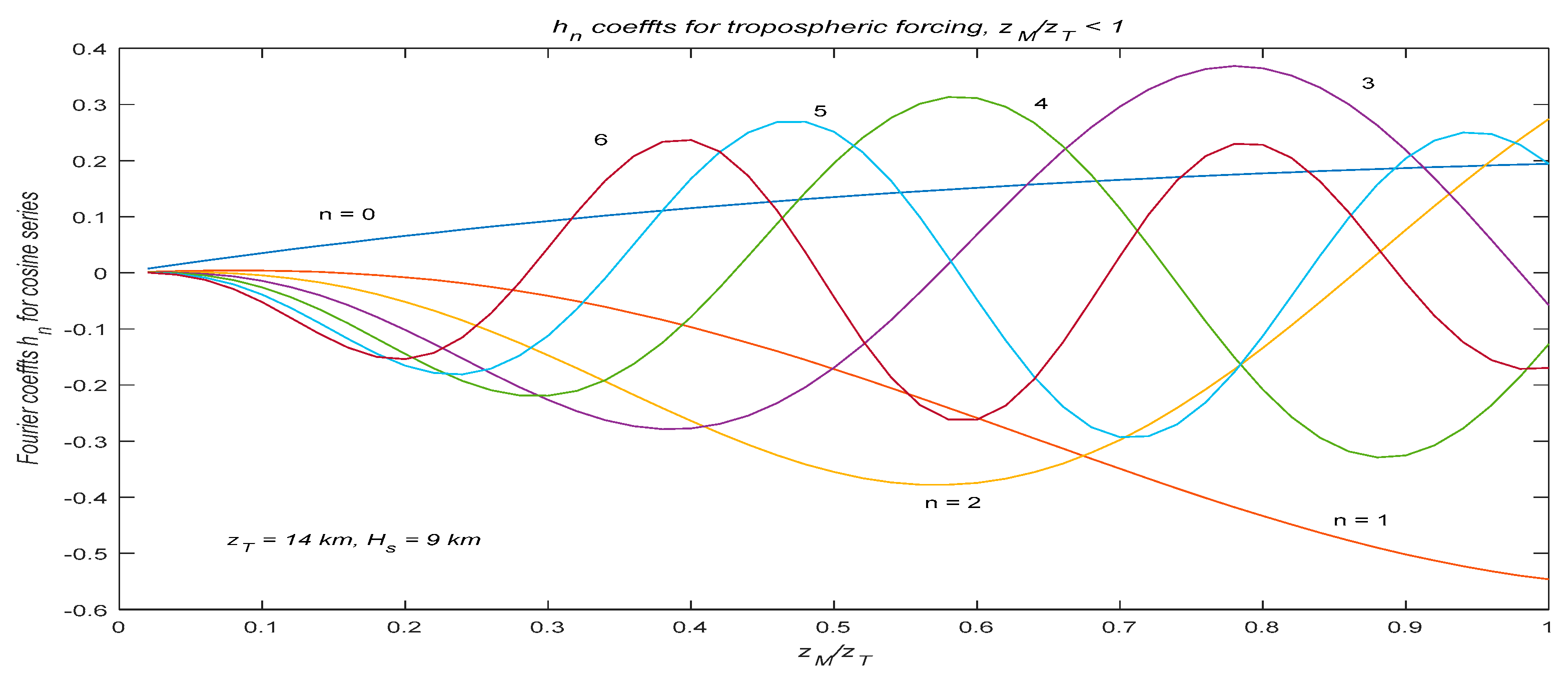
. To compute the internal wave response, we must first obtain the Fourier coefficients
hn from Equation (33) for the specific value of
zM, and then evaluate the integral Equation (38) (
n = 1, 2 and 3 are the most important, but
n = 1:6 are included here). The values of these Fourier coefficients are shown in
Appendix B and those for 0 <
zM ≤
zT in
Figure A2. For the internal waves, it is only necessary to cover the range 0 <
ω <
N1. Here the
N-profile is given by Equation (7),
a = 1 km (
a = 0.5 km gives very similar results), and
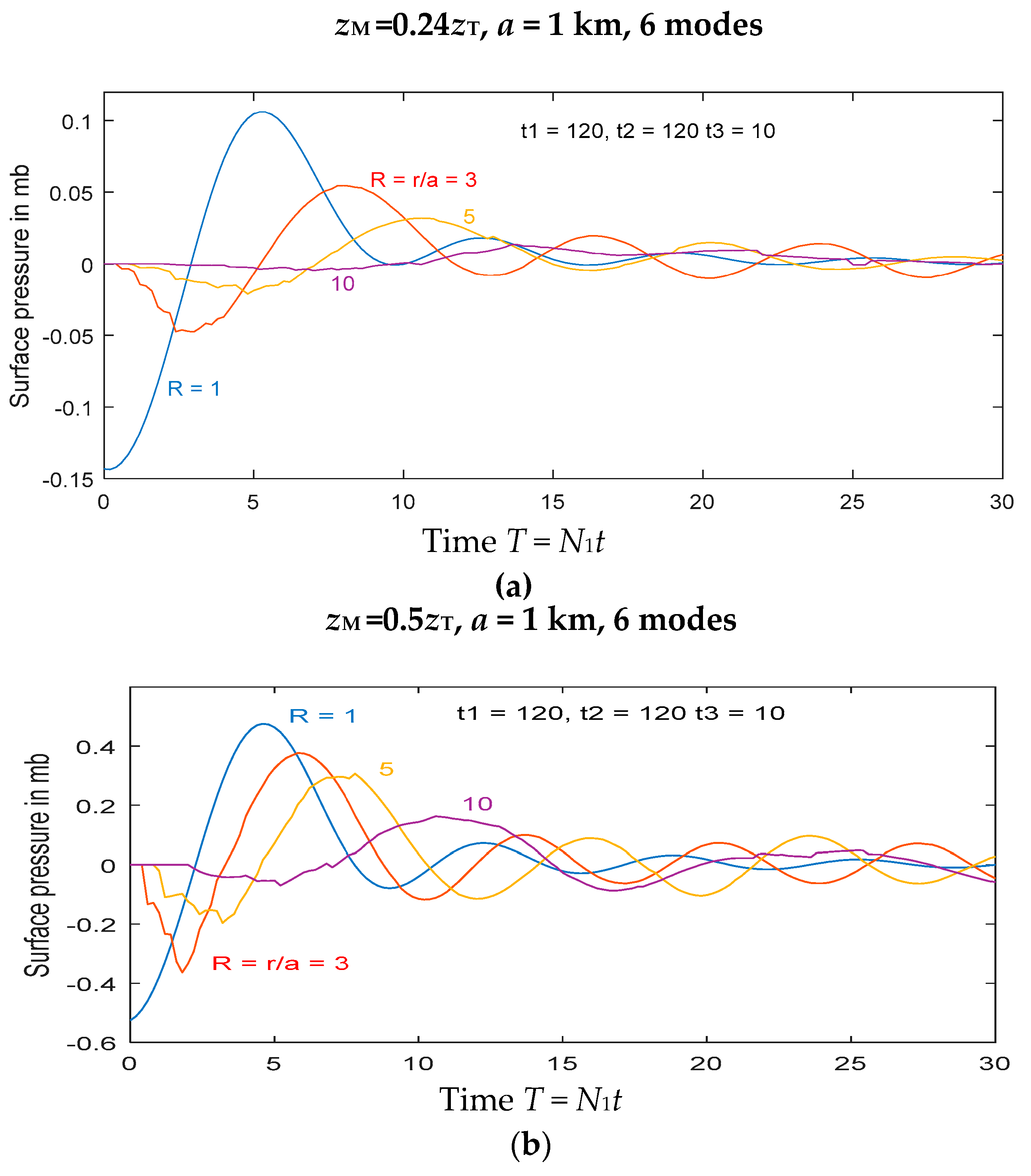
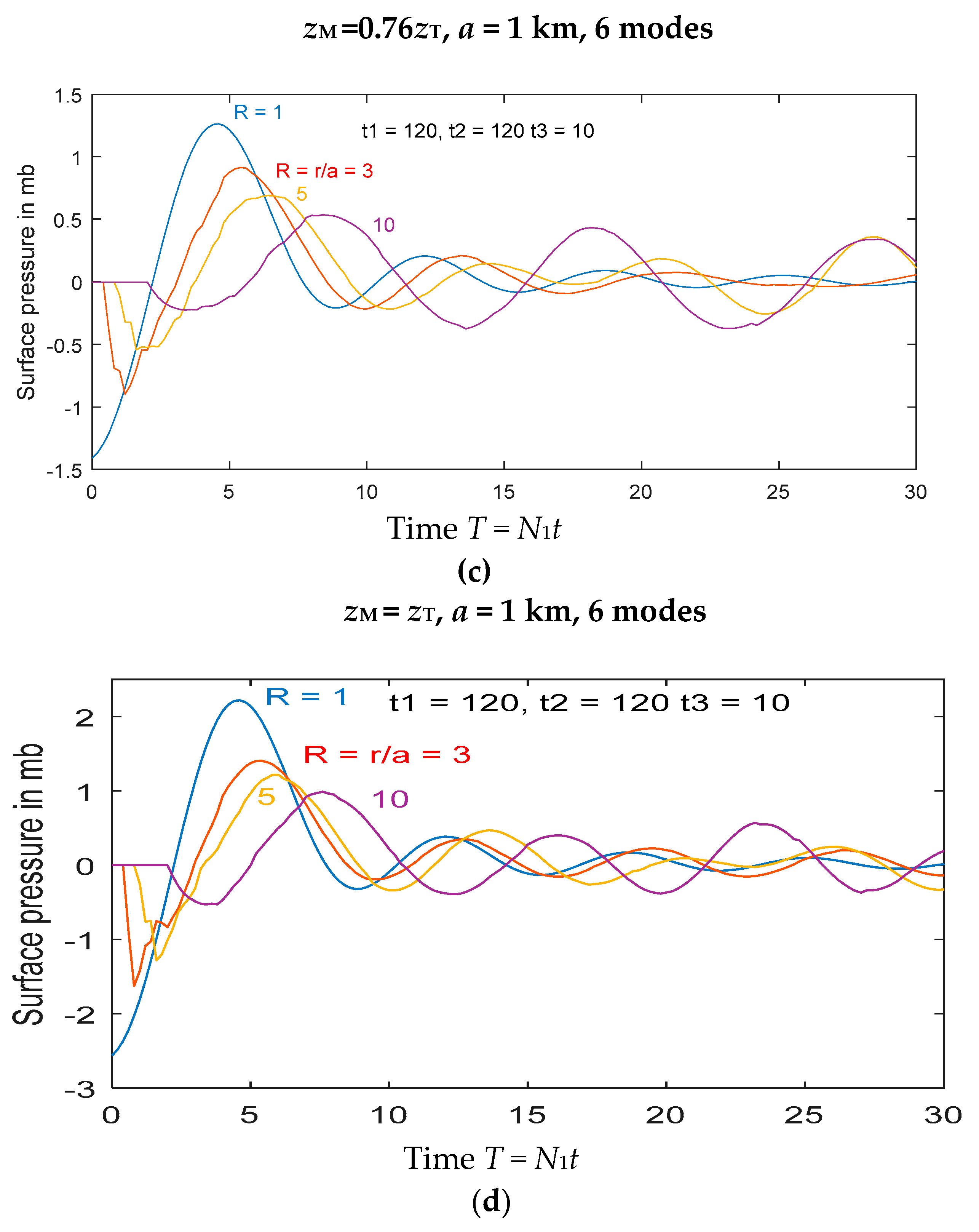
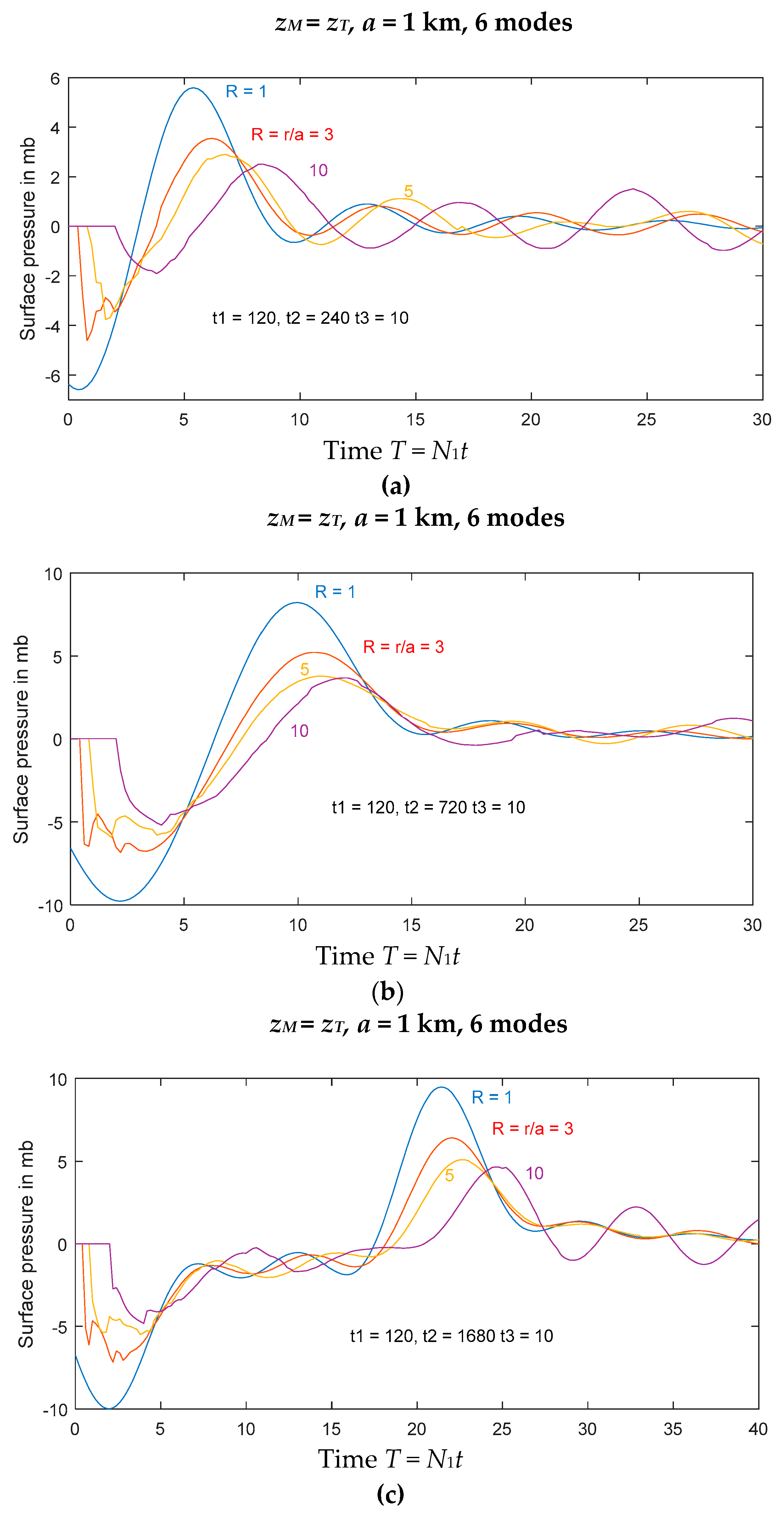
zT = 14 km. Results are shown in
Figure 4 for the “base case” for four different values of
zM: 0.24, 0.5, 0.76 and 1.0. As seen in each figure, at the onset of motion there is an initial abrupt decrease in surface pressure, that decreases with increasing distance. Following this, there is, at each location, a subsequent increase in surface pressure of comparable amplitude. This is followed by oscillations of approximately constant or slowly increasing period as the amplitude decreases with time. The minimum period for gravity waves is the buoyancy period 2π/
N1, which here is 6.28 min, and these waves have periods in the range 8–9 min. We note that the amplitude of the waves (in terms of surface pressure) increases rapidly with the strength and maximum height of the eruption, with typical amplitudes (at
R = 3) of 0.05, 0.35, 0.75 and 1.2 mb as
zM/
zT increases from 0.24 to unity. The number of oscillations in surface pressure depends on the height and strength of the eruption. For the larger eruptions that reach the upper troposphere, these oscillations last for several cycles, but, for the smaller ones (
zM < 0.5
zT), they die out quickly after about two cycles.
There is a tendency for the wave periods to decrease (frequency to increase) with time. In the four cases in
Figure 4, the values of
ω/
N1 (where
ω is the local frequency) at each location are initially about 0.7, but increase to values of 0.9 or more, close to the maximum value of unity, with increasing time. This increase in frequency implies that the phase speed decreases.
The above results are representative of eruptions that last for a period of time that is significantly shorter than the buoyancy period, 2π/
N1 (6.28 min). For eruptions lasting for shorter times than the “basic state” above, the time series at the various locations are collectively similar in shape, but their amplitudes are smaller, being approximately proportional to the length of time of the eruption. If the length of the eruption is increased by increasing time
t2, the wave pattern remains the same but the amplitude continues to increase, in proportion to the time
t2, up until this time becomes comparable with the buoyancy period (here, 6.28 min), as shown in
Figure 5, after which it remains approximately constant. The time of the initial minimum of surface pressure occurs at progressively slightly later times with the increasing length of the eruption, up until the buoyancy period and then remains constant. However, the subsequent maximum in surface pressure continues to increase in proportion to the length of the eruption, regardless of how long this is.
The wave amplitudes reach a maximum when t2 is comparable with the buoyancy period, and decreases if t2 is increased further, to near zero (after the initial wave) for t2 = 800 s. For larger t2, the initial waves occur progressively later, and dominate the wave field. The following wave pattern is complex, and has smaller amplitude for t2 very large.
We have described the flow in terms of time series at fixed distances, but other relevant properties are the wave speed and wavelength. The wavefield here consists of six modes, but is principally dominated by modes 1 and 2, each of which has its own speed and wavelength. If we consider unidirectional waves of the form
where
ω is the frequency and
k the wave number of mode
n = 1, 2 or 3, Equation (22) gives the dispersion relation
where
cw(
n) is the wavespeed for mode
n, and
, is the wavelength for that particular mode. The maximum speed, for very long internal waves, is
. Mode
n = 1 travels faster than the others, and hence is the first to arrive. If
ω ≈ 0.7
N1 for the initial waves, this may be taken to be mode
n = 1, and Equation (44) then gives
which gives a wavelength of about 28 km (for
zT = 14 km) and a wavespeed
of about 38 m/s. Higher order modes travel more slowly. Secondary maxima in wave amplitude at various locations may be attributed to the arrival of higher order modes, principally mode
n = 2.
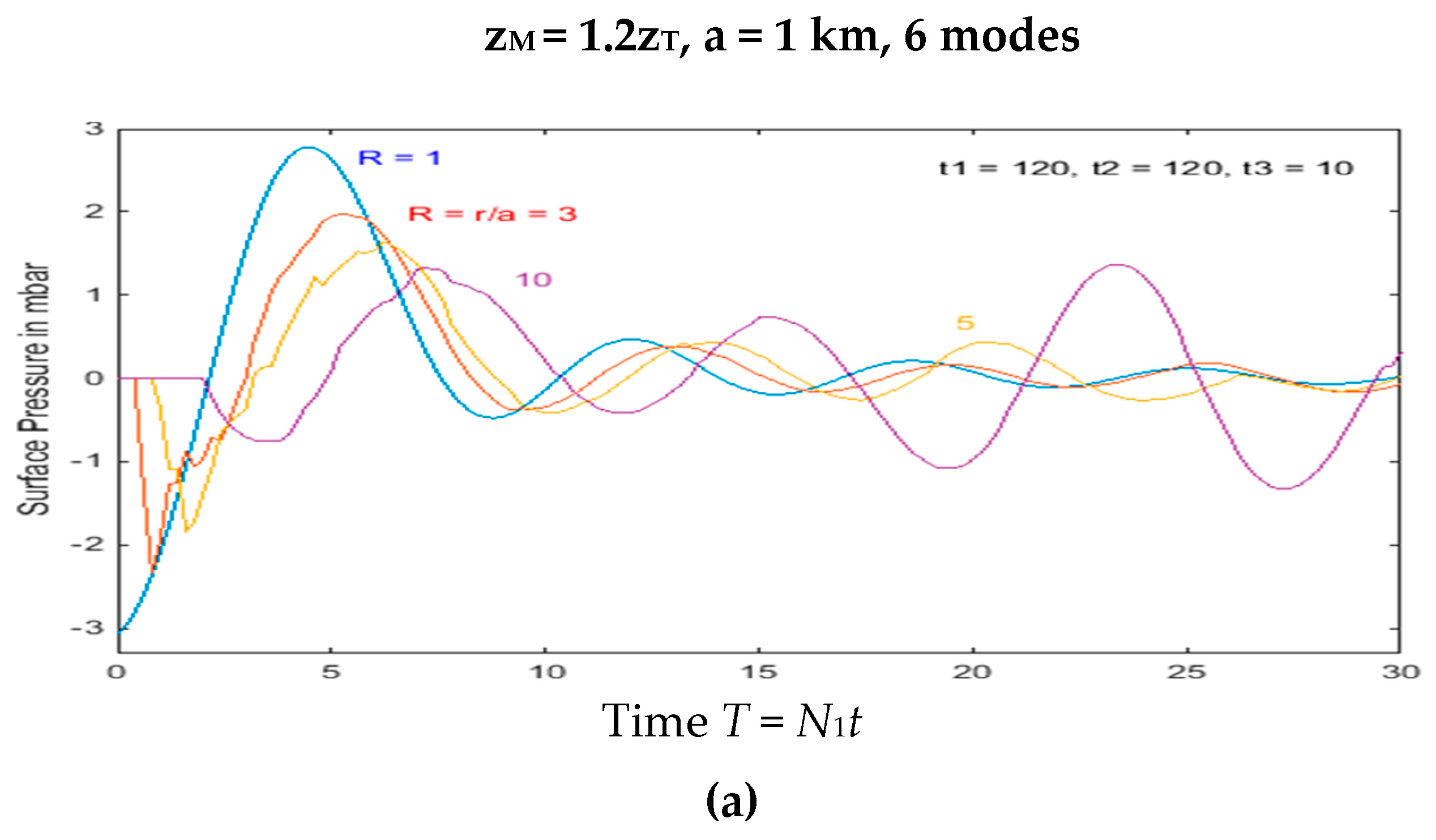
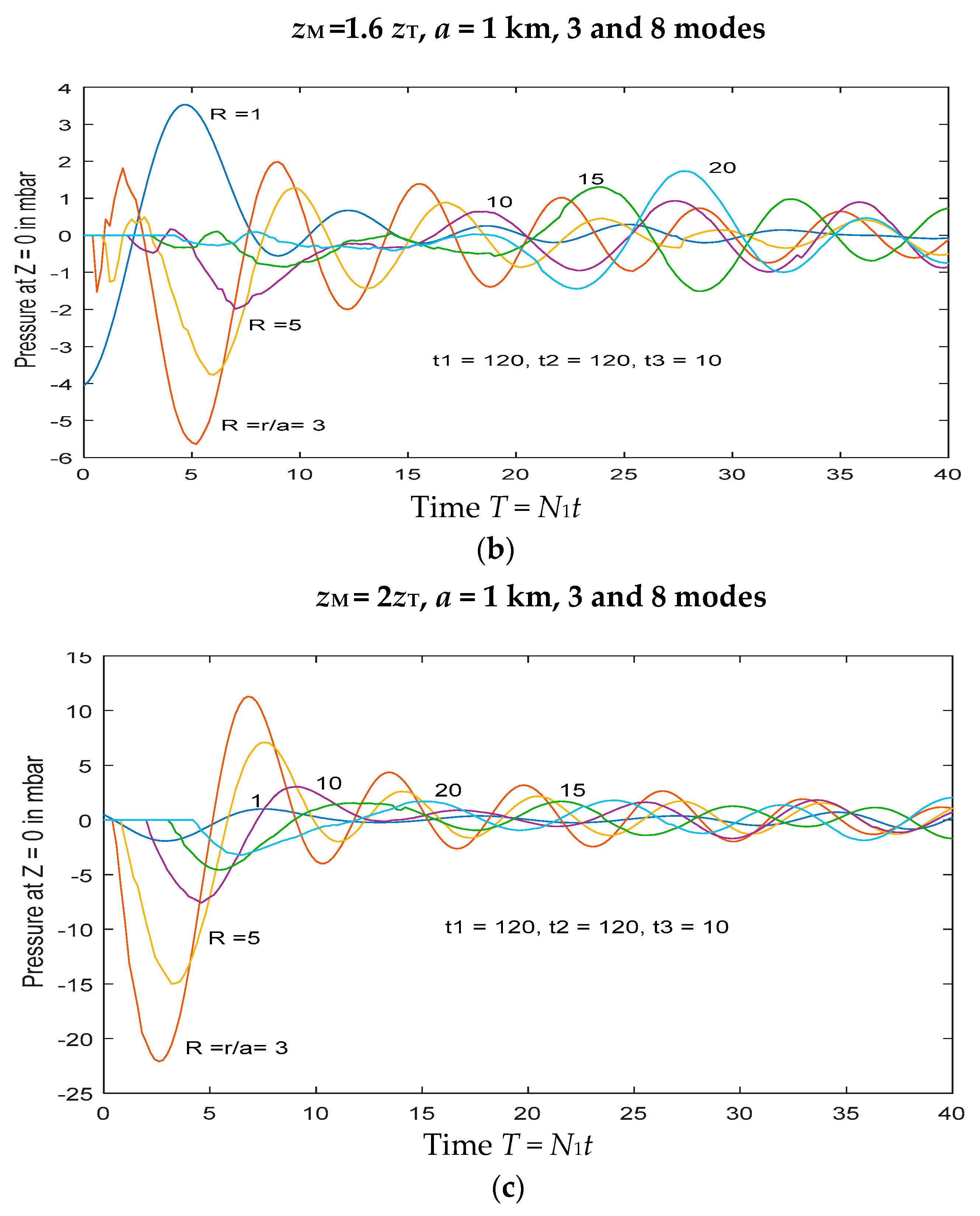
If the eruption reaches into the stratosphere (
zM >
zT), forcing from within the troposphere still occurs, and may be calculated in the same manner. The total effect on surface pressure (and tropospheric wave motion generally) is due to the sum of forcing in both the troposphere and stratosphere. Here we first describe the tropospheric forcing component. For wave forcing in the troposphere, as
zM increases above
zT, the resulting flow remains similar to that for
zM =
zT, but slowly decreases in amplitude, for values up to 1.6
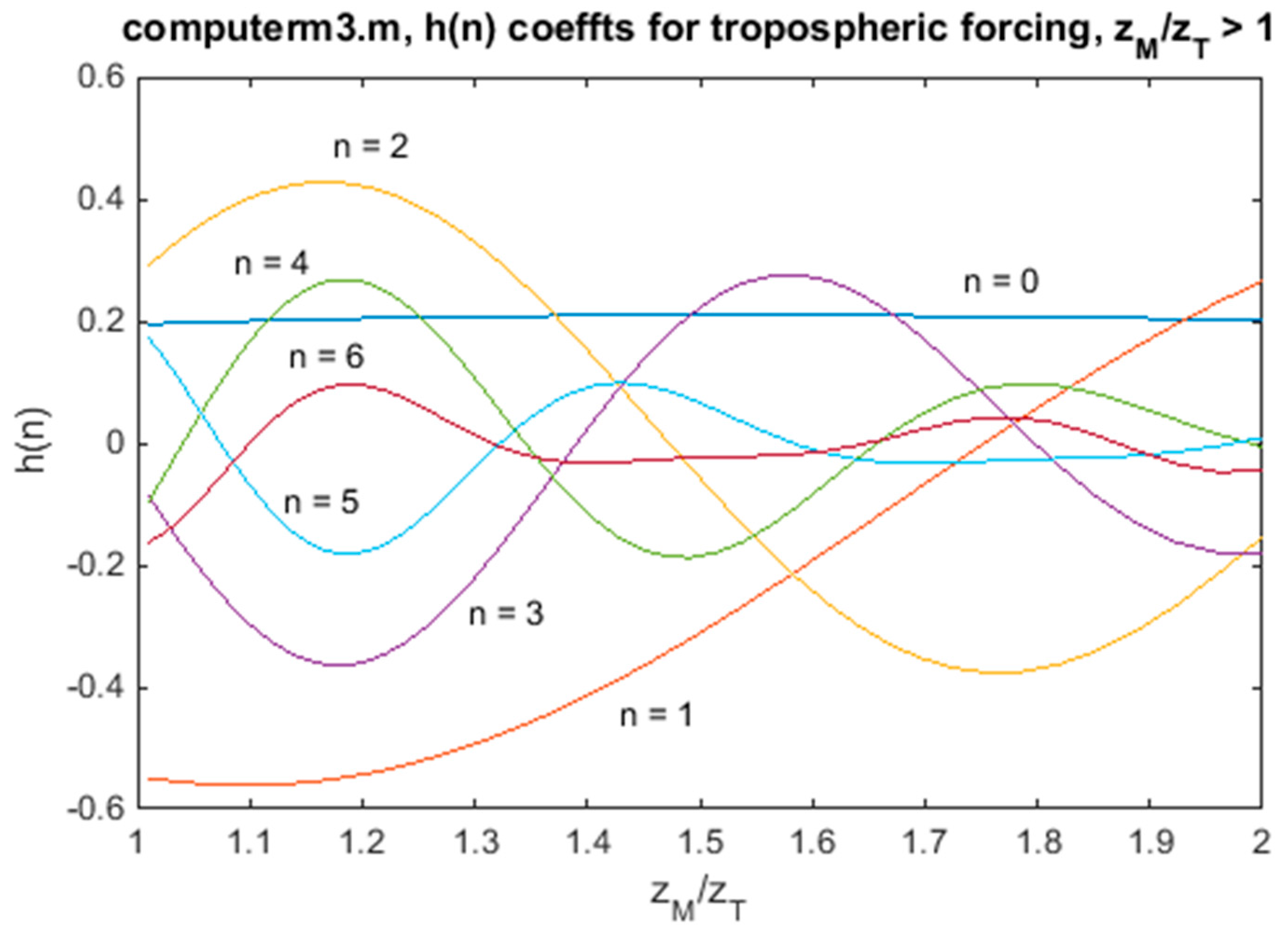
zT. This is seen in
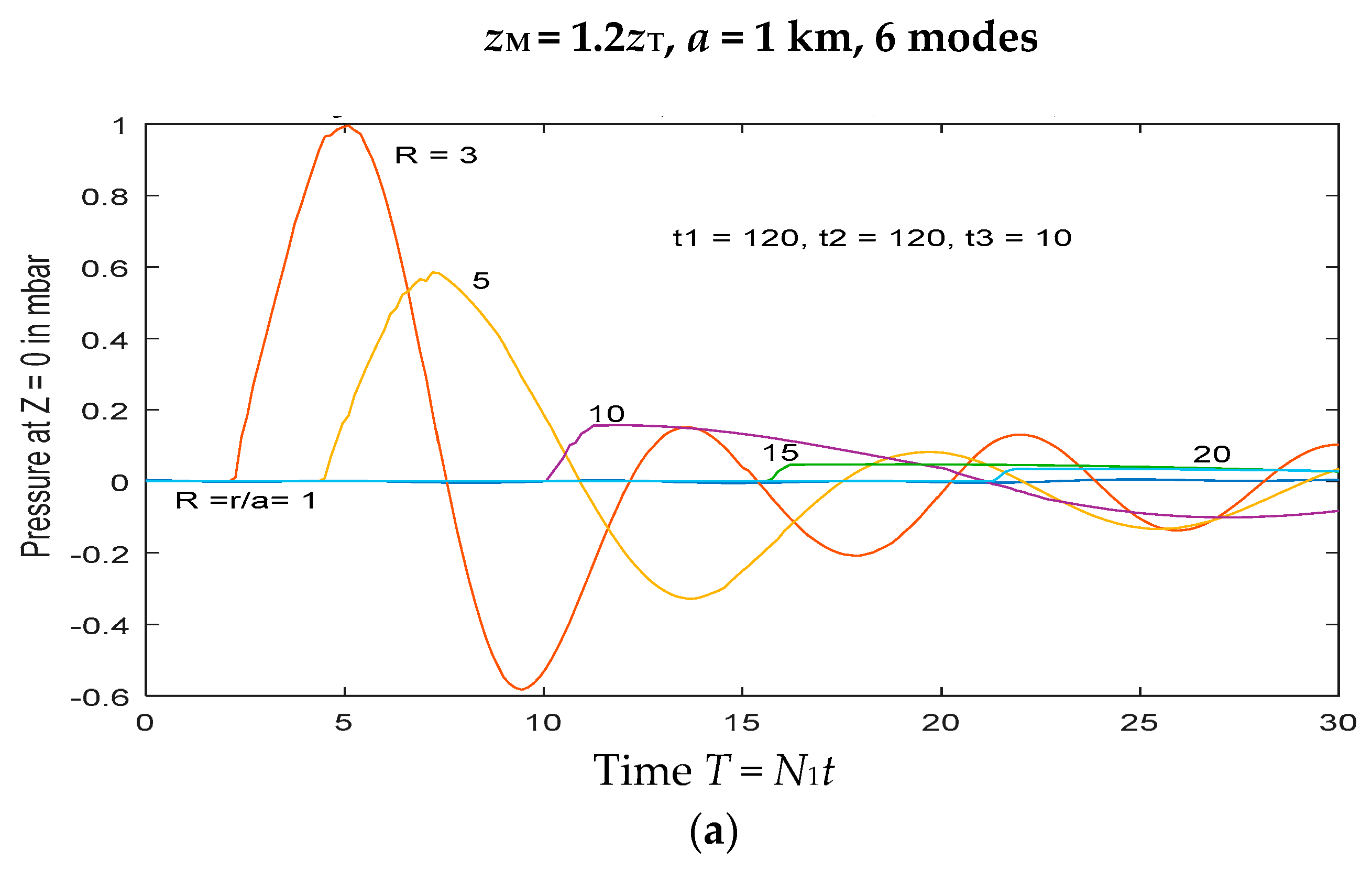
Figure 6, for which the Fourier coefficients
h(
n) are shown in
Appendix Figure A2. For
zM > 1.6
zT, there is a progressive change in sign of the initial waves at each location (out to 10 km), which may be primarily attributed to the change in sign of the forcing term
h(1) for mode 1.
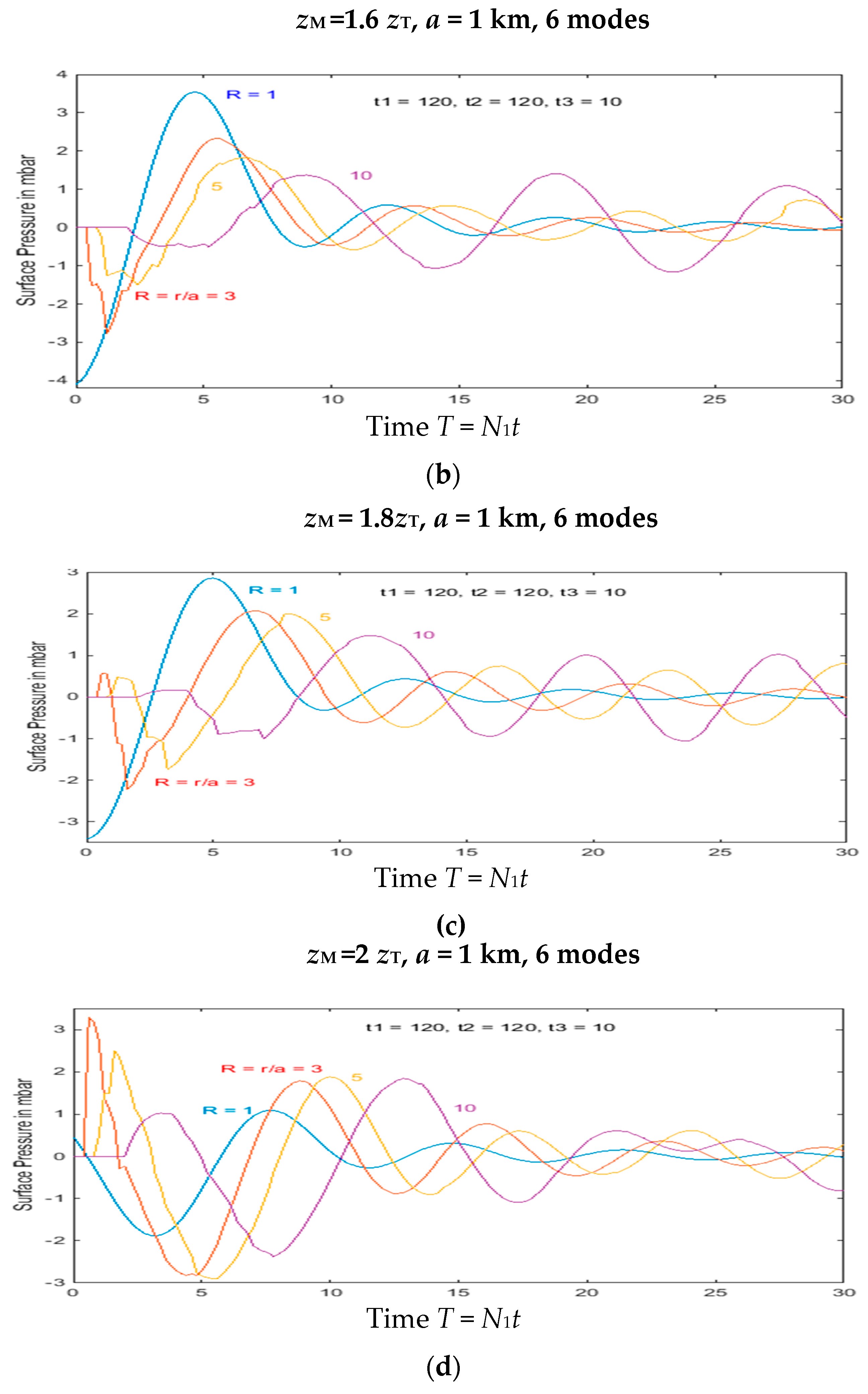
(ii) Stratospheric eruptions
Eruptions that are strong enough to reach levels in the stratosphere generate wave motion in both the troposphere and stratosphere. The equations for stratospheric generation are described in
Appendix A. The wave motion generated at any given frequency
ω < N2 has both upward and downward-propagating components, in approximately equal measure. The wave motion with upward group velocity does not affect the motion in the troposphere, and the only component that does is the motion with downward group velocity (upward phase velocity) with frequency in the range 0 <
ω < N1. This wave motion impacts on the tropopause, and part of the wave energy flux is reflected back upwards, and part enters the troposphere. The formulation in
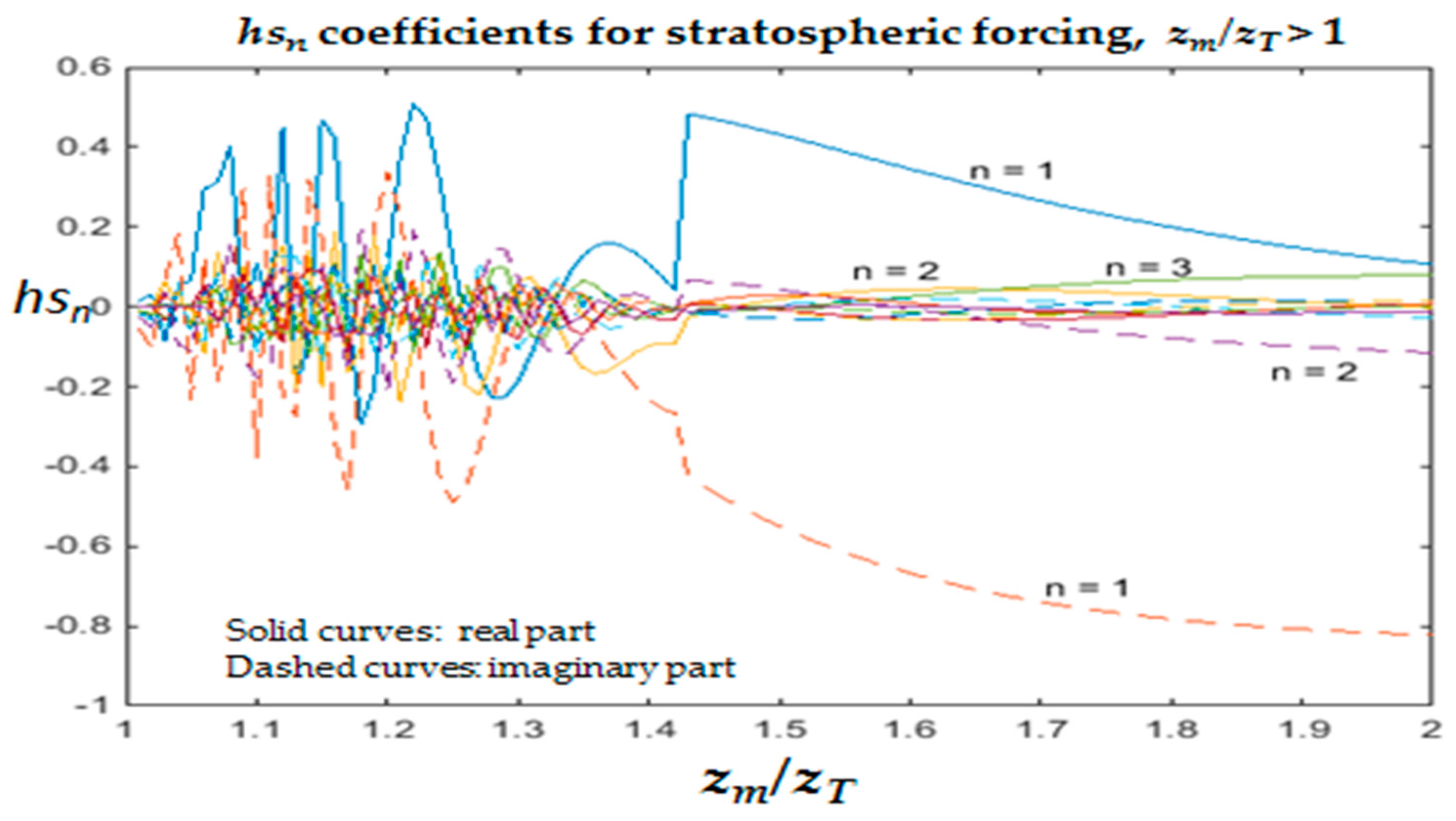
Appendix A captures this latter part, and gives the resulting pressure signal at the surface. The relevant complex Fourier coefficients are shown in
Figure A3. In the range
zT <
zM < 1.35
zT, the forcing amplitude for each mode is generally small, or almost indeterminate, but clear values of significant magnitude are evident for
zM > 1.4
zT. Some representative surface pressure signals in this parameter range are shown for stratospheric forcing in
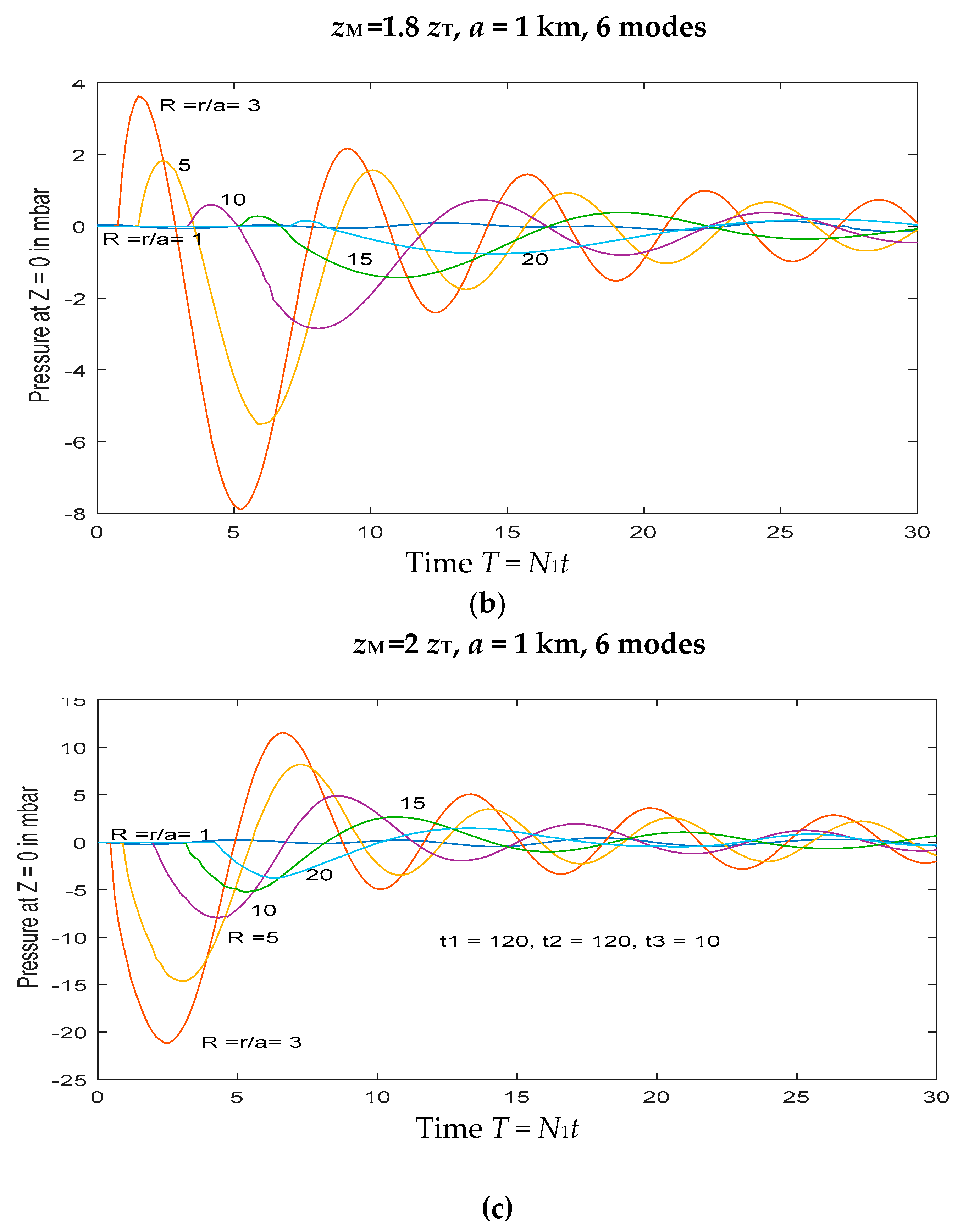
Figure 7.
Figure A3 shows that, when
zM < 1.4, the forcing amplitude is small and rapidly varying. As a result, the resulting surface pressure signal from stratospheric forcing is relatively small and effectively indeterminate.
Figure 7a shows the response for
zM/
zT = 1.22, but this is relatively small and unreliable, in comparison to
Figure 7b–d. Here, the signal is of much larger amplitude, and progressively changes sign as
zM/
zT increases from 1.5 to 2.
If an eruption reaches into the stratosphere, the resultant surface pressure is the sum of the forcing in the troposphere and that of the stratosphere. The higher the eruption reaches the stronger it is, and the larger the overall forcing of internal waves, but the above result implies that in the range 1 < zM/zT < 1.4, most of the response comes from forcing in the troposphere. This is because the upper level spreading is still present there, and the tropospheric forcing profile is more effective. However, if zM/zT > 1.4, the tropospheric forcing is weaker and the stratospheric forcing increases in strength, and the latter dominates the total response. A noteworthy feature of these results is the progressive change in sign as zM/zT increases. Note also the larger amplitude than that for forcing directly in the troposphere. This is because the eruptions that reach deep into the stratosphere have correspondingly larger amplitudes.
The nett signal in surface pressure from eruptions that penetrate the tropopause is the sum of the signals forced separately in the troposphere and stratosphere, and these are shown for a range of parameters in
Figure 8.
6. Comparison with Observations
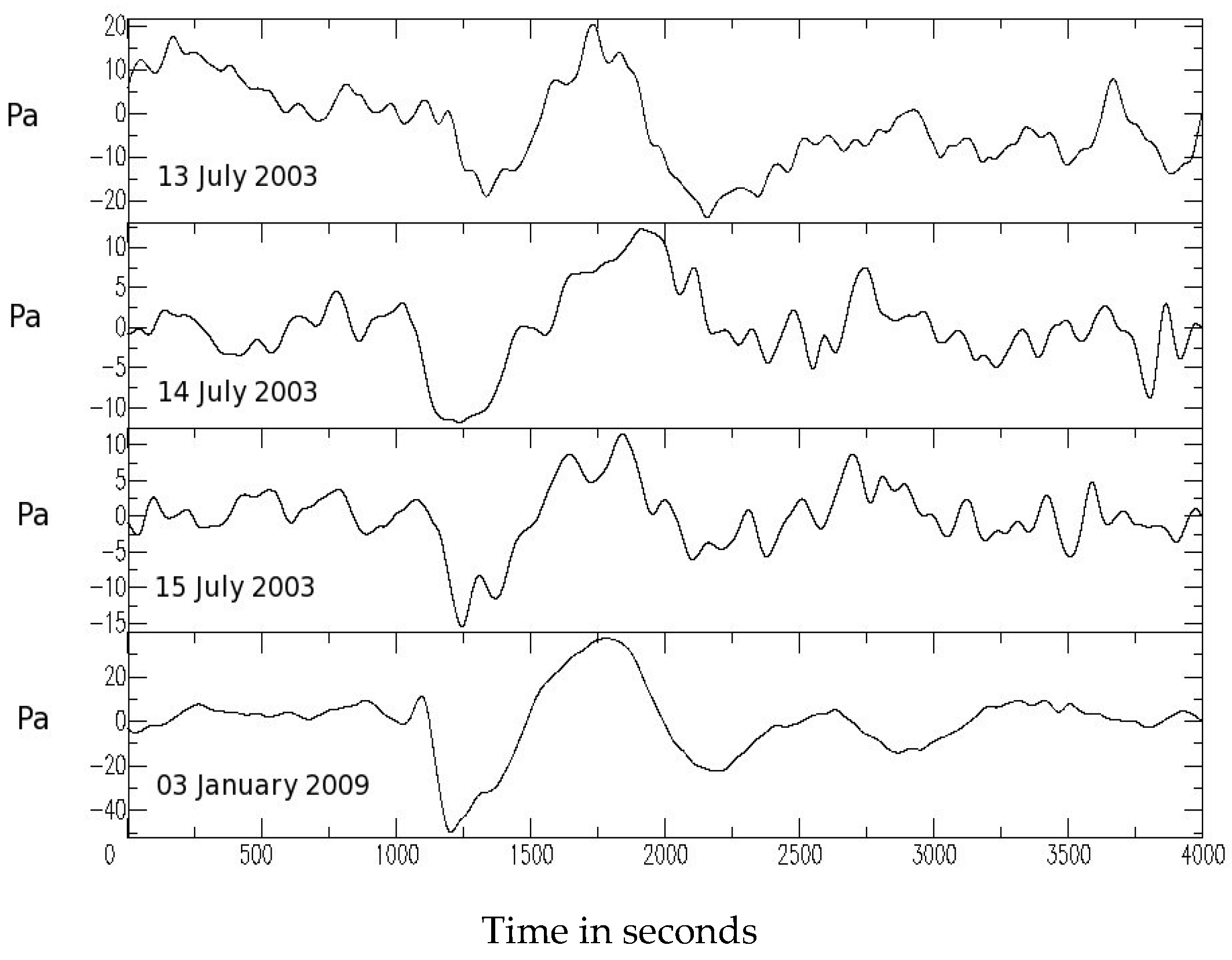
Figure 9 shows some records from surface microbarographs during eruptions of the Soufrière Hills volcano. The amplitude is not large, and, in comparison with the model results in
Figure 4, this implies that the eruptions are of short duration and do not reach more than several km vertically into the troposphere. This is consistent with direct observations of these eruptions: Montserrat is not a very large volcano, in global terms. There have been numerous explosive eruptions of Montserrat over the past 20 years, and the records of
Figure 9 are typical. The periods are of order 800 s, or about 13 min. The records shown in
Figure 4 have generally shorter periods, of about 10 min. This may be due to the fact that the eruptions are confined to the lower troposphere, where the stratification is weaker (
N1 ~ 0.008 s
−1) as seen in
Figure 2. Other eruptions of Montserrat show behaviour with the same general pattern as that displayed in
Figure 4a,b for locations that are close to the source (within 5–10 km): an initial large negative pressure signal followed by a positive one of comparable amplitude, and then rapidly decaying oscillations, for one or two cycles for small eruptions. Data from eruptions of other volcanoes that are larger and/or longer in duration are scarce and of lower quality.
From the microbarograph observations, it is possible to estimate the properties of an eruption.
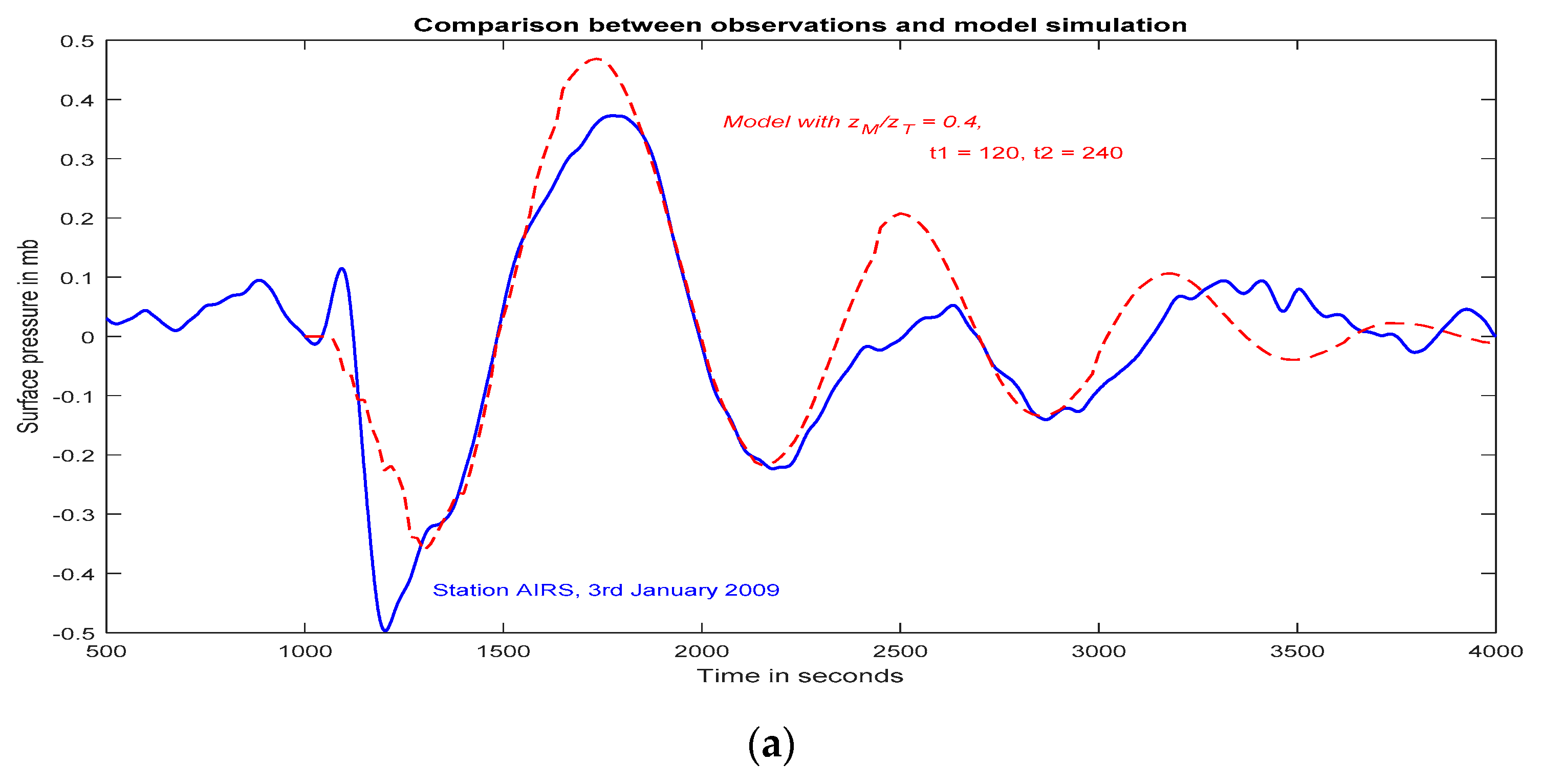
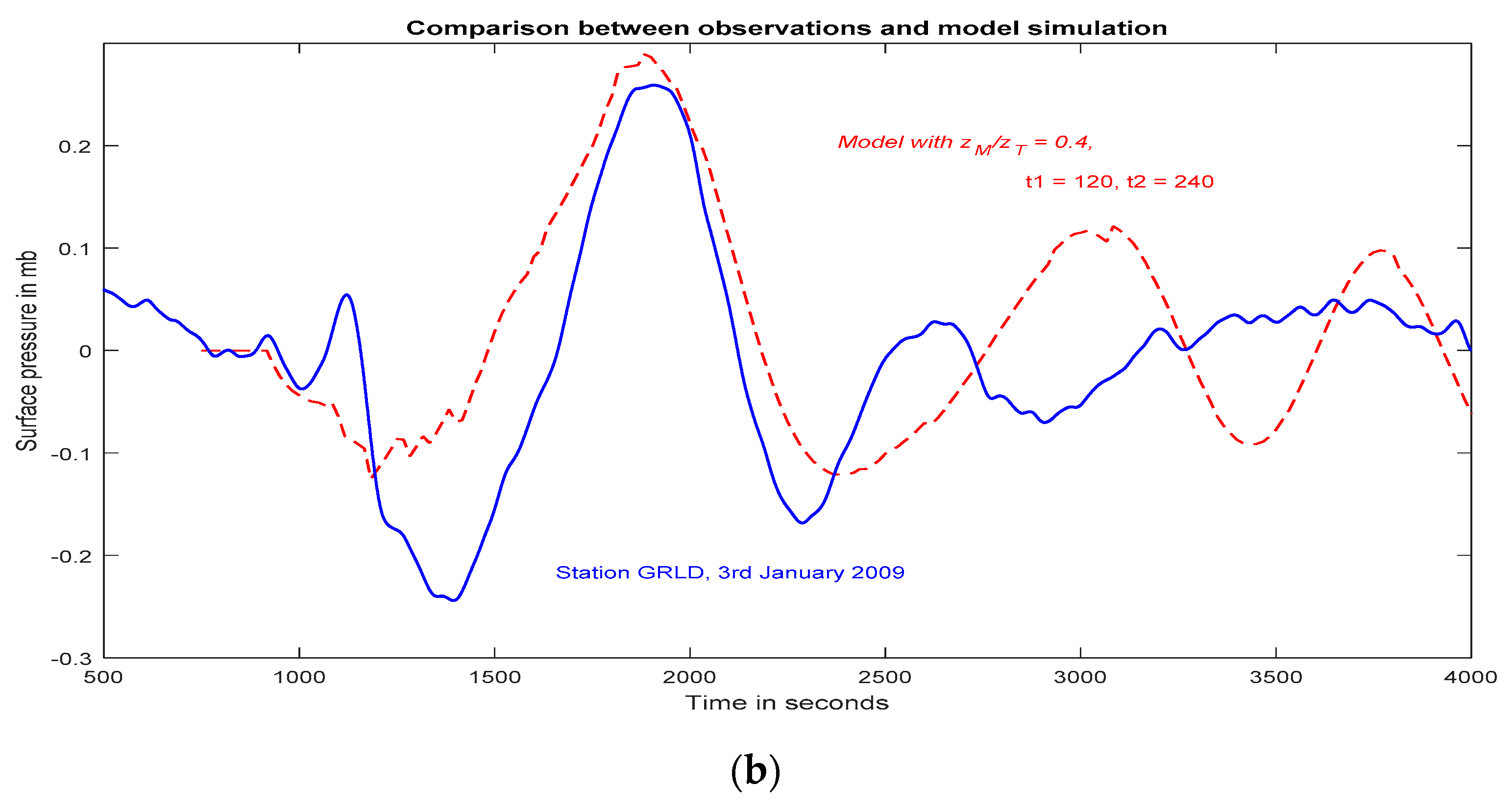
Figure 10 shows a direct comparison between observations from the eruption of 3 January 2009 at stations AIRS (5 km from source) and GRLD (10 km from source), with curves from the model with
zM/
zT = 0.4, and
t1 = 120 s,
t2 = 240 s,
t3 = 10 s. These parameters were chosen to give an approximate fit to the amplitude, and the general similarity between these curves implies that the eruption reached a height of about 5.6 km, with an associated buoyancy flux given by Equation (1), and lasted for about 4 min. Most of the observational records in
Figure 10 and
Figure 11 show a small maximum in surface pressure at the start of the eruption, which is not described by the model. This feature may be attributed to the initial vertical growth of the plume, which will give an initial increase in surface pressure because of the injection of erupted material into the lower atmosphere, before the entrainment process takes effect.
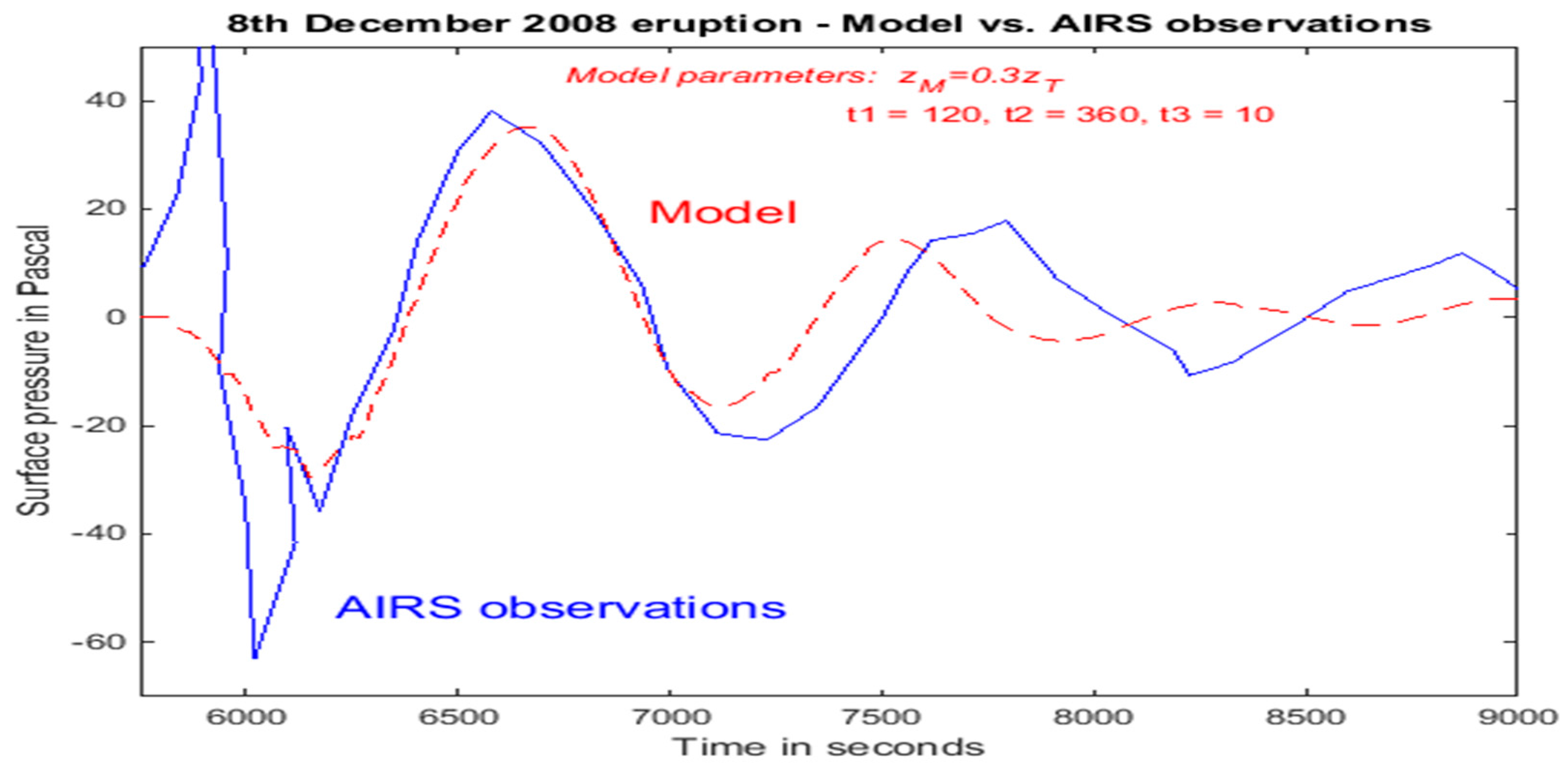
Figure 11 shows an eruption that generated waves with a longer period of about 20 min, with observations described by Ripepe et al. [
3,
9]. The wave amplitude is not large (~35 Pa) implying a shallow eruption, and in the model simulation, has significant contributions from modes with high vertical wavenumber, which implies that they propagate slowly, giving longer period at fixed locations.
7. Conclusions
This paper describes a mathematical model of internal wave generation by explosive (and other) volcanic eruptions. The model is based on the representation of the eruption by a conventional plume model, of the type described by Morton et al. (1956). In comparison with earlier models for internal wave generation based on equations for nuclear explosions (that employ a source of fluid at an elevated point location), this plume-based model contains the effect of entrainment of environmental fluid in the rising region, as well as the spreading region in the upper part of the plume. For the calculations described here, the plume has constant structure that increases in strength linearly with time of a period of about 2 min, maintains its strength for a subsequent period (which may be zero), and then rapidly decays. Such a plume entrains environmental fluid over the lowest 70% of its height, and the inflowing and entrained fluid then spreads horizontally outwards in the upper 30%. The resulting horizontal flow is then employed as a boundary condition on a vertical cylinder that encloses the plume, and the associated horizontal velocity on the surface of this cylinder generates the internal waves.
For small, short-lived eruptions that only reach into the lower part of the troposphere, there is an initial negative surface pressure signal near the source that propagates outward and is followed by a positive pressure signal of comparable magnitude. This is then followed by a decaying oscillation in surface pressure, and as the strength (and therefore height) of the eruption increases, these oscillations become more durable (i.e., longer lasting) and extend to greater distances (see
Figure 4). This behaviour is generally consistent with that observed for explosive eruptions on the island of Montserrat over the past 20 years.
The model is also applied to larger eruptions that may (or may not) reach into the stratosphere, and/or last for much longer periods of time. In the case most studied here, the eruption is assumed to have the form of growth to maximum strength in 2 min (or similar), and then maintains its strength at constant rate for a time T (say), followed by rapid decay. The effect of variation of time T from zero to large values was investigated, with results shown in
Figure 5. As time T increases, the initial pattern shown in
Figure 4 remains unchanged until T exceeds the buoyancy period (2π/
N1 s). As T increases beyond this value, the initial decrease and minimum in pressure remain but the subsequent maximum becomes progressively delayed, in proportion to the length of the period of the eruption, with small signal in between the two. The amplitude of both depend on the amplitude of the eruption (i.e., the surface buoyancy flux, measured by the height), but not its duration. After the passage of the maximum-pressure wave, at any given location the wave amplitude then progressively decreases, as for short eruptions.
Waves that are generated by eruptions that are confined to the troposphere mostly have increasing periods as they propagate further from the source. This effect is most pronounced for small eruptions (that only reach low levels), and at progressively larger distances from the source, but seems to apply generally.
Eruptions that reach into the stratosphere force internal waves from within the troposphere and from within the stratosphere, and the resultant signal seen at ground level is a sum of the forcing from both regions. If the penetration of the eruption into the stratosphere is small (zT < zM <1.4 zT), most of the effect on surface pressure is generated within the troposphere, and the results resemble those for zM = zT. However, for larger amplitudes in the range 1.4zT < zM <2 zT, the stratospheric forcing increases in amplitude, and dominates the pressure signal at the surface. One difference is that the signal from the troposphere arrives first, and the component from the stratosphere arrives later, with the initial maximum arriving at around t ~ 5/N1, but otherwise the character of the surface pressure signal resembles that from the tropospheric eruptions, but at larger amplitude.