Observations of a Cold Front at High Spatiotemporal Resolution Using an X-Band Phased Array Imaging Radar
Abstract
:1. Introduction
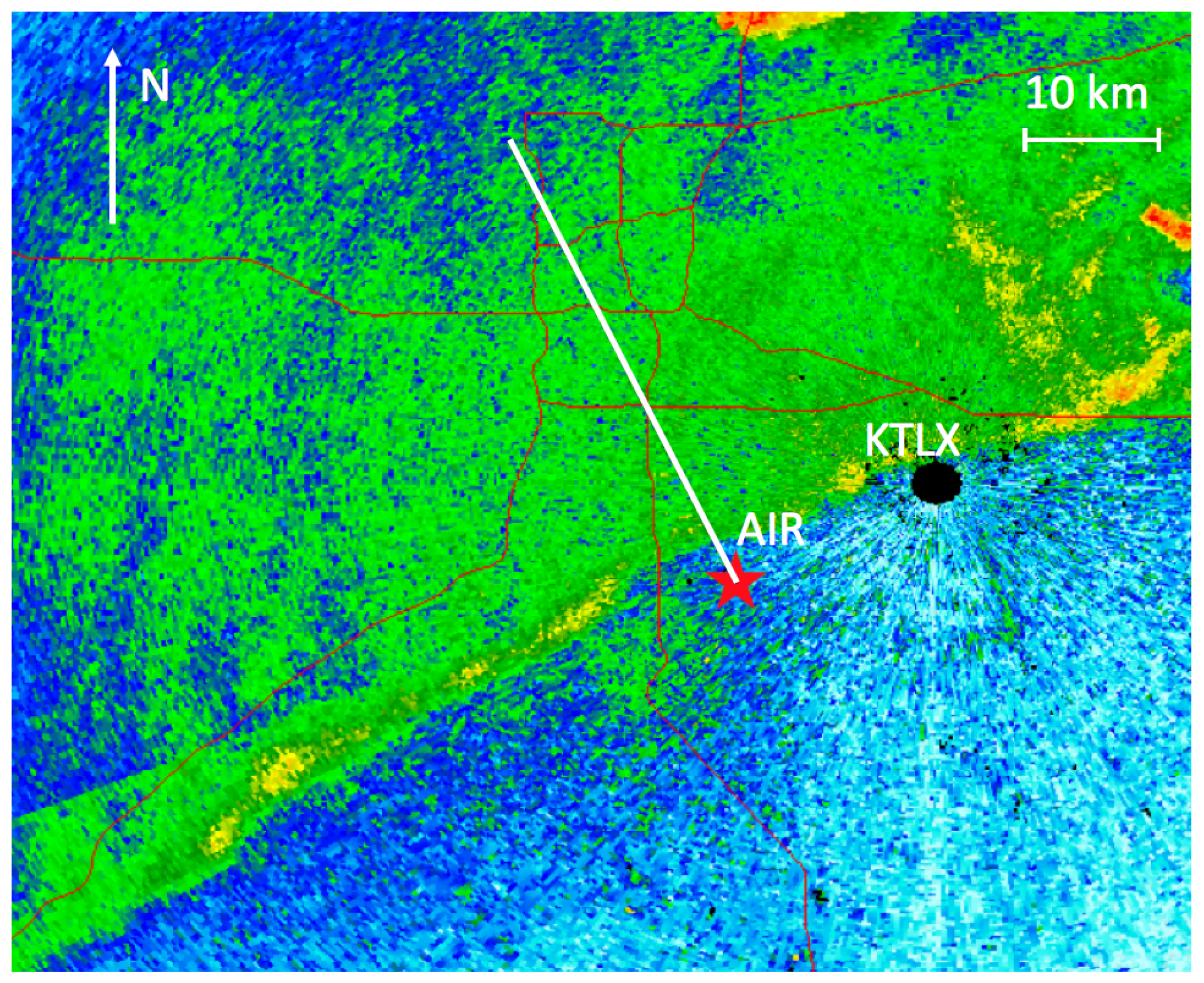
2. Data Collection and Methods
3. Results
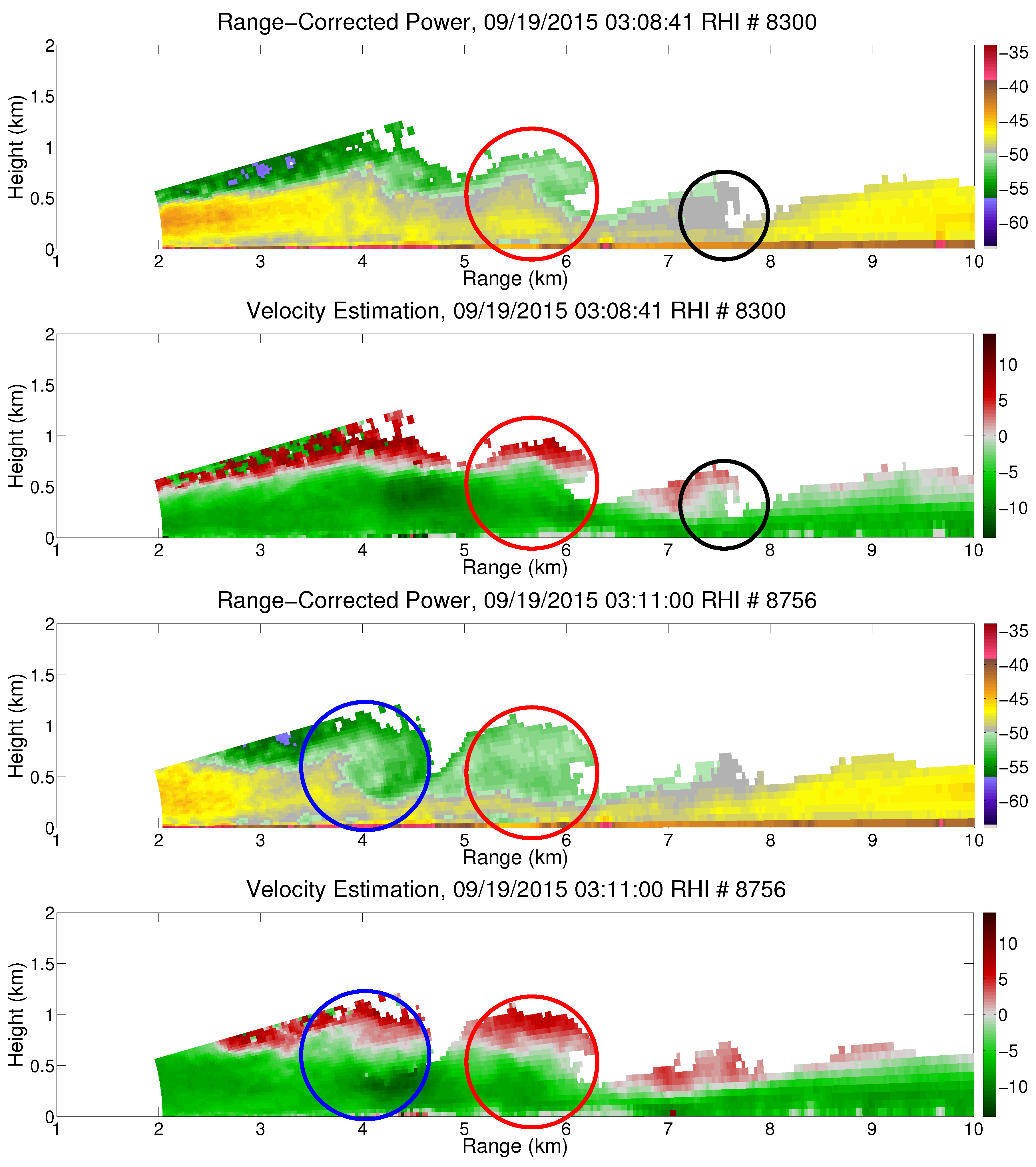
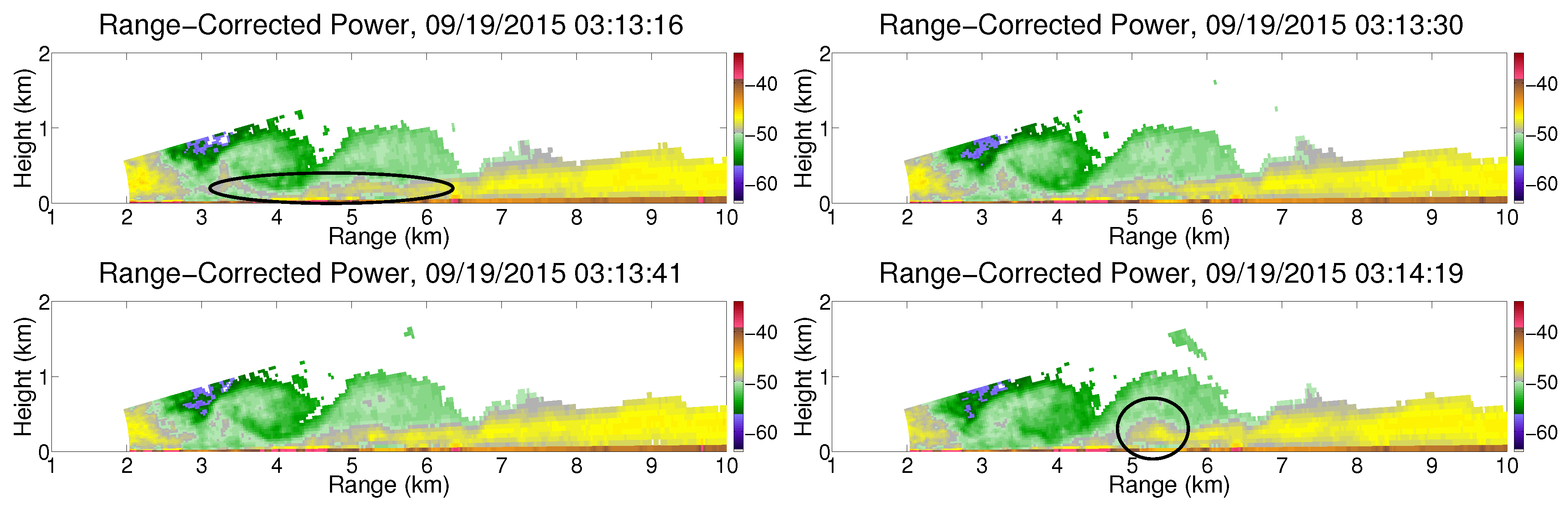
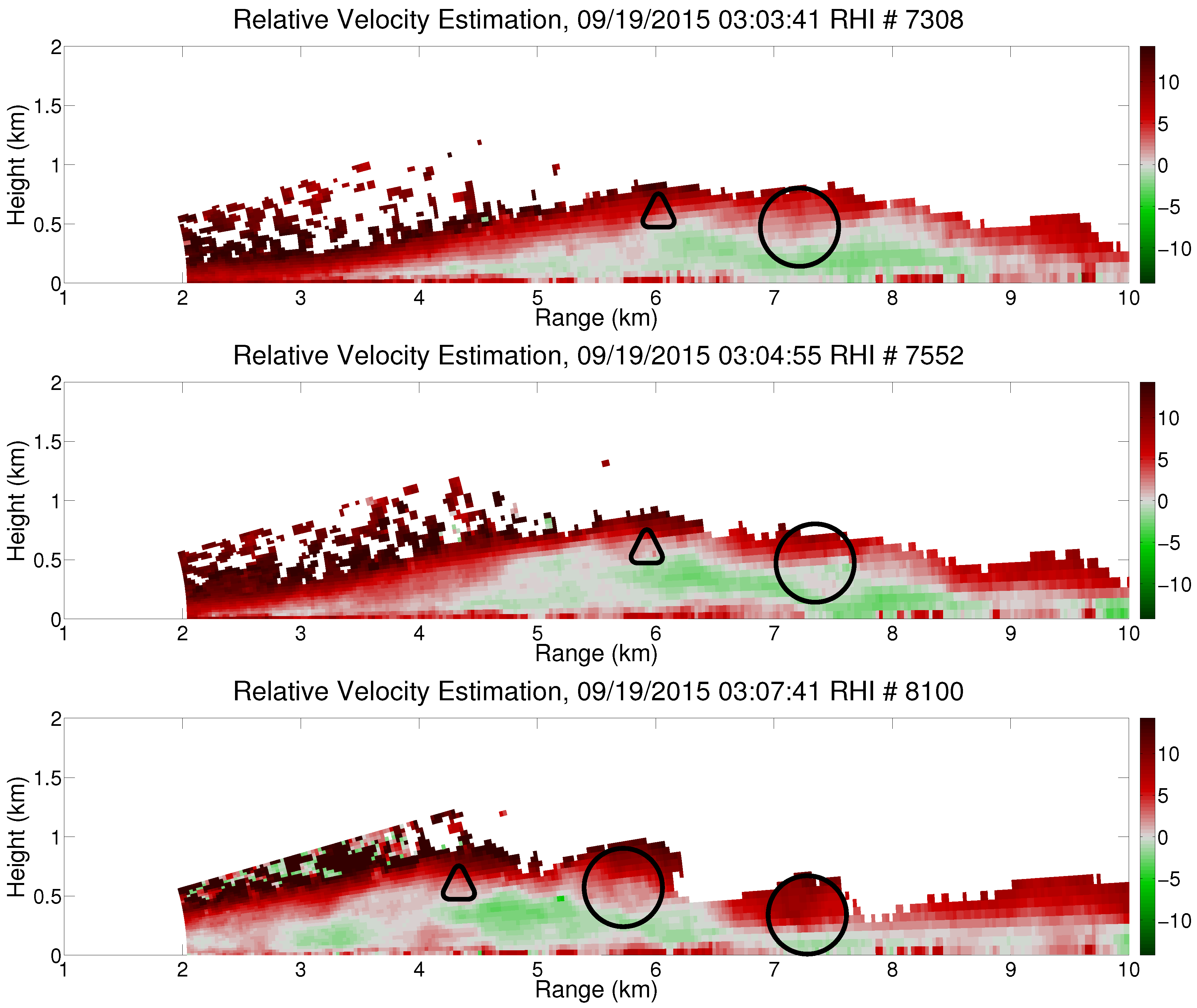
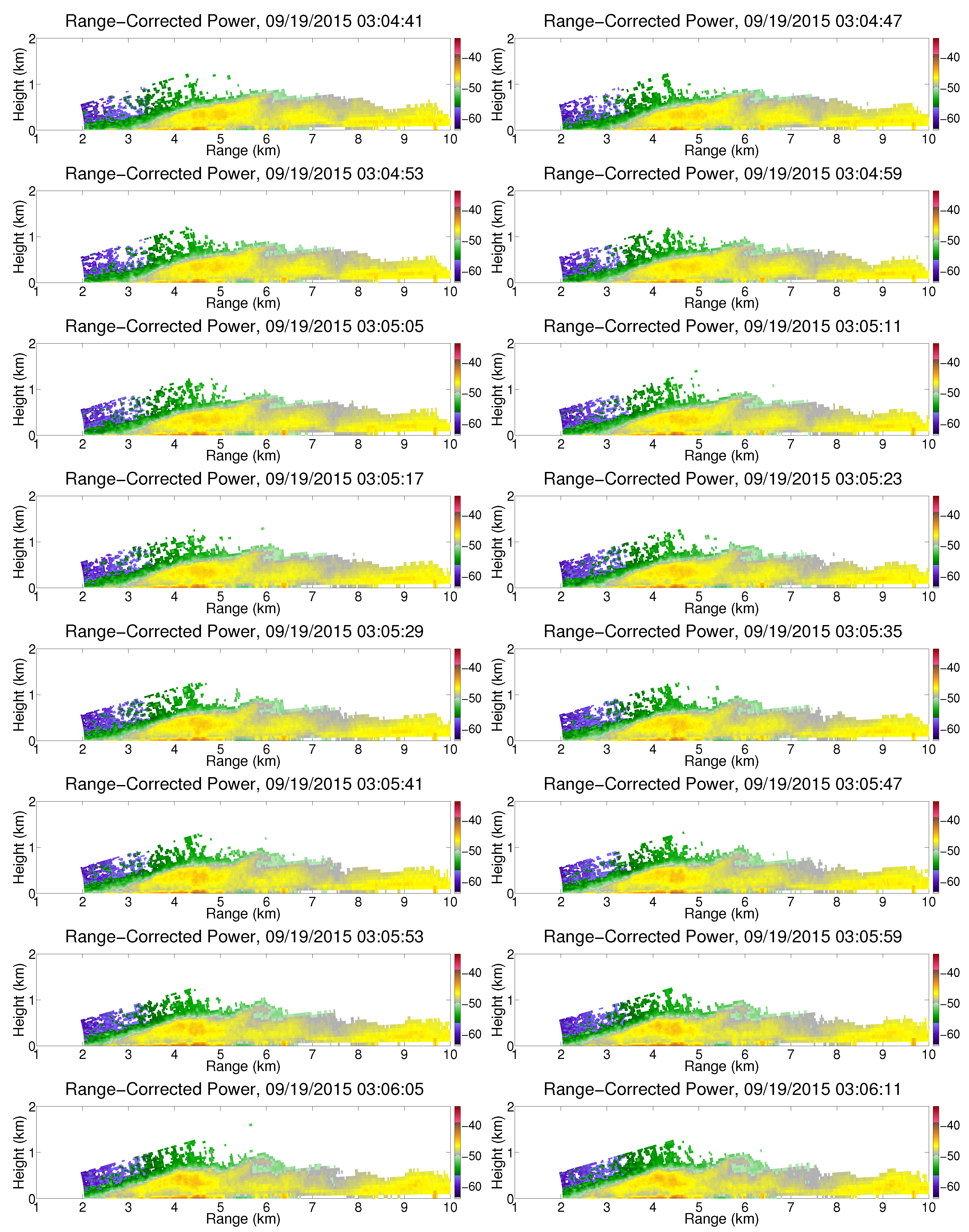
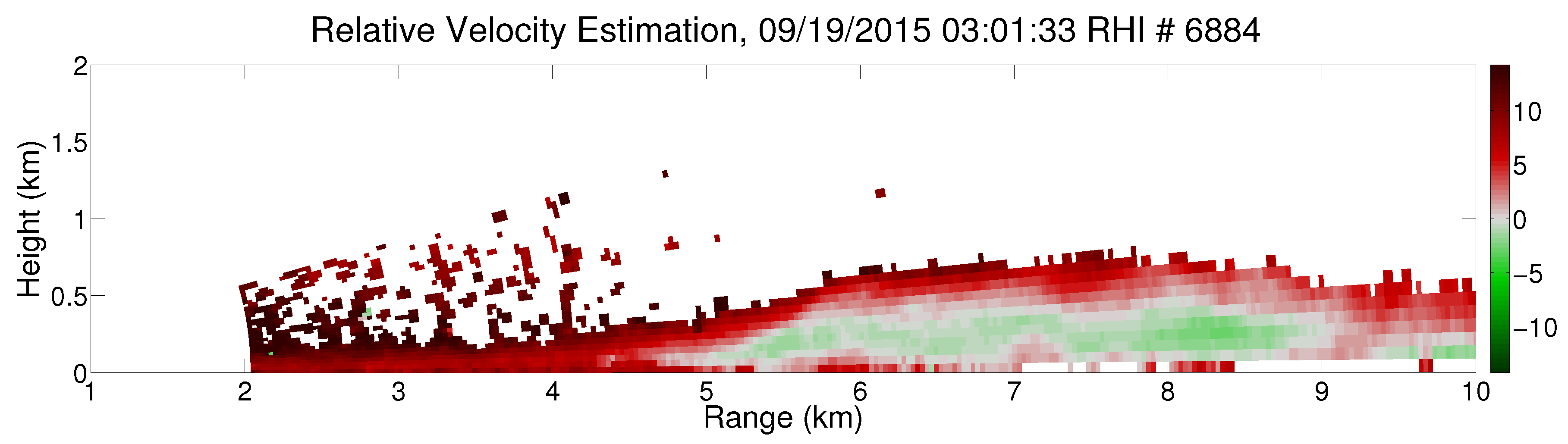
3.1. Kelvin-Helmholtz Instabilities
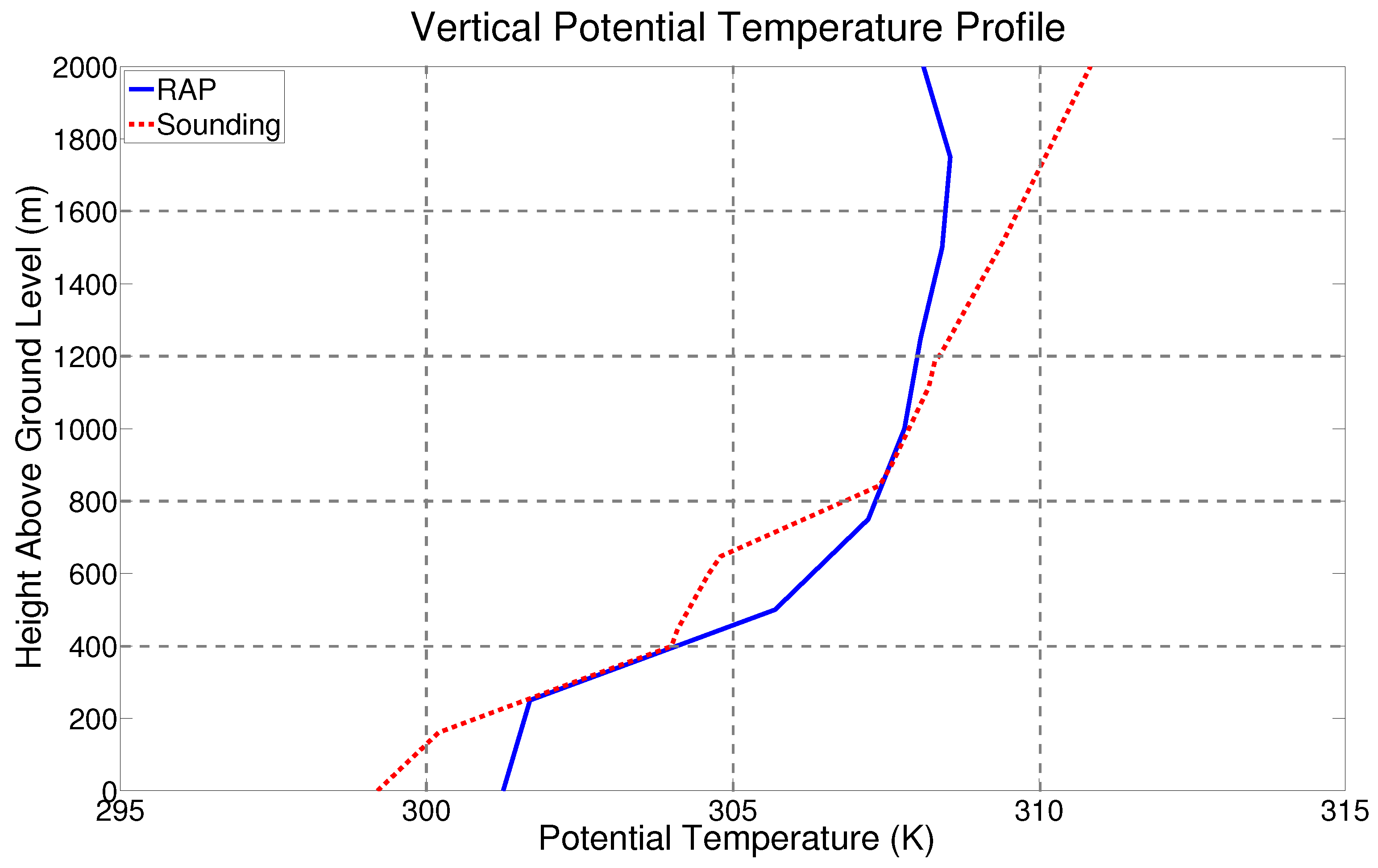
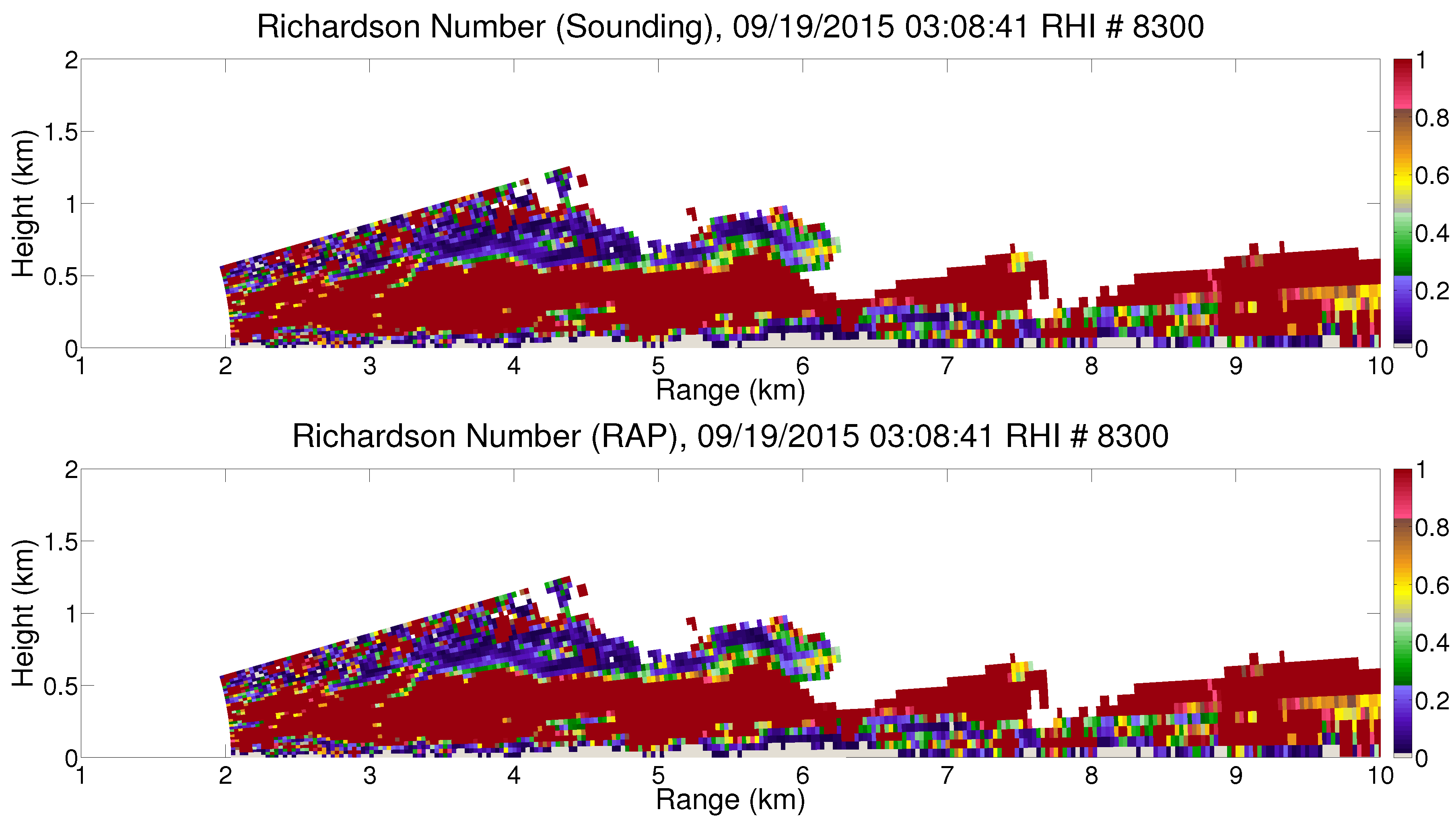
3.2. Richardson Number Estimation
3.3. Feeder Flow
4. Discussion
4.1. KHI Initiation & Formation Observations
4.2. Potential Relationship between Richardson Number and KHI Characteristics
4.3. Proposed Future Work
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Charba, J. Application of Gravity Current Model to Analysis of Squall-Line Gust Front. Mon. Weather Rev. 1974, 102, 140–156. [Google Scholar] [CrossRef]
- Goff, R.C. Vertical Structure of Thunderstorm Outflows. Mon. Weather Rev. 1976, 134, 1429–1440. [Google Scholar] [CrossRef]
- Weckwerth, T.M.; Wakimoto, R.M. The Initiation and Organization of Convective Cells atop a Cold-Air Outflow Boundary. Mon. Weather Rev. 1992, 120, 2169–2187. [Google Scholar] [CrossRef]
- May, P.T. Thermodynamic and Vertical Velocity Structure of Two Gust Fronts Observed with a Wind Profiler/RASS during MCTEX. Mon. Weather Rev. 1999, 127, 1796–1807. [Google Scholar] [CrossRef]
- Wakimoto, R.M.; Bosart, B.L. Airborne Radar Observations of a Cold Front during FASTEX. Mon. Weather Rev. 2000, 128, 2447–2470. [Google Scholar] [CrossRef]
- Geerts, B.; Damiani, R.; Haimov, S. Finescale Vertical Structure of a Cold Front as Revealed by an Airborne Doppler Radar. Mon. Weather Rev. 2006, 134, 251–271. [Google Scholar] [CrossRef]
- Friedrich, K.; Kingsmill, D.E.; Flamant, C.; Murphey, H.V.; Wakimoto, R.M. Kinematic and Moisture Characteristics of a Nonprecipitating Cold Front Observed during IHOP. Part I: Across-Front Structures. Mon. Weather Rev. 2008, 136, 147–172. [Google Scholar] [CrossRef]
- Friedrich, K.; Kingsmill, D.E.; Flamant, C.; Murphey, H.V.; Wakimoto, R.M. Kinematic and Moisture Characteristics of a Nonprecipitating Cold Front Observed during IHOP. Part II: Alongfront Structures. Mon. Weather Rev. 2008, 136, 3796–3821. [Google Scholar] [CrossRef]
- Geerts, B.; Miao, Q. Vertically Pointing Airborne Doppler Radar Observations of Kelvin-Helmholtz Billows. Mon. Weather Rev. 2010, 138, 982–986. [Google Scholar] [CrossRef]
- Mayor, S.D. Observations of Seven Atmospheric Density Current Fronts in Dixon, California. Mon. Weather Rev. 2011, 139, 1338–1351. [Google Scholar] [CrossRef]
- Klingle, D.L. A Gust Front Case Studies Handbook; ATC Proj. Rep. DOT/FAA/PM-84/15; MIT Lincoln Laboratory: Lexington, MA, USA, 1985. [Google Scholar]
- Uyeda, H.; Zrnić, D.S. Automatic Detection of Gust Fronts. J. Atmos. Ocean. Technol. 1986, 3, 36–50. [Google Scholar] [CrossRef]
- Klingle, D.L.; Smith, D.R.; Wolfson, M.M. Gust Front Characteristics as Detected by Doppler Radar. Mon. Weather Rev. 1987, 115, 905–918. [Google Scholar] [CrossRef]
- Whiton, R.C.; Smith, P.L.; Bigler, S.G.; Wilk, K.E.; Harbuck, A.C. History of Operation Use of Weather Radar by U.S. Weather Services. Part II: Development of Operational Doppler Weather Radars. Weather Forecast. 1998, 13, 244–252. [Google Scholar] [CrossRef]
- Delanoy, R.L.; Troxel, S.W. Automated Gust Front Detection Using Knowledge-Based Signal Processing. In Proceedings of the IEEE Radar Conference, Lynnfield, MA, USA, 20–22 April 1993.
- Hermes, L.G.; Witt, A.; Smith, S.D.; Klingle-Wilson, D.; Morris, D.; Stumpf, G.J.; Eilts, M.D. The Gust-Front Detection and Wind-Shift Algorithms for the Terminal Doppler Weather Radar System. J. Atmos. Ocean. Technol. 1993, 10, 693–709. [Google Scholar] [CrossRef]
- Droegemeier, K.K.; Wilhelmson, R.B. Numerical Simulation of Thunderstorm Outflow Dynamics. Part I: Outflow Sensitivity Experiments and Turbulence Dynamics. J. Atmos. Sci. 1987, 44, 1180–1210. [Google Scholar] [CrossRef]
- Smith, R.K.; Reeder, M.J. On the Movement and Low-Level Structure of Cold Fronts. Mon. Weather Rev. 1988, 116, 1927–1944. [Google Scholar] [CrossRef]
- Sinclair, V.A.; Niemelä, S.; Leskinen, M. Structure of a Narrow Cold Front in the Boundary Layer: Observations versus Model Simulation. Mon. Weather Rev. 2012, 140, 2497–2519. [Google Scholar] [CrossRef]
- Young, G.S.; Johnson, R.H. Meso- and Microscale Features of a Colorado Cold Front. J. Clim. Appl. Meteorol. 1984, 23, 1315–1325. [Google Scholar] [CrossRef]
- Nielsen, J.W. In Situ Observations of Kelvin-Helmholtz Waves along a Frontal Inversion. J. Atmos. Sci. 1992, 49, 369–386. [Google Scholar] [CrossRef]
- Wakimoto, R.M. The Life Cycle of Thunderstorm Gust Fronts as Viewed with Doppler Radar and Rawinsonde Data. Mon. Weather Rev. 1982, 110, 1060–1082. [Google Scholar] [CrossRef]
- Martner, B.E. Vertical Velocities in a Thunderstorm Gust Front and Outflow. J. Appl. Meteorol. 1997, 36, 615–622. [Google Scholar] [CrossRef]
- Mueller, C.K.; Carbone, R.E. Dynamics of a Thunderstorm Outflow. J. Atmos. Sci. 1987, 44, 1879–1898. [Google Scholar] [CrossRef]
- Mahoney, W.P., III. Gust Front Characteristics and the Kinematics Associated with Interacting Thunderstorm Outflows. Mon. Weather Rev. 1988, 116, 1474–1491. [Google Scholar] [CrossRef]
- Lothon, M.; Campistron, B.; Chong, M.; Couvreux, F.; Guichard, F.; Rio, C.; Williams, E. Life Cycle of a Mesoscale Circular Gust Front Observed by a C-Band Doppler Radar in West Africa. Mon. Weather Rev. 2011, 139, 1370–1388. [Google Scholar] [CrossRef]
- Simpson, J.E. A Comparison Between Laboratory and Atmospheric Density Currents. Q. J. R. Meteorol. Soc. 1969, 95, 758–765. [Google Scholar] [CrossRef]
- Simpson, J.E. Effects of the Lower Boundary on the Head of a Gravity Current. J. Fluid Mech. 1972, 53, 759–768. [Google Scholar] [CrossRef]
- Simpson, J.E.; Britter, R.E. A Laboratory Model of an Atmospheric Mesofront. Q. J. R. Meteorol. Soc. 1980, 106, 485–500. [Google Scholar] [CrossRef]
- Lindzen, R.S. Stability of a Helmholtz Velocity Profile in a Continuously Stratified, Infinite Boussinesq Fluid–Applications to Clear Air Turbulence. J. Atmos. Sci. 1974, 31, 1507–1514. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Rosenthal, A.J. On the Instability of Helmholtz Velocity Profiles in Stably Stratified Fluids When a Lower Boundary is Present. J. Geophys. Res. 1976, 81, 1561–1571. [Google Scholar] [CrossRef]
- Xue, M.; Xu, Q.; Droegemeier, K.K. A Theoretical and Numerical Study of Density Currents in Nonconstant Shear Flows. J. Atmos. Sci. 1997, 54, 1998–2019. [Google Scholar] [CrossRef]
- Xue, M. Density Current in Two-Layer Shear Flows. Q. J. R. Meteorol. Soc. 2000, 126, 1301–1320. [Google Scholar] [CrossRef]
- Liu, C.; Moncrieff, M.W. Simulated Density Currents in Idealized Stratified Environments. Mon. Weather Rev. 2000, 128, 1420–1437. [Google Scholar] [CrossRef]
- Hazel, P. Numerical Studies of the Stability of Inviscid Stratified Shear Flows. J. Fluid Mech. 1972, 51, 39–61. [Google Scholar] [CrossRef]
- Cushman-Roisin, B. Environmental Fluid Dynamics; John Wiley and Sons, Inc.: New York, NY, USA, 2014. [Google Scholar]
- Thorpe, S.A. Experiments on Instability and Turbulence in a Stratified Shear Flow. J. Fluid Mech. 1973, 61, 731–762. [Google Scholar] [CrossRef]
- Houser, J.L.; Bluestein, H.B. Polarimetric Doppler Radar Observations of Kelvin-Helmholtz Waves in a Winter Storm. J. Atmos. Sci. 2011, 68, 1676–1702. [Google Scholar] [CrossRef]
- Miles, J.W. On the Stability of Heterogeneous Shear Flows. J. Fluid Mech. 1961, 10, 496–508. [Google Scholar] [CrossRef]
- Howard, L.N. Note on a Paper of John W. Miles. J. Fluid Mech. 1961, 10, 509–512. [Google Scholar] [CrossRef]
- Miles, J.W.; Howard, L.N. Note on Heterogeneous Shear Flow. J. Fluid Mech. 1964, 20, 331–336. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American Hourly Assimilation and Model Forecast Cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Yu, T.Y.; Orescanin, M.B.; Curtis, C.D.; Zrnić, D.S.; Forsyth, D.E. Beam Multiplexing Using the Phased-Array Weather Radar. J. Atmos. Ocean. Technol. 2007, 24, 616–626. [Google Scholar] [CrossRef]
- Zrnić, D.S.; Kimpel, J.F.; Forsyth, D.E.; Shapiro, A.; Crain, G.; Ferek, R.; Heimmer, J.; Benner, W.; McNellis, T.J.; Vogt, R.J. Agile-Beam Phased Array Radar for Weather Observations. Bull. Am. Meteorol. Soc. 2007, 88, 1753–1766. [Google Scholar] [CrossRef]
- Weber, M.E.; Cho, J.Y.N.; Herd, J.S.; Flavin, J.M.; Benner, W.E.; Torok, G.S. The Next-Generation Multimission U.S. Surveillance Radar Network. Bull. Am. Meteorol. Soc. 2007, 88, 1739–1751. [Google Scholar] [CrossRef]
- Heinselman, P.L.; Torres, S.M. High-Temporal-Resolution Capabilities of the National Weather Radar Testbed Phased-Array Radar. J. Appl. Meteorol. Climatol. 2011, 50, 579–593. [Google Scholar] [CrossRef]
- Adachi, T.; Kusunoki, K.; Yoshida, S.; Arai, K.I.; Ushio, T. High-Speed Volumetric Observation of a Wet Microburst Using X-Band Phased Array Weather Radar in Japan. Mon. Weather Rev. 2016, 144, 3749–3765. [Google Scholar] [CrossRef]
- Isom, B.; Palmer, R.; Kelley, R.; Meier, J.; Bodine, D.; Yeary, M.; Cheong, B.L.; Zhang, Y.; Yu, T.Y.; Biggerstaff, M.I. The Atmospheric Imaging Radar: Simultaneous Volumetric Observations Using a Phased Array Weather Radar. J. Atmos. Ocean. Technol. 2013, 30, 655–675. [Google Scholar] [CrossRef]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Palmer, R.D.; Gopalam, S.; Yu, T.Y.; Fukao, S. Coherent Radar Imaging Using Capon’s Method. Radio Sci. 1998, 33, 1585–1598. [Google Scholar] [CrossRef]
- Cheong, B.L.; Hoffman, M.W.; Palmer, R.D.; Fraiser, S.J.; López-Dekker, F.J. Pulse Pair Beamforming and the Effects of Reflectivity Field Variations on Imaging Radars. Radio Sci. 2004, 39, RS3014. [Google Scholar] [CrossRef]
- Yoshikawa, E.; Ushio, T.; Kawasaki, Z.; Yoshida, S.; Morimoto, T.; Mizutani, F.; Wada, M. MMSE Beam Forming on Fast-Scanning Phased Array Weather Radar. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3077–3088. [Google Scholar] [CrossRef]
- Nai, F.; Torres, S.M.; Palmer, R.D. Adaptive Beamspace Processing for Phased-Array Weather Radars. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5688–5698. [Google Scholar] [CrossRef]
- Doviak, R.J.; Zrnić, D.S. Doppler Radar & Weather Observations; Dover Publications, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Kurdzo, J.M.; Cheong, B.L.; Palmer, R.D.; Zhang, G.; Meier, J.B. A Pulse Compression Waveform for Improved-Sensitivity Weather Radar Observations. J. Atmos. Ocean. Technol. 2014, 31, 2713–2731. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Nai, F.; Bodine, D.J.; Bonin, T.A.; Palmer, R.D.; Cheong, B.L.; Lujan, J.; Mahre, A.; Byrd, A.D. Observations of Severe Local Storms and Tornadoes with the Atmospheric Imaging Radar. Bull. Am. Meteorol. Soc. 2016. [Google Scholar] [CrossRef]
- Skolnik, M. Radar Handbook; McGraw-Hill Education: Berkshire, UK, 2008. [Google Scholar]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Academic Press: New York, NY, USA, 2006. [Google Scholar]
- Blumen, W.; Banta, R.; Burns, S.P.; Fritts, D.C.; Newsom, R.; Poulos, G.S.; Sun, J. Turbulence Statistics of a Kelvin-Helmholtz Billow Event Observed in the Night-Time Boundary Layer during the Cooperative Atmosphere-Surface Exchange Study Field Program. Dyn. Atmos. Oceans 2001, 34, 189–204. [Google Scholar] [CrossRef]
| Richardson Number Estimation Method | Rimin | Rimax |
|---|---|---|
| Displaced Sounding | 0.13 | 0.20 |
| RAP Model Output | 0.14 | 0.22 |
| Thorpe 1973 Findings | 0.10 | 0.13 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahre, A.; Yu, T.-Y.; Palmer, R.D.; Kurdzo, J.M. Observations of a Cold Front at High Spatiotemporal Resolution Using an X-Band Phased Array Imaging Radar. Atmosphere 2017, 8, 30. https://doi.org/10.3390/atmos8020030
Mahre A, Yu T-Y, Palmer RD, Kurdzo JM. Observations of a Cold Front at High Spatiotemporal Resolution Using an X-Band Phased Array Imaging Radar. Atmosphere. 2017; 8(2):30. https://doi.org/10.3390/atmos8020030
Chicago/Turabian StyleMahre, Andrew, Tian-You Yu, Robert D. Palmer, and James M. Kurdzo. 2017. "Observations of a Cold Front at High Spatiotemporal Resolution Using an X-Band Phased Array Imaging Radar" Atmosphere 8, no. 2: 30. https://doi.org/10.3390/atmos8020030
APA StyleMahre, A., Yu, T.-Y., Palmer, R. D., & Kurdzo, J. M. (2017). Observations of a Cold Front at High Spatiotemporal Resolution Using an X-Band Phased Array Imaging Radar. Atmosphere, 8(2), 30. https://doi.org/10.3390/atmos8020030





