Next Article in Journal
First Results of the “Carbonaceous Aerosol in Rome and Environs (CARE)” Experiment: Beyond Current Standards for PM10
Previous Article in Journal
Modeling the Stepping Process of Negative Lightning Stepped Leaders
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 8
Issue 12
10.3390/atmos8120247
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Urban Roughness Estimation Based on Digital Building Models for Urban Wind and Thermal Condition Estimation—Application of the SkyHelios Model

by
Yu-Cheng Chen
1,
Dominik Fröhlich
2,
Andreas Matzarakis
2 and
Tzu-Ping Lin
1,*
1
Department of Architecture, National Cheng Kung University, 1 University Rd., East Dist., Tainan 701, Taiwan
2
Research Center Human Biometeorology, German Meteorological Service, D-79104 Freiburg, Germany
*
Author to whom correspondence should be addressed.
Atmosphere 2017, 8(12), 247; https://doi.org/10.3390/atmos8120247
Submission received: 1 November 2017 / Revised: 8 December 2017 / Accepted: 8 December 2017 / Published: 10 December 2017
(This article belongs to the Section Biometeorology and Bioclimatology)
Browse Figures
Versions Notes

Abstract

:
Roughness length is a critical parameter for estimation of wind conditions, and it is therefore also relevant for the estimation of human thermal conditions in urban areas. The high density of buildings in urban areas causes large changes in land coverage, thereby increasing surface roughness. This influence atmospheric flow and also leads to a reduction in urban air ventilation, thus increasing the risk of human thermal stress. In this study, a digital building model of Tainan city was used to calculate roughness length using an approach based on Voronoi cells by applying the microclimate model, SkyHelios. The model was also used to estimate the wind conditions, including the wind speed and wind direction. For estimation of the thermal conditions, this study obtained meteorological data for air temperature, relative humidity, globe temperature, wind speed, and wind direction on two specific days (31 July 2015 and 21 January 2016). To quantify the thermal stress, the physiologically equivalent temperature (PET) was used to represent the thermal conditions. The wind conditions results obtained from the model indicate that even microscale conditions with vortices and corner flow can be represented with high precision and resolution. The thermal conditions results demonstrate that different created environments and microclimate conditions affect the thermal environment. The difference in PET can be up to 3 °C. This study confirmed that comparison of microclimate thermal conditions based on measurements and obtained from modeling using SkyHelios are in sufficient agreement and can be used in urban planning in the future.

1. Introduction

Roughness length is an important factor affecting wind conditions and thus the thermal environment within an urban area [1,2,3]. Increase in wind speed (WS) and reduction in heat load are increasing crucial issues that must be addressed [4,5].
WS at the pedestrian level, is strongly affected by obstacles and urban morphology. Roughness length is a factor that can be used to quantify the strength of these effects. Previous research has revealed that the greater the surface roughness length, the poorer the ventilation that can pass through the boundary layer [6,7]. Different obstacles, including buildings, vegetation, and pavement material, may cause variation in roughness length, and WS will be decreased directly above areas that have a high roughness length [8,9]. A high thermal load owing to low wind permeability usually occurs within urbanized areas and increases the heat load on humans [10,11].
In previous studies, wind and thermal conditions were simulated using frontal area index (FAI) [1,12] and computational fluid dynamics (CFD) models [13,14]. However, only considering the FAI of a building is insufficient for considering the surface roughness length and then estimating the urban microclimate, including wind and thermal conditions. In term of CFD approach, wind and thermal conditions can be estimated within urban areas using ENVI-met [15,16] and Wind Perfect [17,18,19], for example, based on an initial meteorological dataset. However, wind conditions are difficult to determine owing to turbulence within the boundary layer.
In small-scale environments, such as in urban areas, WS and wind direction (WD) can be most accurately determined by conducting a measurement campaign [20,21,22]. However, for data with high spatial resolution, a lack of equipment does not allow for the required measurements. Therefore, it is not easy to make wind measurements in urban areas.
To estimate a microclimate without conducting measurements, this study utilized the SkyHelios model [10,23], which was developed for estimating the spatial distribution of wind conditions (e.g., WS and WD) and thermal indicators such as physiologically equivalent temperature (PET) by considering building features and meteorological information [10,24]. The SkyHelios model has been widely used in previous studies in the field of human biometeorology [23,25,26], but the application of the model still requires development and validation.
In this study, a measurement campaign was therefore conducted on 31 July 2015 and 21 January 2016. The data were used for calculating thermal and wind conditions including PET, WS, and WD using the SkyHelios model. The results are intended to confirm that a combination of measurements and building information calculated using the SkyHelios model can be used to estimate urban climate and thermal stress.
Therefore, the aims of this study were as follows: (1) to estimate human thermal sensation based on PET, as calculated without WS measurement; (2) to estimate WS for different WDs and various roughness lengths for calculating PET in different seasons; (3) to analyze the relationship between the WS estimated using the SkyHelios model and the PET obtained using a combination of measurement and the RayMan model [19,27,28,29]; and (4) to visualize microclimate conditions by creating maps for use by urban planners who do not have a meteorological background. The maps can be easily used to identify hotspots within an urban area and to develop countermeasures for mitigation of heat stress.

2. Methods

2.1. Study Area

Tainan (22°59′ N, 120°11′ E) is a highly developed tropical city with 1.88 million inhabitants. It covers 2191.6 km2 (2014) of southern Taiwan. The mean annual temperature (Ta) is 24.6 °C. July is the hottest month, during which the mean Ta is 30.4 °C and the wind is dominated by an orographic wind effect from the west coast (270°). January is the coldest month, during which the mean Ta is 17.6 °C. The annual mean relative humidity (RH) is 74.4%. The WD in January is mainly northerly (0°) (Taiwan Central Weather Bureau).
In this study, the Tainan train station district—the most densely built-up area of Tainan, covering 0.42 km2—was selected as the area of investigation for the comparison of calculated and measured WS and thermal conditions (Figure 1).

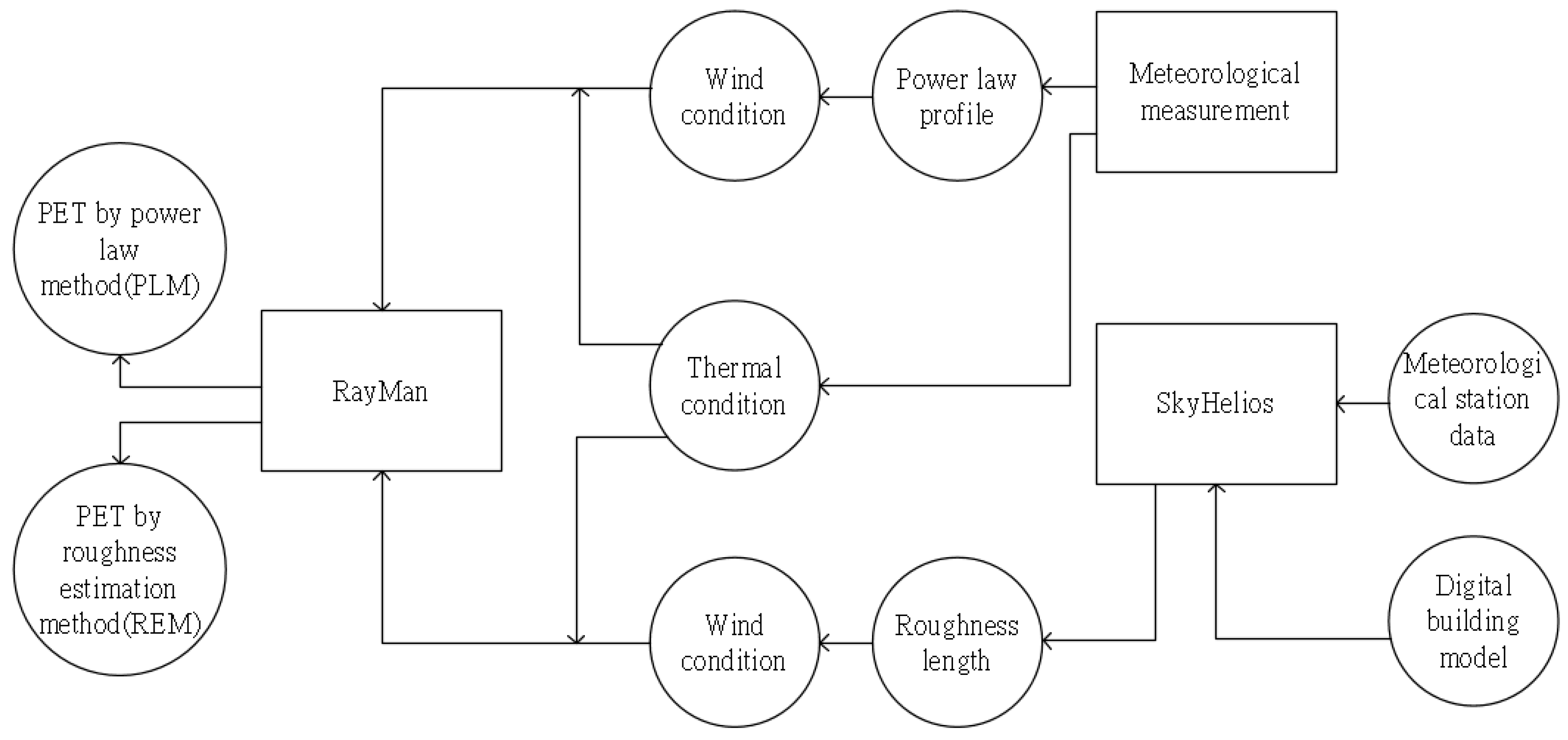
2.2. Research Structure

WS was used in the calculations to obtain PET through two methods (Figure 2), and the advantages and disadvantages of each method were compared. The first method was the power law profile method (PLM), which is based on measured WS data recorded by a meteorological station “HOBO”, located on the rooftop of a building near the study area. The WS was reduced by a power law profile to the pedestrian level. This method combines reduced WS and thermal condition data obtained from measurement to estimate PET by importing wind and thermal condition parameters into RayMan [24,27,28].
The second method is the roughness estimation method (REM), which utilizes WS estimated by roughness spatial data, including building height and shape information, from a digital building model. The SkyHelios model [23,26] estimates the local roughness length based on the building data. Therefore, this method can be considered for calculating spatial WS distribution for the whole area of interest. Thermal conditions measurement data are also used with the WS estimated from roughness length as input factors into the RayMan model [24,27,28] for obtaining the PET.
The PET calculated using the two methods are different for the same measurement points within the study area. The PET distribution conditions are presented in Section 3.2 and Section 3.3.

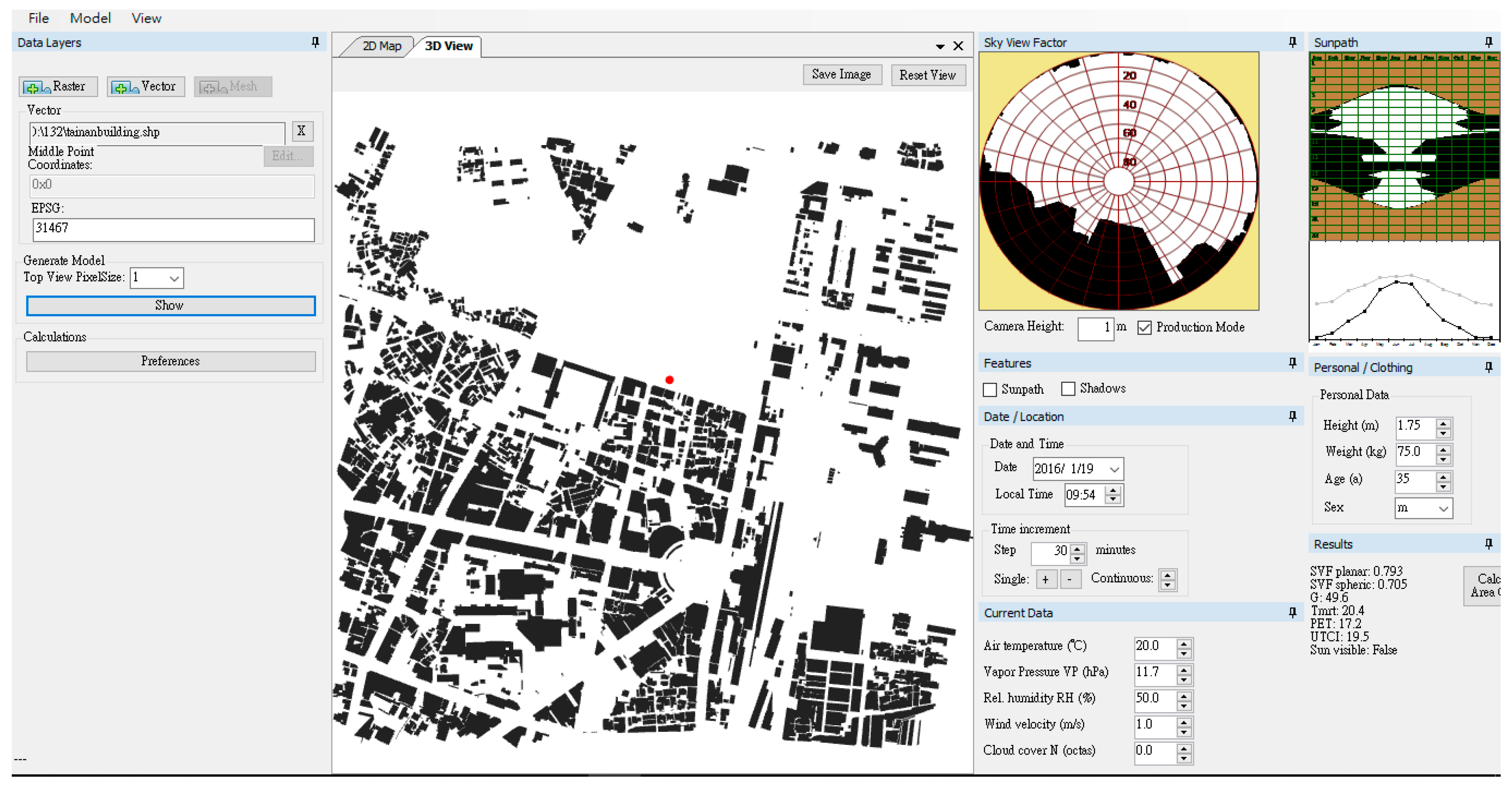
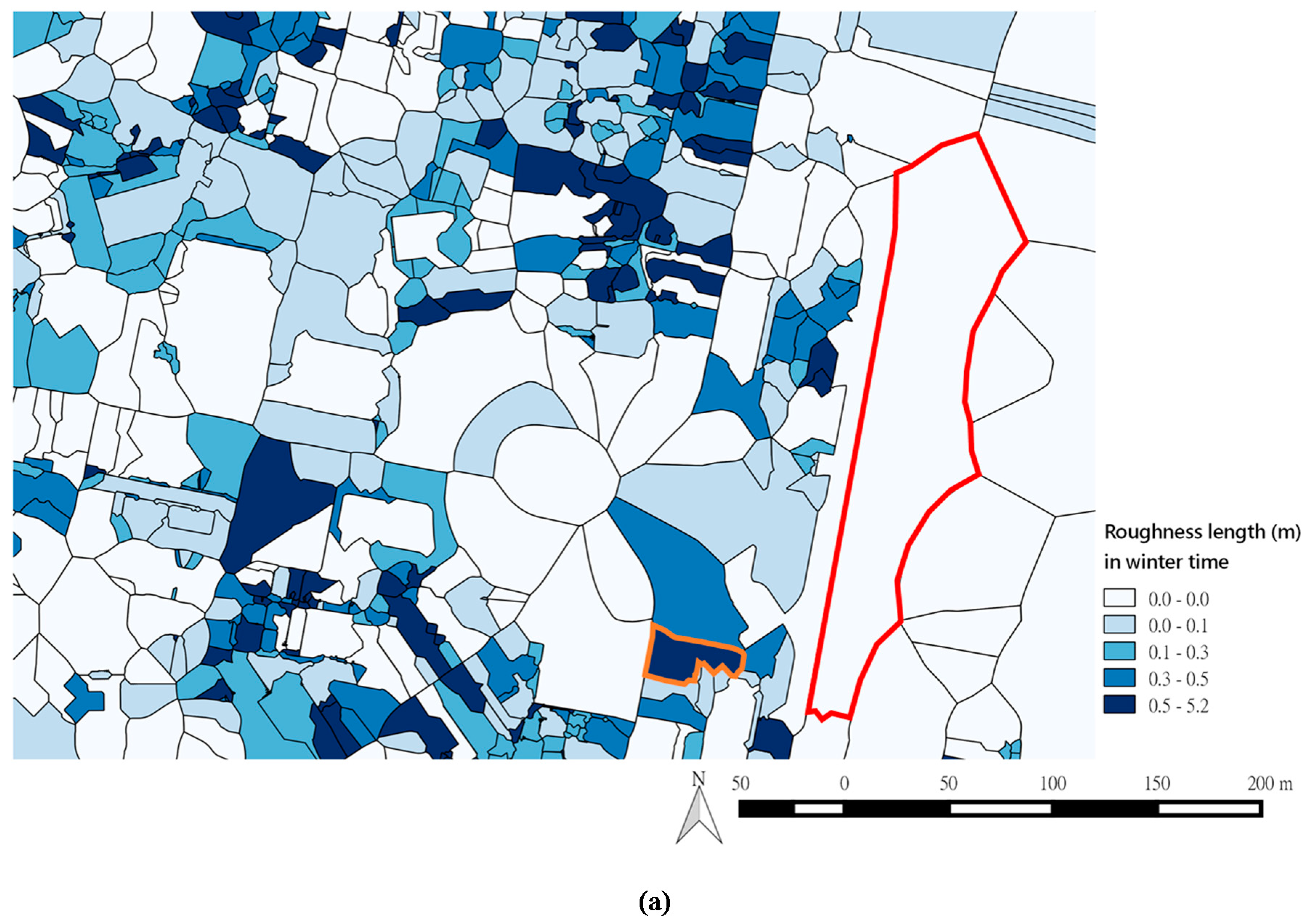
2.3. Local Roughness Estimation

The local roughness length and displacement height employed in the SkyHelios model can be estimated using different approaches [30,31,32]. In this study, the approach reported by Bottema and Mestayer (1998) was used. This approach requires a reference area for each obstacle. In SkyHelios, a Voronoi diagram is computed containing cells for all the obstacles to serve as reference areas [9,10].
The major advantage of using Voronoi diagram compared with arbitrary reference areas such as a regular grid or lot areas is that the dependence of Voronoi cells on the actual obstacles. This ensures that roughness length and displacement height are determined based on the closest obstacle, as shown in Figure 3.

2.4. Estimation of Wind Conditions

WS and WD were estimated using a recent version of the SkyHelios model [33]. This model includes a diagnostic wind model based on the approach reported by Röckle [34]. Different wind field modifications are calculated for each obstacle, which form an initial wind field (Figure 4). The initial wind field initially contains strong divergence, and this divergence must be reduced numerically. The wind model implemented in SkyHelios uses the structure and basics reported by Röckle [34], but considers several modified parameterizations [35,36,37,38]. It is designed to be applicable to complex environments (e.g., city centers and complex urban structures).

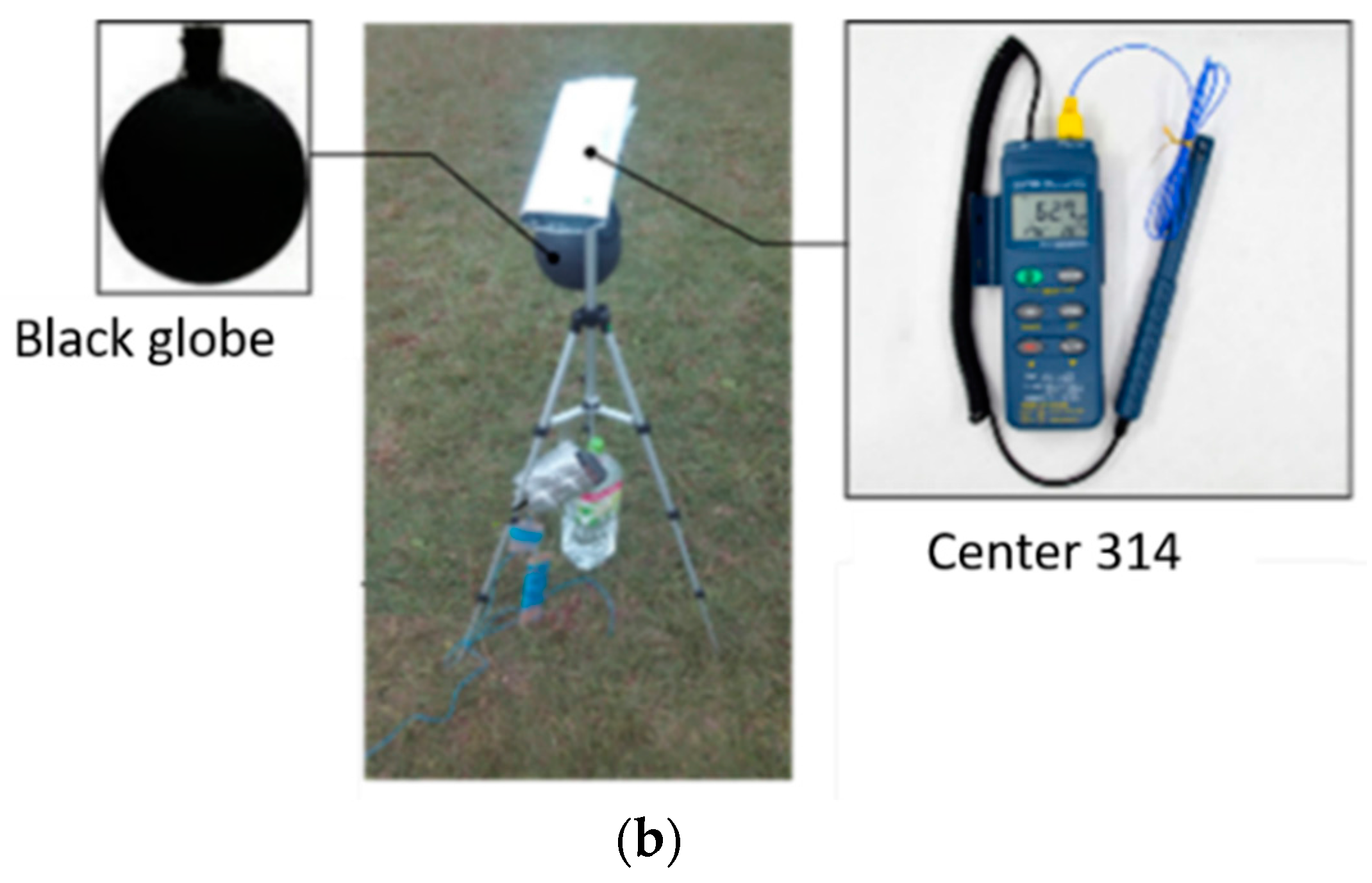
2.5. Meteorological Data Measurement Survey

In this study, 16 measurement locations were selected for conductance of thermal environment surveys on 31 July 2015 and 21 January 2016 at 12:00 p.m. The locations were selected based on their different land use types, including commercial areas, residential areas, schools, hospitals, and open spaces (Figure 5a). Each location was equipped with a “Center314” data-logger that recorded Ta, globe temperature (Tg), and RH (Figure 5b). The precisions of the instruments were ±0.5 °C for the air thermometer, ±2% for the RH meter, and ±0.2 °C for the globe temperature meter.
WS and global radiation data were obtained from meteorological station HOBO, which was located on the roof (approximately 25 m above ground level) of a university building near the study area. The precision of the instruments was ±3% for the WS meter and ±10 W/m2 for the solar radiation quantity meter. Data were recorded every 5 s. The thermal environment map could therefore be generated for several points in time.

2.6. Estimation of Thermal Conditions

PET combines the effect of Ta, RH, WS, and different radiant fluxes on the thermal perception of a human being [24,39]. The index is used for evaluating thermal comfort in complex built-up urban environments [28]. PET can be estimated using measurement data by using a climate model [11,40]. Two methods were employed for obtaining PET: using measurements only and through modeling using SkyHelios.
The PLM uses the measured Ta, RH, and Tg to calculate the PET [27,28,41]. However, owing to a lack of WS sensors, this study employed WS information reduced by the power law profile. All the data were then used together with the RayMan model for the calculation of the PET.
The REM employs modeling based on two types of information. First is a digital building model, which can be applied to determine the local roughness length which use for estimating the wind condition in the SkyHelios model. Second is the initial meteorological data covering a single day, consisting of the parameters Ta, RH, solar irradiation, and WS obtained from the HOBO meteorological station, and loaded as a meteorological data input file in the RayMan model, which then estimated PET in high spatial resolution.

3. Results

The results of this study consist of (1) the WS and WD calculated using the SkyHelios model for summer and wintertime; (2) figures showing the thermal conditions, as determined based on the PLM and REM methods for the summertime; and (3) evaluation of the relationship between the PETs calculated using the PLM and REM.
Climate data gathered from the HOBO meteorological station was used to represent typical meteorological conditions for the selected area. Therefore, the wind field was estimated for a WD of 270° and a WS of 4 m/s using SkyHelios, representing typical summer conditions on 31 July 2015 at 12 p.m. A second set of data was selected to fit the winter conditions on 21 January 2016, when the WD was 0° and WS was 5 m/s.

3.1. Wind Condition Mapping Based on Modeling

Summer and winter wind conditions were selected to demonstrate the effect of the seasonal wind system in the study area. In Tainan, incident wind is typically from 270° in summer. The results for WD in summer show that the WD was between 180° and 210° on the open area including main road, in the plaza, and at the railway. On the leeward side of obstacles, the WD changed to 30–60° or 300–330° because the wake effect modifies the incident WD (Figure 6a). In the winter, the wind was mostly from approximately 0°. However, a WD of 270–330° could be found on the leeward side of buildings. On the main road, which runs east to west, the WD was approximately 180–210° (Figure 6b).
The WS was approximately 0.3–0.4 m/s in open areas on the typical summer day, as opposed to the initial WS input of 2 m/s. This was greater at the corners of buildings, where the WS was up to 0.5 m/s owing to corner flow. However, the WS was decreased to 0.1–0.2 m/s on the leeward side of buildings because of the wake effect (Figure 6c). In winter, the initial input WS had increased to 5 m/s. The WS in the open area was 0.6–0.7 m/s and that at the front of buildings was 1 m/s (Figure 6d).
The spatial distribution of WS in Tainan indicates a relationship between the numerous compact high-rise buildings and the microclimate. The microscale conditions with vortices and corner flow require high model precision and resolution. Therefore, the model can be used to detect potential ventilation paths and can help urban planners to improve their designs for better wind permeability.

3.2. Thermal Environment Conditions Determined Using the PLM

The thermal conditions estimated using the PLM based on the measured Ta, RH, and TG, as well as the WS measured by the HOBO meteorological station. The WS will reduced by approximately 50% according to the power law profile, as shown in Figure 7 by the blue bar.
The results indicate that the PET distribution is strongly related to the presence of a built-up environment: high-rise buildings create long shadows, owing to which the human body is not exposed to direct solar irradiation. Therefore, the PET is lower at locations (e.g., 5, 6, 7, 14, and 15) where obstacles obscure the sun. However, for locations in open spaces or close to low-rise buildings (such as locations 2, 9, and 13), the human body is exposed to direct solar irradiation and long wave reflections by the pavement, thus increasing the thermal load.
The results indicate a strong spatial variation in PET ranging from 36.4 to 58.0 °C. However, because this method applies the same WS of 2 m/s at all locations, the results cannot consider local modifications of WS caused by the built-up environment.

3.3. Thermal Environment Conditions Determined Using the REM

The results for the thermal conditions calculated using the REM at 12 pm show extreme heat (Figure 7), especially in places with no shade and lower WS. Because the SkyHelios model can estimate the WS by considering the built environment and roughness length, the effect of buildings can be determined on the estimation of the PET.
Areas such as locations 4 and 5, which are located within a shaded area, show relatively low thermal stress. However, in some open spaces, such as locations 10 and 15, solar radiation causes high thermal stress. Compared with the results obtained using the PLM, the REM results show a wider range of PETs because the WS was determined more accurately in the estimation process.

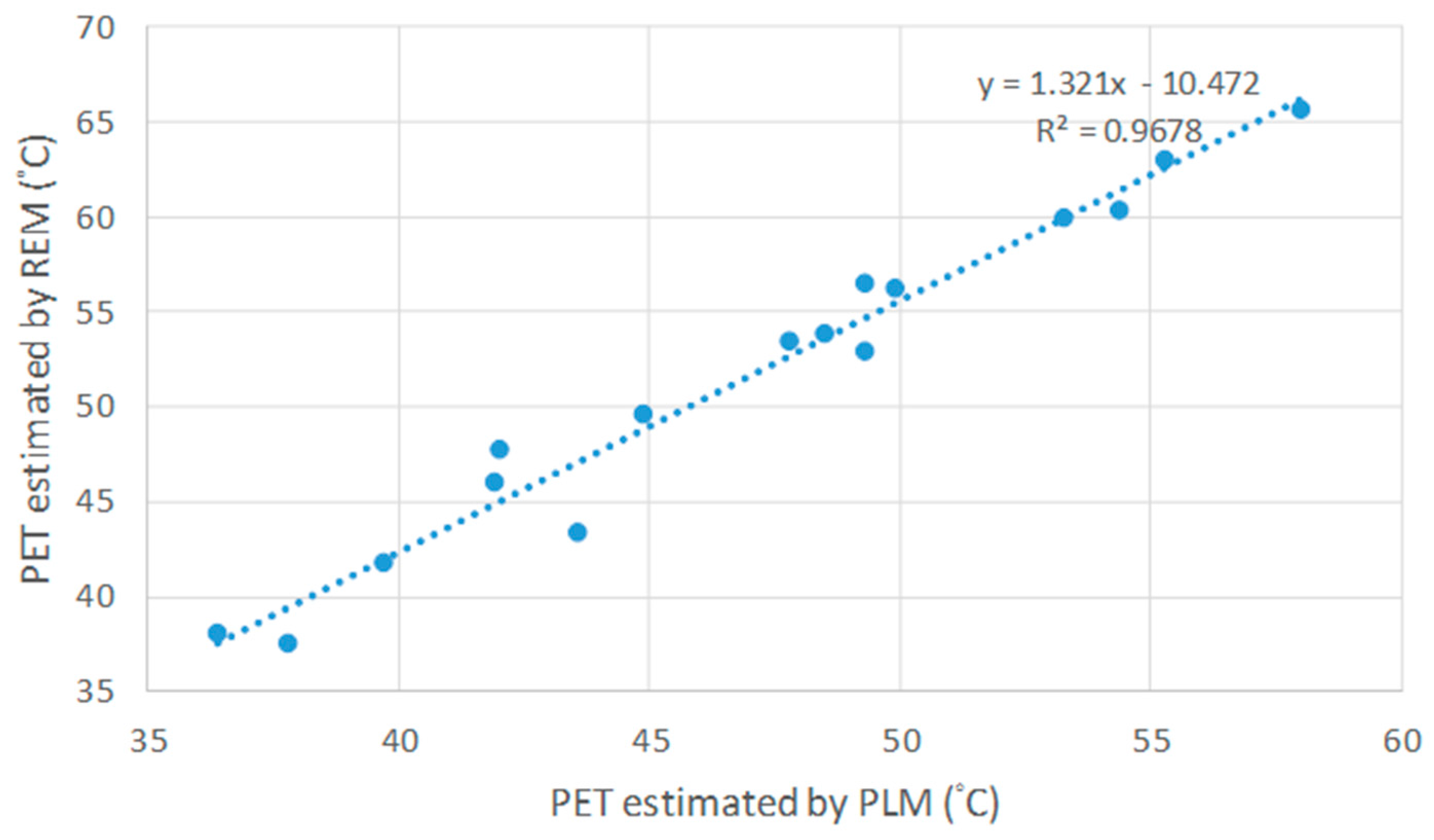
3.4. Correlation between Modeling and Measurements

The correlation coefficient between the PET calculated using the PLM and REM is high (Figure 8), reaching 0.967. This indicates that the SkyHelios model accurately estimates the human thermal bioclimate in urban areas without requiring local wind measurements. However, because the WS modeled by SkyHelios was lower than the WS estimated by the power law profile, as shown in Figure 7, the PET calculated using the REM is higher at each location compared with that calculated using the PLM.
In addition, the results demonstrate that the higher the thermal stress, the larger the gap between the PET results obtained using the two methods is. WS thus critically affects human thermal sensation. During periods of high thermal stress, a high WS immediately reduces the heat load from the human body. In the case of lower thermal stress, the effect of WS on PET is weaker (compared with locations 5, 7, and 14 in Figure 7).

4. Discussion

4.1. WS Difference Obtained Using the Two Methods

This study employs two methods to obtain the WS for PET calculations using the RayMan model [26,27]. The first method is based on the power law profile [42,43], which was applied for the reduction of WS recorded by a rooftop meteorological station.
This method quickly yielded an approximation of ground-level WS without conducting any measurements. However, the surface roughness length was spatially inhomogeneous, and many different obstacles were present (e.g., air flow might have been blocked by compact high-rise buildings), causing strong spatial WS variability in urban areas [44]. If WS is determined by applying a vertical profile to rooftop measurements, the impact of the complex built-up environment cannot be considered. The WS at the surface level therefore suffers from large uncertainties. Because WS is a crucial input parameter to PET, the PET calculated using this approach is unreliable [45].
In this study, WS was therefore also estimated using the SkyHelios model with a digital building model and meteorological data. The WS calculated using the model is lower because SkyHelios considers the roughness length based on the building model and reduces the initial WS, more closely reflecting the actual conditions [10]. WS values obtained from the calculation using SkyHelios are therefore considered to be accurate and suitable for the assessment of thermal microclimate within urban areas.

4.2. Main Findings and Comparison with Previous Studies

Previously, roughness length was mostly estimated based on land use classification or land cover type [46,47], obstacle density [48,49], as well as a combination of FAI and building floor area [32,50,51]. However, these approaches only provide approximate results and cannot assess roughness length within complex environments. Therefore, in this study, the method proposed by Ketterer et al., 2006 was employed to calculate the roughness length based on obstacle distribution considering both buildings and vegetation using SkyHelios [10].
Studies have applied various approaches to obtain the distribution of WS on different scales. Examples of common approaches include models based on weather forecasting models [52,53,54] and measurement campaigns [1,55].
However, these weather forecasting models are only designed for mesoscale conditions, such as the presence of a sea breeze and mountain flow. Their spatial resolution is insufficient to describe the wind conditions within complex built-up urban environments. Because the WS and WD in urban areas are mostly influenced by street orientation and building distribution, models such as SkyHelios, which provide data in high spatial resolution (e.g., 1 m2), should be used in estimating urban wind conditions on the microscale.
The results of this study reveal that the WS obtained using the REM is lower than that obtained using the PLM, because the REM considers the different roughness lengths caused by various types of obstacles and different built environments, whereas the PLM only considers height above the ground.

4.3. Differences in Roughness Length during Different Seasons

The SkyHelios model can estimate the roughness length depending on building height, FAI, and WD. FAI is calculated based on WD, and the most frequent WD changes with the seasons. Therefore, roughness length also changes with the seasons in Tainan. The roughness lengths for summer and winter, which are dependent on WD, are shown by the red and orange frames in Figure 9.
The prevailing WD in Tainan is westerly in the summer and northerly in the winter. Within the study area, two specific areas were selected for comparison during different seasons. Because the red frame (railroad) is located in the north–south direction and the incident wind is from 0°, the railway forms a ventilation path with a low roughness length of 0.0029 m in the winter. In the orange frame area (commercial area), however, the FAI of the buildings is increased and thus the roughness length is increased to 0.6 m (red frame in Figure 9a).
In the summertime, the incident wind is from 270° and causes a high roughness length of approximately 0.03 m in the red frame because of the presence of many buildings crossing the WD. Buildings oriented in the east–west direction, for example, that are located west of the railroad (orange frame in Figure 9b) cause a relatively low roughness length of 0.36 m.

5. Conclusions

In this study, three main questions were addressed: the benefits of considering roughness length during the estimation of microclimate conditions, the advantage of modeling, and the most important input factors for PET estimation.
First, meteorological information, such as WS and radiation flux, is best determined by modeling in urban areas because a survey requires considerable time and effort. The estimation of wind conditions in this study considered the roughness length, allowing for higher precision compared with the application of a power law function.
Second, the REM considers roughness length and can thus obtain more accurate results than other methods because roughness length has a strong effect on microclimate, especially on wind conditions. The WS obtained using the REM is more representative of the actual conditions compared with that obtained using the PLM. Therefore, the REM is more reliable and should be used for providing accurate meteorological information.
Radiation fluxes and WS are the two most crucial factors for the formation and intensity of thermal comfort and heat stress conditions in cities and should be the main focus in the development of climate change adaptation measures due to the PET difference can be up to 3 °C. Therefore, these two factors should be considered in urban planning and building design in future studies on urban microscale environments.
Finally, the SkyHelios model estimates radiation and wind conditions with high spatial and temporal resolution. Areas with high thermal stress can be identified easily and are mostly the areas with less shade and low WS. The results of this study can help urban planners who do not have a meteorological background to identify hotspots and implement appropriate countermeasures to fight the emerging issue of thermal stress in urban areas.

Acknowledgments

The authors would like to thank the Project-based Personnel Exchange Program (PPP) for financially supporting this research under the project of NSC-DAAD “Human-biometeorological information in UCmap in Taiwan and Germany”.

Author Contributions

The manuscript was prepared by Yu-Cheng Chen, technical support was provided by Dominik Fröhlich and organized by Andreas Matzarakis and Tzu-Ping Lin. All the authors reviewed the manuscript and contributed their part to improve the manuscript. All authors have read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wong, M.S.; Nichol, J.E.; To, P.H.; Wang, J. A simple method for designation of urban ventilation corridors and its application to urban heat island analysis. Build. Environ. 2010, 45, 1880–1889. [Google Scholar] [CrossRef]
  2. Atkinson, B.W. Numerical Modelling of Urban Heat-Island Intensity. Bound. Layer Meteorol. 2003, 109, 285–310. [Google Scholar] [CrossRef]
  3. Collier, C.G. The impact of urban area on weather. Q. J. R. Meteorol. Soc. 2006, 132, 1–25. [Google Scholar] [CrossRef]
  4. Müller, N.; Kuttler, W.; Barlag, A. Counteracting urban climate change: Adaptation measures and their effect on thermal comfort. Theor. Appl. Climatol. 2014, 115, 243–257. [Google Scholar] [CrossRef]
  5. Shishegar, N. Street design and urban microclimate: Analyzing the effects of street geometry and orientation on airflow and solar access in urban canyons. J. Clean Energy Technol. 2013, 1, 52–56. [Google Scholar] [CrossRef]
  6. Wever, N. Quantifying trends in surface roughness and the effect on surface WS observations. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
  7. Gunturu, U.B.; Schlosser, C.A. Characterization of wind power resource in the United States. Atmos. Chem. Phys. 2012, 12, 9687–9702. [Google Scholar] [CrossRef] [Green Version]
  8. Van Hove, L.W.A.; Jacobs, C.M.J.; Heusinkveld, B.G.; Elbers, J.A.; van Driel, B.C.; Holtslag, A.A.M. Temporal and spatial variability of urban heat island and thermal comfort within the Rotterdam agglomeration. Build. Environ. 2015, 83, 91–103. [Google Scholar] [CrossRef]
  9. Faivre, R.D.; Colin, J.; Menenti, M. Evaluation of methods for aerodynamic roughness length retrieval from very high-resolution imaging LIDAR observations over the heihe basin in China. Remote Sens. 2017, 9, 63. [Google Scholar] [CrossRef]
  10. Ketterer, C.; Gangwisch, M.; Fröhlich, D.; Matzarakis, A. Comparison of selected approaches for urban roughness determination based on voronoi cells. Int. J. Biometeorol. 2016, 61, 189–198. [Google Scholar] [CrossRef] [PubMed]
  11. Matzarakis, A.; Endler, C. Climate change and thermal bioclimate in cities: Impacts and options for adaptation in Freiburg, Germany. Int. J. Biometeorol. 2010, 54, 479–483. [Google Scholar] [CrossRef] [PubMed]
  12. Grimmond, C.S.B.; King, T.S.; Roth, M.; Oke, T.R. Aerodynamic roughness of urban areas derived from wind observations. Bound. Layer Meteorol. 1998, 89, 1–24. [Google Scholar] [CrossRef]
  13. Houda, S.; Zemmouri, N.; Hasseine, A.; Athmani, R.; Belarbi, R.; Flow, U. A CFD model for simulating urban flow in complex. Online J. Sci. Technol. 2012, 2, 1–10. [Google Scholar]
  14. Fadl, M.S.; Karadelis, J. CFD Simulation for Wind Comfort and Safety in Urban Area: A Case Study of Coventry University Central Campus. Int. J. Archit. Eng. Constr. 2013, 2, 131–143. [Google Scholar] [CrossRef]
  15. Bruse, M. Die Auswirkungen Kleinskaliger Umweltgestaltung auf das Mikroklima. Entwicklung des Prognostischen Numerischen Modells ENVI-met zur Simulation der Wind-, Temperatur- und Feuchteverteilung in Städtischen Strukturen. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 1999. [Google Scholar]
  16. Bruse, M.; Fleer, H. Simulating surface-plant-air interactions inside urban environments with a three dimensional numerical mode. Environ. Model. Softw. 1998, 13, 73–384. [Google Scholar] [CrossRef]
  17. Toparlar, Y.; Blocken, B.; Vos, P.; van Heijst, G.J.F.; Janssen, W.D.; van Hooff, T.; Montazeri, H.; Timmermans, H.J.P. CFD simulation and validation of urban microclimate: A case study for Bergpolder Zuid, Rotterdam. Build. Environ. 2015, 83, 79–90. [Google Scholar] [CrossRef]
  18. Blocken, B.; van der Hout, A.; Dekker, J.; Weiler, O. CFD simulation of wind flow over natural complex terrain: Case study with validation by field measurements for ria de ferrol, galicia, spain. J. Wind Eng. Ind. Aerodyn. 2015, 147, 43–57. [Google Scholar] [CrossRef]
  19. Chen, Y.C.; Lin, T.P.; Matzarakis, A. Comparison of mean radiant temperature from field experiment and modelling: A case study in Freiburg, Germany. Theor. Appl. Climatol. 2014, 118, 535–551. [Google Scholar] [CrossRef]
  20. Papadopoulou, M.; Raphael, B.; Smith, I.; Sekhar, C. Optimal Sensor Placement for Time-Dependent Systems: Application to Wind Studies around Buildings. J. Comput. Civ. Eng. 2015, 30. [Google Scholar] [CrossRef]
  21. Emeis, S. Vertical wind profiles over an urban area. Meteorol. Z. 2004, 13, 353–359. [Google Scholar] [CrossRef]
  22. Blocken, B. Computational fluid dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef] [Green Version]
  23. Matzarakis, A.; Matuschek, O. Sky View Factor as a parameter in applied climatology—Rapid estimation by the SkyHelios Model. Meteorol. Z. 2011, 20, 39–45. [Google Scholar] [CrossRef]
  24. Höppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef] [PubMed]
  25. Lin, T.P.; Tsai, K.T.; Hwang, R.L.; Matzarakis, A. Quantification of the effect of thermal indices and sky view factor on park attendance. Landsc. Urban Plan. 2012, 107, 137–146. [Google Scholar] [CrossRef]
  26. Matuschek, O.; Matzarakis, A. Estimation of sky view factor in complex environment as a tool for applied climatological studies. In Proceedings of the Seventh Conference on Biometeorology, Meteorological Institute of the Albert-Ludwigs-Universität Freiburg Rep, Freiburg im Breisgau, Germany, 12–14 April 2010; Volume 20, pp. 534–539. [Google Scholar]
  27. Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments—Application of the RayMan model. Int. J. Biometeorol. 2007, 51, 23–34. [Google Scholar] [CrossRef] [PubMed]
  28. Matzarakis, A.; Mayer, H.; Iziomon, M.G. Applications of a universal thermal index: Physiological equivalent temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
  29. Lin, T.P.; Matzarakis, A. Tourism climate and thermal comfort in Sun Moon Lake, Taiwan. Int. J. Biometeorol. 2008, 52, 281–290. [Google Scholar] [CrossRef] [PubMed]
  30. Lettau, H. Note on aerodynamic roughness—Parameter estimation on the basis of roughness-element description. J. Appl. Meteorol. 1969, 8, 828–832. [Google Scholar] [CrossRef]
  31. Matzarakis, A.; Mayer, H. Mapping of urban air paths for planning in Munich. In Planning Applications of Urban and Building Climatology; The IFHP/ CIB-symposium: Berlin, Germany, 1992; Volume 16, pp. 13–22. [Google Scholar]
  32. Bottema, M.; Mestayer, P.G. Urban roughness mapping—Validation techniques and some first results. J. Wind Eng. Ind. Aerodyn. 1998, 74, 163–173. [Google Scholar] [CrossRef]
  33. Fröhlich, D. Development of a Microscale Model for the Thermal Environment in Complex Areas. Ph.D. Thesis, Albert-Ludwigs-University Freiburg, Freiburg im Breisgau, Germany, 2016. [Google Scholar]
  34. Röckle, R. Bestimmung der Strömungsverhältnisse im Bereich Komplexer Bebauungsstrukturen. Ph.D. Thesis, Technical University Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
  35. Macdonald, R.W. Modelling the mean velocity profile in the urban canopy layer. Bound. Layer Meteorol. 2000, 97, 25–45. [Google Scholar] [CrossRef]
  36. Bagal, N.; Pardyjak, E.; Brown, M. Improved Upwind Cavity Parameterizations for a Fast Response Urban Wind Model. In Proceedings of the 84th American Meteorological Society (AMS) Annual Meeting, Seattle, WA, USA, 13–16 January 2004; pp. 567–570. [Google Scholar]
  37. Pardyjak, E.R.; Brown, M.J.; Bagal, N. Improved Velocity Deficit Parameterizations for a Fast Response Urban Wind Model. In Proceedings of the 84th American Meteorological Society (AMS) Annual Meeting, Seattle, WA, USA, 13–16 January 2004; pp. 507–511. [Google Scholar]
  38. Singh, B.; Hansen, B.S.; Brown, M.J.; Pardyjak, E.R. Evaluation of the QUIC-URB fast response urban wind model for a cubical building array and wide building street canyon. Environ. Fluid Mech. 2008, 8, 81–312. [Google Scholar] [CrossRef]
  39. Mayer, H.; Höppe, P. Thermal comfort of man in different urban environments. Theor. Appl. Climatol. 1987, 38, 43–49. [Google Scholar] [CrossRef]
  40. Fröhlich, D.; Matzarakis, A. Modeling of changes in thermal bioclimate: Examples based on urban spaces in Freiburg, Germany. Theor. Appl. Climatol. 2013, 111, 547–558. [Google Scholar] [CrossRef]
  41. Gulyas, A.; Unger, J.; Matzarakis, A. Assessment of the microclimatic and human comfort conditions in a complex urban environment: Modelling and measurements. Build. Environ. 2006, 41, 1713–1722. [Google Scholar] [CrossRef]
  42. Peterson, E.W.; Hennessey, J.P., Jr. On the use of power laws for estimates of wind power potential. J. Appl. Meteorol. 1978, 17, 390–394. [Google Scholar] [CrossRef]
  43. Touma, J.S. Dependence of the wind profile power law on stability for various locations. J. Air Pollut. Control Assoc. 1977, 27, 863–866. [Google Scholar] [CrossRef]
  44. Lindén, J.; Holmer, B. Thermally induced wind patterns in the Sahelian city of Ouagadougou, Burkina Faso. Theor. Appl. Climatol. 2011, 105, 1–13. [Google Scholar] [CrossRef]
  45. Newman, J.F.; Klein, P.M. The Impacts of Atmospheric Stability on the Accuracy of WS Extrapolation Methods. Resources 2014, 3, 81–105. [Google Scholar] [CrossRef]
  46. Stewart, I.D.; Oke, T.R. Local Climate Zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
  47. Kalyanapu, A.J.; Burian, S.J.; McPherson, T.N. Effect of land use-based surface roughness on hydrologic model output. J. Spat. Hydrol. 2009, 9, 51–71. [Google Scholar]
  48. Macdonald, R.W.; Griffiths, R.F.; Hall, D.J. An improved method for estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
  49. Holland, D.E.; Berglund, J.A.; Spruce, J.P.; McKellip, R.D. Derivation of effective aerodynamic surface roughness in urban areas from airborne Lidar terrain data. J. Appl. Meteorol. Climatol. 2008, 47, 2614–2626. [Google Scholar] [CrossRef]
  50. Bottema, M. Urban roughness modelling in relation to pollutant dispersion. Atmos. Environ. 1997, 31, 3059–3075. [Google Scholar] [CrossRef]
  51. Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. Climatol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
  52. Kwun, J.H.; Kim, Y.K.; Seo, J.W.; Jeong, J.H.; You, S.H. Sensitivity of MM5 and WRF mesoscale model predictions of surface winds in a typhoon to planetary boundary layer parameterizations. Nat. Hazards 2009, 51, 63–77. [Google Scholar] [CrossRef]
  53. Dudhia, J.; Bresch, J.F. A global version of the PSU-NCAR mesoscale model. Mon. Weather Rev. 2002, 130, 2989–3007. [Google Scholar] [CrossRef]
  54. Nielsen-Gammon, J.W.; McNider, R.T.; Angevine, W.M.; White, A.B.; Knupp, K. Mesoscale model performance with assimilation of wind profiler data: Sensitivity to assimilation parameters and network configuration. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
  55. Childs, P.P.; Raman, S. Observations and numerical simulations of urban heat Island and sea breeze circulations over New York City. Pure Appl. Geophys. 2005, 162, 1955–1980. [Google Scholar] [CrossRef]
Atmosphere 08 00247 g001 550
Figure 1. Location of the study area. The blue mark represents the province of Tainan city, the red frame shows the area of interest.
Figure 1. Location of the study area. The blue mark represents the province of Tainan city, the red frame shows the area of interest.
Atmosphere 08 00247 g001
Atmosphere 08 00247 g002 550
Figure 2. The structure of research.
Figure 2. The structure of research.
Atmosphere 08 00247 g002
Atmosphere 08 00247 g003 550
Figure 3. The digital building model for the area of interest including the Tainan train station.
Figure 3. The digital building model for the area of interest including the Tainan train station.
Atmosphere 08 00247 g003
Atmosphere 08 00247 g004 550
Figure 4. The graphical user interface of the urban climate model SkyHeilos.
Figure 4. The graphical user interface of the urban climate model SkyHeilos.
Atmosphere 08 00247 g004
Atmosphere 08 00247 g005a 550Atmosphere 08 00247 g005b 550
Figure 5. (a) Distribution of measurement points within the study area (b) The measurement instruments.
Figure 5. (a) Distribution of measurement points within the study area (b) The measurement instruments.
Atmosphere 08 00247 g005aAtmosphere 08 00247 g005b
Atmosphere 08 00247 g006 550
Figure 6. (a) WD in 31 July 2015; (b) WD in 21 January 2016; (c) WS in 31 July 2015; and (d) WS in 21 January 2016.
Figure 6. (a) WD in 31 July 2015; (b) WD in 21 January 2016; (c) WS in 31 July 2015; and (d) WS in 21 January 2016.
Atmosphere 08 00247 g006
Atmosphere 08 00247 g007 550
Figure 7. PET difference between PLM and REM.
Figure 7. PET difference between PLM and REM.
Atmosphere 08 00247 g007
Atmosphere 08 00247 g008 550
Figure 8. The correlation result of PET calculated by PLM and REM.
Figure 8. The correlation result of PET calculated by PLM and REM.
Atmosphere 08 00247 g008
Atmosphere 08 00247 g009a 550Atmosphere 08 00247 g009b 550
Figure 9. (a) The roughness length for incident WD of 0° (winter time); (b) The roughness length for incident WD of 270° (summer time).
Figure 9. (a) The roughness length for incident WD of 0° (winter time); (b) The roughness length for incident WD of 270° (summer time).
Atmosphere 08 00247 g009aAtmosphere 08 00247 g009b

Share and Cite

MDPI and ACS Style

Chen, Y.-C.; Fröhlich, D.; Matzarakis, A.; Lin, T.-P. Urban Roughness Estimation Based on Digital Building Models for Urban Wind and Thermal Condition Estimation—Application of the SkyHelios Model. Atmosphere 2017, 8, 247. https://doi.org/10.3390/atmos8120247

AMA Style

Chen Y-C, Fröhlich D, Matzarakis A, Lin T-P. Urban Roughness Estimation Based on Digital Building Models for Urban Wind and Thermal Condition Estimation—Application of the SkyHelios Model. Atmosphere. 2017; 8(12):247. https://doi.org/10.3390/atmos8120247

Chicago/Turabian Style

Chen, Yu-Cheng, Dominik Fröhlich, Andreas Matzarakis, and Tzu-Ping Lin. 2017. "Urban Roughness Estimation Based on Digital Building Models for Urban Wind and Thermal Condition Estimation—Application of the SkyHelios Model" Atmosphere 8, no. 12: 247. https://doi.org/10.3390/atmos8120247

APA Style

Chen, Y. -C., Fröhlich, D., Matzarakis, A., & Lin, T. -P. (2017). Urban Roughness Estimation Based on Digital Building Models for Urban Wind and Thermal Condition Estimation—Application of the SkyHelios Model. Atmosphere, 8(12), 247. https://doi.org/10.3390/atmos8120247

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop