Influence of Raindrop Size Distribution on Throughfall Dynamics under Pine and Birch Trees at the Rainfall Event Level
Abstract
1. Introduction
2. Methods
2.1. Description of the Experimental Setup
2.2. Measurements
2.3. Data Analysis Methods
3. Results
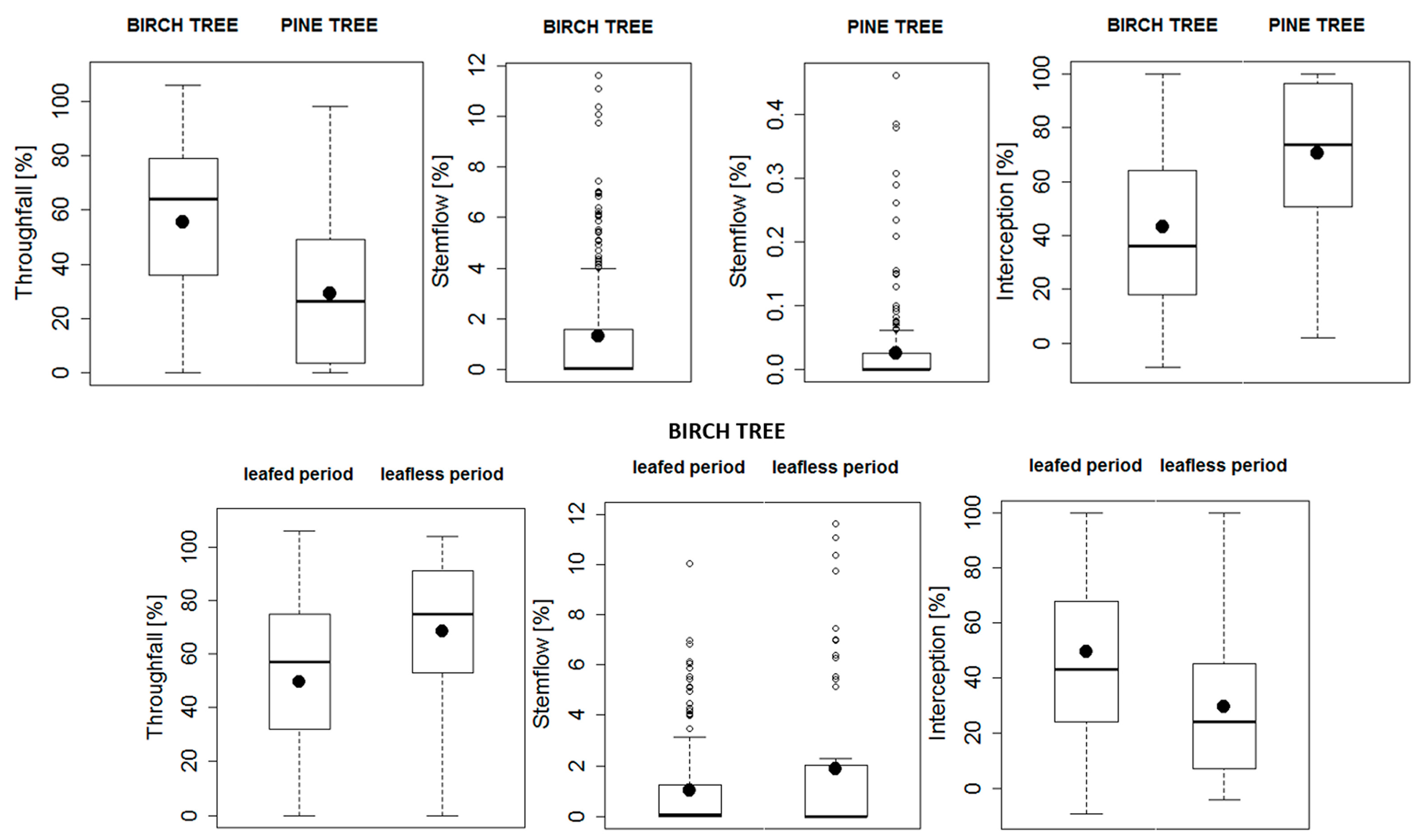
3.1. Throughfall, Stemflow, and Rainfall Interception
3.2. Number of Raindrops, Their Median Volume Diameter, and Kinetic Energy
3.3. Effect of Drop Diameter and Velocity on Throughfall
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brandt, C.J. The size distribution of throughfall drops under vegetation canopies. Catena 1989, 16, 507–524. [Google Scholar] [CrossRef]
- Dunkerley, D. Measuring interception loss and canopy storage in dryland vegetation: A brief review and evaluation of available research strategies. Hydrol. Process. 2000, 14, 669–678. [Google Scholar] [CrossRef]
- Nanko, K.; Hotta, N.; Suzuki, M. Evaluating the influence of canopy species and meteorological factors on throughfall drop size distribution. J. Hydrol. 2006, 329, 422–431. [Google Scholar] [CrossRef]
- Bassette, C.; Bussiere, F. Partitioning of splash and storage during raindrop impacts on banana leaves. Agric. For. Meteorol. 2008, 148, 991–1004. [Google Scholar] [CrossRef]
- Levia, D.F.; Hudson, S.A.; Llorens, P.; Nanko, K. Throughfall drop size distributions: A review and prospectus for future research. WIREs Water 2017, 4, e1225. [Google Scholar] [CrossRef]
- Nanko, K.; Hudson, S.A.; Levia, D.F. Differences in throughfall drop size distributions in the presence and absence of foliage. Hydrol. Sci. J. 2016, 61, 620–627. [Google Scholar] [CrossRef]
- Fleischbein, K.; Wilcke, W.; Goller, R.; Boy, J.; Valarezo, C.; Zech, W.; Knoblich, K. Rainfall interception in a lower montane forest in Ecuador: Effects of canopy properties. Hydrol. Process. 2005, 19, 1355–1371. [Google Scholar] [CrossRef]
- Deguchi, A.; Hattoria, S.; Park, H. The influence of seasonal changes in canopy structure on interception loss: Application of the revised Gash model. J. Hydrol. 2006, 318, 80–102. [Google Scholar] [CrossRef]
- Vilhar, U. Padavinski režim v izbranih vrzelih in sestojih dinarskega jelovo-bukovega gozda. Zbornik Gozdarstva in Lesarstva 2010, 91, 43–58. (In Slovenian) [Google Scholar]
- Zabret, K. The influence of tree characteristics on rainfall interception. Acta Hydrotech. 2013, 26, 99–116. (In Slovenian) [Google Scholar]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Process. 2000, 14, 763–784. [Google Scholar] [CrossRef]
- Andre, F.; Jonard, M.; Ponette, Q. Influence of species and rain event characteristics on stemflow volume in a temperate mixed oak-beech stand. Hydrol. Process. 2008, 22, 4455–4466. [Google Scholar] [CrossRef]
- Šraj, M.; Brilly, M.; Mikoš, M. Rainfall interception by two deciduous Mediterranean forests of contrasting stature in Slovenia. Agric. For. Meteorol. 2008, 148, 121–134. [Google Scholar] [CrossRef]
- Siegert, C.M.; Levia, D.F. Seasonal and meteorological effects on differential stemflow funneling ratios for two deciduous tree species. J. Hydrol. 2014, 519, 446–454. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Sempere Torres, D. Measurement and parameterization of rainfall microstructure. J. Hydrol. 2006, 328, 1–7. [Google Scholar] [CrossRef]
- Calder, I.R. Dependence of rainfall interception on drop size: 1. Development of the two-layer stochastic model. J. Hydrol. 1996, 185, 363–378. [Google Scholar] [CrossRef]
- Hall, R.L. Interception loss as a function of rainfall and forest types: Stochastic modelling for tropical canopies revisited. J. Hydrol. 2003, 280, 1–12. [Google Scholar] [CrossRef]
- Frasson, R.; Krajewski, W. Characterization of the drop-size distribution and velocity–diameter relation of the throughfall under the maize canopy. Agric. For. Meteorol. 2011, 151, 1244–1251. [Google Scholar] [CrossRef]
- Fornis, R.L.; Vermeulen, H.R.; Nieuwenhuis, J.D. Kinetic energy–rainfall intensity relationship for Central Cebu, Philippines, for soil erosion studies. J. Hydrol. 2005, 300, 20–32. [Google Scholar] [CrossRef]
- Petan, S.; Rusjan, S.; Vidmar, A.; Mikoš, M. The rainfall kinetic energy–intensity relationship for rainfall erosivity estimation in the Mediterranean part of Slovenia. J. Hydrol. 2010, 391, 314–321. [Google Scholar] [CrossRef]
- Caracciolo, C.; Napoli, M.; Prodi, F. Raindrop Size Distribution and Soil Erosion. J. Irrig. Drain. Eng. 2012, 138, 461–469. [Google Scholar] [CrossRef]
- Nanko, K.; Watanabe, A.; Hotta, N.; Suzuki, M. Physical interpretation of the difference in drop size distributions of leaf drips among tree species. Agric. For. Meteorol. 2013, 169, 74–84. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Šraj, M. Evaluation of Drop Size Distribution Impact on Rainfall Interception by Trees. Proceedings 2017, 1, 117. [Google Scholar]
- ARSO. Available online: http://www.meteo.si/met/sl/archive/ (accessed on 9 August 2017).
- Tapiador, F.J.; Checa, R.; de Castro, M. An experiment to measure the spatial variability of rain drop size distribution using sixteen laser disdrometers. Geophys. Res. Lett. 2010, 37, L16803. [Google Scholar] [CrossRef]
- You, C.; Lee, D. Decadal Variation in Raindrop Size Distributions in Busan, Korea. Adv. Meteorol. 2015, 2015, 329327. [Google Scholar] [CrossRef]
- Park, S.G.; Kim, H.; Ham, Y.; Jung, S. Comparative Evaluation of the OTT PARSIVEL Using a Collocated Two-Dimensional Video Disdrometer. J. Atmos. Ocean. Technol. 2017, 34, 2059–2082. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Forest Hydrology. In The Forestry Handbook; Evans, J.S., Ed.; Blackwell: Oxford, UK, 2000; Volume 1, Chapter 12; pp. 301–343. [Google Scholar]
- Zimmermann, A.; Zimmermann, B. Requirements for throughfall monitoring: The roles of temporal scale and canopy complexity. Agric. For. Meteorol. 2014, 189–190, 125–139. [Google Scholar] [CrossRef]
- OTT Hydromet. Operating Instructions. Present weather sensor OTT Parsivel. 2016. Available online: http://www.ott.com/en-us/products/download/operating-instructions-present-weather-sensor-ott-parsivel2/ (accessed on 8 November 2017).
- Nanko, K.; Mizugaki, S.; Onda, Y. Estimation of soil splash detachment rates on the forest floor of an unmanaged Japanese cypress plantation based on field measurements of throughfall drop sizes and velocities. Catena 2008, 72, 348–361. [Google Scholar] [CrossRef]
- Ciaccioni, A.; Bezak, N.; Rusjan, S. Analysis of rainfall erosivity using disdrometer data at two stations in central Slovenia. Acta Hydrotech. 2016, 29, 89–102. [Google Scholar]
- Gunn, R.; Kinzer, G.D. The Terminal Fall Velocity for Water Droplets in Stagnant Air. J. Atmos. Sci. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Livesley, S.J.; Baudinette, B.; Glover, D. Rainfall interception and stemflow by eucalypt street trees—The impacts of canopy density and bark type. Urban For. Urban Green. 2014, 13, 192–197. [Google Scholar] [CrossRef]
- Šraj, M. Intercepted precipitation: Measurements and analysis. Geografski Vestnik 2008, 81, 99–111. (In Slovenian) [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing 2015, Vienna, Austria. Available online: http://www.R-project.org/ (accessed on 5 March 2015).
- Xiao, Q.; McPherson, G. Rainfall interception of three trees in Oakland, California. Urban Ecosyst. 2011, 14, 755–769. [Google Scholar] [CrossRef]
- Inkiläinen, N.M.; McHale, M.R.; Blank, G.B.; James, A.L.; Nikinmaa, E. The role of the residential urban forest in regulating throughfall: A case study in Raleigh, North Carolina, USA. Landsc. Urban Plan. 2013, 119, 91–103. [Google Scholar] [CrossRef]
- Cape, J.N.; Brown, A.H.F.; Robertson, S.M.C.; Howson, G.; Paterson, I.S. Interspecies comparisons of throughfall and stemflow at tree sites in nothern Britain. For. Ecol. Manag. 1991, 46, 165–177. [Google Scholar] [CrossRef]
- Buttle, J.M.; Farnsworth, A.G. Measurement and modeling of canopy water partitioning in a reforested landscape: The Ganaraska Forest, southern Ontario, Canada. J. Hydrol. 2012, 466–467, 103–144. [Google Scholar] [CrossRef]
- Asadian, Y.; Weiler, M. A New Approach in Measuring Rainfall Interception by Urban Trees in Coastal British Columbia. Water Qual. Res. J. Can. 2009, 44, 16–25. [Google Scholar]
- Staelens, J.; De Schrijver, A.; Verheyen, K.; Verhoest, N.E.C. Rainfall partitioning into throughfall, stemflow, and interception within a single beech (Fagus sylvatica L.) canopy: Influence of foliation, rain event characteristics, and meteorology. Hydrol. Process. 2008, 22, 33–45. [Google Scholar] [CrossRef]
- Zabret, K.; Mikoš, M.; Rakovec, J.; Šraj, M. Proces prestrezanja padavin: Vpliv vegetacijske dobe, trajanja padavinskega dogodka ter mikrostrukture padavin. In Raziskave s Področja Geodezije in Geofizike 2015, Proceedings of the Redna Letna Skupščina SZGG, Ljubljana, Slovenia, 28 January 2016; Univerza v Ljubljani: Ljubljana, Slovenia, 2016. [Google Scholar]
- Klaassen, W.; Bosveld, F.; de Water, E. Water storage and evaporation as constituents of rainfall interception. J. Hydrol. 1998, 212–213, 36–50. [Google Scholar] [CrossRef]
- Calder, I.R.; Hall, R.L.; Rosier, P.T.W.; Bastable, H.G.; Prasanna, K.T. Dependence of rainfall interception on drop size: 2. Experimental determination of the wetting functions and two-layer stochastic model parameters for five tropical tree species. J. Hydrol. 1996, 185, 379–388. [Google Scholar] [CrossRef]
- Hall, R.L.; Calder, I.R.; Nimal Gunawardena, E.R.; Rosier, P.T.W. Dependence of rainfall interception on drop size: 3. Implementation and comparative performance of the stochastic model using data from a tropical site in Sri Lanka. J. Hydrol. 1996, 185, 389–407. [Google Scholar] [CrossRef]
- Llorens, P.; Gallart, F. A simplified method for forest water storage capacity measurement. J. Hydrol. 2000, 240, 131–144. [Google Scholar] [CrossRef]
- Hutchings, N.J.; Milne, R.; Crowther, J.M. Canopy storage capacity and its vertical distribution in a Sitka spruce canopy. J. Hydrol. 1988, 104, 161–171. [Google Scholar] [CrossRef]
- Keim, R.F.; Skaugset, A.E.; Weiler, M. Storage of water on vegetation under simulated rainfall of varying intensity. Adv. Water Resour. 2006, 29, 974–986. [Google Scholar] [CrossRef]
- Frischbier, N.; Wagner, S. Detection, quantification and modelling of small-scale lateral translocation of throughfall in tree crowns of European beech (Fagus. sylvatica L.) and Norway spruce (Picea. abies (L.) Karst.). J. Hydrol. 2015, 522, 228–238. [Google Scholar] [CrossRef]
- Gomez, J.A.; Vanderlinden, K.; Giraldez, J.V.; Fereres, E. Rainfall concentration under olive trees. Agric. Water Manag. 2002, 55, 53–70. [Google Scholar] [CrossRef]
- Yousefi, S.; Sadeghi, S.H.; Mirzaee, S.; van der Ploeg, M.; Keesstra, S.; Cerdà, A. Spatio-temporal variation of throughfall in a hyrcanian plain forest stand in Northern Iran. J. Hydrol. Hydromech. 2018, 66, 97–106. [Google Scholar] [CrossRef]

| Tree Species | Average Height [m] | Average DBH 1 [cm] | Total Projected Crown Area [m2] | Average Branch Inclination 2 | LAI 3 (Leafed Period) | Bark Characteristics |
|---|---|---|---|---|---|---|
| Birch | 15.7 (±1.0) | 17.9 (±0.4) | 42.3 | 51° | 4.72 | Thin, smooth |
| Pine | 12.6 (±0.6) | 19.0 (±2.3) | 22.7 | 98° | 1.8 | Thick, rough |
| Raindrop Diameter Classes | Raindrop Velocity Classes | ||||
|---|---|---|---|---|---|
| Average Class Value [mm] | Lower Limit [mm] | Upper Limit [mm] | Average Class Value [m/s] | Lower Limit [m/s] | Upper Limit [m/s] |
| 0.05 | 0 | 0.1 | |||
| 0.15 | 0.1 | 0.2 | |||
| 0.312 | 0.2495 | 0.3745 | 0.25 | 0.2 | 0.3 |
| 0.437 | 0.3745 | 0.4995 | 0.35 | 0.3 | 0.4 |
| 0.562 | 0.4995 | 0.6245 | 0.45 | 0.4 | 0.5 |
| 0.687 | 0.6245 | 0.7495 | 0.55 | 0.5 | 0.6 |
| 0.812 | 0.7495 | 0.8745 | 0.65 | 0.6 | 0.7 |
| 0.937 | 0.8745 | 0.9995 | 0.75 | 0.7 | 0.8 |
| 1.062 | 0.9995 | 1.1245 | 0.85 | 0.8 | 0.9 |
| 1.187 | 1.1245 | 1.25 | 0.95 | 0.9 | 1 |
| 1.375 | 1.25 | 1.5 | 1.1 | 1 | 1.2 |
| 1.625 | 1.5 | 1.75 | 1.3 | 1.2 | 1.4 |
| 1.875 | 1.75 | 2 | 1.5 | 1.4 | 1.6 |
| 2.125 | 2 | 2.25 | 1.7 | 1.6 | 1.8 |
| 2.375 | 2.25 | 2.5 | 1.9 | 1.8 | 2 |
| 2.75 | 2.5 | 3 | 2.2 | 2 | 2.4 |
| 3.25 | 3 | 3.5 | 2.6 | 2.4 | 2.8 |
| 3.75 | 3.5 | 4 | 3 | 2.8 | 3.2 |
| 4.25 | 4 | 4.5 | 3.4 | 3.2 | 3.6 |
| 4.75 | 4.5 | 5 | 3.8 | 3.6 | 4 |
| 5.5 | 5 | 6 | 4.4 | 4 | 4.8 |
| 6.5 | 6 | 7 | 5.2 | 4.8 | 5.6 |
| 7.5 | 7 | 8 | 6 | 5.6 | 6.4 |
| 8.5 | 8 | 9 | 6.8 | 6.4 | 7.2 |
| 9.5 | 9 | 10 | 7.6 | 7.2 | 8 |
| 11 | 10 | 12 | 8.8 | 8 | 9.6 |
| 13 | 12 | 14 | 10.4 | 9.6 | 11.2 |
| 15 | 14 | 16 | 12 | 11.2 | 12.8 |
| 17 | 16 | 18 | 13.6 | 12.8 | 14.4 |
| 19 | 18 | 20 | 15.2 | 14.4 | 16 |
| 21.5 | 20 | 23 | 17.6 | 16 | 19.2 |
| 24.5 | 23 | 26 | 20.8 | 19.2 | 22.4 |
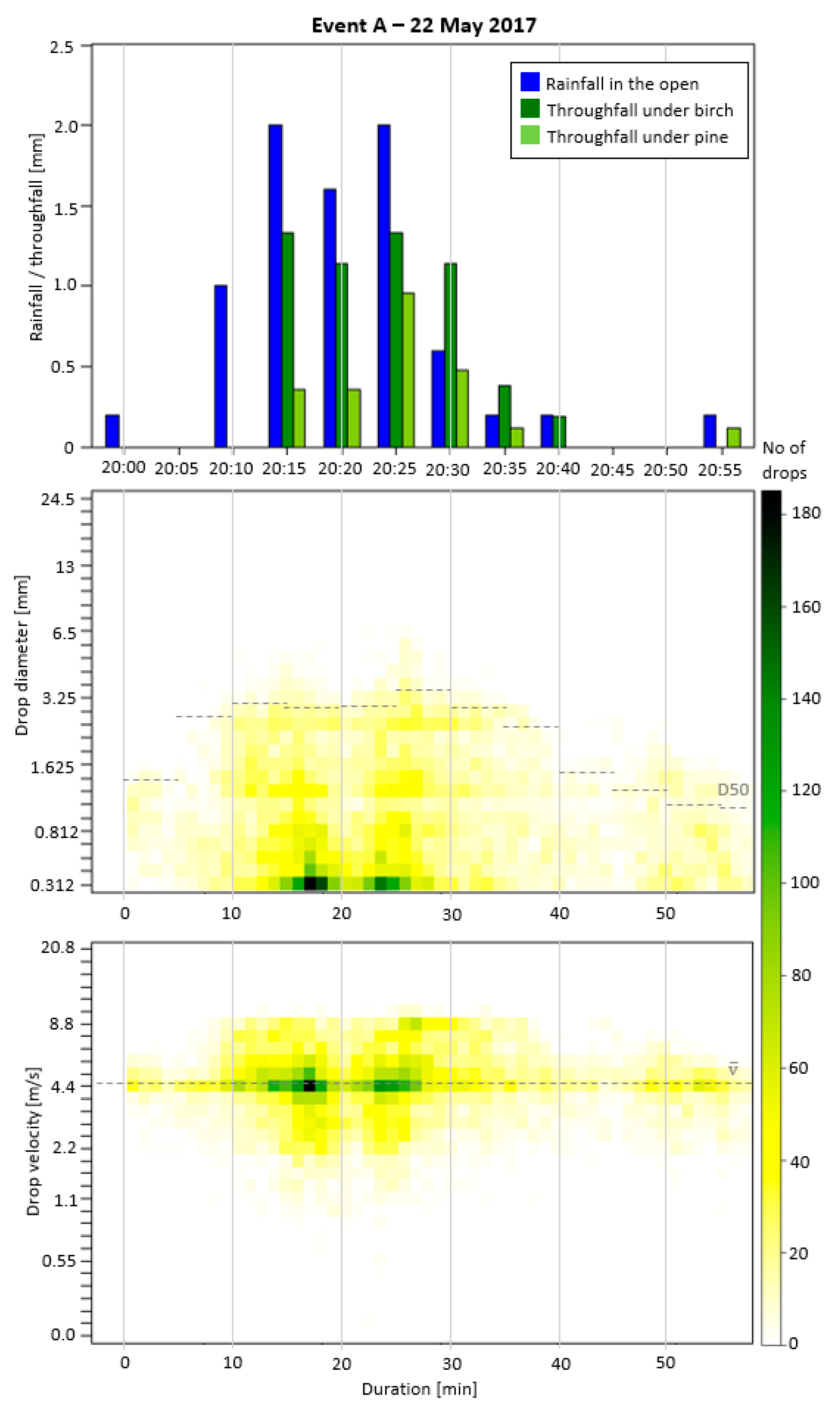
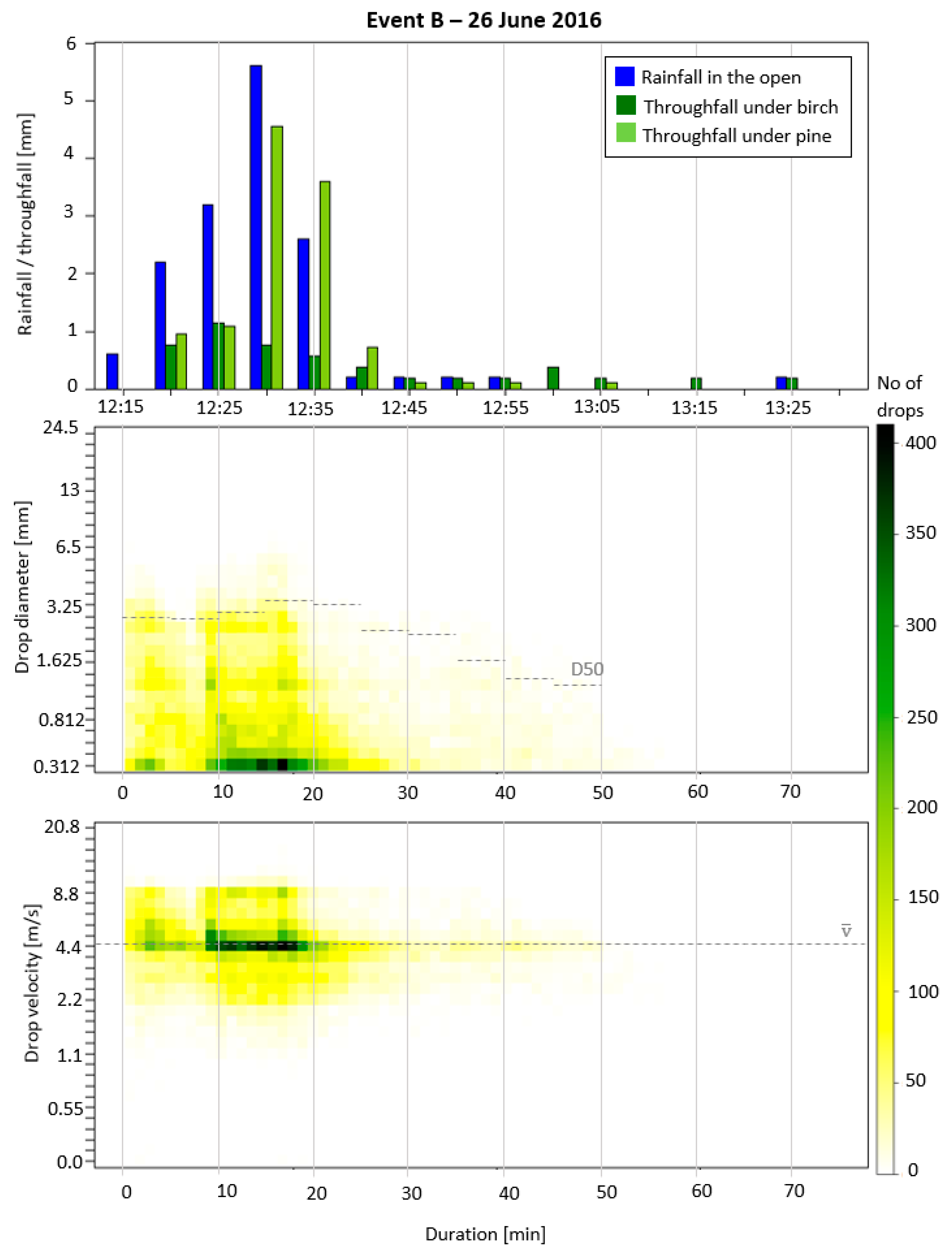
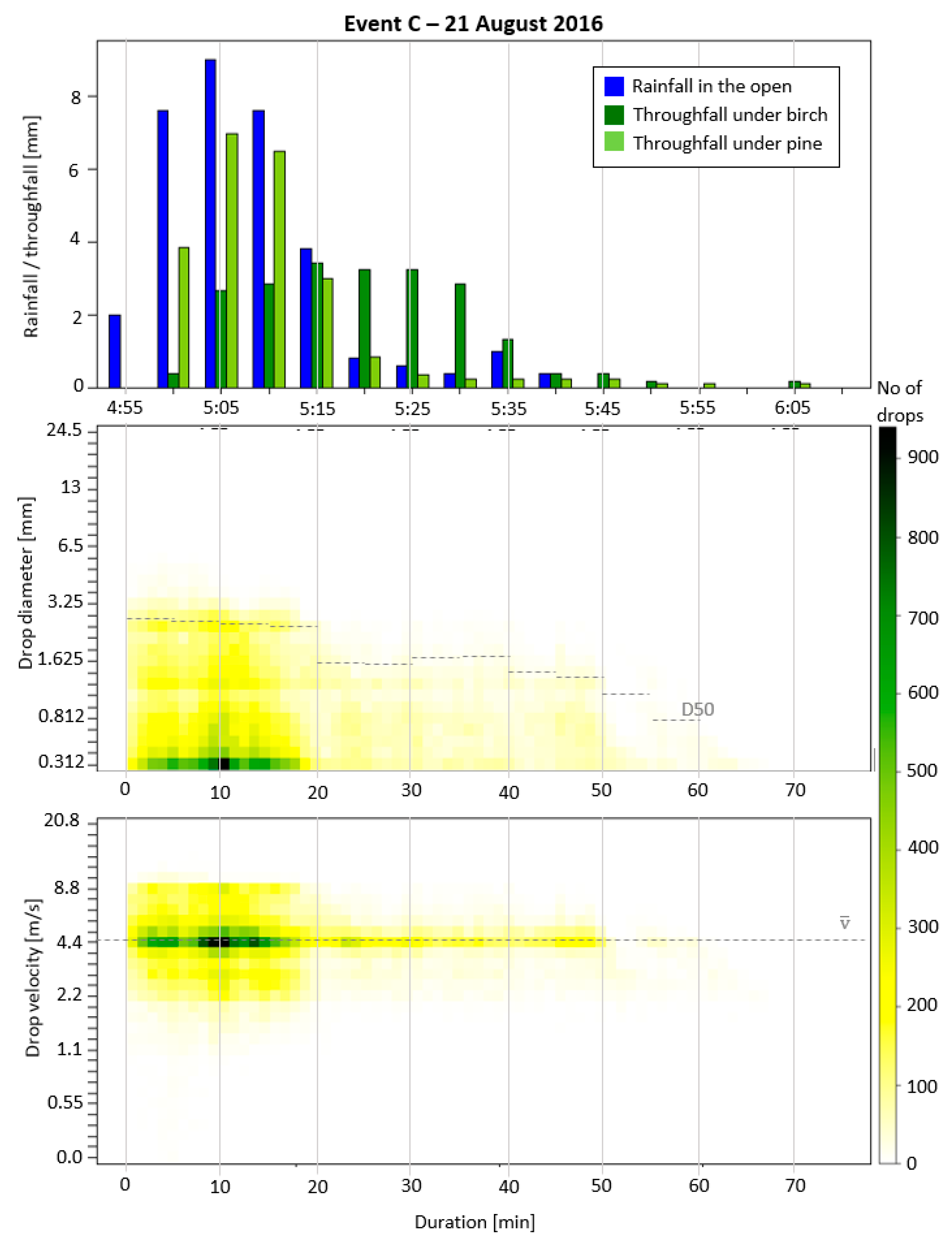
| Event | Duration [min] | Rainfall Amount [mm] | Rainfall Intensity [mm/h] | Average Wind Speed [m/s] | TF Birch | TF Pine | Kinetic Energy [mJ/cm2] | D50 [mm] |
|---|---|---|---|---|---|---|---|---|
| A 22 May 2017 | 54 | 8.0 | 8.9 | 2.67 | 69% | 31% | 1.99 | 2.92 |
| B 26 June 2016 | 69 | 15.2 | 13.2 | 2.28 | 62% | 77% | 2.23 | 2.94 |
| C 21 August 2016 | 71 | 33.4 | 28.2 | 2.80 | 64% | 70% | 5.12 | 2.39 |
| Time | Intensity [mm/5min] | D50 [mm] | Average Drop Velocity [m/s] | TF Pine [%] | TF Birch [%] |
|---|---|---|---|---|---|
| 20:25 | 0.4 | 2.81 | 5.04 | 48% | 67% |
| 20:30 | 0.12 | 3.60 | 5.34 | 80% | 67% |
| 20:35 | 0.04 | 2.76 | 4.94 | 60% | 190% |
| Time | Intensity [mm/5min] | D50 [mm] | Average Drop Velocity [m/s] | TF Pine [%] | TF Birch [%] |
|---|---|---|---|---|---|
| 12:30 | 1.12 | 2.70 | 4.37 | 81% | 14% |
| 12:35 | 0.52 | 3.47 | 4.11 | 138% | 22% |
| 12:40 | 0.04 | 3.35 | 4.11 | 360% | 190% |
| Time | Intensity [mm/5min] | D50 [mm] | Average Drop Velocity [m/s] | TF Pine [%] | TF Birch [%] |
|---|---|---|---|---|---|
| 5:15 | 0.76 | 2.31 | 4.64 | 79% | 90% |
| 5:20 | 0.16 | 1.53 | 4.44 | 105% | 404% |
| 5:25 | 0.12 | 1.45 | 4.41 | 60% | 538% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabret, K.; Rakovec, J.; Mikoš, M.; Šraj, M. Influence of Raindrop Size Distribution on Throughfall Dynamics under Pine and Birch Trees at the Rainfall Event Level. Atmosphere 2017, 8, 240. https://doi.org/10.3390/atmos8120240
Zabret K, Rakovec J, Mikoš M, Šraj M. Influence of Raindrop Size Distribution on Throughfall Dynamics under Pine and Birch Trees at the Rainfall Event Level. Atmosphere. 2017; 8(12):240. https://doi.org/10.3390/atmos8120240
Chicago/Turabian StyleZabret, Katarina, Jože Rakovec, Matjaž Mikoš, and Mojca Šraj. 2017. "Influence of Raindrop Size Distribution on Throughfall Dynamics under Pine and Birch Trees at the Rainfall Event Level" Atmosphere 8, no. 12: 240. https://doi.org/10.3390/atmos8120240
APA StyleZabret, K., Rakovec, J., Mikoš, M., & Šraj, M. (2017). Influence of Raindrop Size Distribution on Throughfall Dynamics under Pine and Birch Trees at the Rainfall Event Level. Atmosphere, 8(12), 240. https://doi.org/10.3390/atmos8120240








