Integrated Regional Enstrophy and Block Intensity as a Measure of Kolmogorov Entropy
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
3. Results—Blocking Case Studies
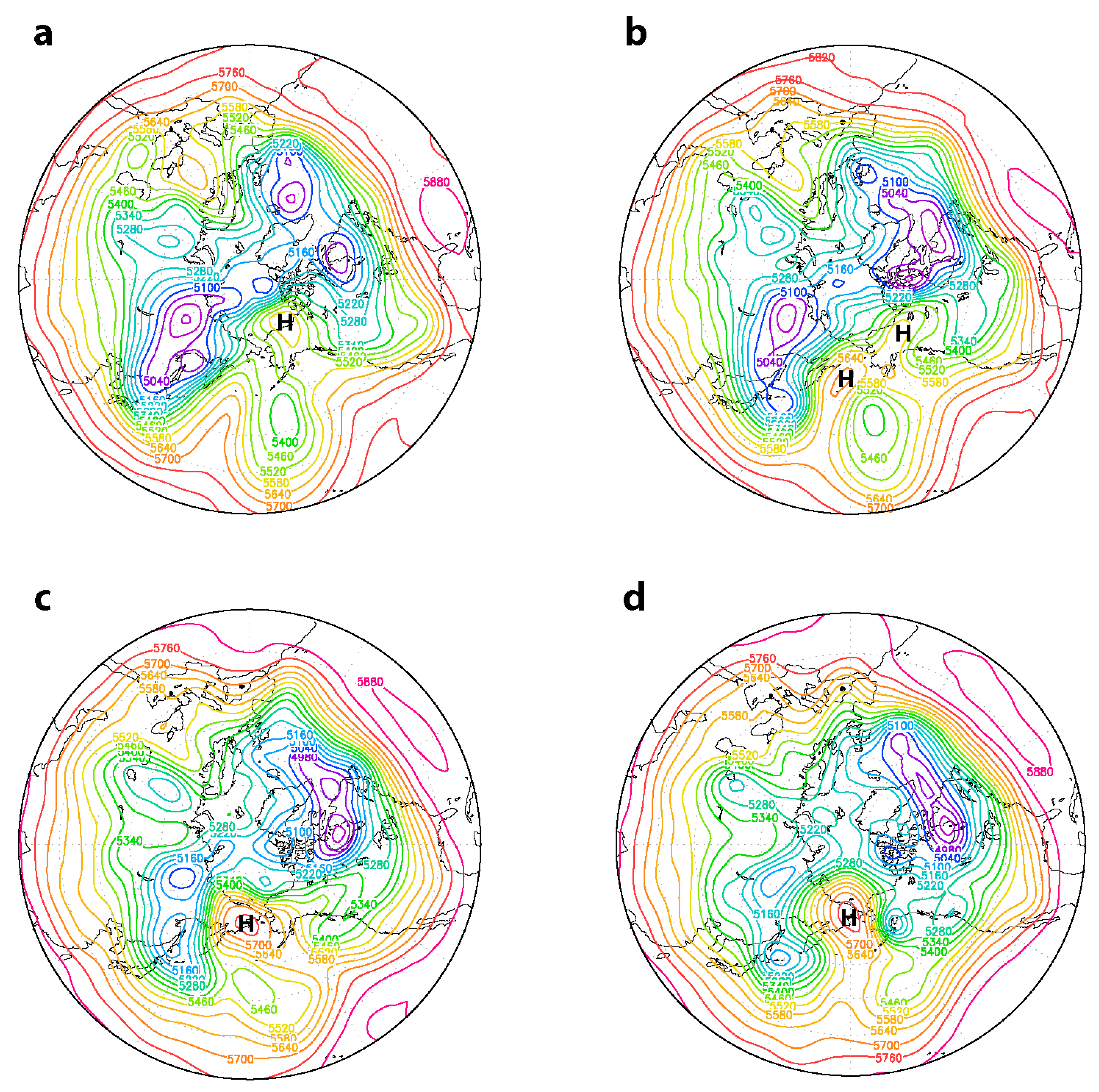
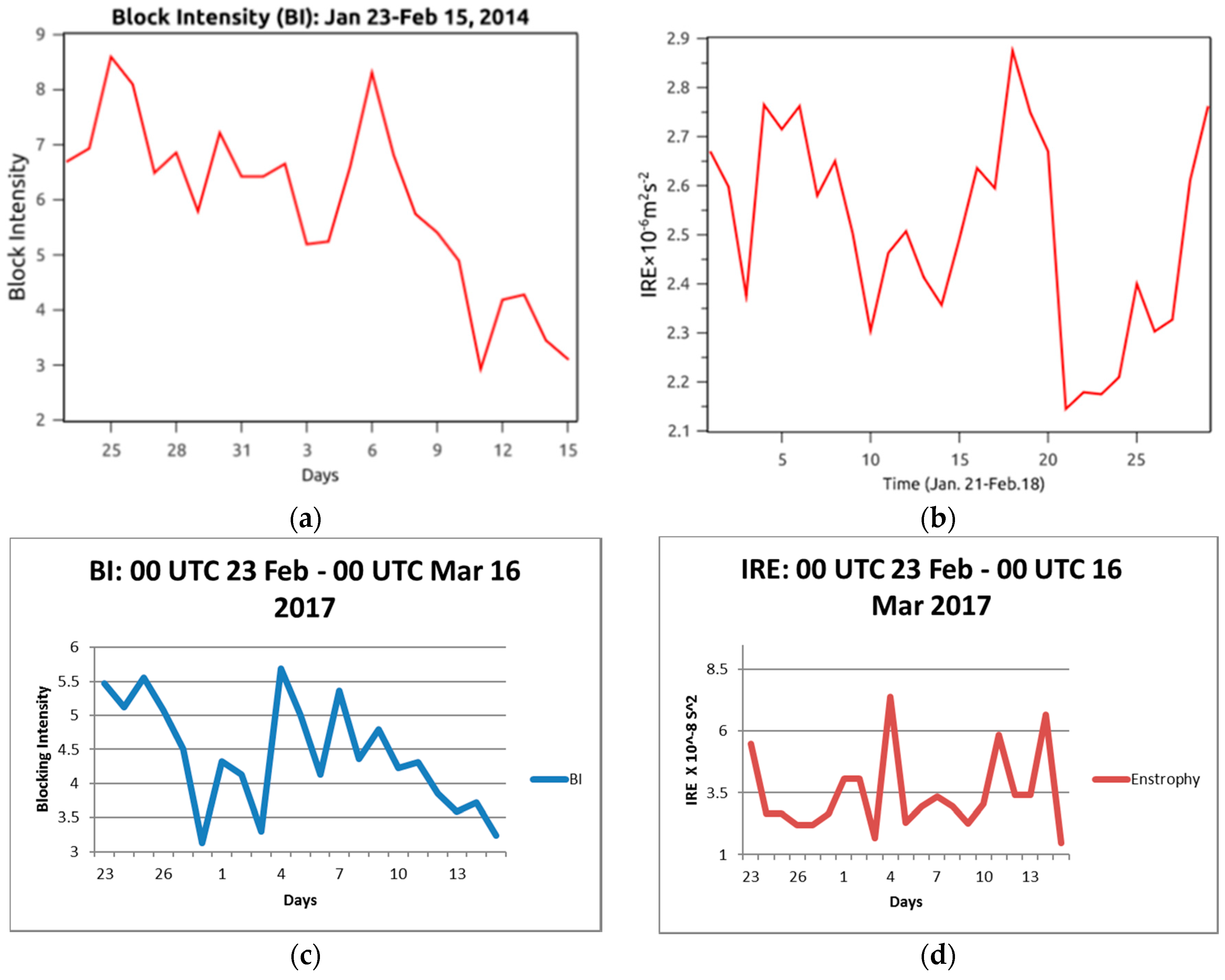
3.1. Blocking Case: January–February 2014
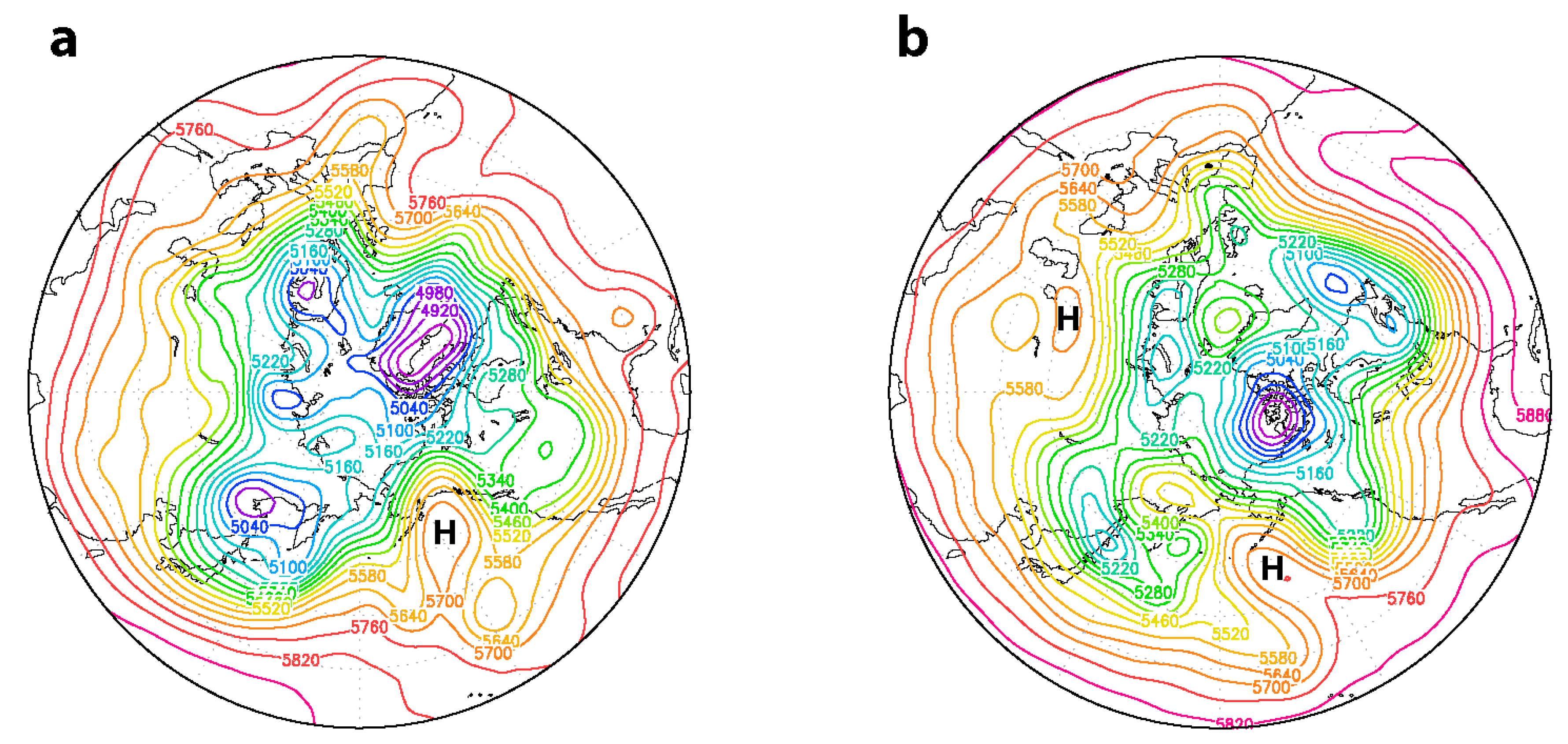
3.2. Blocking Case: February–March 2017
3.3. Blocking Cases: BI, IRE, KSE
4. Discussion, Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lupo, A.R.; Smith, P.J. Climatological features of blocking anticyclones in the Northern Hemisphere. Tellus Ser. A 1995, 47, 439–456. [Google Scholar] [CrossRef]
- Dymnikov, V.P.; Kazantsev, Y.V.; Kharin, V.V. Information entropy and local Lyapunov exponents of barotropic atmospheric circulation. Izv. Atmos. Ocean. Phys. 1992, 28, 425–432. [Google Scholar]
- Lupo, A.R.; Mokhov, I.I.; Dostoglou, S.; Kunz, A.R.; Burkhardt, J.P. Assessment of the impact of the planetary scale on the decay of blocking and the use of phase diagrams and enstrophy as a diagnostic. Izv. Atmos. Ocean. Phys. 2007, 43, 45–51. [Google Scholar] [CrossRef]
- Athar, H.; Lupo, A.R. Scale Analysis of Blocking Evens from 2002 to 2004: A case study of an unusually persistent blocking events leading to a heat wave in the Gulf of Alaska during August 2004. Adv. Meteorol. 2010, 2010. [Google Scholar] [CrossRef]
- Jensen, A.D.; Lupo, A.R. The role of deformation and other quantities in an equation for estrophy as applied to atmospheric blocking. Dyn. Atmos. Oceans 2014, 66, 151–159. [Google Scholar] [CrossRef]
- Haines, K.; Holland, A.J. Vacillation cycles and blocking in a channel. Q. J. R. Meteorol. Soc. 1998, 124, 873–897. [Google Scholar] [CrossRef]
- Colucci, S.J.; Baumhefner, D.P. Numerical prediction of the onset of blocking: A case study with forecast ensembles. Mon. Weather Rev. 1998, 126, 773–784. [Google Scholar] [CrossRef]
- Lupo, A.R.; Mokhov, I.I.; Akperov, M.G.; Chernokulsky, A.V.; Athar, H. A dynamic analysis of the role of the planetary and synoptic-scale in the summer of 2010 blocking episodes over the European Part of Russia. Adv. Meteorol. 2012, 2012. [Google Scholar] [CrossRef]
- Lupo, A.R.; Mokhov, I.I.; Chendev, Y.G.; Lebedeva, M.G.; Akperov, M.G.; Hubbart, J.A. Studying summer season drought in western Russia. Adv. Meteorol. 2014, 2014, 942027. [Google Scholar] [CrossRef]
- Mokhov, I.I. Specific features of the 2010 summer heat formation in the European territory of Russia in the context of general climate changes and climate anomalies. Izv. Atmos. Ocean. Phys. 2011, 47, 653–680. [Google Scholar] [CrossRef]
- Mokhov, I.I.; Akperov, M.G.; Prokofyeva, M.A.; Timazhev, A.V.; Lupo, A.R.; Le Treut, H. Blockings in the Northern Hemisphere and Euro-Atlantic region: Estimates of changes from reanalysis data and model simulations. Doklady Earth Sci. 2013, 499, 430–433. [Google Scholar] [CrossRef]
- Jensen, A.D.; Lupo, A.R. Using enstrophy advection as a diagnostic to identify blocking-regime transition. Q. J. R. Meteorol. Soc. 2014, 140, 1677–1683. [Google Scholar] [CrossRef]
- Jensen, A.D. A dynamic analysis of a record breaking winter season blocking event. Adv. Meteorol. 2015, 2015, 634896. [Google Scholar] [CrossRef]
- Lupo, A.R.; Li, Y.C.; Feng, Z.C.; Fox, N.I.; Rabinowitz, J.L.; Simpson, M.L. Sensitive versus Rough Dependence under Initial Conditions in Atmospheric Flow Regimes. Atmosphere 2016, 7, 11. [Google Scholar] [CrossRef]
- Li, Y.C. The distinction of turbulence from chaos—Rough dependence on initial data. Electron. J. Differ. Equ. 2014, 2014, 1–8. [Google Scholar]
- Ekmann, J.P.; Ruelle, D. Ergodic theory of chaos. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: One Liberty Plaza, NY, USA, 1993. [Google Scholar]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1965, 20, 130–141. [Google Scholar] [CrossRef]
- Schubert, S.; Lucarini, V. Dynamical analysis of blocking events: Spatial and temporal fluctuations of covariant Lyapunov vectors. Q. J. R. Meteorol. Soc. 2016, 142, 2143–2158. [Google Scholar] [CrossRef]
- Oseledets, V.L. A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems. Trans. Mosc. Math. Soc. 1968, 19, 179. [Google Scholar]
- Ruelle, D. An inequality for the entropy of differentiable maps. Bol. Soc. Bras. Math. 1978, 9, 83. [Google Scholar] [CrossRef]
- Persin, J.B. Lyapunov characteristic exponents and smooth ergodic theory. Russ. Math. Matical Surv. 1977, 32, 55–114. [Google Scholar] [CrossRef]
- Zeng, X.; Pielke, R.A.; Eykholt, R. Estimating the fractal dimension and the predictability of the atmosphere. J. Atmos. Sci. 1992, 49, 649–659. [Google Scholar] [CrossRef]
- Wiedenmann, J.M.; Lupo, A.R.; Mokhov, I.I.; Tikhonova, E.A. The climatology of blocking anticyclonesfor the Northern and Southern Hemispheres: Block intensity as a diagnostic. J. Clim. 2002, 15, 3459–3473. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- NCEP/NCAR Reanalyses Project. Available online: http://www.esrl.noaa.gov/psd/data/reanalysis/reanalysis.shtml (accessed on 19 June 2016).
- University of Missouri Blocking Archive. Available online: http://weather.missouri.edu/gcc (accessed on 6 June 2016).
- Shapiro, R. Smoothing, filtering, and boundary effects. Rev. Geophys. 1970, 8, 359–387. [Google Scholar] [CrossRef]
- Bond, N.A.; Cronin, M.F.; Freeland, H.; Mantua, N. Causes and impacts of the 2014 warm anomaly in the NE Pacific. Geophys. Res. Lett. 2015, 42, 3414–3420. [Google Scholar] [CrossRef]
- Bond, N.A.; Cronin, M.F.; Freeland, H. The Blob: An extreme warm anomaly in the Northeast Pacific [in “State of the Climate 2014”]. Bull. Am. Meteorol. Soc. 2015, 96, S62–S63. [Google Scholar]
- Jensen, A.D. The Nonequilbrium Thermodynamics of Atmospheric Blocking. Atmos. Chem. Phys. Discuss. 2017, in press. [Google Scholar] [CrossRef]
- Lupo, A.R.; Colucci, S.J.; Mokhov, I.I.; Wang, Y. Large-scale dynamics, anomalous flows, and teleconnections 2015. Adv. Meteorol. 2016, 2016, 1893468. [Google Scholar] [CrossRef]
- Li, J.; Chylek, P.; Zhang, F. The dissipation structure of extratropical cyclones. J. Atmos. Sci. 2014, 71, 69–88. [Google Scholar] [CrossRef]
- NOAA State of the Climate. Available online: http://www.ncdc.noaa.gov/sotc/synoptic/2014 (accessed on 17 November 2014).
- Reynolds, D.D.; Lupo, A.R.; Jensen, A.D.; Market, P.S. The predictability of Northern Hemisphere blocking using a ensemble mean forecast system. In Proceedings of the 2nd Electronic Conference on Atmospheric Science, Basel, Switzerland, 16–31 July 2017. [Google Scholar]
- Lupo, A.R. A diagnosis of two blocking events that occurred simultaneously in the mid-latitude Northern Hemisphere. Mon. Weather Rev. 1997, 125, 1801–1823. [Google Scholar] [CrossRef]
- Neter, J.; Wasserman, W.; Whitmore, G.A. Applied Statistics, 3rd ed.; Allyn and Bacon: Boston, MA, USA, 1988. [Google Scholar]
- Sanders, F.; Gyakum, J.R. Synoptic-dynamic climatology of the “bomb”. Mon. Weather Rev. 1980, 108, 1577–1589. [Google Scholar] [CrossRef]
- Matsueda, M. Predictability of Euro-Russian blocking in summer of 2010. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
| Block Period | BI | IRE (×10−6 s−2) | KSE |
|---|---|---|---|
| Onset Intensification 1 | 6.90 | 2.56 | 0.86 |
| Mid-block Intensification | 6.46 | 2.57 | 1.39 |
| Block Lifetime | 5.93 | 2.49 | 0.75 |
| Block Period | BI | IRE (×10−6 s−2) | KSE |
|---|---|---|---|
| Onset Intensification 2 | 5.30 | 4.06 | 1.79 |
| Mid-block Intensification | 4.57 | 3.53 | 1.38 |
| Block Lifetime | 4.42 | 3.46 | 1.09 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jensen, A.D.; Lupo, A.R.; Mokhov, I.I.; Akperov, M.G.; Reynolds, D.D. Integrated Regional Enstrophy and Block Intensity as a Measure of Kolmogorov Entropy. Atmosphere 2017, 8, 237. https://doi.org/10.3390/atmos8120237
Jensen AD, Lupo AR, Mokhov II, Akperov MG, Reynolds DD. Integrated Regional Enstrophy and Block Intensity as a Measure of Kolmogorov Entropy. Atmosphere. 2017; 8(12):237. https://doi.org/10.3390/atmos8120237
Chicago/Turabian StyleJensen, Andrew D., Anthony R. Lupo, Igor I. Mokhov, Mirseid G. Akperov, and DeVondria D. Reynolds. 2017. "Integrated Regional Enstrophy and Block Intensity as a Measure of Kolmogorov Entropy" Atmosphere 8, no. 12: 237. https://doi.org/10.3390/atmos8120237
APA StyleJensen, A. D., Lupo, A. R., Mokhov, I. I., Akperov, M. G., & Reynolds, D. D. (2017). Integrated Regional Enstrophy and Block Intensity as a Measure of Kolmogorov Entropy. Atmosphere, 8(12), 237. https://doi.org/10.3390/atmos8120237






