Abstract
An objectively trained model for tropical cyclone intensity estimation from routine satellite infrared images over the Northwestern Pacific Ocean is presented in this paper. The intensity is correlated to some critical signals extracted from the satellite infrared images, by training the 325 tropical cyclone cases from 1996 to 2007 typhoon seasons. To begin with, deviation angles and radial profiles of infrared images are calculated to extract as much potential predicators for intensity as possible. These predicators are examined strictly and included into (or excluded from) the initial predicator pool for regression manually. Then, the “thinned” potential predicators are regressed to the intensity by performing a stepwise regression procedure, according to their accumulated variance contribution rates to the model. Finally, the regressed model is verified using 52 cases from 2008 to 2009 typhoon seasons. The R2 and Root Mean Square Error are 0.77 and 12.01 knot in the independent validation tests, respectively. Analysis results demonstrate that this model performs well for strong typhoons, but produces relatively large errors for weak tropical cyclones.
1. Introduction
Tropical Cyclones (TCs) are some of the most damaging natural hazards [1]. The intensity (here refers to the maximum sustained wind) is generally used as a main indicator for quantifying the damage potential of TCs. Because it is difficult to obtain direct in-situ measurements of TC intensity [2], satellite remote sensing, especially geostationary meteorological satellite (GMS) remote sensing, has been heavily relied upon in related studies and operational forecasts. On the one hand, GMS has higher temporal and spatial resolution compared to polar satellite microwave remote sensing [3,4,5] and air reconnaissance [6,7,8]. On the other hand, GMS could cover the vast tropical ocean continually, and thereby provide valuable datasets concerning the genesis, track, intensity and other well-concerned information about TCs throughout their life cycles. The Northwestern Pacific Ocean (NWP), which is characterized with frequent cyclone activities, is heavily dependent on GMS for TC intensity estimation and forecast [3,9,10].
During the beginning years (1970s) of satellites, Dvorak summarized previous research [11,12] and proposed a comprehensive pattern recognition technique for tropical cyclone (TC) intensity estimation from satellite imagery, which is known as Dvorak Technique (DT) [13,14]. However, DT depends on experts’ experience, and therefore is subjective and time intensive. Several revisions of the DT technique were developed during the later decades. The Objective Dvorak Technique (ODT) [15] recognized patterns in satellite imagery using computer-based algorithm, and created a look-up table. The shortcoming of ODT is that centers of TCs are determined either manually or with the aid of external resources [16]. The more recently developed Advanced Dvorak technique (ADT), which is regarded as the latest version of DT method, advances the original Dvorak technique through modifications based on rigorous statistical and empirical analysis [17,18]. Despite the continual development of the DT method, all versions of DT technique (except for ADT) estimate TC intensity based on cloud features and patterns recognition.
Apart from the DT method, some other techniques have also been developed. Mueller (2006) used geostationary IR data to estimate wind field structure of TCs through estimates of radius of maximum wind (RMAX)and wind at 182 km (V182) with 405 cases from the 1995–2003 Atlantic and Eastern Pacific typhoon seasons [19]. Chao (2011) made use of both IR and visible satellite images to estimate TC rotation speed and then sought to predict TC wind intensity using estimated rotation speeds at the 130–260 km ring [10]. Fetanat (2013) proposed a new technique for TC intensity estimation using the spatial feature analogs in satellite imagery. The technique was testified as on par with other objective techniques [20]. Zhuge (2015) combined information from geostationary satellite infrared window (IR) and water vapor (WV) imagery, and proposed a WV-IRW-to-IRW ratio (WIRa)-based indicator to estimate TC intensity over NWP [3]. The results showed that the WIRa-based indicator gives a more accurate estimation of TC intensities.
Another approach for characterizing TC cloud dynamics was initially discussed by Piñeros (2008) [21]. In that study, the deviation angle variance (DAV) was used to describe the degree of asymmetry and “organization” of TC cloud. This was then developed into the Deviation Angle Technique (DAV-T) which was applied into many aspects of TC related research [16,22,23,24]. In particular, it has been proved that DAV-T can be a reliable tool in hurricane intensity estimation [16,22]. The DAV-T was lately applied into estimating TC intensity over NWP. Results showed an accurate estimation with a Root Mean Square Error (RMSE) of 14.3 knot in the 2007–2011 NWP typhoon seasons [25]. More recently, a non-dimensional TC intensity (TI) index was proposed by combining some statistical parameters of DAVs [26]. The TI index was reported to be more suitable for TCs with axisymmetric, non-sheared cloud systems.
Despite the aforementioned new techniques for TC intensity estimation, each with its strengths and drawbacks, there is still need to improve the precision and accuracy of TC intensity estimation technique making use of satellite images for the aim of better forecast. Therefore, in this research, we seek to extract the most significant signals and parameters from IR images so as to develop an objective technique to estimate current intensity of TCs. The objective of this paper is to provide another reference for improving our capability of TC intensity estimation. The remaining parts of this paper are organized as follows. Data collection and preprocessing are discussed in Section 2. Section 3 describes the procedures for developing the model. The model is tested and discussed in Section 4. The main conclusions are summarized in Section 5.
2. Data Collection and Preprocessing
To date, a wide breadth of scientific measurements from in-situ, aircraft, and satellite instruments are readily available for TC related research [27]. However, it is still difficult to gather all information (including both images and data) that pertain to a particular TC or an ocean basin [28]. The JPL Tropical Cyclone Information System (TCIS) includes a comprehensive set of multi-parameter observations and model outputs that are relevant to both large-scale and storm-scale processes in the atmosphere and in the ocean. The TCIS data archive, including AIRS, CloudSAT, MLS, AMSU-B, QuikSCAT, Argo floats, GPS, and many others, pertains to the thermodynamic and microphysical structure of the storms, the air-sea interaction processes and the larger-scale environment over the globe from 1999 to 2010. Storm data are subsetted to a 2000 × 2000 km2 window around the hurricane track for six geographic regions [29].
The region of interest in this paper covers the NWP basin from 5° to 45°N and from 100° to 165°E (Figure 1). The inputs include digital brightness temperatures (BTs) of the IR (10.3–11.3 um) and water vapor (WV, 6.5–7.0 um) channel images with spatial and temporal resolution of 8 km and 3 h, respectively. It was noted that the TCIS satellite images are actually produced by Hurricane satellite data (HURSAT-B1, version 05) [30]. While the HURSAT-B1 covers TCs in Western Pacific Ocean from 1978 to 2009, the earliest WV data provider for NWP is GMS-5 from 1996. Therefore, satellite images from 1996 to 2009 are used. The HURSAT-B1 images were downloaded from HURSAT and TCIS for the years 1996–1998 and 1999–2009, respectively. All images were filtered using a low-pass filter in order to exclude unreasonable increment or decrement in BTs. In addition, the images were screened and preprocessed carefully to avoid introducing uncertain errors. For example, images with “missing belt” are cubic interpolated.
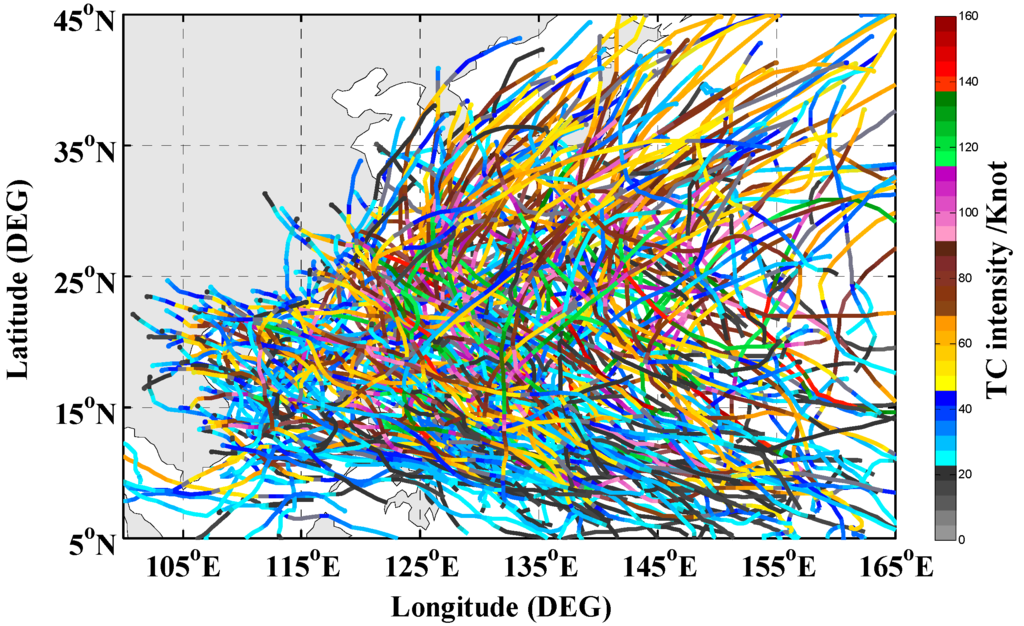
Figure 1.
The region of interest in this paper, and tracks of the 325 cases adopted in training the model.
The selected dataset comprises 18,108 three-hourly satellite images of 377 tropical cyclone cases from 1996 to 2009 NWP typhoon season. Of the 377 cases, 118 are tropical depression, 53 are tropical storm, 54 are typhoons, 36 are moderate typhoons, 26 are severe typhoons, 57 are super typhoons, and 33 are extreme typhoons. The 377 cases are divided into two groups. They are, 325 (16,126 images) from 1996 to 2007 and 52 (1982 images) from 2008 to 2009 typhoon seasons, performing as training and validation datasets, respectively. More specifically, of all the 16,126 training images, 4752 are tropical depression (29.47%), 5513 are tropical storms (34.19%), 2444 are typhoons (15.16%), 1522 are moderate typhoons (7.70%), 910 are severe typhoons (5.64%), 1041 are super typhoons (6.46%), and 252 are extreme typhoons (1.39%), as shown in Figure 1 and Table 1.

Table 1.
Number and percent of images in each category of tropical cyclones for training and validating the model. The terminologies of the typhoon categories are included in the brackets behind the category number.
Among TC best-track information archives, the dataset from Joint Typhoon Warning Center (JTWC) is one of the most broadly used ones [31], and has been proved to be more reliable compared to other best-track datasets available for NWP basin [32,33,34]. JTWC best-track dataset is thus adopted as verification. To match the three-hourly satellite images, the 6-h interval archived best-track data are interpolated using the linear interpolation method.
3. Methodologies
3.1. Estimation and Development of DAV
As aforementioned in the introduction section, DAV-T is another reliable approach for TC intensity estimation by quantifying the degree of axisymmetry and “organization” of IR brightness temperatures. In this paper, gradient vectors of BTs are computed by performing the sobel template. For each pixel within 300-km radius from the center pixel, the deviation angle between the gradient vector and corresponding radial extending from the TC center is calculated, and the DAV is then determined. Ritchie (2014) [25] relates the DAV to TC intensity via a sigmoid model. We tested that model using the 325 cases in the training datasets. However, the R2 is only 0.36. Therefore, we endeavor to develop the DAV-T through adding some statistical parameters.
Since the interpolated best-track information, especially the locations might be inconsistent with satellite images, we here adopt a center region, which is assumed as the nine pixels surrounding corresponding JTWC best-track center location on each image. The deviation angles and all undermentioned parameters are hence computed upon the center region. Accordingly, the average values of the center regions are determined as optimal ones in order to minimize errors caused by inaccurate TC center positions.
The first statistical parameter, the probability density of mean deviation angle (P_MDA) proposed by Liu (2015) [26] is included. Liu found that P_MDA is positively related with intensity. Nevertheless, the P_MDA here is derived using accumulating probability densities between and , where DAs denote deviation angles. Because this could take most of significant peaks in the histogram of the deviation angles into account, which means that the P_MDA would not be decided solely by the probability density at the mean deviation angle which might be an uncertain noise, and hence reduce uncertain errors. The second statistical parameter is the interquartile range (IQR) of deviation angles. The advantage of IQR is that this could effectively exclude unreasonable extremums and some possible noises derived from BTs.
After obtaining parameters DAV, P_MDA and IQR, we concentrate on developing a new index by combining effects of these three. According to previous studies, a weak cyclone system is featured with disorganized and asymmetrical cloud cluster. Therefore, gradient vectors of the brightness temperatures would be extremely disorganized, and thereby the higher the DAV. Accordingly, the stronger the TC, the larger the P_MDA and the smaller the IQR. That being said, we are not going to build proportional (or reciprocal) relationships between the intensity and the three parameters, but try to seek a mode that could improve the explanatory power of these parameters to intensity as large as possible. After times of tests (not shown here), the new index DAO is eventually determined as follows:
where the amplification factor 100 is added to raise the order of the magnitude of DAO while it does not influence DAO’s behaviors. Here we take a weak TC as an example to clarify the mechanism of DAO, for such a case, the DAV would be relatively large compared with those strong TC. According to Figure 3 in Ritchie (2013) [25], large increment of DAV corresponds to small intensity change for weak TCs, and vice versa. Therefore, the Logarithmic operation is performed on DAV to compress changes in large DAVs and expand changes in small DAVs. The P_MDA acts as an exponent. That is, for cases with differing intensities but possibly the same DAV, the power function distinguish the intensity based on the mechanism that for weaker TCs, much fewer peak deviation angles would distribute within the vicinity of the mean deviation angle, and therefore the smaller the DAO. The performance of DAO and the three parameters are tested individually. Results prove that the DAO performs better than using any of the three parameters alone on the 325 cases. Specifically, by testing the 16,126 images, the correlation coefficient between DAO and TC intensity is proved to be higher (0.74) compared with DAV (−0.62), P_MDA (0.60) and IQR (−0.63).
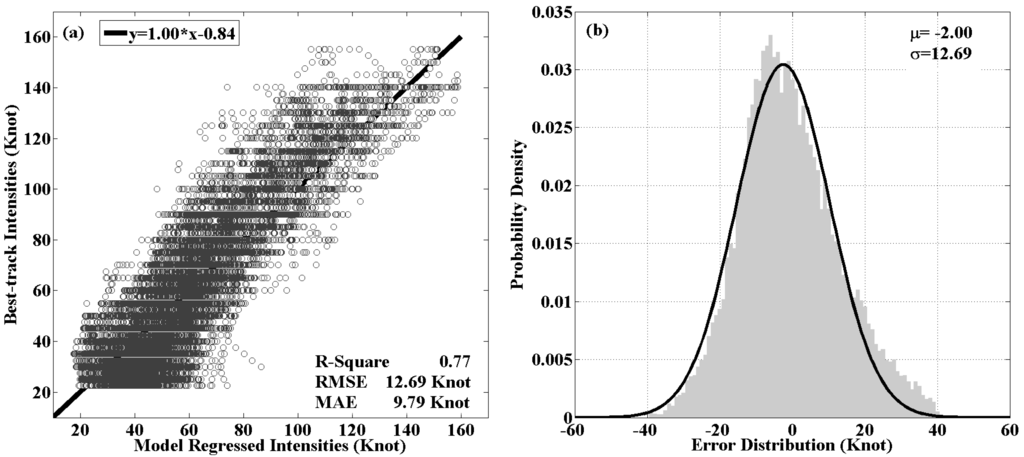
Figure 3.
(a) Scatterplot of model regressed vs. interpolated best-track intensities in the dependent test. The solid line was derived by a linear regression procedure using least square method; (b) The distribution of the errors. The solid curve represents a Gaussian model which was derived by fitting the error distribution.
3.2. Potential Predicators Extraction
Radial profiles of the IR brightness temperature (IRBT for short) form the other basis for extracting possible predicators for TC intensity. This is achieved by converting the Cartesian latitude and longitude gridded data into a polar coordinate system. Then, the BT data are azimuthally averaged at 4 km intervals from the TC center. Note that the radial profiles may differ slightly if they are calculated according to different TC center locations. This could introduce uncertain errors in computing radial profiles of the IRBTs. Therefore, as down in calculating DAVs, a mine-pixel center region is taken to create the azimuthally averaged IRBT profiles. The mean of the nine profiles obtained in this region is finally adopted as the optimal one. The Empirical orthogonal function (EOF) analysis is commonly used to extract crucial information from IRBT [7,19,35]. However, here we do not correlate TC intensity directly to IRBT profiles, because by testing the 325 cases we found that taking the EOFs as predicators for intensity contributes very little to improving the regression. Instead, we extract critical signals from the profiles to represent characters of satellite images.
As defined by [36,37,38], the core region of TC could be divided into inner core and outer core regions (from 0° to 1° and from 1° to 2.5° radially respectively). Thus, the inner core average BT (ICBT) and the outer core average BT (OCBT) are estimated. In addition, the minimum and the maximum BT within the outer core region are also derived (hereinafter denoted as MIBT and MABT, respectively). Figure 2 shows the Schematic diagram of the distribution of aforementioned parameters. In Figure 2, the solid curve represents the mean of the 16,126 IRBT profiles.
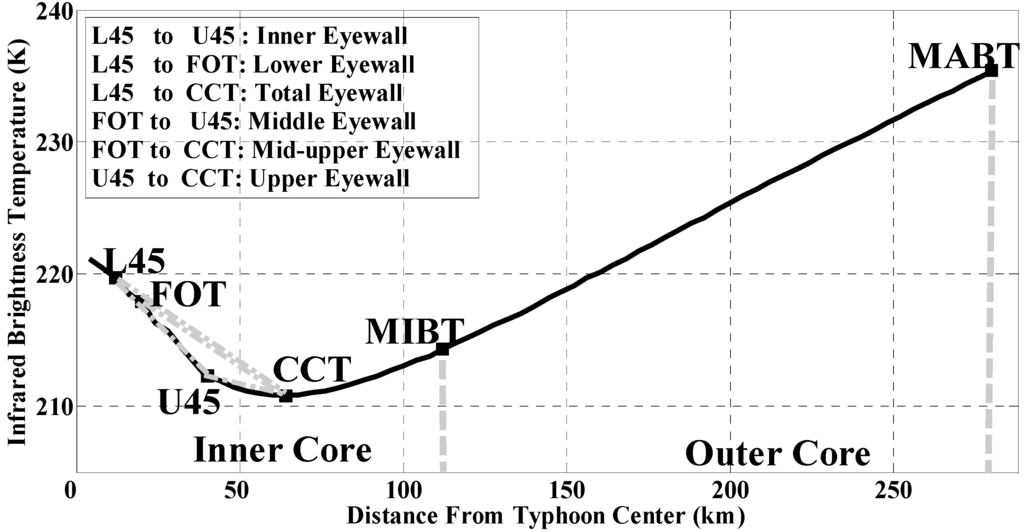
Figure 2.
Schematic diagram of the radial profile (solid curve, calculated by averaging the radial profiles of the 16,126 images) of the IR brightness temperature. The vertical gray dashed line divides the core region into inner and outer core, respectively.
According to Sanabia (2014) [39], IR profiles in the TC inner core could be represented by four critical points which locate mainly within 100 km from the TC center. The first critical point is the radial location of the coldest cloud top (CCT) within 200 km from the TC center. Note that here the CCT differs from the location of MIBT. The second critical point, the radial location of the first overshooting top (FOT hereinafter), is defined using the BT difference (TWV-IR) between water vapor (WV) and IR brightness temperature [40]. The third and fourth critical points are selected to define a lower and upper extent (hereinafter denoted as L45 and U45) of the inner eyewall, respectively. The L45 in this paper is identified as the first 45° downturn inflection point, which is the location at which the orientation of the IR profile changes from vertical to the horizontal, and vice versa the U45, because we adopted normal cartesian coordinate system without inverting the y axis as did in Sanabia (2014). The mean location of the four critical points are plotted in Figure 2.
One of the premises for locating L45 and U45 is that the CCTs do not locate in TC centers. However, not all images meet this criterium. Therefore, for such cases, we subjectively define L45, U45 and CCT as the mean of those whose L45 and U45 could be identified. The other obstacle for identifying L45 and U45 is, for some cases, it is inevitable that the eye and eyewall do not exist, and therefore the radial profile do not slope to register a 45° angle. For such occasions, we adjust the threshold angle to a smaller one iteratively until finding the point where the profile changes from vertical to horizontal, and from horizontal to vertical.Nevertheless, the minimum threshold angle for L45 and U45 cannot be less than 35°. As shown in Figure 2, six slopes of the IR brightness temperature between the four critical points are calculated. These six slopes can be regarded as proxies for inner-core convections. For example, SL45-FOT represents the slope between the locations of L45 and FOT, which is obtained by dividing the change in IRBT between L45 and FOT by the radial distance. Finally, the mean brightness temperature between every two critical points are calculated. Table 2 lists all the potential predicators. All these predicators are probably relevant to TC intensity, while the significance of each one is not determined. Note that in Table 2, all terms of the eyewall follow previous studies [39,41].

Table 2.
Potential predicator pool for intensity estimation from the IR images.
3.3. Multiple Linear Regression Model Development
Although it is encouraged to seek potential predicators as much as possible, it is unadvisable to take all the potential predicators into the final regression, because some of them may mutually correlated and thus provide redundant information. Therefore, it is necessary to “thin” the initial pool of the potential predictors. Note that for the aim of training an objective method of TC intensity estimation without knowing any information of the TC in advance, any variables that represent TC itself are not included, they had been testified as significant in estimating TC wind structure though [7,8,19,35].
For DAV-T related parameters, the new index DAO and the square of the DAV (DAV2) are selected. For predicators extracted from IRBT profiles, we manually exclude those which are weakly related to the TC intensity by testing the 325 cases. After this, the potential predicator pool initially contains 12 predicators: DAV2. DAO, ICBT, OCBT, MIBT, SL45-U45, SL45-CCT, SFOT-U45, AL45-U45, AL45-CCT, AFOT-U45 and AU45-CCT. For ICBT and OCBT, we divide them by AL45-U45, AL45-CCT, AFOT-U45 and AU45-CCT, respectively and introduce eight new parameters into the pool.
The regression is performed using a stepwise regression method. In the selection procedure, predicators are either added or removed from the multilinear model according to their statistical significance. The initial model contains no predicators other than the constant term. From then on, the model compares the explanatory power of incrementally larger and smaller models. At each step, the p-value of an F-statistic is computed to test models with and without a potential predicator. If a predicator is not currently in the model, the null hypothesis is that the predicator would have a zero coefficient if added to the model. If there is sufficient evidence to reject the null hypothesis, the predicator is added to the model. Conversely, if a predicator is currently in the model, the null hypothesis is that the predicator has a zero coefficient. If there is insufficient evidence to reject the null hypothesis, the predicator is removed from the model. The model terminates when no single inputting predicator improves the model. Here, we set the lowest confidence level as 99.99%. That is, we require the maximum p-value for a predicator to be added as 0.0005, and the minimum p-value for a predicator to be removed as 0.0001.
After selection by the stepwise regression procedure, eventually, seven predicators are involved into regression. They are DAV2, DAO, ICBT/AFOT-U45, ICBT/AL45-U45, OCBT/AU45-CCT, OCBT/AL45-FOT and SL45-U45. The DAV2 is included as the first as previous studies have proved its significance. The order by which the remaining predicators are input (Column 2 in Table 3) are decided according to their contribution rates to the accumulated variance. Table 3 lists some statistics produced while training the model. In order to quantify the relative contributions of all predictors to the model, all these predicators were normalized, and the stepwise regression was performed again. As shown in the last two columns in Table 3, the predicators ICBT/AL45-U45 and ICBT/AFOT-U45 dominate the regression (41.92% and 40.31%, respectively). This is then followed by SL45-U45 (6.28%) and OCBT/AL45-FOT (4.26%). It is obvious that the inputting predicators in this model improves the accuracy of the regression considerably (with a net difference of 18.42 knot and a net improvement of 59.21%).

Table 3.
Statistics related to the regression model.
4. Results and Discussions
4.1. Dependent Tests and Results
The final regressed model is as following:
where TCI represents TC intensity estimated using the trained model. Figure 3a shows the scatterplot of the model estimated vs. interpolated best-track intensities. It can be seen that for weak Tcs, the model overestimates intensities noticeably. Figure 3b plots the distribution of the errors, which fitted a Gauss model well (the black solid curve). From the curve, 68.26% of the errors lie within the region between −14.69 knot and 11.69 knot, and 95.44% lie within the region between −27.38 knot and 23.38 knot.
The model is validated several times to justify its accuracy. First of all, we adopted the n-fold cross validation method to examine the accuracy of the model for individual TCs. To begin with, the 16,126 images are divided into mutually exclusive 325 individual TC groups. Then, the validation are performed 325 times. For each time, we leave one case out and train the model using the remaining 324 cases iteratively. After that, the trained model is validated using the one which was not included into training the model. Note although this produced 325 models, the differences among these 325 models are quite small (not shown here for avoiding redundancy) and are similar with the one showed above. In each validation process, the distribution of the mean absolute error (MAE), the RMSE and the mean absolute relative error (MARE) are calculated (Figure 4). Figure 4a plots the distribution of the errors which is obtained by an accumulating procedure of the 16,126 images. It can be seen that 50%, 75% and 90% of the model estimated intensities are with the MAE less than 7, 13, and 20 knot, respectively. Figure 4b shows the average of RMSE for individual TCs. For the 325 cases in the dependent test, well over 75% of their intensities are estimated with a mean RMSE less than 12 knot, while only 18 TCs over 15 knot. The averaged RMSE is 18.52 knot for the overall 325 cases. Figure 4c,d plots the averaged MARE and averaged bias (defined as the average differences between the estimated intensity and the best-track intensity) for the 325 cases, respectively. The mean MARE is 19.91% and the mean bias is −0.56 knot (while the mean absolute bias is 4.47 knot).
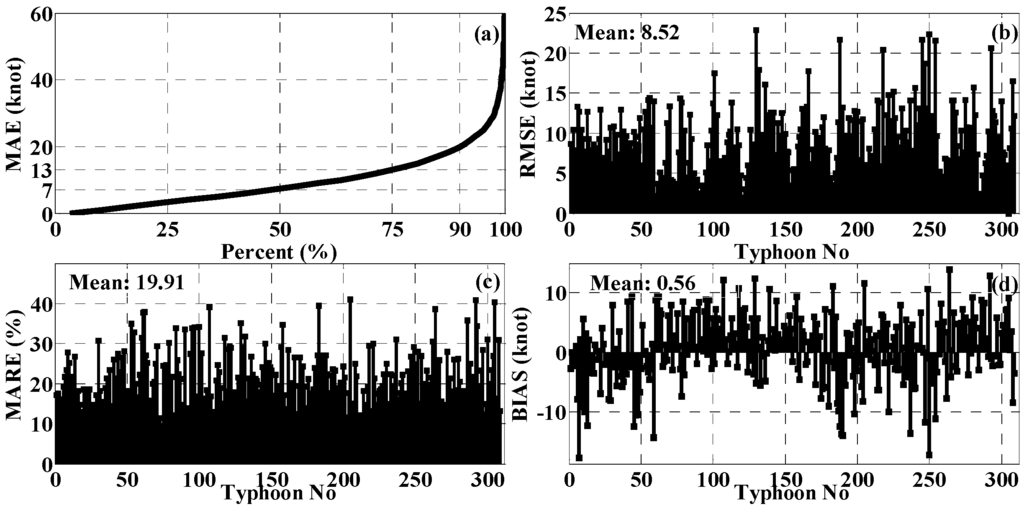
Figure 4.
N-fold cross validation of the model using the 325 cases in the northwestern pacific Ocean during the time period from 1996 to 2007. (a) The cumulative distribution of the absolute errors; (b) The root mean square error for each left out case; (c) The absolute relative error for each left out case; (d) The bias for each left out case.
In order to examine whether the performance of the model relies on the category of the TC intensity, the 16,126 images are divided into every 5 knot bins. Figure 5a shows the counts of TCs in each intensity bins in the dependent tests. Figure 5b shows that the mean RMSE generally increases with intensity but for intense typhoons (≥130 Knot). However, from Figure 5c, the MARE, it can be found that the absolute relative error is not significant (≤15%) for TCs stronger than 60 knot, which means that although more errors could be expected for intense typhoons, the relative error is quite small. From Figure 5d, the model generates noticeable (absolute bias > 10 Knot) overestimation in cases of weak systems (≤25 knot) and underestimation in cases of intense (≥150 knot).
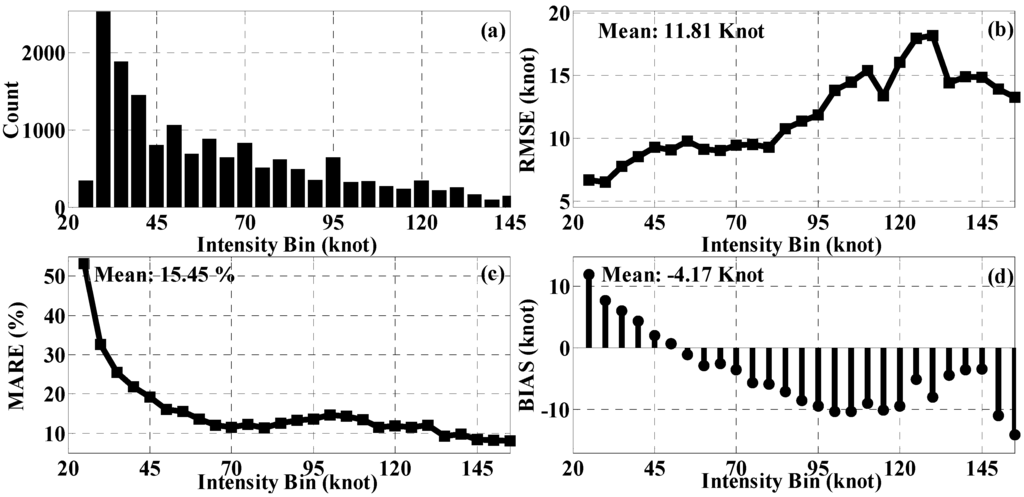
Figure 5.
Results of the dependent tests by intensities bins. (a) The frequency distribution of the cyclones by intensity in the dependent tests; The average: (b) root mean square error; (c) absolute relative error; and (d) bias for each intensity bin.
To facilitate further analysis, the 16,126 images are then divided into seven groupsaccording to Saffir–Simpson Scale. The RMSE and MARE are calculated for each group. Table 4 shows the results. In general, the error increases with intensity, with the RMSE 10.52, 12.94, 15.68, 17.49 and 18.93 knot for category 1–5 typhoons, respectively. However, from the MARE (last column in Table 4), it can be found that the model performs well but for tropical depressions and storms (also see Figure 3 and Figure 5) which has the highest proportion of samples (63.66%). The MARE between the regressed and the interpolated best-track intensities for tropical depressions is as high as 30.35% although the RMSE is relatively small (7.77 knot). Figure 3a and Figure 5d, Table 4 all suggest that this is due to an overestimate (96.74%) for this category, while for category 1–5 typhoons, the model tends to produce underestimations. As a whole, for all the 16,126 images, 57.76% (9314) are overestimated while 42.24% (6812) are underestimated. The overall RMSE is 12.69 knot (also see Table 4 and Figure 3a). Meanwhile, the overall MARE is 19.78% which is resulted primarily from tropical storms and depressions, when they are removed from the dependent tests, the overall MARE deceases to 12.55% for all category 1–5 typhoons.

Table 4.
Dependent tests of the model by dividing the cyclones into seven groups according to Saffir–Simpson Scale. The number and ratio of underestimated or overestimated images are listed in the table.
4.2. Independent Tests Results
The developed model is run on 52 cases (see Figure 6 and Table 1 for detail number and percent of images in each group) from the 2008 to 2009 typhoon season for validation. Of the 52 cases, five are tropical depressions, 23 are tropical storms, five are typhoons, six are moderate typhoons, three are severe typhoons, five are super typhoons, and fvie are extreme typhoons. Because this 52 cases are not included in training the model, the results of the independent tests are indicative of what we can expect when this model is applied into real-time estimation process. For the aim of comparison among groups with approximately same size. The 52 cases are divided into three groups by thresholds <60 knot, 60 to 120 knot and ≥120 to <100 knot, and 100 to 130 knot and ≥130 knot, according to their maximum intensity (hereinafter denoted as G1, G2 and G3, respectively), producing 690, 689 and 603 images in each group, respectively. After that, validations are performed independently. Figure 7 shows the accuracy of the model in estimating intensity of the 52 cases in three groups. Comparing to best-track intensities, the results indicate a high accuracy, especially for intense typhoons (G3). As shown, for G1 (Figure 7a), more errors exist as there are more images on which TCs are weak and the model tends to overestimate their intensities. For G2 (Figure 7b), the model performs better with an R2 of 0.66, while for G3 (Figure 7c), in which the typhoons are quite strong, the model can estimate intensities with a much higher accuracy (R2 of 0.84). Table 5 lists statistics produced in testing the three groups. The mean of RMSE, MAE, bias, MARE and R2 are 12.01 knot, 9.50 knot, 2.00 knot, 21.67%, and 0.77 for the overall cases, respectively.
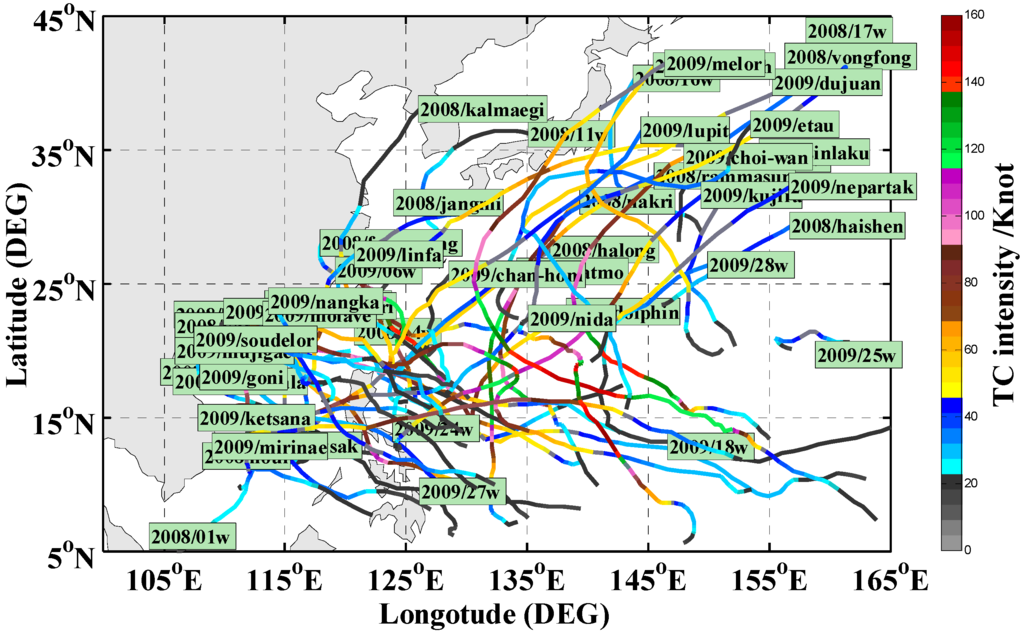
Figure 6.
Same as Figure 1 but for cases from 2008 to 2009 typhoon season used in the independent tests. The green boxes represents the name of the cyclones.
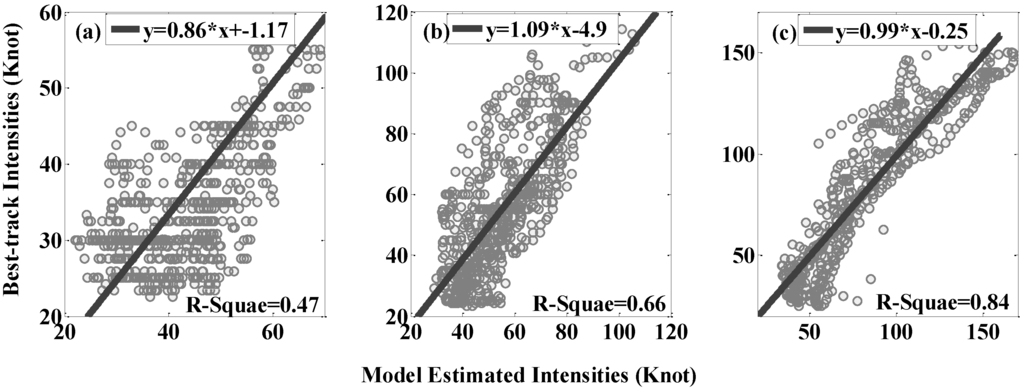
Figure 7.
Scatterplots of the model estimated vs. best-track intensities for groups in which the maximum intensity: (a) <60 knot; (b) 60–120; and (c) >120 knot in the independent tests. The solid lines indicates the goodness of the regression of the scatterplot, which are obtained using the least square method.

Table 5.
Statistics produced in the independent tests.
Figure 8 shows the intensity sequences of TCs in the three groups. The model estimated intensities sequence for G3 (Figure 8c) shows high consistence with the best-track over time. Meanwhile, more errors could be found for weak typhoons TCs as expected (top panel in Figure 8 for G1). Figure 8 also indicates that variations of the BTs in satellite images do not necessarily produce changes in intensities.
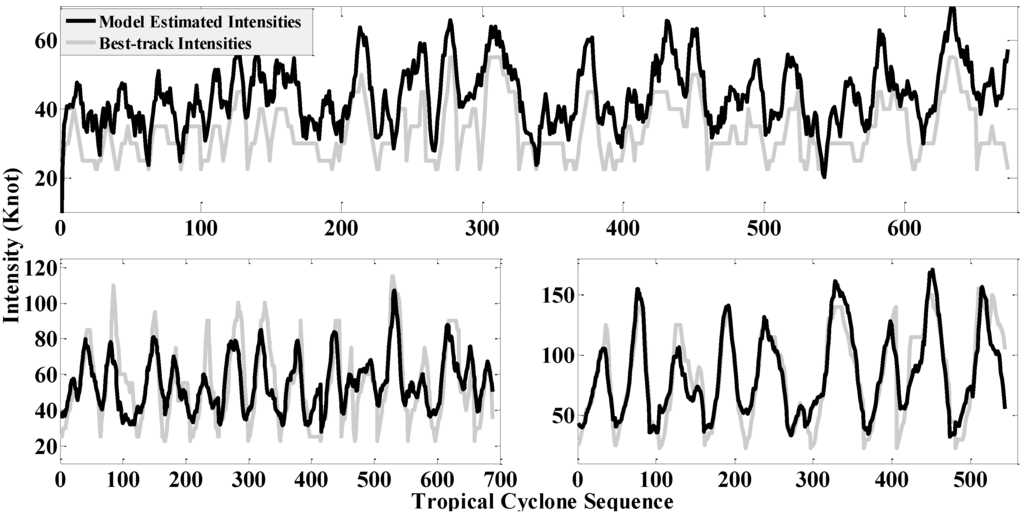
Figure 8.
The sequences of the intensity of the 52 typhoons divided into three groups. The gray line indicates the best-track intensities and the black line represents the model estimated ones.
4.3. Case Analysis of Extreme Typhoon Melor (No. 202009)
For investigating factors that could be attributed as the source of errors, the extreme typhoon Melor—No. 202009—is selected to analyze further as it is the strongest case in the independent validation tests. Typhoon Melor (2009), known as Typhoon Quedan in the Philippines, was the second category 5 typhoon in 2009. It reached 150 knot (central pressure 911 hPa) at 12:00 p.m. UTC 4 October. Figure 9a shows an image of Melor (2009) reaching the peak intensity, and Figure 9b shows the intensity sequence estimated using the model. In addition, the model estimated intensity curve was 12-h smoothed (black solid line). The smoothed curve is consistent with the best-track curve (R2 of 0.91).
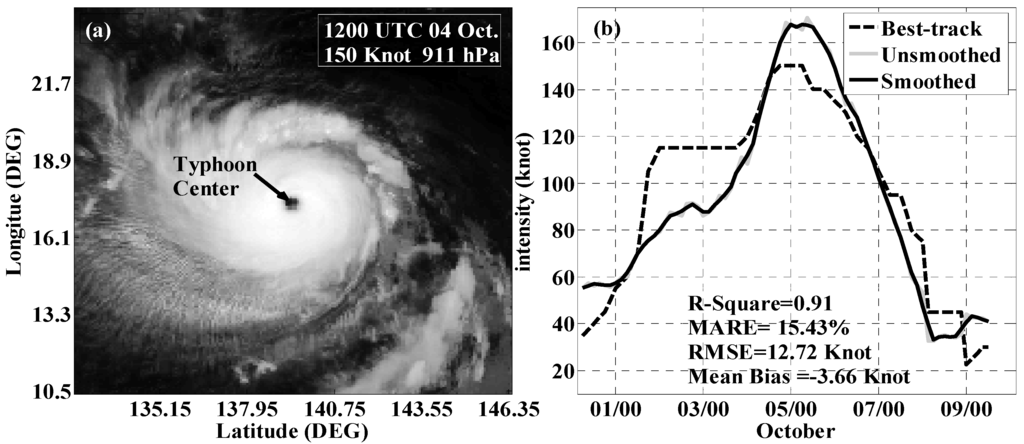
Figure 9.
(a) IR image of typhoon Melor (2009) at 12:00 p.m. UTC 4 October, the arrow indicates the typhoon center derived from JTWC best-track dataset; (b) The intensity sequence estimated using the model developed in this paper (gray solid curve), the curve that is 12-h smoothed (black solid curve), and that from best-track (black dashed curve).
The model underestimates intensity of Melor (mean bias of −3.66 Knot) in most cases while the peak intensity and intensities in the following 48 h are slightly overestimated. By examing the images within this 48-h time interval, we found that there is no L45 or U45 points on the radial profiles of most images. We doubt that assuming the location of L45 and U45 as the average values might introduce errors but further examination is in need. As described in the data section, since the existence of the “missing belt” in the Satellite images, which is filled by interpolation, we doubt that this also results in uncertain errors as it produces considerable errors in computing gradient vectors of the brightness temperatures. Nonetheless, further improvements are needed to perfect the model developed in this study. In addition, the patterns of these images are similar within the core region but vary substantially outside the core. Since the fixed radius (300 km) was adopted in computing deviation angle related parameters, it is possible that errors could be introduced by this fixed radius.
From best-track intensity curve, it is clear that typhoon Melor experienced a time period (approximately from 2 October to 4 October) of stable intensities. However, from the model estimated curve, the intensity see an steadily rising trend. Meanwhile, the intensities within this time period are observably underestimated. By examing both the best-track and the model estimated intensities, we found the intensity of Melor did remain stable from 0:00 UTC 2 Oct to 6:00 UTC 3 October as recorded by the original JTWC best-track, but it increased to 120 knot at 12:00 UTC Oct. 03 and later to 130 knot. Therefore, it is likely that the interpolation process of the best-track data produced such errors. To test this, the original best-track intensities and the IR images of corresponding time are used to perform the regression again. The comparison of statistics of the errors between the model regressed using the interpolated best-track and the original intensities are listed in Table 6. It is clear that results derived using the original best-track intensities are much better than that using the interpolated ones. Therefore, we are confident that the accuracy of the model could be improved if accurate and high temporal resolution historical typhoon intensities could be provided.

Table 6.
Comparison of the regressed model between using the original and interpolated best-track intensities.
Finally, Following Fetanat (2013) [20], a short comparison of statistics produced in validations of existing algorithms for estimating TC intensity was made, the technique introduced by Kossin (2007) [42], the improved DAV-T developed by Ritchie (2014) [25], the feature analogs in satellite imagery (FASI) proposed by Fetanat (2013) [20], and the developed TI index [26] are considered. The overall RMSE produced both in the dependent and independent tests of our models which were developed using the three-hourly interpolated and the original six-hourly archived intensities are used to compare with these techniques, results are listed in Table 7. It is noteworthy that in this paper we use the largest set of tropical cyclone cases into developing the model compared with the aforementioned techniques. The accuracy of our model, however, is on par with these techniques. Furthermore, it is obvious that the retrained model using the original three-hourly archived best-track intensities performs even better.

Table 7.
Comparison of the model estimated typhoon intensities with previous developed technique using the statistics RMSE.
5. Conclusions
Cloud-top brightness temperatures have long been correlated with surface wind structure of tropical cyclones [7,8,10,19,43]. More recently, several new techniques have been developed to estimate TC intensity from satellite measured brightness temperature in the northwestern pacific basin [3,16,20,25]. This paper presents an objective model for tropical cyclone intensity estimation over northwestern pacific Ocean using geostationary IR data.
The final obtained model is developed using tropical cyclone cases (16,126 three-hourly images) from the 1996 to 2009 Northwestern Pacific typhoon seasons, with a multiple linear regression technique. The independent validations are performed on 52 cases from 2008 to 2009 typhoon season. Before regression, significant signals and parameters of satellite IR images are extracted by several steps (as described in Section 3). The predicators that are eventually involved in the model include the square of deviation angle variance (DAV2), the new developed index DAO, the inner core mean brightness temperature (ICBT), the outer core brightness temperature (OCBT), the mean brightness temperature between FOT and U45 (AFOT-U45), the mean brightness temperature between CCT and U45 (AU45-CCT), the mean brightness temperature between L45 and FOT (AFOT-U45), and the slope between L45 and U45 (Sl45-u45).
The regressed model is shown in Section 4.1. Various tests are performed to statistically justify the accuracy of the developed model. From the dependent test, the model could perform with a reasonable accuracy (with a mean RMSE of 12.69 knot and mean absolute relative errors of 19.78% for the overall cases). However, the model generally overestimates weak cyclones while underestimates intense typhoons. In the independent tests, it is proven that the model could be regarded as a reference in determining TC intensities in real-time, especially for intense typhoons. By dividing the 52 cases in the independent tests into three groups of approximately equal size, we show that there more errors could be expected when the model is applied into deterring intensities of weak systems. In short, the model can estimate tropical cyclone intensities relatively accurate in the independent tests (a RMSE of 12.01 Knot).
In order to quantify the influence of the interpolation of the best-track intensities on the performance of the model, the original best-track intensities are adopted to perform the regression again (results are listed in Table 6 and Table 7). Noticeable improvements could be seen using original best-track intensities. Specifically, this produces a decrease in RMSE of around 2 Knot. Therefore, we have confidence that this model could be improved, providing an accurate and high temporal resolution historical intensity dataset. Many factors may be attributed as error sources and further studies are in need to improve the model.
In conclusion, the model developed in this paper provides another reference for tropical cyclone intensity estimation over North Western Pacific Ocean. Future works will focus mainly on the improvement of the model and the application of the model in estimating surface wind structure of typhoons from satellite images.
Acknowledgments
Tropical cyclone best-track data were downloaded from the Joint Typhoon Warning Center. Tropical cyclone satellite images were obtained from HURSAT and the JPL Tropical Cyclone Information System. This work is supported by Shandong Joint Fund for Marine Science Research Center (No. U1406404), the National High Technology Research and Development Program of China (863 Program, No. 2013AA09A505), and the National Basic Research Program of China (973 Program, No. 2012CB955600). Special appreciation is extended to Professor Elizabeth A. Ritchie (University of New South Wales) for explaining the DAV-T and for her insightful comments. The authors are grateful for valuable comments from Kenneth Knapp and other two anonymous reviewers.
Author Contributions
Yong Zhao and Chaofang Zhao conceived and designed the framework of this research and wrote the paper. The remaining two authors contributed to the experiments.
Conflicts of Interest
The authors declare that there are no research conflicts to report, but just provide another reference for related research.
Abbreviations
The following abbreviations are used in this manuscript:
| TC | Tropical Cyclone |
| BT | Brightness Temperature |
| NWP | Northwestern Pacific Ocean |
| TCIS | The JPL Tropical Cyclone Information System |
| GMS | Geostationary Meteorological Satellite |
| IRBT | Infrared Brightness Temperature |
| MSW | Maximum Sustained Wind |
| JTWC | National Joint Typhoon Warning Center |
| DAV | The Variance of Deviation Angles |
| DAV-T | The Deviation-Angle Variance Technique |
| P_MDA | The Probability Density of Mean Deviation Angle |
| IQR | Interquartile Range of the DAs |
| ICBT | The Inner Core Average BT |
| OCBT | The Outer Core Average BT |
| MIBT (MABT) | Azimuthally Averaged Minimum (Maximum) BT within the Outer Core |
| CCT | The Radial Location of the Coldest Cloud |
| FOT | The Radial Location of the First Overshooting Top |
| L45 (U45) | The Lower (Upper) Extent of the Inner Eyewall |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| MARE | Mean Absolute Relative Error |
References
- Tang, D.L.; Sui, G.; Lavy, G.; Pozdnyakov, D.; Song, Y.T.; Switzer, A.D. Typhoon Impact and Crisis Management; Springer: New York, NY, USA, 2014. [Google Scholar]
- Liu, C.-C.; Shyu, T.-Y.; Chao, C.-C.; Lin, Y.-F. Analysis on typhoon longwang intensity changes over the ocean via satellite data. J. Mar. Sci. Technol. 2009, 17, 23–28. [Google Scholar]
- Zhuge, X.-Y.; Guan, J.; Yu, F.; Wang, Y. A new satellite-based indicator for estimation of the western North Pacific tropical cyclone current intensity. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5661–5676. [Google Scholar] [CrossRef]
- Velden, C.S.; Goodman, B.M.; Merrill, R.T. Western North Pacific tropical cyclone intensity estimation from noaa polar-orbiting satellite microwave data. Mon. Weather Rev. 1991, 119, 159–168. [Google Scholar] [CrossRef]
- Brueske, K.F.; Velden, C.S. Satellite-based tropical cyclone intensity estimation using the NOAA-KLM series Advanced Microwave Sounding Unit (AMSU). Mon. Weather Rev. 2003, 131, 687–697. [Google Scholar] [CrossRef]
- Aberson, S.D.; Black, M.L.; Black, R.A.; Cione, J.J.; Landsea, C.W.; Marks, F.D., Jr.; Burpee, R.W. Thirty years of tropical cyclone research with the NOAA P-3 aircraft. Bull. Am. Meteorol. Soc. 2006, 87, 1039–1055. [Google Scholar] [CrossRef]
- Kossin, J.P.; Knaff, J.A.; Berger, H.I.; Herndon, D.C.; Cram, T.A.; Velden, C.S.; Murnane, R.J.; Hawkins, J.D. Estimating hurricane wind structure in the absence of aircraft reconnaissance. Weather Forecast. 2007, 22, 89–101. [Google Scholar] [CrossRef]
- Knaff, J.A.; Longmore, S.P.; DeMaria, R.T.; Molenar, D.A. Improved tropical-cyclone flight-level wind estimates using routine infrared satellite reconnaissance. J. Appl. Meteorol. Climatol. 2015, 54, 463–478. [Google Scholar] [CrossRef]
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L.; Zehr, R.; Olander, T.; Mayfield, M.; Guard, C.C.; Lander, M.; Edson, R. The dvorak tropical cyclone intensity estimation technique: A satellite-based method that has endured for over 30 years. Bull. Am. Meteorol. Soc. 2006, 87, 1195–1210. [Google Scholar] [CrossRef]
- Chao, C.-C.; Liu, G.-R.; Liu, C.-C. Estimation of the upper-layer rotation and maximum wind speed of tropical cyclones via satellite imagery. J. Appl. Meteorol. Climatol. 2011, 50, 750–766. [Google Scholar] [CrossRef]
- Sadler, J.C. Tropical cyclones of the Eastern North Pacific as revealed by TIROS observations. J. Appl. Meteorol. 1964, 3, 347–366. [Google Scholar] [CrossRef]
- Hubert, L.F.; Timchalk, A. Estimating hurricane wind speeds from satellite pictures. Mon. Weather Rev. 1969, 97, 382–383. [Google Scholar] [CrossRef]
- Dvorak, V.F. Tropical Cyclone Intensity Analysis Using Satellite Data; US Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service: Washington, DC, USA, 1984.
- Dvorak, V.F. Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Weather Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Velden, C.S.; Olander, T.L.; Zehr, R.M. Development of an objective scheme to estimate tropical cyclone intensity from digital geostationary satellite infrared imagery. Weather Forecast. 1998, 13, 172–186. [Google Scholar] [CrossRef]
- Piñeros, M.F.; Ritchie, E.A.; Tyo, J.S. Estimating tropical cyclone intensity from infrared image data. Weather Forecast. 2011, 26, 690–698. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S.; Turk, M.A. Development of the Advanced Objective Dvorak Technique (AODT)—Current progress and future directions. In Proceedings of the 25th Conference on Hurricanes and Tropical Meteorology, San Diego, CA, USA, 29 April–3 May 2002.
- Olander, T.L.; Velden, C.S. The advanced dvorak technique: Continued development of an objective scheme to estimate tropical cyclone intensity using geostationary infrared satellite imagery. Weather Forecast. 2007, 22, 287–298. [Google Scholar] [CrossRef]
- Mueller, K.J.; DeMaria, M.; Knaff, J.; Kossin, J.P.; Vonder Haar, T.H. Objective estimation of tropical cyclone wind structure from infrared satellite data. Weather Forecast. 2006, 21, 990–1005. [Google Scholar] [CrossRef]
- Fetanat, G.; Homaifar, A.; Knapp, K.R. Objective tropical cyclone intensity estimation using analogs of spatial features in satellite data. Weather Forecast. 2013, 28, 1446–1459. [Google Scholar] [CrossRef]
- Piñeros, M.F.; Ritchie, E.A.; Tyo, J.S. Objective measures of tropical cyclone structure and intensity change from remotely sensed infrared image data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3574–3580. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Valliere-Kelley, G.; Piñeros, M.F.; Tyo, J.S. Tropical cyclone intensity estimation in the north Atlantic basin using an improved deviation angle variance technique. Weather Forecast. 2012, 27, 1264–1277. [Google Scholar] [CrossRef]
- Piñeros, M.F.; Ritchie, E.; Tyo, J.S. Detecting tropical cyclone genesis from remotely sensed infrared image data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 826–830. [Google Scholar] [CrossRef]
- Rodríguez-Herrera, O.G.; Wood, K.M.; Dolling, K.P.; Black, W.T.; Ritchie, E.; Tyo, J.S. Automatic tracking of pregenesis tropical disturbances within the deviation angle variance system. IEEE Geosci. Remote Sens. Lett. 2015, 12, 254–258. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Wood, K.M.; Rodríguez-Herrera, O.G.; Piñeros, M.F.; Tyo, J.S. Satellite-derived tropical cyclone intensity in the north pacific ocean using the deviation-angle variance technique. Weather Forecast. 2014, 29, 505–516. [Google Scholar] [CrossRef]
- Liu, C.-C.; Liu, C.-Y.; Lin, T.-H.; Chen, L.-D. A satellite-derived typhoon intensity index using a deviation angle technique. Int. J. Remote Sens. 2015, 36, 1216–1234. [Google Scholar]
- Hristova-Veleva, S.M. Using the JPL tropical cyclone information system for research and applications. In Proceedings of the 28th Conference on Hurricanes and Tropical Meteorology, Orlando, FL, USA, 28 April–2 May 2008.
- Knosp, B.W. The JPL tropical cyclone information system: Design and implementation. In Proceedings of the 28th Conference on Hurricanes and Tropical Meteorology, Orlando, FL, USA, 28 April–2 May 2008.
- Knosp, B.; Ao, C.; Chao, Y.; Dang, V.; Garay, M.; Haddad, Z.; Hristova-Veleva, S.; Lambrigtsen, B.; Li, P.; Park, K. The JPL Tropical Cyclone Information System: Data and Tools for Researchers; AGU: San Francisco, CA, USA, 2008. [Google Scholar]
- Knapp, K.R.; Kossin, J.P. New global tropical cyclone data set from ISCCP b1 geostationary satellite observations. J. Appl. Remote Sens. 2007, 1, 013505–013506. [Google Scholar]
- Chu, J.-H.; Sampson, C.R.; Levine, A.S.; Fukada, E. The joint typhoon warning center tropical cyclone best-tracks, 1945–2000. Available online: http://www.usno.navy.mil/JTWC (accessed on 9 March 2016).
- Zhao, H.; Wu, L.; Wang, R. Decadal variations of intense tropical cyclones over the Western North Pacific during 1948–2010. Adv. Atmos. Sci. 2014, 31, 57–65. [Google Scholar] [CrossRef]
- Chan, J.C. Decadal variations of intense typhoon occurrence in the Western North Pacific. R. Soc. 2008, 464. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, L.; Zhou, W. Interannual changes of tropical cyclone intensity in the Western North Pacific. J. Meteorol. Soc. Jpn. 2011, 89, 243–253. [Google Scholar] [CrossRef]
- Knaff, J.A.; Longmore, S.P.; Molenar, D.A. An objective satellite-based tropical cyclone size climatology. J. Clim. 2014, 27, 455–476. [Google Scholar] [CrossRef]
- Croxford, M.; Barnes, G.M. Inner core strength of atlantic tropical cyclones. Mon. Weather Rev. 2002, 130, 127–139. [Google Scholar] [CrossRef]
- Weatherford, C.L.; Gray, W.M. Typhoon structure as revealed by aircraft reconnaissance. Part I: Data analysis and climatology. Mon. Weather Rev. 1988, 116, 1032–1043. [Google Scholar] [CrossRef]
- Weatherford, C.L.; Gray, W.M. Typhoon structure as revealed by aircraft reconnaissance. Part II: Structural variability. Mon. Weather Rev. 1988, 116, 1044–1056. [Google Scholar] [CrossRef]
- Sanabia, E.R.; Barrett, B.S.; Fine, C.M. Relationships between tropical cyclone intensity and eyewall structure as determined by radial profiles of inner-core infrared brightness temperature. Mon. Weather Rev. 2014, 142, 4581–4599. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S. Tropical cyclone convection and intensity analysis using differenced infrared and water vapor imagery. Weather Forecast. 2009, 24, 1558–1572. [Google Scholar] [CrossRef]
- Hazelton, A.T.; Hart, R.E. Hurricane eyewall slope as determined from airborne radar reflectivity data: Composites and case studies. Weather Forecast. 2013, 28, 368–386. [Google Scholar] [CrossRef]
- Kossin, J.; Knapp, K.; Vimont, D.; Murnane, R.; Harper, B. A globally consistent reanalysis of hurricane variability and trends. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Lajoie, F.; Walsh, K. A technique to determine the radius of maximum wind of a tropical cyclone. Weather Forecast. 2008, 23, 1007–1015. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).