The Application of TAPM for Site Specific Wind Energy Forecasting
Abstract
:1. Introduction
2. Observational and Forecast Model Data

2.1. Wind Data Analysis

| Region | Wind Speed Range * | Operational Features of Each Region |
|---|---|---|
| ~3 m/s | The wind speed that is sufficient for wind turbine to commence operation |
| ~3–15 m/s | The output power rises approximately as the cube of the wind speed following the wind power equation, Note that the increase in output tapers off as the wind approaches the rated output speed |
| 15–25 m/s | In this region, the power output remains constant despite further increases in wind speed. |
| 25 m/s | This curtailing of output is done deliberately to prevent structural damage to the turbine and typically involves both blade design and active control of blade pitch to “spill” the excess wind energy [25]. |
| >25 m/s | For wind speeds exceeding the cut-off speed, the turbine is shut down to prevent structural/mechanical damage to the turbine. |
3. Correction Methodology and Forecast Verification
4. Results
4.1. Assessment of TAPM for Wind Forecasting
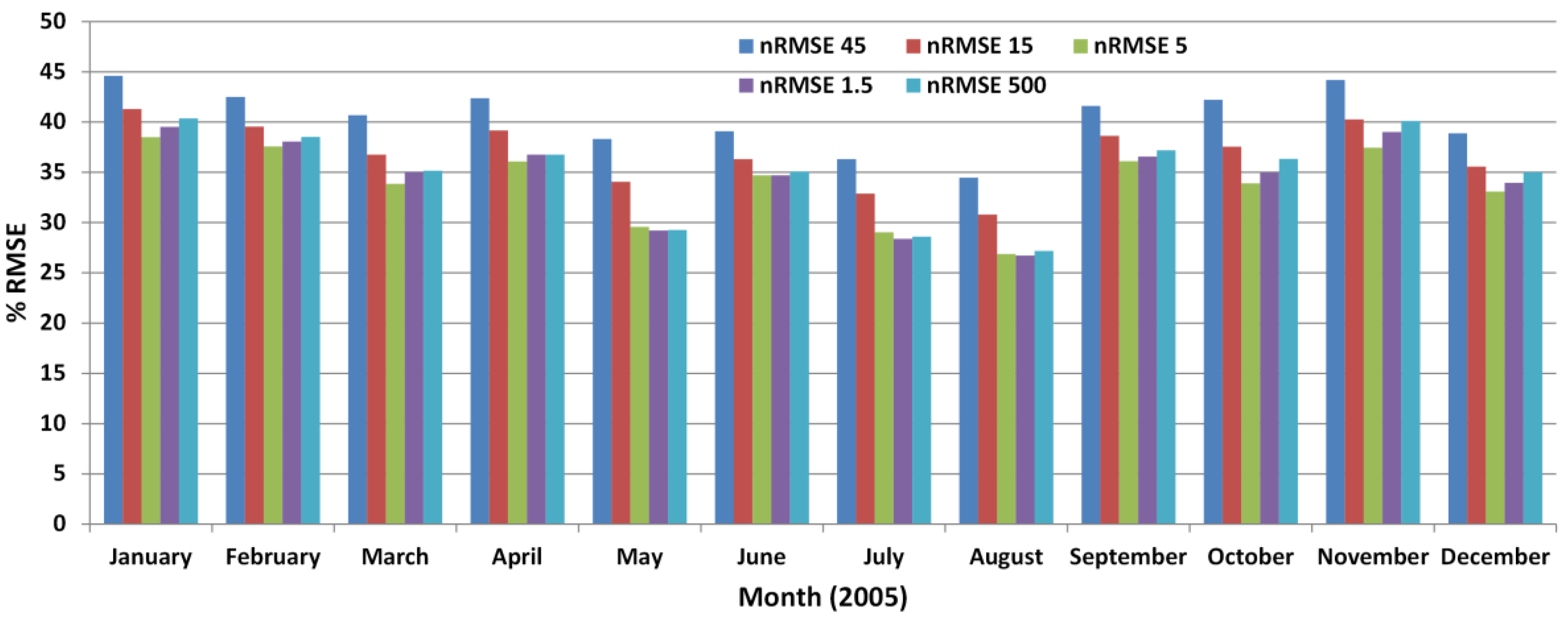
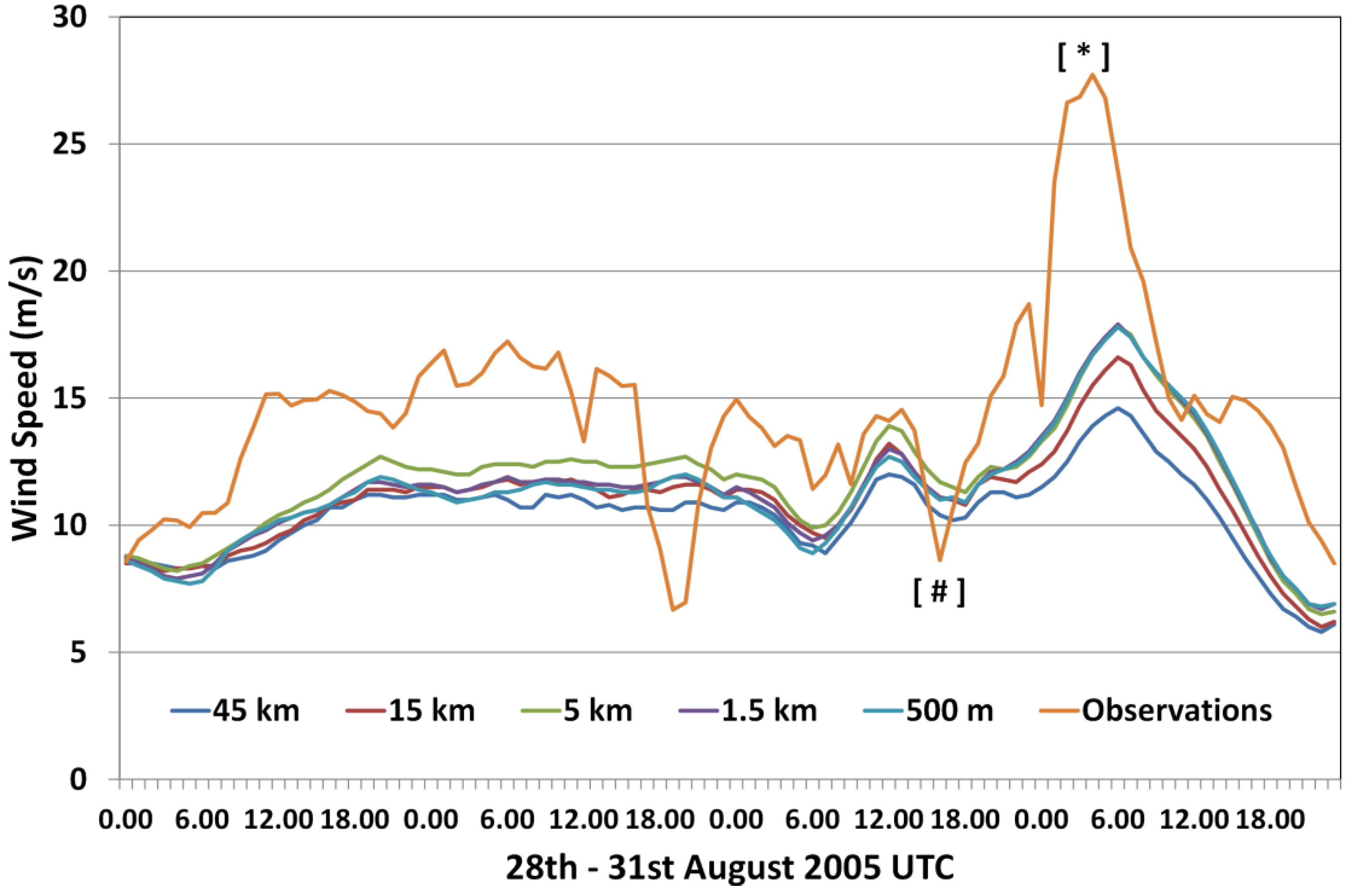

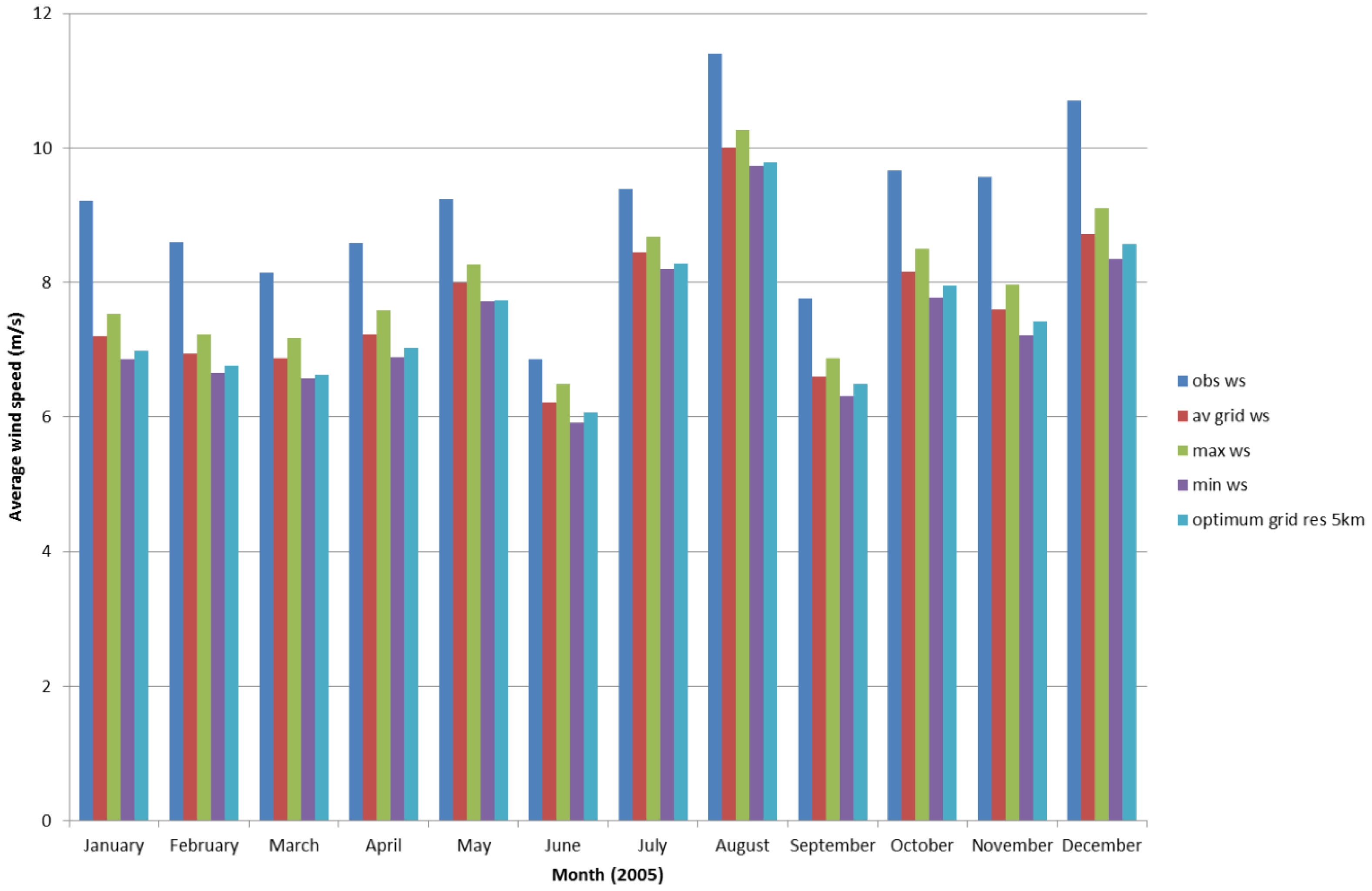
4.2. Correction Methodology Analysis
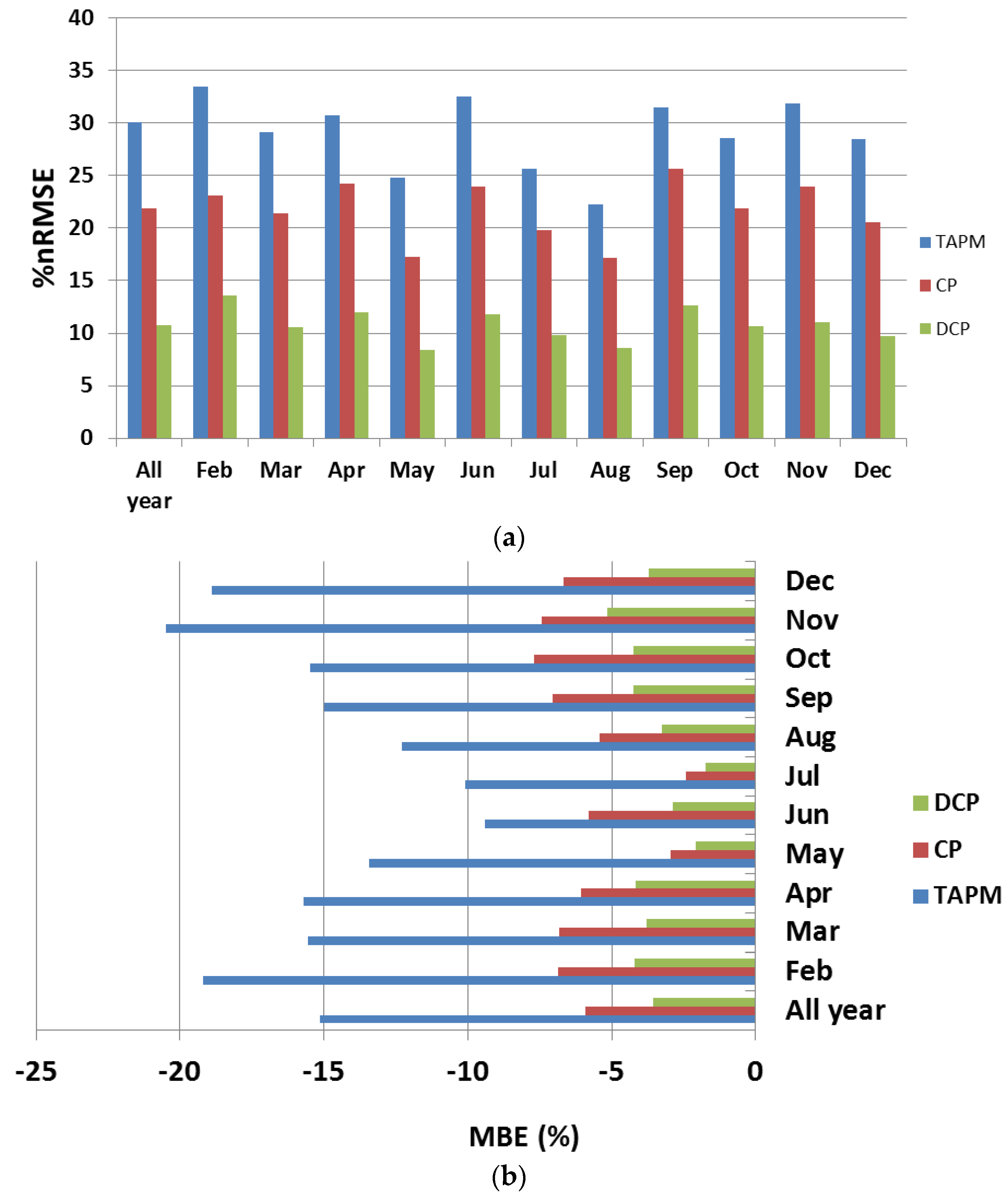
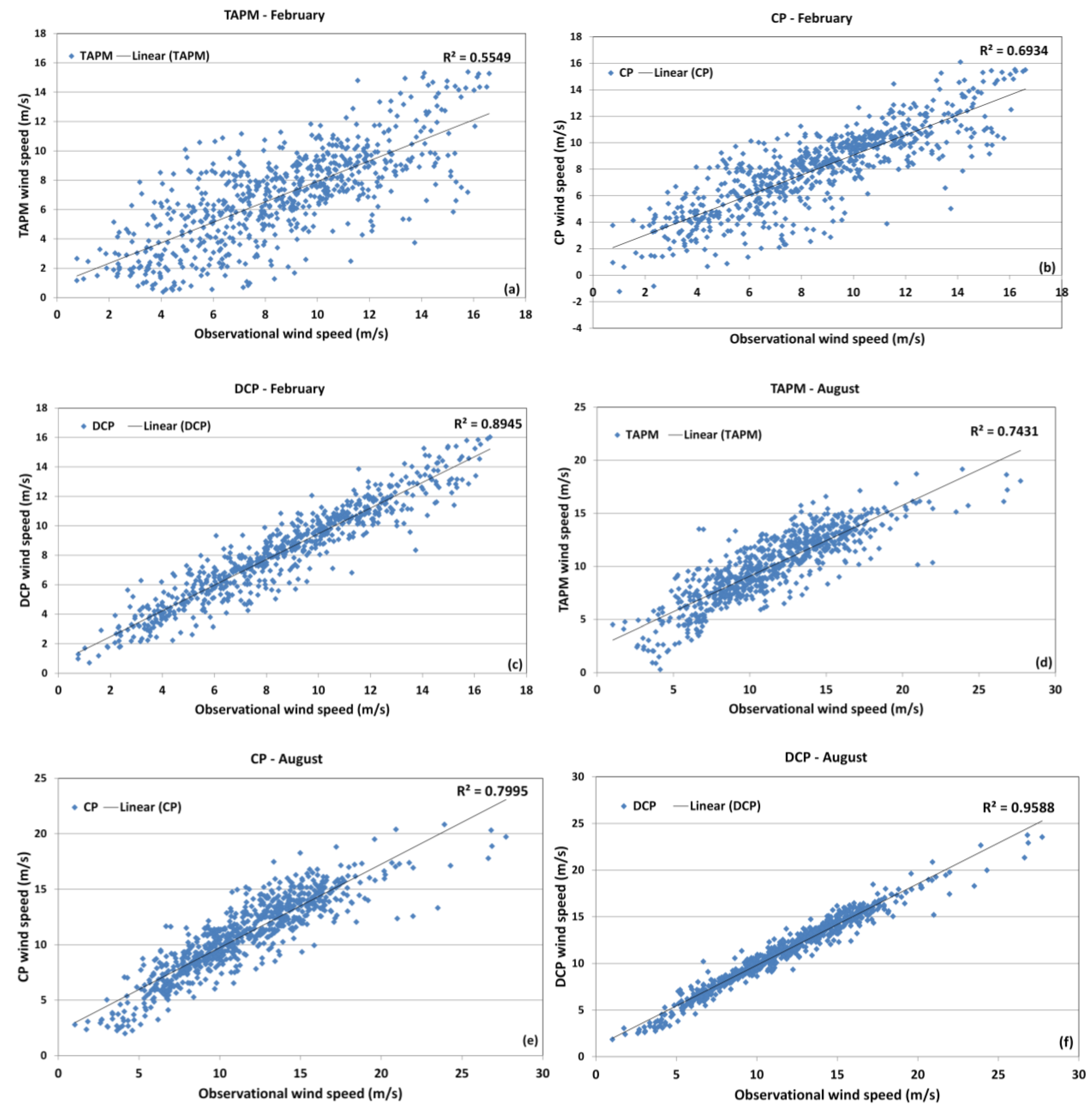
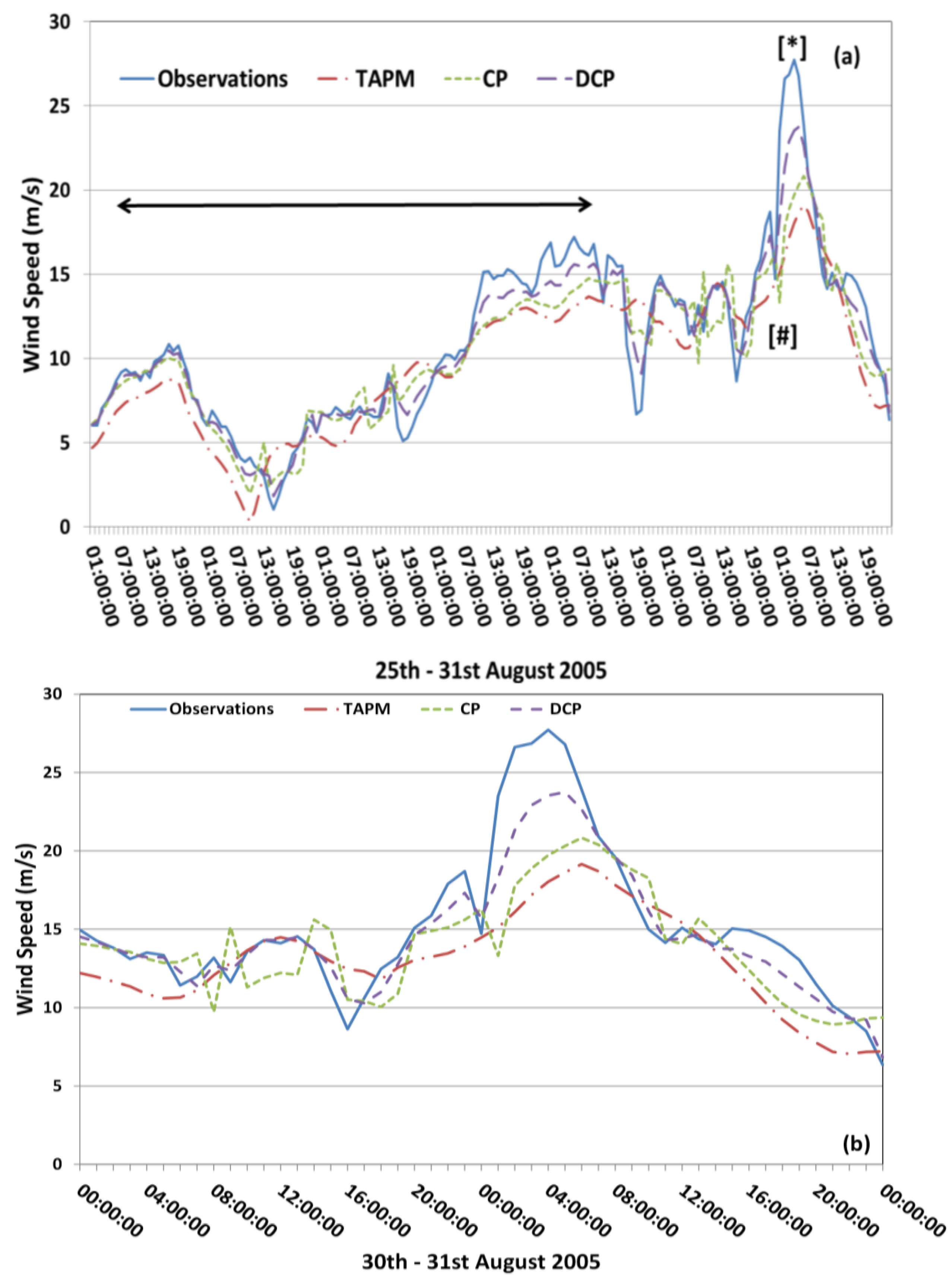
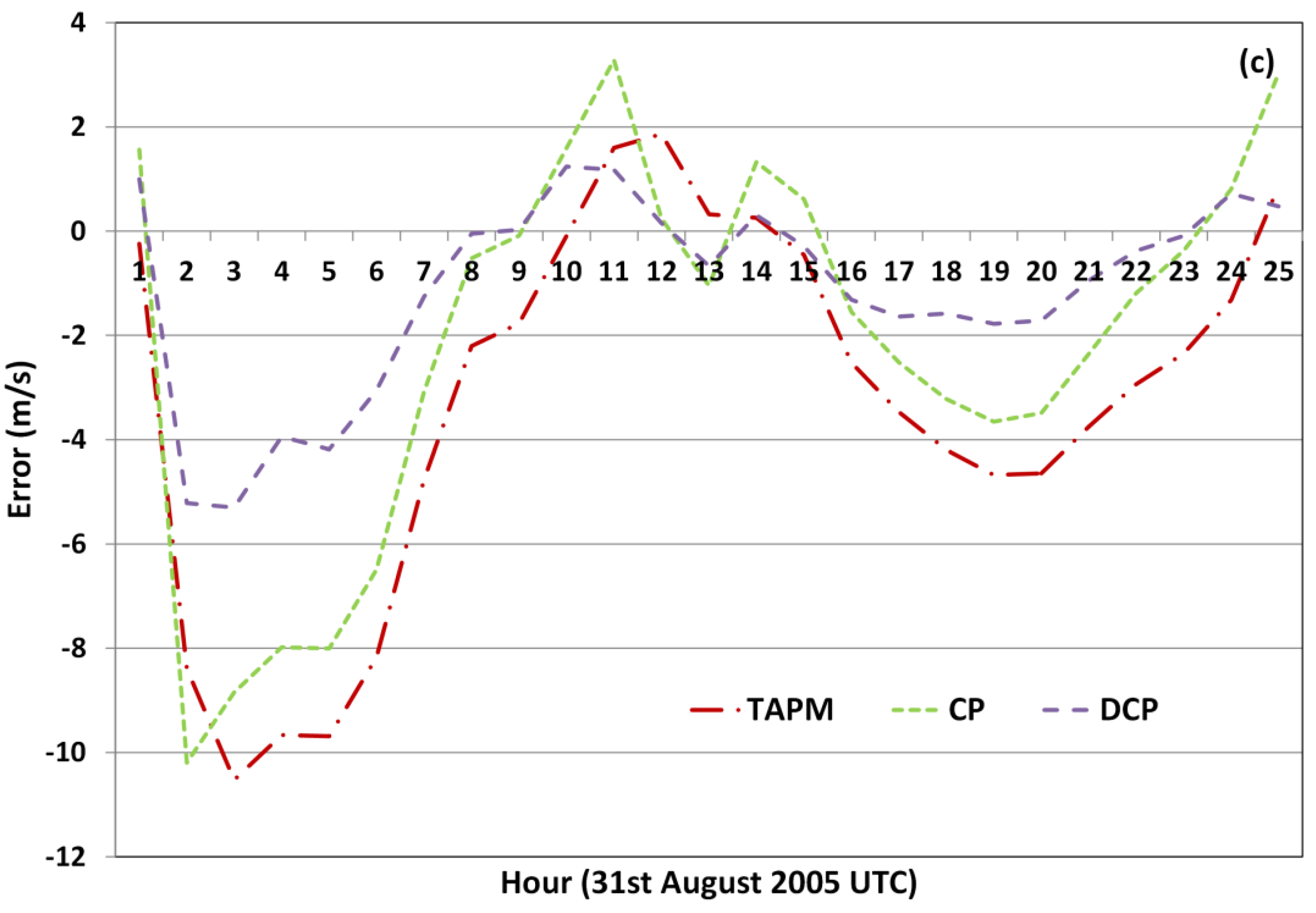

5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Feinberg, E.A.; Genethliou, D. Load Forecasting. In Applied Mathematics for Restructured Electric Power Systems: Optimization, Control, and Computational Intelligence; Chow, J.H., Wu, F.F., Momoh, J.J., Eds.; Spinger: New York, NY, USA, 2005; pp. 269–285. [Google Scholar]
- Sanchez, I. Short-term prediction of wind energy production. Int. J. Forecast. 2006, 22, 43–65. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Evaluation of global wind power. J. Geophys. Res. 2005, 11, D1211. [Google Scholar] [CrossRef]
- Wiser, R.; Bolinger, M. 2011 Wind Energy Technologies Market Report; Lawrence Berkeley Laboratories, US Department of Energy: Oak Ridge, TN, USA, August 2012. [Google Scholar]
- Möhrlen, C.; Jørgensen, J.U. A new algorithm for Upscaling and Short-term forecasting of windpower using Ensemble forecasts. In Proceedings of the 8th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Farms, Bremen, Germany, 14–15 October 2009.
- Wind Energy Forecasting, a Collaboration of the National Centre for Atmospheric Research (NCAR) and Xcel Energy. Available online: http://www.nrel.gov/docs/fy12osti/52233.pdf (accessed on 10 July 2015).
- Blonbou, R. Very Short Term Wind Power Forecasting with Neural Networks and Adaptive Bayesian learning. Renew. Energy 2011, 36, 1118–1124. [Google Scholar] [CrossRef]
- Marquis, M.; Wilczak, J.; Ahlstrom, M.; Sharp, J.; Stern, A.; Smith, J.C.; Calvert, S. Forecasting the Wind to Reach Significant Penetration Levels of Wind Energy. Bull. Am. Meteorol. Soc. 2011, 92, 1159–1171. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Junk, C.; Monache, L.D.; Alessandrini, S.; Cervone, G.; von Bremen, L. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z. 2015, 24, 361–379. [Google Scholar]
- Milligan, M.; Schwartz, M.; Wan, Y. Statistical Wind Power Forecasting Models: Results for U.S. Wind Farms; National Renewable Energy Laboratory: Golden, CO, USA, 2003; p. 17.
- Torres, J.L.; Garcia, A.; de Blas, M.; Francisco, A. Forecast of hourly averages wind speed with ARMA models in Navarre. Sol. Energy 2005, 70, 65–77. [Google Scholar] [CrossRef]
- Potter, C.W.; Negnevitsky, M. Very short-term wind forecasting for Tasmanian power generation. IEEE Trans. Power Syst. 2006, 21, 965–972. [Google Scholar] [CrossRef]
- Agrawal, M.; Boland, J.; Ridley, B. Analysis of wind farm output: Estimation of volatility using high frequency data. Environ. Model. Assess. 2013. [Google Scholar] [CrossRef]
- Vincent, C.; Bourke, W.; Kepert, J.D.; Chattopadhyay, M.; Ma, Y.; Steinle, P.J.; Tingwell, C.I.W. Verification of a high-resolution mesoscale NWP system. Aust. Meteorol. Mag. 2008, 57, 213–233. [Google Scholar]
- Huang, X.; Ma, Y.; Mills, G. Verification of Mesoscale NWP Forecasts of Abrupt Wind Changes; CAWCR Technical Report No. 008; The Centre for Australian Weather and Climate Research: Melbourne, Australia, 2008; p. 72. [Google Scholar]
- Giebel, G.; Landberg, L.; Kariniotakis, G.; Brownsword, R. State-of-the-Art on Methods and Software Tools for Short-Term Prediction of Wind Energy Production; EWEC: Madrid, Spain, 2003. [Google Scholar]
- Landberg, L.; Giebel, G.; Nielsen, H.A.; Nielsen, T.; Madsen, H. Short-term prediction—An overview. Wind Energy 2003, 6, 273–280. [Google Scholar] [CrossRef]
- Focken, U.; Lange, M. Final report—Wind power forecasting pilot project in Alberta, Canada. In Wind Power Forecasting PILOT Project; Energy & Meteo Systems: Oldenburg, Germany, 2008; p. 21. [Google Scholar]
- Jørgensen, J.; Möhrlen, C. AESO wind power forecasting PILOT project: Final project report. In Wind Power Forecasting PILOT Project; Weprog: Ebberup, Denmark, 2008; p. 102. [Google Scholar]
- Shi, J.; Guo, J.M.; Zheng, S.T. Evaluation of Hybrid Forecasting Approaches for Wind Speed and Power Generation Time Series. Renew. Sustain. Energy Rev. 2012, 16, 3471–3480. [Google Scholar] [CrossRef]
- Roaring 40s. Available online: http://www.hydro.com.au/energy/our-power-stations/wind-power (accessed on 18 November 2015).
- Hurley, P. TAPM V4. Part 1: Technical Description; CSIRO Marine and Atmospheric Research Paper No. 25; Commonwealth Scientific and Industrial Research Organisation: Canberra, Australia, 2008. [Google Scholar]
- Google Earth (Data SIO NOAA US Navy, NGA, GEBCO, Image CNES/Astrium). Available online: https://www.google.com/maps/@-40.729434,144.6883667,9879m/data=!3m1!1e3 (accessed on 18 January 2016).
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained, Theory, Design and Application; John Wiley & Sons Ltd.: West Sussex, UK, 2006. [Google Scholar]
- Kay, M.J.; Cutler, N.; Micolich, A.; MacGill, I.; Outhred, H. Emerging Challenges in Wind Energy Forecasting for Australia. Aust. Meteorol. Ocean. J. 2009, 58, 99–106. [Google Scholar]
- Murphy, A.H. What is a good forecast? An essay on the nature of goodness in weather forecasting. Weather Forecast. 1993, 8, 281–293. [Google Scholar] [CrossRef]
- Murphy, A.H. The coefficients of correlation and determination as measures of performance in forecast verification. Weather Forecast. 1995, 10, 681–688. [Google Scholar] [CrossRef]
- Woodcock, F.; Engel, C. Operational Consensus Forecasts. Weather Forecast. 2005, 20, 101–111. [Google Scholar] [CrossRef]
- Kay, M.; MacGill, I. Improving NWP Forecasts for the Wind Energy Sector. In Weather Matters for Energy; Springer: New York, NY, USA, 2014. [Google Scholar]
- Wonnacott, T.H.; Wonnacott, R.J. Introductory Statistics; Wiley: New York, NY, USA, 1977; p. 650. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977; p. 688. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kay, M. The Application of TAPM for Site Specific Wind Energy Forecasting. Atmosphere 2016, 7, 23. https://doi.org/10.3390/atmos7020023
Kay M. The Application of TAPM for Site Specific Wind Energy Forecasting. Atmosphere. 2016; 7(2):23. https://doi.org/10.3390/atmos7020023
Chicago/Turabian StyleKay, Merlinde. 2016. "The Application of TAPM for Site Specific Wind Energy Forecasting" Atmosphere 7, no. 2: 23. https://doi.org/10.3390/atmos7020023
APA StyleKay, M. (2016). The Application of TAPM for Site Specific Wind Energy Forecasting. Atmosphere, 7(2), 23. https://doi.org/10.3390/atmos7020023





