Statistical Modeling Approaches for PM₁₀ Prediction in Urban Areas; A Review of 21st-Century Studies

Abstract

PM₁₀ prediction has attracted special legislative and scientific attention due to its harmful effects on human health. Statistical techniques have the potential for high-accuracy PM₁₀ prediction and accordingly, previous studies on statistical methods for temporal, spatial and spatio-temporal prediction of PM₁₀ are reviewed and discussed in this paper. A review of previous studies demonstrates that Support Vector Machines, Artificial Neural Networks and hybrid techniques show promise for suitable temporal PM₁₀ prediction. A review of the spatial predictions of PM₁₀ shows that the LUR (Land Use Regression) approach has been successfully utilized for spatial prediction of PM₁₀ in urban areas. Of the six introduced approaches for spatio-temporal prediction of PM₁₀, only one approach is suitable for high-resolved prediction (Spatial resolution < 100 m; Temporal resolution ≤ 24 h). In this approach, based upon the LUR modeling method, short-term dynamic input variables are employed as explanatory variables alongside typical non-dynamic input variables in a non-linear modeling procedure.

1. Introduction

Ambient respirable particles [1], or particulate matter with a diameter of less than 10 µm (PM₁₀), have attracted special legislative and scientific attention due to their effects on human health. Particles with a diameter of less than 10 µm constitute the so-called inhalable fraction of particles, which are able to reach the bronchi-tracheal area [2]. PM₁₀ is made up of a variety of solid and liquid substances derived from natural sources (e.g., volcanoes, dust storms, forest and grassland fires, living vegetation, and marine salts) and human activities (e.g., central heating, industry, construction works, vehicular traffic, domestic heating, and incinerators) [2,3,4]. From a chemical point of view, a complex mixture of organic and inorganic carbon, metals (lead, arsenic, mercury, cadmium, chrome, nickel, and vanadium), nitrates, sulphates and phosphates are present in the particulates [2].

PM₁₀ has primary and secondary origins [5]. The major primary sources of PM₁₀ in urban areas are road traffic (e.g., carbonaceous compounds from exhaust emissions [6], re-suspension of road dust [7], and tyre abrasion [8]) and combustion processes. Secondary particles are mainly formed by the condensation of vapors, or chemical reactions such as atmospheric oxidation of SO₂ to H₂SO₄, and NO₂ to HNO₃ [9].

PM₁₀ concentration in urban areas is the result of a combination of regional background, urban and traffic concentrations [8,10,11,12,13]. For example, Figure 1 shows the source apportionment of PM₁₀ in Berlin.

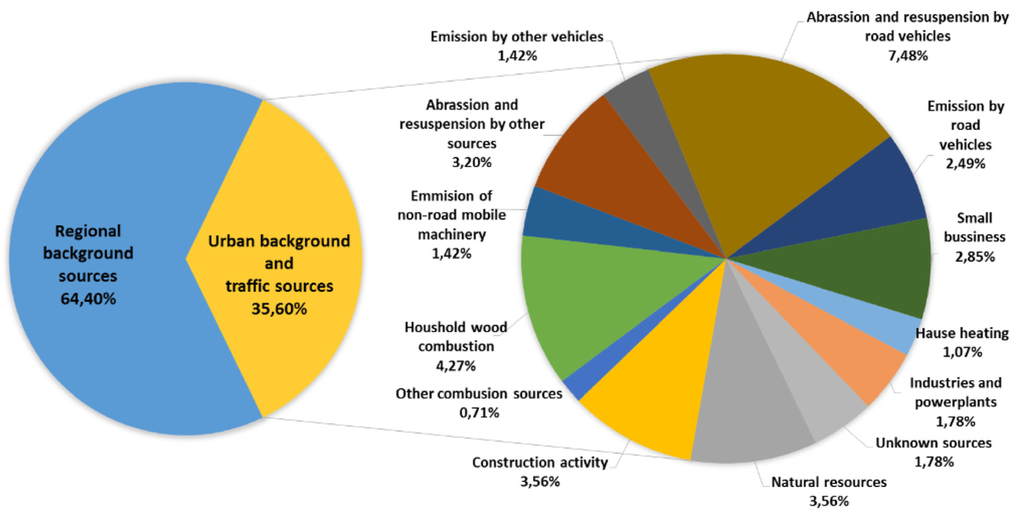
Figure 1. Source apportionment of PM₁₀ in Berlin [14].

Figure 1. Source apportionment of PM₁₀ in Berlin [14].

Particulate matter significantly affects aspects of atmospheric chemistry and air quality, such as dry and wet deposition, visibility, solar radiation, and cloud formation [5,15,16]. PM₁₀ also has a direct effect on health via inhalation [5]. Glinianaia et al. [17] and Šrám et al. [18] have reported the effects of particulate matter on infant birth weight. Samet et al. [19] found that an elevated PM₁₀ concentration can increase mortality rates the following day. In some studies, a significant relationship between health effects (mortality and morbidity) and elevated concentration of particulate matter was found (e.g., [20,21,22,23,24,25,26]). Moreover, it has been demonstrated by a number of epidemiological studies (e.g., [27,28,29]) that low concentrations of particulate matter can also have a large effect on human health. To address the PM₁₀ problem, the European Union has set two limit values on PM₁₀. According to these limits, the mean daily PM₁₀ concentration may not exceed 50 (µg/m³) more than 35 times per year, and the mean annual PM₁₀ concentration may not exceed 40 (µg/m³) [30].

Most major European urban areas experience severe short-term PM₁₀ episodes that are harmful to the environment and human health [31]. The public must be informed when high PM₁₀ concentration conditions are present [5]. Furthermore, administrations must attempt to reduce pollutant concentrations by limiting vehicular traffic on some days (e.g., alternative circulation of even and odd number plate alteration and “Sundays on foot”) [2,32], industrial emission restriction, and urban planning [33].

Long-term forecasting is employed for urban planning and design, as well as transportation networks, industrial sites and residential areas management, in order to minimize unacceptable risks to public health [31].

In order to diminish or prevent the risk of critical concentration levels, abatement actions (such as traffic reduction) should be planned at least one or two days in advance [31]. Therefore, a short-term forecasting platform must be developed and used as a rapid alert system to inform the public of harmful air pollution events, as well as to adapt air pollution control strategies [2,31,32,33,34]. When air pollution concentration exceeds imposed (limit) values, the use of forecasting models could inform decisions on the enforcement of regulations. This would prevent unnecessary inconvenience to the city's residents [2].

Spatial and temporal variations of PM₁₀ concentration are related to complex interactions among many parameters [5], and PM₁₀ prediction in urban areas is more difficult than the prediction of other air pollutants (e.g., NO₂) [35]. Therefore, despite the need for an accurate air quality forecasting model to alert the public and activate pollution control activities [31,34], often no effective action can be imposed during elevated PM₁₀ conditions because of non-existent or inadequate forecasting models [31].

There are two main approaches to the prediction of PM₁₀ in urban areas; mechanistic and statistical models.

A mechanistic (deterministic) approach involves numerically solving a set of differential equations. This approach does not require a large amount of measured data, but it does require a complete knowledge of pollutant sources, and temporal variation of the emission quantity, chemical composition of emissions, and physical processes in the atmosphere [36]. Detailed information about the source of pollutants and other parameters is often unavailable. These parameters must be estimated or simply ignored due to a lack of available information [37], and these simplifications increase the uncertainty of the results. One of the major properties of mechanistic models is causality. Mechanistic models predict more frequent events reasonably accurately, but they are not able to accurately predict extreme events [38], due to the complexity and inherent uncertainty associated with turbulent flow [38]. Because of the complex transportation and transformation of PM₁₀, the development of mechanistic models that can accurately predict the spatio-temporal variation of air pollutants is not easy [39], and these models are not capable of the accurate prediction of time series for short and medium time ranges. Therefore, these models are not suitable for planning and regulation [37,38].

Insufficient knowledge of pollutant sources and emission inventories, and inaccurate description of physico-chemical processes, can lead to significant bias and error in air quality estimations of mechanistic models [40,41,42,43]. However, assimilation and mapping techniques (e.g., bias correction, model output statistics, ensemble Kalman filtering, statistical approaches, geostatistical approaches) can improve the air quality estimations of mechanistic models (e.g., [44,45,46,47,48]). Some studies have generated high-resolution maps of air quality in urban areas by combining regional mechanistic and local dispersion models, which estimate regional (or background) and near-road concentrations, respectively (e.g., [49,50]). Furthermore, the strong physical and mechanical bases of mechanistic models should not be ignored. In the future, as the structure of mechanistic models improves, and computational power increases, these models will have more potential for accurate air quality predictions and short-term warnings. The current models are complex, time consuming and inaccurate [51]. Accordingly, a suitable methodology should be adopted for PM forecasting in urban areas [51].

To overcome the limitations of mechanistic models, statistical models are employed for air pollution predictions [37], and they have been successfully developed for the spatio-temporal prediction of air pollutants [39]. Statistical models are suitable for the description of the complex site-specific relationship between air pollutants and explanatory variables, and they often make predictions with a higher accuracy than mechanistic models [36]. However, one drawback of statistical models is that they do not consider the physics behind the data and consequently, the developed model for a study area is not applicable to other sites [5,36]. Fernando et al. [51] compared a mechanistic model with a statistical modeling approach for daily PM₁₀ forecasting in 2005 at Central Phoenix station in Phoenix, Arizona, USA. A Neural network was employed as the statistical model. The utilized mechanistic model was MODEL3-CMAQ, which consists of the MM5 (Mesoscale Meteorological Model) model for the simulation of meteorological parameters, the SMOKE (Sparse Matrix Operator Kernel Emission) model for the simulation of emission processing, and the CMAQ (Community Multi-scale Air Quality) model for the simulation of PM₁₀ concentration. The statistical model was found to be easier, faster, and more accurate than the mechanistic model, and it did not require costly emission inventories and computer resources.

Given the importance of PM₁₀ prediction in urban areas, this paper reviews the existing statistical approaches for PM₁₀ prediction (1-temporal, 2-spatial and 3-spatio-temporal prediction).

2. Search Strategy and Study Selection

We systematically identified and reviewed the statistical approaches to PM₁₀ prediction in urban areas. The Google Scholar database was searched for relevant literature published since 2000. Search terms included “Particulate matter”, “PM₁₀”, “urban area”, “city”, “prediction”, “forecasting”, “simulation”, “modeling”, “geostatistical” and “statistical” with different combinations. Titles and abstracts were read to select relevant articles, and the full texts were then downloaded. In addition, the bibliographies of the selected articles and relevant review papers were investigated to identify further reading. We only selected articles published in English. Most were published in peer-reviewed journals as full publications. Some conference papers and books were also selected. We selected articles in which the air pollutant, modeling approach and case study were outdoor PM₁₀, statistical approach and an urban area, respectively. The articles were then categorized according to the presentation of the detailed necessary information (e.g., input variables, modeling procedure, time scale of forecasting, and period of observations).

3. PM₁₀ Predictors in Statistical Models

Statistical modeling techniques require input (explanatory) variables. In this section, PM₁₀ predictors that have often been employed in PM₁₀ prediction studies are introduced, and their relation to PM₁₀ is briefly explained. High accuracy input data is very important in the prediction of PM₁₀. The utilization of the results of numerical weather forecast models as input variables in statistical PM₁₀ models can add some uncertainties to PM₁₀ predictions because of the uncertainties associated with numerical weather forecast models [33]. Consequently, the results of numerical weather forecasts are rarely used as the input variables of statistical models.

PM₁₀ values in preceding time steps are similar to the initial conditions for the PM₁₀ prediction in the following time steps [5], and they have often been considered as an explanatory variable in forecasting models. Including lagged PM₁₀ in the set of input variables is expected to improve modeling results [52]. Stadlober et al. [32] showed that lagged PM₁₀ is a more important variable than temporal or meteorological variables in the forecasting of PM₁₀ in urban areas.

Wind speed is a major meteorological parameter that determines the horizontal transport, dispersion and re-suspension of air pollutants. Low wind speed is associated with high PM₁₀ concentration [53,54,55,56,57]. Wind speed is a suitable indicator for the transport of PM₁₀; it has a direct relation to the atmospheric dispersion processes, and is a principal factor in the control of air pollution levels [58].

Wind direction can be related to the PM₁₀ concentration under non-homogeneous spatio-temporal PM₁₀ emission conditions [5], and it has a major role in the transport, dilution and re-suspension of PM₁₀ [53,57].

Solar radiation, cloud cover and air temperature are the effective parameters in the formation of secondary PM₁₀ [5,56,58]. In addition, high air temperature in an area leads to slow moving high-pressure atmosphere systems, clear and sunny skies, stable atmospheric condition with subsiding air, accumulation of air pollutants, and high PM₁₀ concentration [56]. Hence, temperature is considered as one of the strongest predictors of PM₁₀ concentration [56]. Furthermore, air temperature change is related to incoming solar radiation, and enhances turbulence kinetic energy, influencing the mixing layer height. A shallow mixing layer leads to an increase in PM₁₀ concentration at ground level. Perez and Reyes [59] observed that high PM₁₀ concentration occurs when the difference between maximum and minimum daily temperature in winter is large, and this temperature difference is an important meteorological parameter for the forecasting of daily maximum PM₁₀ concentration.

Motor vehicle exhaust is a source of PM₁₀ [60], and vehicular traffic re-suspends PM₁₀ [8]. Road transport is one of the major sources of primary PM₁₀, and annual average daily traffic and other derived traffic variables are often suitable parameters for incorporation into long-term models. However, these parameters may not always be suitable for short-term spatial modeling, as traffic has short-term variations and its variability is unpredictable [39].

When data on traffic flow and speed are not available, CO and NOx can be employed as surrogates for traffic variables [57]. Moreover, SO₂ and NOx are considered to be sources of secondary PM₁₀ concentration [61].

Land use patterns can also influence air pollution. For example, plants reduce PM₁₀ [62] and water bodies prevent PM₁₀ re-suspension [60]. Population density and meteorological parameters can influence the spatial pattern of PM₁₀ [60].

Short-term variations of city activities, such as traffic intensity, influence the short-term variation of PM₁₀ emission [56]. In addition, long-term variation of PM₁₀ (monthly or seasonally), which can be attributed to central heating (as winter months show higher PM₁₀ values than other months), can influence the long-term variations of PM₁₀ sources. Temporal variables (e.g., hour of day, day of week, month of year and day of year) can be used in the presentation of information on the intensity of PM₁₀ emission sources [58].

4. Temporal Prediction (Forecasting) of PM₁₀ in Urban Areas

In temporal prediction studies, the PM₁₀ concentration in one or more stations in the urban area is simulated and forecast. Different statistical techniques have been employed for the temporal prediction of PM₁₀ in urban areas, and they are introduced in this section.

4.1. Multi-Variate Linear Regression (MLR)

MLR has been widely used for PM₁₀ forecasting in urban areas. Although it has an accuracy problem due to linear representation of non-linear systems, and it is not able to capture extreme values (episodes) [37], it does not require continuous historical data [63]. Table 1 exhibits the main recent studies on the temporal prediction of PM₁₀ in different urban areas.

Table 1. Recent studies on PM₁₀ forecasting in one or more stations in urban areas, using MLR and ANN techniques.

PM10 Parameter	Method **	Forecasting Time-Scale	Case Study	Country	Inputs *	Results ***	Time Series	Ref.
Monthly	MLP	-****	One station in Janipur	India	TV, WS, WD, RH, Ta	RMSE = 7.9, R = 0.7	1993–1998	[64]
Daily	MLP	Mean and maximum one day ahead	One station in Lawer Fraster Valley	Canada	PM10, PM2.5, NO, CO, NO2, MVs and TVs	Mean PM10: R = 0.65	1995–1999	[65]
						Maximum PM10: R = 0.66
Daily	MLR	Mean and maximum one day ahead	One station in Lawer Fraster Valley	Canada	PM10, PM2.5, NO, CO, NO2, MVs and TVs	Mean PM10: R = 0.7	1995–1999	[65]
						Maximum PM10: R = 0.69
Daily	MLP	One-day	One station in Athens	Greece	Model 1: WS, DT, DOW, RH, WDI Model2: Lagged PM10, WS, DT, DOW, RH, WDI	Model 1: MAE = 16.0, RMSE = 21.2, R2 = 0.47	1 June 1999–31 May 2001	[66]
						Model 2: MAE = 12.6, RMSE = 16.9, R2 = 0.65
Daily	MLR	One-day	One station in Athens	Greece	Model 1: WS, DT, DOW, RH, WDI Model 2: Lagged PM10, WS, DT, DOW, RH, WDI	Model 1: MAE = 18.0, RMSE = 23.4, R2 = 0.34	1 June 1999–31 May 2001	[66]
						Model 2: MAE = 14.7, RMSE = 18.37, R2 = 0.6
Hourly	MLR	One hour	2 stations in Helsinki	Finland	TVs (e.g., CDAY and HOD), MVs, and traffic flow variables	R = 0.2–0.24	1996–1999	[35]
Hourly	MLP	One hour	2 stations in Helsinki	Finland	TVs (e.g., CDAY and HOD), MVs, and traffic flow variables	R = 0.31–0.42	1996–1999	[35]
Daily	RBF	3 days ahead	One station in Hong Kong	Hong Kong	PM10, SO2, NO, CO, NO2, NOx, WA; WD; SR; Ta	MAE = 12.5, RMSE = 16.3	2000	[67]
Daily	RBF	3 days ahead	One station in Hong Kong	Hong Kong	6 PCs of combination of PM10, SO2, NO, CO, NO2, NOx, WS, WD, SR and Ta	MAE = 16.4, RMSE = 21.4	2000	[67]
Daily	MLP	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.88 MAE = 8.59	1999–2002	[68]
Daily	PNN	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.89 MAE = 8.55	1999–2002	[68]
Daily	LL	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.90 MAE= 8.25	1999–2002	[68]
Daily	MLP	One-day ahead	10 Urban stations in 10 cities	Belgium	First 9-hourly PM10 in current day and daily forecasts of BLH, WS, Ta, CC, WD, DOW for one-day ahead	RMSE: about 12–24 R: about 0.67–0.81	1997–2001	[5]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	PM10 (t−24), PM10 (t−25), PM10 (t−26), WS, Ta, RH, SR, WD, DOW, SEA, SDAY, CDAY	R = 0.7–0.82	2001–2002	[58]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	PM10 (t−24), PM10 (t−25), PM10 (t−26)	R = 0.43–0.54	2001–2002	[58]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	Different set of variables were selected for the 4 stations	R = 0.65–0.83	2001–2002	[58]
Hourly	MLR	24 h ahead	4 stations in Athens	Greece	10 variables were selected	R = 0.55–0.59	2001-2002	[58]
Daily	MLP and MLR	Maximum one-day ahead	5 stations in Santiago	Chile	Some hourly PM10 in day t−1, and some meteorological observations and forecasts	Contingency table	2001–2004	[69]
Daily maximum	ELMAN	Two-days ahead	Five stations in Palermo	Italy	Hourly WS, WD, Ta, P	RMSE = 4.53–6.47 R = 0.93–0.97 MAE = 2.77–5.58	1 January 2003–31 December 2004	[2]
Daily	MLP	One day ahead	One station in Volos	Greece	PM10 (t−1), DOW; MOY, Tmax-Tmin, WS	R = 0.78 RMSE = 11.4	2001–2003	[56]
Daily	MLR	One day ahead	One station in Volos	Greece	PM10 (t−1), DOW; MOY, Tmax-Tmin, WS	R = 0.74 RMSE = 11.2	2001–2003	[56]
Daily	MLR	Daily	One station in Graz	Austria	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.69	2001–2007	[32]
Daily	MLR	Daily	One station in Klagenfurt	Austria	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.7	2003–2005	[32]
Daily	MLR	Daily	One station in Bolzano	Italy	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.55	2001–2006	[32]
Hourly	MLP	Hourly	Three traffic sites in Guangzhou	China	7 MVs: WS, Ta, P, WD, Rf, SR, RH 3 background parameters: PM10 (t−1), PM10 (t−2), PM10 (t−3) 2 TVs: DOW, HOD; TrV; 3 geographical parameters: DRC, SD, SAR	One hour ahead: MAPE = 12.9%; MAE = 15.5; RMSE = 20.1 R = 0.961 Some hours ahead: MAPE = 22.4%; MAE = 35; RMSE = 57.5; R = 0.912	2007	[70]
Hourly	MLR	Hourly	Three traffic sites in Guangzhou	China	WS, SR, RH, PM10 (t−1), PM10 (t−2), PM10 (t−3) TrV DRC	One hour ahead: R = 0.971 Some hours ahead: R= 0.894	2007	[70]
Hourly	MLP	One hour ahead	One station in Zagreb	Croatia	PM10(t−1), MVs, TVs	R = 0.72 MAE = 9.34 RMSE = 13.3	2004–2005	[36]
Hourly	MLP	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.65–0.76 RMSE = 13–32	2006–2008	[33]
Hourly	RBF	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.37–0.43 RMSE = 19.5–35	2006–2008	[33]
Hourly	PCRA	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.33–0.38 RMSE = 17.8–26.2	2006–2008	[33]
Hourly	MLP	24 h ahead	One station, Phoenix	Arizona	PM10, meteorological data	R2 = 0.38	2005	[51]
Daily maximum	MLP	One day ahead	8 stations in Santiago	Chile	PM10, meteorological information	MPAE = 14%–27%	2006–2011	[71]
Daily	MLP	Maximum one day ahead	9 stations in Tehran	Iran	PM10, NO, CO, MVs, TVs	R = 0.05–0.72	2001–2009	[72]
Hourly	MLP	2 h ahead	One station in London	UK	PM10 (t−2), WS (t−2), WD (t-2)	R2 = 0.98	January 2009	[73]
Daily	MLP	-	36 stations in Changsha	China	MVs	R2 = 0.89	April 2013–April 2014	[74]
Daily	MLR	-	36 stations in Changsha	China	MVs	R2 = 0.47	April 2013–April 2014	[74]

* Abbreviations of the parameters: BLH: Boundary layer height; CC: Cloud cover; CDAY: Cosine of hour of the day; DOW: Day of week; DT: Difference between daily maximum and minimum temperatures; DRC: Distance to road center; HOD: Hour of day; MOY: Month of year; MVs: Meteorological variables; P: Atmospheric pressure; PCs: Principal components; Rf: Rainfall; RH: Relative humidity; SD: Street direction; SAR: Street aspect ratio; SDAY: Sine of hour of the day; SEA: Binary seasonal index; SR: Solar radiation; Ta: Air temperature; Tmin: Minimum temperature; Tmax: Maximum temperature; TrV: Traffic volume; TVs: Temporal variables; WD: Wind direction; WDI: Wind direction index; WS: Wind speed; ** Abbreviations of the methods: ANN: Artificial Neural Networks; LL: Lazy Learning; MLP: Multi-variate Linear Regression; MLP: Multi Layer Perceptron; NPR: Non-Parametric Regression; PCRA: Principal component Regression Analysis, PNN: Pruned Neural Networks; RBF: Radial Basis Function; *** Unit of the presented RMSE and MAE values is µg/m³; **** Real time simulation has been performed.

Table 1. Recent studies on PM₁₀ forecasting in one or more stations in urban areas, using MLR and ANN techniques.

PM10 Parameter	Method **	Forecasting Time-Scale	Case Study	Country	Inputs *	Results ***	Time Series	Ref.
Monthly	MLP	-****	One station in Janipur	India	TV, WS, WD, RH, Ta	RMSE = 7.9, R = 0.7	1993–1998	[64]
Daily	MLP	Mean and maximum one day ahead	One station in Lawer Fraster Valley	Canada	PM10, PM2.5, NO, CO, NO2, MVs and TVs	Mean PM10: R = 0.65	1995–1999	[65]
						Maximum PM10: R = 0.66
Daily	MLR	Mean and maximum one day ahead	One station in Lawer Fraster Valley	Canada	PM10, PM2.5, NO, CO, NO2, MVs and TVs	Mean PM10: R = 0.7	1995–1999	[65]
						Maximum PM10: R = 0.69
Daily	MLP	One-day	One station in Athens	Greece	Model 1: WS, DT, DOW, RH, WDI Model2: Lagged PM10, WS, DT, DOW, RH, WDI	Model 1: MAE = 16.0, RMSE = 21.2, R2 = 0.47	1 June 1999–31 May 2001	[66]
						Model 2: MAE = 12.6, RMSE = 16.9, R2 = 0.65
Daily	MLR	One-day	One station in Athens	Greece	Model 1: WS, DT, DOW, RH, WDI Model 2: Lagged PM10, WS, DT, DOW, RH, WDI	Model 1: MAE = 18.0, RMSE = 23.4, R2 = 0.34	1 June 1999–31 May 2001	[66]
						Model 2: MAE = 14.7, RMSE = 18.37, R2 = 0.6
Hourly	MLR	One hour	2 stations in Helsinki	Finland	TVs (e.g., CDAY and HOD), MVs, and traffic flow variables	R = 0.2–0.24	1996–1999	[35]
Hourly	MLP	One hour	2 stations in Helsinki	Finland	TVs (e.g., CDAY and HOD), MVs, and traffic flow variables	R = 0.31–0.42	1996–1999	[35]
Daily	RBF	3 days ahead	One station in Hong Kong	Hong Kong	PM10, SO2, NO, CO, NO2, NOx, WA; WD; SR; Ta	MAE = 12.5, RMSE = 16.3	2000	[67]
Daily	RBF	3 days ahead	One station in Hong Kong	Hong Kong	6 PCs of combination of PM10, SO2, NO, CO, NO2, NOx, WS, WD, SR and Ta	MAE = 16.4, RMSE = 21.4	2000	[67]
Daily	MLP	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.88 MAE = 8.59	1999–2002	[68]
Daily	PNN	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.89 MAE = 8.55	1999–2002	[68]
Daily	LL	One day	One station in Milan	Italy	PM10, SO2, Ta, P	R = 0.90 MAE= 8.25	1999–2002	[68]
Daily	MLP	One-day ahead	10 Urban stations in 10 cities	Belgium	First 9-hourly PM10 in current day and daily forecasts of BLH, WS, Ta, CC, WD, DOW for one-day ahead	RMSE: about 12–24 R: about 0.67–0.81	1997–2001	[5]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	PM10 (t−24), PM10 (t−25), PM10 (t−26), WS, Ta, RH, SR, WD, DOW, SEA, SDAY, CDAY	R = 0.7–0.82	2001–2002	[58]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	PM10 (t−24), PM10 (t−25), PM10 (t−26)	R = 0.43–0.54	2001–2002	[58]
Hourly	MLP	24 h ahead	4 stations in Athens	Greece	Different set of variables were selected for the 4 stations	R = 0.65–0.83	2001–2002	[58]
Hourly	MLR	24 h ahead	4 stations in Athens	Greece	10 variables were selected	R = 0.55–0.59	2001-2002	[58]
Daily	MLP and MLR	Maximum one-day ahead	5 stations in Santiago	Chile	Some hourly PM10 in day t−1, and some meteorological observations and forecasts	Contingency table	2001–2004	[69]
Daily maximum	ELMAN	Two-days ahead	Five stations in Palermo	Italy	Hourly WS, WD, Ta, P	RMSE = 4.53–6.47 R = 0.93–0.97 MAE = 2.77–5.58	1 January 2003–31 December 2004	[2]
Daily	MLP	One day ahead	One station in Volos	Greece	PM10 (t−1), DOW; MOY, Tmax-Tmin, WS	R = 0.78 RMSE = 11.4	2001–2003	[56]
Daily	MLR	One day ahead	One station in Volos	Greece	PM10 (t−1), DOW; MOY, Tmax-Tmin, WS	R = 0.74 RMSE = 11.2	2001–2003	[56]
Daily	MLR	Daily	One station in Graz	Austria	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.69	2001–2007	[32]
Daily	MLR	Daily	One station in Klagenfurt	Austria	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.7	2003–2005	[32]
Daily	MLR	Daily	One station in Bolzano	Italy	Meteorological forecasts and TVs; PM10 (t−1) and Ta (t−1)	R2 = 0.55	2001–2006	[32]
Hourly	MLP	Hourly	Three traffic sites in Guangzhou	China	7 MVs: WS, Ta, P, WD, Rf, SR, RH 3 background parameters: PM10 (t−1), PM10 (t−2), PM10 (t−3) 2 TVs: DOW, HOD; TrV; 3 geographical parameters: DRC, SD, SAR	One hour ahead: MAPE = 12.9%; MAE = 15.5; RMSE = 20.1 R = 0.961 Some hours ahead: MAPE = 22.4%; MAE = 35; RMSE = 57.5; R = 0.912	2007	[70]
Hourly	MLR	Hourly	Three traffic sites in Guangzhou	China	WS, SR, RH, PM10 (t−1), PM10 (t−2), PM10 (t−3) TrV DRC	One hour ahead: R = 0.971 Some hours ahead: R= 0.894	2007	[70]
Hourly	MLP	One hour ahead	One station in Zagreb	Croatia	PM10(t−1), MVs, TVs	R = 0.72 MAE = 9.34 RMSE = 13.3	2004–2005	[36]
Hourly	MLP	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.65–0.76 RMSE = 13–32	2006–2008	[33]
Hourly	RBF	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.37–0.43 RMSE = 19.5–35	2006–2008	[33]
Hourly	PCRA	One hour ahead	4 stations in four urban areas	Cyprus	PM10 (t−24), PM10 (t−25), PM10 (t−26), MVs, TVs	R2 = 0.33–0.38 RMSE = 17.8–26.2	2006–2008	[33]
Hourly	MLP	24 h ahead	One station, Phoenix	Arizona	PM10, meteorological data	R2 = 0.38	2005	[51]
Daily maximum	MLP	One day ahead	8 stations in Santiago	Chile	PM10, meteorological information	MPAE = 14%–27%	2006–2011	[71]
Daily	MLP	Maximum one day ahead	9 stations in Tehran	Iran	PM10, NO, CO, MVs, TVs	R = 0.05–0.72	2001–2009	[72]
Hourly	MLP	2 h ahead	One station in London	UK	PM10 (t−2), WS (t−2), WD (t-2)	R2 = 0.98	January 2009	[73]
Daily	MLP	-	36 stations in Changsha	China	MVs	R2 = 0.89	April 2013–April 2014	[74]
Daily	MLR	-	36 stations in Changsha	China	MVs	R2 = 0.47	April 2013–April 2014	[74]

* Abbreviations of the parameters: BLH: Boundary layer height; CC: Cloud cover; CDAY: Cosine of hour of the day; DOW: Day of week; DT: Difference between daily maximum and minimum temperatures; DRC: Distance to road center; HOD: Hour of day; MOY: Month of year; MVs: Meteorological variables; P: Atmospheric pressure; PCs: Principal components; Rf: Rainfall; RH: Relative humidity; SD: Street direction; SAR: Street aspect ratio; SDAY: Sine of hour of the day; SEA: Binary seasonal index; SR: Solar radiation; Ta: Air temperature; Tmin: Minimum temperature; Tmax: Maximum temperature; TrV: Traffic volume; TVs: Temporal variables; WD: Wind direction; WDI: Wind direction index; WS: Wind speed; ** Abbreviations of the methods: ANN: Artificial Neural Networks; LL: Lazy Learning; MLP: Multi-variate Linear Regression; MLP: Multi Layer Perceptron; NPR: Non-Parametric Regression; PCRA: Principal component Regression Analysis, PNN: Pruned Neural Networks; RBF: Radial Basis Function; *** Unit of the presented RMSE and MAE values is µg/m³; **** Real time simulation has been performed.

Although Table 1 implies that MLR has been widely used for PM₁₀ forecasting, comparison between the results of MLR and other techniques demonstrates the weakness of the MLR approach. The stepwise input variable selection technique is often used in MLR for the determination of suitable explanatory variables for regression. Collinearity among the input parameters has often occurred in different MLR studies, and sometimes PCRA (Principal Component Regression Analysis) is used to overcome the problem of collinearity [33]. Another linear regression technique, which has been applied for temporal prediction of PM₁₀ in urban areas, is Lazy Learning (LL). LL is a local linear forecasting technique, which employs the local learning algorithm when a forecast is required. This technique showed better performance than MLP (Multi Layer Perceptron) and PNN (Pruned Neural Network) in a study on the daily forecasting of PM₁₀ in Milan, Italy [68].

4.2. Artificial Neural Networks

Artificial Neural networks (ANNs) have been used for the forecast of a wide range of pollutants and their concentrations at various time scales with very good results. Nagendra and Khare [75] pointed out that ANNs have recently become an alternative to conventional methods, and in the near future they will become an important tool for modeling air pollutant distribution. The most widely used non-linear techniques for the temporal prediction of PM₁₀ are neural networks with different structures (MLP: Multi Layer Perceptron; ELMAN; PNNs: Pruned Neural Networks; RBF: Radial Basis Function). MLP has been utilized more than the other structures of ANNs. Table 1 presents the major recent studies on the application of ANN for temporal prediction of PM₁₀ in urban areas.

The main advantages of ANNs are their application in cases in which a full theoretical approach is not available, incorporation of a large number of heterogeneous variables, implementation speed, and their ability to simulate complex problems with non-linear behavior [64,66]. In addition, the main advantages of an ANN forecasting system, compared to mechanistic atmospheric modeling systems, are that less input data and computational time are required (in operation mode) [5]. Moreover, ANN models, unlike stochastic models, do not require pre-assumptions about the data distribution [70].

Chaloulakou et al. [66] compared the MLR and ANN techniques for daily forecasting of PM₁₀ in one station in Athens, Greece. They evaluated the developed models (Model 1: without lagged PM₁₀; Model 2: with lagged PM₁₀ data as an input variable) for the forecasting of high PM₁₀ (>75 µg/m³). They demonstrated that the utilization of PM₁₀ as an input variable can significantly improve the forecasting results (See Table 2). In total, ANNs performed better than MLR in forecasting high PM₁₀ concentration events.

Table 2. Evaluation statistics for forecasting of high values (PM₁₀ > 75 µg/m³) using MLR and ANNs [66], reprinted by permission of the Air & Waste Management Association.

Evaluation Statistics	Abbreviation	Model 1: MLR	Model 1: ANN	Model 2: MLR	Model 2: ANN
Probability of Detection or Fraction of Correctly Forecasted exceedances	$PODorFCF=A/\left(A+B\right)$	0.91	0.93	0.93	0.93
False Alarm Rate	$FAR=C/\left(C+A\right)$	0.3	0.2	0.17	0.13
Threat Score or Success Index	$TSorSI=A/\left(A+B+C\right)$	0.65	0.75	0.78	0.82

A, B and C are the number of forecasted and observed exceedances of the limit value, number of observed exceedances but not forecasted, and number of forecasted exceedances but not observed, respectively.

Table 2. Evaluation statistics for forecasting of high values (PM₁₀ > 75 µg/m³) using MLR and ANNs [66], reprinted by permission of the Air & Waste Management Association.

Evaluation Statistics	Abbreviation	Model 1: MLR	Model 1: ANN	Model 2: MLR	Model 2: ANN
Probability of Detection or Fraction of Correctly Forecasted exceedances	$PODorFCF=A/\left(A+B\right)$	0.91	0.93	0.93	0.93
False Alarm Rate	$FAR=C/\left(C+A\right)$	0.3	0.2	0.17	0.13
Threat Score or Success Index	$TSorSI=A/\left(A+B+C\right)$	0.65	0.75	0.78	0.82

A, B and C are the number of forecasted and observed exceedances of the limit value, number of observed exceedances but not forecasted, and number of forecasted exceedances but not observed, respectively.

McKendry [65] reported the inability of MLR and MLP to make daily forecasts of extreme PM₁₀ concentrations in Lower Fraster Valley, Canada. Hence, he proposed the development of a more sophisticated training approach for ANNs, or the use of fuzzy or neuro-fuzzy techniques for the forecasting of extreme events [65]. Kukkonen et al. [35] employed MLR and MLP for the hourly forecasting of PM₁₀ in two stations in Helsinki, Finland. They pointed out that the developed ANN is only applicable for the period and location of the training dataset. Therefore, it cannot be applied to the analysis of different abatement scenarios for the future. This is one of the major limitations of ANNs. Kukkonen et al. [35] used a limited number of input variables and consequently, they concluded that the currently available ANN models are not applicable for future PM₁₀ prediction in urban areas. This conclusion seems incorrect. They could have incorporated the suitable explanatory variables into ANNs, which are able to consider the effects of different abatement scenarios on PM₁₀ concentration.

Better forecasting of high PM₁₀ concentration conditions is more important than that of normal PM₁₀ conditions [69]. Therefore, in some studies, a training dataset was designed so that the frequency distribution of its output variable (PM₁₀ concentration) was uniform, and the employment of this training dataset led to an appropriate model for the forecasting of high PM₁₀ concentration conditions (e.g., [5,69]). However, utilization of this training database reduces the accuracy of low and normal PM₁₀ concentration forecasts [69].

In some studies, the feature selection technique was employed for the selection of suitable variables for modeling, because the appropriate selection of the input variables may be more important than the type of utilized model [69]. For example, Chaloulakou et al. [66], Diaz-Robles et al. [34] and Paschalidou et al. [33] utilized stepwise regression analysis technique for input variables selection. Hooybergs et al. [5] plotted the inputs against output, divided the input variables into some bins, calculated the average of the bins, and determined the general behavior of the output against inputs for the investigation of the importance of the variables. Perez and Reyes [69] used “self-organizing maps”, and “mutual information and false nearest neighbor” for determination of suitable meteorological and hourly PM₁₀ variables, respectively. Grivas and Chaloulakou [58] used a genetic algorithm for input feature selection.

MLP models have some problems in dealing with high dimensional input variables (the curse of dimensionality) [67]. Another problem with the use of MLP is the local minima. Computational penalty for the mitigation of this problem is unavoidable [67]. Lu et al. [67] used PCA to decrease the dimension of the input variables and utilized RBF (Radial Basis Function) neural network for PM₁₀ forecasting in Hong Kong. They stated that the RBF has a lower computational cost than MLP. However, Paschalidou et al. [33] showed that the MLP performs better than RBF at the hourly forecasting of PM₁₀. In addition, they showed that the developed MLP model is suitable for extreme events forecasting in a case over Cyprus (POD = 0.68–0.71, FAR < 30%).

In total, ANNs have performed better than MLR. Inclusion of PM₁₀ in the input variables list improves the forecasting results significantly. Although MLP has been employed more than other ANN structures for PM₁₀ forecasting, the best ANN structure is still unknown. In addition, frequency distribution of PM₁₀ in the training dataset may highly influence the modeling results, and the utilization of PM₁₀ with uniform frequency distribution may lead to an appropriate model for the forecasting of extreme events. Therefore, combining two PM₁₀ forecasting models, developed using two training datasets with different frequency distributions, may lead to a suitable model for the forecasting of low to high PM₁₀ concentrations.

4.3. Other Techniques

Besides linear and ANN techniques, other techniques have occasionally been employed for temporal prediction of PM₁₀ in urban areas, obtaining results comparable with the two widely used techniques (MLR and ANNs). Some of these techniques are ARIMA (Auto-Regressive Integrated Moving Average), hybrid models, BRT (Boosted Regression Tree), CART (Classification And Regression Trees), GAM (Generalized Additive Model), QRM (Quantile Regression Model) fuzzy, and SVM (Support Vector Machines). Table 3 presents the recent studies on temporal PM₁₀ prediction using these techniques and their comparison with MLR and ANNs.

Table 3. Results of the application of other techniques for PM₁₀ forecasting, and their comparison with MLR and ANN techniques.

PM10 Parameter	Method **	Forecasting Time-Scale	Case Study	Country	Inputs *	Results ***	Time Series	Source
Hourly	GAM	-****	Four stations in Oslo	Norway	TVs, MVs, and traffic variables	R2 = 0.48–0.72	November 2001–May 2003	[76]
Daily	MLR	One-day	One station in Delhi	India	WS, RH, SR, Ta	R2 = 0.58	2000–2002	[37]
Daily	ARIMA	One-day	One station in Delhi	India	Daily PM10	R2 = 0.73	2000–2002	[37]
Daily	Hybrid MLR and ARIMA	One-day	One station in Delhi	India	WS, RH, SR, Ta, Daily PM10	R2 = 0.77	2000–2002	[37]
Daily	MLR	One-day	One station in Hong Kong	Hong Kong	WS, RH, SR, Ta	R2 = 0.54	2000–2001	[37]
Daily	ARIMA	One-day	One station in Hong Kong	Hong Kong	Daily PM10	R2 = 0.8	2000–2001	[37]
Daily	Hybrid MLR and ARIMA	One-day	One station in Hong Kong	Hong Kong	WS, RH, SR, Ta, Daily PM10	R2 = 0.84	2000–2001	[37]
Daily	MLR	Daily	One station in Thessaloniki	Greece	MVs	R = 0.297	1994–2000	[52]
						MAE = 49
	PCR					R = 0.235
						MAE = 34
	CART					R = 0.386
						MAE = 28
	MLP					R = 0.249
						MAE = 25
Daily	MLP	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.6, R2 = 0.78	2000–2006	[34]
Daily	MLR	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.4, R2 = 0.78	2000–2006	[34]
Daily	ARMAX	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.5, R2 = 0.77	2000–2006	[34]
Daily	Hybrid ARMAX-ANN	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 8.8, R2 = 0.98	2000–2006	[34]
Monthly	MLP	-	Some stations in Avilés	Spain	O3, CO, NO, NO2, SO2	R = 0.42	2006–2008	[77]
	SVM					R = 0.62
Daily	GAM	-	One station in Makkah	Saudi Arabia	SO2, NO, NO2, O3 and CO concentration (t); PM10 (t-1); WS, RH, WD, Rf, P and Ta (t)	R2 = 0.52	November 2011–July 2012	[78]
Monthly	MLP	-	Some stations in Gijón	Spain	O3, CO, NO, NO2, SO2	R = 0.62	2006–2008	[79]
	SVM					R = 0.8
Daily	MLR	-	One station in Makkah	Saudi Arabia	SO2,NOx and CO (t); PM10 (t-1); WS, RH and Ta (t)	R = 0.51	2012	[57]
	GAM					R = 0.6
	QRM					R = 0.81
	BRT					R = 0.54–0.61

* For abbreviation of the input parameters refer to Table 1; ** Abbreviation of the methods: ARIMA: Auto-Regressive Integrated Moving Average; BRT: Boosted Regression Tree;.CART: Classification And Regression Trees; GAM: Generalized Additive Model; QRM: Quantile Regression Model; SVM: Support Vector Machines; *** Unit of the presented RMSE and MAE values is µg/m³; **** Real time simulation has been performed.

Table 3. Results of the application of other techniques for PM₁₀ forecasting, and their comparison with MLR and ANN techniques.

PM10 Parameter	Method **	Forecasting Time-Scale	Case Study	Country	Inputs *	Results ***	Time Series	Source
Hourly	GAM	-****	Four stations in Oslo	Norway	TVs, MVs, and traffic variables	R2 = 0.48–0.72	November 2001–May 2003	[76]
Daily	MLR	One-day	One station in Delhi	India	WS, RH, SR, Ta	R2 = 0.58	2000–2002	[37]
Daily	ARIMA	One-day	One station in Delhi	India	Daily PM10	R2 = 0.73	2000–2002	[37]
Daily	Hybrid MLR and ARIMA	One-day	One station in Delhi	India	WS, RH, SR, Ta, Daily PM10	R2 = 0.77	2000–2002	[37]
Daily	MLR	One-day	One station in Hong Kong	Hong Kong	WS, RH, SR, Ta	R2 = 0.54	2000–2001	[37]
Daily	ARIMA	One-day	One station in Hong Kong	Hong Kong	Daily PM10	R2 = 0.8	2000–2001	[37]
Daily	Hybrid MLR and ARIMA	One-day	One station in Hong Kong	Hong Kong	WS, RH, SR, Ta, Daily PM10	R2 = 0.84	2000–2001	[37]
Daily	MLR	Daily	One station in Thessaloniki	Greece	MVs	R = 0.297	1994–2000	[52]
						MAE = 49
	PCR					R = 0.235
						MAE = 34
	CART					R = 0.386
						MAE = 28
	MLP					R = 0.249
						MAE = 25
Daily	MLP	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.6, R2 = 0.78	2000–2006	[34]
Daily	MLR	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.4, R2 = 0.78	2000–2006	[34]
Daily	ARMAX	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 28.5, R2 = 0.77	2000–2006	[34]
Daily	Hybrid ARMAX-ANN	One-day	One station in Temuco	Chile	WS, Tmin, Tmax, hourly maximum PM10	RMSE = 8.8, R2 = 0.98	2000–2006	[34]
Monthly	MLP	-	Some stations in Avilés	Spain	O3, CO, NO, NO2, SO2	R = 0.42	2006–2008	[77]
	SVM					R = 0.62
Daily	GAM	-	One station in Makkah	Saudi Arabia	SO2, NO, NO2, O3 and CO concentration (t); PM10 (t-1); WS, RH, WD, Rf, P and Ta (t)	R2 = 0.52	November 2011–July 2012	[78]
Monthly	MLP	-	Some stations in Gijón	Spain	O3, CO, NO, NO2, SO2	R = 0.62	2006–2008	[79]
	SVM					R = 0.8
Daily	MLR	-	One station in Makkah	Saudi Arabia	SO2,NOx and CO (t); PM10 (t-1); WS, RH and Ta (t)	R = 0.51	2012	[57]
	GAM					R = 0.6
	QRM					R = 0.81
	BRT					R = 0.54–0.61

* For abbreviation of the input parameters refer to Table 1; ** Abbreviation of the methods: ARIMA: Auto-Regressive Integrated Moving Average; BRT: Boosted Regression Tree;.CART: Classification And Regression Trees; GAM: Generalized Additive Model; QRM: Quantile Regression Model; SVM: Support Vector Machines; *** Unit of the presented RMSE and MAE values is µg/m³; **** Real time simulation has been performed.

ARMA (Auto Regressive Integrated Moving Average) and ARIMA (Auto Regressive Integrated Moving Average) [80] have been employed in some studies for PM₁₀ forecasting (e.g., see [34,37] in Table 3). However, these techniques have an accuracy problem due to the linear representation of non-linear systems, and are not able to capture extreme concentrations [34]. In addition, these methods require continuous historical data [63]. ARMA and ARIMA models have the capability to include external explanatory variables and in this case, they are named ARMAX and ARIMAX, respectively.

In some studies, the ARMA or ARIMA have been coupled with other methods such as ANNs, and the developed models are called hybrid models. In hybrid ANN and ARIMAX, an ARIMAX model is first developed, and then the ANN model is used to describe the residuals of ARIMAX [37]. Diaz-Robles et al. [37] evaluated the performance of ARMAX, ANNs, MLR and hybrid ARIMAX-ANN for the forecasting of daily maximum PM₁₀ moving average values in one station in Temuco, Chile. The hybrid ARIMAX-ANN was the best model (See Table 3), and its input variables were not only the inputs, employed by an ANN, but also the ARIMAX model outputs and the residuals of ARIMAX.

Goyal et al. [34] presented a hybrid of MLR and ARIMA, whose structure is almost the same as the ARIMAX model. They also demonstrated that the hybrid model performs better than ARIMA and MLR (See Table 3).

The foundation of Support Vector Machines (SVM) is a machine learning technique that was initially developed for classification problems by Cortes and Vapnik [81]. A regression technique based upon SVM was then developed [82]. SVM is able to perform linear and non-linear regressions. The advantages of SVM, compared with MLP, are its better generalization ability and its capability for learning, using a small number of training data and huge number of input variables [77]. Suárez Sánchez et al. [77] employed SVM for simulation of PM₁₀ in Avilés, Spain and they showed that SVM with different Kernel function performs better than MLP (See Table 3). Suárez Sánchez et al. [79] reported similar findings (See Table 3).

Raimondo et al. [83] compared SVM and ANN for temporal Prediction of PM₁₀ in a station in Goteborg, Sweden, and they found that the SVM produced better hourly PM₁₀ forecasting results than an ANN. In addition, Sotomayor-Olmedo et al. [84] demonstrated the appropriate performance of SVM with Gaussian kernel function for the forecasting of monthly PM₁₀ in Mexico City.

GAM (Generalized Additive Model) [85] is an extension of Generalized Linear Model (GLM). This technique has also been employed in a few studies for modeling PM₁₀ in urban areas (See [57,76,78] in Table 3).

QRM (Quantile Regression Model) has occasionally been employed for modeling PM₁₀ in urban areas. Sayegh et al. [57] showed that QRM outperforms MLR, GAM, and BRT in the modeling of daily PM₁₀ in Makkah, Saudi Arabia (See Table 3). For details about QRM refer to Koenker [86].

CART (Classification And Regression Trees) analysis is a statistical procedure, introduced by Breiman et al. [87]. The methodology used by CART is known as binary recursive partitioning. The CART technique splits the data into two groups-nodes and this binary splitting is repeated until some conditions are satisfied [52]. Slini et al. [52] showed that CART technique preforms better than linear regression techniques (See Table 3). The CART technique results in new methods for analysis and forecasting such as BRT, which was employed for daily PM₁₀ simulation in Makkah, Saudi Arabia [57].

Yetilmezsoy and Abdul-Wahab [88] utilized CH₄, CO, wind speed and direction, relative humidity and solar radiation as the input variables of fuzzy and linear regression techniques for the estimation of PM₁₀ in Khaldiya, Kuwait. The fuzzy method outperformed the linear technique (MLR: R² = 0.756; Fuzzy technique: R² = 0.997).

In general, among the rarely used approaches, the SVM and hybrid models outperform ANNs, and these techniques are promising for suitable temporal PM₁₀ prediction. Hence, based upon previous studies, ANN, SVM and hybrid techniques can be considered as suitable techniques for temporal prediction of PM₁₀ in urban areas.

5. Spatial Prediction (Spatial Distribution) of PM₁₀ in Urban Areas

One technique for the spatial prediction of air pollution is spatial interpolation. Some air pollution studies have employed deterministic (e.g., Inverse Distance Weighting (IDW), nearest-neighbor, and splines) and geostatistical (e.g., Kriging) interpolation techniques [89]. Kanakiya et al. [90] used Kriging, IDW, nearest-neighbor and splines for spatial prediction of PM₁₀ in Prune, India. Kriging and IDW were employed for spatial prediction of PM₁₀ in Istanbul, Turkey [91] and Phoenix, Arizona, USA [92]. In total, Kriging has been applied more often in urban areas (e.g., metropolitan areas of Barcelona and Bilbao, Spain [93], an urban scale in Europa [94], Phoenix metropolitan region, Arizona [95] and Mumbai, India [96]), than have other typical deterministic interpolation techniques.

Although spatial interpolation techniques (relying on conventional geostatistical techniques), are suitable for spatial prediction of air pollutants at national, regional and global scales [97,98], they are not suitable for spatial prediction at smaller scales such as urban areas [99,100]. Conventional geostatistical techniques consider the spatial autocorrelation information with or without broad scale variations (or trends) (e.g., ordinary Kriging, universal Kriging and Kriging with external drift). Air pollution sources in urban areas are extremely varied and complex. There are many local emission sources, and there is a steep gradient of pollutant concentration away from these sources [100,101]. Accordingly, a dense air pollution monitoring network must be employed if conventional geostatistical techniques are to be used. This is rarely available in urban areas [102,103,104,105], and interpolation using an inadequate number of monitoring stations can lead to highly biased and smoothed results [89,100]. Consequently, the number of published applications of Kriging on spatial prediction of air pollutants is relatively low [100,105].

Recently, some promising new approaches to spatial interpolation techniques, based upon geostatistical techniques, have been introduced and applied to spatial prediction of PM₁₀ in urban areas. Co-kriging technique, using PM₁₀ predictions of Transport Chemical Aerosol Model (TCAM) [106] as a secondary variable, was successfully applied for spatial prediction of PM₁₀ over Milan metropolitan area, Italy [107,108], and it forecast with higher accuracy than the Kriging technique [107]. Pollice and Lasinio [109] employed the Bayesian Kriging-based technique [110] for spatial prediction of daily PM₁₀ in Taranto, Italy. This technique is characterized by the utilization of time varying weather covariates [109]. Park [111] employed a spatio-temporal Kriging technique for spatial prediction of monthly PM₁₀ in Seoul metropolitan area, South Korea, and demonstrated that this technique outperforms conventional Kriging. In addition, Functional Kriging (an alternative to spatio-temporal Kriging) was successfully applied for spatial prediction of PM₁₀ in Madrid, Spain [112].

LUR (Land Use Regression) has been introduced as a credible alternative technique for the spatial prediction of air pollutants in urban areas with small number of monitoring stations [89], [104]. LUR has frequently been used for air pollution exposure assessment, and modeling of small-scale spatial variation of air pollutants in urban areas using different predictor variables [113,114,115]. There is no standard method for conducting LUR, but some explanations about the general approach can be found in the literature (e.g., [98,116,117,118]. In LUR, a statistical relationship between air pollutants and some urban characteristics (e.g., land use characteristics, traffic intensity, and population density) is established [39,119]. In some studies, air pollution emission sources (i.e., traffic and industrial point sources data) and the concentration of some pollutants at particular locations are also included in the list of predictor variables (e.g., [39,120,121,122]). In total, the explanatory variables in different LUR models are not unique, due to the city characteristics and data availability [74]. LUR models have seldom employed the morphological parameters, which may consider the dispersion field near to the pollution sources [123]. Tang et al. [123] added 4 morphological parameters to the traditional LUR model and improved the performance of the LUR model.

Hoek et al. [113] reviewed the studies on the application of LUR for spatial modeling of air pollutants. They showed that the main studies have focused on PM_2.5 and NOx, and the LUR approach has rarely been employed for the spatial modeling of PM₁₀ in urban areas. Table 4 shows the main studies on the application of LUR for the modeling of spatial distribution of PM₁₀ in urban areas.

Table 4. Recent studies on the spatial modeling of PM₁₀ in urban areas.

PM10 Parameter	Case Study	Country	Inputs	Number of Stations	Buffer Radii (m)	Results	Time Series	Source
Heating season	Tianjin	China	Major roads, land use, population, meteorological and distance to sea parameters	30	500–2000	R2 = 0.49	2006	[60]
Heating season	Tianjin	China	Major roads, land use, population, meteorological and distance to sea parameters	30	500–2000	R2 = 0.72	2006	[60]
Annual	Jinan	China	Traffic, land use, population, meteorological and distance to sea parameters	14	500–2000	R2 = 0.6	August 2008–July 2009	[120]
Annual	London	UK	Traffic volume, land cover, altitude	52	20–300	R2 = 0.47	1997–2005	[124]
Annual	Oslo	Norway	Traffic, population and land use parameters	20	25–1000	R2 = 0.64	October 2008–April 2011	[125]
	Stockholm county	Sweden				0.77
	Helsinki/Turku	Finland				0.42
	Copenhagen	Denmark				0.64
	Kaunas	Lithuania				0.3
	Manchester	UK				0.75
	London/Oxford	UK				0.88
	Munich/Augsburg	Germany				0.75
	Vorarlberg	Austria				0.71
	Paris	France				0.77
	Gyor	Hungary				0.54
	Lugano	Italy				0.8
	Turin	Italy				0.69
	Rome	Italy				0.59
	Barcelona	Spain				0.82
	Catalunya	Spain				0.71
	Athens	Greece				0.6
	Heraklion	Greece				0.38
Annual	Urban core area of Taiyuan	China	Meteorological parameters, emission data, altitude	-	-	R2 = 0.72	2000–2008	[126]
Annual	Tehran	Iran	Geographic, traffic, land use, distance, population and product variables	21	100–3000	Adjustd R2 = 0.53	2010	[127]
Cooler season						Adjustd R2 = 0.58
Warmer Season						Adjustd R2 = 0.55
Annual	Taipei	Taiwan	Road and land use parameters	20	25–5000	R2 = 0.69	October 2009–August 2010	[128]
Seasonal	Changsha	China	Road network and land use parameters	40	300–1200	R2 (Spring) = 0.48–0.7	2010	[129]
						R2 (Summer) = 0.39–0.6
						R2 (Autumn) = 0.3–0.72
						R2 (Winter) = 0.34–0.36
Annual	Changsha	China	Traffic conditions and land use type	36	300–1200	R2 = 0.58	2010	[74]
Four-year average	London	UK	Traffic and land use parameters	42	20–5000	R2 = 0.71	2008–2011	[123]
Four-year average	London	UK	Traffic and land use parameters + 4 morphological parameters	42	20–5000	R2 = 0.73	2008–2011	[123]

Table 4. Recent studies on the spatial modeling of PM₁₀ in urban areas.

PM10 Parameter	Case Study	Country	Inputs	Number of Stations	Buffer Radii (m)	Results	Time Series	Source
Heating season	Tianjin	China	Major roads, land use, population, meteorological and distance to sea parameters	30	500–2000	R2 = 0.49	2006	[60]
Heating season	Tianjin	China	Major roads, land use, population, meteorological and distance to sea parameters	30	500–2000	R2 = 0.72	2006	[60]
Annual	Jinan	China	Traffic, land use, population, meteorological and distance to sea parameters	14	500–2000	R2 = 0.6	August 2008–July 2009	[120]
Annual	London	UK	Traffic volume, land cover, altitude	52	20–300	R2 = 0.47	1997–2005	[124]
Annual	Oslo	Norway	Traffic, population and land use parameters	20	25–1000	R2 = 0.64	October 2008–April 2011	[125]
	Stockholm county	Sweden				0.77
	Helsinki/Turku	Finland				0.42
	Copenhagen	Denmark				0.64
	Kaunas	Lithuania				0.3
	Manchester	UK				0.75
	London/Oxford	UK				0.88
	Munich/Augsburg	Germany				0.75
	Vorarlberg	Austria				0.71
	Paris	France				0.77
	Gyor	Hungary				0.54
	Lugano	Italy				0.8
	Turin	Italy				0.69
	Rome	Italy				0.59
	Barcelona	Spain				0.82
	Catalunya	Spain				0.71
	Athens	Greece				0.6
	Heraklion	Greece				0.38
Annual	Urban core area of Taiyuan	China	Meteorological parameters, emission data, altitude	-	-	R2 = 0.72	2000–2008	[126]
Annual	Tehran	Iran	Geographic, traffic, land use, distance, population and product variables	21	100–3000	Adjustd R2 = 0.53	2010	[127]
Cooler season						Adjustd R2 = 0.58
Warmer Season						Adjustd R2 = 0.55
Annual	Taipei	Taiwan	Road and land use parameters	20	25–5000	R2 = 0.69	October 2009–August 2010	[128]
Seasonal	Changsha	China	Road network and land use parameters	40	300–1200	R2 (Spring) = 0.48–0.7	2010	[129]
						R2 (Summer) = 0.39–0.6
						R2 (Autumn) = 0.3–0.72
						R2 (Winter) = 0.34–0.36
Annual	Changsha	China	Traffic conditions and land use type	36	300–1200	R2 = 0.58	2010	[74]
Four-year average	London	UK	Traffic and land use parameters	42	20–5000	R2 = 0.71	2008–2011	[123]
Four-year average	London	UK	Traffic and land use parameters + 4 morphological parameters	42	20–5000	R2 = 0.73	2008–2011	[123]

There is no specific method for the determination of the optimum number of monitoring stations for developing LUR models [113,125,127]. The studies use data measured in 20–100 monitoring stations [89], and most studies have a small to medium number of sampling stations (20–60) [130]. Table 4 shows that the number of stations employed in the spatial modeling of PM₁₀ in urban areas is between 14 and 52. Basagaña et al. [130] employed 147 stations for LUR modeling of NO₂ in the cities of Girona and Salt, Spain, and they tried to determine the effect the number of monitoring stations had on the modeling results. They found that a high number of sampling stations leads to better performance in LUR modeling. However, this effect may be masked by the adjusted R² and Leave-One-Out Cross Validation (LOOCV) [130]. In addition, a large number of measurement sites (more than 80 stations for Girona and Salt) are required for the characterization of local air pollution levels in complex urban settings [130]. European cities typically have a limited number of air pollution monitoring stations, so some additional in-situ measurements are necessary for appropriate spatial prediction of PM₁₀ [131]. However, obtaining data from additional stations consumes time, cost and resources [113,132,133,134]. This is the main constraint on the development of dense air pollution monitoring networks in urban areas [135].

Taheri Shahraiyni et al. [136,137] presented a new technique for the development of dense air pollution monitoring networks for urban areas, by generating virtual stations. They successfully implemented their technique in the development of a dense PM₁₀ monitoring network in Berlin, Germany. The presented technique by Taheri Shahraiyni et al. [136,137] reduces the need for additional in-situ measurement data, and enables a low-cost method for spatial prediction of PM₁₀, which is suitable for policy making. Although the MLR technique is often utilized for LUR model development, Zhang et al. [126] used MLP for spatial simulation of the annual PM₁₀ concentration in the urban core area of Taiyuan, China. The intercept of MLR in the LUR approach implies the background concentration values [60], [113] but Chen et al. [120] found that the intercept of the MLR model for PM₁₀ in Jinan, China, is higher than the background values.

Previous studies showed that the initial input variables, utilized for PM₁₀ modeling, are often collinear. A reduction of collinearity is sought (e.g., [74,125], and [127]) as a developed model using collinear input variables is not robust, and is sensitive to small changes in the data [138,139]. Hence, a collinearity reduction technique is applied to the input variables. The different thresholds for correlation coefficients have been considered for the collinearity reduction in different LUR studies on PM₁₀ (e.g., 0.6 [74]; 0.67 [125]; 0.75 [127]). Li et al. [129] introduced LUR modeling with a semi-circular buffer that is able to incorporate wind direction into the LUR model, and it performs better than the LUR model with circular buffer in the modeling of seasonal PM₁₀ in Changsha, China.

In general, the LUR modeling approach has presented different results for different urban areas (R² = 0.3–0.88).

LUR studies have mainly been focused on the spatial modeling of seasonal or annual PM₁₀. Accordingly, the developed PM₁₀ models have high spatial resolution, but they have no temporal variation [74], [134]. Short-term PM₁₀ prediction models are important for the evaluation of short-term exposure in human health studies [74], rapid decision-making to inform and alert the public of harmful air pollution events, and to adapt air pollution control strategies [2,31,32,33,34]. Short-term variations of PM₁₀ have often been ignored in previous studies, and many studies have assumed that they have no impact on long-term exposure. This assumption is only valid, however, if temporal changes in PM₁₀ in the whole study area are equal [134]. This assumption is not valid in urban areas.

It is possible to develop an LUR model at any given time frame. A few studies, which have focused on the development of spatio-temporal variations of air pollutants using LUR models [134], are presented in the next section.

6. Spatio-Temporal Prediction (Forecasting of Spatial Distribution) of PM₁₀ in Urban Areas

Given the importance of improving the temporal resolution of spatial PM₁₀ models, some studies have tried to develop spatio-temporal models for air pollutants in urban areas.

The developed methods for spatio-temporal modeling of PM₁₀ can be categorized into the following groups:

• Temporal trend: The simplest method is the utilization of the temporal trend of the air pollutant, derived from the local background monitoring stations, for the adjustment of LUR results for past years. The disadvantage of this technique is that the trend of the monitoring station is extended throughout the urban area [134,140]. This approach is easy and it can be suitable if a representative fixed station is employed. However, a fixed station, which is affected by local air pollution sources (a non-representative station), cannot properly calibrate the pollutant concentration [74]. Taheri Shahraiyni et al. [141] presented a technique for the determination of the most representative stations in urban areas. Combining this new technique with temporal trend may lead to an appropriate spatio-temporal model for long-term variations of PM₁₀.
• Temporal adjustment: Another approach is the temporal adjustment of the values of the model’s predictors. This approach has some disadvantages. Many predictors change very slowly over time (e.g., land use) and consequently, this approach only predicts long-term variations in PM₁₀ levels. In addition, the temporal changes of the predictors do not necessarily reflect the temporal changes of the pollutants [134], and this method does not account for changes in the relationship between predictors and air pollutants [140].
• Temporal adjustment and trend: The combination of the previous two approaches (temporal adjustment and temporal trend) can be considered as an approach for spatio-temporal prediction of PM₁₀. In this approach, the spatio-temporal PM₁₀ concentration is first calculated by the temporal adjustment technique, and then the temporal trend is added to the developed model [140].
• Temporal recalibration: The change, or recalibration of the coefficients of the existing model, is another approach for the development of a suitable model for other times [134,140]. Mölter et al. [134] recalibrated the LUR model for calculation of annual spatial variations of PM₁₀ in Manchester, UK, over a long period. They concluded that this technique allows for the extrapolation of the LUR model over a long period. Wang et al. [140] compared different approaches (approaches 1–4) for hindcast and forecast of NO and NO₂ in Vancouver, Canada and showed that the best approach is the recalibration technique.
• Temporal model development: Some studies develop several models in different time steps (e.g., [142]). However, this approach requires a huge amount of human and material resources for data collection and model development [74]. Consequently, it is not time or cost-effective.
• Employment of temporal predictors: Although the previous approaches (approaches 1–5) derived a spatio-temporal PM₁₀ model, they have been utilized for long-term variations of air pollutants, and accordingly are not useful for the derivation of short-term variations of PM₁₀. Employment of temporal predictors enables the estimation of short-term variation of air pollutants, by the utilization of some short-term dynamic input variables in the spatio-temporal model. For example, Gryparis et al. [143] and Maynard et al. [144] employed the temporal, meteorological, location (latitude and longitude) and traffic variables, along with black carbon levels measured at one monitoring station, for the development of a daily black carbon model for Boston, USA. However, they did not consider land use parameters. Su et al. [145] incorporated meteorological parameters into LUR models and utilized them for hourly NO₂ estimation in Vancouver, Canada. Alam and McNabola [39] utilized the daily traffic and meteorological parameters, temporal parameter, and transboundary air pollution, derived from back trajectory analysis and population density, as input variables of the different statistical techniques (MLR, NPR (Non-Parametric Regression), ANN) within the LUR conceptual framework for the spatial simulation of daily PM₁₀ concentration in Vienna (Austria) and Dublin (Ireland). The results showed that ANN (Dublin: R² = 0.51; Vienna: R² = 0.66) outperforms MLR (Dublin: R² = 0.38–0.43; Vienna: R² = 0.35–0.39) and NPR (Dublin: R² = 0.45; Vienna: R² = 0.51). They showed that the utilization of a non-linear technique, instead of linear techniques, can lead to an acceptable level of accuracy.

In conclusion, further studies into the development of high-resolved spatio-temporal PM₁₀ prediction in urban areas are necessary. Future studies may attempt to develop new techniques for high-resolved spatio-temporal PM₁₀ prediction in urban areas. Non-linear approaches seem better than linear models for the development of spatial and spatio-temporal models with higher accuracy. Therefore, future studies may attempt to develop different non-linear spatial and spatio-temporal PM₁₀ prediction models.

In order to diminish or prevent the risk of critical concentration levels, abatement actions should be planned at least one or two days in advance [31]. Consequently, PM₁₀ forecasting with daily or smaller time steps can be considered as high temporal resolution (Short-term forecasts). In order to perform suitable monitoring at the urban scale, the grid size should be comparable with urban blocks (often less than 100 m) [146]. In addition, Merbitz et al. [147] showed that PM₁₀ concentration in urban areas decreases exponentially from the emission source, and the effect of the emission source is dampened at a very short distance (about 100 m). Therefore, to suitably consider short-range PM₁₀ variations, the grid size for high-resolved spatial PM₁₀ prediction in urban areas should be less than 100 m.

7. Summary and Conclusions

Figure 2 depicts the summary of this study.

The review of previous studies on the statistical modeling of PM₁₀ in urban areas showed that non-linear techniques outperform linear techniques for temporal prediction of PM₁₀. Among the introduced techniques, ANN, SVM and hybrid models have the most potential for better performance. In addition, including PM₁₀ in the input variables significantly improves the forecasting results. Although MLP has been employed more than other ANN structures for the temporal prediction of PM₁₀, the best ANN structure is still unknown.

Frequency distribution of PM₁₀ in the training dataset may strongly influence the modeling results, and the utilization of PM₁₀ data with uniform distribution may lead to an appropriate model for the forecasting of extreme events. However, utilization of this training database reduces the accuracy of low and normal PM₁₀ concentration forecasts. Accordingly, combining two PM₁₀ forecasting models, which have been developed using two training datasets with different frequency distributions, may lead to a suitable model for forecasting low to high PM₁₀ concentrations.

Linear approaches are often used for the development of LUR models for spatial prediction of PM₁₀. However, non-linear approaches have recently been employed and they can improve results. Consequently, future studies may develop non-linear LUR models for spatial and spatio-temporal PM₁₀ prediction in urban areas. Although LUR modeling with a high number of sampling stations leads to better performance, there is no specific method for the determination of the optimum number of monitoring stations for the development of the LUR model. Recently, a new technique has been developed for the generation of virtual PM₁₀ stations, and it can be employed in the densification of the PM₁₀ monitoring network. This approach reduces the need for additional in-situ measurement data and enables a low-cost method for spatial prediction of PM₁₀.

LUR studies have mainly been focused on the spatial modeling of seasonal or annual PM₁₀, but it is possible to develop an LUR model at any given time. A few studies have focused on the development of spatio-temporal variations of air pollutants using LUR models. Among six different approaches to the spatio-temporal modeling of PM₁₀, only one approach (employment of temporal predictors) enables the estimation of short-term variation in the levels of air pollutants. This is achieved by the utilization of some short-term dynamic input variables in the spatio-temporal model. This approach has rarely been used for high-resolved spatio-temporal prediction of PM₁₀ in urban areas, and future studies may focus on the development of a high resolved spatio-temporal statistical model for PM₁₀ prediction in urban areas.

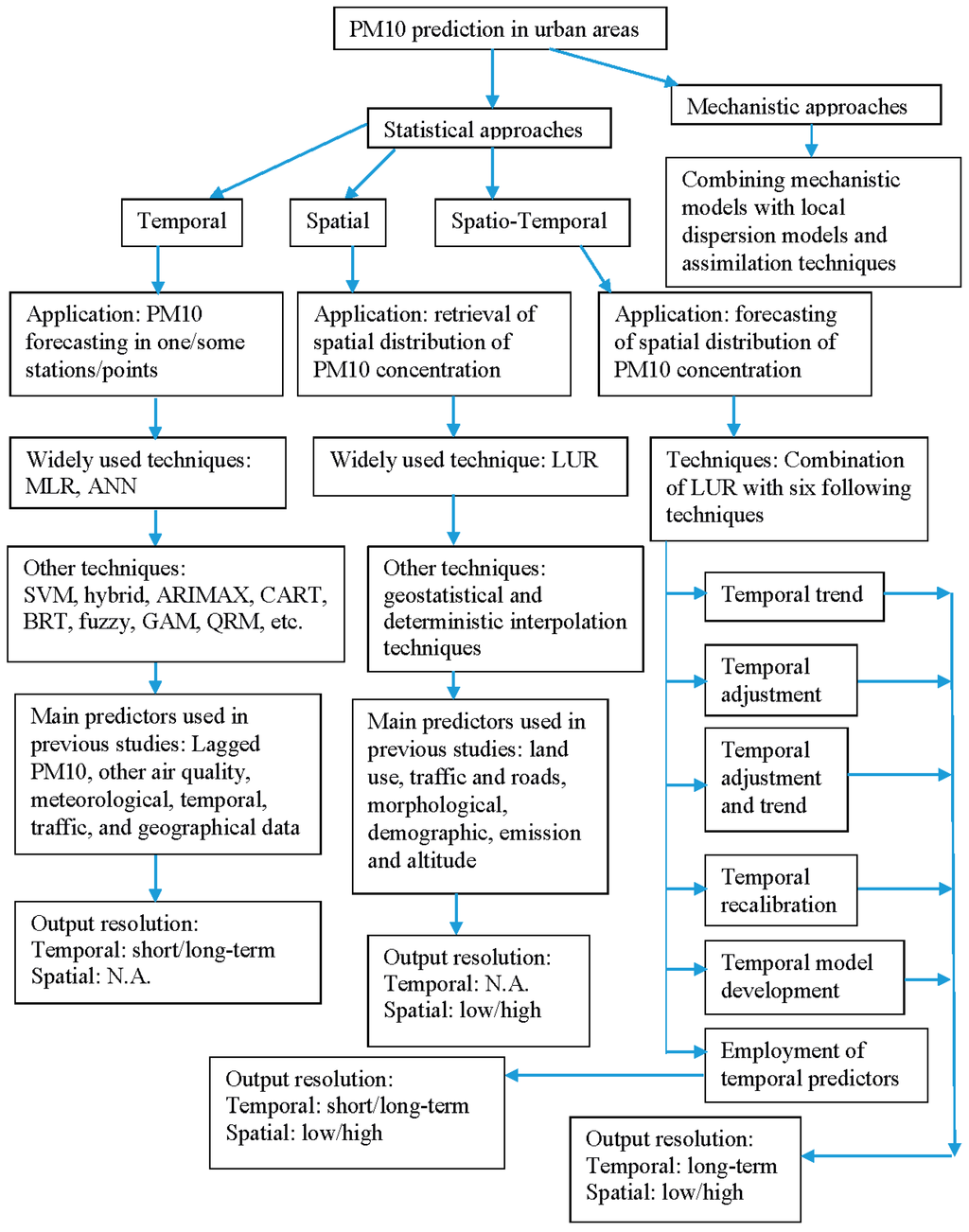
Figure 2. Summary of the review.

Figure 2. Summary of the review.