Evaluation of Optimized WRF Precipitation Forecast over a Complex Topography Region during Flood Season
Abstract
:1. Introduction
2. Data and Methodology
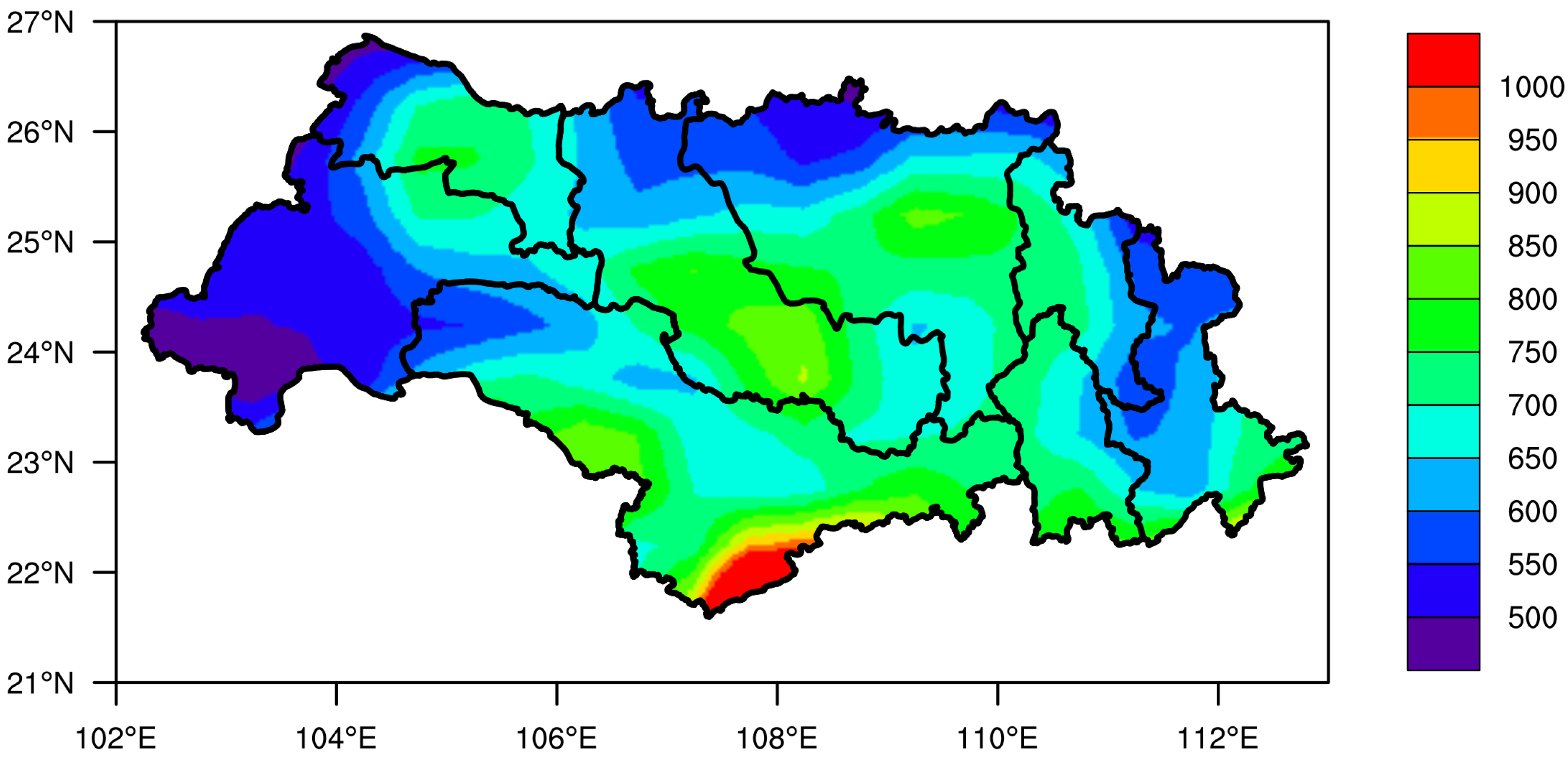
2.1. Study Area and Data Sources
2.2. Experimental Design of Sensitivity Tests
2.2.1. Experimental Design of Horizontal Resolution and Domain Size Sensitivity
2.2.2. Experimental Design of Physical Parameterization Sensitivity
2.3. Model Evaluation
3. Results
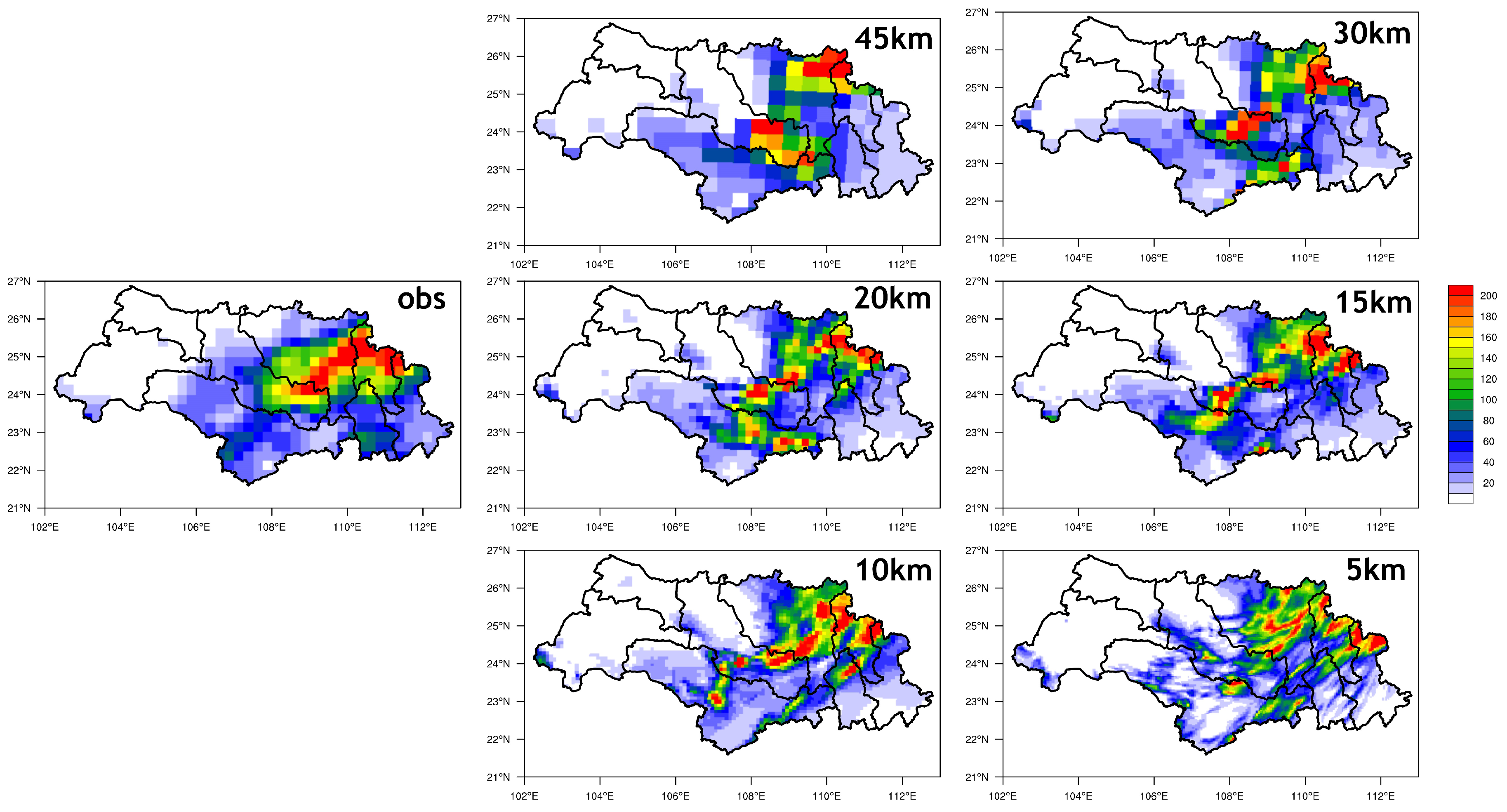
3.1. Influence of Horizontal Resolution and Domain Size on Simulations
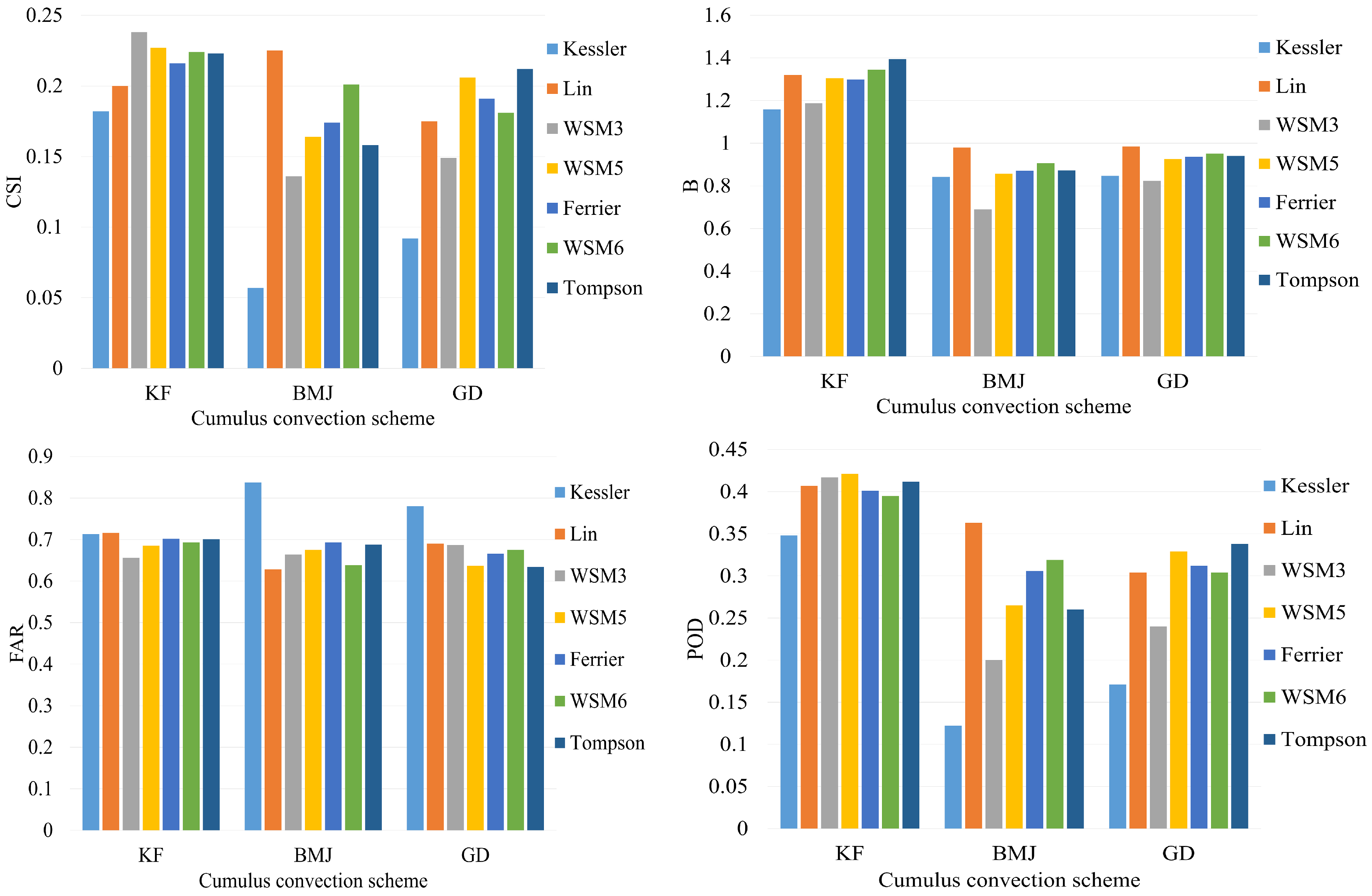
3.2. Influence of Physical Parameterization Scheme on Simulations
3.3. Evaluation of Precipitation Forecast with the Optimized Configuration
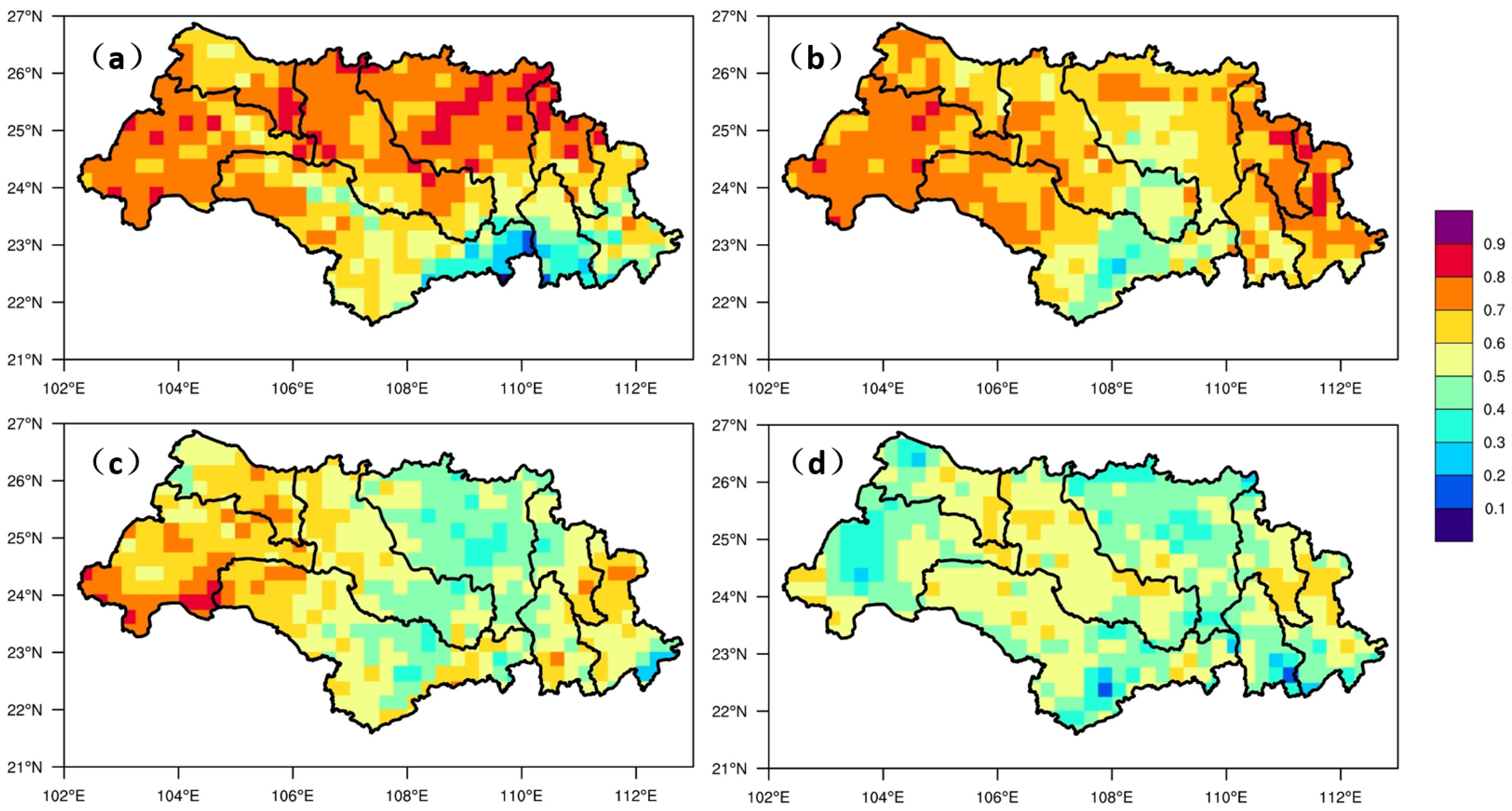
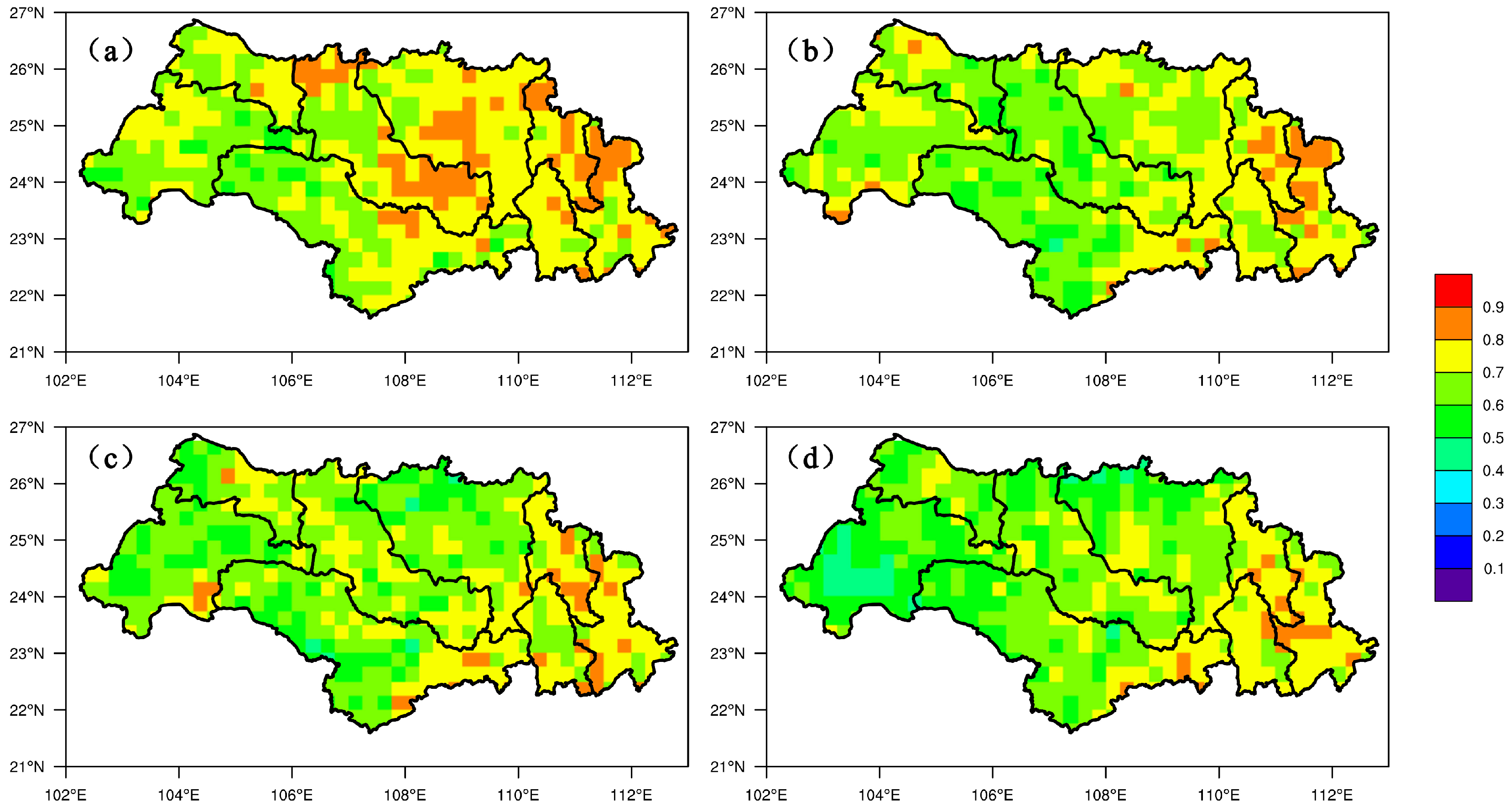
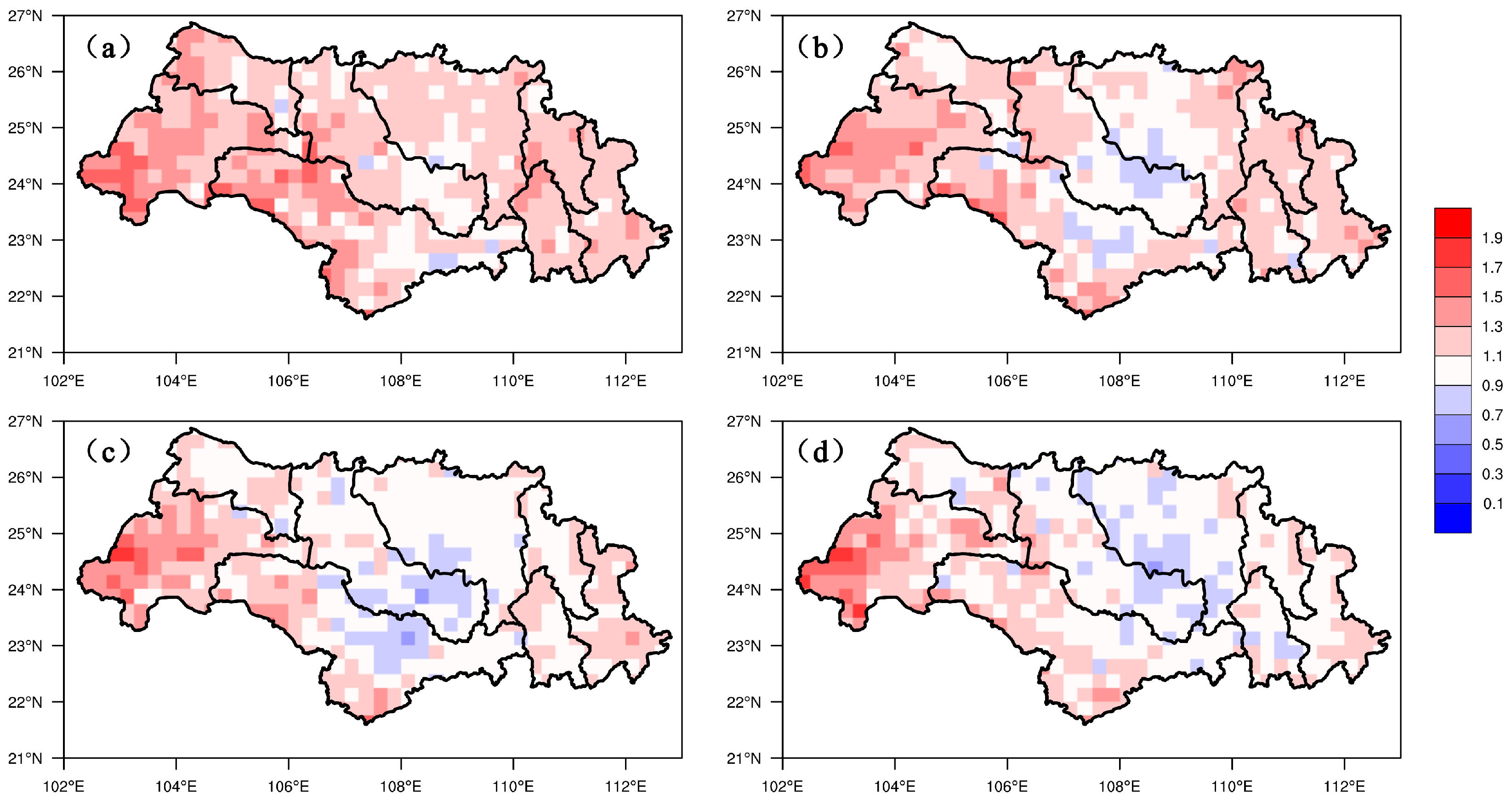
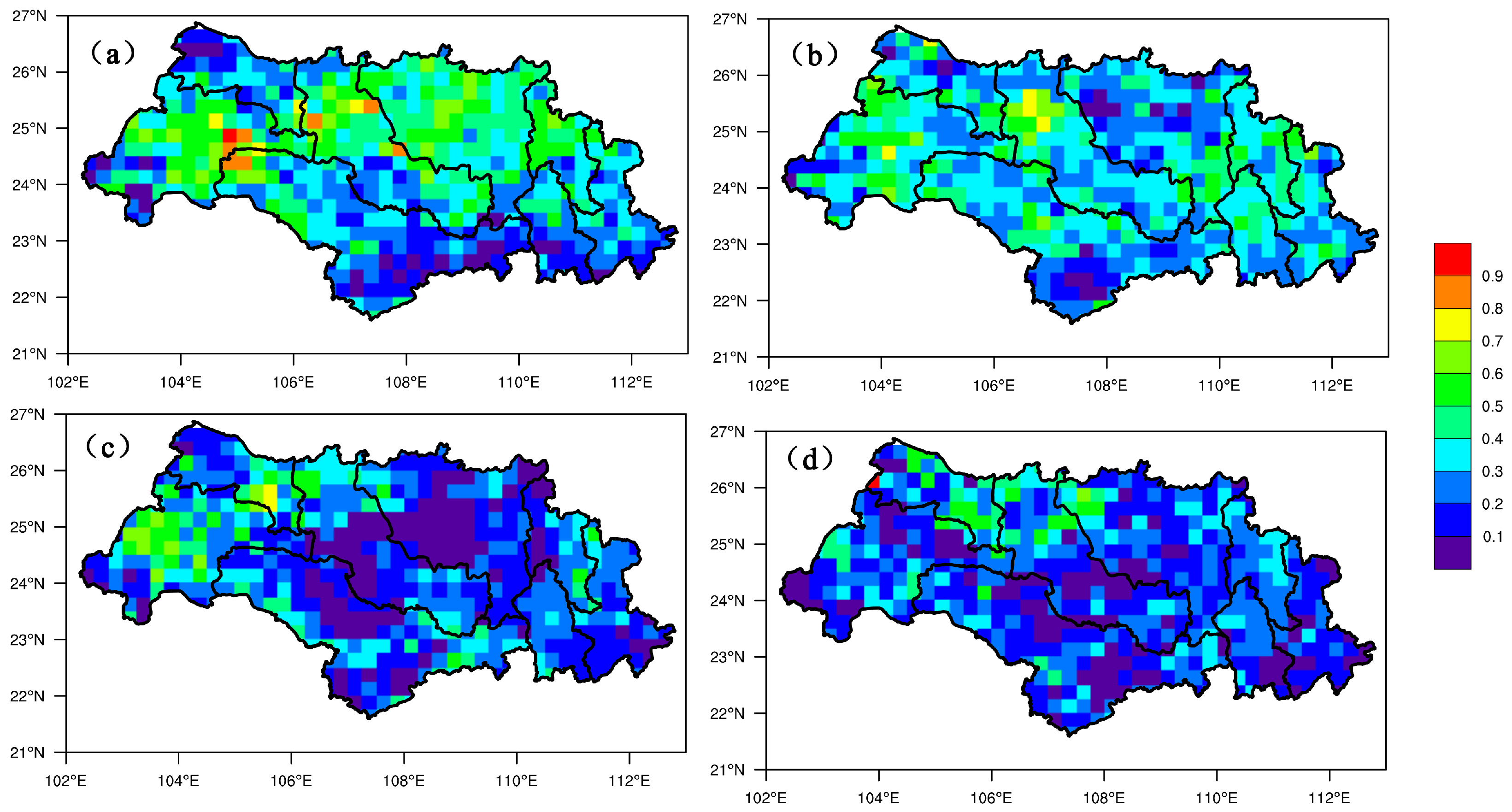
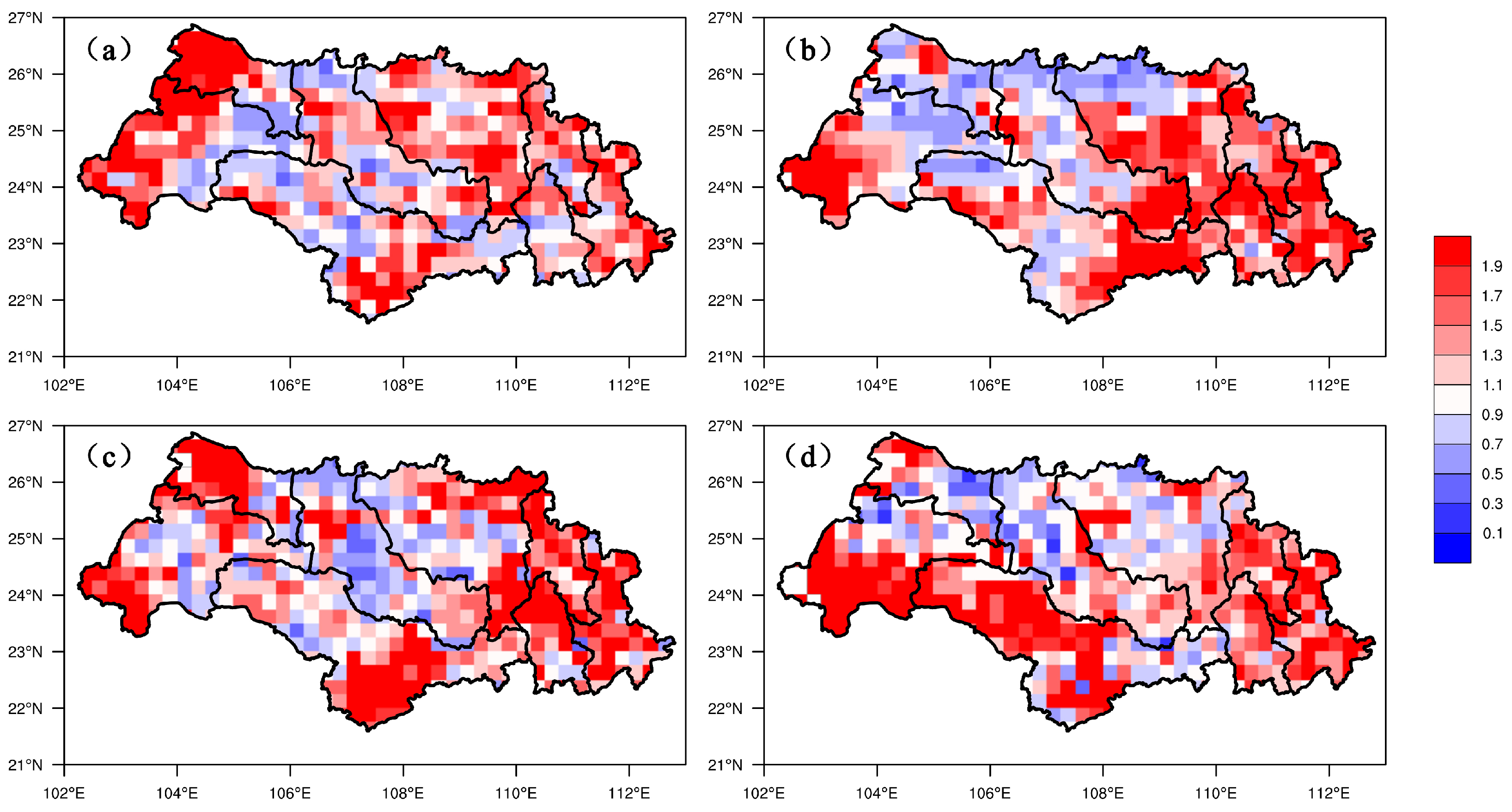
3.3.1. Evaluation of Grid Point Forecast
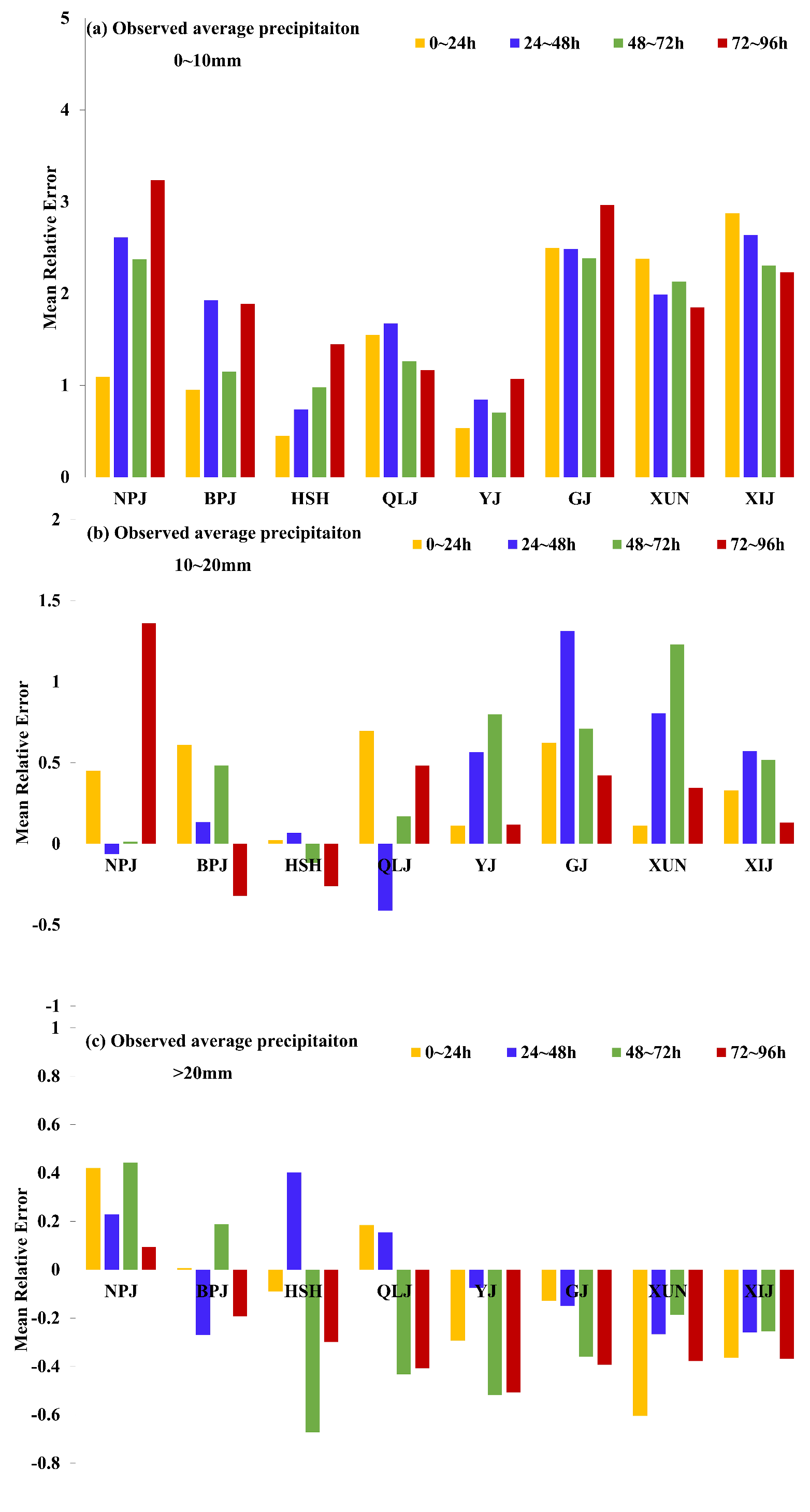
3.3.2. Evaluation of Average Precipitation Forecast
3.4. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, Z.Y.; Lin, Q.X.; Lu, G.H.; Wen, L.; Zhang, S.L.; Hu, J.W. A comprehensive assessment of extending the lead time of precipitation and streamflow forecast by using coupled hydrological and atmospheric modeling system. Disaster Adv. 2013, 6, 519–528. [Google Scholar]
- Wu, J.; Lu, G.H.; Wu, Z.Y. Flood forecasts based on multi-model ensemble precipitation forecasting using a coupled atmospheric-hydrological modeling system. Nat. Hazards 2014, 74, 325–340. [Google Scholar] [CrossRef]
- Baldauf, M.; Seifert, A.; Forstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities. Mon. Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Lee, C.S.; Ho, H.Y.; Lee, K.T.; Wang, Y.C.; Guo, W.D.; Chen, D.Y.C.; Hsiao, L.F.; Chen, C.H.; Chiang, C.C.; Yang, M.J.; et al. Assessment of sewer flooding model based on ensemble quantitative precipitation forecast. J. Hydrol. 2013, 506, 101–113. [Google Scholar] [CrossRef]
- Novak, D.R.; Bailey, C.; Brill, K.F.; Burke, P.; Hogsett, W.A.; Rausch, R.; Schichtel, M. Precipitation and Temperature Forecast Performance at the Weather Prediction Center. Weather Forecast. 2014, 29, 489–504. [Google Scholar] [CrossRef]
- Liu, X.L.; Coulibaly, P. Downscaling Ensemble Weather Predictions for Improved Week-2 Hydrologic Forecasting. J. Hydrometeoro. 2011, 12, 1564–1580. [Google Scholar] [CrossRef]
- Liu, J.; Bray, M.; Han, D.W. Sensitivity of the Weather Research and Forecasting (WRF) model to downscaling ratios and storm types in rainfall simulation. Hydrol. Process. 2012, 26, 3012–3031. [Google Scholar] [CrossRef]
- Matsangouras, I.; Pytharoulis, I.; Nastos, P. Numerical modeling and analysis of the effect of Greek complex topography on tornado genesis. Nat. Hazards Earth Syst. Sci. Discuss. 2014, 2, 1433–1464. [Google Scholar] [CrossRef]
- Teixeira, J.; Carvalho, A.; Luna, T.; Rocha, A. Sensitivity of the WRF model to the lower boundary in an extreme precipitation event-Madeira Island case study. Nat. Hazards Earth Syst. Sci. Discuss. 2013, 1, 5603–5641. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gomez-Gesteira, M.; Santos, C. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pu, Z.X.; Zhang, X.B. Examination of Errors in Near-Surface Temperature and Wind from WRF Numerical Simulations in Regions of Complex Terrain. Weather Forecast. 2013, 28, 893–914. [Google Scholar] [CrossRef]
- Cheng, W.Y.Y.; Steenburgh, W.J. Evaluation of surface sensible weather forecasts by the WRF and the Eta Models over the western United States. Weather Forecast. 2005, 20, 812–821. [Google Scholar] [CrossRef]
- Wen, M.; Yang, S.; Vintzileos, A.; Higgins, W.; Zhang, R.H. Impacts of Model Resolutions and Initial Conditions on Predictions of the Asian Summer Monsoon by the NCEP Climate Forecast System. Weather Forecast. 2012, 27, 629–646. [Google Scholar] [CrossRef]
- Xue, Y.K.; Janjic, Z.; Dudhia, J.; Vasic, R.; de Sales, F. A review on regional dynamical downscaling in intraseasonal to seasonal simulation/prediction and major factors that affect downscaling ability. Atmos. Res. 2014, 147, 68–85. [Google Scholar] [CrossRef]
- Bhaskaran, B.; Ramachandran, A.; Jones, R.; Moufouma-Okia, W. Regional climate model applications on sub-regional scales over the Indian monsoon region: The role of domain size on downscaling uncertainty. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Haghroosta, T.; Ismail, W.; Ghafarian, P.; Barekati, S. The efficiency of the WRF model for simulating typhoons. Nat. Hazards Earth Syst. Sci. Discuss. 2014, 2, 287–313. [Google Scholar] [CrossRef]
- Lowrey, M.R.K.; Yang, Z.L. Assessing the Capability of a Regional-Scale Weather Model to Simulate Extreme Precipitation Patterns and Flooding in Central Texas. Weather Forecast. 2008, 23, 1102–1126. [Google Scholar] [CrossRef]
- Zhang, S.R.; Lu, X.X.; Higgitt, D.L.; Chen, C.T.A.; Han, J.T.; Sun, H.G. Recent changes of water discharge and sediment load in the Zhujiang (Pearl River) Basin, China. Glob. Planet. Change 2008, 60, 365–380. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Duda, M.; Huang, X.; Wang, W. A description of the Advanced Research WRF version 3. Available online: http://opensky.ucar.edu/islandora/object/ technotes:500 (accessed on 10 November 2016).
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 2. Available online: http://oai.dtic.mil/oai/ oai?verb=getRecord&metadataPrefix=html&identifier=ADA487419 (accessed on 10 November 2016).
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Kessler, E. On the continuity and distribution of water substance in atmospheric circulations. Atmos. Res. 1996, 41, 179. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). Asia Pac. J. Atmos. Sci. 2006, 42, 129–151. [Google Scholar]
- Ferrier, B.S.; Houze, R.A., Jr. One-dimensional time-dependent modeling of GATE cumulonimbus convection. J. Atmos. Sci. 1989, 46, 330–352. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Grell, G.A.; Devenyi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 381–384. [Google Scholar] [CrossRef]
- Wu, L.; Liu, B.; Chen, X.; Lu, W. Uncertainty of Extreme Precipitation Threshold in Pearl River Basin. J. China Hydrol. 2013, 33, 59–64. [Google Scholar]
- Zhao, J.; Luo, J.; Gao, A.; Zeng, X. Analysis on a Heavy Rain Process in a Warm Sector in Guangxi in June 2008. Trop. Geogr. 2010, 30, 145–150. [Google Scholar]
- Chen, Y.; Nong, M. Diagnosis and numerical simulation of the persistent heavy rainfall in Guangxi in June 2008. J. Meteorol. Sci. 2010, 30, 250–255. [Google Scholar]
- Bresch, J.F.; Reed, R.J.; Albright, M.D. A polar-low development over the Bering Sea: Analysis, numerical simulation, and sensitivity experiments. Mon. Weather Rev. 1997, 125, 3109–3130. [Google Scholar] [CrossRef]
- Gallus, W.A. Eta simulations of three extreme precipitation events: Sensitivity to resolution and convective parameterization. Weather Forecast. 1999, 14, 405–426. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteorol. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
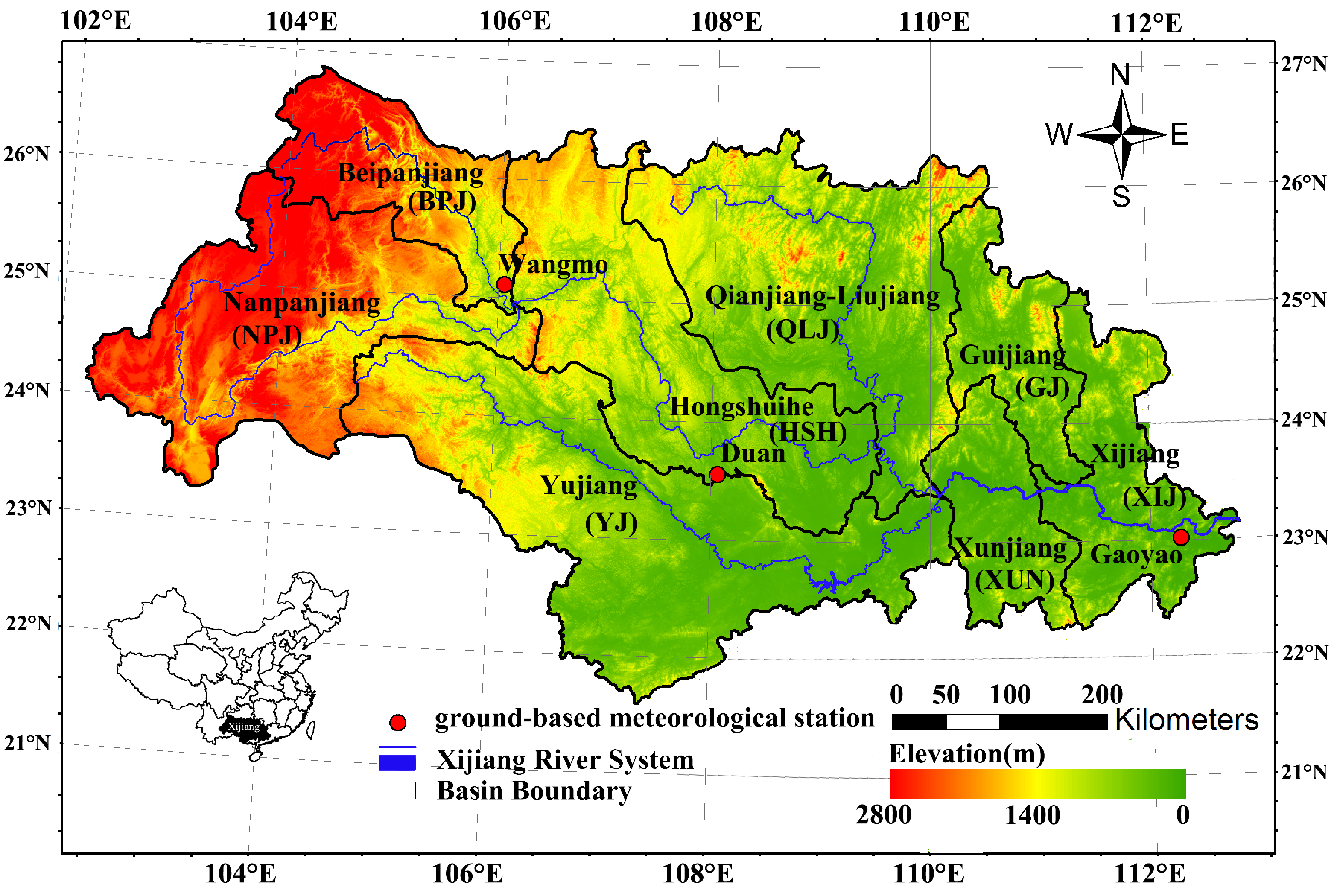
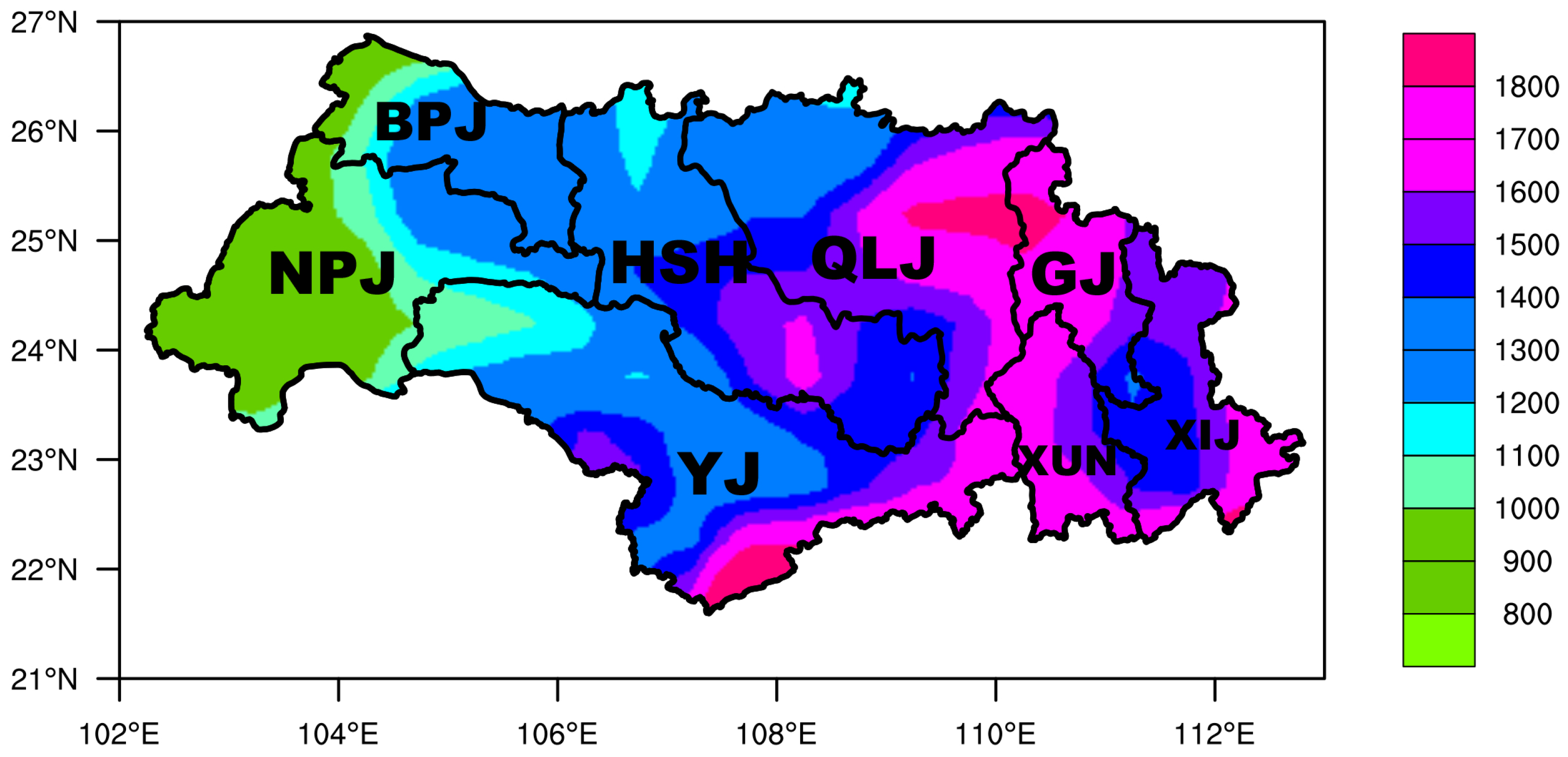
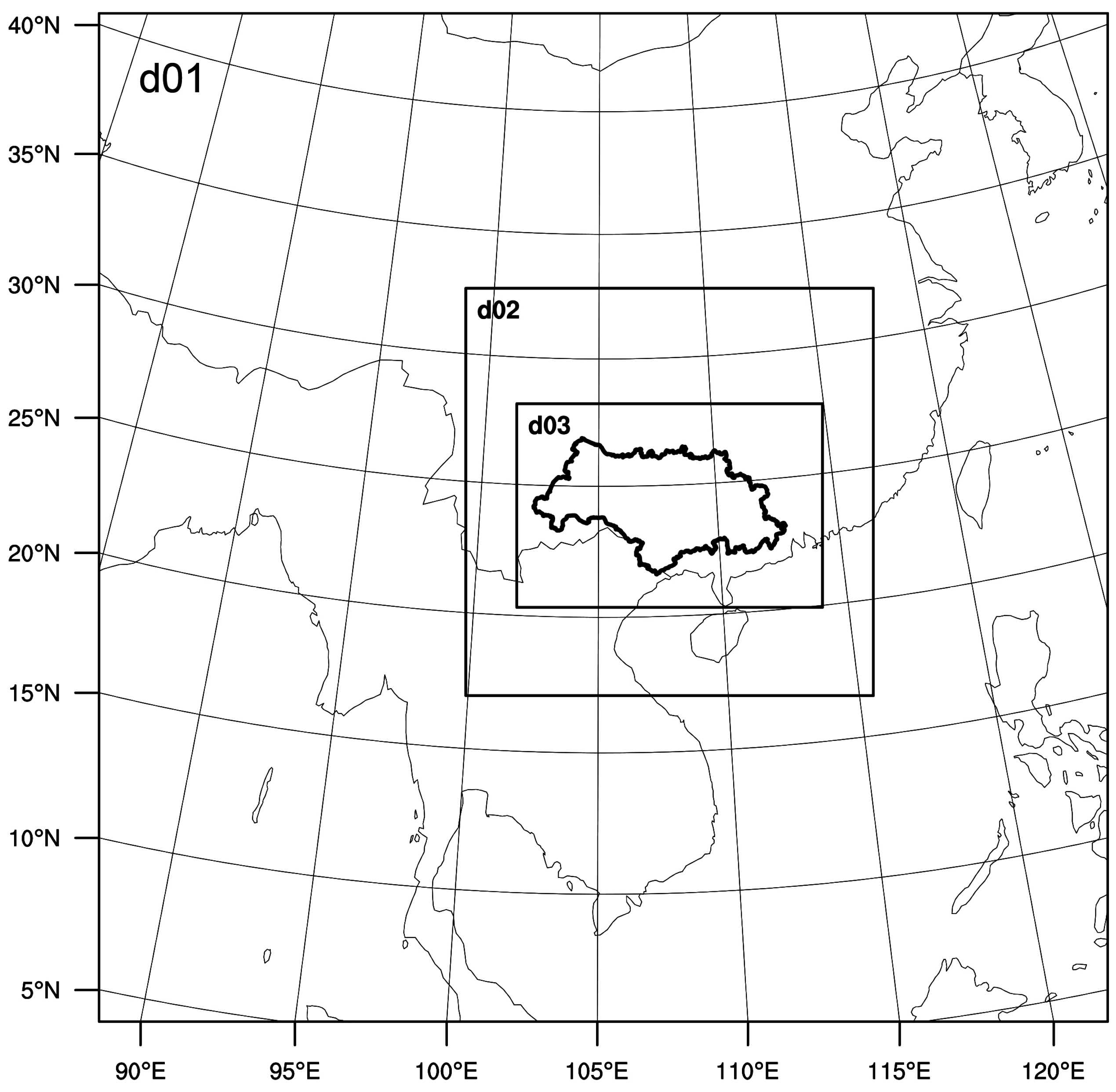
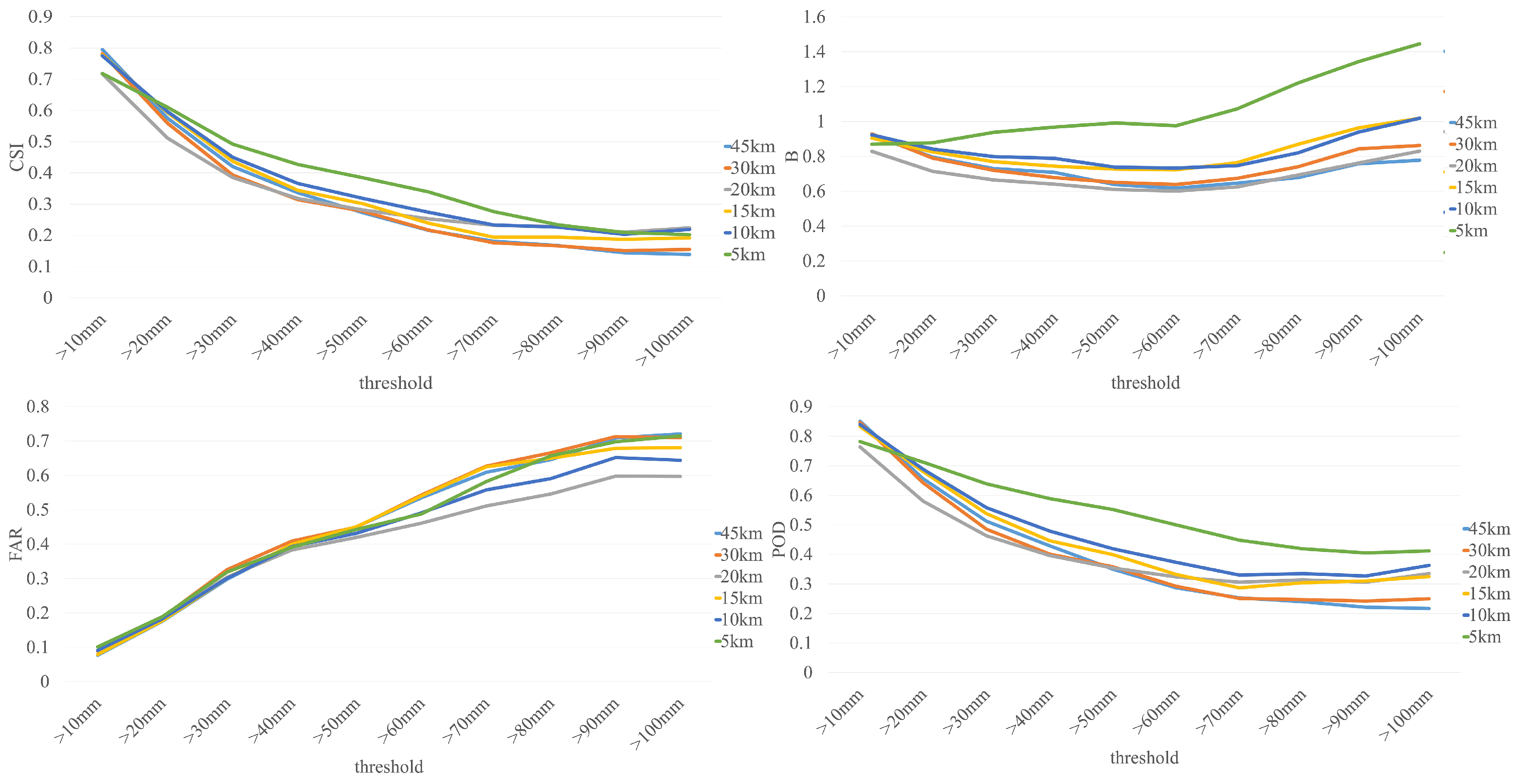
| Sub Basin | |
|---|---|
| Nanpanjiang (NPJ) | 67,191 |
| Beipanjiang (BPJ) | 31,399 |
| Hongshuihe (HSH) | 64,288 |
| Yujiang (YJ) | 92,515 |
| Qianjiang–Liujiang (QLJ) | 75,208 |
| Guijiang (GJ) | 22,611 |
| Xunjiang (XUN) | 21,694 |
| Xijiang (XIJ) | 31,794 |
| Event | Occurrence Time | Areal Average in Proceedings of the Precipitation (mm/day) | Weather System | Location of Rainstorm Center | Maximum Grid Precipitation (mm/day) |
|---|---|---|---|---|---|
| Case1 | 0000 UTC 5–6 June 2005 | 54.1 | South Asia High and Southwest monsoon | 106.42 E 23.13 N | |
| Case2 | 45.3 | Southwest vortex | 110.68 E 23.65 N | ||
| 0000 UTC | High-Level trough | ||||
| 21–22 June 2005 | and Shear line | ||||
| Case3 | 0000 UTC | 57.4 | Tropical storm | 110.18 E 24.14 N | |
| 16–17 July 2006 | |||||
| Case4 | 47.0 | High and low | 109.4 E 24.35 N | ||
| 0000 UTC | level jet | ||||
| 12–13 June 2007 | Shear Line | ||||
| Case5 | 0000 UTC | 83.1 | South Asia High | 109.26 E 24.15 N | |
| 12–13 June 2008 | and Trough | ||||
| Case6 | 49.9 | High-Level trough | 109.2 E 23.5 N | ||
| 0000 UTC | Shear line and | ||||
| 3-4 July 2009 | Southwest monsoon | ||||
| Case7 | 0000 UTC | 39.0 | Southwest vortex | 110.82 E 22.86 N | |
| 1–2 June 2010 |
| Nesting Strategy | Horizontal Resolution for Each Domain |
|---|---|
| Single domain | d01 (45 km) |
| Single domain | d01 (30 km) |
| Single domain | d01 (20 km) |
| Two domain nested | d01 (45 km), d02 (15 km) |
| Two domain nested | d01 (30 km), d02 (10 km) |
| Three domain nested | d01 (45 km), d02 (15 km), d03 (5 km) |
| Forecast | Observation | |
|---|---|---|
| YES | NO | |
| YES | a | b |
| NO | c | d |
| Microphysics Scheme | Ice Phase Transformation | Phase Transformation of Mixed Phase Clouds |
|---|---|---|
| Kessler | NO | NO |
| Lin | YES | YES |
| WSM3 | YES | NO |
| WSM5 | YES | NO |
| Ferrier | YES | YES |
| WSM6 | YES | YES |
| Thompson | YES | YES |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lu, G.; Wu, Z.; He, H.; Shi, J.; Ma, Y.; Weng, S. Evaluation of Optimized WRF Precipitation Forecast over a Complex Topography Region during Flood Season. Atmosphere 2016, 7, 145. https://doi.org/10.3390/atmos7110145
Li Y, Lu G, Wu Z, He H, Shi J, Ma Y, Weng S. Evaluation of Optimized WRF Precipitation Forecast over a Complex Topography Region during Flood Season. Atmosphere. 2016; 7(11):145. https://doi.org/10.3390/atmos7110145
Chicago/Turabian StyleLi, Yuan, Guihua Lu, Zhiyong Wu, Hai He, Jun Shi, Yuexiong Ma, and Shichuang Weng. 2016. "Evaluation of Optimized WRF Precipitation Forecast over a Complex Topography Region during Flood Season" Atmosphere 7, no. 11: 145. https://doi.org/10.3390/atmos7110145
APA StyleLi, Y., Lu, G., Wu, Z., He, H., Shi, J., Ma, Y., & Weng, S. (2016). Evaluation of Optimized WRF Precipitation Forecast over a Complex Topography Region during Flood Season. Atmosphere, 7(11), 145. https://doi.org/10.3390/atmos7110145






