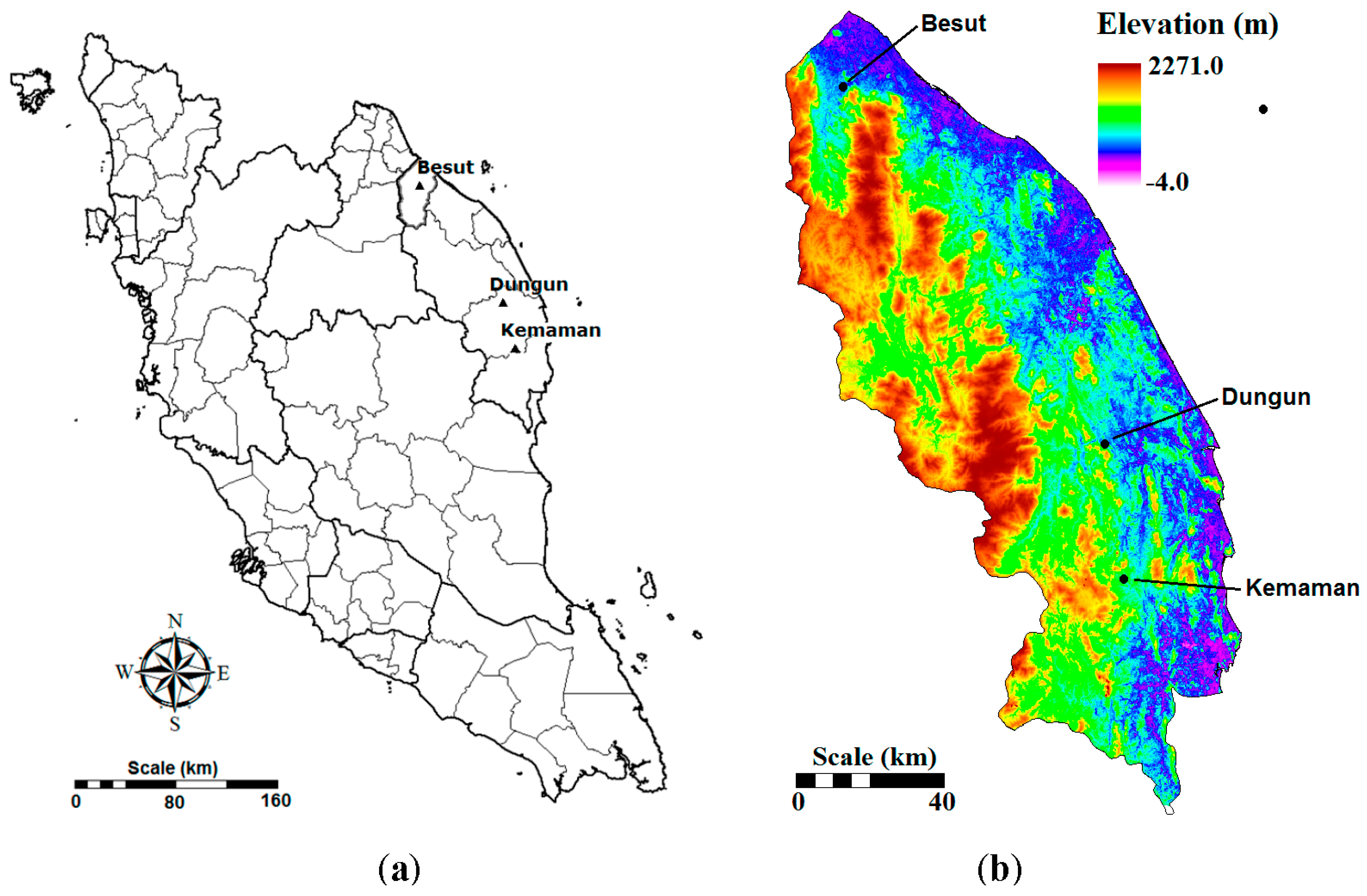
3.1. Selection of Predictors
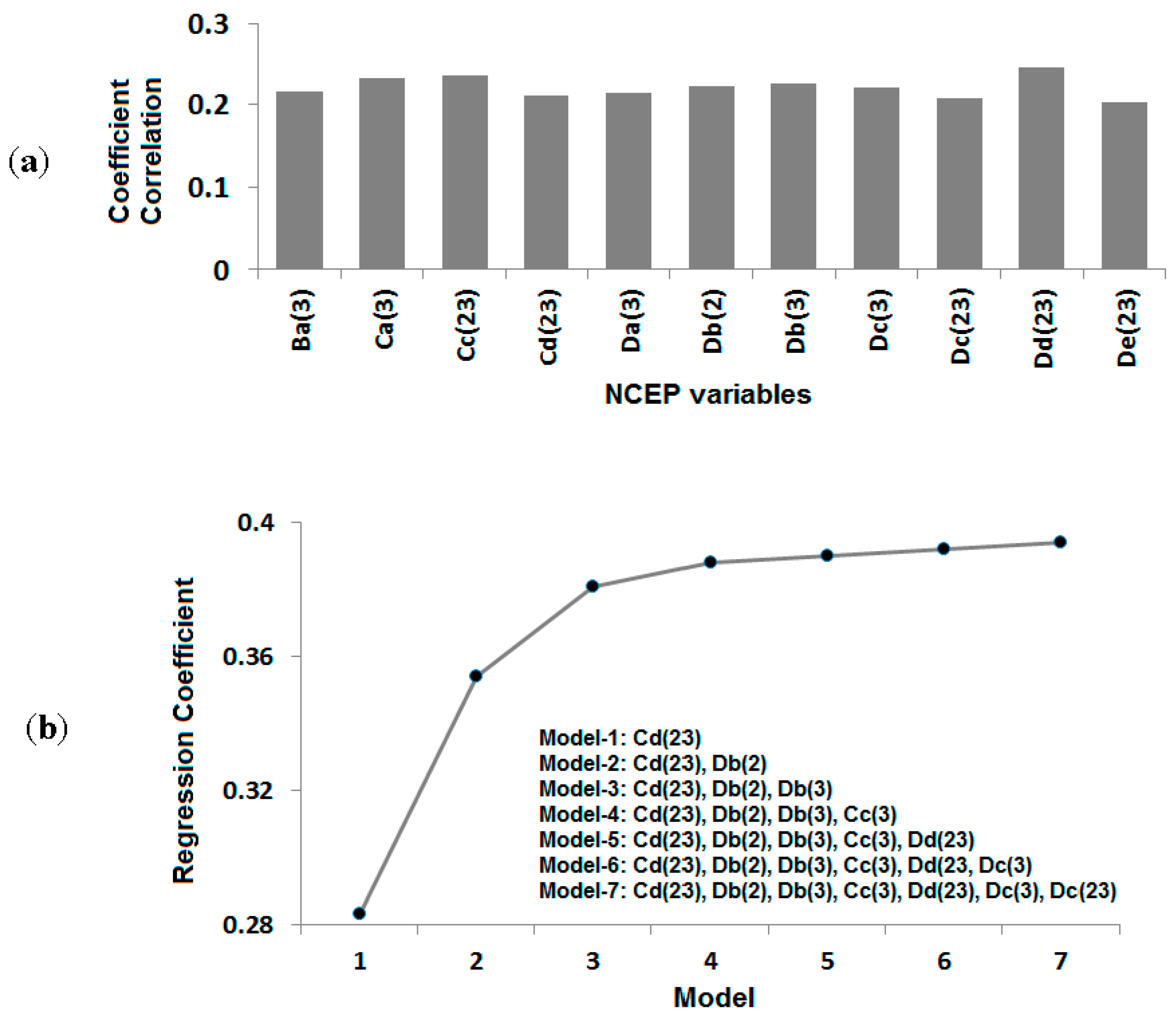
For the selection of predictors, the NCEP variables from 42 grid points surrounding the study area were individually correlated with local rainfall events. The NCEP variables from different grid points, having high correlation with heavy rainfall event at Dungun station, are shown in
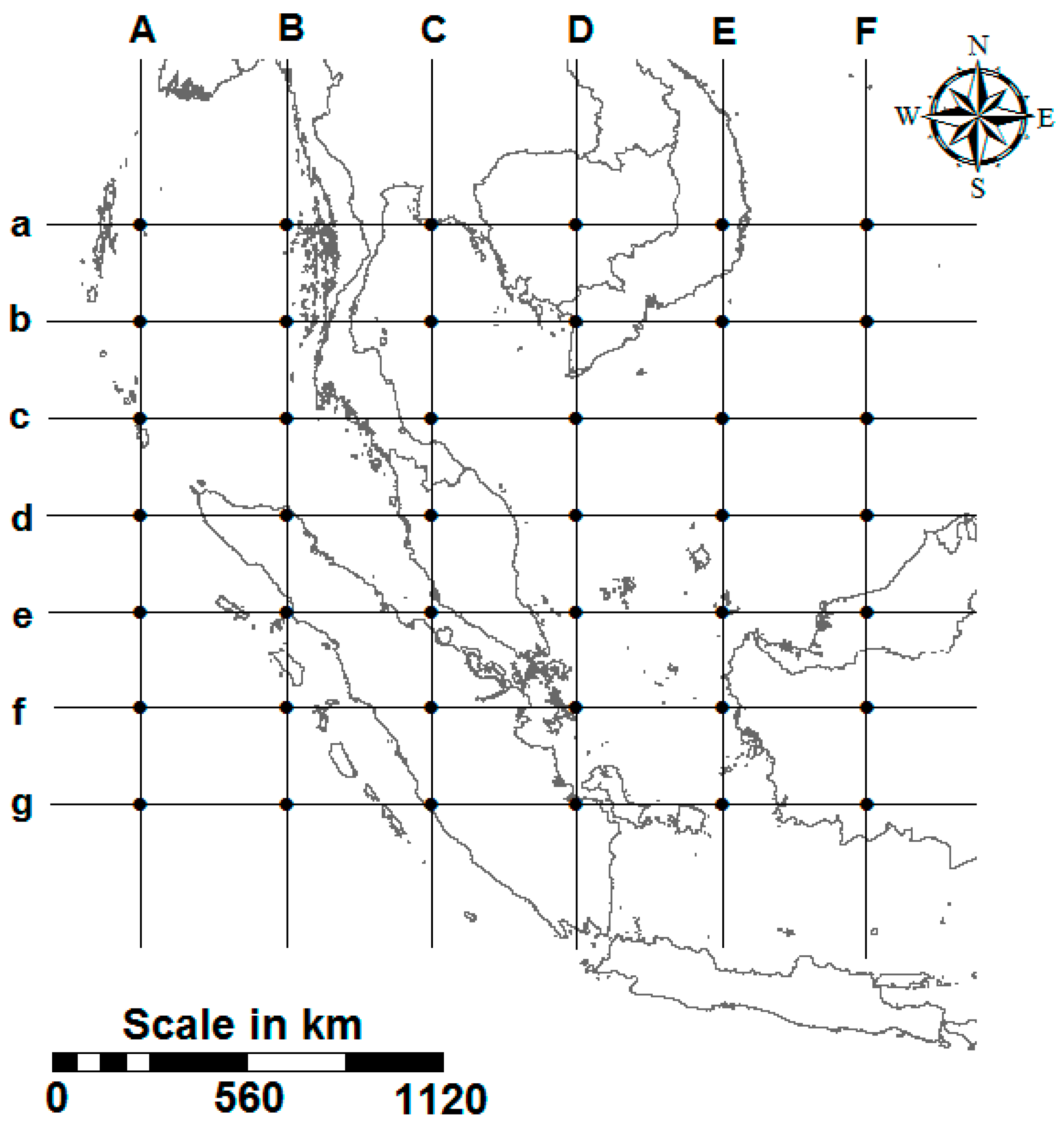
Figure 3a. In the figure, the capital letter in an NCEP variable name represents the column and the lower case letter represents the row of the NCEP grid point, as shown in
Figure 2. The number in brackets represents the NCEP variable, as described in
Table 1. Therefore, Cd(23) represents relative humidity at 500 hPa at the grid point located in column “C” and row “d”. Eleven NCEP variables from different grid points were found to have high correlation with a heavy rainfall event. These NCEP variables were used to select the final set of predictors for the downscaling using stepwise multiple regression. Stepwise multiple regression is a way of choosing predictors of a particular dependent variable on the basis of statistical criteria, such as an F-test or adjusted R-squared test. Stepwise multiple regression adds and removes predictors, in a stepwise manner, until there is no justifiable reason to add or remove more. Therefore, it allows the selection of the subset of independent variables that is the best predictor. The plot of regression coefficients between different subsets of independent variables and 90th percentile rainfall events at Dungun station is shown in
Figure 3b. The figure shows that the model performance increases with the inclusion of more NCEP variables. However, it does not increase substantially after the inclusion of more variables with three independent variables, namely Cd(23), Db(2) and Db(3). Therefore, these three NCEP variables were finally chosen as predictors for the downscaling of heavy rainfall days at Dungun station.
Figure 3.
(a) The NCEP variables from different grid points with good correlation with heavy rainfall events during the NE monsoon; (b) the plot of regression coefficients between different subsets of NCEP variables and heavy rainfall events at Dungun station.
Figure 3.
(a) The NCEP variables from different grid points with good correlation with heavy rainfall events during the NE monsoon; (b) the plot of regression coefficients between different subsets of NCEP variables and heavy rainfall events at Dungun station.
The process produced the same set of NCEP variables for all three stations. The NCEP variables selected as predictors for different rainfall indices are given in
Table 3. NCEP variables at grid points located in the NE direction have more influence on the rainfall of the study area. This is justifiable, as the rainfall in the study area is influenced by the NE monsoon.
Table 3 shows that the NCEP variables selected for downscaling rainfall indices are relative humidity at 500 and 850 hPa, surface airflow strength and surface zonal velocity. Precipitation at a location depends on the available air moisture content and flow of moist air. Relative humidity at 500 and 850 hPa represents the water vapor available in the air; surface airflow strength represents the regime of near surface air flow and surface zonal velocity on the equator cause zonal wind stress. Therefore, selection of these variables is physically plausible for rainfall downscaling. Other researchers also used those variables as predictors for rainfall downscaling in Malaysia [
67,
68]. It is very important to remember that the predictors used for downscaling should be reliably simulated by GCMs. The predictors selected in the present study are well simulated by many GCMs, including Hadley Centre Coupled Model, version 2 (HadCM2), Canadian Global Coupled Model, version 2 (CGCM2),
etc. Therefore, these predictors have been widely used for the downscaling and projection of future rainfall [
67,
68,
69].
Table 3.
NCEP variables used to build downscaled models.
Table 3.
NCEP variables used to build downscaled models.
| Event | Predictor | Code | Description |
|---|
| 90th percentile rainfall event | P1 | Cd(23) | Relative humidity at 500 hPa at grid point Cd |
| P2 | Db(2) | Surface airflow strength at grid point Db |
| P3 | Dc(3) | Surface zonal velocity at grid point Dc |
| Rainfall event | P1 | Cd(23) | Relative humidity at 500 hPa at grid point Cd |
| P2 | Dd(24) | Relative humidity at 850 hPa at grid point Dd |
| P3 | Db(3) | Surface zonal velocity at grid point Db |
3.2. Downscaling Using GP
The goal of a GP downscaling process is to produce an algebraic expression or model that best describes the daily rainfall from predictors. For this purpose, the GP algorithm works with solution candidates, which are tree structure representations of symbolic expressions. The function set used for non-terminal nodes includes +, −, ×, /, %, square root, log, as well as logical and other commonly-used trigonometric operators. As the goal is to find the extreme rainfall from NCEP variables, the terminal nodes must consist of selected NCEP variables, as well as constants. The obtained results are discussed below.
3.2.1. Downscaling Heavy Rainfall Days
A GP model for the downscaling of the days with larger than or equal to 90th percentile rainfall was developed first. The amounts of 90th percentile daily rainfall over the normal climate period (1961–1990) defined by the World Meteorological Organization [
44] are 23.2, 24.6 and 25.8 mm at Besut, Dungun and Kemaman stations, respectively. GP-based logistic regression was used to decide whether 90th percentile rainfall will occur or not during a day from the NCEP variables.
The GP software (Discipulus) used in the present study performs multiple runs by default. In the present study, 100 runs were used to produce a wide range of results. Termination of each run was considered as 200 generations without any improvement in fitness function. The distribution of results from multiple GP runs includes a distributional tail of excellent solutions. The best solution is selected based on the hit rate. The highest overall hit rates were obtained in downscaling heavy rainfall days in run 52 after 652 generations at Besut station, in run 47 after 712 generations at Dungun and in run 34 after 512 generations at Kemaman. The highest overall hit rates obtained at different stations is given in
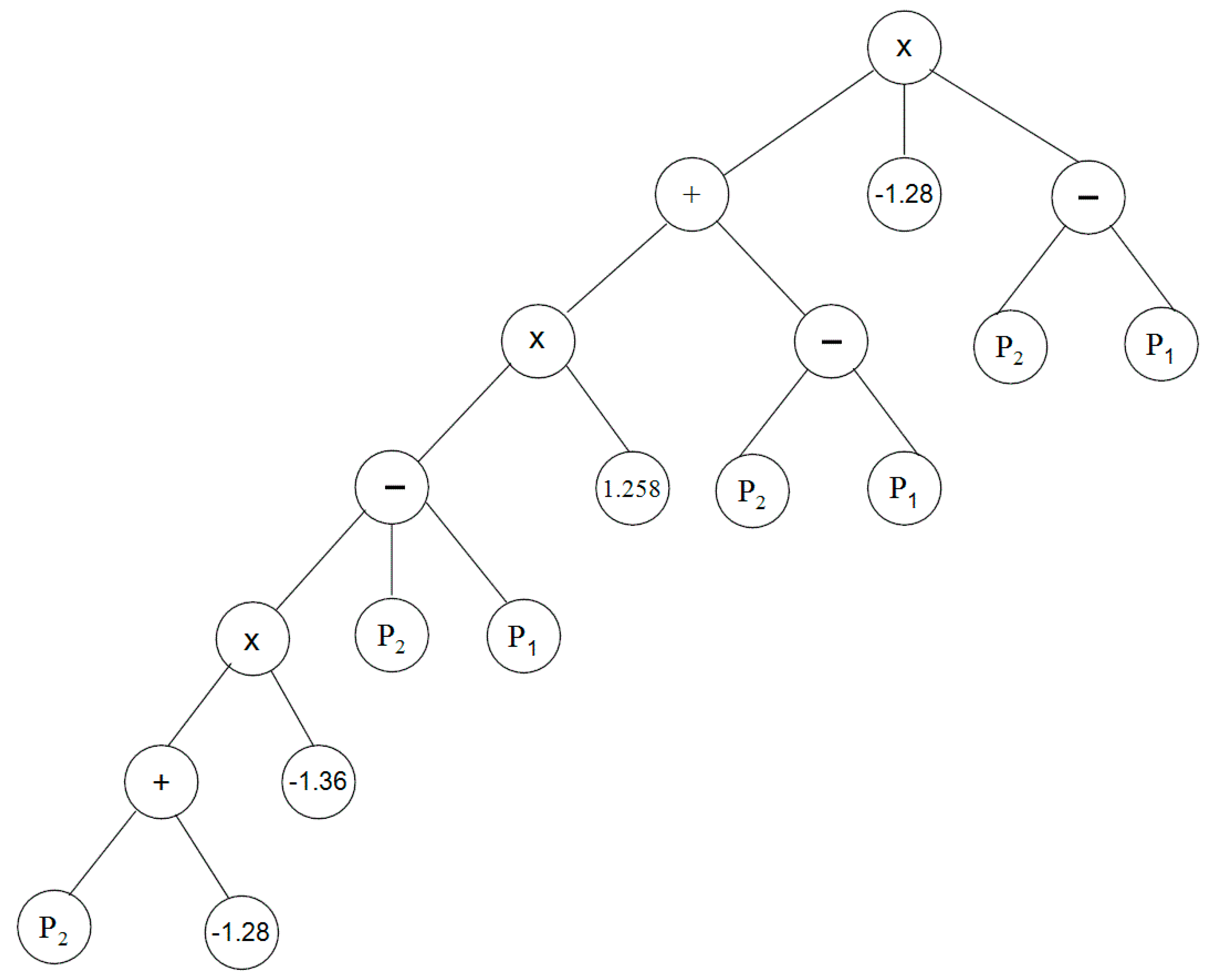
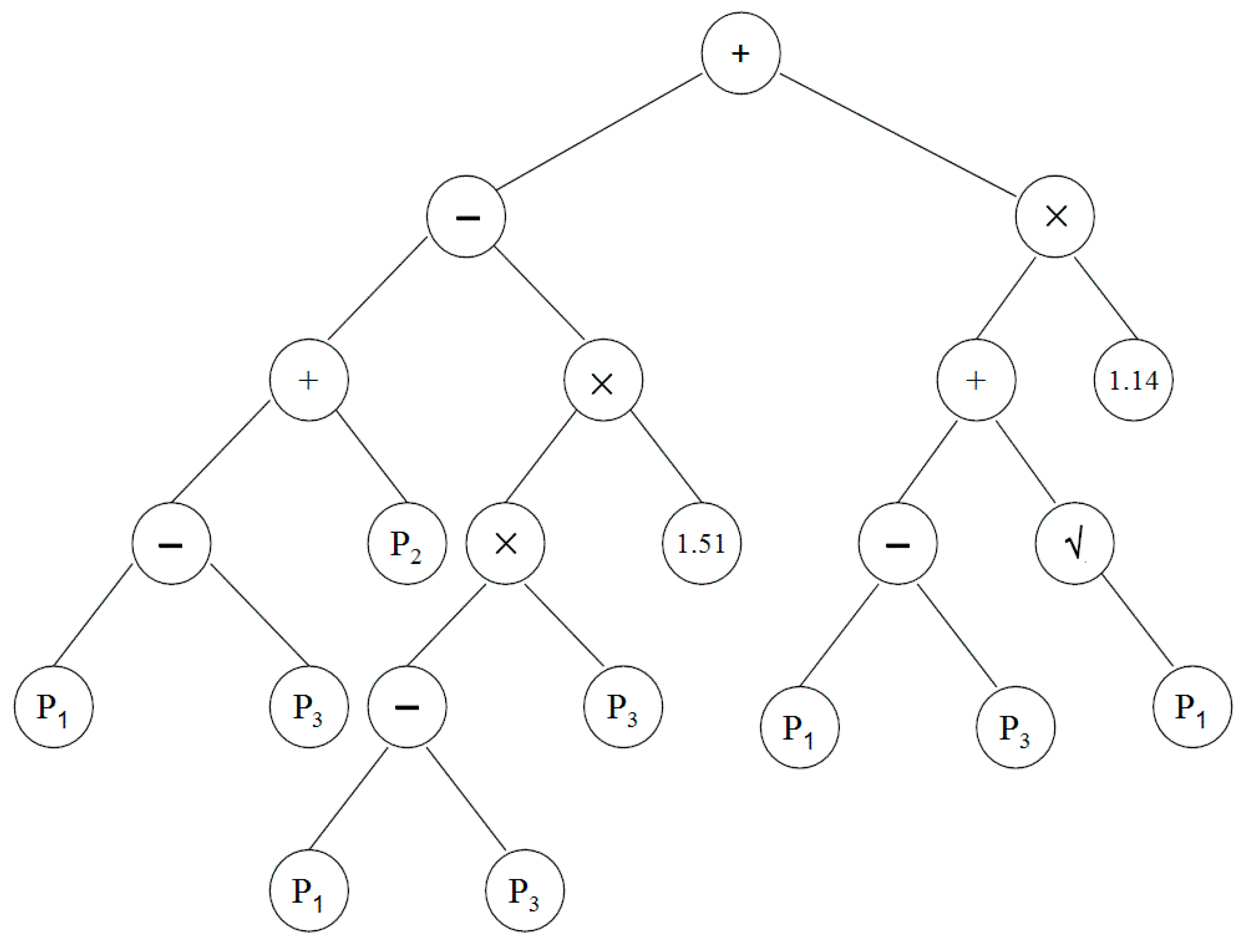
Table 4. It can be seen from the table that GP is able to model the 90th percentile rainfall index in 78.3%–81.1% of cases during calibration and 75.9%–78.0% of cases during validation. This means that GP-based logistic regression is successful in downscaling heavy rainfall days in more than 78.3% of cases. The best tree structure representations of symbolic expressions produced by GP in downscaling heavy rainfall days at Besut station is shown in
Figure 4. The simplified equations obtained from the GP structures that can be used to downscale the number of heavy rainfall days in the vicinity of three rainfall stations is given in
Table 5.
Table 4.
Overall hit rates during training and validation of genetic programming (GP) models in downscaling rainfall indices.
Table 4.
Overall hit rates during training and validation of genetic programming (GP) models in downscaling rainfall indices.
| Rainfall Indices | Station Name | Hit Rate (%) |
|---|
| Training | Validation |
|---|
| Days with larger than or equal to 90th percentile rainfall | Besut | 81.1 | 78.0 |
| Dungun | 80.1 | 76.8 |
| Kemaman | 78.3 | 75.9 |
| Rainy days | Besut | 86.1 | 82.0 |
| Dungun | 84.5 | 80.2 |
| Kemaman | 83.9 | 81.0 |
Figure 4.
The tree structure representations of symbolic expressions produced by GP for heavy rainfall event downscaling at Besut (descriptions of
P1,
P2 and
P3 are given in
Table 3).
Figure 4.
The tree structure representations of symbolic expressions produced by GP for heavy rainfall event downscaling at Besut (descriptions of
P1,
P2 and
P3 are given in
Table 3).
Table 5.
The simplified equations derived by GP for the downscaling of extreme rainfall indices (descriptions of
P1,
P2 and
P3 are given in
Table 3).
Table 5.
The simplified equations derived by GP for the downscaling of extreme rainfall indices (descriptions of P1, P2 and P3 are given in Table 3).
| Rainfall Indices | Station Name | Equation |
|---|
| Days with larger than or equal to 90th percentile rainfall | Besut | −1.28[P2 − P1 + 1.258[P2 − P1 − 1.36[P2 + P3]]] × [P2 − P1] |
| Dungun | [P2 + P1 − 2.56[P2 + P1 − 3.26[P1 + P2 + P3]]] × 1.23P2 |
| Kemaman | −1.11[P2 − P1 + 1.56[P2 − P1 − 1.45[P2 + P3]]] × [P2 − P1 + P3] |
| Rainy days | Besut | (P3 − P1 + P2) − 1.51(P3 × P2 − P1) + 1.14(P1 − P3 + sqrt(P1)) |
| Dungun | 1.23 × (P1 + P2) − 1.26(P3 × P2 − P1) + 0.86(P1 − P2) |
| Kemaman | 2.34 × P2 − 2.13(P3 × 1.54 − P1) + 1.45(P1 − P3 × P1) |
3.2.2. Downscaling Consecutive Wet and Dry Days
For downscaling of consecutive wet and dry days, a GP model was developed to predict whether rainfall will occur or not during a day. This produced a binary time series for the whole period, which was used to compute the consecutive wet and dry days in a year.
The GP model required different numbers of generations to give the highest overall hit rates at different stations. The best hit rates in downscaling rainy days at different stations is given in
Table 4. It can be seen from the table that GP-based logistic regression was successful in downscaling rainfall days in 83.9%–86.1% of cases during calibration and 80.2%–82.0% of cases during validation. The best tree structure produced by the GP in downscaling rainy days at Besut is shown in
Figure 5. The simplified equations obtained from the structures that can be used for downscaling rainy days at different stations are given in
Table 5.
Figure 5.
The tree structure representations of symbolic expressions produced by GP for the downscaling of rainy days at Besut (descriptions of
P1,
P2 and
P3 are given in
Table 3).
Figure 5.
The tree structure representations of symbolic expressions produced by GP for the downscaling of rainy days at Besut (descriptions of
P1,
P2 and
P3 are given in
Table 3).
3.4. Downscaling Using the SDSM
The SDSM package was also used to downscale daily rainfall with the same predictors used for GP (given in
Table 3). Daily rainfall data for the time periods 1961–1990 and 1991–2000 were used for calibration and validation of the SDSM, respectively. The extreme rainfall indices were then estimated from the daily rainfall downscaled by the SDSM. In the present study, extreme rainfall indices during the validation period were computed and compared with observed and GP-based downscaled results.
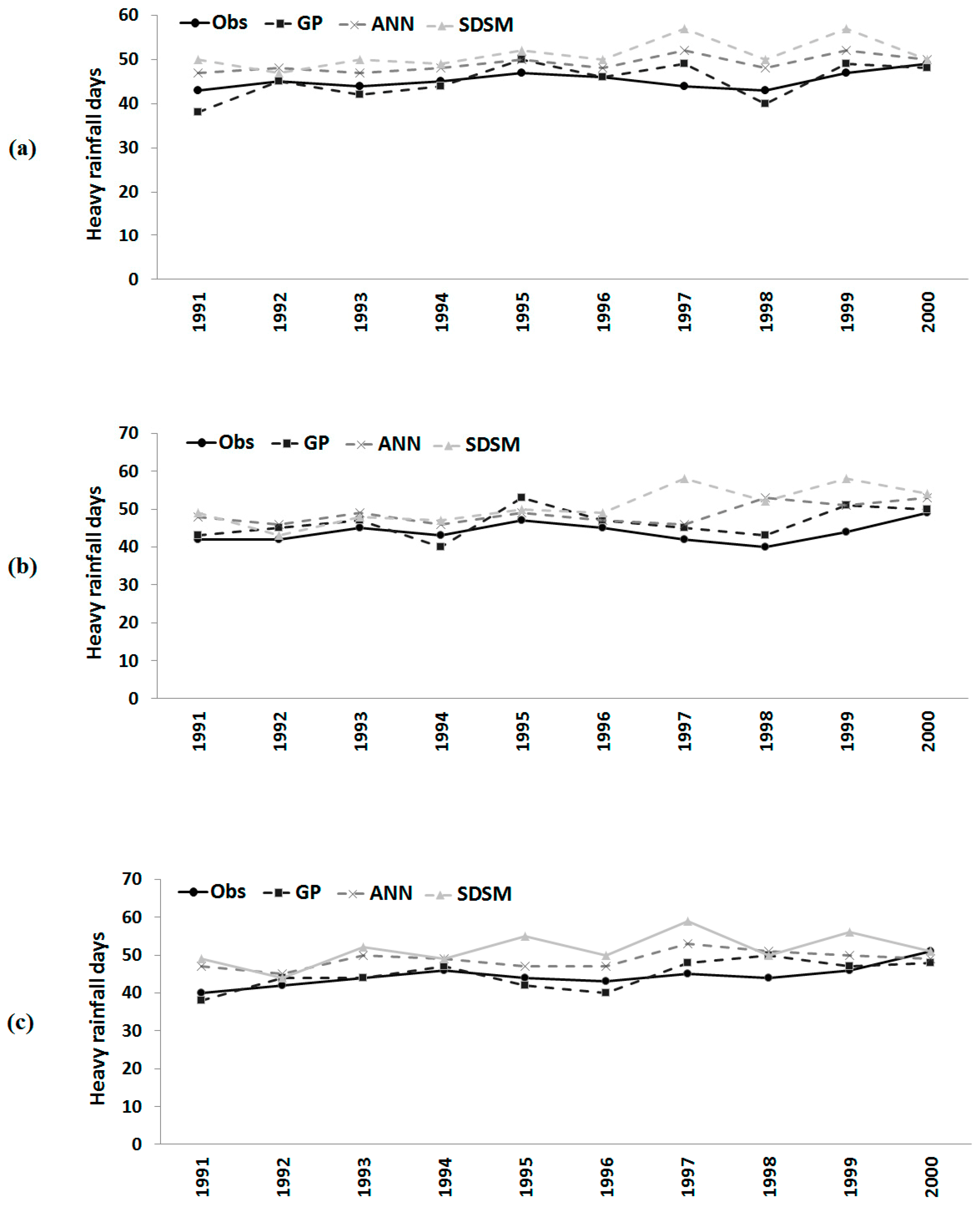
Figure 6.
Observed number of heavy rainfall days and those downscaled by GP, the ANN and the statistical downscaling model (SDSM) during model validation at: (a) Besut; (b) Dungun; and (c) Kemaman.
Figure 6.
Observed number of heavy rainfall days and those downscaled by GP, the ANN and the statistical downscaling model (SDSM) during model validation at: (a) Besut; (b) Dungun; and (c) Kemaman.
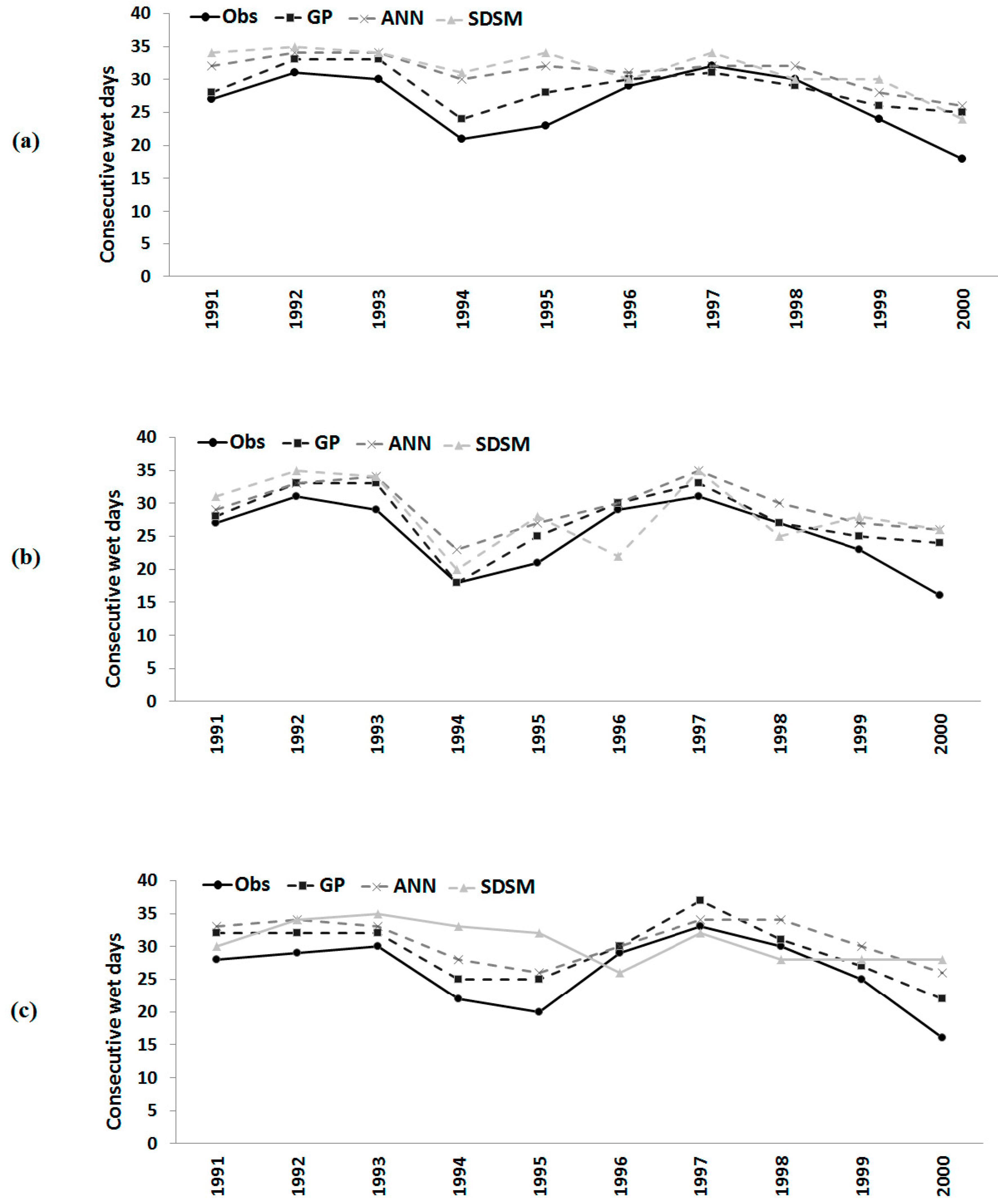
Figure 7.
Observed number of consecutive wet days and those downscaled by GP, the ANN and the SDSM during model validation at: (a) Besut; (b) Dungun; and (c) Kemaman.
Figure 7.
Observed number of consecutive wet days and those downscaled by GP, the ANN and the SDSM during model validation at: (a) Besut; (b) Dungun; and (c) Kemaman.
3.5. Comparison of Results
Comparisons of observed and downscaled heavy rainfall days during monsoon, as well as consecutive wet days and consecutive dry days in a year over the model validation period (1991–2000) are shown in
Figure 6,
Figure 7 and
Figure 8, respectively. It can be seen in
Figure 6 that all of the methods estimated the number of heavy rainfall days successfully over the evaluation period. However, the downscaled output from GP is closer to the observed values compared to those estimated by the ANN and the SDSM. In most of the years, both the ANN model and SDSM overestimated the number of heavy rainfall days. Compared to the ANN, the SDSM overestimated heavy rainfall days more often. On the other hand, GP underestimated the number of days in certain years, but the estimated GP values were found to be very close to observed values in almost all of the years and at all of the stations. The root mean squared error (RMSE) and correlation coefficient (expressed as r
2) between observed and downscaled values during validation are given in
Table 6. The table shows that the errors in estimation of the number of heavy rainfall days by GP are always significantly less compared to ANN and SDSM estimations. The correlation coefficient between observed values and GP downscaled values during the validation period was also found to be higher compared to ANN and SDSM downscaling.
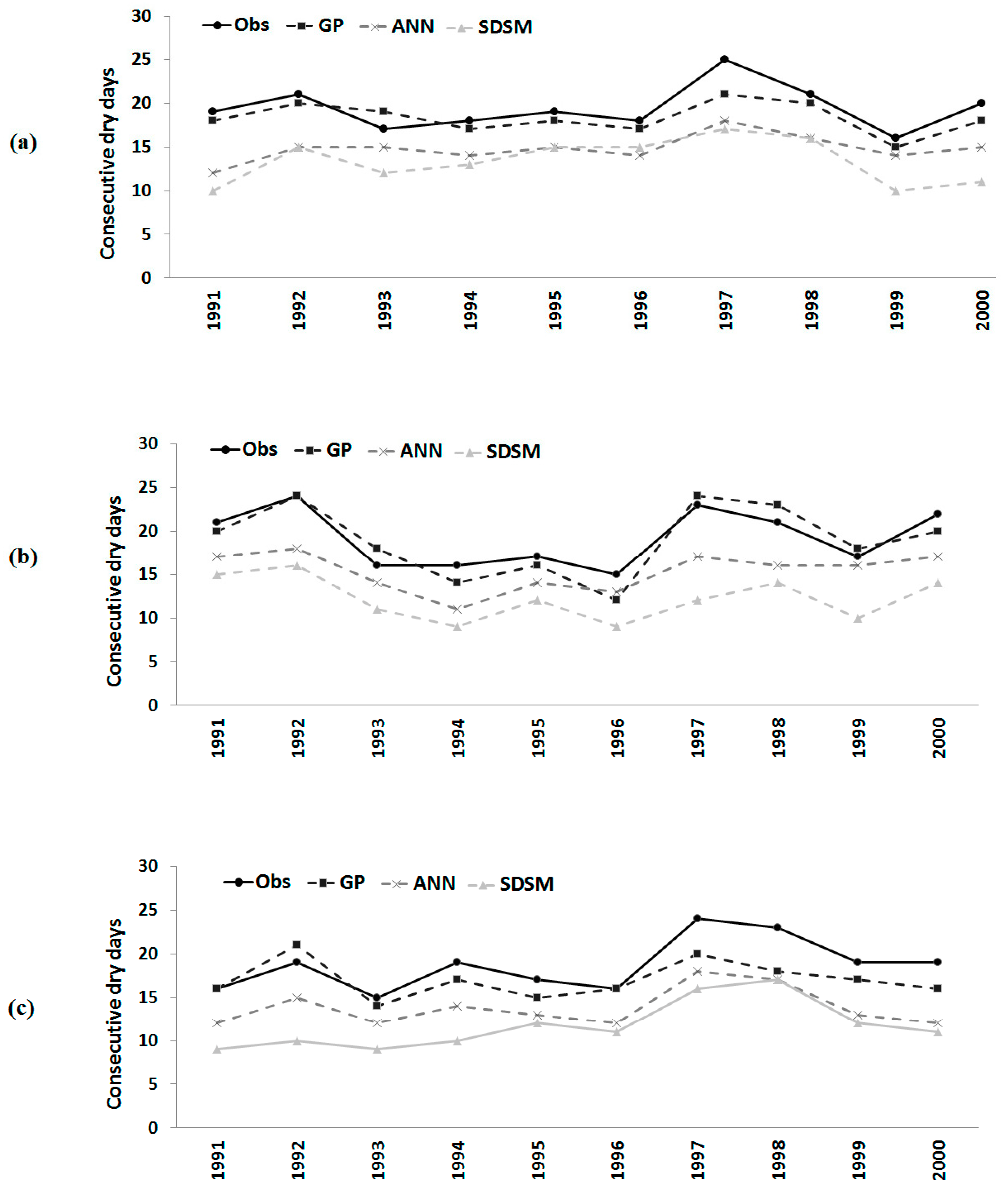
Figure 8.
Observed number of consecutive dry days and those downscaled by GP, the ANN and the SDSM during model validation at (a) Besut; (b) Dungun; and (c) Kemaman.
Figure 8.
Observed number of consecutive dry days and those downscaled by GP, the ANN and the SDSM during model validation at (a) Besut; (b) Dungun; and (c) Kemaman.
Similar results were obtained for consecutive wet days and consecutive dry days in a year. It can be seen from
Figure 7 that the number of consecutive wet days in a year was overestimated by the ANN model and SDSM in most of the years at all three stations during the validation period. GP also overestimated the number of consecutive wet days in certain years. However, GP downscaled values are found to be closer to observed values compared to those downscaled by the ANN and SDSM at all of the stations.
Table 6 shows that the errors in the number of consecutive wet days in a year estimated by GP is always significantly less compared to ANN and SDSM estimations. The correlation coefficient between observed and GP downscaled values during the validation period was also found to be higher.
Errors in GP downscaling of the number of consecutive dry days in a year were found to be similar to those in the estimations of the other two extreme indices. It can be seen from
Figure 8 that the downscaled number of consecutive dry days in a year by GP, the ANN and SDSM is less than the observed number of days in most of the years at all three stations. However, GP downscaled values are still found to be closer compared to those downscaled by the ANN and SDSM.
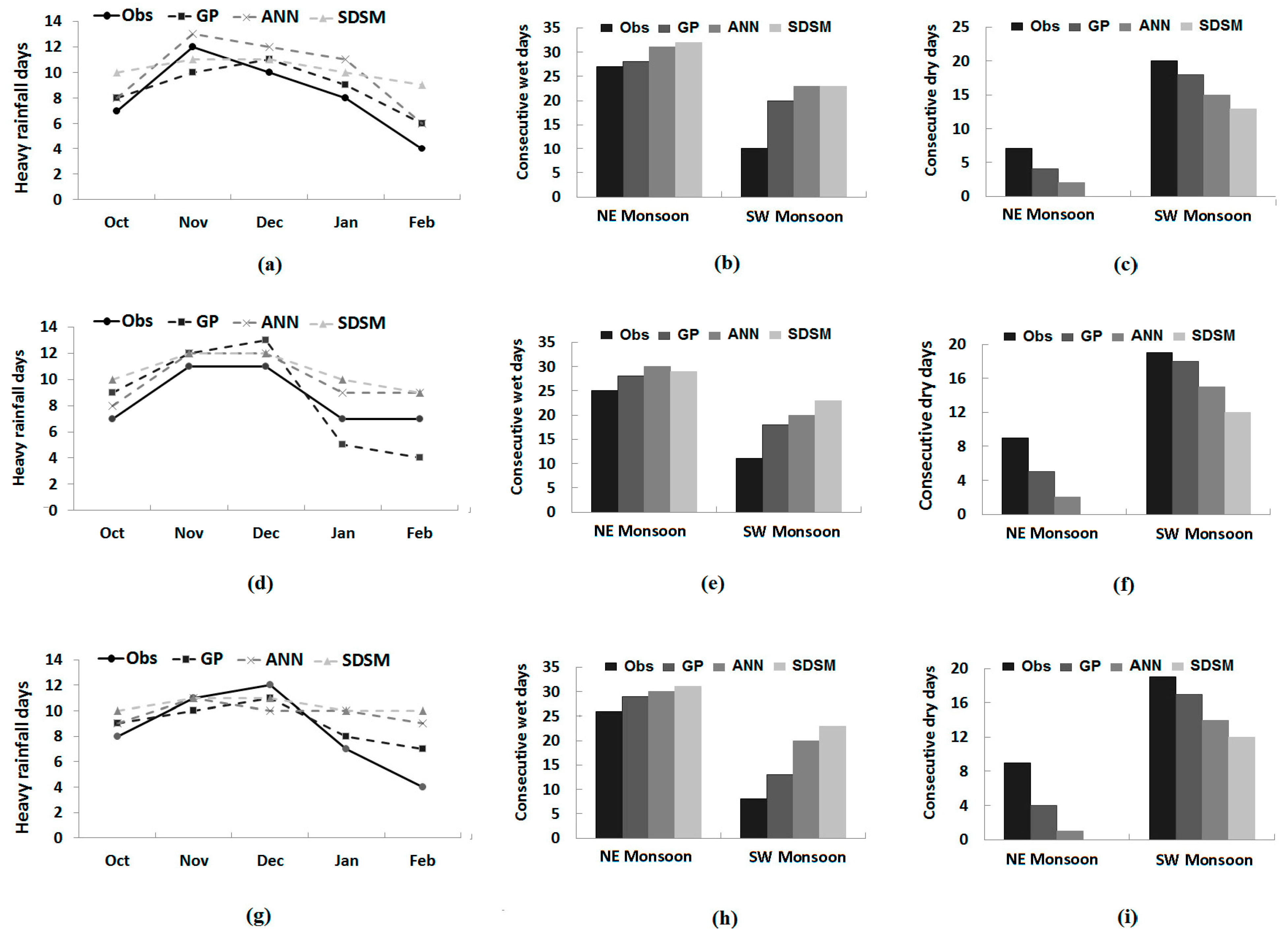
Comparison of observed and downscaled heavy rainfall days during different months of the NE monsoon, as well as continuous wet days and continuous dry days during NE and SW monsoons at different stations during model validation is shown in
Figure 9. It can be seen from
Figure 9 that seasonal or monthly variations in extreme rainfall indices are well reconstructed by GP compared to those by the ANN and SDSM. In the case of heavy rainfall days, the SDSM was found to downscale almost to the same number in all of the NE monsoon months. The ANN is able to show some variation in the number of heavy rainfall days, but not like GP. It can also be noted from the values in
Figure 9 that all of the methods overestimated the number of heavy rainfall days in most of the months. Still, the values estimated by GP are closer to the observed values compared to those estimated by the ANN and SDSM. The RMSEs between the observed and estimated number of heavy rainfall days using different methods during model validation are given in
Table 7. The table shows that the error in the estimation of the number of heavy rainfall days by GP is always less compared to the ANN and SDSM.
Table 6.
The RMSEs and correlation coefficients (r2) between observed and downscaled extreme indices estimated by GP, the ANN and the SDSM during model validation.
Table 6.
The RMSEs and correlation coefficients (r2) between observed and downscaled extreme indices estimated by GP, the ANN and the SDSM during model validation.
| Indices | Station | GP | ANN | SDSM |
|---|
| RMSE | r2 | RMSE | r2 | RMSE | r2 |
|---|
| 90th percentile rainfall days | Besut | 1.08 | 0.75 | 1.31 | 0.58 | 2.16 | 0.43 |
| Dungun | 1.14 | 0.73 | 1.83 | 0.58 | 2.69 | 0.41 |
| Kemaman | 1.13 | 0.67 | 1.62 | 0.61 | 2.57 | 0.51 |
| Consecutive wet days | Besut | 1.02 | 0.88 | 1.73 | 0.80 | 1.95 | 0.65 |
| Dungun | 1.05 | 0.89 | 1.54 | 0.83 | 1.74 | 0.61 |
| Kemaman | 1.10 | 0.96 | 1.66 | 0.92 | 2.20 | 0.46 |
| Consecutive dry days | Besut | 1.06 | 0.83 | 1.55 | 0.73 | 1.99 | 0.67 |
| Dungun | 1.04 | 0.91 | 1.65 | 0.87 | 2.28 | 0.85 |
| Kemaman | 1.23 | 0.82 | 1.60 | 0.82 | 2.26 | 0.77 |
Figure 9.
Monthly/seasonal distribution of: (a) heavy rainfall days, (b) consecutive wet days and (c) consecutive dry days at Besut; (d) heavy rainfall days; (e) consecutive wet days and (f) consecutive dry days at Dungun; and (g) heavy rainfall days, (h) consecutive wet days and (i) consecutive dry days at Kemaman.
Figure 9.
Monthly/seasonal distribution of: (a) heavy rainfall days, (b) consecutive wet days and (c) consecutive dry days at Besut; (d) heavy rainfall days; (e) consecutive wet days and (f) consecutive dry days at Dungun; and (g) heavy rainfall days, (h) consecutive wet days and (i) consecutive dry days at Kemaman.
Table 7.
The RMSE in downscaled seasonal extreme indices using GP, the ANN and the SDSM during model validation.
Table 7.
The RMSE in downscaled seasonal extreme indices using GP, the ANN and the SDSM during model validation.
| Indices | Station | GP | ANN | SDSM |
|---|
| 90th percentile rainfall days | Besut | 1.66 | 2.18 | 3.16 |
| Dungun | 1.68 | 2.35 | 2.45 |
| Kemaman | 1.80 | 3.12 | 3.54 |
| Consecutive wet days | Besut | 5.02 | 6.80 | 6.96 |
| Dungun | 3.81 | 5.15 | 6.32 |
| Kemaman | 2.92 | 6.96 | 7.91 |
| Consecutive dry days | Besut | 1.80 | 3.54 | 4.95 |
| Dungun | 2.06 | 4.03 | 5.70 |
| Kemaman | 2.69 | 4.72 | 5.70 |
The number of consecutive wet days in two major seasons (SW monsoon and NE monsoon) was overestimated by the ANN and SDSM during the validation period at all three stations (
Figure 9). GP also overestimated the number of consecutive wet days, but GP downscaled values were found to be closer to observed values compared to those downscaled by the ANN and SDSM in both of the seasons and at all of the stations.
Table 7 shows that the errors in estimation of seasonal consecutive wet spells estimated by GP are always less compared to those estimated by the ANN and SDSM. Errors in the downscaling number of seasonal dry spells are also found to be less for GP. It can be seen from
Figure 9 that downscaled lengths of seasonal dry spells estimated by GP, the ANN and the SDSM are lower than the observed number of consecutive dry days in both seasons at all of the stations. However, GP downscaled values were still found to be closer compared to those downscaled by the ANN and SDSM.