The Rectification of ENSO into the Mean State: A Review of Theory, Mechanisms, and Implications

Abstract

The El Niño–Southern Oscillation (ENSO) is the most consequential mode of interannual climate variability on the planet, yet its prediction has become complex due to the inability of classical paradigms to explain the observed co-evolution of the tropical mean state and interannual variability on decadal timescales. This article synthesizes the extensive research on ENSO rectification, exploring a paradigm that resolves this causality problem by recasting ENSO as an active architect of its own mean state. Tracing the intellectual development of this theory, starting from fundamental concepts such as the “dynamical thermostat” and “heat pump” hypotheses, modern analysis has identified the core physical mechanism as nonlinear dynamical heating (NDH), which is rooted in nonlinear heat advection during asymmetric ENSO cycles. The convergence of evidence from forced ocean models and observational diagnostics confirms a rectified signal characterized by an off-equatorial spatial pattern, providing a primary mechanism for tropical Pacific decadal variability (TPDV). By establishing a coherent framework linking high-frequency asymmetry with low-frequency variations, this review lays the foundation for future research and emphasizes the critical role of the rectification effect in improving decadal climate prediction.

1. Introduction

The El Niño–Southern Oscillation (ENSO) represents the dominant source of interannual climate variability on Earth, with profound global consequences [1,2]. These impacts manifest globally, ranging from the modulation of Atlantic hurricane season length, where La Niña conditions during autumn can foster an extended season [3], to significant disruptions of major regional climate systems [4,5,6]. For decades, the scientific understanding of this phenomenon has been rooted in Bjerknes’s [7] groundbreaking work, which first revealed that the air–sea positive feedback mechanism drives the development of warm and cold anomalies. In this classical paradigm, ENSO is regarded as a quasi-periodic, self-sustaining coupled system instability phenomenon, and its typical evolution process was extensively documented by Rasmusson and Carpenter [8]. This perspective has driven the development of powerful theoretical frameworks, such as delay oscillator theory [9] and recharge–discharge oscillator theory [10,11], and has been successfully reflected in intermediate complex models such as in Zebiak and Cane [12]. As summarized in the groundbreaking works of Philander [13] and Neelin et al. [14], the tremendous success of this paradigm has greatly propelled progress in climate prediction, making ENSO one of the most predictable climate phenomena on seasonal to interannual time scales [15,16]. From this perspective, the core focus of research is to understand how changes in the mean state, such as those driven by anthropogenic greenhouse gas warming, regulate the characteristics of ENSO variability [17,18]. This viewpoint implicitly considers the mean state as the main driving factor, with ENSO being its response.

However, this paradigm of one-way causal relationships is increasingly being challenged by a range of observational evidence that reveals a more complex and interactive system than imagined. The mean state of the tropical Pacific is not static and unchanging, but undergoes significant changes on decadal scale, a phenomenon widely known as the TPDV. The most notable event was the abrupt climate pattern shift around 1976, which altered the time-averaged conditions of the entire basin and was marked by a substantial increase in the amplitude and frequency of ENSO events [19,20]. Another significant shift occurred around 2000. Following this event, it was observed that the interannual variability of the tropical Pacific had weakened [21]. This significant low-frequency modulation is also a prominent feature in multi-millennium scale general circulation model (GCM) simulations [22], which has practical significance for predictability. As shown by Zheng et al. [23], the decadal variation of background state can significantly modulate the intensity of Bjerknes feedback, consequently changing the predictability time limit of ENSO. The co-evolution of observed background climate and its dominant interannual variability raises a fundamental “chicken and egg” question: Is the decadal warming in the Eastern Pacific a result or a cause of the increased ENSO activity? [19,24,25,26]. Answering this question is not merely an academic exercise. It is one of the central challenges in climate dynamics, as TPDV is a primary source of uncertainty in near-term global warming projections [27] and a key challenge for decadal predictions [26,28]. It is precisely this critical need to resolve the causality dilemma that motivates this review.

The complexity of the problem is further exacerbated as people realize that ENSO itself is not a single, perfectly periodic oscillation. Numerous studies have confirmed its profound diversity, irregularity, and asymmetry [18]. The identification of distinct types of El Niño events, with different dynamic and teleconnection characteristics, challenges the notion of a single unified mechanism [29,30,31,32]. In addition, the significant asymmetry between oscillation phases, where strong El Niño events are usually stronger and structurally different than strong La Niña events, cannot be fully explained by linear oscillator theory [33,34]. This has led to an alternative view of ENSO that it acts as an internally stable mode rather than a self-sustaining oscillator whose irregularity is reflected by high-frequency random atmospheric forcing excitation [35]. This type of forcing is typically associated with western wind bursts and is now considered a key factor in generating ENSO diversity and extreme phenomena [36,37]. These complexities bring significant obstacles to prediction, with a well-known example being the spring predictability barrier. This phenomenon is related to annual cycles, specific structures of initial errors, and nonlinear growth [38,39,40]. The classical linear paradigm cannot fully explain TPDV, and the diversity and asymmetry of ENSO highlight the necessity of constructing a more comprehensive framework.

The key to solving this causal puzzle lies in a new framework that redefines ENSO as an active architect that shapes its own mean state, rather than a passive anomaly. This alternative paradigm is based on the ENSO rectification theory, which suggests that the transient and asymmetric oscillations of ENSO will leave permanent non-zero influence in the time-averaged climate. The physical basis of rectification is the asymmetry that is difficult to explain by linear theory. Driven by nonlinear processes in the ocean and atmosphere, the impacts of El Niño and La Niña on the climate system do not cancel each other out on a multi-year timescale. On the contrary, they leave behind a rectified or residual signal that systematically alters the long-term average state [41,42]. This process provides a powerful internal physical mechanism for the generation of low-frequency decadal climate anomalies due to high-frequency interannual variability. As shown by Kim and Kug [43] in their comprehensive multi-model analysis, this ENSO residual spatial pattern is surprisingly similar to the observed zonal dipole pattern of TPDV, directly solving the problem of “chicken and egg.”

This review synthesizes the body of literature that has developed and tests the theory of ENSO rectification. We first trace the theoretical origins of ENSO regulatory perspective, from the fundamental concept of tropical “dynamical thermostat” to the first direct confirmation of its stabilizing effect on mean climate through numerical simulations. Subsequently, we follow the scientific process to explain how the theory was formalized, how the primary physical mechanisms were identified, and the characteristic spatial pattern of the rectified signal through multilevel models and observational analysis is confirmed. Finally, we explore the frontiers of this research, including the significant challenges faced by current state-of-the-art climate models in simulating rectification processes, their controversial role in the broader framework of TPDV, and the profound impact of this paradigm on model development, decadal prediction, and projection of future climate change responses in the tropical Pacific. We argue that treating ENSO as a fundamental nonlinear regulator of its own background state is crucial for advancing our understanding of coupled climate systems.

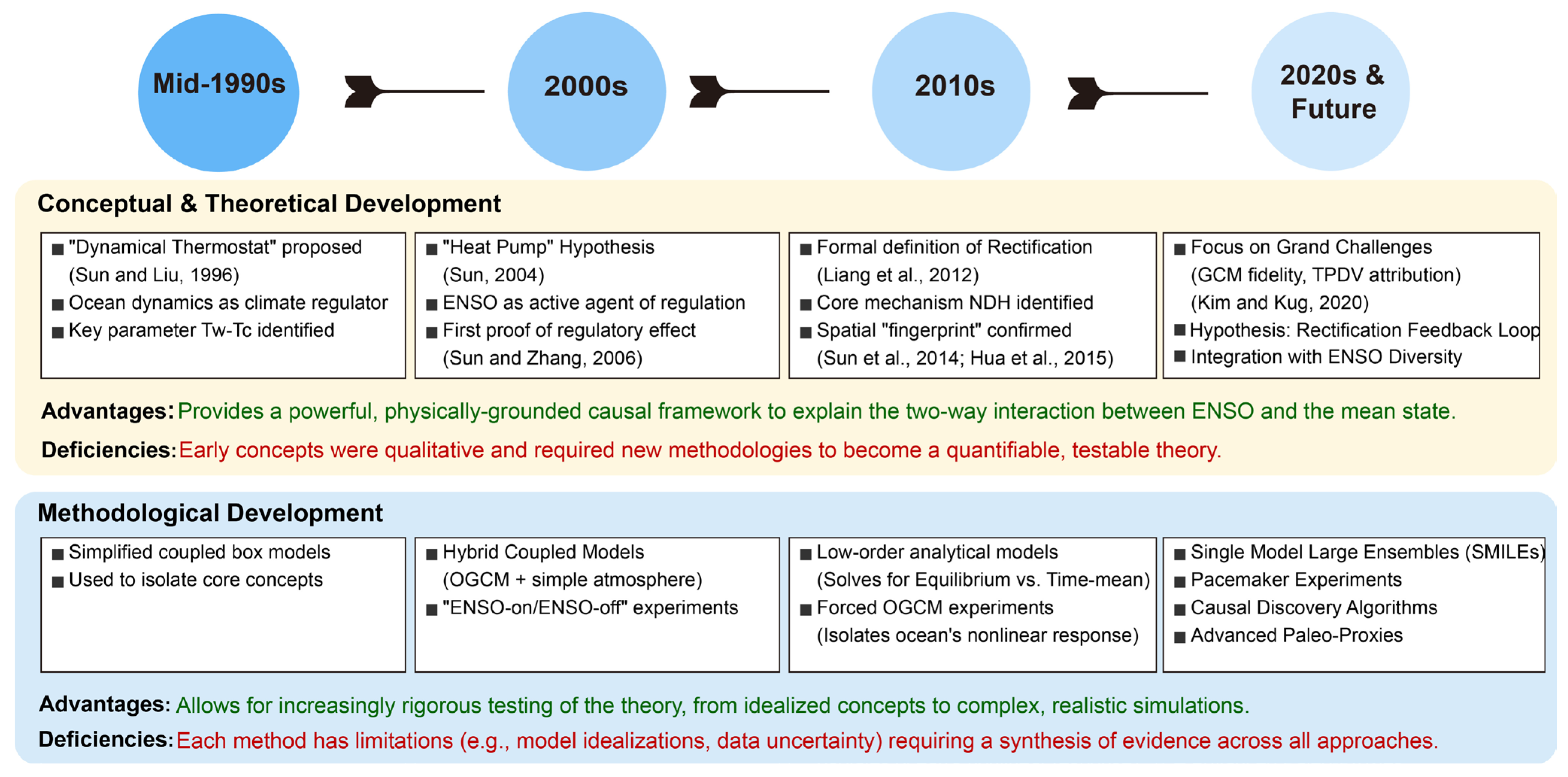
2. Conceptual Origins of the Regulatory View

The theory of ENSO rectification was not a sudden breakthrough, but rather the culmination of a deliberate and progressive intellectual shift. This shift challenged the traditional view of the tropical climate system at the time, which believed that the system was dominated by a relatively static average state that governed variability behavior. This process began with a fundamental rethinking of the thermal balance process in the tropical Pacific, shifting the research focus from simple atmospheric feedbacks to the complex dynamics of coupled ocean–atmosphere systems. This new perspective has given rise to a regulatory perspective in which ENSO is no longer seen as a simple instability, but as a key and active participant in maintaining the long-term stability of its own background climate.

The first major step in this paradigm shift was the concept of “dynamical thermostat” proposed by Sun and Liu [44]. This concept can be understood through an analogy with a home thermostat. The entire tropical Pacific is constantly being heated by an external forcing, solar radiation. A simple response would be for the entire basin to warm uniformly. The ocean–atmosphere system, however, possesses an intrinsic cooling mechanism: the upwelling of cold, deep water in the eastern Pacific, which acts like a powerful air-conditioning vent. The thermostat controlling this vent is the Bjerknes feedback. As the basin warms, the east–west temperature gradient strengthens, which in turn intensifies the Walker circulation and associated trade winds. These stronger winds drive more vigorous upwelling, effectively turning up the air-conditioning in the east to counteract the heating and maintain a stable basin-wide temperature. This elegant concept redefined the stability of the tropical Pacific climate, identifying the vertical thermal contrast between the warm western surface (Tw) and the cold upwelled water (Tc) as the fundamental parameter that sets the system’s sensitivity.

This new framework set the stage for the “heat pump” hypothesis, which explicitly casts the ENSO cycle itself as the primary agent of regulation [45]. If the dynamical thermostat is the system’s steady-state regulator, the heat pump is its episodic pressure-release valve. The process can be visualized as a cycle, beginning with a recharge phase during La Niña or neutral conditions. During this period, the strong and steady trade winds continuously push warm surface water to the west, causing heat energy to accumulate in the subsurface of the western Pacific and progressively increasing the unstable Tw–Tc contrast. Once the system becomes sufficiently unstable, an El Niño event is triggered, acting as a massive discharge of this accumulated heat. The event not only sloshes warm water eastward across the surface, but critically, transports it poleward and mixes it downward into the deeper ocean, effectively purging the excess heat from the equatorial system. This hypothesis provided a compelling narrative: if an external forcing attempts to destabilize the system, the natural response is to trigger a more powerful discharge—a stronger El Niño—to maintain long-term thermal balance. In this view, ENSO is not a malfunction, but a necessary and fundamental negative feedback, the climate’s machinery for self-regulation.

Although this hypothesis is highly convincing conceptually, it still requires direct experimental verification. Sun and Zhang [46] provided conclusive evidence for the first time through a series of innovative numerical experiments conducted in a mixed coupled model. Their research method aimed to unambiguously isolate the regulatory role of ENSO. They conducted paired simulations: in the “ENSO-on” experiment, the ocean and atmosphere were fully coupled, allowing ENSO to form naturally. In the parallel “ENSO-off” experiment, the coupling of equatorial wind and sea surface temperature (SST) was artificially suppressed, preventing the formation of ENSO. When external unstable forces corresponding to enhanced tropical heating were applied to the two experiments, the results were drastically different. In the “ENSO-off” world, the system is in a passive state: Tw–Tc contrast shows a sensitive and linear increase in response to forcing. However, in the “ENSO-on” world, the system exhibits active response. It is not a change in the average state, but a change in variability: the model produces stronger El Niño events. These more powerful events are more effective in mixing heat, warming the thermocline (Tc) while cooling the surface (Tw), resulting in almost no external forcing on the time-averaged Tw–Tc contrast. The physical mechanism behind this buffering is that ENSO acts as a basin-scale heat mixer, transporting anomalous heat from the surface deep into the subsurface thermocline, a process shown in Figure 1. This is the first direct and clear demonstration of the positive regulatory effect of ENSO on its own background state. Experiments have shown that in a world with ENSO, the average state of the tropical Pacific is highly resilient, as the oscillations themselves actively buffer the system from external disturbances by adjusting their amplitude. This study provides decisive modeling evidence for the heat pump hypothesis, completing the theoretical transition from a static, atmosphere-centered tropical climate perspective to a dynamic regulation framework centered on a coupled ocean–atmosphere system. The progress from the development of hypothesis to experimental verification lays the conceptual and empirical foundation for formalizing and quantifying this regulatory effect through rectification theory.

While these foundational concepts were instrumental in shifting the paradigm toward a regulatory view of ENSO, their limitations must be recognized. Both the “dynamical thermostat” and the “heat pump” were primarily qualitative and descriptive frameworks. They provided a powerful new narrative for understanding the two-way interaction between ENSO and the mean state, but they lacked a rigorous, quantitative method for diagnosing the net effect of this interaction from data or models. Furthermore, these early concepts did not inherently address or explain the source of ENSO asymmetry, which would later be identified as the essential ingredient for producing a non-zero rectified signal. In essence, these hypotheses brilliantly established that ENSO regulates its background state, but they could not fully explain how this process worked or provide a method to precisely measure it. This gap highlighted the urgent need for a new theoretical framework that could formalize and quantify the rectification effect, a challenge that the field would address in the following decade.

3. The Formal Theory and Physical Mechanism

The conceptual framework constructed by the dynamical thermostat and heat pump hypothesis provides a convincing and qualitative description of the regulatory role of ENSO. However, in order to transform this attractive concept into a rigorous scientific theory, a new conceptual framework is necessary to enable a precise quantitative assessment of ENSO’s net influence on the mean climate and to identify its main physical mechanisms. This critical step involves a methodological innovation in which the effects of ENSO should be separated from the background state, and also a detailed analysis of the ocean thermal balance to determine the source of the rectified signal.

3.1. The New Framework: Quantitative Assessment of the Rectification as the Difference Between the Time-Mean Value and the Equilibrium State

The main challenge in diagnosing the impact of ENSO based on observational data or standard climate models is that the observed climatological state is not purely a background state. In fact, it is a time-averaged state in which the constant effects of several interannual variabilities are embedded. It is not possible to simply subtract ENSO anomalies from the records to determine the background, since the background itself is determined by these anomalies. This analytical difficulty requires a new approach to defining a hypothetical state without ENSO for comparison with the actual climate.

The breakthrough in methodology came from the research of Liang et al. [24], who utilized a low-order, but physically comprehensive analytical model of a coupled tropical Pacific system. The model is simple enough in that its steady-state solution can be obtained through mathematical derivation, while also being complex enough to generate self-sustaining oscillations similar to ENSO oscillations. This enables them to define and compare two vastly different climate states. The equilibrium state is the steady state, a non-oscillatory state that a system is in where Bjerknes feedback is insufficient to induce instability. Although this state can be obtained through mathematical derivation, it is unstable under current climate conditions and therefore unobservable in nature. It represents the real background climate that is not affected by oscillations. The time-mean state is the long-term average of variables that the model operates in an oscillatory, ENSO-active regime. This state is equivalent to the model’s equivalence of observational climatology.

The rectification effect is then strictly and explicitly defined as the discrepancy between the time-mean state and the equilibrium state. From their low-order model, Liang et al. [24] derived an analytical expression that directly links these two states:

$$\overline{T_2}\approx T_{2\mathrm{e}\mathrm{q}}+{\displaystyle \frac{\overline{T_2^{\mathrm{\prime }2}}}{\overline{T_1}-\overline{T_2}}}$$

(1)

where $\overline{T_2}$ is the time-mean SST in the eastern Pacific, $T_{2\mathrm{e}\mathrm{q}}$ is its corresponding equilibrium value, $\overline{T_2^{\mathrm{\prime }2}}$ is the variance of SST anomalies in the eastern Pacific (a measure of ENSO amplitude), and $\overline{T_1}-\overline{T_2}$ is the time-mean zonal SST gradient. This result provides the first formal, quantitative proof that the net effect of ENSO is to create a mean climate that is fundamentally different from the underlying equilibrium. Equation (1) shows mathematically that the rectified warming (the second term) is directly proportional to the amplitude of the ENSO oscillations. Their findings directly address the “chicken and egg” problem, pointing out that the decadal warming in the eastern tropical Pacific in recent decades may be more of a result of enhanced ENSO activity during the same period, rather than its cause. This framework also provides a powerful explanation for the difficulty in detecting clear external forcing trends in indicators such as zonal SST gradient in observations: the regulatory role of ENSO rectification mechanisms may be actively offsetting or masking forcing signals.

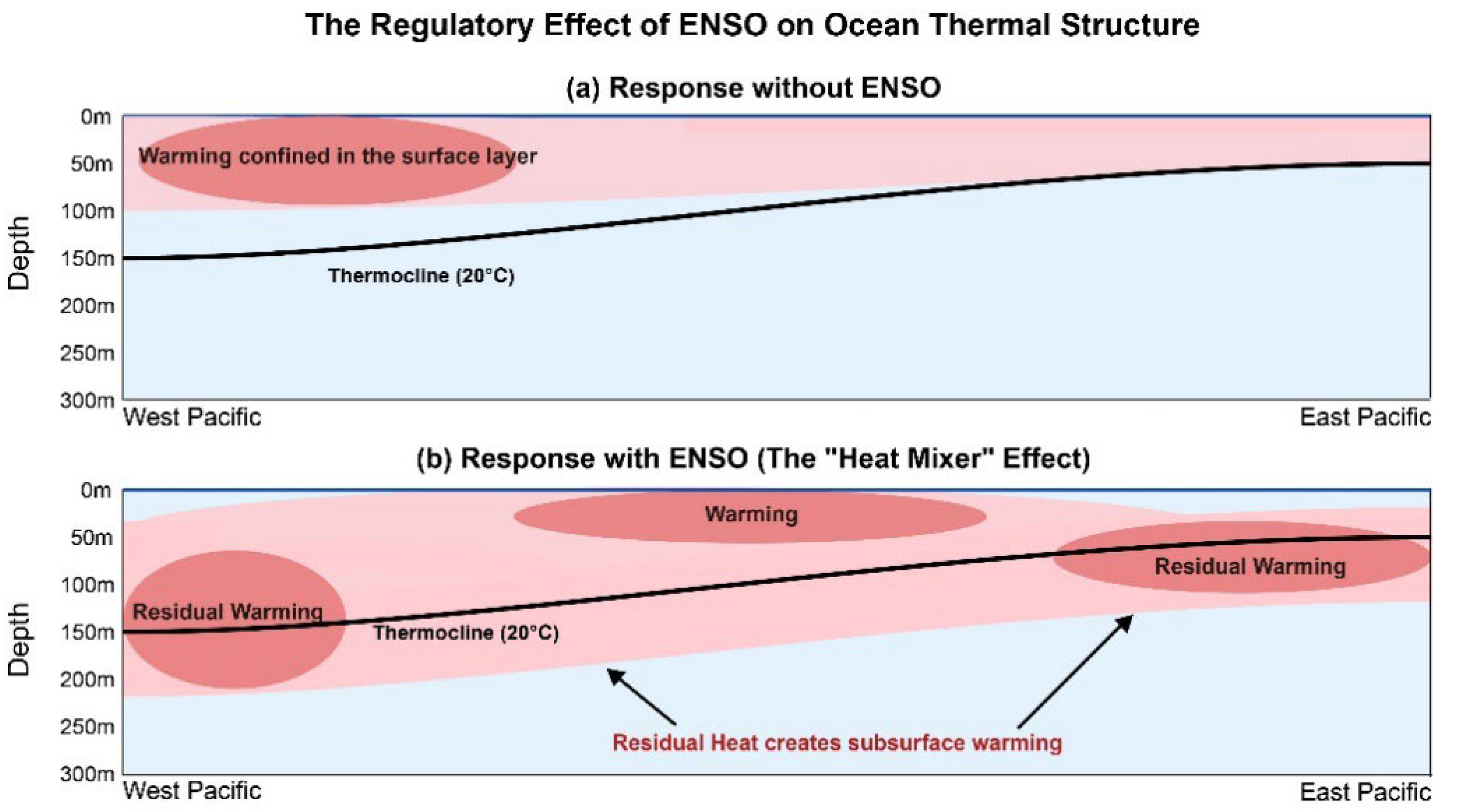
3.2. Pinpointing the Cause: Nonlinear Dynamical Heating as the Core Physical Process

After proving the existence of rectification phenomenon, the next step is to determine how it occurs. By systematically analyzing the various terms of the upper-ocean thermal budget equation in the model, Liang et al. [24] identified nonlinear heat conduction as the core physical process causing this phenomenon. In a purely linear system, the response of the ocean to El Niño warming and La Niña cooling should be completely symmetrical and their effects cancel each other out over time. However, the governing equations of fluid dynamics are essentially nonlinear. The key term they identified is the time-mean nonlinear advection of heat, which can be expressed as:

NDH = −⟨v′·∇T′⟩

(2)

where NDH is the nonlinear dynamical heating, the angle brackets ⟨ ⟩ denote a long-term time average, v′ represents the anomalous ocean currents (the deviation from the time-mean), and ∇T′ is the gradient of the anomalous temperature.

NDH can be intuitively understood as the net effect of anomalous currents flowing across anomalous temperature gradients. For example, a persistent anomalous eastward current (v′ > 0) flowing into a region with an anomalous warm gradient (∇T′ < 0, i.e., warmer water upstream) will produce a net warming effect. Because the strength and patterns of both the anomalous currents and the temperature gradients are different between El Niño and La Niña (i.e., they are asymmetric), their product does not average to zero over many cycles. This non-zero residual constitutes the rectified signal that systematically heats or cools the mean state over time.

While nonlinear advection is considered the dominant dynamical driver of rectification, it should be noted that other nonlinear processes have been proposed. For instance, Schopf and Burgman [41] described a kinematic mechanism, whereby a symmetric oscillation of the thermocline against a nonlinear mean vertical temperature profile can produce asymmetric surface temperature anomalies and a non-zero residual. However, the majority of evidence from both analytical models and GCM heat budget analyses points to the dynamical process of NDH as the primary contributor. The detailed heat budget analysis conducted by Su et al. [47] decomposed this item and found that the nonlinear zonal and meridional temperature advection were the primary contributing factors to the anomalous positive skewness of the east Pacific SST, while the nonlinear vertical advection may actually produce the opposite symmetry effect. This discovery is crucial, as it elevates the explanation of rectification from a statistical attribute, namely the observational asymmetry of ENSO, to a specific physical process rooted in the original equations of ocean dynamics. The importance of this mechanism has been strongly supported by other research. For example, Duan et al. [34] emphasized the decisive role of nonlinear temperature advection in explaining ENSO amplitude asymmetry. Hayashi and Jin [48], in a follow-up study, provided strong evidence for the role of subsurface NDH by using ocean reanalysis data. They found that there is a sharp increase in NDH near the equatorial thermocline after the peak of a strong El Niño event, which weakens the subsequent La Niña event and directly leads to the asymmetry and net rectification warming of ENSO. Kohyama and Hartmann [49] further proposed the concept of nonlinear ENSO warming suppression and suggested that this NDH is essential for the occurrence of extreme El Niño events, and that its potential weakening under global warming may lead to average state changes similar to La Niña. The multi-model study by Kim and Kug [43] confirmed the central role of this mechanism. They found that in models with strong ENSO asymmetry, the spatiotemporal pattern of time-mean NDH caused by ENSO anomalies was highly consistent with the dipole pattern dominated by the model’s decadal variability pattern.

The role of NDH is not merely theoretical—it is also vividly demonstrated in the evolution of extreme El Niño events, with the 1997–1998 event being a typical case study. The event is characterized by unprecedented eastward expansion of the western Pacific warm pool and intense deepening of the equatorial thermocline, creating ideal conditions for strong nonlinear advection [50]. Hayashi and Jin [48] used ocean reanalysis products to diagnose and analyze this event, directly confirming this process. They found that after the surface warming of the event reached its peak, there was a strong outbreak of subsurface NDH near the thermocline. This strong subsurface warming rapidly discharged accumulated heat, which played a key role in the subsequent weakening of La Niña events. This process directly led to significant asymmetry in the 1997–1999 ENSO cycle and net rectified warming in the mean state. Therefore, the 1997–1998 event provided clear observational evidence for NDH as a powerful physical process that actively shapes the life cycle and asymmetry of major ENSO events.

3.3. The Role of ENSO Asymmetry in the Rectification Process

It is critical to emphasize the distinction between the root cause of rectification and its behavioral manifestation. The ultimate cause of rectification is the inherent nonlinearity of the coupled climate system—the processes described in Section 3.2 that break the perfect symmetry of a linear world. ENSO asymmetry, whereby strong El Niño events are significantly stronger and often spatially different from strong La Niña events, is the direct manifestation of the underlying nonlinear dynamics [33]. Therefore, asymmetry is not the root cause of rectification, but rather the crucial proximate mechanism through which it operates. A perfectly symmetric, linear oscillation would average to zero over time: this is the asymmetry of the cycle that ensures a non-zero residual is left behind, thus driving the rectification process. This asymmetry arises from a confluence of deterministic nonlinearities, such as the nonlinear response of atmospheric deep convection to SST [51], the nonlinear relationship between wind speed and wind stress, and asymmetric thermodynamic damping from surface heat fluxes [52]. Superimposed on these deterministic processes is high-frequency, stochastic atmospheric forcing. The key is that this noise is not simply additive, but state-dependent. For example, westerly wind bursts tend to be more frequent and intense under warm background conditions, resulting in multiplicative or semistochastic feedback that preferentially amplifies El Niño events [36,37,53]. In fact, the specific timing and intensity of these wind bursts have proven to be important factors in determining the diversity of the development of El Niño events [54]. As shown by Levine et al. [55], this state-dependent noise forcing is a powerful mechanism for generating El Niño-La Niña asymmetry and is particularly essential for generating extreme El Niño events. In a novel approach, Martinez-Villalobos et al. [56] showed that the observed El Niño–La Niña asymmetry can be reproduced in an entirely linear model as long as it is driven by this correlated additive multiplicative noise, highlighting the important impact of the structure of the noise itself. A comprehensive analysis of these processes shows that the asymmetry driving rectification is a complex emergent property. As shown by Geng and Jin [57] in models of intermediate complexity, the parametric space for obtaining a real positive asymmetry is a relatively narrow and specific region, which gracefully explains the persistent difficulties encountered by many GCMs to simulate this fundamental characteristic.

4. Evidence from Models and Observations

The formal theory of ENSO rectification based on the NDH mechanism presents a clear and verifiable hypothesis: in the presence of ENSO, there is a significant difference between the time-mean state of the tropical Pacific and the assumed equilibrium state without ENSO. To verify this hypothesis, we need to go beyond theoretical models and look for evidence in more complex and realistic systems. This section integrates key evidence from two major research areas: controlled experiments using advanced ocean general circulation models (OGCMs) and advanced diagnostic analysis of observation and reanalysis datasets. These research clues provide robust and consistent validation of rectification effects and their characteristic signatures in the climate system.

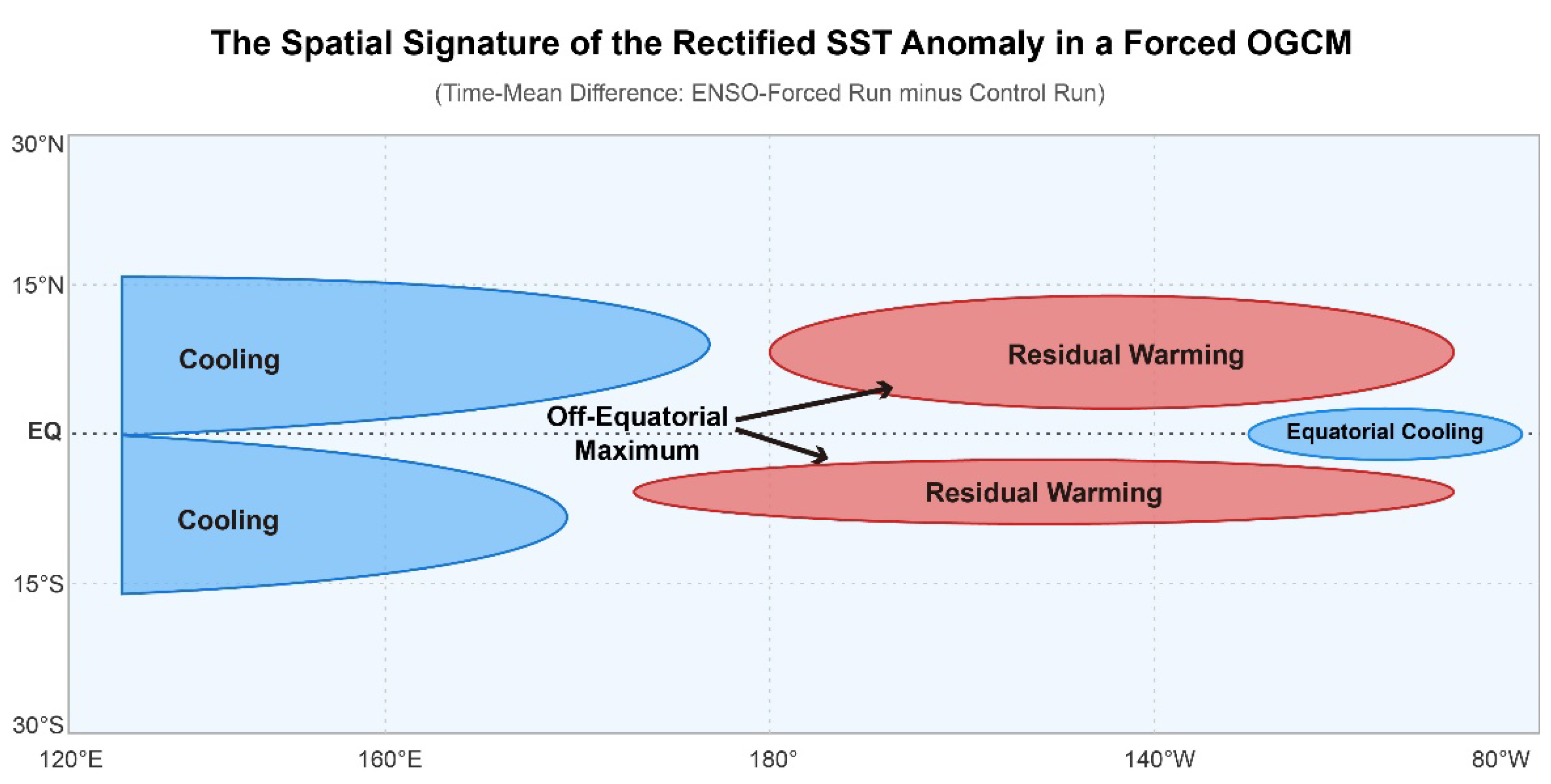
4.1. Evidence from OGCMs

The most direct and powerful test of the rectification hypothesis was performed using numerical experiments with OGCMs. These experiments provided the closest simulations to controlled laboratory studies, making it possible to definitively isolate the effects of ENSO variability. The main method, pioneered by Sun et al. [25], involves a pair of simulations designed to be identical in all respects, the only difference being the presence or absence of wind forcing associated with ENSO. The control experiment forces the OGCM with climatological mean surface wind stress, representing a baseline climate state that does not contain interannual atmospheric variability. In contrast, the perturbation experiment uses the same OGCM, but imposing the same climatological mean wind stress plus the observed interannual wind stress anomalies over a multi-decadal period, which represents a climate state with a real history of ENSO events.

By construction, the long-term mean atmospheric forcing applied to both simulations is the same. In a linear ocean system, the resulting time-mean oceanic state should also be the same. However, the research results of Sun et al. [25] showed significant and systematic differences. The runs that include ENSO variability show that the western Pacific warm pool is colder, the subsurface thermocline is warmer, and most importantly, the surface temperature in the eastern Pacific is higher than controlled runs. The robustness of these findings was subsequently validated by Hua et al. [58] using another OGCM model that included complete seasonal cycles. Their research not only replicated key results, but also provided deeper mechanistic insights through heat budget analysis, indicating that the pattern of time-mean NDH terms closely matches the rectified temperature change pattern.

The key finding of these forced OGCM experiments is the distinction between true rectified signals and simple diagnostic indicators known as ENSO residuals. The residuals are usually calculated by linearly summing the composite SST patterns of El Niño and La Niña, with the maximum asymmetric signals centered on the equator. In sharp contrast, the dynamically driven rectified signal revealed in OGCM exhibits a significant peak of warming outside the equator. As Sun et al. [25] pointed out in their analysis, this difference has profound significance: it indicates that the rectification process is not simply a linear addition of surface anomalies, but a unique spatial fingerprint generated by complex nonlinear ocean dynamics. It is this off-equatorial pattern rather than equatorial residuals that bears a striking resemblance to the observational structure of the TPDV, providing the strongest evidence that the rectification may be the key physical mechanism for its generation (Figure 2).

The experimental evidence from forced OGCMs is consistent with the analysis of long-running, freely evolving coupled GCMs. For example, Choi et al. [59] analyzed TPDV in multiple CGCMs and were able to distinguish between “ENSO-like TPDV,” which derives from slower and intrinsic oceanic adjustments, and “ENSO-induced TPDV,” which is closely associated with decadal modulation of ENSO amplitude and represents rectified residuals of ENSO. In a subsequent comprehensive multi-model analysis, Kim and Kug [43] confirmed that a large group of Coupled Model Intercomparison Project (CMIP5) models with strong ENSO asymmetry internally generate a TPDV mode characterized by a zonal dipole closely resembling the ENSO residual pattern. These studies collectively indicate that the rectified effect of ENSO is an identifiable and important source of decadal variability in fully coupled climate models.

4.2. Evidence from Observational and Reanalysis-Based Analyses

Although the OGCM experiment provides a controlled environment, it is more difficult to confirm the existence of rectification phenomena in the real world due to the inability to observe the equilibrium state. Therefore, researchers have developed a series of clever diagnostic techniques to separate rectified signals from observed and reanalyzed data products. These methods provide evidence that the rectification effect is not just about model construction, but about observing active processes in the climate system.

One of the earliest methods was to diagnose ENSO residuals. As outlined by Choi and An [42], this method decomposes the observed SST records into low-frequency (decadal variation) and high-frequency (ENSO) components through statistical decomposition. They found statistically significant non-zero residuals in the time-averaged ENSO components, which were correlated with the decadal variation of ENSO skewness. A more direct physical method is to calculate NDH directly from modern high-resolution ocean reanalysis products. A key study by Liu et al. [60] established a clear lead–lag relationship and found that the NDH signal consistently led the quasi-decadal SST anomaly by about 30 months, providing strong causal evidence for the rectification effect driving low-frequency variability. The third new technique is to construct a rectification-free background state through statistical methods, as shown by Huang et al. [61]. This method independently confirms that the observed average state is warmer in the eastern Pacific, which is a direct consequence of asymmetric El Niño events. These techniques represent a clear evolution in diagnostic approaches. While the early ENSO residual method provided the first statistical hint of a rectified signal, its physical basis was indirect. The subsequent move to direct calculation of NDH from reanalysis marked a significant advance by grounding the analysis in the ocean’s physical heat budget. The most recent statistical reconstruction methods offer a third, independent line of evidence, confirming the findings of the physical diagnostics through a completely different methodological lens.

These targeted diagnostic analyses are strongly supported by a broader analysis of the decadal changes observed in the tropical Pacific. For example, McPhaden [62] documented a significant shift in the relationship between upper-ocean warm water volume, a key precursor to ENSO, and SST anomalies since the 21st century, indicating a correlation between shortened lead times and increased frequency of central Pacific (CP) El Niño events. Similarly, Wen et al. [63] found that the relationship between the depth of the thermocline and ENSO has undergone significant changes since 1999 and is increasingly influenced by regions outside the equator. In addition, robust decadal scale variations have been identified in large scale circulation features such as the bifurcation of the North Equatorial Current that are highly correlated with the TPDV index in multiple ocean reanalysis products [64]. The long-term control simulation using GCMs also provides a laboratory environment for studying these interactions. Okumura et al. [65] analyzed the 1300-year simulation run of the Community Climate System Model 4.0 and found that El Niño and La Niña phenomena exhibit significant asymmetric modulation, which is closely related to the TPDV generated within the model. Although these studies did not isolate the rectification mechanism like targeted diagnosis, they collectively outline a system undergoing significant, physically coherent decadal-scale reorganization, providing the necessary real-world background for the TPDV explained by the rectification mechanism. In addition, other nonlinear processes, such as tropical instability waves (TIWs), which have decadal changes in their behavior, also contribute to the heat budget of the equatorial cold tongue in a nonlinear way [66].

4.3. Synthesis of Evidence and Methodological Caveats

The diverse and independent lines of investigation presented above, ranging from the controlled environment of forced OGCMs to the statistical and physical diagnostics of reanalysis data, converge on a consistent and robust picture, though the evidence from controlled OGCM experiments is arguably more direct and convincing for isolating the physical mechanism. The evidence overwhelmingly supports the conclusion that ENSO, through the mechanism of nonlinear ocean dynamics, actively rectifies its variability into the mean climate. However, a critical assessment requires acknowledging the inherent limitations and uncertainties associated with each approach. The forced OGCM experiments, while powerful in their ability to isolate the rectified signal, are by design an idealized representation of the climate system. The ocean-only configuration neglects potentially important coupled feedbacks from the atmosphere that could either dampen or amplify the rectified response in the real world. Furthermore, the results are sensitive to the fidelity of the wind stress forcing used and the specific physics and biases of the OGCM itself.

On the other hand, while observational and reanalysis-based analyses provide a real-world perspective, they face their own set of significant uncertainties. Ocean reanalysis products, which are a blend of models and sparse observations, can have substantial disagreements, particularly in subsurface velocity and temperature fields prior to the widespread deployment of the Argo float array in the early 2000s. These data uncertainties can directly impact the accuracy of NDH budget calculations. Moreover, the instrumental record is relatively short, making it challenging to robustly separate internal decadal variability, such as that generated by rectification, from externally forced long-term trends or from lower-frequency internal variability that may not be related to ENSO. Despite these caveats, the remarkable consistency in the qualitative findings across these fundamentally different methodologies provides a strong foundation of confidence in the existence and importance of the ENSO rectification effect. The OGCM experiments provide the cleanest proof of the physical mechanism, while the observational diagnostics, despite their uncertainties, are crucial for confirming that this mechanism is indeed active in the real-world climate system.

5. Grand Challenges in Rectification Research

The establishment of ENSO rectification as a robust physical process has opened up a series of complex and thought-provoking questions. Although the fundamental theory is well supported, there are still several significant challenges that need to be fully addressed to integrate it into the broader framework of climate science. These challenges lie at the intersection of climate modeling, the attribution of decadal variability, and the fundamental nature of diverse expressions of ENSO. Progress in these areas is crucial for improving the accuracy of long-range forecasting and future climate predictions using the rectification paradigm.

5.1. The GCM Fidelity Problem

A major and persistent obstacle in climate science is that most state-of-the-art GCMs are systematically unable to simulate real-world ENSO asymmetry. A large number of studies evaluating the CMIP set consistently indicate that this is a long-standing issue. As Bellenger et al. [67] pointed out in their comparison, ENSO performance has not achieved a leap from CMIP3 to CMIP5, and its basic characteristics have not been well characterized. Observational data show that extreme warm events are significantly stronger than cold events, exhibiting strong positive skewness, while the model set shows a broad and unrealistic distribution, with many models even producing ENSO that is nearly symmetric or negatively skewed [68,69]. This persistent challenge across model generations is quantitatively summarized in

Table 1. ENSO asymmetry metrics in observations and CMIP ensembles. The table summarizes the skewness of the Niño-3.4 SST index, a primary metric of ENSO asymmetry. Note the strong positive value in observations, contrasted with the wide, nearly zero-mean spread in the multi-model ensembles, which highlights the persistent challenge for climate models. Data are synthesized from key multi-model intercomparison studies [68,69,72]. Note: N/A indicates “Not applicable,” meaning the data is not available or not relevant.

Dataset	Number of Models Analyzed	Ensemble Mean Skewness	Range of Skewness	Fraction with Negative Skewness
Observations	N/A	0.88	N/A	N/A
CMIP3 Ensemble	19	−0.02	−0.88 to +0.80	~50%
CMIP5 Ensemble	14	~0.0	−0.8 to +0.8	~50%
CMIP6 Ensemble	19	0.16	−0.34 to +0.88	~16% (3 of 19)

. While there has been some incremental progress, with the CMIP6 ensemble showing a slight positive mean skewness and fewer models exhibiting a negative skewness compared to CMIP3 and CMIP5, the overall model spread remains large, and the majority of models still significantly underestimate the strong positive asymmetry observed in nature [69]. This is not a negligible model bias. Due to ENSO asymmetry being the fundamental driving force of the rectification process, its inadequate characterization means that the critical rectification feedback of ENSO on the mean state is either missing, too weak, or modeled incorrectly in our state-of-the-art climate models [70]. This fidelity problem has direct consequences for the simulation of decadal variability, as demonstrated by the model classification in Kim and Kug [43]. Their work explicitly shows that models with weak ENSO asymmetry fail to reproduce the correct zonal dipole mode of TPDV, highlighting how a failure in simulating interannual nonlinearity cascades directly into errors in the simulation of low-frequency climate modes. This has tangible consequences for climate projections, as Sutton et al. [71] demonstrated that the rectification of ENSO in models can lead to a significant underestimation of the asymmetry in its teleconnections over regions like North America.

Recent diagnostic research has begun to reveal the fundamental cause of this fidelity issue. It is indicated by numerous pieces of evidence that there is a corresponding relationship between the weakening of ENSO asymmetry and the weakening of NDH simulations. For example, a significant correlation between simulated NDH intensity and ENSO asymmetry in the CMIP5 dataset was found by Hayashi et al. [73], and they pointed out that most models suffer from insufficient NDH. There is a close relationship between this oceanic dynamic defect and the persistent bias in the mean state of the model climatology. The most famous deviation among them may be regarded as the equatorial cold tongue bias, which means that the model usually simulates a state where the eastern equatorial Pacific is too cold and extends too far westward [74]. This erroneous cold equilibrium suppresses deep atmospheric convection, which is crucial for generating strong nonlinear coupling feedback required for extreme El Niño events and their associated NDH [75]. The further complexity of the problem lies in the deviation in atmospheric components. As shown by Fang et al. [76], the unrealistic cloud radiation effects in many CMIP5 models exacerbate the intensity asymmetry bias. This may form a self-reinforcing negative feedback loop: the average state of deviation leads to a weakening of nonlinear intensity and asymmetry, which means that the feedback mechanism that should have shaped the warming of the eastern Pacific is too weak, thus continuing to strengthen the initial cold bias.

5.2. Quantifying the Contribution of Rectification to TPDV

Although the spatial signature of the rectified signal provides strong indirect evidence for its contribution to the TPDV [25], its precise role relative to other proposed mechanisms remains a major unresolved issue. The research field of TPDV is active and multidimensional, with multiple mechanisms currently being studied, as summarized in comprehensive reviews by Power et al. [26] and Capotondi et al. [28]. For clarity, it is useful to distinguish which of these processes may act as competitors to rectification by generating TPDV independently and which may act as complements by modulating the ENSO cycle that is then rectified.

One main mechanism involves extratropical forcing. A significant fraction of TPDV may be energized by the ocean’s integration of atmospheric variability originating in the midlatitude. For example, the seasonal footprint mechanism describes how the winter atmospheric variability (e.g., North Pacific Oscillation) in the north Pacific leaves imprints on the subtropical ocean surface SST. These imprints form anomalies that then propagate towards the equator through a coupled feedback mechanism, affecting tropical regions in subsequent seasons [77]. The specific mechanisms involve thermodynamic coupling between the ocean and atmosphere, which allows the midlatitude forced SST anomalies to persist and expand [78]. The path has been clearly validated and confirmed by the coupled model experiment in Alexander et al. [79]. To the extent that these processes can directly force decadal anomalies in the tropics, they can be considered a competing mechanism. However, the meridional patterns in both the north and south Pacific have been identified as key transmission channels for this mid- to extratropical influence, although they may affect different types of ENSO and act on different timescales [80,81]. This process is often manifested in the form of the Pacific Meridional Mode (PMM), which has been confirmed as a key precursor to ENSO [82]. In this role, extratropical forcing acts as a complementary process that influences TPDV by first modulating ENSO.

Another important mechanism is stochastic forcing, suggesting TPDV can be generated as a slow and comprehensive response of the upper ocean to high-frequency random atmospheric weather noise [83,84,85]. Based on this view, structured low-frequency variability driven by uncertainty can be generated by accumulated random forcing from processes such as sudden westerly winds. Holmes et al. [86] proposed an updated and more subtle viewpoint. They argued that the ocean itself generates a stochastic forcing through the chaotic and high-frequency variability of TIWs, and it can directly affect the evolution of ENSO and contribute to its irregularity. Like the PMM, stochastic forcing primarily acts as a complementary mechanism that influences TPDV by shaping the character of the ENSO variability that is subsequently rectified.

Finally, inter-basin teleconnections are considered the source of decadal modulation. For example, it is shown that the Atlantic Multidecadal Oscillation affects the Pacific Walker circulation and is associated with an increase in El Niño events in the central Pacific [87]. The decadal warming of the Indian Ocean can also modulate the intensity of Pacific trade winds similarly, and it thereby establishes feedback pathways between the two ocean basins [88,89]. A dramatic case was observed in the year 2014, when unusually warm Indian Ocean SSTs helped to arrest the development of what was projected to be a major El Niño event [90]. As these teleconnections primarily influence TPDV by altering the background state in which ENSO operates, they are best viewed as another complementary mechanism. The major challenge for future research is to develop robust attribution methodologies that can separate these overlapping processes, including the influence of pan-tropical climate change driven by the Atlantic [91]. Additionally, quantifying the fractional contribution of tropically generated rectification versus other driving factors will also be a significant task.

5.3. The Role of ENSO Diversity in Rectification

Recognizing that ENSO is not a monolithic phenomenon, but a spectrum of events adds another layer of complexity to the rectification problem. The main manifestation of this ENSO diversity lies the differences between the eastern Pacific (EP) El Niño events and the CP El Niño events (also known as “El Niño Modoki” [29]), where SST anomalies of CP El Niño events are mainly concentrated near the International Date Line [30,92]. These types are related to different intrinsic dynamics and initiation mechanisms. Kug et al. [31] first pointed out that EP El Niño is mainly driven by thermocline feedback and involves basin-scale wave mechanics. In contrast, CP El Niño relies more on local zonal advective feedback in the central Pacific. This is reflected in Bjerknes feedback itself, which has been shown to operate asymmetrically between the two types of El Niño [93]. The initiation mechanisms of CP and EP events are also different. For example, specific subtropical precursors and oceanic pathways are associated with the initiation of some CP events, which are fundamentally different from the mechanisms of EP events [94]. These precursors can lead to different optimal growth pathways for central versus eastern Pacific events [95]. Furthermore, the response of ENSO to these precursors, such as the PMM, can itself be nonlinear, and the character of the resulting ENSO event (e.g., EP or CP El Niño) depends on the initial state of the tropical Pacific [96].

This diversity has direct implications for rectification. EP El Niño events typically have greater intensity, stronger nonlinearity, and more significant asymmetry, indicating the net rectified signal may be primarily dominated by their occurrence. Paek et al. [50] highlighted these different evolutionary paths in their case studies of the 1997–1998 (strong EP) and 2015–2016 (strong, but with significant CP characteristics) events. However, there is strong evidence to suggest that the frequency of CP events has increased in the past few decades [97], and this trend is projected to continue under global warming by some models [98]. It raises several key and unanswered questions: What is the net rectification signal generated by a climate system that experiences a mixture of EP and CP events? Will the transition of ENSO dominant types lead to changes in spatial patterns or overall intensity of rectification effects on the mean state? Answering these questions is crucial for correctly interpreting past decade shifts and predicting the future evolution of the tropical Pacific.

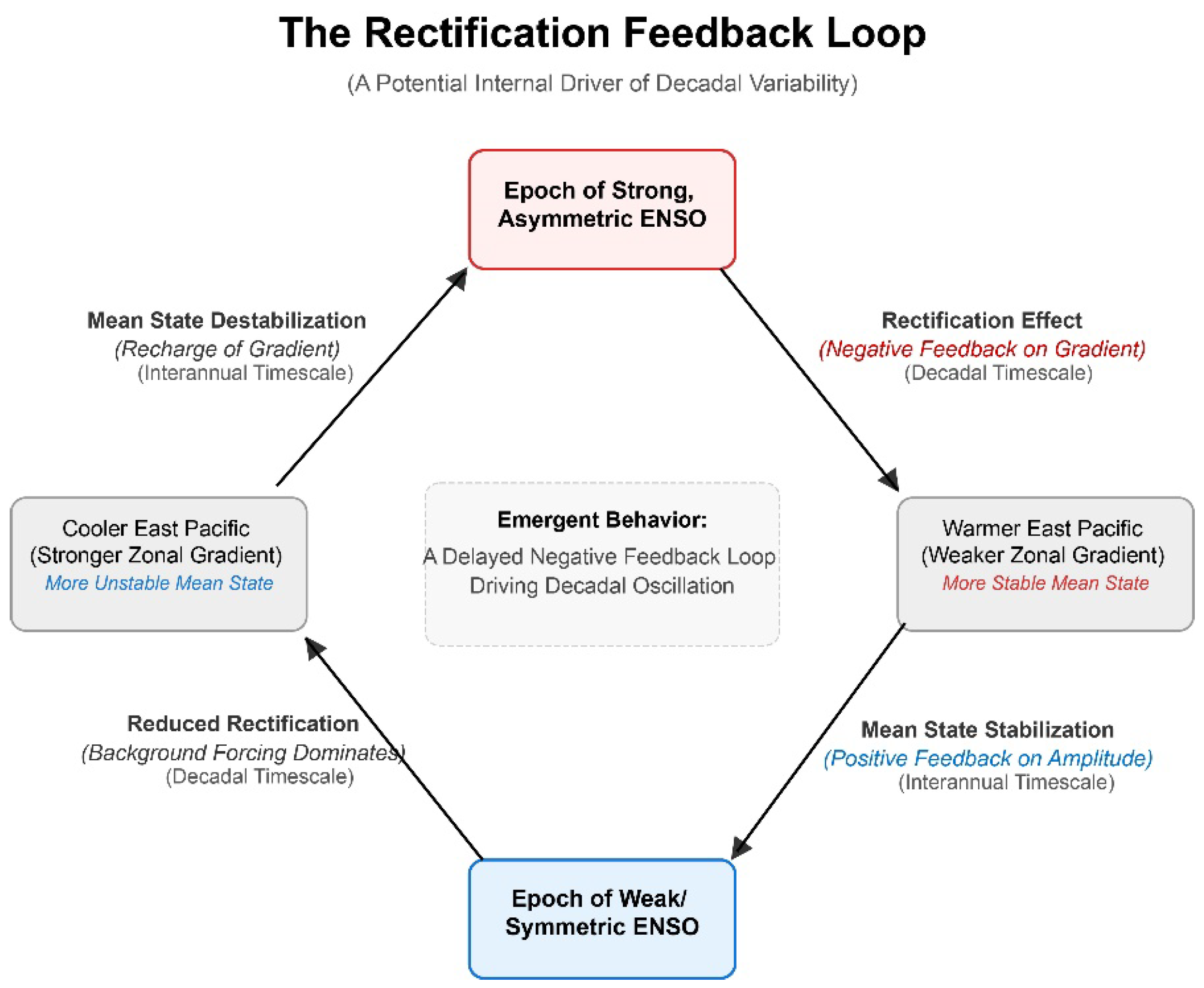
5.4. The Rectification Feedback Loop as a Decadal Oscillator

Perhaps the most speculative, yet compelling frontier is the hypothesis of a closed feedback loop that can generate self-sustaining decadal oscillations within the tropical Pacific. This hypothesis integrates two competitive paradigms of ENSO and mean-state relationships into a dynamic cycle. To understand this loop, it is best deconstructed into its two constituent feedback arms, which operate on different timescales. The first arm is the decadal-scale negative feedback of ENSO variability on the mean state, which is regarded as the core rectification process itself. The epoch of high ENSO activity dominated by strong and asymmetric El Niño events generates a strong rectification effect, then systematically warming the eastern Pacific and weakening the mean zonal SST gradient [24,25,43]. The residuals of asymmetric events alter the background in this process [41], making a strong negative feedback effect on the thermal gradient of the mean state. The variability of the system here works to neutralize the background instability that drives its development, a process that can be considered rectification damping. The degree of this damping derives from a quantifiable effect of ENSO, as shown by recent studies [99]. The second arm is the interannual-scale positive feedback of the mean state on ENSO variability, which represents the classic view of mean-state control. A background state with a weaker zonal SST gradient and a deeper eastern thermocline is dynamically more stable and less conducive to the growth of strong Bjerknes feedback, thereby suppressing the amplitude and frequency of subsequent ENSO events. This stabilizing influence of a warmer mean state has been a cornerstone of ENSO theory for decades, as demonstrated in seminal theoretical work by Fedorov and Philander [100,101] and supported by stability analyses in a range of models [102]. In this arm, a weaker gradient leads to weaker ENSO, and a stronger gradient leads to stronger ENSO. This is a positive link between the mean state’s instability and the resulting variability. This hypothesized sequence thus connects the two competing causal arrows—ENSO shaping the mean state, and the mean state modulating ENSO—into a single, oscillating feedback loop.

The hypothesis posits that the combination of these two arms creates a delayed negative feedback loop that drives decadal oscillation (Figure 3). An epoch of strong ENSO (the cause) leads to a more stable mean state (the effect) via rectification. This stable mean state then suppresses ENSO, leading to a quiescent period. During this lull, the rectifying feedback is diminished, allowing background radiative forcing to slowly recharge the zonal SST gradient, making the system progressively more unstable until it is primed for another epoch of strong ENSO. The “delay” in the loop is the multi-year timescale required for the rectified signal to accumulate and significantly alter the mean state and the subsequent time required for the mean state to recover. While the full, closed-loop oscillation remains unproven, study documenting interactive feedbacks between ENSO and TPDV in coupled models [103] provides the kind of evidence this hypothesis seeks to explain. Validating this complete feedback loop hypothesis represents a major challenge that will require innovative analysis of long-term observational data and multi-millennial simulation using coupled models.

5.5. A Roadmap for Future Research

Addressing the grand challenges outlined above requires a concerted and methodologically innovative research effort. To resolve the persistent fidelity problem in GCMs, future efforts must move beyond simply documenting biases and toward isolating their root causes through initiatives like a rectification model intercomparison project. Such a project would enable a systematic assessment of how biases in ocean physics, atmospheric convection, and air–sea coupling contribute to errors in the simulated rectification feedback. Beyond model evaluation, attributing the causes of TPDV requires moving from correlation to causation. Promising methodologies include pacemaker experiments, which can cleanly isolate the influence of one ocean basin’s variability on the global system [104,105], and the application of advanced causal network discovery algorithms to generate causal fingerprints that can provide stronger emergent constraints on future projections [106]. A parallel research effort must focus on ENSO diversity by conducting targeted OGCM forcing experiments using wind anomalies exclusively from either EP-type or CP-type events, in order to produce the first quantitative maps of their distinct rectified imprints.

Testing the most ambitious hypothesis of the decadal feedback loop requires leveraging long timescales that extend beyond the instrumental record. The growing number of multi-millennial “pre-industrial control” simulations from GCMs provides one such laboratory, allowing for time-lagged correlational analysis between metrics of ENSO variance and the mean state to search for the proposed oscillatory behavior. The most compelling evidence, however, would come from paleoclimate archives. A major research effort should focus on synthesizing high-resolution proxy records that can simultaneously reconstruct both ENSO variance and the background mean state over past millennia. The recent breakthrough in measuring trace elements on individual foraminifera shells enables us to reconstruct ENSO-like variability in past abrupt climate events with unprecedented resolution. Glaubke et al. [107] found that the background average state seems to mediate the response of ENSO to meltwater forcing, which strongly supports the bidirectional feedback mechanism proposed by the decadal loop hypothesis. Applying these technologies to Holocene research will provide a definitive test for rectification feedback loops as the fundamental mode of the climate system.

6. Consequences for Climate Science and Prediction

The rectification theory of ENSO has evolved from a nascent hypothesis to a clear physical mechanism, which has a deep and broad impact on the core disciplines of climate science. It requires revising the development and diagnostic frameworks of existing models, opening up new avenues for decadal forecasting, and fundamentally reshaping our understanding of how the tropical Pacific responds to anthropogenic climate change. This paradigm shift goes beyond simple descriptions of climate change and provides new tools and perspectives for analyzing and predicting climate change.

6.1. For Model Development: Moving Beyond Linear Dynamics to Improve Mean-State Simulations

A significant and persistent flaw in improving average-state simulations in state-of-the-art GCMs is their systematic failure to simulate the real ENSO asymmetry [68,69]. This revised framework not only diagnoses this issue, but also provides clear and physics-based goals for model improvement. This study comprehensively indicates that the weak ENSO asymmetry in the model is directly related to the insufficient characterization of NDH, which is closely related to the sustained bias in the simulated average state, with the most significant being the equatorial cold tongue bias [70,73]. Therefore, future model development must prioritize improving the accuracy of characterizing nonlinear processes in the tropical Pacific. This requires a multifaceted approach to address the interconnected nature of the problem: while improving nonlinear ocean transport simulations, it is necessary to simultaneously reduce the persistent cold tongue bias, as a more realistic mean state is a prerequisite for the nonlinear atmospheric response that drives the asymmetry [75]. Furthermore, these improvements must be coupled with an enhancement of key air–sea feedbacks to ensure the entire system responds with the correct sensitivity [52]. The rectification paradigm makes it clear that these are not independent issues. A model’s ability to simulate the mean state, its interannual variability, and the asymmetry of that variability are deeply interconnected through nonlinear feedbacks.

6.2. For Diagnostics and Attribution: Rectification as a Necessary Metric

In order to track the progress of model development and better attribute observed climate variability, the climate science community should adopt diagnostic methods specifically designed to quantify rectification effects. The traditional approach of analyzing linear trends or low-frequency variability in isolation is insufficient in a system where high-frequency variability also systematically shapes the mean state. Therefore, a new set of standard diagnostics is needed to move beyond simple pattern evaluation and toward a more process-based understanding. In

Table 2. Proposed diagnostics for quantifying the ENSO rectification effect in climate models.

Diagnostic Method	Scientific Purpose/Question Addressed	Key Reference(s)
1. Forced OGCM “ENSO-on/off” Experiments	Isolates the ocean’s intrinsic nonlinear response to wind forcing. Quantifies the spatial pattern of the rectified signal.	[25,58]
2. NDH Budget Calculation	Directly quantifies the strength of the primary physical mechanism (⟨v′·∇T′⟩) in both coupled models and reanalyses.	[24,60]
3. ENSO Asymmetry Metrics	Provides a statistical measure of the behavioral prerequisite for rectification. Essential for model fidelity evaluation.	[33,68]
4. Equilibrium vs. Time-Mean State Analysis	(For simpler/analytical models) Provides a formal, rigorous quantification of the total rectified effect.	[24]

, we propose a concise set of key diagnostics, which can be used to rigorously quantify the rectification effect in climate models. These include both controlled numerical experiments designed to isolate the mechanism, as well as specific statistical and physical metrics that can be calculated from standard model output. By making the quantification of the rectification effect a standard component of model evaluation, the research community can more effectively diagnose the sources of model errors and better attribute observed decadal changes between internal, rectified variability and external forcing.

6.3. For Decadal Prediction: From Concept to Operational Forecast

The memory provided by rectification can be harnessed for practical decadal prediction. We propose a specific and feasible pathway to operationalize this predictability: the development of a hybrid statistical-dynamical forecasting system. While such a system using asymmetry as a direct predictor has not yet been fully implemented, the core components required are areas of active research and development. The statistical component will use time series of observed ENSO statistical data (such as running mean of its variance and skewness) as predictors to make probabilistic predictions of the TPDV index 5–10 years ahead. The dynamical component would then use this statistical forecast to improve initialization and constrain a fully coupled forecast model. The most crucial and practically feasible step is to improve the initialization of the dynamical model to incorporate the rectified signal. This requires the use of advanced ocean data assimilation systems, such as four-dimensional variational schemes, which are designed to produce dynamical and consistent evolution of ocean states [108]. By accurately assimilating sparse observational data, especially in the subsurface, these systems can better capture slow, accumulated heat content anomalies associated with NDH. These anomalies are a key source of interdecadal predictability [109]. Therefore, a coordinated effort to assimilate data more effectively can better constrain the rectified signal, thereby enhancing the skill of operational decadal prediction systems. This approach is both practical and promising.

6.4. For Climate Change Projections: Disentangling the Forced Response

The rectification paradigm regards that in the real world, forced responses to greenhouse gases and internal regulatory feedback are inseparable. To clarify these impacts and test the paradigm, the climate modeling community must make greater use of single-model initial-condition large ensembles (SMILEs). As outlined by Maher et al. [110], these ensembles involve running a single climate model dozens or hundreds of times under initial conditions with small perturbations, and are powerful tools for separating forced climate change signals from noise of internal variability. The average of all ensemble members reveals a clear, externally forced trend, while the distribution of members quantifies the model’s simulated internal variability, including the impact of ENSO rectification. This method has proven highly effective in quantifying how internal variability, such as interdecadal Pacific oscillations (IPOs), can mask or enhance forced trends in observed records. Recent studies using large CMIP6 ensembles have powerfully demonstrated this, with Wu et al. [111] showing that the IPO can account for the majority of the observed tropical expansion, and Chan et al. [112] using a SMILE to show that internal variability can conceal emerging forced trends in hydrology for decades. A powerful future study will compare two different large ensembles: one from models with realistic, strong ENSO rectification, and the other from models with weaker or nonexistent rectification. By comparing the ensemble mean and propagation of these two SMILEs, we can quantitatively evaluate for the first time how the presence of strong rectifying feedback modulates the forced response of the tropical Pacific to global warming. This will provide a definitive test of the revised paradigm and is a crucial step in building confidence in future climate predictions.

7. Conclusions

The theory of ENSO rectification marks a significant advancement in our comprehension of tropical climate systems. It marks a paradigm shift from viewing ENSO as a transient anomaly on a static background to recognizing it as a fundamental framework of the mean climate itself. The research results reviewed in this article demonstrate a clear knowledge process, which is summarized in Figure 4. The extensive body of research synthesized in this review can be distilled into four main conclusions, as follows.

• ENSO rectification is a robust physical process supported by multiple, convergent lines of evidence. The existence of a rectified signal that alters the mean state is not a theoretical curiosity, but has been confirmed through a hierarchy of methods, from analytical models and controlled OGCM experiments to advanced diagnostics of observational data.
• NDH is the dominant physical mechanism, but it is systematically underrepresented in climate models. The nonlinear advection of heat during asymmetric ENSO cycles is the primary driver of the rectified signal. The persistent failure of state-of-the-art GCMs to simulate this process realistically, due to mean-state biases and weak nonlinearity, is a critical barrier to progress.
• Rectification contributes substantially to TPDV, but its fractional role remains uncertain. The off-equatorial spatial pattern of the rectified signal provides a compelling physical explanation for the observed structure of TPDV. However, quantifying its precise contribution relative to other mechanisms, such as extratropical and stochastic forcing, is a major unresolved challenge.
• Future progress depends on resolving ENSO asymmetry in models and adopting new rectification metrics. Improving decadal predictions and long-term climate projections requires not only the development of models that can capture the nonlinear dynamics of ENSO, but also the adoption of a new suite of process-based diagnostics to track and attribute the effects of rectification.

Ultimately, the study of ENSO rectification provides a convincing case study for a broader principle in Earth system science: the complex interaction between high-frequency variability and long-term average states is not just noise, but a fundamental system-organizing process. Therefore, the continued exploration of this adiabatic and nonlinear perspective is crucial for the future of climate science, as well as for advancing our fundamental understanding of how complex natural systems regulate themselves in a constantly changing world.