Dynamic Risk Assessment of Collapse Geological Hazards on Highway Slopes in Basalt Regions During Rainy Seasons
Abstract
1. Introduction
2. Methodology
2.1. Research Area and Data
2.2. Data Sources
2.3. Theoretical Basis
 ”, accumulated or depleted via flows, thereby reflecting the cumulative outcomes of past system behaviors, and stands as the core determinant of the system’s future evolutionary trends) can be expressed as
”, accumulated or depleted via flows, thereby reflecting the cumulative outcomes of past system behaviors, and stands as the core determinant of the system’s future evolutionary trends) can be expressed as ” in the SD model, determines the rate at which state variables increase or decrease, and acts as a pivotal factor that connects distinct state variables and drives the system’s dynamic changes), K and L, respectively, represent the present and future moments, and C is the initial value of the state variable.
” in the SD model, determines the rate at which state variables increase or decrease, and acts as a pivotal factor that connects distinct state variables and drives the system’s dynamic changes), K and L, respectively, represent the present and future moments, and C is the initial value of the state variable.2.4. Establishment of the SD Model
2.5. Basis for Calculating Important Parameters of the SD Model
3. Simulation and Risk Assessment
3.1. Computer Simulation Program Design
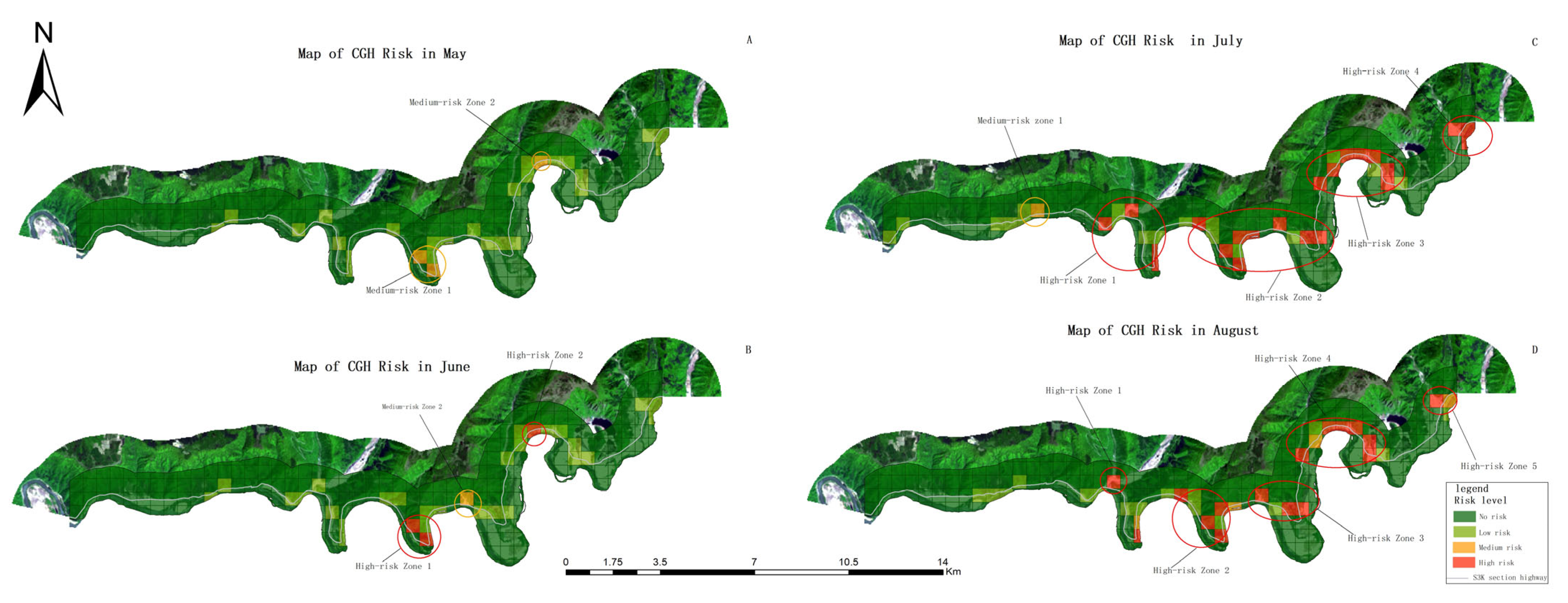
3.2. Risk Mapping
4. Results and Discussion
- (A)
- Advancements in dynamic risk assessment.
- (B)
- Improvements in spatial precision.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, S.; Xu, C.; Ma, J.; Gao, H. Escalating risks and impacts of rainfall-induced geohazards. Nat. Hazards Res. 2025, in press. [Google Scholar] [CrossRef]
- de Souza, D.C.; Crespo, N.M.; da Silva, D.V.; Harada, L.M.; de Godoy, R.M.P.; Domingues, L.M.; Luiz, R.; Bortolozo, C.A.; Metodiev, D.; de Andrade, M.R.M.; et al. Extreme rainfall and landslides as a response to human-induced climate change: A case study at Baixada Santista, Brazil, 2020. Nat. Hazards 2024, 120, 10835–10860. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Liu, X.; Terfa, B.K.; Nam, W.-H.; Gu, X.; Zhang, X.; Wang, C.; Yang, J.; Wang, P.; et al. Review on the progress and future prospects of geological disasters prediction in the era of artificial intelligence. Nat. Hazards 2024, 120, 11485–11525. [Google Scholar] [CrossRef]
- Zhang, G. Principles and Methods of Natural Disaster Risk Assessment and Zoning; China Meteorological Press: Beijing, China, 2014; pp. 16–17. [Google Scholar]
- Yu, P.; Dong, J.; Hao, H.; Xie, Y.; Zhang, H.; Wang, J.; Zhu, C.; Guan, Y.; Yu, H. Risk Assessment and Prevention Planning for Collapse Geological Hazards Considering Extreme Rainfall—A Case Study of Laoshan District in Eastern China. Land 2023, 12, 1558. [Google Scholar] [CrossRef]
- Aubrecht, C.; Özceylan, D.; Steinnocher, K.; Freire, S. Multi-level geospatial modeling of human exposure patterns and vulnerability indicators. Nat. Hazards 2013, 68, 147–163. [Google Scholar] [CrossRef]
- Sun, R.; Gao, G.; Gong, Z.; Wu, J. A review of risk analysis methods for natural disasters. Nat. Hazards 2020, 100, 571–593. [Google Scholar] [CrossRef]
- Lai, J.-S.; Tsai, F. Improving GIS-Based Landslide Susceptibility Assessments with Multi-temporal Remote Sensing and Machine Learning. Sensors 2019, 19, 3717. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Zheng, Y.; Zhou, Y.; Daud, H. Deep Learning and Machine Learning Models for Landslide Susceptibility Mapping with Remote Sensing Data. Remote Sens. 2023, 15, 4703. [Google Scholar] [CrossRef]
- Saha, S.; Majumdar, P.; Bera, B. Deep learning and benchmark machine learning based landslide susceptibility investigation, Garhwal Himalaya (India). Quat. Sci. Adv. 2023, 10, 100075. [Google Scholar] [CrossRef]
- Moos, C.; Bontognali, Z.; Dorren, L.; Jaboyedoff, M.; Hantz, D. Estimating Rockfall and Block Volume Scenarios Based on a Straightforward Rockfall Frequency Model. Eng. Geol. 2022, 309, 106828. [Google Scholar] [CrossRef]
- Monisha, P.J.; Obaid, S.; Madhavan, S.; Sivagami, S.; Saranya, N.N. Landslide Detection and Early Warning System Using Extended Kalman Filter with Convolutional Neural Networks Based Long Short-Term Memory. In Proceedings of the 2024 International Conference on Integrated Intelligence and Communication Systems (ICIICS), Kalaburagi, India, 22–23 November 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Wei, L.; Xu, Y.; Lv, D.; Cui, H.; Liu, S.; Ao, M. Rockfall susceptibility assessment in Kuandian County (Northeast. China) by combining information content method and analytic hierarchy process. Bull. Eng. Geol. Environ. 2024, 83, 240. [Google Scholar] [CrossRef]
- Yan, D.; Zhang, H.; Xie, M.; Jiang, Y.; Li, S.; Liu, J. Review on the monitoring and early warning technology of large-scale unstable rock collapse. Adv. Eng. Sci. 2024, 56, 10–23. [Google Scholar] [CrossRef]
- Lei, Y.; Huang, J.; Cui, Y.; Jiang, S.H.; Wu, S.; Ching, J. Time capsule for landslide risk assessment. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 613–634. [Google Scholar] [CrossRef]
- Zhan, Q.; Wang, S.; Wang, L.; Guo, F.; Zhao, D.; Yan, J. Analysis of Failure Models and Deformation Evolution Process of Geological Hazards in Ganzhou City, China. Front. Earth Sci. 2021, 9, 731447. [Google Scholar] [CrossRef] [PubMed]
- van Westen, C.; van Asch, T.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Fu, X.; Yang, Y.; Wang, M.; Zhang, Z. Advances in modeling, assessment, and prevention of geotechnical and geological disasters. Front. Earth Sci. 2022, 10, 999365. [Google Scholar] [CrossRef]
- Lee, J.J.; Song, M.S.; Yun, H.S.; Yum, S.G. Dynamic landslide susceptibility analysis that combines rainfall period, accumulated rainfall, and geospatial information. Sci. Rep. 2022, 12, 18429. [Google Scholar] [CrossRef]
- Mihailović, D.T.; Malinović-Milićević, S. A Novel Approach to Understanding the Complexity of Precipitation. Atmosphere 2025, 16, 706. [Google Scholar] [CrossRef]
- Fan, Q.; Sui, J.; Wang, T.; Li, N.; Sun, Q. Eruption history and magma evolution of the trachybasalt in the Tianchivolcano, Changbaishan. Acta Petrol. Sin. 2006, 22, 1449–1457. Available online: https://geology.nju.edu.cn/CN/abstract/abstract8560.shtml (accessed on 13 August 2025).
- Wang, Y. Stability Analysis and Control Engineering of Landslide in S3k Section of Yangjiang Highway in Changbai County, Jilin. Master’s Thesis, Jilin University, Changchun, China, 2017. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10183-1018000028.htm (accessed on 13 August 2025).
- Qian, L.; Zang, S.; Man, H.; Sun, L.; Wu, X. Determination of the Stability of a High and Steep Highway Slope in a Basalt Area Based on Iron Staining Anomalies. Remote Sens. 2023, 15, 3021. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Okada, N.; Tatano, H. Integrated natural disaster risk mangement comprehensive and integrated model and Chinese strategy choice. J. Nat. Disasters 2006, 15, 29–37. [Google Scholar] [CrossRef]
- Zhong, Y.; Jia, X.; Qian, Y. Frontiers and Applications of System Dynamics; Science Press: Beijing, China, 2016. [Google Scholar]
- Zhu, Q.; Jia, R.; Xu, X.; Feng, L. System Dynamics Modeling and Reserch on Theory and Application of Feedback Loop Analysis; Economic & Management Publishing House: Beijing, China, 2022. [Google Scholar]
- Jiang, X.D.; Hou, T.S.; Guo, S.L.; Chen, Y. Influence of cracks on loess collapse under heavy rainfall. CATENA 2023, 223, 106959. [Google Scholar] [CrossRef]
- Jones, J.N.; Boulton, S.J.; Stokes, M.; Bennett, G.L.; Whitworth, M.R. 30-year record of Himalaya mass-wasting reveals landscape perturbations by extreme events. Nat. Commun. 2021, 12, 6701. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.; Zang, S. Differentiation Rule and Driving Mechanisms of Collapse Disasters in Changbai County. Sustainability 2022, 14, 2074. [Google Scholar] [CrossRef]
- Ge, Q.S.; Zou, M.; Zheng, J.Y. Integrated Assessment of Natural Disaster Risks in China; Cience Press: Beijing, China, 2008; pp. 102–122. [Google Scholar]
- Li, Z.; Nadim, F.; Huang, H.; Uzielli, M.; Lacasse, S. Quantitative Vulnerability Estimation for Scenario-based Landslide Hazards. Landslides 2010, 7, 125–134. Available online: https://link.springer.com/article/10.1007/s10346-009-0190-3 (accessed on 13 August 2025). [CrossRef]
- Di Felice, P. Ranking of Assets with Respect to Their Exposure to the Landslide Hazard: A GIS Proposal. ISPRS Int. J. Geo-Inf. 2020, 9, 326. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, Y. Risk investigation method and practice of geohazard. Geol. Bull. China 2008, 27, 1205–1216. Available online: http://dzhtb.cgs.cn/article/id/20080816 (accessed on 13 August 2025).
- Lollino, P.; Pagliarulo, R.; Trizzino, R.; Santaloia, F.; Pisano, L.; Zumpano, V.; Fazio, N.L. Multi-scale approach to analyse the evolution of soft rock coastal cliffs and role of controlling factors: A case study in South-Eastern Italy. Geomat. Nat. Hazards Risk 2021, 12, 1058–1081. [Google Scholar] [CrossRef]
- Zhao, F.; Miao, F.; Wu, Y.; Ke, C.; Gong, S.; Ding, Y. Refined landslide susceptibility mapping in township area using ensemble machine learning method under dataset replenishment strategy. Gondwana Res. 2024, 131, 20–37. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; Science and Education Administration, United States Department of Agriculture: Washington, DC, USA, 1978; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=ce79cdb85a57324b5f094b598fadfb78 (accessed on 13 August 2025).
- Zhao, Y.; Tian, Z.; Liang, Y.; Zhao, Y. Changing trend of soil erodibility factor based on two national mappings of it. Sci. Soil. Water Conserv. 2024, 22, 146–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, B.; Shi, P.; Jiang, Z. Crop cover factor estimating for soil loss prediction. Acta Ecol. Sin. 2001, 21, 1050–1056. Available online: https://www.ecologica.cn/stxb/article/abstract/010702?st=search (accessed on 13 August 2025).
- Thakuriah, G. GIS-based revised universal soil loss equation for estimating annual soil erosion: A case of lower Kulsi basin, India. SN Appl. Sci. 2023, 5, 81. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Li, H.; Liu, H.; Xiao, J.; Yin, J. Soil erosion changes based on GIS/RS and USLE in Poyang Lake basin. Trans. Chin. Soc. Agric. Eng. 2011, 27, 337–344. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=0eadd6fad631e015e3eb84d2e14b3ba0&site=xueshu_se (accessed on 13 August 2025).
- Xu, X.Q.; Fan, H.M.; Tan, J.; Jia, Y.; Wu, M. Comparison of Practice Values of Soil and Water Conservation Measures Under the Condition of Snow Melting and Rainfall Erosion. Res. Soil. Water Conserv. 2017, 24, 29–38. Available online: http://stbcyj.paperonce.org/oa/DArticle.aspx?type=view&id=20170306 (accessed on 13 August 2025).
- Li, J. A Study on Regional Gravitation Erosion Hazrad Based on RS and GIS. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2006. [Google Scholar]
- Ahmad, M.; Ansari, M.K.; Singh, T.N. Instability investigations of basaltic soil slopes along SH-72, Maharashtra, India. Geomat. Nat. Hazards Risk 2013, 6, 115–130. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Su, M.; Zhang, S.; Lu, D. Stability Analysis of a Weathered-Basalt Soil Slope Using the Double Strength Reduction Method. Adv. Civ. Eng. 2021, 2021, 6640698. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Cui, P.; Chen, D.; Tang, J.; Ou, T.; Hao, J.; Wang, J.; Zhang, G.; Lei, Y.; et al. Disaster effects of climate change and the associated scientific challenges. Sci. Bull. 2024, 69, 286–300. [Google Scholar] [CrossRef]
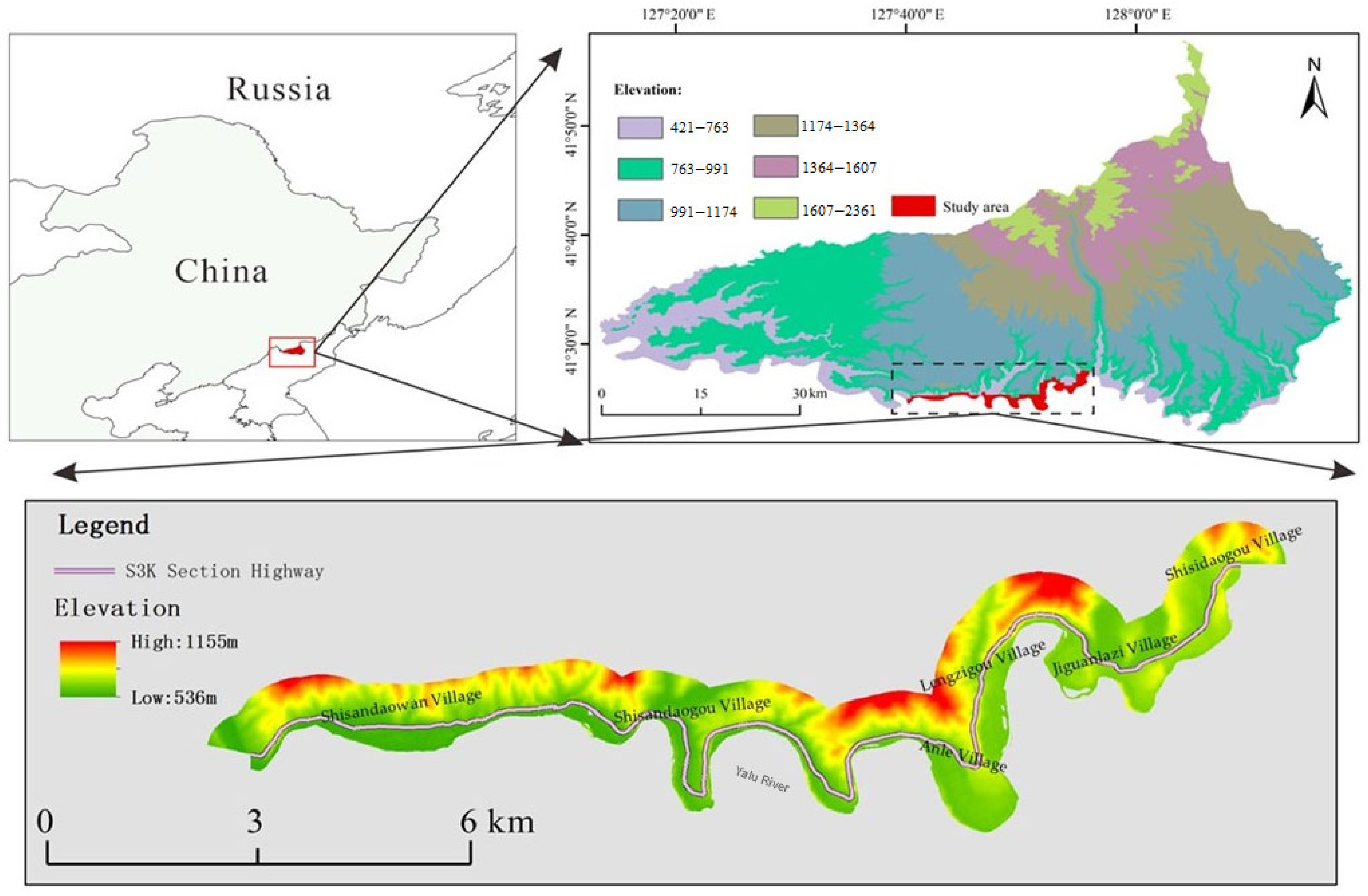

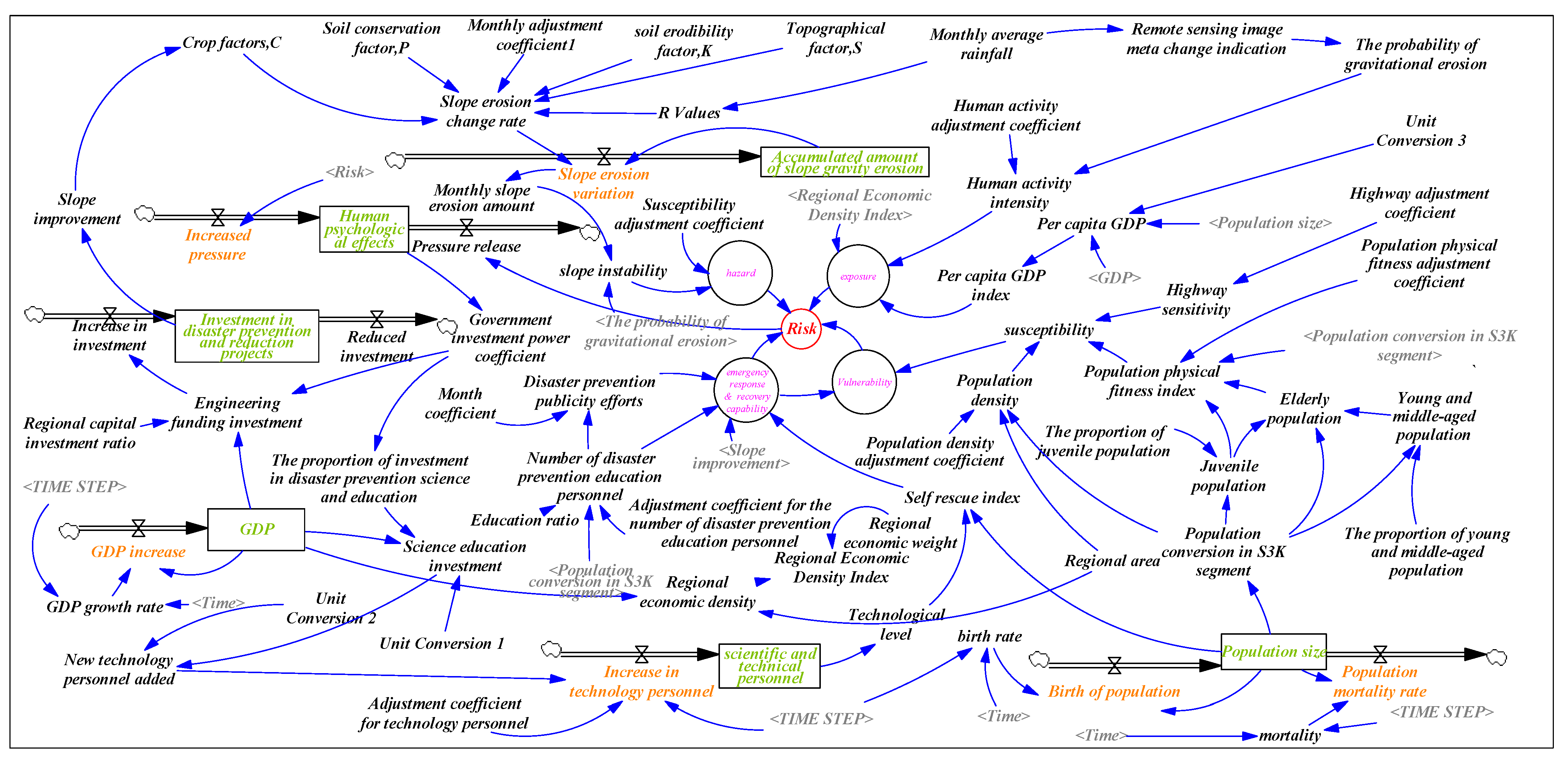

| Data Types | Information Mining of Key Parameters in the SD Model |
|---|---|
| Socioeconomic data | It is used to calculate GDP, population, income level, scientific research level, education, etc., as shown in Equations (3) and (4). |
| RS images | For slope stability studies; they involve the calculation of parameter C (Equation (7)), etc. |
| Topographic | The overview is shown in Figure 1, including the determination of S and L (Equations (8) and (9)) and the calculation of slope stability. |
| Land use data | It involves calculating slope stability, conducting exposure analysis and research, and determining parameter P. |
| Meteorological data | To calculate the important parameters of slope erosion, see Equation (5). Additionally, it is used for research on the exposure of hazard-bearing bodies. |
| Regional geological maps | They are applied to slope stability analysis. |
| Highway traffic | It is applicable to the highway sensitivity index. |
| Administrative area maps | They are used in the calculation and statistics of processes. |
| Year | Month | Rainfall (mm) | Year | Month | Rainfall (mm) | Year | Month | Rainfall (mm) |
|---|---|---|---|---|---|---|---|---|
| 2026 | 5 | 68.0 | 2028 | 5 | 68.4 | 2030 | 5 | 68.9 |
| 6 | 85.4 | 6 | 89.2 | 6 | 88.7 | |||
| 7 | 167.2 | 7 | 167.1 | 7 | 166.9 | |||
| 8 | 137.2 | 8 | 135.7 | 8 | 134.2 | |||
| 9 | 53.5 | 9 | 52.7 | 9 | 52.0 | |||
| 2027 | 5 | 68.2 | 2029 | 5 | 68.6 | |||
| 6 | 87.9 | 6 | 87.7 | |||||
| 7 | 167.2 | 7 | 167.0 | |||||
| 8 | 136.4 | 8 | 134.9 | |||||
| 9 | 53.1 | 9 | 52.4 |
| Risk Level | Month | Spatial Location | Township to Which it Belongs | Corresponding Grid Number |
|---|---|---|---|---|
| Low risk or no risk | 1,2,3,4, 9,10,11,12 | -- | -- | -- |
| Medium-risk Zone 1 | 5 | 127°49′12″ E, 41°24′51″ N | Anle Village | 201,254 |
| Medium-risk Zone 2 | 127°52′21″ E, 41°26′47″ N | Lenggouzi Village | 929 | |
| Medium-risk Zone 1 | 6 | 127°50′38″ E, 41°25′24″ N | Anle Village | 403 |
| High-risk Zone 1 | 127°49′12″ E, 41°24′51″ N | Anle Village | 201,254 | |
| High-risk Zone 2 | 127°52′21″ E, 41°26′47″ N | Lenggouzi Village | 929 | |
| Medium-risk Zone 1 | 7 | 127°44′10″ E, 41°25′36″ N | Shisandaowan Village | 474 |
| High-risk Zone 1 | 127°46′39″ E, 41°25′38″ N | Shisandaogou Village | 390,481 | |
| High-risk Zone 2 | 127°50′38″ E, 41°25′24″ N | Anle Village | 201,254,321,322,326,327,403 | |
| High-risk Zone 3 | 127°52′23″ E, 41°26′47″ N | The section from Lenggouzi Village to Jiguanlazi Village | 699,811,815,704,929,930,931 | |
| High-risk Zone 4 | 127°55′16″ E, 41°27′20″ N | Shisidaogou Village | 1056,1173,1174 | |
| High-risk Zone 1 | 8 | 127°46′39″ E, 41°25′38″ N | Shisandaogou Village | 481 |
| High-risk Zone 2 | 127°49′12″ E, 41°24′51″ N | Anle Village | 201,254,321,397 | |
| High-risk Zone 3 | 127°51′21″ E, 41°25′8″ N | Anle Village | 326,327,403 | |
| High-risk Zone 4 | 127°52′21″ E, 41°26′47″ N | The section from Lenggouzi Village to Jiguanlazi Village | 174,196,197,704,815,931 | |
| High-risk Zone 5 | 127°55′16″ E, 41°27′20″ N | Shisidaogou Village | 1173 |
| Corresponding Grid Number | On-Site Investigation Situation | Photo | Corresponding Grid Number | On-Site Investigation Situation | Photo |
|---|---|---|---|---|---|
| 1173 | The slope has a height difference of 25 m, with an estimated volume of 9100 m3. The volume of debris accumulated at the foot of the slope is 11.88 m3. A collapse occurred in 2012, which posed a threat to both residents and the highway infrastructure. The designation of this area as high-risk during heavy rainfall periods is consistent with the research findings. |  | 811 | The slope height difference is about 15 m, and the predicted volume is 4800 m3. This is identified as a high-risk area. |  |
| 704, 815, 929, 930 | A protective net has been installed on the slope; however, multiple areas have sustained damage. The predicted collapse volume is 26,000 m3, with an average weathered layer thickness of about 2 m and an unloading depth of about 1.2 m. The designation of this area as high-risk during heavy rainfall periods is consistent with the research findings. |  | 931 | The rock slope has a height difference of about 45 m, with a predicted volume of about 10,000 m3. Eight clustered disaster points have been identified within 1 km. This area is classified as high-risk. |  |
| 390 | The height difference in the slope is about 20 m, with an estimated volume of 6100 m3. The structure is predominantly blocky, with an accumulation volume of about 9 m3. This condition poses a threat to the highway, resulting in a high-risk classification during the rainy season. |  | 474 | The predicted volume of unstable material is about 9000 m3. The top of the slope is unstable, and there is a risk of rockfall, posing a threat to the highway. |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, L.; Zhao, P.; Li, Z. Dynamic Risk Assessment of Collapse Geological Hazards on Highway Slopes in Basalt Regions During Rainy Seasons. Atmosphere 2025, 16, 978. https://doi.org/10.3390/atmos16080978
Qian L, Zhao P, Li Z. Dynamic Risk Assessment of Collapse Geological Hazards on Highway Slopes in Basalt Regions During Rainy Seasons. Atmosphere. 2025; 16(8):978. https://doi.org/10.3390/atmos16080978
Chicago/Turabian StyleQian, Lihui, Peng Zhao, and Zhongshui Li. 2025. "Dynamic Risk Assessment of Collapse Geological Hazards on Highway Slopes in Basalt Regions During Rainy Seasons" Atmosphere 16, no. 8: 978. https://doi.org/10.3390/atmos16080978
APA StyleQian, L., Zhao, P., & Li, Z. (2025). Dynamic Risk Assessment of Collapse Geological Hazards on Highway Slopes in Basalt Regions During Rainy Seasons. Atmosphere, 16(8), 978. https://doi.org/10.3390/atmos16080978





