Dataset Construction for Radiative Transfer Modeling: Accounting for Spherical Curvature Effect on the Simulation of Radiative Transfer Under Diverse Atmospheric Scenarios
Abstract
1. Introduction
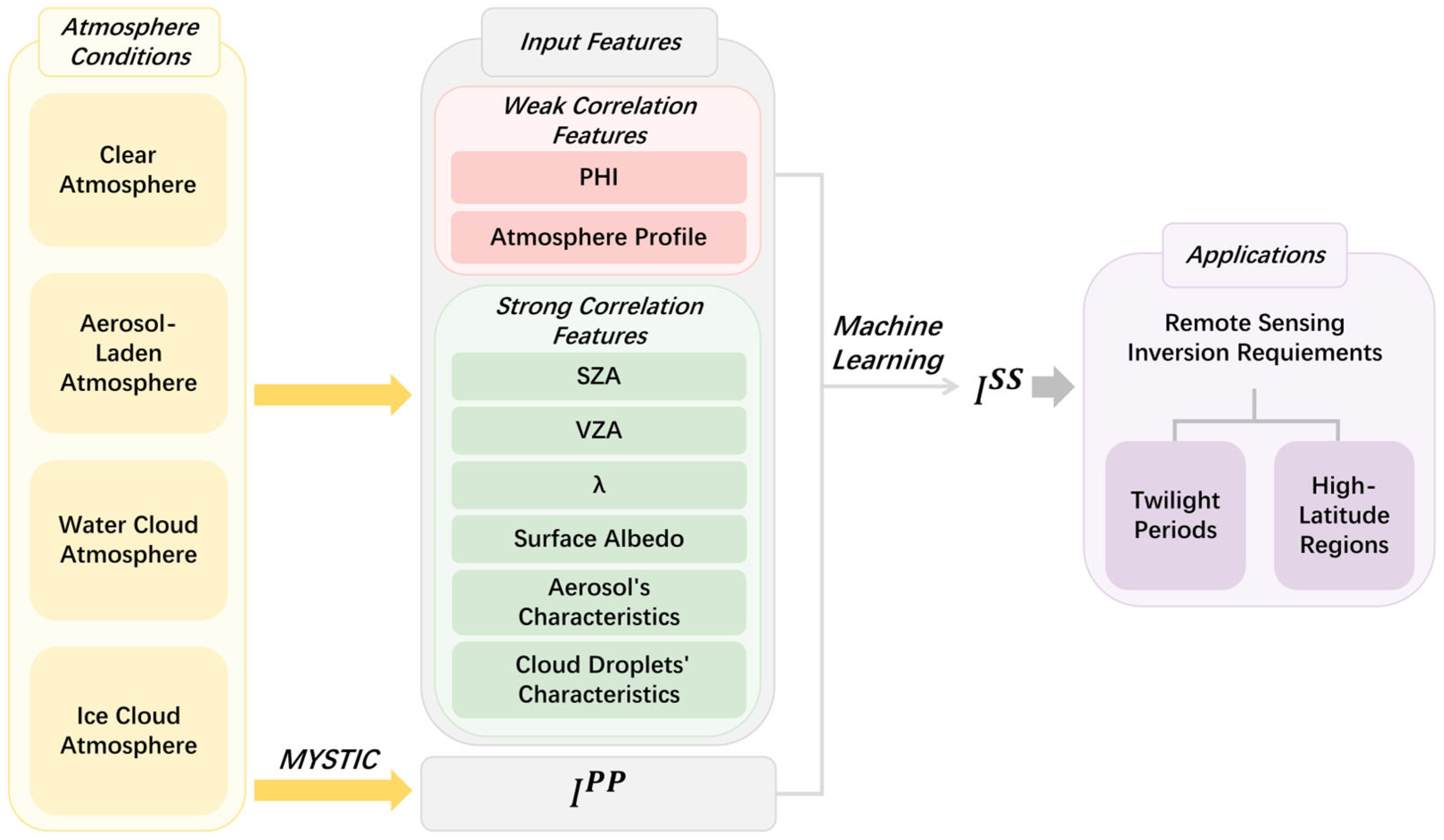
2. Data and Methods
3. Results Analysis
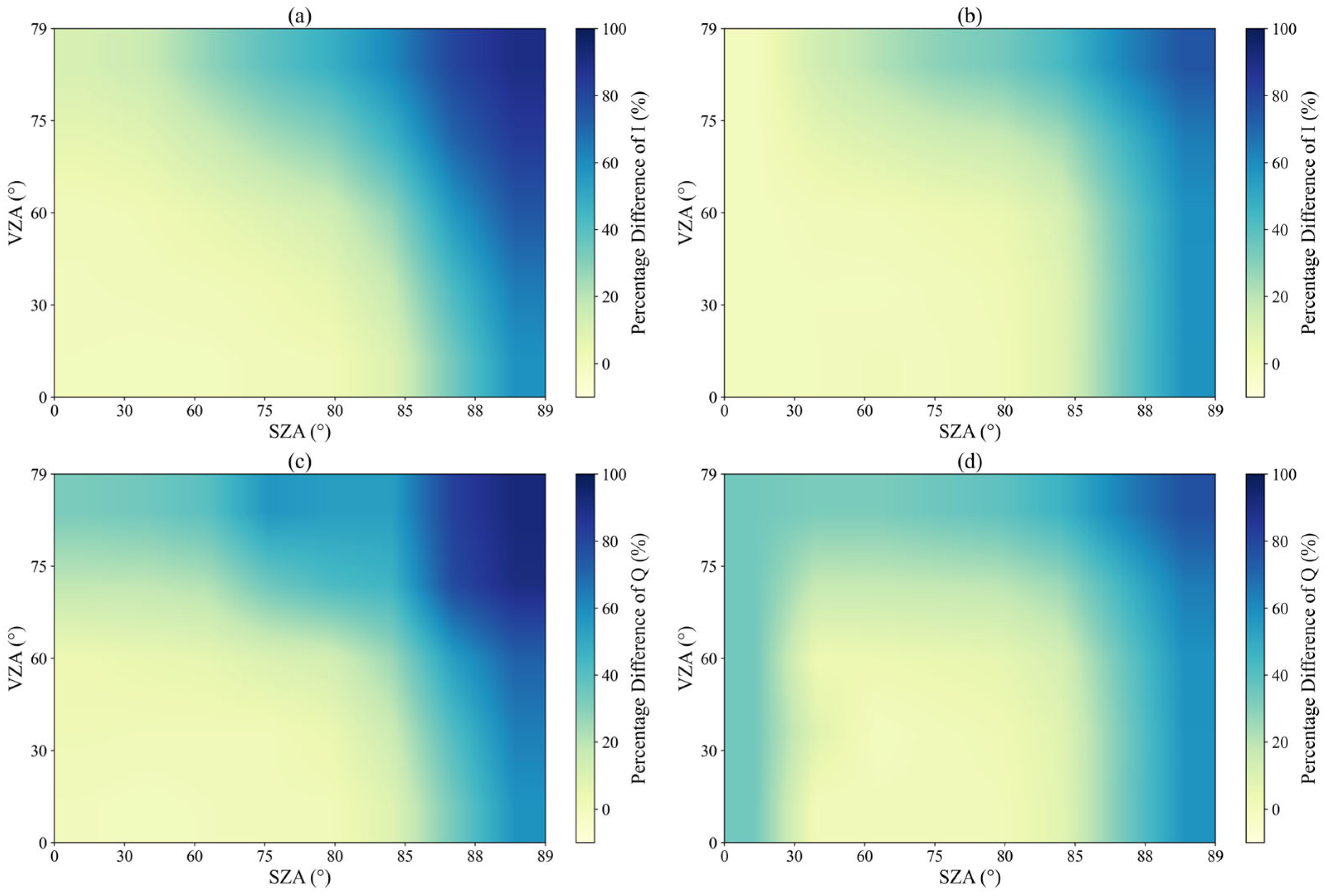
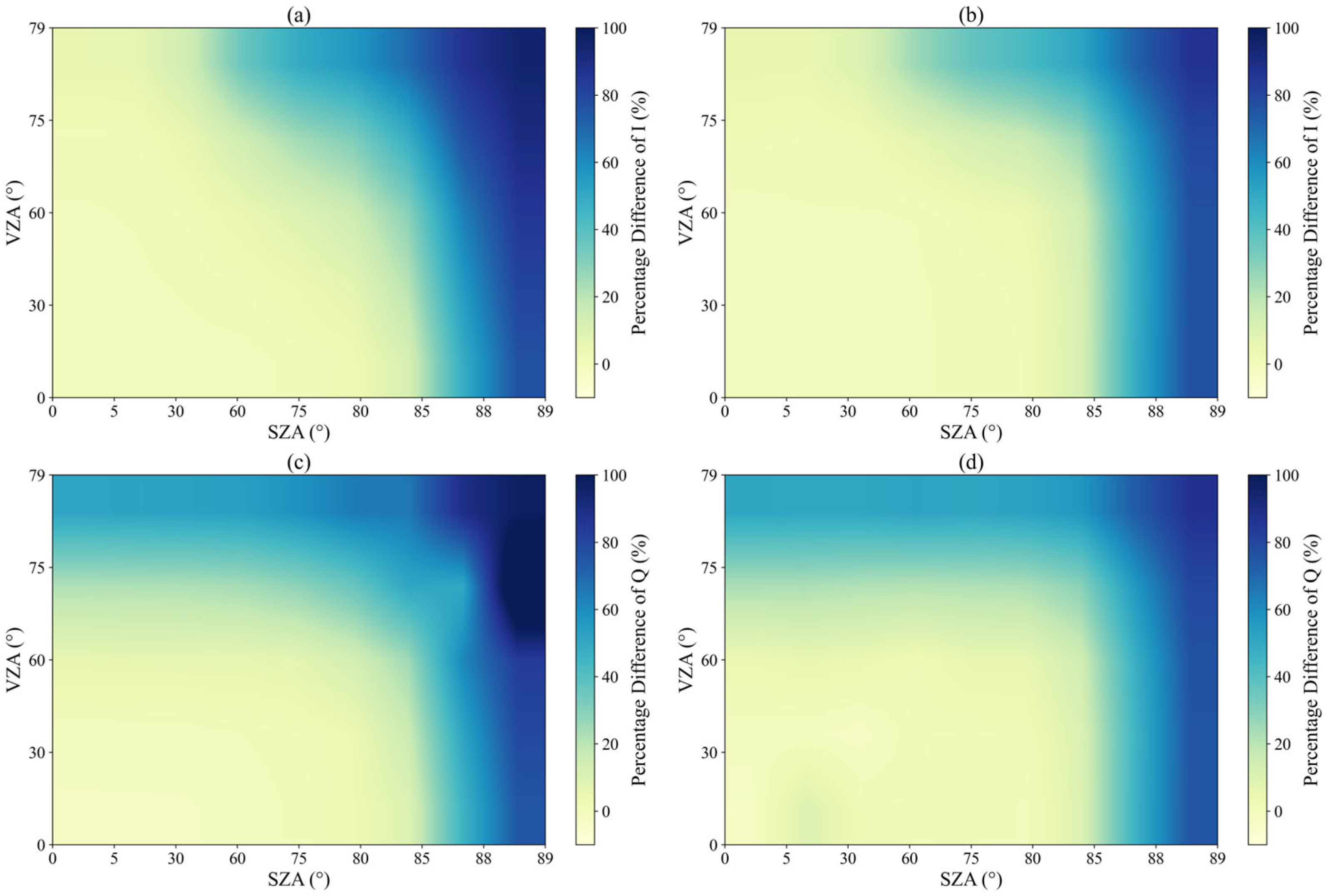
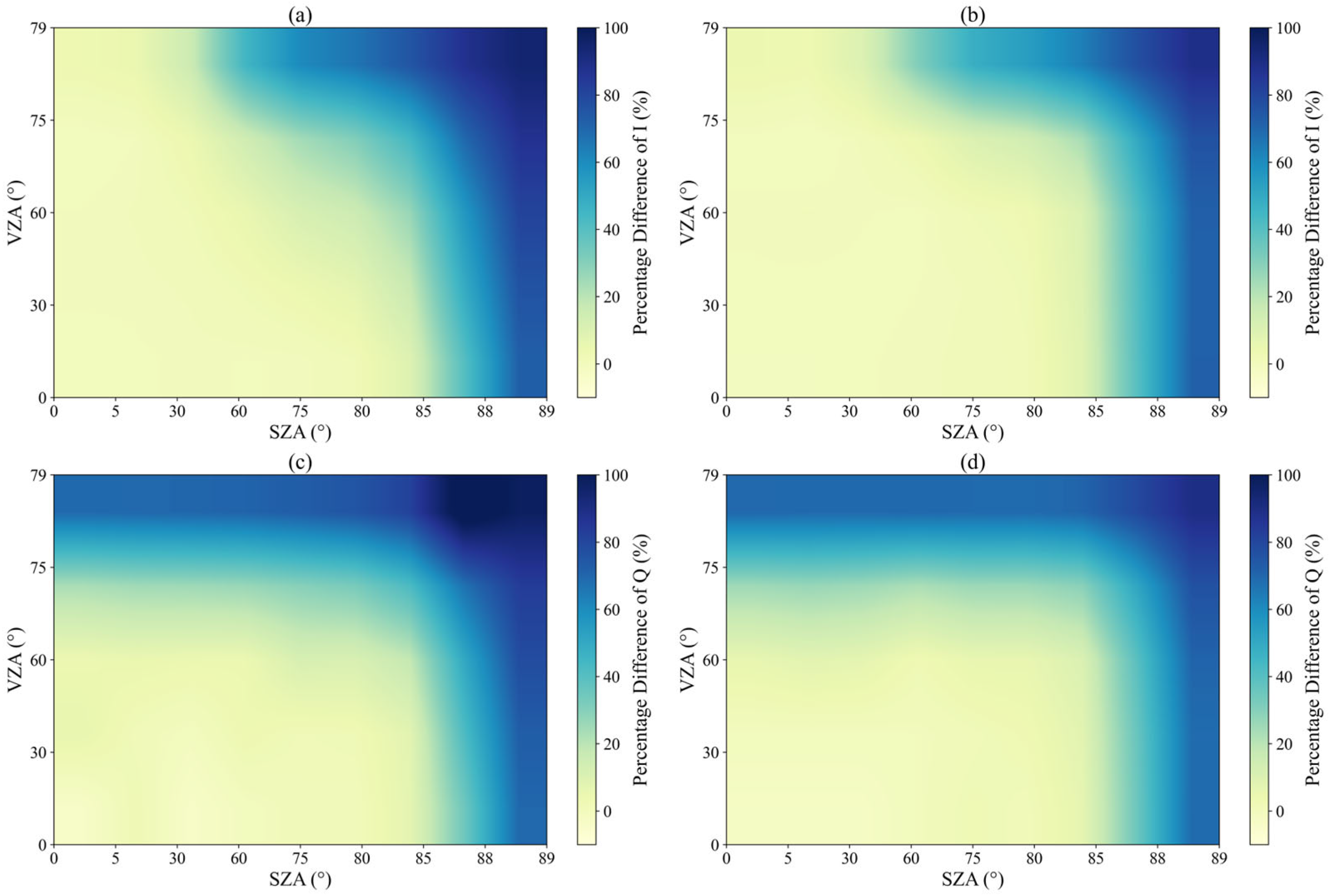
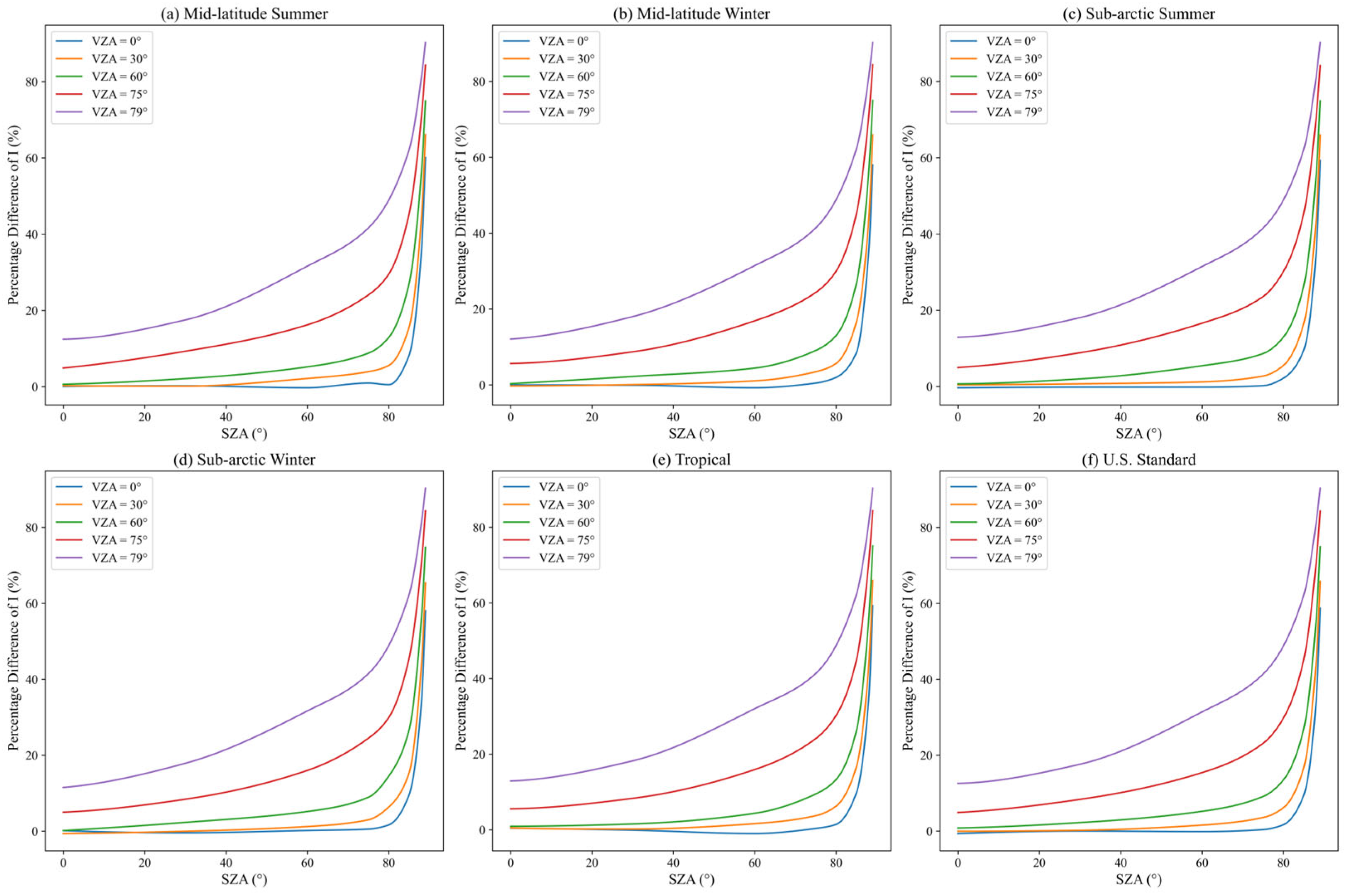
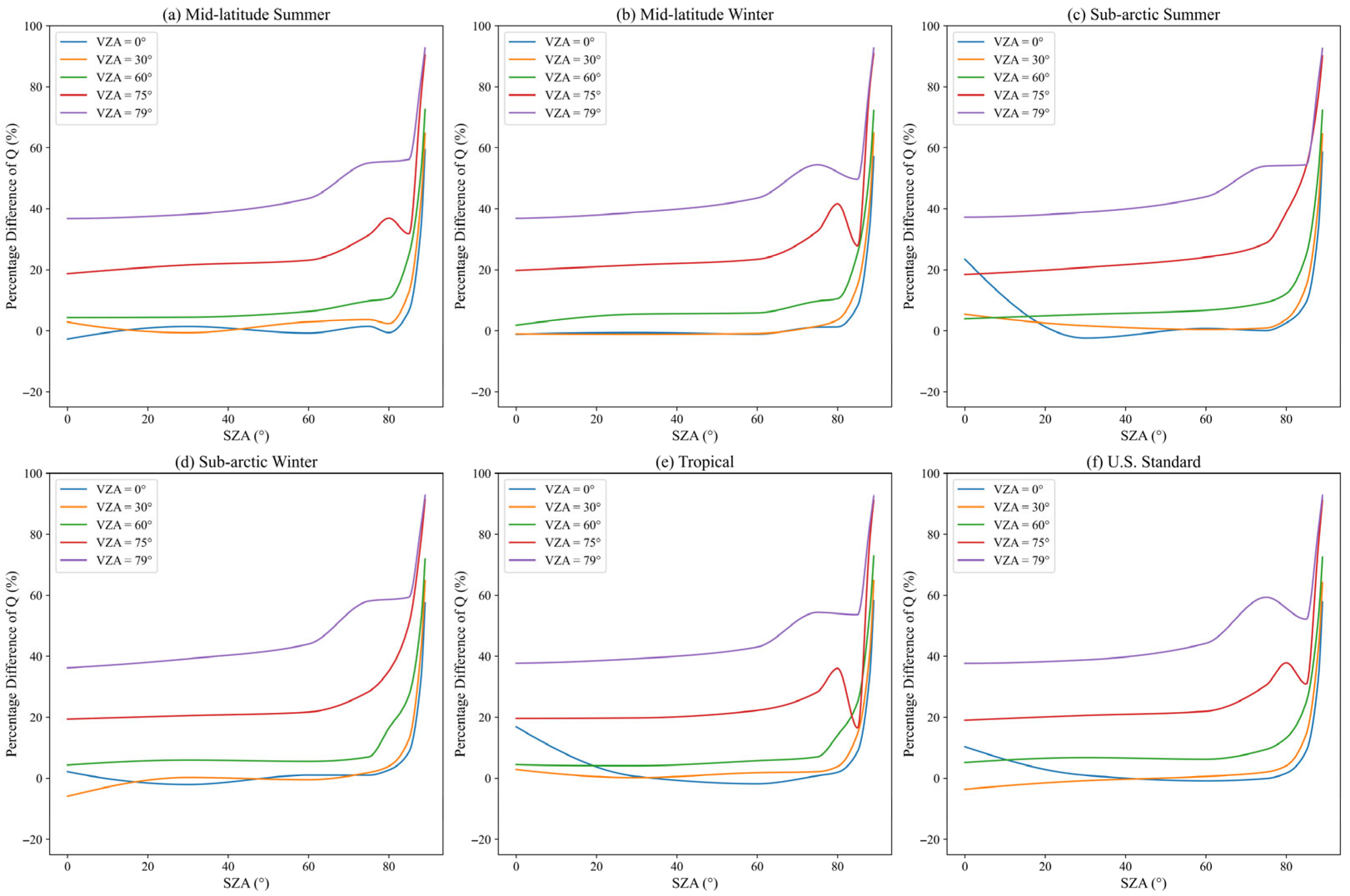
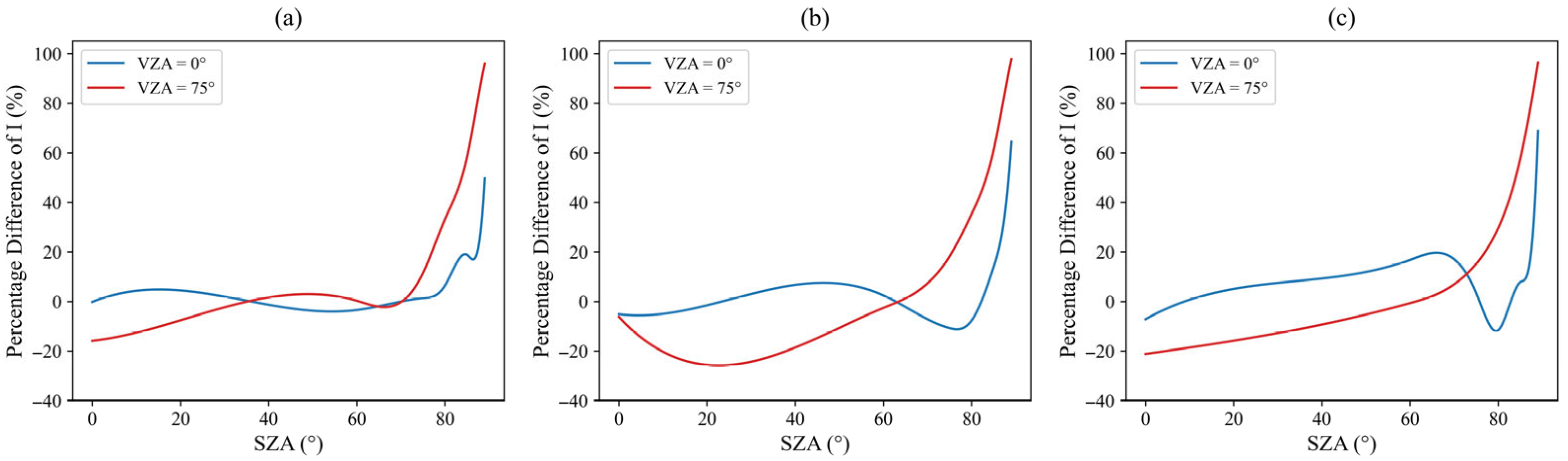
3.1. Clear Atmosphere
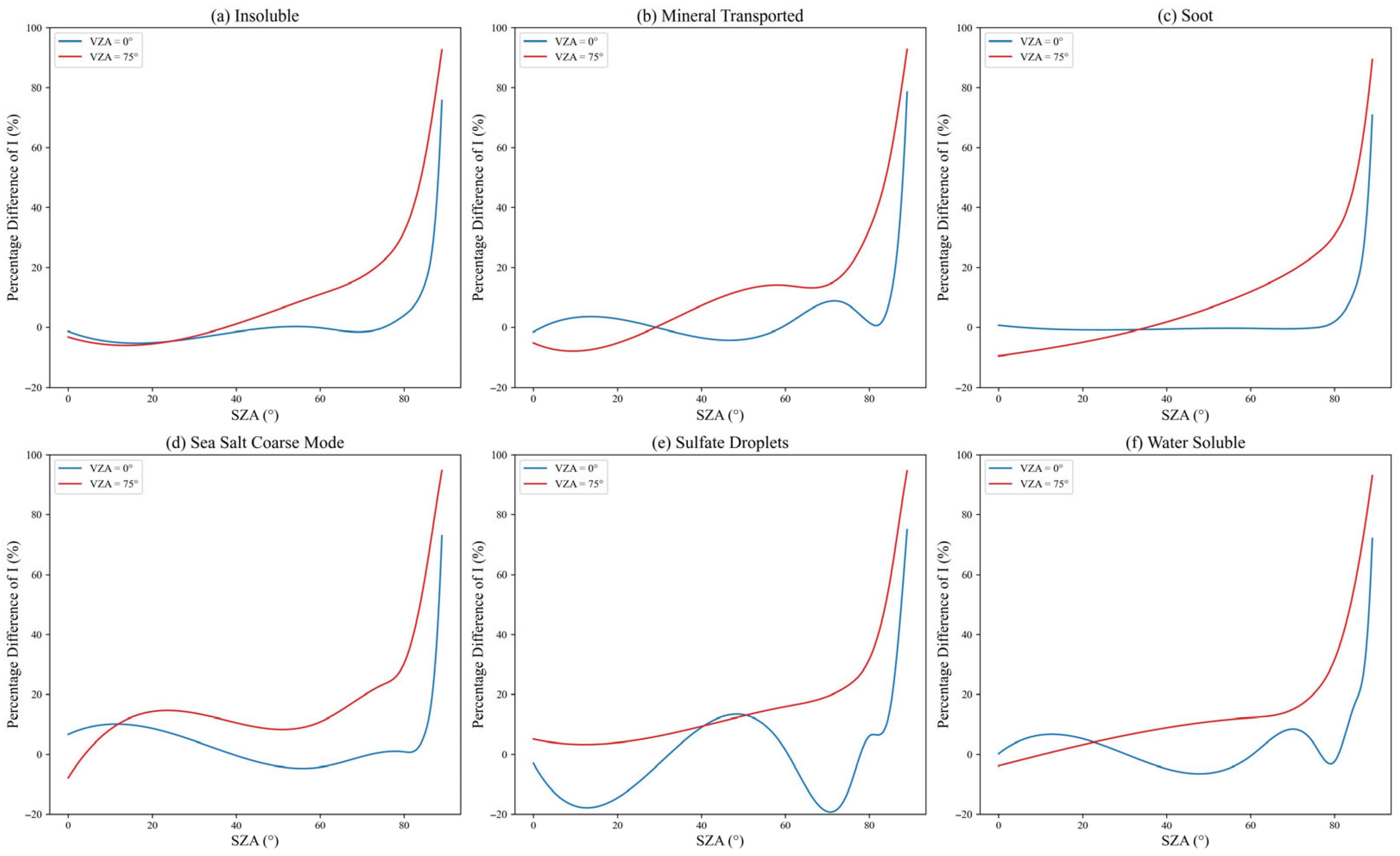
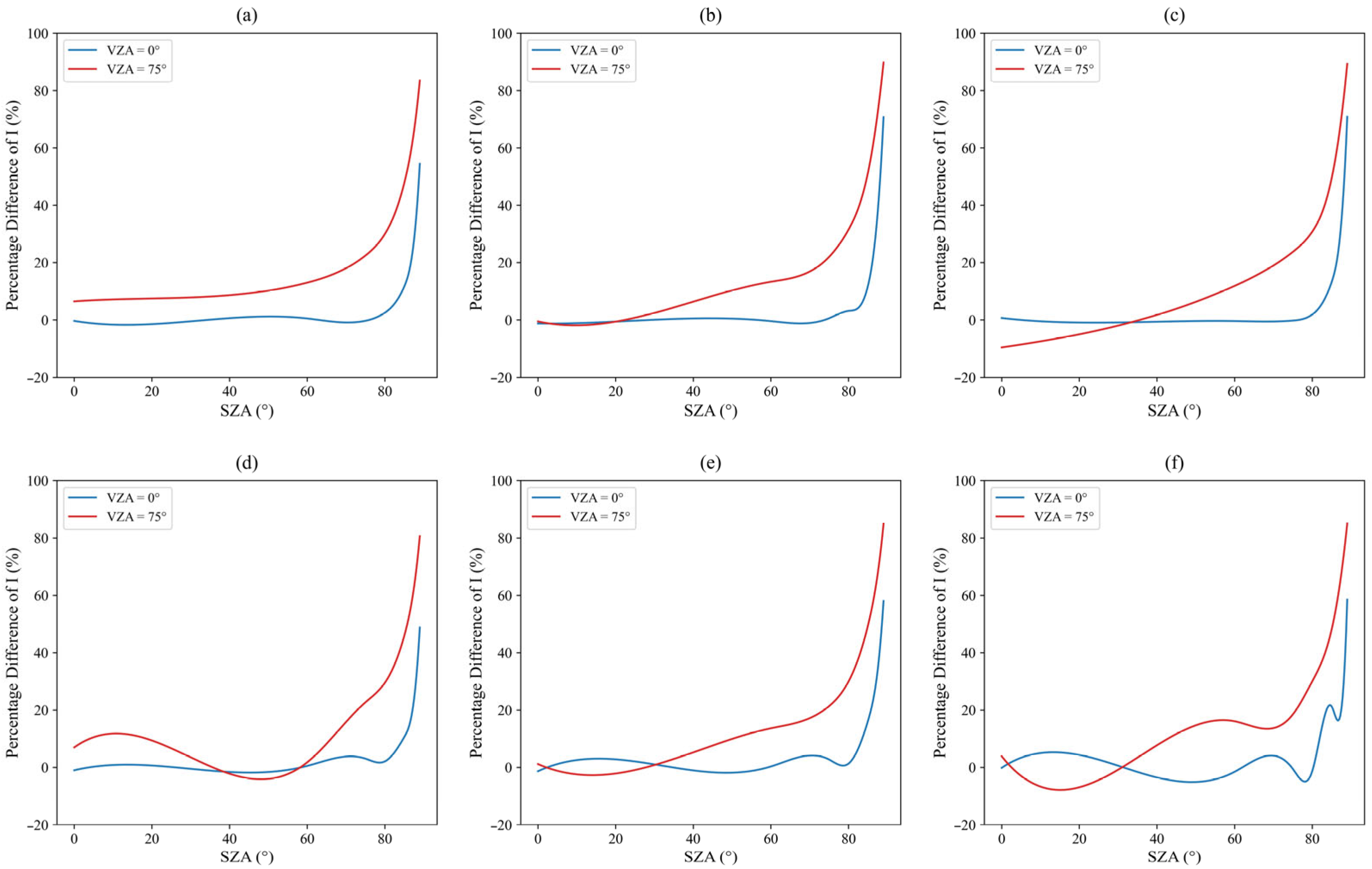
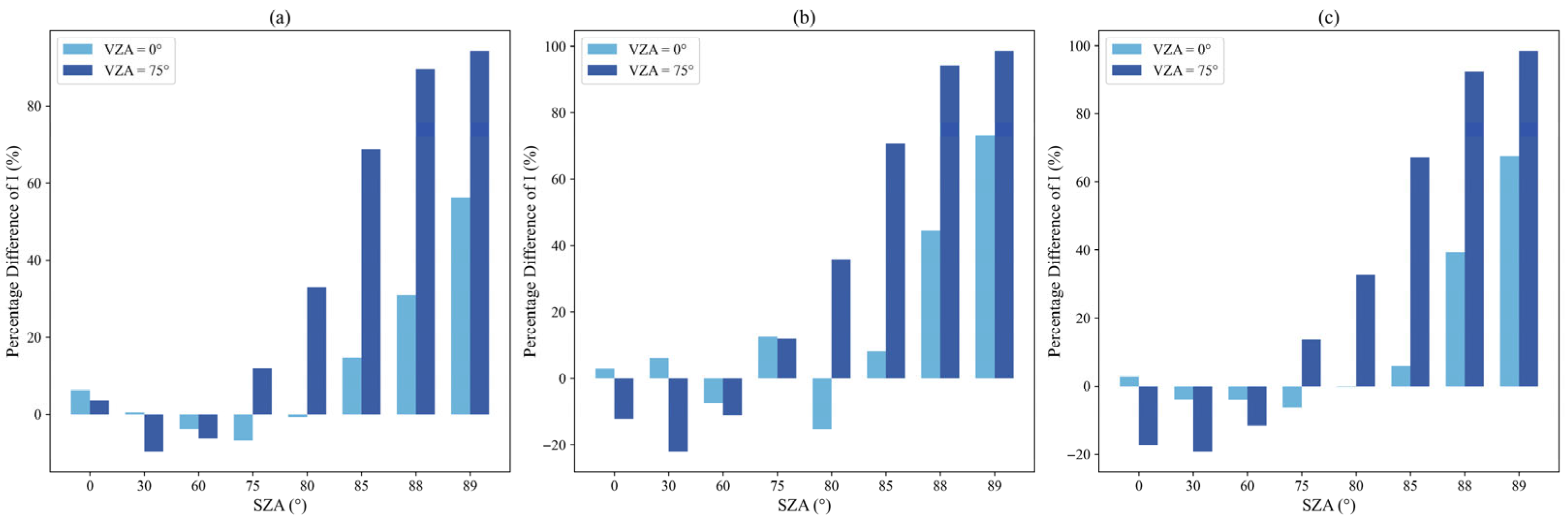
3.2. Aerosol-Laden Atmosphere
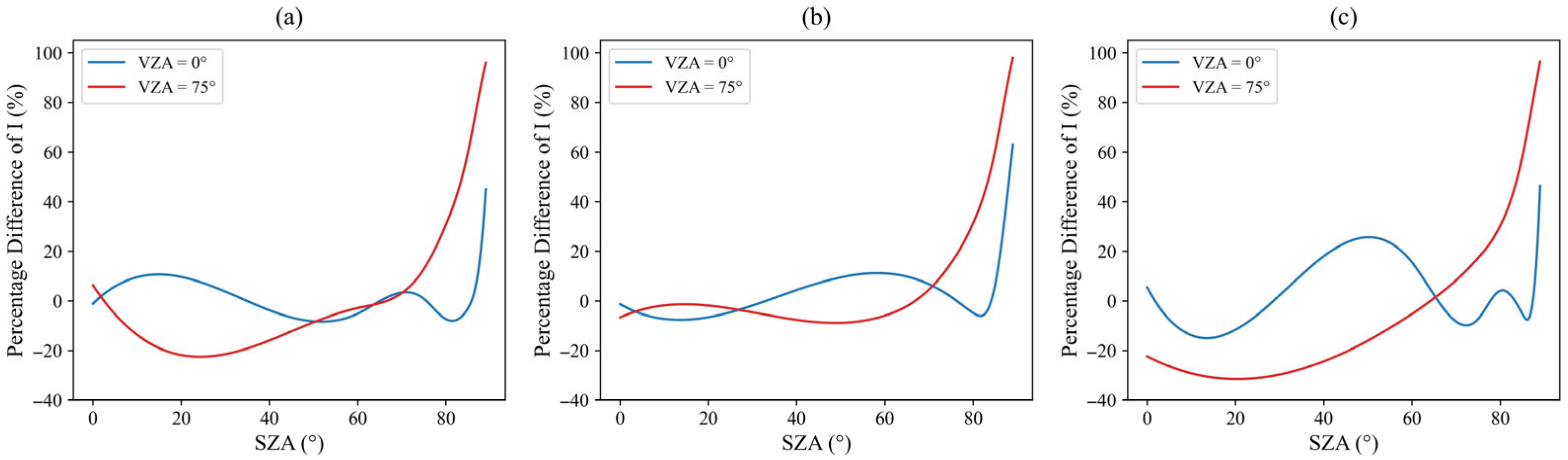
3.3. Liquid Water Cloud Atmosphere
3.4. Ice Cloud Atmosphere
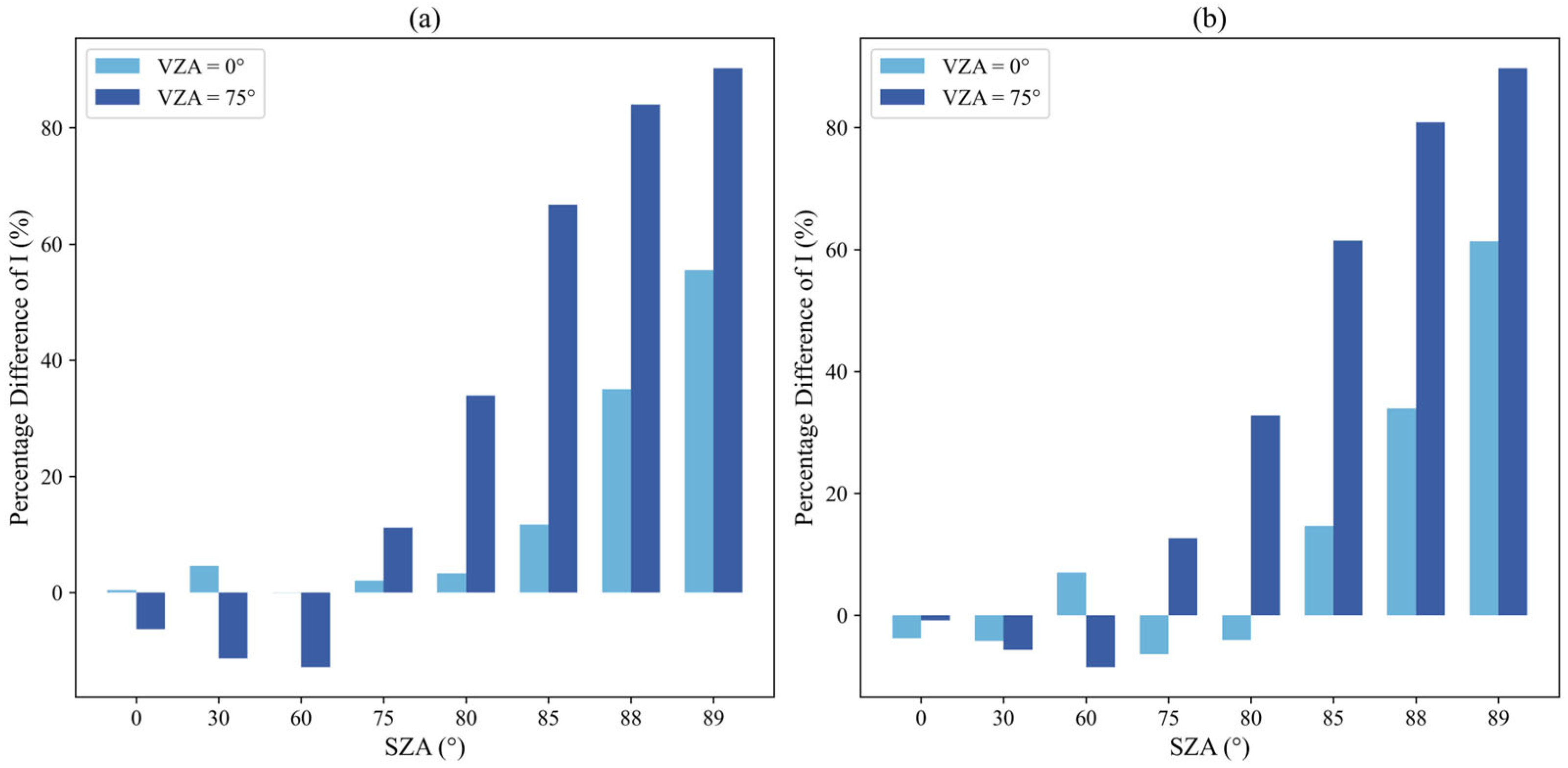
3.5. Liquid Water Cloud and Aerosol-Laden Atmosphere
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RT | Radiative Transfer |
| PP | Plane-Parallel |
| PSS | Pseudo-Spherical |
| IPSS | Improved Pseudo-Spherical |
| SZA | Solar Zenith Angles |
| VZA | Viewing Zenith Angle |
| MYSTIC | Monte Carlo Code |
| SPARTA | Spherical Planetary Atmospheric Radiative Transfer Algorithm |
| RTE | Radiative Transfer Equation |
| DISORT | Discrete Ordinates Radiative Transfer |
| TRO | Tropical |
| MLS | Mid-Latitude Summer |
| MLW | Mid-Latitude Winter |
| SAS | Sub-Polar Summer |
| SAW | Sub-Polar Winter |
| STA | U.S. Standard |
| SSA | Single Scattering Albedo |
| gg | Asymmetry Factor |
| INSO | Water-Insoluble |
| WASO | Water-Soluble |
| SOOT | Black Carbon |
| SUSO | Sulfate Droplets |
| SSCM | Sea Salt Coarse Mode |
| MITR | Mineral Transport |
| OPAC | Optical Properties of Aerosols and Clouds |
| MERSI-III | Medium Resolution Spectral Imager-III |
| AOD | Aerosol Optical Depth |
References
- Plass, G.N.; Kattawar, G.W. Radiative transfer in an atmosphere–ocean system. Appl. Opt. 1969, 8, 455–466. [Google Scholar] [CrossRef] [PubMed]
- Lenoble, J.; Sekera, Z. Equation of radiative transfer in a planetary spherical atmosphere. Proc. Natl. Acad. Sci. USA 1961, 47, 372–378. [Google Scholar] [CrossRef]
- Smokty, O.I. Multiple light scattering in the spherical planetary atmosphere. Pure Appl. Geophys. 1969, 72, 214–225. [Google Scholar] [CrossRef]
- Meinel, A.B.; Meinel, M.P. Optical Phenomena in the Atmosphere. (Book Reviews: Twilight: A Study in Atmospheric Optics). Science 1966, 154, 1160. [Google Scholar] [CrossRef]
- Marchuk, G.I.; Mikhailov, G.A.; Nazaraliev, M.A.; Darbinjan, R.A.; Kargin, B.A.; Elepov, B.S. The Monte Carlo Methods in Atmospheric Optics; Springer: Berlin, Germany, 1980; Volume 12, pp. 54–86. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1–772. [Google Scholar]
- Xu, F.; He, X.; Jin, X.; Cai, W.; Bai, Y.; Wang, D.; Gong, F.; Zhu, Q. Spherical vector radiative transfer model for satellite ocean color remote sensing. Opt. Express 2023, 31, 11192–11212. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Handscomb, D.C. Monte Carlo Methods; Methuen & Co Ltd.: London, UK, 1964; p. 178. [Google Scholar]
- Caudill, T.R.; Flittner, D.E.; Herman, B.M.; Torres, O.; McPeters, R.D. Evaluation of the pseudo-spherical approximation for backscattered ultraviolet radiances and ozone retrieval. J. Geophys. Res. Atmos. 1997, 102, 3881–3890. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Rozanov, A.; Burrows, J.P. SCIATRAN software package (V4.6): Update and further development of aerosol, clouds, surface reflectance databases and models. Geosci. Model Dev. 2023, 16, 1511–1536. [Google Scholar] [CrossRef]
- Spurr, R. VLIDORT: A linearized pseudo-spherical vector discrete ordinate radiative transfer code for forward model and retrieval studies in multilayer multiple scattering media. J. Quant. Spectrosc. Radiat. Transf. 2006, 102, 316–342. [Google Scholar] [CrossRef]
- Spurr, R.; Christi, M. The LIDORT and VLIDORT linearized scalar and vector discrete ordinate radiative transfer models: Updates in the last 10 years. In Springer Series in Light Scattering; Kokhanovsky, A., Ed.; Springer: Berlin, Germany, 2019; Volume 3, pp. 1–62. [Google Scholar]
- Korkin, S.; Yang, E.; Spurr, R.; Emde, C.; Krotkov, N.; Vasilkov, A.; Haffner, D.; Mok, J.; Lyapustin, A. Revised and extended benchmark results for Rayleigh scattering of sunlight in spherical atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2020, 254, 107181. [Google Scholar] [CrossRef]
- Korkin, S.; Yang, E.-S.; Marchuk, E. Numerical results for polarized light scattering in a spherical atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2022, 287, 108194. [Google Scholar] [CrossRef]
- He, X.; Stamnes, K.; Bai, Y.; Li, W.; Wang, D.; Fan, Y. Effects of Earth curvature on atmospheric correction for ocean color remote sensing. Remote Sens. Environ. 2018, 209, 118–133. [Google Scholar] [CrossRef]
- Zhai, P.-W.; Hu, Y. An improved pseudo spherical shell algorithm for vector radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2022, 282, 108132. [Google Scholar] [CrossRef]
- Adams, C.N.; Kattawar, G.W. Radiative transfer in spherical shell atmospheres: I. Rayleigh scattering. Icarus 1978, 35, 139–151. [Google Scholar] [CrossRef]
- Adams, C.N.; Kattawar, G.W. Radiative transfer in spherical shell atmospheres: II. Asymmetric phase functions. Icarus 1978, 35, 436–449. [Google Scholar] [CrossRef]
- Li, H.; He, X.; Bai, Y.; Shanmugam, P.; Park, Y.J.; Liu, J.; Zhu, Q.; Gong, F.; Wang, D.; Huang, H. Atmospheric correction of geostationary satellite ocean color data under high solar zenith angles in open oceans. Remote Sens. Environ. 2020, 249, 112022. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.-C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Three-Dimensional Radiative Transfer Calculations with the MYSTIC Model. In Proceedings of the EGS 2000, Nice, France, 25–29 April 2000; DLR: Cologne, Germany, 2000. [Google Scholar]
- Mayer, B. Radiative transfer in the cloudy atmosphere. Eur. Phys. J. Conf. 2009, 1, 75–99. [Google Scholar] [CrossRef]
- Duhis, A.H.; Aljanabi, M.; Al-Kafaji, M.S.S. Increasing photovoltaic system power output with white paint albedo—A scenario in Al-Mausaib City using PVSyst. software. Int. J. Power Electron. Drive Syst. 2023, 14, 1149–1159. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Zege, E.P. The effect of hygroscopic growth on the optical properties of aerosols. J. Aerosol Sci. 2015, 81, 1–14. [Google Scholar]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Koepke, P.; Gasteiger, J.; Hess, M. Technical Note: Optical properties of desert aerosol with non-spherical mineral particles: Data incorporated to OPAC. Atmos. Chem. Phys. 2015, 15, 5947–5956. [Google Scholar] [CrossRef]





| Atmospheric Type | Parameter | Values/Options |
|---|---|---|
| Clear atmosphere | Atmospheric Profile File | TRO, MLS, MLW, SAS, SAW, STA |
| Wavelength | 450 nm, 550 nm, 650 nm | |
| Solar Zenith Angle (SZA) | [0°, 89°] | |
| Sensor Azimuth Angle (PHI) | 0°, 90° | |
| Viewing Zenith Angle (VZA) | [0°, 79°] | |
| Surface Albedo () | 0.08 (ocean), 0.15 (tree), 0.2 (grass), 0.3 (stone), 0.4 (ice), 0.8 (snow) [25] | |
| Aerosol-laden atmosphere | Aerosol Type | Water-insoluble (INSO), Water-soluble (WASO), Black Carbon (SOOT), Sulfate Droplets (SUSO), Sea Salt Coarse Mode (SSCM), Transported Mineral (MITR) |
| Single Scattering Albedo (SSA) | Based on the OPAC database: (450 nm): 0.705586, 0.968506, 0.245706, 0.999999, 0.999996, 0.755423 (550 nm): 0.730000, 0.961548, 0.208889, 0.999999, 0.999999, 0.837441 (650 nm): 0.750693, 0.953461, 0.175677, 0.999999, 0.999993, 0.876215 | |
| Asymmetry Factor (gg) | Based on the OPAC database: (450 nm): 0.915526, 0.908406, 0.509439, 0.941813, 0.943903, 0.908330 (550 nm): 0.911533, 0.895515, 0.469539, 0.940180, 0.942755, 0.896900 (650 nm): 0.908112, 0.881702, 0.431983, 0.936384, 0.941450, 0.889530 | |
| Optical depth | Angstrom parameters: 1 | |
| Water cloud atmosphere | Asymmetry Factor (gg) | Based on the OPAC database: 0.950884 (450 nm), 0.950601 (550 nm), 0.949917 (650 nm) |
| Ice cloud atmosphere | Asymmetry Factor (gg) | Based on OPAC database: Columnar ice cloud: 0.864696 (450 nm), 0.868618 (550 nm), 0.871774 (650 nm) Platelike ice cloud: 0.874529 (450 nm), 0.885377 (550 nm), 0.891587 (650 nm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Q.; Wu, K.; Wang, X.; Xin, Q.; Chen, L. Dataset Construction for Radiative Transfer Modeling: Accounting for Spherical Curvature Effect on the Simulation of Radiative Transfer Under Diverse Atmospheric Scenarios. Atmosphere 2025, 16, 977. https://doi.org/10.3390/atmos16080977
Gu Q, Wu K, Wang X, Xin Q, Chen L. Dataset Construction for Radiative Transfer Modeling: Accounting for Spherical Curvature Effect on the Simulation of Radiative Transfer Under Diverse Atmospheric Scenarios. Atmosphere. 2025; 16(8):977. https://doi.org/10.3390/atmos16080977
Chicago/Turabian StyleGu, Qingyang, Kun Wu, Xinyi Wang, Qijia Xin, and Luyao Chen. 2025. "Dataset Construction for Radiative Transfer Modeling: Accounting for Spherical Curvature Effect on the Simulation of Radiative Transfer Under Diverse Atmospheric Scenarios" Atmosphere 16, no. 8: 977. https://doi.org/10.3390/atmos16080977
APA StyleGu, Q., Wu, K., Wang, X., Xin, Q., & Chen, L. (2025). Dataset Construction for Radiative Transfer Modeling: Accounting for Spherical Curvature Effect on the Simulation of Radiative Transfer Under Diverse Atmospheric Scenarios. Atmosphere, 16(8), 977. https://doi.org/10.3390/atmos16080977






