Energy Sustainability of Urban Areas by Green Systems: Applied Thermodynamic Entropy and Strategic Modeling Means
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Framework
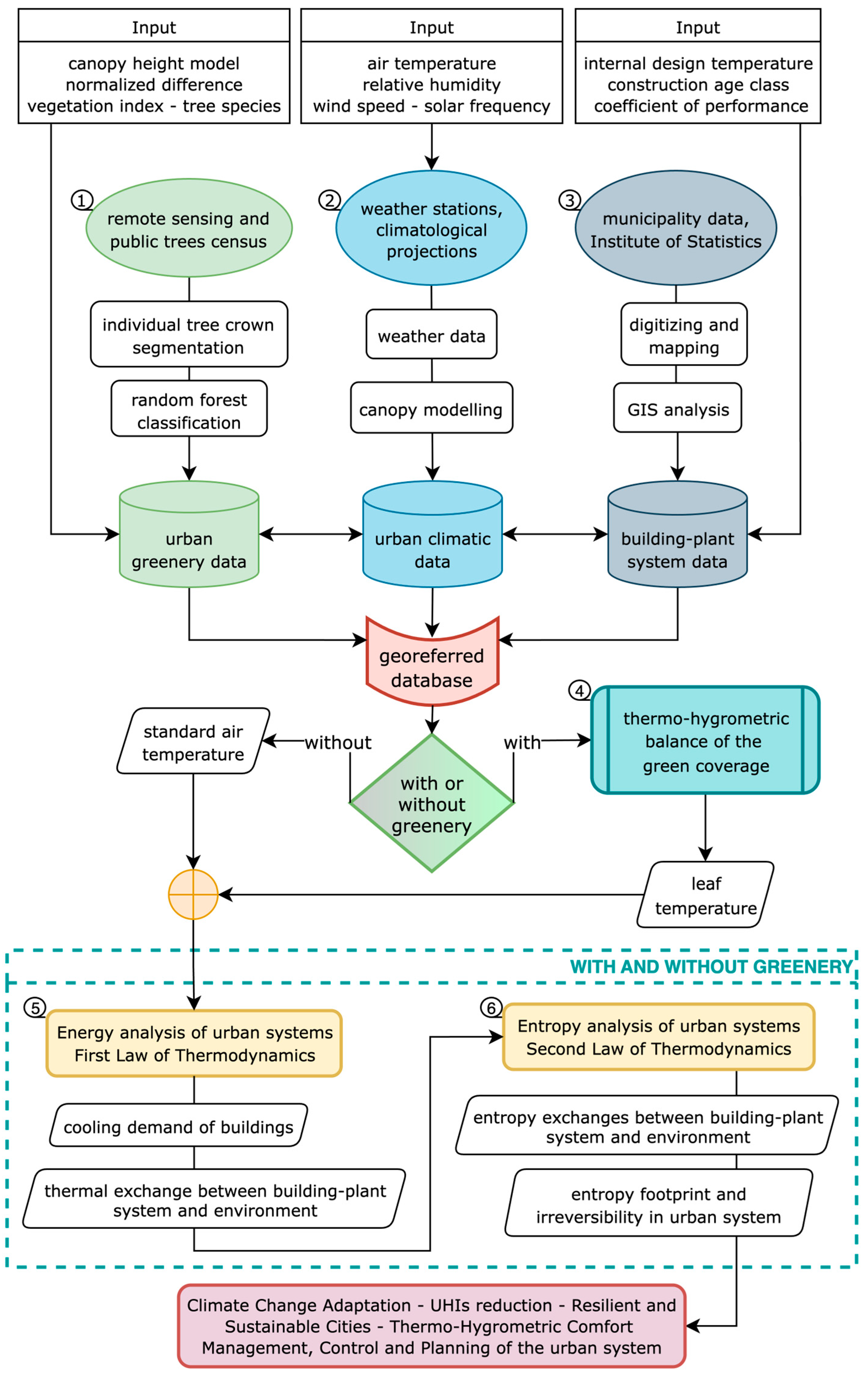
2.2. Modeling Approach, Data Sources, and Pre-Processing
2.3. The Case Study: Typical Built-Up Urban Area of Florence
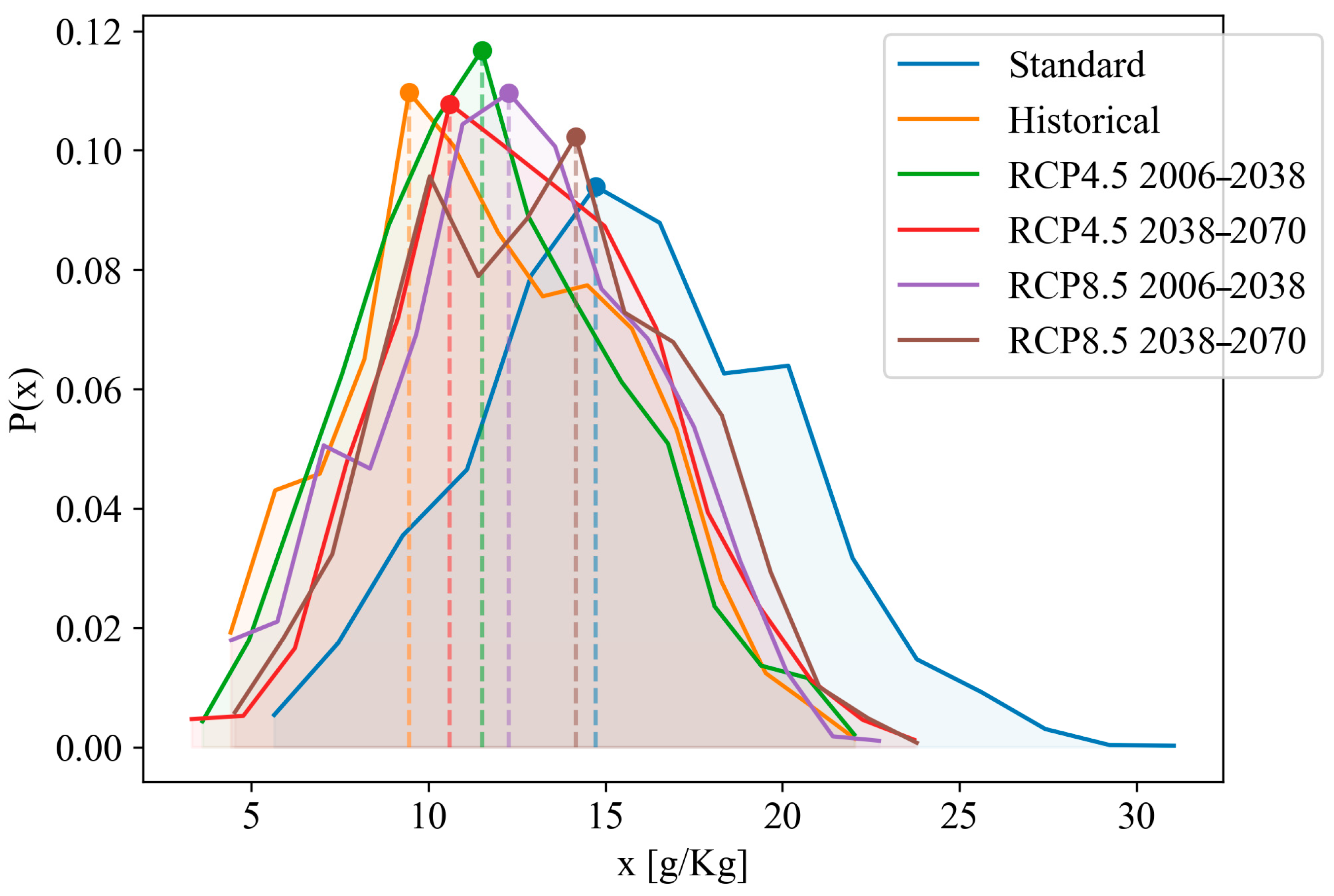
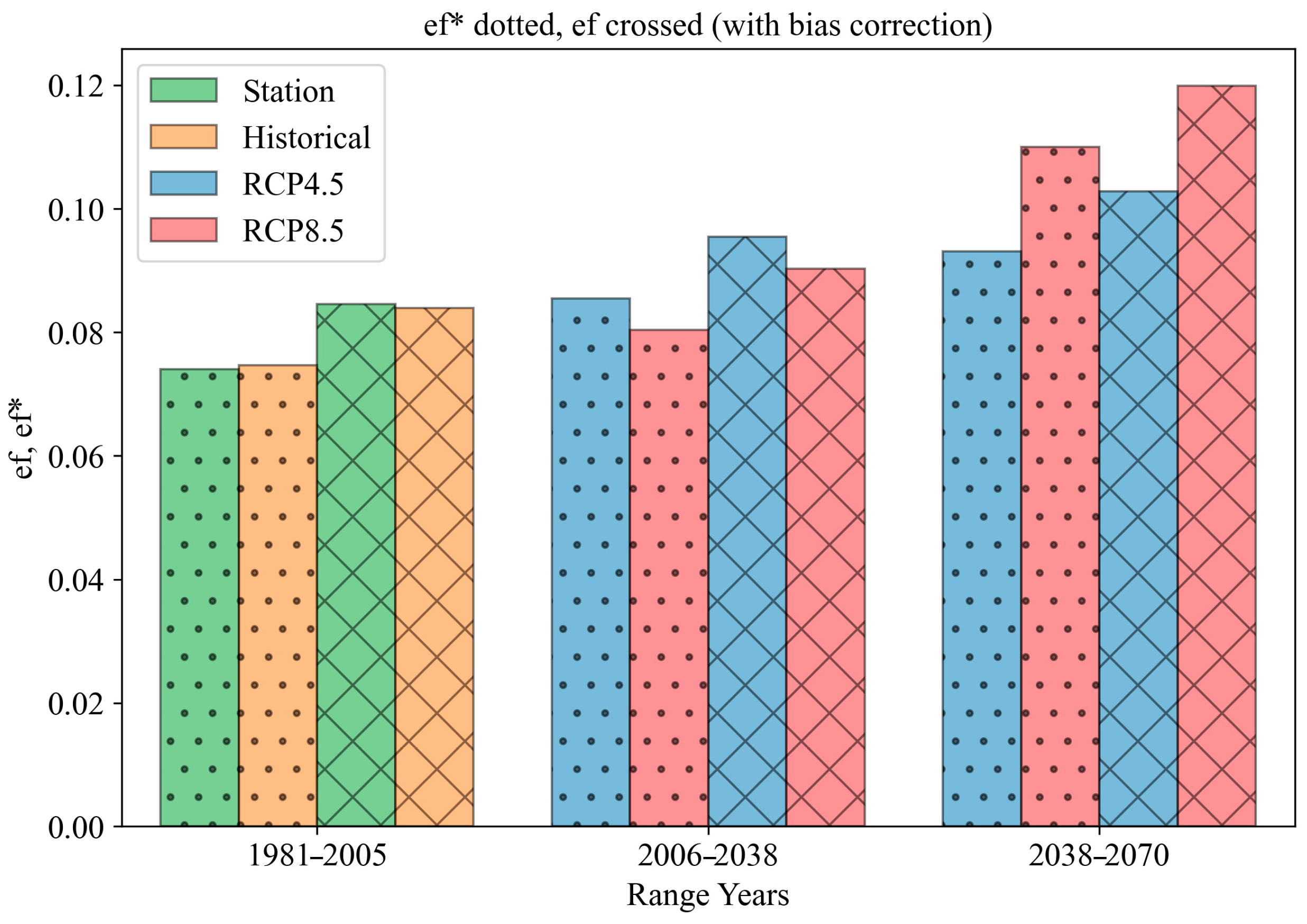
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ab | dispersing surface of the buildings in the investigated area [m2] |
| Aurban | urban area considered for the analysis [m2] |
| b | correction factor for the entropy weights [-] |
| SCOP | mean coefficient of performance for heat pumps [-] |
| Dl | characteristic dimension of the leaves in the wind direction [m] |
| ef | entropy weight without the presence of the greenery [-] |
| ef* | entropy weight with the presence of the greenery [-] |
| GHI | global horizontal irradiation on a specific site [W/m2] |
| hl | heat transfer coefficient by natural convection between leaves and the air below [W/m2 °C] |
| hs | heat transfer coefficient of natural convection between ground and the air above [W/m2 °C] |
| k1 | empirical coefficient [J/m2·s1/2·°C1] |
| k2 | empirical coefficient [s1/2·m1] |
| Ll | latent heat of vaporization at the surface temperature of the leaves [J/kg] |
| m | air flow rate on the considered surface as a function of the wind velocity [kg/s m2] |
| Qb | cooling power for buildings in the summer period without the presence of greenery [W] |
| Qb−G | cooling power for buildings in the summer period with the presence of greenery [W] |
| Qb_rel | thermal power released to the environment without the presence of greenery [W] |
| Qb-G_rel | thermal power released to the environment with the presence of greenery [W] |
| QSun | total horizontal Sun radiation hitting the urban area in the summer period [W/m2] |
| rl | evaporation resistance of the leaves [s/m] |
| RHa | relative humidity of the air [-] |
| Ta | ambient temperature [K] |
| Ta−g | air temperature above the ground [K] |
| Te | external mean air temperature in the summer period without the presence of greenery [K] |
| Te−G | external mean air temperature in the summer period with the presence of greenery [K] |
| Tg | temperature of the ground surface [K] |
| Ti | indoor temperature for the buildings in the summer period [K] |
| Tl | surface temperature of the leaves [K] |
| U | global heat exchange coefficient for the building (W/m2K] |
| vw | wind velocity [m/s] |
| Wl | characteristic dimension of the leaves in the direction transverse to the wind [m] |
| Geek symbols | |
| αa | adsorption coefficient of the air in the visible range [-] |
| αg | adsorption coefficient of the ground across the entire spectrum [-] |
| αl | absorption coefficient [-] for the leaves across the entire spectrum [-] |
| αm | mean absorption coefficient [-] for the urban area across the entire spectrum [-] |
| entropy generation due to the buildings without the presence of greenery [J/K] | |
| entropy generation due to the buildings with the presence of greenery [J/K] | |
| entropy generation due to Sun radiation hitting the urban area without greenery [J/K] | |
| entropy generation due to Sun radiation hitting the urban area with greenery [J/K] | |
| εa | emissivity coefficient of the air in the infrared range [-] |
| εeffective | emissivity between two bodies/surfaces as a function of the emissivity of each [-] |
| εg | emissivity coefficient for the ground in the infrared range [-] |
| εl | emissivity coefficient of leaves in the infrared range [-] |
| ρa | density of the air at ambient temperature [kg/m3] |
| ρva | vapor density at the ambient temperature [kg/m3] |
| ρvl | vapor density at the surface temperature of the leaves [kg/m3] |
| σ | Stefan–Boltzmann constant [W/m2K4] |
Appendix A
Appendix A.1
Appendix A.2
| Weather Index | wj | Weather Index | wj |
|---|---|---|---|
| Maximum dry bulb temperature | 1/24 | Mean dew bulb temperature | 2/24 |
| Minimum dry bulb temperature | 1/24 | Maximum wind velocity | 2/24 |
| Mean dry bulb temperature | 2/24 | Mean wind velocity | 2/24 |
| Maximum dew bulb temperature | 1/24 | Total horizontal solar radiation | 11/24 |
References
- Tamang, B. Global Climate Change: Challenges, Opportunities, and Multilateral Strategies for Sustainable Development. NPRC J. Multidiscip. Res. 2024, 1, 65–76. [Google Scholar] [CrossRef]
- Afifa; Arshad, K.; Hussain, N.; Ashraf, M.H.; Saleem, M.Z. Air Pollution and Climate Change as Grand Challenges to Sustainability. Sci. Total Environ. 2024, 928, 172370. [Google Scholar] [CrossRef] [PubMed]
- Malakar, K.D.; Kumar, M.; Anand, S.; Kuzur, G. Climate Crisis and Socio-Ecological Sustainability. In Climate Change and Socio-Ecological Transformation; Springer: Singapore, 2023; pp. 439–494. [Google Scholar]
- Cornell, S.E.; Gupta, A. Is Climate Change the Most Important Challenge of Our Times? In Contemporary Climate Change Debates; Routledge: Oxfordshire, UK, 2019; pp. 6–20. [Google Scholar]
- Meerab, K. Addressing the Global Environmental Crisis: A Comprehensive Review of Current Strategies and Challenges. Int. Res. J. Arts Soc. Sci. 2023, 11, 1–4. [Google Scholar] [CrossRef]
- Francini, S.; Chirici, G.; Chiesi, L.; Costa, P.; Caldarelli, G.; Mancuso, S. Global Spatial Assessment of Potential for New Peri-Urban Forests to Combat Climate Change. Nat. Cities 2024, 1, 286–294. [Google Scholar] [CrossRef]
- Gao, J.; O’Neill, B.C. Mapping Global Urban Land for the 21st Century with Data-Driven Simulations and Shared Socioeconomic Pathways. Nat. Commun. 2020, 11, 2302. [Google Scholar] [CrossRef] [PubMed]
- IISD. International Day of Forests. Available online: https://sdg.iisd.org/events/international-day-of-forests-2018/ (accessed on 12 August 2025).
- Netto, V.M.; Meirelles, J.; Ribeiro, F.L. Cities and Entropy: Assessing Urban Sustainability. In Sustainability Assessment of Urban Systems; Cambridge University Press: Cambridge, UK, 2020; p. 438. Available online: https://www.cambridge.org/core/books/abs/sustainability-assessment-of-urban-systems/cities-and-entropy-assessing-urban-sustainability-as-a-problem-of-coordination/83D93195E53A8B8579E974CEF9AEEB81#chapter (accessed on 12 August 2025).
- Purvis, B.; Mao, Y.; Robinson, D. Entropy and Its Application to Urban Systems. Entropy 2019, 21, 56. [Google Scholar] [CrossRef]
- Schneider, E.D.; Kay, J.J. Life as a Manifestation of the Second Law of Thermodynamics. Math. Comput. Model. 1994, 19, 25–48. [Google Scholar] [CrossRef]
- Roach, T.N.F. Use and Abuse of Entropy in Biology: A Case for Caliber. Entropy 2020, 22, 1335. [Google Scholar] [CrossRef]
- Zhao, S.; Ren, Y.; Mao, C.; Yue, A. Are Cities Healthy? A City Health Diagnose Framework from the Perspective of Living Organism. Ecol. Indic. 2024, 160, 111834. [Google Scholar] [CrossRef]
- Modonesi, C.; Serafini, S.; Giuliani, A. Urban Systems Between the Environment, Human Health and Society: An Overview. Systems 2025, 13, 487. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Li, W. Analyses of Urban Ecosystem Based on Information Entropy. Ecol. Modell. 2006, 197, 1–12. [Google Scholar] [CrossRef]
- Rondinel-Oviedo, D.R.; Keena, N. Entropy and Cities: A Bibliographic Analysis towards More Circular and Sustainable Urban Environments. Entropy 2023, 25, 532. [Google Scholar] [CrossRef]
- Al Mashagbah, A.F. The Use of GIS, Remote Sensing and Shannon’s Entropy Statistical Techniques to Analyze and Monitor the Spatial and Temporal Patterns of Urbanization and Sprawl in Zarqa City, Jordan. J. Geogr. Inf. Syst. 2016, 8, 293–300. [Google Scholar] [CrossRef]
- Gaur, A.; Eichenbaum, M.K.; Simonovic, S.P. Analysis and Modelling of Surface Urban Heat Island in 20 Canadian Cities under Climate and Land-Cover Change. J. Environ. Manag. 2018, 206, 145–157. [Google Scholar] [CrossRef]
- Mohajerani, A.; Bakaric, J.; Jeffrey-Bailey, T. The Urban Heat Island Effect, Its Causes, and Mitigation, with Reference to the Thermal Properties of Asphalt Concrete. J. Environ. Manag. 2017, 197, 522–538. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Huang, Y.; Irga, P.; Kumar, P.; Li, W.; Wei, W.; Shon, H.K.; Lei, C.; Zhou, J.L. Synergistic Control of Urban Heat Island and Urban Pollution Island Effects Using Green Infrastructure. J. Environ. Manag. 2024, 370, 122985. [Google Scholar] [CrossRef] [PubMed]
- Kleidon, A.; Malhi, Y.; Cox, P.M. Maximum Entropy Production in Environmental and Ecological Systems. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Aoki, I. Entropy Budgets of Deciduous Plant Leaves and a Theorem of Oscillating Entropy Production. Bull. Math. Biol. 1987, 49, 449–460. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Feng, J. Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy. Entropy 2017, 19, 600. [Google Scholar] [CrossRef]
- Free, G.; Poikane, S.; Solheim, A.L.; Bussettini, M.; Bradley, C.; Smith, J.; Caroni, R.; Bresciani, M.; Pinardi, M.; Giardino, C.; et al. Climate Change and Ecological Assessment in Europe under the WFD—Hitting Moving Targets with Shifting Baselines? J. Environ. Manag. 2024, 370, 122884. [Google Scholar] [CrossRef]
- Repo, A.; Albrich, K.; Jantunen, A.; Aalto, J.; Lehtonen, I.; Honkaniemi, J. Contrasting Forest Management Strategies: Impacts on Biodiversity and Ecosystem Services under Changing Climate and Disturbance Regimes. J. Environ. Manag. 2024, 371, 123124. [Google Scholar] [CrossRef]
- Pelorosso, R.; Gobattoni, F.; Leone, A. The Low-Entropy City: A Thermodynamic Approach to Reconnect Urban Systems with Nature. Landsc. Urban Plan. 2017, 168, 22–30. [Google Scholar] [CrossRef]
- Fistola, R.; Gargiulo, C.; La Rocca, R.A. Rethinking Vulnerability in City-Systems: A Methodological Proposal to Assess “Urban Entropy”. Environ. Impact Assess. Rev. 2020, 85, 106464. [Google Scholar] [CrossRef]
- Fistola, R. Urban Entropy vs Sustainability: A New Town Planning Perspective. In Proceedings of the 7th International Conference on Urban Regeneration and Sustainability, Ancona, Italy, 7 May 2012; pp. 195–204. [Google Scholar]
- Sun, X. Green City and Regional Environmental Economic Evaluation Based on Entropy Method and GIS. Environ. Technol. Innov. 2021, 23, 101667. [Google Scholar] [CrossRef]
- Prigogine, I.; Stengers, I. La Nouvelle Alliance: Métamorphose de La Science. Contemp. Fr. Civiliz. 1979, 7, 305. [Google Scholar]
- Pulselli, M.R.; Tiezzi, E. Città Fuori Dal Caos; Donzelli Editor, Series: Essays; Nature and Artifact: Rome, Italy, 2008; ISBN 9788860362582. [Google Scholar]
- Zuo, S.; Dai, S.; Ju, J.; Meng, F.; Ren, Y.; Tian, Y.; Wang, K. The Importance of the Functional Mixed Entropy for the Explanation of Residential and Transport CO2 Emissions in the Urban Center of China. J. Clean. Prod. 2022, 380, 134947. [Google Scholar] [CrossRef]
- JRC. Urban Heat Islands: Managing Extreme Heat to Keep Cities Cool. Available online: https://joint-research-centre.ec.europa.eu/jrc-news-and-updates/urban-heat-islands-managing-extreme-heat-keep-cities-cool-2024-07-22_en (accessed on 22 July 2024).
- Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Costa, Á.M. Analysis and Comparison of Spatial–Temporal Entropy Variability of Tehran City Microclimate Based on Climate Change Scenarios. Entropy 2018, 21, 13. [Google Scholar] [CrossRef]
- Cabral, P.; Augusto, G.; Tewolde, M.; Araya, Y. Entropy in Urban Systems. Entropy 2013, 15, 5223–5236. [Google Scholar] [CrossRef]
- Rapf, M.; Kranert, M. Irreversible Entropy to Account for Environmental Impacts and Sustainability. Procedia CIRP 2021, 98, 601–606. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing Climate Information Needs at the Regional Level: The CORDEX Framework. Organ. Bull. 2009, 58, 175–183. [Google Scholar]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New High-Resolution Climate Change Projections for European Impact Research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Rizwan, A.M.; Dennis, L.Y.C.; Liu, C. A Review on the Generation, Determination and Mitigation of Urban Heat Island. J. Environ. Sci. 2008, 20, 120–128. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kotlarski, S.; Keuler, K.; Christensen, O.B.; Colette, A.; Déqué, M.; Gobiet, A.; Goergen, K.; Jacob, D.; Lüthi, D.; van Meijgaard, E.; et al. Regional Climate Modeling on European Scales: A Joint Standard Evaluation of the EURO-CORDEX RCM Ensemble. Geosci. Model Dev. 2014, 7, 1297–1333. [Google Scholar] [CrossRef]
- Boberg, F.; Christensen, J.H. Overestimation of Mediterranean Summer Temperature Projections Due to Model Deficiencies. Nat. Clim. Change 2012, 2, 433–436. [Google Scholar] [CrossRef]
- Colmet-Daage, A.; Sanchez-Gomez, E.; Ricci, S.; Llovel, C.; Borrell Estupina, V.; Quintana-Seguí, P.; Llasat, M.C.; Servat, E. Evaluation of Uncertainties in Mean and Extreme Precipitation under Climate Change for Northwestern Mediterranean Watersheds from High-Resolution Med and Euro-CORDEX Ensembles. Hydrol. Earth Syst. Sci. 2018, 22, 673–687. [Google Scholar] [CrossRef]
- Derdour, S.; Ghenim, A.N.; Megnounif, A.; Tangang, F.; Chung, J.X.; Ayoub, A.B. Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria). Atmosphere 2022, 13, 1876. [Google Scholar] [CrossRef]
- Prein, A.F.; Langhans, W.; Fosser, G.; Ferrone, A.; Ban, N.; Goergen, K.; Keller, M.; Tölle, M.; Gutjahr, O.; Feser, F.; et al. A Review on Regional Convection-permitting Climate Modeling: Demonstrations, Prospects, and Challenges. Rev. Geophys. 2015, 53, 323–361. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Emission Scenarios. Available online: https://www.ipcc.ch/report/emissions-scenarios (accessed on 7 March 2025).
- Balocco, C.; Grazzini, G. Thermodynamic Parameters for Energy Sustainability of Urban Areas. Sol. Energy 2000, 69, 351–356. [Google Scholar] [CrossRef]
- Gates, D. Physical Processes in Ecosystems; University of Washington Center for Quantitative Science: Seattle, WA, USA, 2020. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 2010; ISBN 0–07–352936–2. [Google Scholar]
- Gazzetta Ufficiale. Norme per L’attuazione Del Piano Energetico Nazionale in Materia Di Uso Razionale Dell’energia, Di Risparmio Energetico e Di Sviluppo Delle Fonti Rinnovabili Di Energia. 1991. Available online: https://www.gazzettaufficiale.it/gunewsletter/dettaglio.jsp?service=1&datagu=2010-04-21&task=dettaglio&numgu=92&redaz=010G0078&tmstp=1273049012988 (accessed on 12 August 2025).
- Gazzetta Ufficiale. Regolamento Recante Norme per la Progettazione, L’installazione, l’esercizio e La Manutenzione Degli Impianti Termici Degli Edifici Ai Fini Del Contenimento Dei Consumi Di Energia 1993. Available online: https://www.gazzettaufficiale.it/eli/id/1993/10/14/093G0451/sg (accessed on 12 August 2025).
- UNI UNI/TS 11300-1:2014; Energy Performance of Buildings-Part 1: Evaluation of Energy Need for Space Heating and Cooling. British Standards Institution (BSI): London, UK, 2014.
- WMO. Guidance to Measuring, Modelling and Monitoring the Canopy Layer Urban Heat Island; WMO: Geneva, Switzerland, 2023; ISBN 9789263112. [Google Scholar]
- Pena Acosta, M.; Vahdatikhaki, F.; Santos, J.; Dorée, A.G. A Comparative Analysis of Surface and Canopy Layer Urban Heat Island at the Micro Level Using a Data-Driven Approach. Sustain. Cities Soc. 2023, 99, 104944. [Google Scholar] [CrossRef]
- Raffa, M.; Adinolfi, M.; Reder, A.; Marras, G.F.; Mancini, M.; Scipione, G.; Santini, M.; Mercogliano, P. Very High Resolution Projections over Italy under Different CMIP5 IPCC Scenarios. Sci. Data 2023, 10, 238. [Google Scholar] [CrossRef] [PubMed]
- CMCC DDS. Climate Projections RCP4.5 and RCP8.5 Downscaled @2.2 Km over Italy. Available online: https://doi.org/10.25424/CMCC-J90A-5P12 (accessed on 7 August 2025).
- Douss, R.; Farah, I.R. Extraction of Individual Trees Based on Canopy Height Model to Monitor the State of the Forest. Trees For. People 2022, 8, 100257. [Google Scholar] [CrossRef]
- Mohan, M.; Leite, R.V.; Broadbent, E.N.; Wan Mohd Jaafar, W.S.; Srinivasan, S.; Bajaj, S.; Dalla Corte, A.P.; do Amaral, C.H.; Gopan, G.; Saad, S.N.M.; et al. Individual Tree Detection Using UAV-Lidar and UAV-SfM Data: A Tutorial for Beginners. Open Geosci. 2021, 13, 1028–1039. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Mohan, M.; Mendonça, B.A.F.; de Silva, C.A.; Klauberg, C.; de Saboya Ribeiro, A.S.; Araújo, E.J.G.; de Monte, M.A.; Cardil, A. Optimizing Individual Tree Detection Accuracy and Measuring Forest Uniformity in Coconut (Cocos nucifera L.) Plantations Using Airborne Laser Scanning. Ecol. Modell. 2019, 409, 108736. [Google Scholar] [CrossRef]
- Yu, K.; Hao, Z.; Post, C.J.; Mikhailova, E.A.; Lin, L.; Zhao, G.; Tian, S.; Liu, J. Comparison of Classical Methods and Mask R-CNN for Automatic Tree Detection and Mapping Using UAV Imagery. Remote Sens. 2022, 14, 295. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Francini, S.; Schelhaas, M.-J.; Vangi, E.; Lerink, B.; Nabuurs, G.-J.; McRoberts, R.E.; Chirici, G. Forest Species Mapping and Area Proportion Estimation Combining Sentinel-2 Harmonic Predictors and National Forest Inventory Data. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103935. [Google Scholar] [CrossRef]
- Francini, S.; Cocozza, C.; Hölttä, T.; Lintunen, A.; Paljakka, T.; Chirici, G.; Traversi, M.L.; Giovannelli, A. A Temporal Segmentation Approach for Dendrometers Signal-to-Noise Discrimination. Comput. Electron. Agric. 2023, 210, 107925. [Google Scholar] [CrossRef]
- Hermosilla, T.; Bastyr, A.; Coops, N.C.; White, J.C.; Wulder, M.A. Mapping the Presence and Distribution of Tree Species in Canada’s Forested Ecosystems. Remote Sens. Environ. 2022, 282, 113276. [Google Scholar] [CrossRef]
- Lindquist, M.A. The Statistical Analysis of FMRI Data. Stat. Sci. 2008, 23, 439–464. [Google Scholar] [CrossRef]
- Fuchs, M.; Tanner, C.B. Infrared Thermometry of Vegetation 1. Agron. J. 1966, 58, 597–601. [Google Scholar] [CrossRef]
- Mashabatu, M.; Ntshidi, Z.; Dzikiti, S.; Jovanovic, N.; Dube, T.; Taylor, N.J. Deriving Crop Coefficients for Evergreen and Deciduous Fruit Orchards in South Africa Using the Fraction of Vegetation Cover and Tree Height Data. Agric. Water Manag. 2023, 286, 108389. [Google Scholar] [CrossRef]
- Tiralla, N.; Panferov, O.; Kreilein, H.; Olchev, A.; Ali, A.A.; Knohl, A. Quantification of Leaf Emissivities of Forest Species: Effects on Modelled Energy and Matter Fluxes in Forest Ecosystems. Geogr. Environ. Sustain. 2019, 12, 245–258. [Google Scholar] [CrossRef]
- Comune di Firenze Piano Strutturale e Piano Operativo. Available online: https://www.comune.fi.it/dalle-redazioni/piano-operativo-e-piano-strutturale-2023 (accessed on 7 March 2025).
- Istat. Basi Territoriali: Anni 1991, 2001, 2011 E 2021. Note Legali: Responsabilità E Licenza. 2024. Available online: https://www.istat.it/wp-content/uploads/2024/07/Descrizione-dei-dati-Basi-territoriali.pdf (accessed on 7 March 2025).
- Grazzini, G.; Gonnelli, A. Il Piano Energetico Ambientale Comunale di Firenze. In Proceedings of the II Congresso Nazionale AIGE, Pisa, Italy, 4–5 September 2008. [Google Scholar]
- Regione Toscana Geoscopio—Cartoteca. Available online: https://www502.regione.toscana.it/geoscopio/cartoteca.html (accessed on 7 March 2025).
- Martinez, A.; de la, I.; Labib, S.M. Demystifying Normalized Difference Vegetation Index (NDVI) for Greenness Exposure Assessments and Policy Interventions in Urban Greening. Environ. Res. 2023, 220, 115155. [Google Scholar] [CrossRef]
- Hawryło, P.; Francini, S.; Chirici, G.; Giannetti, F.; Parkitna, K.; Krok, G.; Mitelsztedt, K.; Lisańczuk, M.; Stereńczak, K.; Ciesielski, M.; et al. The Use of Remotely Sensed Data and Polish NFI Plots for Prediction of Growing Stock Volume Using Different Predictive Methods. Remote Sens. 2020, 12, 3331. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation. BMC Genomics 2020, 21, 6. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme. BBA—Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Rubio, E. Emissivity Measurements of Several Soils and Vegetation Types in the 8–14, Μm Wave Band: Analysis of Two Field Methods. Remote Sens. Environ. 1997, 59, 490–521. [Google Scholar] [CrossRef]
- Turner, N.C.; Heichel, G.H. Stomatal Development and Seasonal Changes in Diffusive Resistance of Primary and Regrowth Foliage of Red Oak (Quercus rubra L.) and Red Maple (Acer rubrum L.). New Phytol. 1977, 78, 71–81. [Google Scholar] [CrossRef]
- WMO. Comité Météorologique International, Procès-Verbaux de La Session de Paris; Imprimerie La Concorde: El Baten, Tunisia, 1–12 July 1946. [Google Scholar]
- Du, H.; Cai, W.; Xu, Y.; Wang, Z.; Wang, Y.; Cai, Y. Quantifying the Cool Island Effects of Urban Green Spaces Using Remote Sensing Data. Urban For. Urban Green. 2017, 27, 24–31. [Google Scholar] [CrossRef]
- Arellano, B.; Roca, J. Assessing Urban Greenery Using Remote Sensing. In Proceedings of the SPIE—The International Society for Optical Engineering, Conference: SPIE Optical Engineering + Applications, San Diego, CA, USA, 21–26 August 2022. Proceedings Volume 12232, Earth Observing Systems XXVII. [Google Scholar]
- Sharmin, M.; Tjoelker, M.G.; Pfautsch, S.; Esperon-Rodriguez, M.; Rymer, P.D.; Power, S.A. Tree Crown Traits and Planting Context Contribute to Reducing Urban Heat. Urban For. Urban Green. 2023, 83, 127913. [Google Scholar] [CrossRef]
- Speak, A.; Montagnani, L.; Wellstein, C.; Zerbe, S. The Influence of Tree Traits on Urban Ground Surface Shade Cooling. Landsc. Urban Plan. 2020, 197, 103748. [Google Scholar] [CrossRef]
- He, T.; Hu, Y.; Guo, A.; Chen, Y.; Yang, J.; Li, M.; Zhang, M. Quantifying the Impact of Urban Trees on Land Surface Temperature in Global Cities. ISPRS J. Photogramm. Remote Sens. 2024, 210, 69–79. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.Y.; Jia, B.; Wang, C. Cooling Effect of Urban Greenery: A Bibliometric Analysis. Urban For. Urban Green. 2024, 99, 128453. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Dahanayake, K.W.D.K.C.; Ng, E.; Chow, C.L. Temperature and Cooling Demand Reduction by Green-Roof Types in Different Climates and Urban Densities: A Co-Simulation Parametric Study. Energy Build. 2017, 145, 226–237. [Google Scholar] [CrossRef]
- Meili, N.; Zheng, X.; Takane, Y.; Nakajima, K.; Yamaguchi, K.; Chi, D.; Zhu, Y.; Wang, J.; Qiu, Y.; Paschalis, A.; et al. Modeling the Effect of Trees on Energy Demand for Indoor Cooling and Dehumidification Across Cities and Climates. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004590. [Google Scholar] [CrossRef]
- Mohammed, A.; Khan, A.; Khan, H.S.; Santamouris, M. Cooling Energy Benefits of Increased Green Infrastructure in Subtropical Urban Building Environments. Buildings 2023, 13, 2257. [Google Scholar] [CrossRef]
- Lloyd, G.; Ossola, A.; Burley, H.; Evans, K. Climate Change Threatens Carbon Storage in Europe’s Urban Trees. Urban For. Urban Green. 2024, 101, 128532. [Google Scholar] [CrossRef]
- Croeser, T.; Garrard, G.E.; Visintin, C.; Kirk, H.; Ossola, A.; Furlong, C.; Clements, R.; Butt, A.; Taylor, E.; Bekessy, S.A. Finding Space for Nature in Cities: The Considerable Potential of Redundant Car Parking. NPJ Urban Sustain. 2022, 2, 27. [Google Scholar] [CrossRef]
- Pattnaik, N.; Honold, M.; Franceschi, E.; Moser-Reischl, A.; Rötzer, T.; Pretzsch, H.; Pauleit, S.; Rahman, M.A. Growth and Cooling Potential of Urban Trees across Different Levels of Imperviousness. J. Environ. Manag. 2024, 361, 121242. [Google Scholar] [CrossRef] [PubMed]
- Sjöman, H.; Watkins, H.; Kelly, L.J.; Hirons, A.; Kainulainen, K.; Martin, K.W.E.; Antonelli, A. Resilient Trees for Urban Environments: The Importance of Intraspecific Variation. Plants People Planet 2024, 6, 1180–1189. [Google Scholar] [CrossRef]


| Age Class | <1940 | 1940–1970 | 1971–1980 | >1980 |
|---|---|---|---|---|
| U [W/m2K] | 2.4 | 1.9 | 1.8 | 1.2 |
| Standard TWY | Historical TWY | RCP4.5 2006–2038 TWY | RCP4.5 2039–2070 TWY | RCP8.5 2006–2038 TWY | RCP8.5 2039–2070 TWY | |
|---|---|---|---|---|---|---|
| [°C] | 28.0 | |||||
| [m2] | 64,645,324 | |||||
| [m2] | 192,582,468 | |||||
| U [W/m2K] | 2.1 | |||||
| [°C] | 31.8 | 32.5 | 33.0 | 33.1 | 32.7 | 33.8 |
| [°C] | 31.3 | 32.1 | 32.5 | 32.7 | 32.3 | 33.4 |
| W/m2] | 641.3 | 610.6 | 606.4 | 589.6 | 597.0 | 581.3 |
| [MWh] | 1540 | 1831 | 2016 | 2085 | 1897 | 2337 |
| [MWh] | 1347 | 1670 | 1844 | 1921 | 1731 | 2174 |
| [MWh] | 2110 | 2509 | 2763 | 2857 | 2600 | 3202 |
| [MWh] | 1846 | 2289 | 2527 | 2633 | 2372 | 2979 |
| [MJ/K] | 293,658 | 278,941 | 276,589 | 268,791 | 272,575 | 264,473 |
| [MJ/K] | 294,117 | 279,303 | 276,973 | 269,146 | 272,942 | 264,819 |
| [MJ/K] | 24,925 | 29,566 | 32,510 | 33,597 | 30,620 | 35,578 |
| [MJ/K] | 21,836 | 27,008 | 29,777 | 31,001 | 27,967 | 35,006 |
| [%] | 8.5% | 8.5% | 9.7% | 10.4% | 9.1% | 12.1% |
| [%] | 7.4% | 7.6% | 8.7% | 9.4% | 8.1% | 11.1% |
| [%] | 87.5% | 89.1% | 89.6% | 90.6% | 89.2% | 91.8% |
| Standard | Historical | RCP4.5 2006–2038 | RCP4.5 2039–2070 | RCP8.5 2006–2038 | RCP8.5 2039–2070 |
|---|---|---|---|---|---|
| 36.8 | 40.0 | 42.9 | 41.9 | 43.3 | 43.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balocco, C.; Pierucci, G.; Baia, M.; Borghi, C.; Francini, S.; Chirici, G.; Mancuso, S. Energy Sustainability of Urban Areas by Green Systems: Applied Thermodynamic Entropy and Strategic Modeling Means. Atmosphere 2025, 16, 975. https://doi.org/10.3390/atmos16080975
Balocco C, Pierucci G, Baia M, Borghi C, Francini S, Chirici G, Mancuso S. Energy Sustainability of Urban Areas by Green Systems: Applied Thermodynamic Entropy and Strategic Modeling Means. Atmosphere. 2025; 16(8):975. https://doi.org/10.3390/atmos16080975
Chicago/Turabian StyleBalocco, Carla, Giacomo Pierucci, Michele Baia, Costanza Borghi, Saverio Francini, Gherardo Chirici, and Stefano Mancuso. 2025. "Energy Sustainability of Urban Areas by Green Systems: Applied Thermodynamic Entropy and Strategic Modeling Means" Atmosphere 16, no. 8: 975. https://doi.org/10.3390/atmos16080975
APA StyleBalocco, C., Pierucci, G., Baia, M., Borghi, C., Francini, S., Chirici, G., & Mancuso, S. (2025). Energy Sustainability of Urban Areas by Green Systems: Applied Thermodynamic Entropy and Strategic Modeling Means. Atmosphere, 16(8), 975. https://doi.org/10.3390/atmos16080975










