Complementary Relationship-Based Validation and Analysis of Evapotranspiration in the Permafrost Region of the Qinghai–Tibetan Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites and Data Collection
2.2. Methodologies Adopted
2.2.1. The Generalized Nonlinear Complementary Relationship
2.2.2. Analysis Method
3. Results
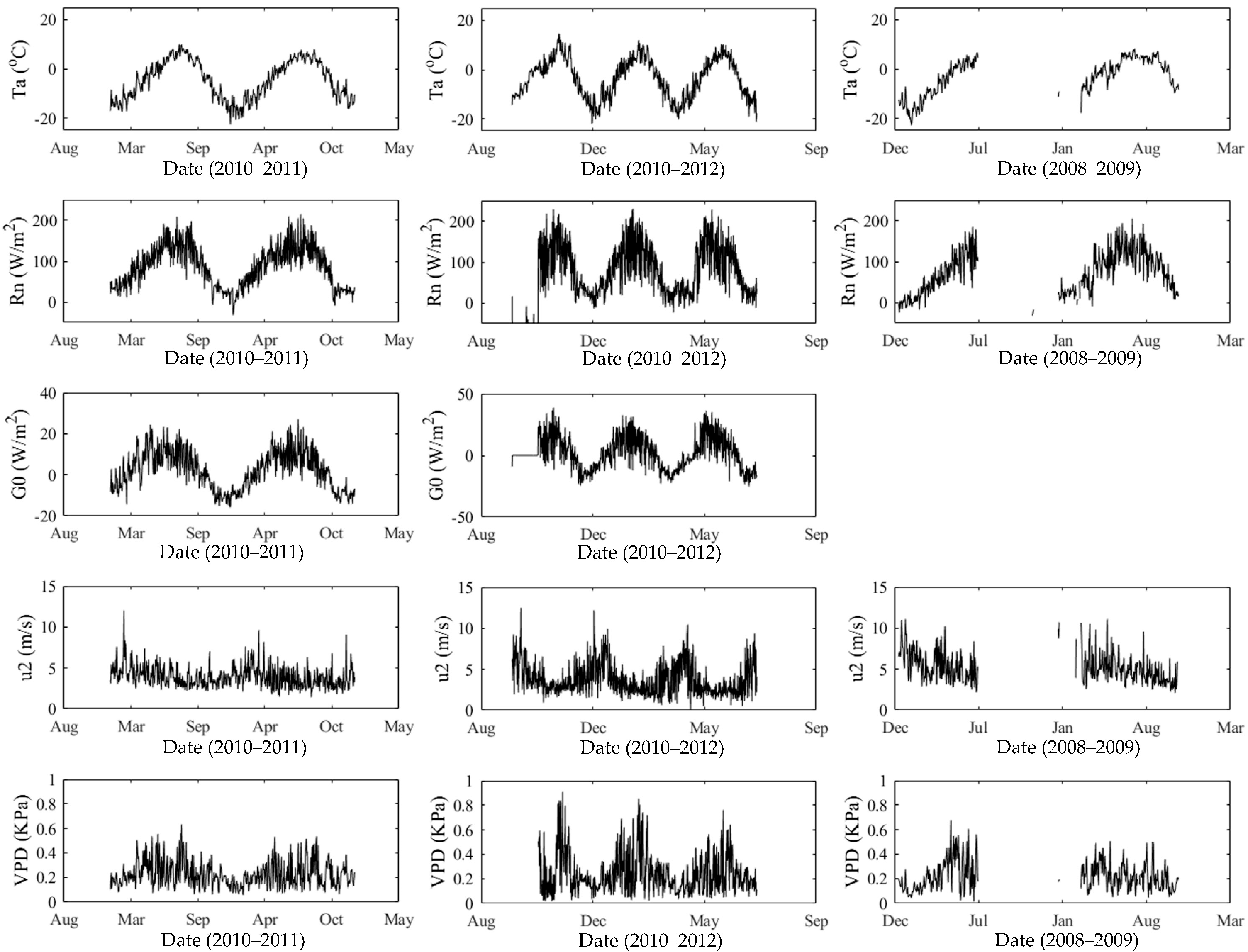
3.1. Change in the Meteorological Factors
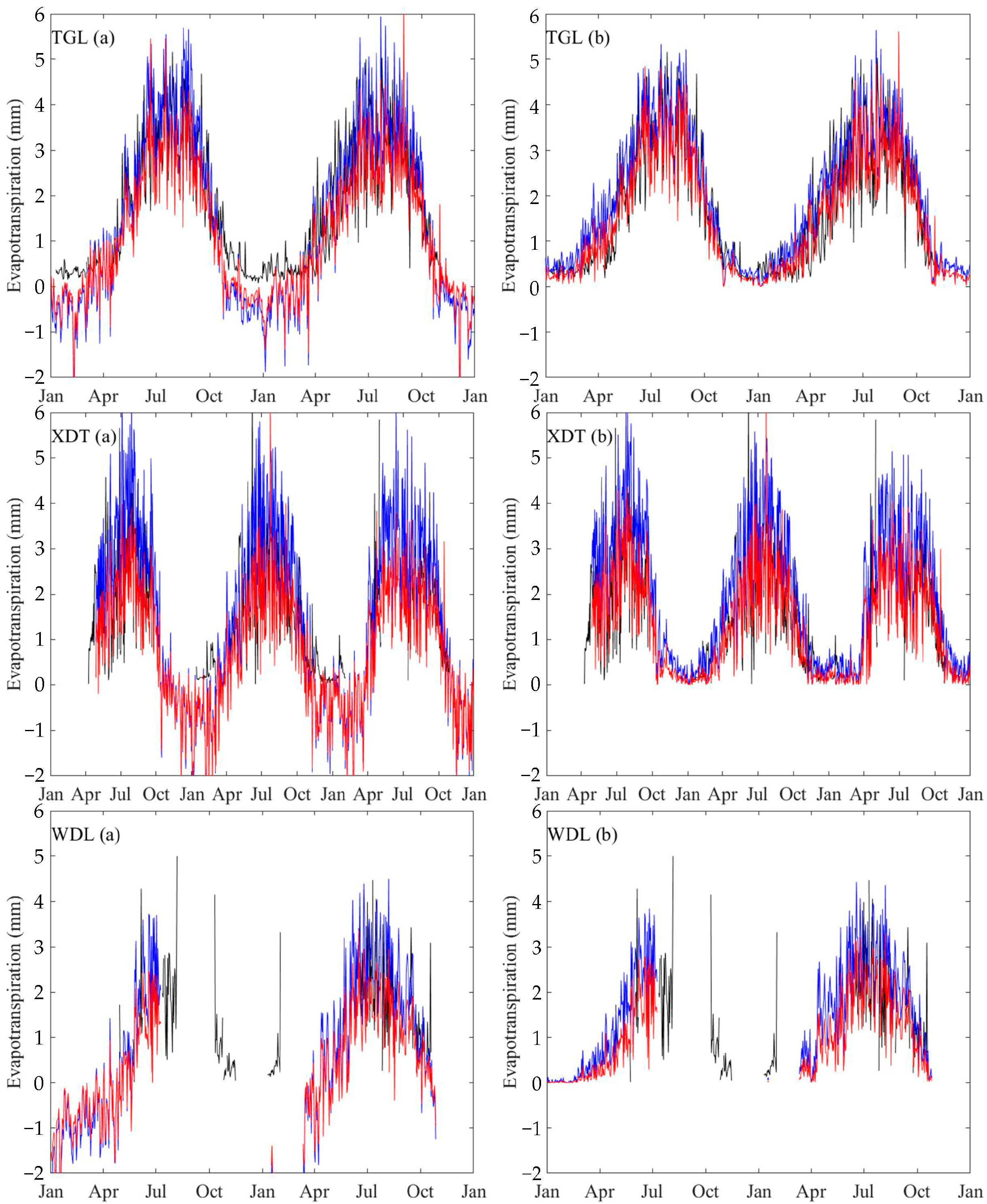
3.2. Performance of the Complementary Relationship (CR)
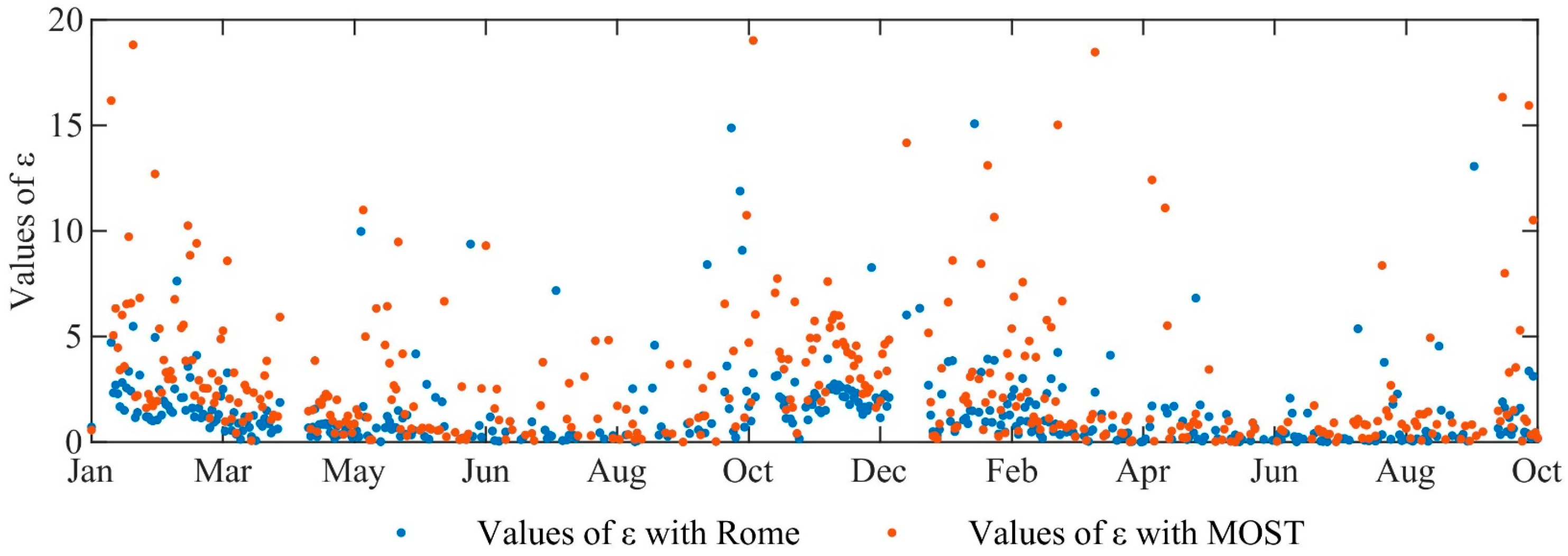
3.3. Validation of the Complementary Relationship (CR)
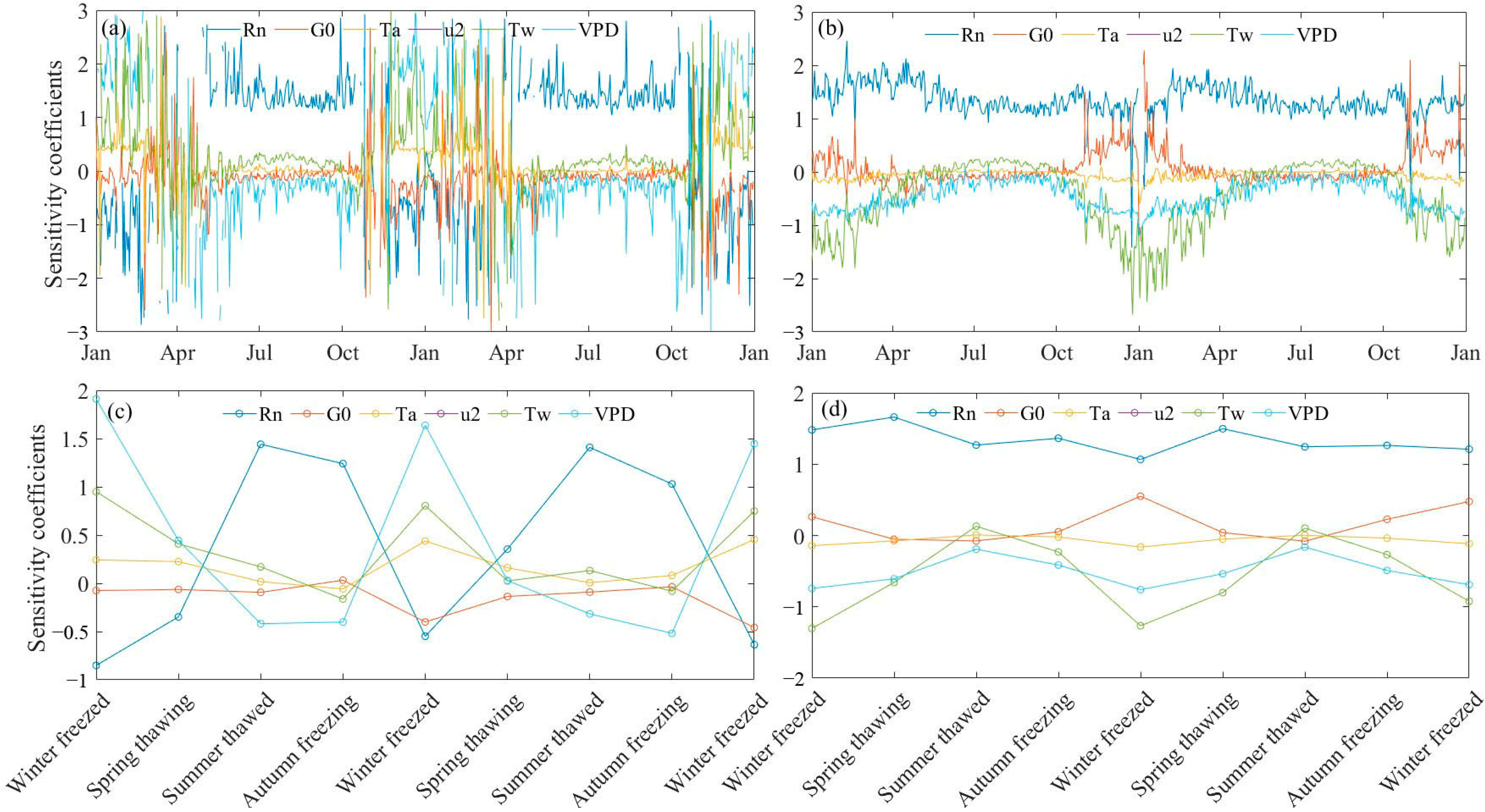
3.4. Sensitivity of the Meteorological Factors to ETa
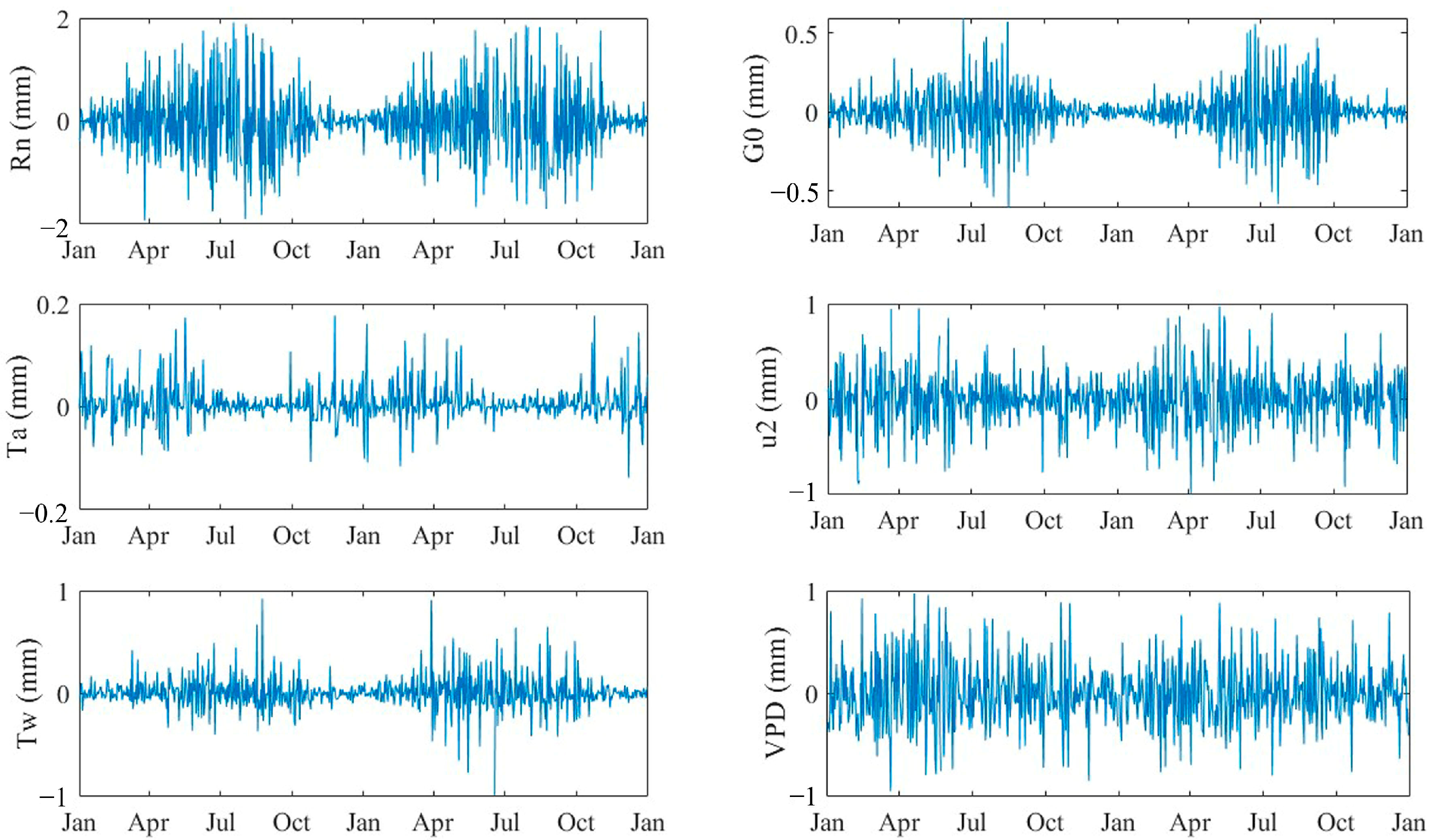
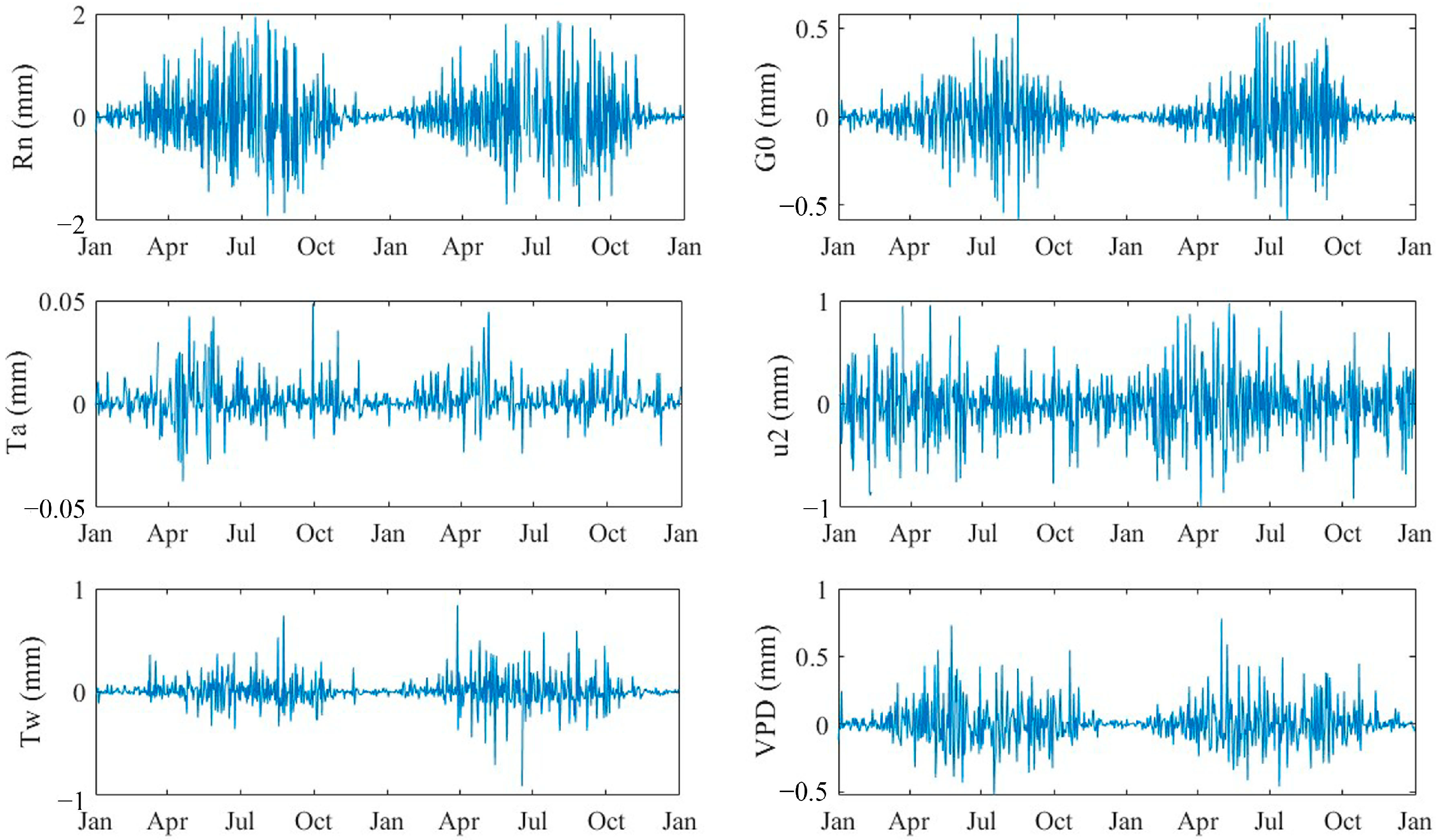
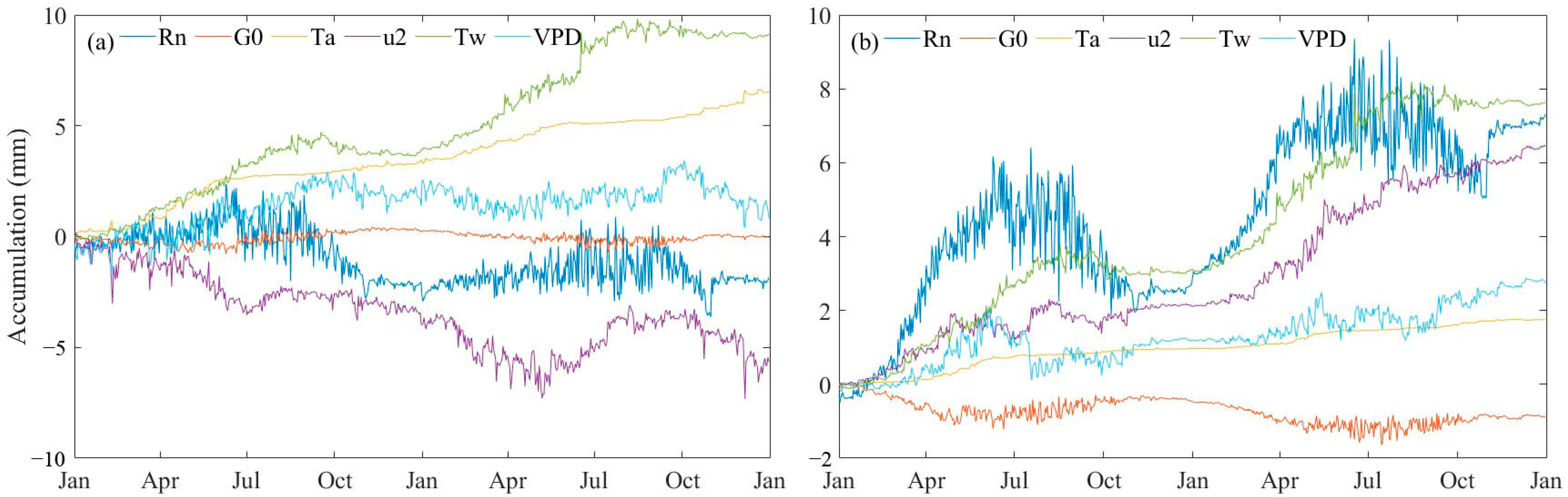
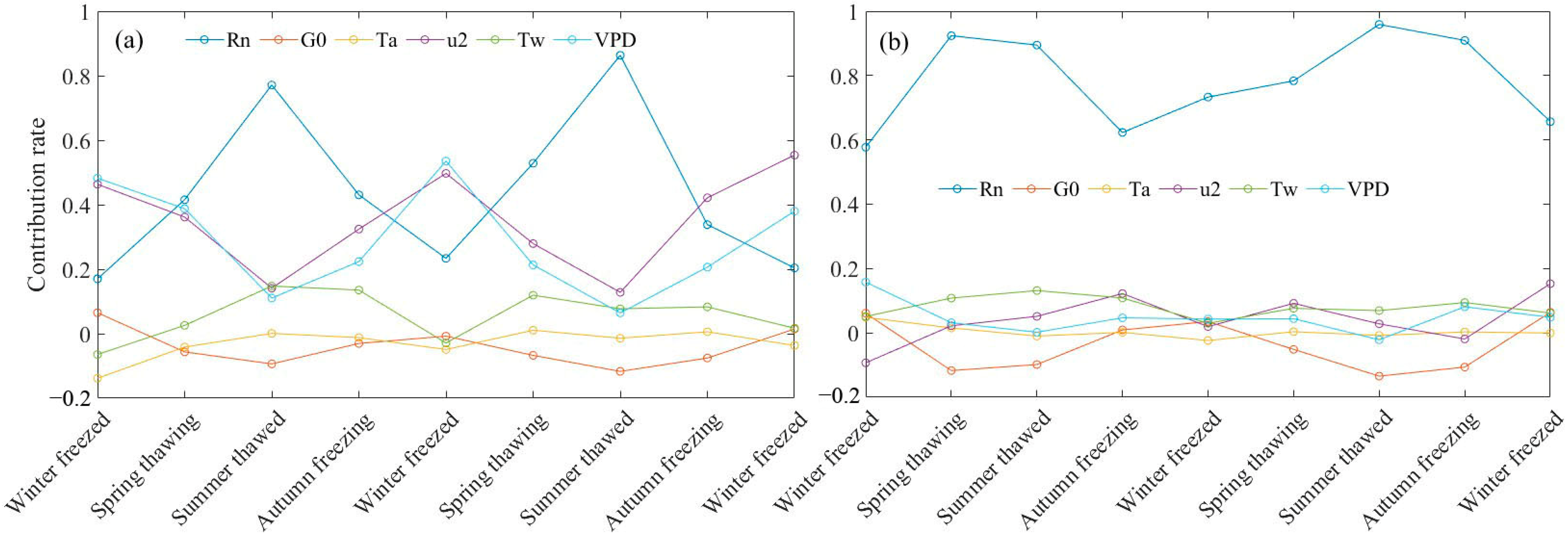
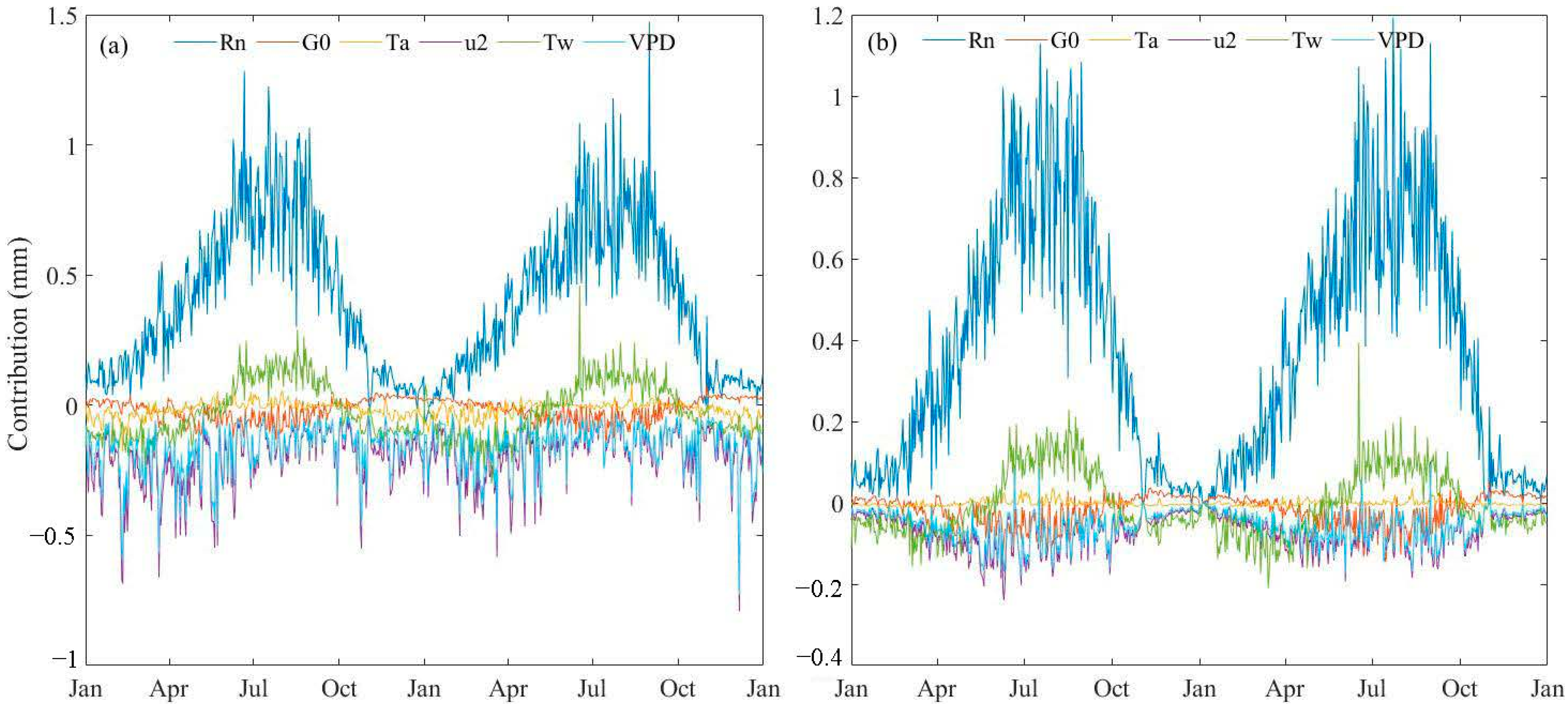
3.5. Contribution of Meteorological Factors to ETa
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QTP | Qinghai–Tibetan Plateau |
| ETa | Actual Evapotranspiration |
| ETp | Potential Evapotranspiration |
| CR | Complementary Relationship |
| EC | Eddy Covariance |
| MOST | Monin–Obukhov Similarity Theory |
| RMSE | Root Mean Square Error |
| Rn | Net Radiation |
| Ta | Air Temperature |
| RH | Relative Humidity |
| u2 | Wind Speed |
| Tw | Air temperature in a wet environment |
| VPD | Saturation and actual vapor pressure deficit |
References
- Swelam, A.; Jomaa, I.; Shapland, T.; Snyder, R.; Moratiel, R. Evapotranspiration response to climate change. In Proceedings of the XXVIII International Horticultural Congress on Science and Horticulture for People (IHC2010): International Symposium on 922, Lisbon, Portugal, 22 August 2010. [Google Scholar]
- Abtew, W.; Melesse, A. Climate change and evapotranspiration. In Evaporation and Evapotranspiration: Measurements and Estimations; Springer: Dordrecht, The Netherlands, 2013; pp. 197–202. [Google Scholar]
- Zhao, L.; Cheng, G.; Li, S.; Zhao, X.; Wang, S. Thawing and freezing processes of active layer in Wudaoliang region of Tibetan Plateau. Chin. Sci. Bull. 2000, 45, 2181–2187. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Change 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Lei, Y.; Shi, J.; Xiong, C.; Ji, D. Tracking the atmospheric–terrestrial water cycle over the Tibetan Plateau based on ERA5 and grace. J. Clim. 2021, 34, 6459–6471. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Li, Z.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. 1978, 193, 120–145. [Google Scholar]
- Monteith, J.L. Evaporation and environment. Symposia of the society for experimental biology. Camb. Univ. Press (CUP) Camb. 1965, 19, 205–234. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Oku, Y.; Ishikawa, H.; Su, Z. Estimation of land surface heat fluxes over the Tibetan Plateau using GMS data. J. Appl. Meteorol. Climatol. 2007, 46, 183–195. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Su, Z.; Ma, Y.; Yang, K.; Wen, J.; Zhang, Y. An improvement of roughness height parameterization of the Surface Energy Balance System (SEBS) over the Tibetan Plateau. J. Appl. Meteorol. Climatol. 2013, 52, 607–622. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Zhang, Y. Calibration-free complementary relationship estimates terrestrial evapotranspiration globally. Water Resour. Res. 2021, 57, e2021WR029691. [Google Scholar] [CrossRef]
- Ma, W.; Ma, Y.; Ishikawa, H. Evaluation of the SEBS for upscaling the evapotranspiration based on in-situ observations over the Tibetan Plateau. Atmos. Res. 2014, 138, 91–97. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Chen, X.; Ma, Y.; Su, Z. Comparison of satellite-based evapotranspiration estimates over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2016, 20, 3167–3182. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, K.; Chao, L.; Liu, L. An improved process-based evapotranspiration/heat fluxes remote sensing algorithm based on the Bayesian and Sobol’ uncertainty analysis framework using eddy covariance observations of Tibetan grass-lands. J. Hydrol. 2022, 613, 128384. [Google Scholar] [CrossRef]
- Hobbins, M.T.; Ramírez, J.A.; Brown, T.C.; Claessens, L.H. The complementary relationship in estimation of regional evapotranspiration: The complementary relationship areal evapotranspiration and advection-aridity models. Water Resour. Res. 2001, 37, 1367–1387. [Google Scholar] [CrossRef]
- Huntington, J.; Szilagyi, J.; Tyler, S.; Pohll, G. Evaluating the complementary relationship for estimating evapotranspiration from arid shrublands. Water Resour. Res. 2011, 47, W05533. [Google Scholar] [CrossRef]
- Bouchet, R.J. Evapotranspiration réelle et potentielle, signification climatique. Int. Assoc. Sci. Hydrol. Pub. 1963, 62, 134–142. [Google Scholar]
- Ramírez, J.A.; Hobbins, M.T.; Brown, T.C. Observational evidence of the complementary relationship in regional evaporation lends strong support for Bouchet’s hypothesis. Geophys. Res. Lett. 2005, 32, L15402. [Google Scholar] [CrossRef]
- Soylu, M.; Istanbulluoglu, E.; Lenters, J.; Wang, T. Quantifying the impact of groundwater depth on evapotranspiration in a semi-arid grassland region. Hydrol. Earth Syst. Sci. 2011, 15, 787–806. [Google Scholar] [CrossRef]
- Li, X.; Gemmer, M.; Zhai, J.; Liu, X.; Su, B.; Wang, Y. Spatio-temporal variation of actual evapotranspiration in the Haihe River Basin of the past 50 years. Quat. Int. 2013, 304, 133–141. [Google Scholar] [CrossRef]
- Chu, R.; Li, M.; Islam, A.R.M.T.; Fei, D.; Shen, S. Attribution analysis of actual and potential evapotranspiration changes based on the complementary relationship theory in the Huai River basin of eastern China. Int. J. Climatol. 2019, 39, 4072–4090. [Google Scholar] [CrossRef]
- Morton, F.I. Operational estimates of areal evapotranspiration and their significance to the science and practice of hydrology. J. Hydrol. 1983, 66, 1–76. [Google Scholar] [CrossRef]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Granger, R.J.; Gray, D. Evaporation from natural nonsaturated surfaces. J. Hydrol. 1989, 111, 21–29. [Google Scholar] [CrossRef]
- Brutsaert, W. A generalized complementary principle with physical constraints for land-surface evaporation. Water Resour. Res. 2015, 51, 8087–8093. [Google Scholar] [CrossRef]
- Brutsaert, W.; Cheng, L.; Zhang, L. Spatial distribution of global landscape evaporation in the early twenty-first century by means of a generalized complementary approach. J. Hydrometeorol. 2020, 21, 287–298. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36, L20403. [Google Scholar] [CrossRef]
- Pan, S.; Tian, H.; Dangal, S.R.; Yang, Q.; Yang, J.; Lu, C.; Ouyang, Z. Responses of global terrestrial evapotranspiration to climate change and increasing atmospheric CO2 in the 21st century. Earth’s Future 2015, 3, 15–35. [Google Scholar] [CrossRef]
- Teuling, A.J.; De Badts, E.A.; Jansen, F.A.; Fuchs, R.; Buitink, J.; Hoek van Dijke, A.J.; Sterling, S.M. Climate change, reforestation/afforestation, and urbanization impacts on evapotranspiration and streamflow in Europe. Hydrol. Earth Syst. Sci. 2019, 23, 3631–3652. [Google Scholar] [CrossRef]
- McKenney, M.S.; Rosenberg, N. Sensitivity of some potential evapotranspiration estimation methods to climate change. Agric. For. Meteorol. 1993, 64, 81–110. [Google Scholar] [CrossRef]
- Chattopadhyay, N.; Hulme, M. Evaporation and potential evapotranspiration in India under conditions of recent and future climate change. Agric. For. Meteorol. 1997, 87, 55–73. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Hong, H. Assessing the effect of climate change on reference evapotranspiration in China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1871–1881. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Miralles, D.G.; Fisher, J.B.; Martens, B.; Jimenez, C.; Purdy, A.J. Sensitivity of evapotranspiration components in remote sensing-based models. Remote Sens. 2018, 10, 1601. [Google Scholar] [CrossRef]
- Cawse-Nicholson, K.; Braverman, A.; Kang, E.L.; Li, M.; Johnson, M.; Halverson, G.; Anderson, M.; Hain, C.; Gunson, M.; Hook, S. Sensitivity and un-certainty quantification for the ECOSTRESS evapotranspiration algorithm–DisALEXI. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102088. [Google Scholar]
- Schuur, E.A.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- Chen, R.; Kang, E.; Zhang, Z. Integrated study on the eco-hydrological process in cold regions of China. Adv. Earth Sci. 2013, 28, 355–364. [Google Scholar]
- Wu, Q.; Zhang, T. Recent permafrost warming on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2008, 113, D13108. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, C.; Yang, N.; Li, Y. Diurnal and seasonal variations of surface energy and CO2 fluxes over a site in Western Tibetan Plateau. Atmosphere 2020, 11, 260. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Song, Y.; Han, C.; Liu, Z.; Liu, J. Evaluation of five complementary relationship models for estimating actual evapotranspiration during soil freeze-thaw cycles. Hydrol. Res. 2021, 52, 431–449. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An Introduction; Cambridge Univ. Press: New York, NY, USA, 2005; 605p. [Google Scholar]
- Brutsaert, W. Evaporation into the atmosphere: Theory, history and applications. Springer Sci. Bus. Media 2013, 299, 40–55. [Google Scholar]
- Szilagyi, J.; Jozsa, J. New findings about the complementary relationship-based evaporation estimation methods. J. Hydrol. 1982, 354, 171–186. [Google Scholar] [CrossRef]
- McCuen, R.H. A sensitivity and error analysis CF procedures used for estimating evaporation. J. Am. Water Resour. Assoc. 1974, 10, 486–497. [Google Scholar] [CrossRef]
- Liu, X.; Yang, W.; Zhao, H.; Wang, Y.; Wang, G. Effects of the freeze-thaw cycle on potential evapotranspiration in the permafrost regions of the Qinghai-Tibet Plateau, China. Sci. Total Environ. 2019, 687, 257–266. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, Y.; Szilagyi, J.; Guo, Y.; Zhai, J.; Gao, H. Evaluating the complementary relationship of evapotranspiration in the alpine steppe of the Tibetan Plateau. Water Resour. Res. 2015, 51, 1069–1083. [Google Scholar] [CrossRef]
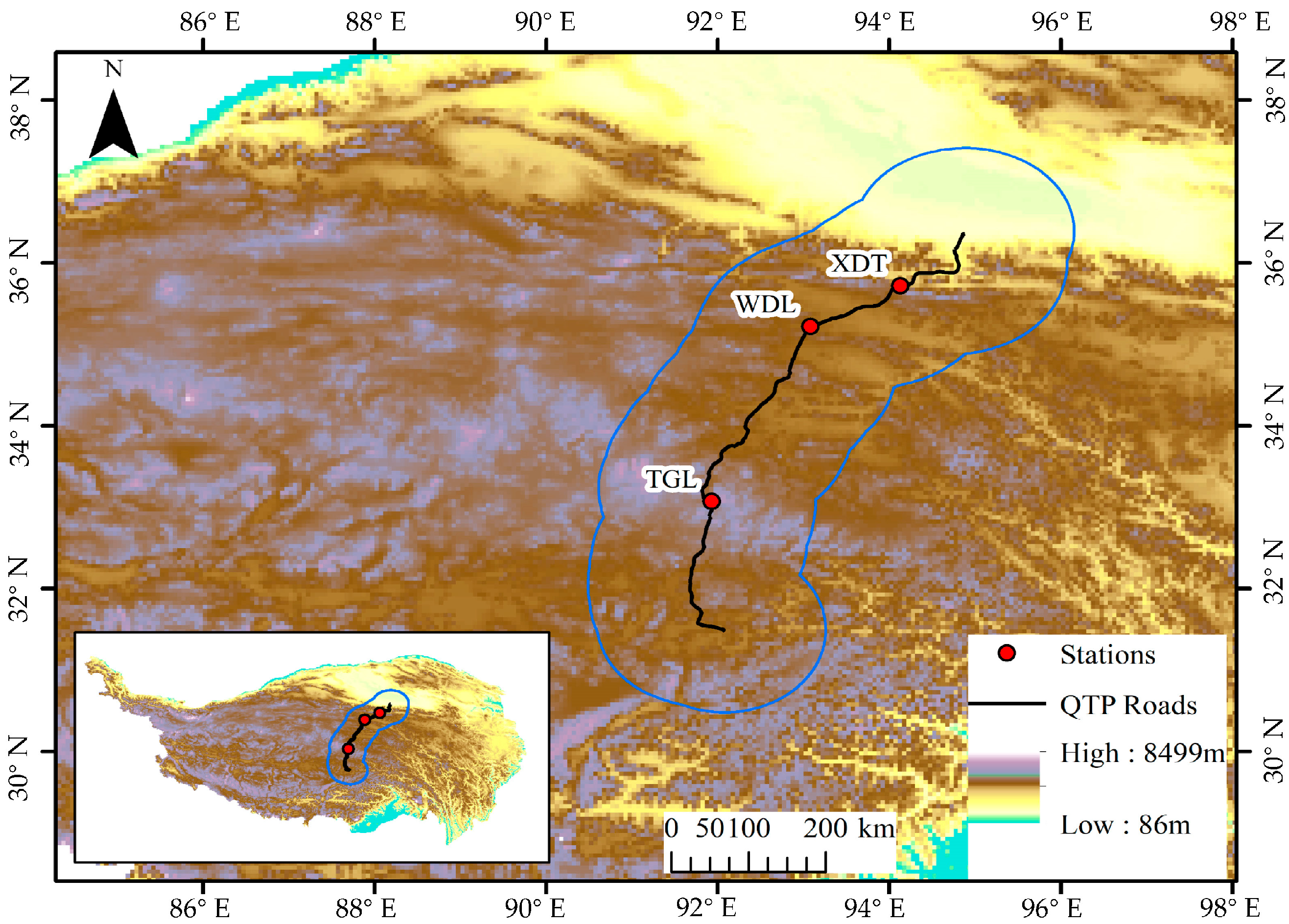

| Sites (Abbr.) | Longitude (E) Latitude (N) | Elevation (m asl) | Topography | Soil Type | Grass Types | Observed Items | Time |
|---|---|---|---|---|---|---|---|
| TGL | 91.93° | 5100 | High-altitude mountain, gentle slopes | Permafrost soils | Meadow steppe | u2, HR, Ta, Pres, P, R, heat flux, soil temperature, and moisture | 2010–2011 |
| 33.07° | |||||||
| XDT | 94.13° | 4538 | Gently sloped or flat | Alpine meadow soils, cryosols | Alpine meadow | 2010–2012 | |
| 35.72° | |||||||
| WDL | 93.08° | 4783 | Plateau basin, flat terrain | Cryosols, gravelly soils | Alpine desert steppe | 2008–2009 | |
| 35.22° |
| Study Sites | Ta (°C) | Rn (W/m2) | G0 (W/m2) | u2 (m/s) | VPD (kPa) |
|---|---|---|---|---|---|
| TGL | −4.36 | 85.57 | 2.19 | 3.94 | 0.23 |
| XDT | −3.44 | 61.21 | 1.69 | 3.76 | 0.24 |
| WDL | −3.01 | 71.51 | — | 5.19 | 0.22 |
| Sits | Counts of Available Data | ETa | RMSE | r |
|---|---|---|---|---|
| TGL | 643 | ETa1_Rome | 0.97 | 0.86 |
| ETa2_Rome | 0.80 | 0.85 | ||
| ETa1_MOST | 0.87 | 0.85 | ||
| ETa2_MOST | 0.70 | 0.86 | ||
| XDT | 621 | ETa1_Rome | 1.17 | 0.79 |
| ETa2_Rome | 1.03 | 0.85 | ||
| ETa1_MOST | 0.98 | 0.74 | ||
| ETa2_MOST | 0.67 | 0.81 | ||
| WDL | 183 | ETa1_Rome | 0.80 | 0.62 |
| ETa2_Rome | 0.73 | 0.58 | ||
| ETa1_MOST | 0.75 | 0.63 | ||
| ETa2_MOST | 0.62 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Xie, Y.; Li, Y.; Kumar, A.; Shao, W.; Zhao, Y. Complementary Relationship-Based Validation and Analysis of Evapotranspiration in the Permafrost Region of the Qinghai–Tibetan Plateau. Atmosphere 2025, 16, 932. https://doi.org/10.3390/atmos16080932
Yu W, Xie Y, Li Y, Kumar A, Shao W, Zhao Y. Complementary Relationship-Based Validation and Analysis of Evapotranspiration in the Permafrost Region of the Qinghai–Tibetan Plateau. Atmosphere. 2025; 16(8):932. https://doi.org/10.3390/atmos16080932
Chicago/Turabian StyleYu, Wenjun, Yining Xie, Yanzhong Li, Amit Kumar, Wei Shao, and Yonghua Zhao. 2025. "Complementary Relationship-Based Validation and Analysis of Evapotranspiration in the Permafrost Region of the Qinghai–Tibetan Plateau" Atmosphere 16, no. 8: 932. https://doi.org/10.3390/atmos16080932
APA StyleYu, W., Xie, Y., Li, Y., Kumar, A., Shao, W., & Zhao, Y. (2025). Complementary Relationship-Based Validation and Analysis of Evapotranspiration in the Permafrost Region of the Qinghai–Tibetan Plateau. Atmosphere, 16(8), 932. https://doi.org/10.3390/atmos16080932








