Abstract
To accurately estimate Zenith Tropospheric Delay (ZTD) for high-precision positioning of the Global Navigation Satellite System (GNSS), this study proposes a modeling method of ZTD based on the UNB3m model and Kriging spatial interpolation, in which the optimal spatial interpolation parameters are determined based on the errors corresponding to different combinations of the interpolation parameters, and the spatial distribution of the GNSS modeling stations is determined by the interpolation errors of the randomly selected GNSS stations for several times. To verify the accuracy and reliability of the proposed model, the ZTD estimates of 132,685 epochs with 1 h or 2 h temporal resolution for 28 years from 1997 to 2025 of the global network of continuously operating GNSS tracking stations are used as inputs; the ZTD results at any position and the corresponding observation moment can be obtained with the proposed model. The experimental results show that the model error is less than 30 mm in more than 85% of the observation epochs, the ZTD estimation results are less affected by the horizontal position and height of the GNSS stations than traditional models, and the ZTD interpolation error is improved by 10–40 mm compared to the GPT3 and UNB3m models at the four GNSS checking stations. Therefore, this technology can provide ZTD estimation results for single- and dual-frequency hybrid deformation monitoring, as well as dense ZTD data for Precipitable Water Vapor (PWV) inversion. Since the proposed method has the advantages of simple implementation, high accuracy, high reliability, and ease of promotion, it is expected to be fully applied in other high-precision positioning applications.
1. Introduction
Tropospheric delay error is a major error in Global Navigation Satellite System (GNSS) applications [1,2,3], and effective correction of tropospheric error at GNSS stations can significantly improve the accuracy of GNSS coordinates. Since the tropospheric delay error is highly correlated with the regional water vapor, it exhibits high spatial and temporal dynamics [4,5], and it is difficult to directly eliminate through the differential processing of station observation data. Without refinement correction, the influence of tropospheric errors on the positioning results can reach the meter scale [6], which seriously hinders the application and promotion of GNSS technology in millimeter-scale high-precision positioning scenarios. In order to reduce the impact of tropospheric errors on the positioning accuracy of GNSS stations, the existing data processing methods generally use parameter estimation [7] and posteriori empirical modeling [8] for tropospheric error correction, and each of the two methods has its own advantages and disadvantages, as well as applicable scenarios.
Among the above two methods, the parameter estimation method can better eliminate the tropospheric error when the meteorological conditions are stable, but under complicated observation conditions, such as a large height difference between the two ends of the baseline [9], rapid changes in meteorological conditions [10], poor quality of observation data [11], and single-frequency observation of the GNSS station [12,13], it is difficult to accurately separate the tropospheric delay error by parameter estimation at this time, which can easily lead to a significant impact on the accuracy of elevation direction. The posteriori empirical model can provide relatively accurate tropospheric delay estimation results for GNSS data processing. According to whether it needs meteorological parameters as input, the posteriori empirical model can be classified into the meteorological parameter model [14] and the non-meteorological parameter model [15]. Because of its advantages of simple implementation, efficient calculation, and wide range of application, the meteorological parameter model represented by the UNB series model [16,17] and the GPT series model [18,19,20] has been more widely used. Its disadvantages are that the magnitude of the error is related to the spatial location, and the model accuracy and temporal resolution are low, which makes it difficult to be applied to regional GNSS high-precision dynamic positioning.
With the increase in the number of continuously operating GNSS stations worldwide and the abundance of Zenith Tropospheric Delay (ZTD) estimation products [21,22], spatial interpolation of regional tropospheric delays based on high-precision ZTD products from GNSS stations has become an important tropospheric modeling idea. Zus et al. [23] used the benchmark data collected in the European COST Action ES1206 to improve the interpolation of GNSS Zenithal Wet Delay (ZWD) by tropospheric gradient and verified the reliability of the interpolation method by simulation experiments and measured data, respectively; the results show that the accuracy of the interpolated ZWD can be improved by 10% when the tropospheric gradient is considered. Akar et al. [24] replaced the European gridded VMF1 by spatially interpolating the station-specific VMF1 product and compared the effectiveness of the ordinary Kriging method and the Inverse Distance Weighting (IDW) prediction using data collected at 24 GNSS stations in 2020; the results show that both spatial interpolation methods improve the quality of the gridded product and that the success rate of the ordinary Kriging method is 6.1% higher than the IDW method.
The above research on spatial interpolation based on tropospheric delay valuation or meteorological parameter grids of GNSS stations can reduce the influence of tropospheric errors in GNSS data processing. However, the shortcoming of the current study is that the ZTD interpolation process is not separated from the influence of horizontal coordinates (X and Y coordinates) and elevation (H coordinates), and the spatial interpolation modeling is directly based on the observation data of multiple stations, whereas the correlation between the ZTD data and elevations is obviously stronger than that of horizontal coordinates, which leads to disadvantages such as the complexity of the modeling process and the lack of applicability of the model in different regions.
To address the shortcomings of the ZTD spatial interpolation model, Wang et al. [25] developed a ZTD vertical profile grid model by considering the height scale factor that varies with time in China. Zhao et al. [26] developed a high-precision ZTD interpolation method by considering the influence of height differences. However, the models proposed in these studies involve cumbersome steps and are difficult to implement. To meet the needs of regional deformation monitoring and other high-precision application scenarios, and to improve the applicability of the ZTD spatial interpolation model as well as reduce the complexity, this paper builds the ZTD spatial interpolation model, aiming to provide high-precision tropospheric delay products for GNSS stations. This research can be used for ZTD estimation of single-frequency stations in single- and dual-frequency hybrid deformation monitoring projects, as well as for ZTD data spatial densification in Precipitable Water Vapor (PWV) inversion.
This paper first introduces the ZTD modeling method based on the UNB3m model and Kriging spatial interpolation and then builds a global ZTD model using the ZTD products as inputs; finally, it verifies the accuracy of the interpolation model by using the uninvolved GNSS stations and the existing empirical models, as well as discusses and analyzes the strengths and weaknesses of the modeling method.
2. Materials and Methods
The ZTD spatial interpolation modeling method proposed in this paper utilizes the data source of ZTD data from GNSS stations and combines the spatial location of GNSS stations, the GPT3 model [20], the Saastamoinen model [27], the UNB3m model [16,17], and Kriging interpolation [28] to ultimately obtain the ZTD on the unknown GNSS stations. The ZTD data can be estimated by inputting the observed data from continuously operating GNSS stations into high-precision data-processing software [29,30], or by directly downloading the released tropospheric products from the International GNSS Service (IGS) and its data processing facilities.
The modeling method is based on the spatial coordinates of the GNSS stations and the observation time information and includes the following steps:
(1) Use the GPT3 model to estimate meteorological parameters, substitute them into the Saastamoinen model to calculate the Zenith Hydrostatic Delay (ZHD) component, and then subtract ZHD from ZTD to obtain ZWD;
(2) Project ZWD onto sea level using the UNB3m model to obtain ZWD0, thereby eliminating the influence of elevation on ZWD interpolation results and simplifying the ZWD interpolation process into a two-dimensional planar interpolation problem;
(3) Apply the Kriging spatial interpolation algorithm to the ZWD0 of GNSS stations to obtain ZWD0 of unknown stations, and then reproject these values to the stations’ elevation using the UNB3m model to obtain ZWD interpolation results;
(4) Substitute the spatial coordinates and observation time information of the GNSS stations into the GPT3 model and Saastamoinen model to calculate ZHD, and combine it with the ZWD interpolation results to obtain the ZTD estimates for unknown stations.
The overall idea behind interpolation modeling is to divide ZTD into two parts, ZHD and ZWD, and process them separately. Step (1) obtaining ZHD, steps (2) and (3) obtaining ZWD, and step (4) combining ZHD and ZWD to obtain ZTD. The specific data processing flow is shown in Figure 1.
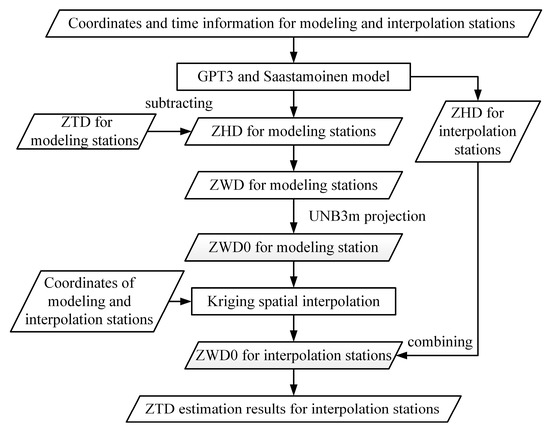
Figure 1.
Flowchart of data processing for ZTD spatial interpolation modeling.
2.1. Calculation of ZHD
The GPT3 model [20] discretizes the coefficients of annual mean, annual variation, and semiannual variation required for the calculation of meteorological parameters and stores them in a grid file, which is available in 1° × 1° and 5° × 5°, respectively. By inputting the station coordinates and observation time information into the GPT3 model, meteorological parameters required for tropospheric estimation can be obtained, such as barometric pressure, temperature, water vapor pressure, weighted average temperature, and so on. Taking barometric pressure calculation as an example, the meteorological parameter calculation formula of the GPT3 model is listed in Equation (1),
where is the value of barometric pressure (hPa) at the GNSS station, denotes the day of year, denotes the annual mean value of barometric pressure, and , , , and denote the coefficients of variation in the annual and semiannual amplitude of barometric pressure, respectively, which can be obtained by the gridded parameter information file of the GPT3 model.
When calculating the ZHD, the GPT3 model is first used to obtain the barometric pressure parameters based on the location of the GNSS station and the observation moment, and then the barometric pressure parameters are substituted into the Saastamoinen model to calculate the ZHD of the GNSS station. The barometric pressure parameters are calculated as shown in Equation (1), and the Saastamoinen model calculation formula is shown as follows:
where is the ZHD of the GNSS station (m), is the latitude (rad), and is the elevation (km).
2.2. Projection of ZWD
The ZWD value of the GNSS station can be obtained by subtracting the ZHD from the ZTD. Since the ZWD is related to the elevation of the GNSS station, the spatial interpolation of the ZWD is still a three-dimensional interpolation problem. To reduce the difficulty of spatial interpolation modeling as well as improve the accuracy of the interpolation results, this paper uses the projection function model to project the ZWD to the sea level position where the station is located, removing the influence of elevation variables.
The UNB3m model [16,17] is a commonly used empirical model for tropospheric delay correction, which is used to estimate parameters such as oblique path tropospheric delay, ZTD, and the Niell mapping function. With the UNB3m model, the projection function of the ZWD between elevation and sea level can be calculated by inputting the day of the year, station latitude, longitude, elevation and altitude angles with the following formula:
where and are the ZWD values of the GNSS station at sea level and elevation, respectively, is the rate of temperature decrease (K/m), is the station elevation (m), is the temperature at sea level (K), λ is the elevation decrease factor of the water vapor pressure, denotes the acceleration of gravity (9.80665 m/s2), and is the gas constant of dry air (287.054 Jkg−1K−1).
Since the meteorological parameter estimation accuracy of the GPT3 model is relatively higher, the ZWD projection coefficients are calculated using Equation (3), in which the meteorological parameters , , and are all estimated by the GPT3 model.
2.3. Kriging Spatial Interpolation Modeling
Kriging interpolation is a spatial interpolation method based on geostatistics, which predicts the values of unsampled locations based on the data of known observation stations, and is widely used in the fields of geography, geology, and environmental science. The basic principle of Kriging interpolation is based on the covariance function of random fields and stochastic processes for spatial modeling and predictive interpolation, and its internal theory is Gaussian process regression in one-dimensional to three-dimensional space [28]. The principle of spatial interpolation schematic is shown in Figure 2.
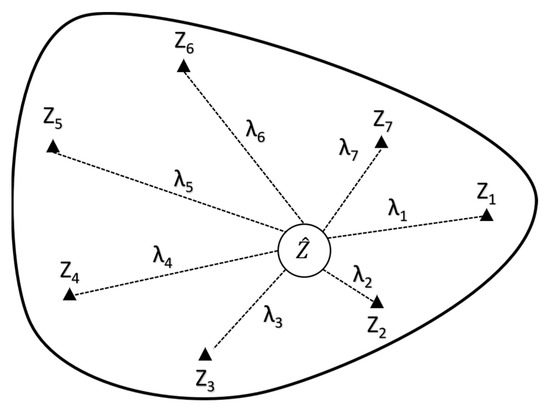
Figure 2.
Schematic diagram of Kriging spatial interpolation.
As shown in Figure 2, the Kriging spatial interpolation is calculated as follows:
where denotes the attribute value of the station to be interpolated, denotes the number of known stations falling within the interpolation range, denotes the weight of the i’th known station, and denotes the attribute value of the i’th known station.
Based on Equation (4), Kriging interpolation can use different correlation models and regression models to solve the nonlinear least squares problem for the given data set to obtain the fitting function and predict the attribute values on the stations to be interpolated. Among these, the relevant models are based on two assumptions: first, the attribute value of a station is related to the attribute values of its neighboring stations and can be inferred from them (spatial correlation assumption); second, the difference in attribute values between two stations is positively correlated with the distance between them within a certain range (distance correlation assumption). The selection of correlation models is related to the variability of the data. For example, the exponential model is suitable for cases where spatial correlation decays exponentially with distance, the Gaussian model is suitable for cases where spatial correlation decays Gaussian with distance, and the spherical model is suitable for cases where spatial correlation remains stable within a certain distance and decays rapidly beyond that distance. The specific formula is shown as follows:
where is the valuation of the ’th attribute at location , is the number of attributes, is the coefficient of the regression function, is the regression function, is the variance of the ’th attribute, is the correlation model with as the parameter, and is another location.
According to the above theory and formula, the of the GNSS stations projected to the sea level obtained in Section 2.2 and the coordinates of the stations are used as inputs, and the of the interpolated GNSS stations at the sea level can be obtained by interpolating with the Kriging spatial interpolation method using the selected correlation and regression models. Then the ZWD at the station elevation can be obtained by substituting the meteorological parameters and elevation of the interpolated GNSS stations with those of the UNB3m model (another transformation of Equation (3)). Finally, the ZWD valuation of the interpolated GNSS stations is combined with the ZHD calculated according to the method introduced in Section 2.1 to complete the Kriging spatial interpolation modeling process and obtain the ZTD of the interpolated GNSS stations.
3. Results
3.1. Data Sources
For continuously operating GNSS stations, their ZTD can be estimated more accurately because they have more accurate station coordinate information, and most of the errors can be eliminated by differential processing between station observations. In addition, thanks to the International GNSS Service (IGS) and the implementation of the open sharing policy of the data processing and analysis centers, the Center for Orbit Determination in Europe (CODE) has been continuously releasing ZTD product files since 1997, which provide a reliable database for the study of ZTD modeling and meteorological forecasting.
In this paper, the ZTD temporal interpolation modeling is carried out by the method introduced in Section 2, and the coordinates of the GNSS stations and the ZTD data used in the study are downloaded from CODE “http://ftp.aiub.unibe.ch/CODE/ (accessed on 27 February 2025)”, and the time span is from 1 January 1997 to 22 February 2025, with a time resolution of 2 h for data before 7 January 2023 (including 7 January 2023) and 1 h for data after 7 January 2023, involving 573 GNSS stations and 132,685 observation epochs. The spatial distribution of all GNSS stations is shown in Figure 3.
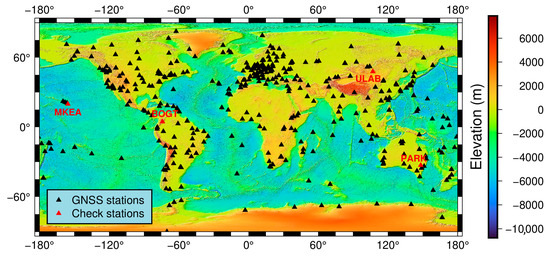
Figure 3.
Spatial distribution of the 573 GNSS stations worldwide.
Due to the different starting and ending times of the observation data from different GNSS stations, to show the number of GNSS stations during the whole observation period, the number of GNSS stations is counted and plotted in Figure 4.
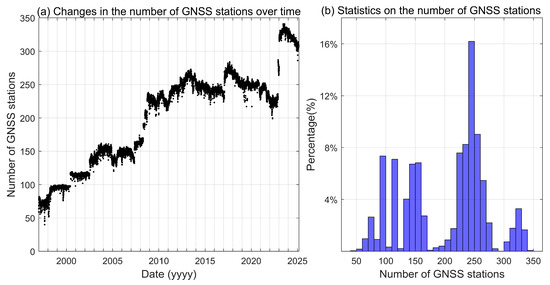
Figure 4.
Variation in the number of GNSS stations during the observation period.
3.2. Experimental Results
To compare the difference between the ZWD at the elevation of the GNSS station and the ZWD converted to the sea level, four GNSS stations with varying elevation gradients and station dispersion are selected for display in Figure 5, including PARK station with an elevation of only 397.4 m, ULAB station with an elevation of 1575.5 m, BOGT station with an elevation of 2576.2 m, and MKEA station with an elevation of 3754.6 m.
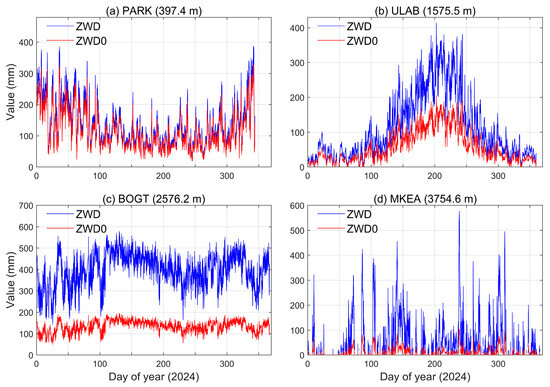
Figure 5.
ZWD values at elevation and sea level for four GNSS stations.
According to the Kriging spatial interpolation modeling method introduced in Section 2.3, the interpolation effect is not only related to the spatial distribution of the GNSS stations but also to the selected correlation and regression models. To obtain the correlation and regression models (optimal spatial interpolation parameters) that best fit the ZTD data of the adopted GNSS stations, each observation moment of the 132,685 observation epochs is cycled sequentially. Firstly, the current observation moment is determined, and the GNSS stations with ZTD data are selected based on the observation moments. Then, 90% of the stations are randomly selected for the Kriging spatial interpolation modeling, and 10% of the stations are not involved in the modeling but only for checking purposes; the error between the ZTD data at the checking stations and the model estimation results is counted. To weaken the influence of GNSS stations on the selection of optimal spatial interpolation parameters, GNSS stations are randomly selected for 100 runs at each observation moment, and the Root Mean Square (RMS) error values of different interpolation parameter combinations at the checking stations are finally counted. There is a total of 90 combinations of interpolation parameters; the regression model includes zero-order polynomial, first-order polynomial, and second-order polynomial; the correlation model includes cubic, exponential, Gaussian, linear, spherical, and cubic spline; and the upper limits include 10, 20, 50, 100 and 200. The upper limit parameter is used to restrict the range of relevant function parameters, ensuring that the parameters do not exceed a reasonable range during the optimization process, thereby improving the stability and prediction accuracy of the model. The error variations in different interpolation parameters are listed in Table 1.

Table 1.
Statistics on the variation in errors for different combinations of interpolation parameters.
As shown in Table 1, among the different Kriging spatial interpolation parameter combinations, the combinations of first-order polynomial, spherical and 50 correspond to the smallest RMS error values. Based on this, the regression model of the final spatial interpolation adopts first-order polynomial, the correlation model adopts spherical, and the upper limit value adopts 50.
Based on the above experimental results, the optimal Kriging interpolation parameters suitable for the ZTD data of the GNSS stations are obtained; at this time, the influence of different GNSS station selection schemes on the ZWD spatial interpolation results is not clear. To discuss the influence of GNSS modeling station selection on the interpolation results, the 30,000th, 60,000th, 90,000th, and 120,000th epochs are selected as the objects for discussion. For each epoch, 90% and 10% of the GNSS stations are randomly selected for modeling and checking, respectively, and 100 runs are made to count the errors of the modeling results and ZTD data on the checking stations for each run to analyze the influences of different GNSS modeling station selection schemes on the model interpolation accuracy. The observation moments, the total number of GNSS stations, the number of modeling stations, and the number of checking stations corresponding to the four epochs are shown in Table 2, and the statistical results of the error distribution on the checking stations corresponding to the 100 GNSS station selection schemes for the four epochs are plotted in Figure 6.

Table 2.
Statistics of observation moments, number of stations, number of modeling stations and number of checking stations corresponding to the four epochs.
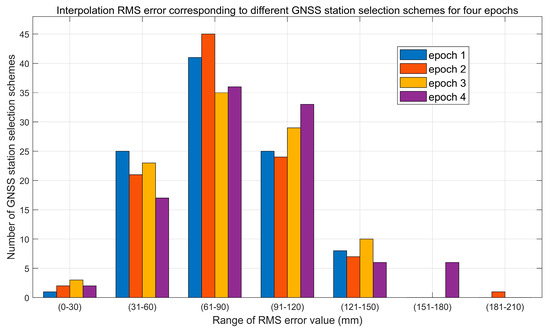
Figure 6.
Statistical distribution chart of RMS error of ZWD interpolation error corresponding to different GNSS station selection schemes for four epochs.
As shown in Figure 6, different GNSS interpolation station selection schemes have a large impact on the ZWD interpolation effect of the model. Therefore, when using the proposed method for spatial interpolation modeling of the ZTD data, the regression model of spatial interpolation adopts the first-order polynomial, the correlation model adopts the spherical, the upper limit value adopts the value of 50, and the selection of the GNSS modeling station is taken by multiple runs to select the station corresponding to the smallest RMS error. According to the above strategy, PARK, ULAB, BOGT, and MKEA stations are used as checking stations, then spatial interpolation modeling of ZTD data in 2024 and statistical error on the checking stations. For each epoch in 2024, the PARK, ULAB, BOGT, and MKEA stations are first selected from the GNSS stations, and then the modeling and checking stations are selected from the remaining GNSS stations. After the modeling, the ZTD data from the GNSS stations, the proposed model, the GPT3 model (the GPT3 model is used to calculate the meteorological parameters, the Saastamoinen model is used to calculate the ZHD, and the ZWD is calculated by the model in [31]), and the UNB3m model are compared, as shown in Figure 7.
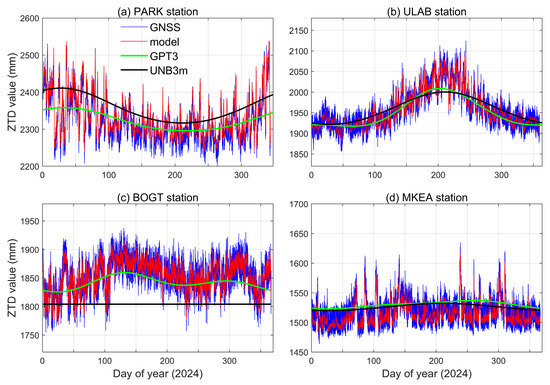
Figure 7.
Comparison of measured values with different model calculations at four GNSS checking stations in 2024.
To analyze the errors between this model and the ZTD data of the GNSS stations, the distribution of the errors between the proposed model and the ZTD data, as well as the error distribution between the traditional model (direct three-dimensional interpolation of ZWD) and the ZTD data at the four GNSS checking stations, are calculated and plotted in Figure 8. To compare the errors between the computed results of the proposed model, the traditional model, the UNB3m model, the GPT3 model and the ZTD data, the RMS error values of each model at the four checking stations, as well as the information of the station coordinates, are statistically presented in Table 3.
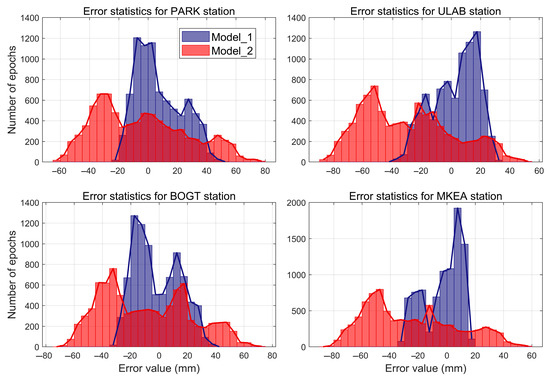
Figure 8.
Error statistics of measured values and Kriging interpolation model calculations at the four GNSS checking stations in 2024. Model_1 refers to the model proposed in this paper, while Model_2 refers to the traditional model that directly performs three-dimensional spatial interpolation on ZWD.

Table 3.
RMS error values (mm) of ZTD calculation results for different models.
In order to further discuss and analyze the influence of GNSS modeling station selection on the model results and verify the accuracy of the proposed model as well as the relation with the number of GNSS stations, the GNSS spatial interpolation modeling method is used to process 132,685 observation epochs, and the modeling and checking stations are randomly selected (90% and 10% of the GNSS stations for modeling and checking) and run for 100 times in the interpolation process so as to statistically analyze the accuracy of checking stations on each observation epoch. The number of epochs in different error intervals and the percentage of GNSS stations in different error intervals are counted and listed in Table 4.

Table 4.
RMS error values of GNSS spatial interpolation modeling on 132,685 observation epochs at the checking stations.
4. Discussion
As shown in Figure 3, the 573 GNSS stations selected in this paper are relatively evenly distributed around the world, but the stations are relatively dense in Europe, more stations are attached to the coastlines of North and South America, and they are relatively sparse in the northern part of Asia and the northern part of Africa. As shown in Figure 4a, the number of GNSS stations basically shows a gradual upward trend over time, which is attributed to the global emphasis on the deployment and maintenance of continuously operating GNSS tracking stations, as well as the implementation of the GNSS data open sharing policy. Figure 4b, on the other hand, shows that most of the epochs have GNSS stations between 200 and 300, followed by those between 100 and 200, and the least number of epochs with the number of GNSS stations below 100 or above 300.
Figure 5 illustrates the changes in the values of ZWD at four GNSS stations before and after projecting from the station elevation to the sea level. From Figure 5, when the ZWD at the station elevation is projected to the sea level by the UNB3m projection function, there is an amplification effect and the numerical change in ZWD is more significant, showing obvious time dispersion. Taking the MKEA station at elevation 3754.6 m as an example, the ZWD values before projection are all below 100 mm, and the ZWD values after projection vary from 0 to 600 mm. Therefore, for smaller numerical changes in the temporal domain, the changes in ZWD values projected onto sea level are more obvious, and the numerical changes in the temporal domain are more distinguishable, which is conducive to establishing a spatial interpolation model to estimate ZWD. On the one hand, the projection function eliminates the influence of ZWD with elevation change and simplifies the spatial interpolation modeling of ZWD from three-dimensional space to a two-dimensional plane. On the other hand, due to the magnification of ZWD by the projection function, the interpolation error can be effectively suppressed when restoring the interpolation result of sea-level ZWD to the elevation of the GNSS station (the inverse process of projecting from the GNSS station elevation to the sea level), which can help the model to more accurately characterize the numerical variation in ZTD.
According to the introduction of the ZTD spatial interpolation modeling method in the previous section, the accuracy of the model is mainly related to the regression model, correlation model, upper limit value included in the Kriging interpolation parameters, and spatial distribution of the GNSS stations. For the selection of the optimal spatial interpolation parameters, 132,685 observation epochs are looped sequentially, and the modeling and checking stations are randomly selected on each epoch for 100 runs to classify and analyze the ZWD interpolation errors corresponding to different combinations of Kriging interpolation parameters. As each of the modeling stations selected for GNSS spatial interpolation is different, multiple runs (100 runs in this paper, or according to the computer arithmetic power to carry out the appropriate increase or decrease) can weaken the impact of the spatial distribution of the GNSS station on the accuracy of the model, highlighting the impact of the Kriging interpolation parameter selection. At this time, according to the different spatial interpolation parameters corresponding to the checking station on the error changes (as shown in Table 1), the optimal spatial interpolation parameters can be determined. For the influence of the GNSS station spatial distribution, after determining the optimal interpolation parameter, it can be discussed and analyzed by using the optimal spatial interpolation parameter to deal with different spatial distributions of the GNSS modeling stations and determine the interpolation station selection based on the error variation in the checking stations (as shown in Figure 6).
The statistical results of the error values between the interpolation results of with different Kriging interpolation parameters (as shown in Table 1) show that the interpolation results are related to the selection of the regression model, the correlation model, and the upper limit value to a certain extent. Overall, the selection of the correlation model has the greatest influence, the correlation model has the second greatest influence, and the upper limit value has the least influence. For the regression models, first-order polynomial is the best, zero-order polynomial is the next best, and second-order polynomial is the worst; for the correlation model, exponential, linear, and spherical have smaller errors; cubic is the next best; Gaussian and cubic spline are the worst, and the error fluctuates significantly; among the upper limit values, the interpolation effect of 50 and 100 is better, 20 and 200 are next, and 10 is the worst. In summary, the most suitable combination of Kriging interpolation parameters for the GNSS station ZTD data adopted in this paper is the first-order polynomial regression model, the spherical correlation model, and the upper limit value of 50. In the selection process of Kriging interpolation parameters, the interpolation model that best describes the spatio-temporal correlation of the current ZTD data is selected as a service to the later ZTD high-precision spatial interpolation modeling. Moreover, due to the differences in the internal factors (mainly meteorological parameters) that lead to spatial and temporal variations in ZTD, the process of optimal Kriging parameter selection needs to be re-executed when spatially interpolating ZTD data from different regions using this method.
As shown in Figure 6, for four epochs, 5 November 2003 23:00, 9 September 2010 23:00, 14 July 2017 23:00, and 13 September 2023 11:00, the GNSS modeling stations are randomly selected and run 100 times to obtain the ZWD valuation of the sea level at the checking stations. Comparing the RMS error values of sea level ZWD estimation errors corresponding to different GNSS station selection schemes, the modeling effects corresponding to different GNSS modeling stations on the four epochs vary greatly. Taking “epoch 1” as an example, the minimum RMS error value is less than 30 mm, and the maximum RMS error value is greater than 120 mm. This shows that when using the proposed method for ZTD spatial interpolation modeling, the accurate selection of GNSS modeling stations will directly affect the modeling accuracy. Analyzing the occurrence of smaller RMS error in Figure 6, for the four modeling epochs, among the 100 GNSS station selection schemes, there is at least one optimal GNSS site selection scheme with an error of less than 30 mm for each epoch.
The number of GNSS stations corresponding to the four modeling epochs counted in Table 2 shows that the number of GNSS stations has no significant relationship with the ZWD interpolation effect. Specifically, comparing the results of randomly selected 290 GNSS stations for spatial interpolation modeling in “epoch 4” and 137 GNSS stations for spatial interpolation modeling in “epoch 1”, both have the same problem of RMS error value, which fluctuates with different station selection schemes. In fact, the process of GNSS modeling station selection is searching for a set of GNSS stations that best characterize the spatial distribution of ZTD values. In summary, when determining the GNSS modeling stations, the optimal selection scheme can be obtained by randomly selecting the modeling stations and checking stations several times (more than 50 times) and counting the RMS error value of the checking stations; according to the smallest RMS error, selecting the corresponding GNSS station selection scheme thus weakens the influence of the spatial distribution of GNSS stations.
As shown in Figure 7, for the comparison of ZTD data and the Kriging interpolation model in 2024, the model can well reflect the ZTD numerical changes in the four checking stations with elevations of 397.4, 1575.5, 2576.2, and 3754.6 m, respectively. The differences between the interpolated model and the ZTD values of the GNSS stations are basically kept within 20 mm. Although there are significant differences in elevation among different checking stations, the model performance is almost unrelated to station elevation. This is because the proposed method considers the influence of station elevation, enabling the model results to reflect both minor changes and obvious jumps in ZTD over its temporal domain. Compared with the UNB3m and GPT3 models, the Kriging interpolation model is in better agreement with the ZTD data, and the difference between the Kriging interpolation model and ZTD data is enough to accurately reflect the fluctuations within a small range. The UNB3m and GPT3 models can roughly simulate the general trend of the ZTD, but in the period of 150~250 days of the year, when the ZTD values at the GNSS stations are more variable, the GPT3 model deviates more from the ZTD values at the GNSS stations, showing obvious underestimation or overestimation, and the UNB3m model deviation is more obvious. For the BOGT station near the equator, the Kriging interpolation model is in better agreement with the GNSS-measured values, and the GPT3 model can basically match the overall trend of the ZTD values, but the UNB3m model is greatly affected by the latitude, and the values show an almost unchanged “straight line” pattern, which is related to the fact that the UNB3m model does not fully take into account the spatial and temporal changes in the troposphere near the equator [16,17]. However, since the results calculated using the UNB3m and GPT3 models are not directly used in actual applications, this comparison only serves to demonstrate the reliability of the proposed method and does not negate the validity of the UNB3m and GPT3 models.
The distribution of the errors between the measured values and the results of the interpolation model at the four GNSS checking stations in 2024 (Figure 8) shows that most of the errors are within 20 mm, but the distribution of the error concentration varies among the different stations and exhibits a non-Gaussian distribution, with the PARK station concentrating on the error within ±15 mm, the ULAB and BOGT stations concentrating on the error within ±20 mm, and the MKEA station concentrating on the error within ±10 mm. This is primarily since the GNSS stations used for interpolation are constantly changing (see Figure 4), making it impossible to guarantee that errors will follow a Gaussian distribution throughout the whole year of 2024. By comparing the error values between the proposed model and the traditional model, it can be observed that the proposed model outperforms the traditional model in terms of both the magnitude and distribution of error values (direct three-dimensional spatial interpolation of ZWD). This is due to the proposed model projecting ZWD onto sea level using the UNB3m model, making the changes in projected ZWD values more pronounced and conducive to spatial interpolation (see Figure 5), and the interpolation error is further reduced as the interpolation results are restored to the station elevation. Overall, the distribution of errors at the different stations is skewed normal, with a high number of small errors near 0 and relatively few larger error values (more than 30 mm) on either side. For the error variation range of the model results, there are a small number of epochs with error more than 50 mm at PARK station, which is related to the number of GNSS stations corresponding to the current epochs and the spatial distribution, but the frequency of such large error values is small.
As shown in Table 3, on the four GNSS checking stations with large differences in latitude, longitude and elevation, the interpolation model is less affected by the changes in the station horizontal coordinates and elevation, there is no obvious change in the RMS errors on different stations, and the RMS error is basically around 15 mm, which reflects the validity and reliability of the proposed ZTD spatial interpolation model to take into account the elevation of the GNSS station through the UNB3m projection function. In terms of the RMS error values, the proposed model is smaller than those of the traditional model, GPT3, and UNB3m models. For the PARK station, the RMS error values of the Kriging interpolation model have an improvement of about 14 mm with respect to the traditional model and about 30 mm with respect to those of the GPT3 and UNB3m models. For the ULAB and MKEA stations, the RMS error values of the proposed model are about 27 mm smaller than those of the traditional model and about 10 mm smaller than those of the GPT3 and UNB3m models. At the BOGT station, the RMS error values of the proposed model are about 10, 16 and 40 mm smaller than those of the traditional model, GPT3, and UNB3m models, respectively. In addition, the temporal resolution of the interpolation model is consistent with the data involved in the modeling up to one or two hours, which makes it more suitable for high temporal dynamics application scenarios than the GPT3 and UNB3m models with single-day resolution. Comparing the GPT3 model and the UNB3m model, the accuracy of the calculation results of both models is comparable at PARK, ULAB and BOGT stations, and the GPT3 model is slightly better than the UNB3m model. However, at the low-latitude BOGT station (latitude 4.6401), the RMS error value of the GPT3 model shows an improvement of about 40 mm compared to the UNB3m model, indicating that the UNB3m model does not run well at low latitudes, which is consistent with the findings of existing scholars [32].
The RMS error values of the ZTD spatial interpolation modeling at the checking stations for 132,685 observation epochs shown in Table 4 indicate that the error of the interpolation model falls between 10 and 30 mm in most of the epochs (accounting for up to 85% of the epochs), about 10% of the epochs have errors from 30 to 50 mm, and the percentage of the epochs with error over 50 mm is less than 0.3%, indicating that the overall ZTD interpolation effect is relatively satisfactory, and the model can give more accurate ZTD valuation in most of the ranges in the whole modeling period. Since the modeling stations and checking stations used for interpolation are randomly selected, the number of stations (as shown in Figure 4) and their spatial locations vary, but the model still maintains an accuracy of around 30 mm, indicating that the model has good stability in ZTD spatial interpolation. Analyzing the epoch percentage of different numbers of GNSS stations in each error interval, the number of stations has a certain relationship with the spatial interpolation effect of GNSS stations, but it is not absolute. Taking the smaller interpolation RMS error value of 15 mm as an example, the percentage of epochs below 100 stations (1.15%) is significantly lower than that above 100 (5.38% for 100~200, 6.47% for 200~300, and 2.28% for above 300). Taking the larger interpolation RMS error value of 30~50 mm as an example, the percentage of epochs below 100 stations (1.67%) is slightly smaller than the percentage of epochs above 300 (1.9%). All of this indicates that the number of stations is not a decisive factor, but the spatial distribution of stations and the ability of the selected GNSS stations to represent the spatial and temporal variations in the ZTD values in the whole modeling region are the key factors.
5. Conclusions
This paper focuses on analyzing the relationship between ZWD data and elevation at GNSS stations and introduces a method for modeling ZTD based on the UNB3m model and Kriging spatial interpolation. The spatial interpolation modeling based on 28 years of observation data from global GNSS stations released by CODE and the discussion and analysis of the results lead to the following main conclusions:
(1) The UNB3m function projects the ZWD to the sea level. The UNB3m function can project the ZWD at the elevation of the GNSS stations to the sea level, enlarge the range of the value change in the ZWD, simplify the interpolation of the ZWD from three-dimensional to two-dimensional, and the error of the interpolation result has the effect of “compression”;
(2) Parameters of the Kriging spatial interpolation model and selection of GNSS stations. In the process of realizing the Kriging spatial interpolation model, the optimal spatial interpolation parameters are selected according to the ZWD interpolation errors corresponding to different combinations of Kriging interpolation parameters, and the spatial distribution of GNSS modeling stations is determined by the modeling errors of randomly selected GNSS stations after selecting spatial interpolation parameters;
(3) Relationship between the modeling effect of the Kriging spatial interpolation model and the GNSS stations. There is no absolute relationship between the modeling effect of the model and the number of GNSS stations; the modeling accuracy of better than 5 mm can be achieved even when the number of GNSS stations is lower than 100; the modeling effect is highly correlated with the spatial distribution uniformity of GNSS stations and the density of GNSS stations in heterogeneous regions; and the accuracy of the model is guaranteed when the selected modeling stations can characterize the spatial-temporal evolution characteristics of the ZTD in the whole study area;
(4) Accuracy and reliability of the Kriging spatial interpolation model. In the results of spatial interpolation modeling of 132,685 observations of ZTD data with 1 or 2 h resolution in 28 years, more than 85% of the observations have modeling accuracies of better than 30 mm, and the model has reliable accuracies at low-latitude or high-elevation GNSS stations, with no obvious error ups and downs in the time domain, and the model accuracy has improved by 10~40 mm compared with that of the GPT3 model and the UNB3m model, and its reliability and stability are significantly enhanced by separating the influences of elevation through the UNB3m model.
In conclusion, this study gives full play to the advantages of the UNB3m model in removing the influence of elevation, simplifies the ZTD spatial interpolation process into a two-dimensional planar interpolation process, and establishes a ZTD spatial interpolation model with rigorous logic, a simple process, and convenient implementation. In terms of model validation, the accuracy and reliability of the model are repeatedly verified by measured data, which proves that the modeling method has a broad application market in high-precision positioning scenarios, such as single- and dual-frequency hybrid deformation monitoring. With the increase in the number of GNSS stations and the abundance of shared ZTD data, high spatial and temporal resolution ZTD observation data will no longer be the main factor limiting the interpolation modeling in the future. Combining methods such as graph theory to improve the computational efficiency and accuracy of optimal GNSS station spatial distribution selection is expected to further improve the accuracy and practicality of ZTD spatial interpolation modeling.
Author Contributions
H.Y., conceptualization, methodology, writing—original draft, formal analysis, supervision, software. Z.L., data curation, visualization, writing—review and editing. F.L. (Fang Li), conceptualization, data curation, supervision. Y.L., data curation, methodology, writing—review and editing. F.L. (Fuping Li), investigation, validation, visualization. R.W., methodology, visualization, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (No. 52364018), the Science and Technology Research Project of Jiangxi Provincial Department of Education (No. GJJ2403702), and the Science and Technology Research Project of Jiangxi Provincial Department of Education (No. GJJ2403703).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The coordinates of the GNSS stations and the ZTD data used in the study are downloaded from the official website of CODE (http://ftp.aiub.unibe.ch/CODE/ accessed on 27 February 2025).
Acknowledgments
We would like to thank CODE for providing open access to the GNSS station coordinates and the ZTD data. The maps and plots in the paper were made using the Generic Mapping Tools (v6.0) and MATLAB (R2022a).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GNSS | Global Navigation Satellite System |
| ZTD | Zenith Tropospheric Delay |
| ZWD | Zenith Wet Delay |
| ZHD | Zenith Hydrostatic Delay |
| IGS | International GNSS Service |
| CODE | Center for Orbit Determination in Europe |
| RMS | Root Mean Square |
| PWV | Precipitable Water Vapor |
References
- Li, H.; Zhu, G.; Kang, Q.; Huang, L.; Wang, H. A Global Zenith Tropospheric Delay Model with ERA5 and GNSS-Based ZTD Difference Correction. GPS Solut. 2023, 27, 154. [Google Scholar] [CrossRef]
- Akar, A.U.; Inal, C. Prediction of Zenith Tropospheric Delay in GNSS Observations Using Support Vector Regression. Adv. Space Res. 2023, 71, 4659–4680. [Google Scholar] [CrossRef]
- Yuan, Z.; Lin, X.; Xu, Y.; Zhao, J.; Du, N.; Cai, X.; Li, M. Zenith Tropospheric Delay Forecasting in the European Region Using the Informer–Long Short-Term Memory Networks Hybrid Prediction Model. Atmosphere 2024, 16, 31. [Google Scholar] [CrossRef]
- Vieira, I.; Verbeeck, H.; Meunier, F.; Peaucelle, M.; Sibret, T.; Lefevre, L.; Cheesman, A.W.; Brown, F.; Sitch, S.; Mbifo, J.; et al. Global Reanalysis Products Cannot Reproduce Seasonal and Diurnal Cycles of Tropospheric Ozone in the Congo Basin. Atmos. Environ. 2023, 304, 119773. [Google Scholar] [CrossRef]
- Zhang, Z.; Lou, Y.; Zhang, W.; Wang, Z.; Zhou, Y.; Bai, J.; Zhang, Z.; Shi, C. Dynamic Stochastic Model for Estimating GNSS Tropospheric Delays from Air-Borne Platforms. GPS Solut. 2023, 27, 39. [Google Scholar] [CrossRef]
- Li, X.; Barriot, J.-P.; Lou, Y.; Zhang, W.; Li, P.; Shi, C. Towards Millimeter-Level Accuracy in GNSS-Based Space Geodesy: A Review of Error Budget for GNSS Precise Point Positioning. Surv. Geophys. 2023, 44, 1691–1780. [Google Scholar] [CrossRef]
- Stauffer, R.; Hohensinn, R.; Pinzón, I.H.; Moeller, G.; Pan, Y.; Kłopotek, G.; Soja, B.; Brockmann, E.; Rothacher, M. Estimation of Tropospheric Parameters with GNSS Smartphones in a Differential Approach. Meas. Sci. Technol. 2023, 34, 095126. [Google Scholar] [CrossRef]
- Huang, L.; Lan, S.; Zhu, G.; Chen, F.; Li, J.; Liu, L. A Global Grid Model for the Estimation of Zenith Tropospheric Delay Considering the Variations at Different Altitudes. Geosci. Model Dev. Discuss. 2023, 2023, 1–18. [Google Scholar] [CrossRef]
- Wang, P.; Liu, H.; Wen, J.; Zhou, B.; Qian, C.; Zhang, Y. Improvement Analysis of a Height-Deviation Compensation-Based Linear Interpolation Method for Multi-Station Regional Troposphere. Earth Space Sci. 2023, 10, e2023EA002946. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Zhang, J.; Qiu, C.; Zhang, S.; Li, L. An Improved Model for Detecting Heavy Precipitation Using GNSS-Derived Zenith Total Delay Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5392–5405. [Google Scholar] [CrossRef]
- Stępniak, K.; Paziewski, J. On the Quality of Tropospheric Estimates from Low-Cost GNSS Receiver Data Processing. Measurement 2022, 198, 111350. [Google Scholar] [CrossRef]
- Zhu, S.; Yue, D.; He, L.; Chen, J.; Liu, Z. Comparative Analysis of Four Different Single-Frequency PPP Models on Positioning Performance and Atmosphere Delay Retrieval. Adv. Space Res. 2021, 67, 3994–4010. [Google Scholar] [CrossRef]
- Adavi, Z.; Weber, R.; Glaner, M.F. Assessment of Regularization Techniques in GNSS Tropospheric Tomography Based on Single-and Dual-Frequency Observations. GPS Solut. 2022, 26, 1–16. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Yao, Y.; Yu, S.; Wang, W.; Yang, A. Refining Empirical Tropospheric Model with Meteorological Stations for Large Height Difference RTK Positioning. GPS Solut. 2023, 27, 138. [Google Scholar] [CrossRef]
- Haji-Aghajany, A.S.; Rohm, B.W.; Kryza, C.M.; Smolak, D.K. Machine Learning-Based Wet Refractivity Prediction through GNSS Troposphere Tomography for Ensemble Troposphere Conditions Forecasting. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4106118. [Google Scholar] [CrossRef]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Leandro, R.F.; Santos, M.C.; Langley, R.B. A North America Wide Area Neutral Atmosphere Model for GNSS Applications. Navigation 2009, 56, 57–71. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Tasan, M.; Ghorbaninasab, Z.; Haji-Aghajany, S.; Ghiasvand, A. Leveraging GNSS Tropospheric Products for Machine Learning-Based Land Subsidence Prediction. Earth Sci. Inform. 2023, 16, 3039–3056. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, Q.; Yao, W.; Guo, H.; Yin, J.; Xu, Y.; Zhai, Y.; Yao, Y.; Gao, Y. Assimilating GNSS Tropospheric Products and Quantitative Evaluation of Their Contributions to Numerical Weather Prediction. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5801413. [Google Scholar] [CrossRef]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sens. 2019, 11, 674. [Google Scholar] [CrossRef]
- Akar, A.U.; Inal, C. Performance of Spatial Interpolation Methods in Predicting GNSS Zenith Total Delay. Measurement 2024, 227, 114189. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, G.; Huang, L.; Wang, H.; Yang, Y.; Li, J.; Huang, L.; Zhou, L.; Liu, L. Development of a ZTD Vertical Profile Model Considering the Spatiotemporal Variation of Height Scale Factor with Different Reanalysis Products in China. Atmosphere 2022, 13, 1469. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, W.; Li, Z.; Du, Z.; Yang, P.; Yao, W.; Yao, Y. A High-Precision ZTD Interpolation Method Considering Large Area and Height Differences. GPS Solut. 2024, 28, 4. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A Method of Interpolation for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Xia, P.; Tong, M.; Ye, S.; Qian, J.; Fangxin, H. Establishing a High-Precision Real-Time ZTD Model of China with GPS and ERA5 Historical Data and Its Application in PPP. GPS Solut. 2023, 27, 2. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, L.; Zhang, F.; Chen, X.; Yang, Z. Accuracy Analysis of Real-Time Precise Point Positioning—Estimated Precipitable Water Vapor under Different Meteorological Conditions: A Case Study in Hong Kong. Atmosphere 2023, 14, 650. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Isioye, O.A.; Combrinck, L.; Botai, J. Performance Evaluation of Blind Tropospheric Delay Correction Models over Africa. S. Afr. J. Geomat. 2015, 4, 502–525. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).