Mapping Solar Future Perspectives of a Climate Change Hotspot: An In-Depth Study of Greece’s Regional Solar Energy Potential, Climatic Trends Influences and Insights for Sustainable Development
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
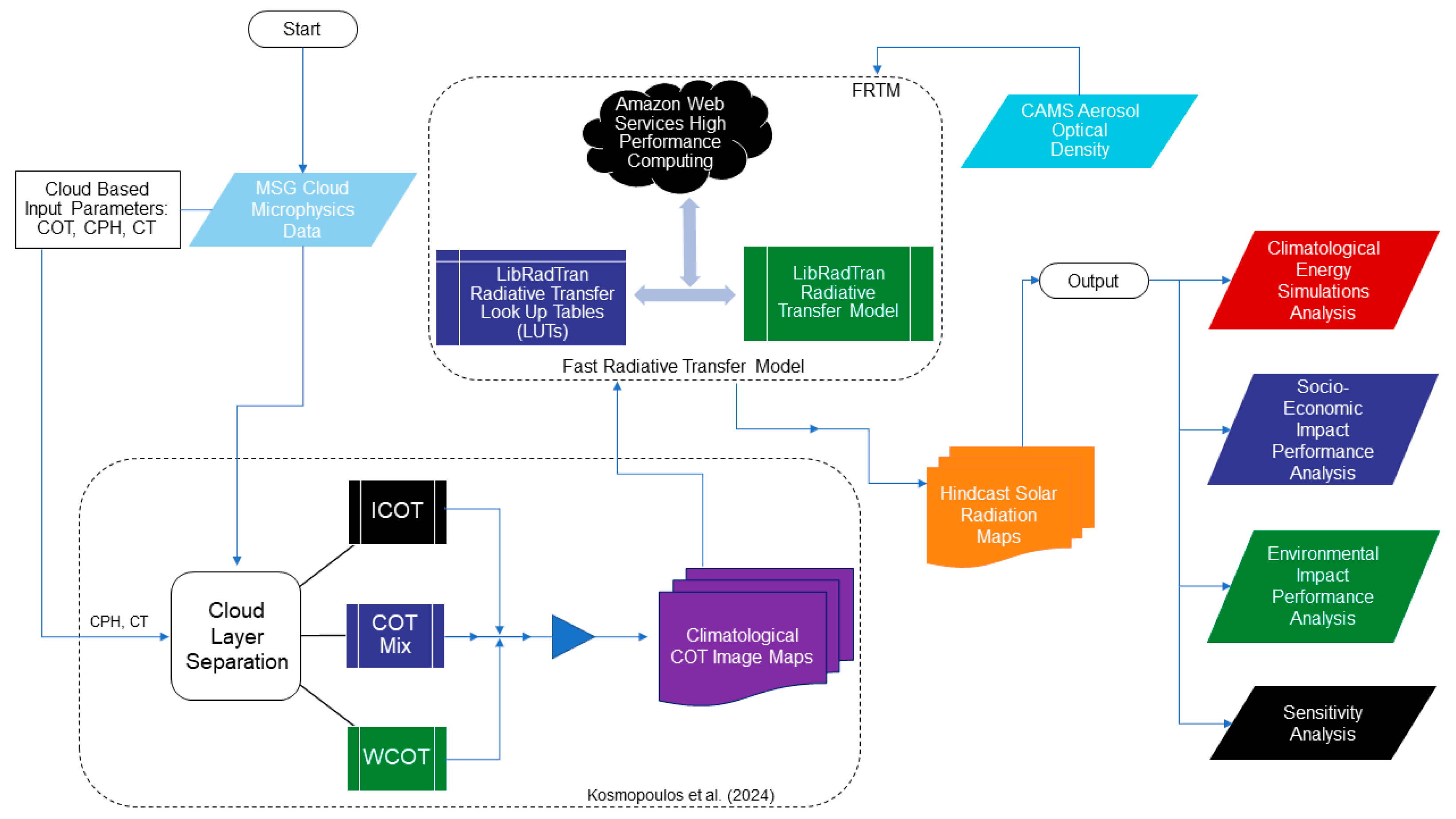
2.2. Fast Radiative Transfer Model (FRTM)
2.3. Metadata Processing and Visualization
3. Results
3.1. Solar Resources of Greece: The Most Up-to-Date PV Power Potential Map
3.2. GHI Variation
3.3. Fluctuations in PV Production
3.4. Energy Planning Scheme
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Estimation of per-1 kWp Metrics and Sensitivity Analysis
| Region | PVoutput (kWh) | GHI (W/m2) | GHI (kWh/m2) | Clear Sky Annual Error (2%) (kWh/m2) | All Sky Annual Error (5%) (kWh/m2) |
|---|---|---|---|---|---|
| EastMac&Thrc | 1548.41 | 200.89 | 1759.82 | 35.20 | 87.99 |
| CentrMac | 1544.36 | 197.21 | 1727.56 | 34.55 | 86.38 |
| WestMac | 1532.19 | 186.15 | 1630.66 | 32.61 | 81.53 |
| Epirus | 1541.94 | 195.01 | 1708.30 | 34.17 | 85.41 |
| Thessaly | 1547.51 | 200.07 | 1752.63 | 35.05 | 87.63 |
| CentrGR | 1557.62 | 209.26 | 1833.12 | 36.66 | 91.66 |
| IonianIslands | 1557.07 | 208.77 | 1828.79 | 36.58 | 91.44 |
| WestGR | 1556.79 | 208.50 | 1826.50 | 36.53 | 91.32 |
| Peloponnese | 1561.72 | 212.99 | 1865.78 | 37.32 | 93.29 |
| Attica | 1571.72 | 222.08 | 1945.45 | 38.91 | 97.27 |
| NorthAegean | 1580.20 | 229.79 | 2012.94 | 40.26 | 100.65 |
| SouthAegean | 1596.61 | 244.71 | 2143.66 | 42.87 | 107.18 |
| Crete | 1596.23 | 244.36 | 2140.60 | 42.81 | 107.03 |
| Region | Δ(PVoutput) (2%) (kWh) | Δ(PVoutput) (5%) (kWh) | Δ(Revenue) (2%) (€/kWh) | Δ(Revenue) (5%) (€/kWh) | Δ(CO2) (2%) (metric tons) | Δ(CO2) (5%) (metric tons) |
|---|---|---|---|---|---|---|
| EastMac&Thrc | 30.97 | 77.42 | 1.67 | 4.18 | 0.022 | 0.054 |
| CentrMac | 30.89 | 77.22 | 1.67 | 4.17 | 0.022 | 0.054 |
| WestMac | 30.64 | 76.61 | 1.65 | 4.14 | 0.021 | 0.054 |
| Epirus | 30.84 | 77.10 | 1.67 | 4.16 | 0.022 | 0.054 |
| Thessaly | 30.95 | 77.38 | 1.67 | 4.18 | 0.022 | 0.054 |
| CentrGR | 31.15 | 77.88 | 1.68 | 4.21 | 0.022 | 0.055 |
| IonianIslands | 31.14 | 77.85 | 1.68 | 4.20 | 0.022 | 0.054 |
| WestGR | 31.14 | 77.84 | 1.68 | 4.20 | 0.022 | 0.054 |
| Peloponnese | 31.23 | 78.09 | 1.69 | 4.22 | 0.022 | 0.055 |
| Attica | 31.43 | 78.59 | 1.70 | 4.24 | 0.022 | 0.055 |
| NorthAegean | 31.60 | 79.01 | 1.71 | 4.27 | 0.022 | 0.055 |
| SouthAegean | 31.93 | 79.83 | 1.72 | 4.31 | 0.022 | 0.056 |
| Crete | 31.92 | 79.81 | 1.72 | 4.31 | 0.022 | 0.056 |
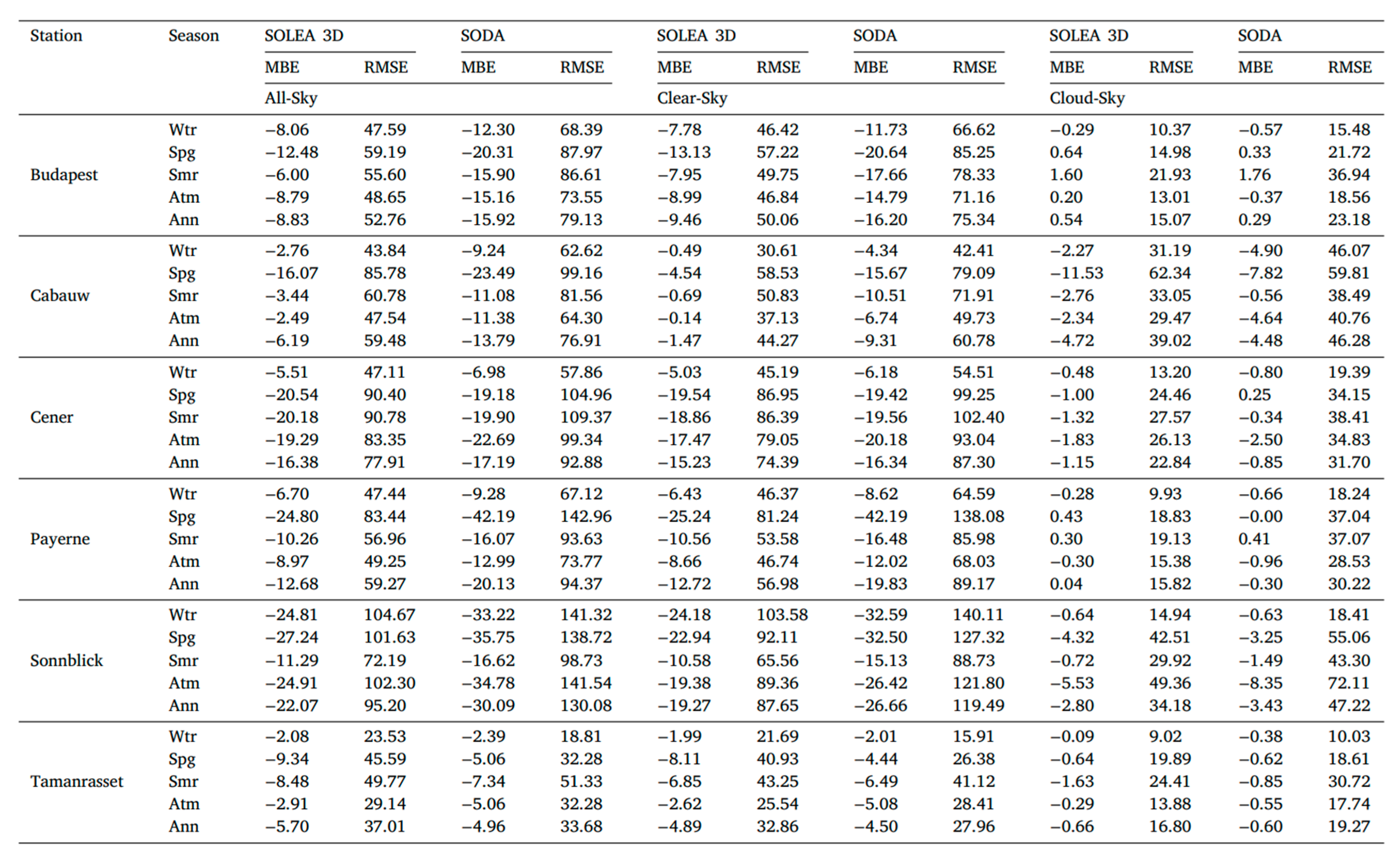
Appendix B
Appendix B.1. Multi-Layer Radiative Transfer in Cloud Atmospheres
Appendix B.2. Multi-Layer Radiative Transfer Equation
- represents the specific intensity at optical depth τ in layer i.
- is the single scattering albedo, defining the fraction of light scattered rather than absorbed in layer i.
- is the scattering phase function that characterizes the angular redistribution of radiation in layer i.
- is the Planck function that describes thermal emission from layer i.
Appendix B.3. Cloud Layer Classifications and Explanations
Appendix B.4. Boundary Conditions
Appendix C
Limitations and Refinement of PVGIS Calibration Utilized
References
- Stamatis, M.; Hatzianastassiou, N.; Korras-Carraca, M.-B.; Matsoukas, C.; Wild, M.; Vardavas, I. How strong are the links between global warming and surface solar radiation changes? Clim. Change 2024, 177, 156. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Makowski, K. Impact of global dimming and brightening on global warming. Geophys. Res. Lett. 2007, 34, L04702. [Google Scholar] [CrossRef]
- Soni, V.K.; Pandithurai, G.; Pai, D.S. Evaluation of long-term changes of solar radiation in India. Int. J. Climatol. 2012, 32, 540–551. [Google Scholar] [CrossRef]
- Hou, X.; Wild, M.; Folini, D.; Kazadzis, S.; Wohland, J. Climate change impacts on solar power generation and its spatial variability in Europe based on CMIP6. Earth Syst. Dynam. 2021, 12, 1099–1113. [Google Scholar] [CrossRef]
- Müller, S.; Remund, J. Satellite based shortest term solar energy forecast system for entire Europe for the next hours. In Proceedings of the 29th European Photovoltaic Solar Energy Conference and Exhibition, EUREC, Amsterdam, The Netherlands, 22–26 September 2014; pp. 2589–2590. [Google Scholar]
- Greece Installs 2.6 GW of PV Capacity in 2024. pv Magazine—Photovoltaics Markets and Technology. Available online: https://www.pv-magazine.com/2025/02/05/greece-installs-2-6-gw-of-pv-capacity-in-2024/ (accessed on 25 February 2025).
- Greece Unveils Revised National Energy and Climate Plan: Aiming for Carbon Neutrality by 2050. Greek News Agenda. Available online: https://www.greeknewsagenda.gr/greece-revised-national-energy-and-climate-plan/ (accessed on 25 November 2024).
- Energy Storage Is the Real Game Changer in Greece. PV Tech. Available online: https://www.pv-tech.org/energy-storage-real-game-changer-greece/ (accessed on 17 November 2024).
- Kitsara, G.; Papaioannou, G.; Papathanasiou, A.; Retalis, A. Dimming/brightening in Athens: Trends in Sunshine Duration, Cloud Cover and Reference Evapotranspiration. Water Resour. Manag. 2013, 27, 1623–1633. [Google Scholar] [CrossRef]
- Founda, D.; Pierros, F.; Sarantopoulos, A. Evidence of Dimming/Brightening Over Greece from Long-Term Observations of Sunshine Duration and Cloud Cover. In Perspectives on Atmospheric Sciences. Springer Atmospheric Sciences; Karacostas, T., Bais, A., Nastos, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Panagea, I.S.; Tsanis, I.K.; Koutroulis, A.G.; Grillakis, M.G. Climate Change Impact on Photovoltaic Energy Output: The Case of Greece. Adv. Meteorol. 2014, 2014, 264506. [Google Scholar] [CrossRef]
- Kosmopoulos, P.; Dhake, H.; Melita, N.; Tagarakis, K.; Georgakis, A.; Stefas, A.; Vaggelis, O.; Korre, V.; Kashyap, Y. Mul-ti-Layer Cloud Motion Vector Forecasting for Solar Energy Applications. Appl. Energy 2024, 353, 122144. [Google Scholar] [CrossRef]
- Sifakis, N.I.; Iossifidis, C.; Kontoes, C.; Keramitsoglou, I. Wildfire Detection and Tracking over Greece Using MSG-SEVIRI Satellite Data. Remote Sens. 2011, 3, 524–538. [Google Scholar] [CrossRef]
- Bedka, K.M. Overshooting cloud top detections using MSG SEVIRI infrared brightness temperatures and their relationship to severe weather over Europe. Atmos. Res. 2011, 99, 175–189. [Google Scholar] [CrossRef]
- Copernicus Atmosphere Monitoring Service (CAMS). Available online: https://atmosphere.copernicus.eu/global-forecast-plots (accessed on 15 August 2024).
- CAMS Radiation Service—SoDa. Available online: https://www.soda-pro.com/web-services/radiation/cams-radiation-service (accessed on 15 August 2024).
- CAMS-AOD—SoDa. Available online: https://www.soda-pro.com/web-services/atmosphere/cams-aod (accessed on 15 August 2024).
- Eskes, H.; Gaudel, A.; Griesfeller, J.; Jones, L.; Kapsomenakis, J.; Katragkou, E.; Kinne, S.; Langerock, B.; Razinger, M.; Richter, A.; et al. Validation of reactive gases and aerosols in the MACC global analysis and forecast system. Geosci. Model Dev. 2015, 8, 3523–3543. [Google Scholar] [CrossRef]
- Derrien, M.; Le Gléau, H. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Feijt, A.J.; Stammes, P. Cloud property retrievals for climate monitoring: Implications of differences between Spinning Enhanced Visible and Infrared Imager (SEVIRI) on METEOSAT-8 and Advanced Very High Resolution Radiometer (AVHRR) on NOAA-17. J. Geophys. Res. 2006, 111, D20210. [Google Scholar] [CrossRef]
- Kosmopoulos, P.; Dhake, H.; Kartoudi, D.; Tsavalos, A.; Koutsantoni, P.; Katranitsas, A.; Lavdakis, N.; Mengou, E.; Kashyap, Y. Ray-Tracing modeling for urban photovoltaic energy planning and management. Appl. Energy 2024, 369, 123516. [Google Scholar] [CrossRef]
- Kosmopoulos, P.; Kouroutsidis, D.; Papachristopoulou, K.; Raptis, P.I.; Masoom, A.; Saint-Drenan, Y.-M.; Blanc, P.; Kontoes, C.; Kazadzis, S. Short-Term Forecasting of Large-Scale Clouds Impact on Downwelling Surface Solar Irradiation. Energies 2020, 13, 6555. [Google Scholar] [CrossRef]
- Choudhury, G.; Block, K.; Haghighatnasab, M.; Quaas, J.; Goren, T.; Tesche, M. Pristine oceans are a significant source of uncertainty in quantifying global cloud condensation nuclei, Atmos. Chem. Phys. 2025, 25, 3841–3856. [Google Scholar] [CrossRef]
- Block, K.; Haghighatnasab, M.; Partridge, D.G.; Stier, P.; Quaas, J. Cloud condensation nuclei concentrations derived from the CAMS reanalysis. Earth Syst. Sci. Data 2024, 16, 443–470. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Huang, G.; Zhang, S. Comprehensive Assessment and Analysis of the Current Global Aerosol Optical Depth Products. Remote Sens. 2024, 16, 1425. [Google Scholar] [CrossRef]
- Garrigues, S.; Remy, S.; Chimot, J.; Ades, M.; Inness, A.; Flemming, J.; Kipling, Z.; Laszlo, I.; Benedetti, A.; Ribas, R.; et al. Monitoring multiple satellite aerosol optical depth (AOD) products within the Copernicus Atmosphere Monitoring Service (CAMS) data assimilation system, Atmos. Chem. Phys. 2022, 22, 14657–14692. [Google Scholar] [CrossRef]
- HEDNO, S.A. (Hellenic Electricity Distribution Network Operator S.A.). Available online: https://deddie.gr/en/ (accessed on 11 November 2024).
- Pawlowicz, R. M_Map: A Mapping Package for MATLAB, Version 1.4m, [Computer Software]. 2020. Available online: https://www-old.eoas.ubc.ca/~rich/map.html (accessed on 17 October 2024).
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/ (accessed on 22 October 2024).
- Sethi, D.; Kosmopoulos, P.G. Rooftop Solar Photovoltaic Potential in Polluted Indian Cities: Atmospheric and Urban Impacts, Climate Trends, Societal Gains, and Economic Opportunities. Remote Sens. 2025, 17, 1221. [Google Scholar] [CrossRef]
- Dhake, H.; Kosmopoulos, P.; Mantakas, A.; Kashyap, Y.; El-Askary, H.; Elbadawy, O. Climatological Trends and Effects of Aerosols and Clouds on Large Solar Parks: Application Examples in Benban (Egypt) and Al Dhafrah (UAE). Remote Sens. 2024, 16, 4379. [Google Scholar] [CrossRef]
- Vigkos, S.; Kosmopoulos, P.G. Photovoltaics Energy Potential in the Largest Greek Cities: Atmospheric and Urban Fabric Effects, Climatic Trends Influences and Socio-Economic Benefits. Energies 2024, 17, 3821. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Mechilis, M.T.; Kaoura, P. Solar Energy Production Planning in Antikythera: Adequacy Scenarios and the Effect of the Atmospheric Parameters. Energies 2022, 15, 9406. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kosmopoulos, P.G.; Patel, P.N.; Sheoran, R. Can Forest Fires Be an Important Factor in the Reduction in Solar Power Production in India? Remote Sens. 2022, 14, 549. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kosmopoulos, P.G.; Ningombam, S.S.; Masoom, A. Impact of Aerosol and Cloud on the Solar Energy Potential over the Central Gangetic Himalayan Region. Remote Sens. 2021, 13, 3248. [Google Scholar] [CrossRef]
- Masoom, A.; Kosmopoulos, P.; Kashyap, Y.; Kumar, S.; Bansal, A. Rooftop Photovoltaic Energy Production Management in India Using Earth-Observation Data and Modeling Techniques. Remote Sens. 2020, 12, 1921. [Google Scholar] [CrossRef]
- Vigkos, S.; Kosmopoulos, P.G.; Papayannis, A. Solar Photovoltaic Energy Production Conditions in the Urban Environment of Athens, Cairo, Granada and Vienna. Environ. Sci. Proc. 2023, 26, 24. [Google Scholar] [CrossRef]
- Vigkos, S.; Kosmopoulos, P.G.; Papayannis, A. Conditions for Producing Solar Photovoltaic Energy in European and North African Cities. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 3845–3849. [Google Scholar] [CrossRef]
- Greenhouse Gas Equivalencies Calculator|US EPA. Available online: https://www.epa.gov/energy/greenhouse-gas-equivalencies-calculator (accessed on 22 October 2024).
- Bellos, E. A geospatial comparative analysis of solar thermal concentrating power systems in Greece. Cleaner Energy Syst. 2023, 4, 100055. [Google Scholar] [CrossRef]
- Climatological Maps of Solar Energy in Greece. Laboratory of Atmospheric Physics of the University of Patras. Available online: https://www.atmosphere-upatras.gr/en/solarmaps (accessed on 28 October 2024).
- Global Solar Atlas. Available online: https://globalsolaratlas.info/map?c=38.358888,24.488525,6&r=GRC (accessed on 28 October 2024).
- SOLCAST. Solar Irradiance Data for Greece. Available online: https://www.solcast.com/solar-radiation-map/greece (accessed on 28 October 2024).
- Solea. Solar Atlas of Greece. Available online: https://solea.gr/solar-atlas-of-greece/ (accessed on 28 October 2024).
- Rasvanis, E.; Tselios, V. Do geography and institutions affect entrepreneurs’ future business plans? Insights from Greece. J. Innov. Entrep. 2023, 12, 3. [Google Scholar] [CrossRef]
- Katopodis, T.; Markantonis, I.; Politi, N.; Vlachogiannis, D.; Sfetsos, A. High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model. Atmosphere 2020, 11, 761. [Google Scholar] [CrossRef]
- Nikitidou, E.; Tzoumanikas, P.; Bais, A.F.; Kazantzidis, A. The Effect of Clouds on Surface Solar Irradiance, from an All-Sky Camera, in Thessaloniki, Greece. In Perspectives on Atmospheric Sciences. Springer Atmospheric Sciences; Karacostas, T., Bais, A., Nastos, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Kouklaki, D.; Papachristopoulou, K.; Fountoulakis, I.; Tsekeri, A.; Raptis, P.-I.; Kazadzis, S.; Eleftheratos, K. Impact of Aerosols on Surface Solar Radiation and Solar Energy in the Mediterranean Basin. Environ. Sci. Proc. 2023, 26, 56. [Google Scholar] [CrossRef]
- Natsis, A.; Bais, A.; Meleti, C.; Tourpali, K. Long-term changes surface solar shortwave irradiance at Thessaloniki, Greece under clear- and all-sky conditions. AIP Conf. Proc. 2024, 2988, 060007. [Google Scholar] [CrossRef]
- Banias, G.; Lampridi, M.; Pediaditi, K.; Achillas, C.; Sartzetakis, E.; Bochtis, D.; Berruto, R.; Busato, P. Evaluation of environmental impact assessment framework effectiveness. Chem. Eng. Trans. 2017, 58, 805–810. [Google Scholar] [CrossRef]
- Cuevas-Agulló, E.; Barriopedro, D.; García, R.D.; Alonso-Pérez, S.; González-Alemán, J.J.; Werner, E.; Suárez, D.; Bustos, J.J.; García-Castrillo, G.; García, O.; et al. Sharp increase in Saharan dust intrusions over the western Euro-Mediterranean in February–March 2020–2022 and associated atmospheric circulation. Atmos. Chem. Phys. 2024, 24, 4083–4104. [Google Scholar] [CrossRef]
- Philippopoulos, K.; Deligiorgi, D.; Mavrakou, T.; Cheliotis, J. Winter atmospheric circulation patterns and their relationship with the meteorological conditions in Greece. Meteorol. Atmos. Phys. 2014, 124, 195–204. [Google Scholar] [CrossRef]
- Philippopoulos, K.; Tzanis, C.G.; Deligiorgi, D.; Alimissis, A. Climatology of the impact of atmospheric circulation on surface meteorological conditions over Greece. In Proceedings of the 17th International Conference on Environmental Science and Technology, CEST2021_00486, Athens, Greece, 1–4 September 2021. [Google Scholar]
- Song, Z.; Wang, M.; Yang, H. Quantification of the Impact of Fine Particulate Matter on Solar Energy Resources and Energy Performance of Different Photovoltaic Technologies. ACS Environ. Au. 2022, 2, 275–286. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Yoo, Y.; Cho, S. Analysis of the Impact of Particulate Matter on Net Load and Behind-the-Meter PV Decoupling. Electronics 2022, 11, 2261. [Google Scholar] [CrossRef]
- Hajat, S. Health effects of milder winters: A review of evidence from the United Kingdom. Environ. Health 2017, 16 (Suppl. 1), 109. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; El-Askary, H.; Taylor, M.; Gkikas, A.; Proestakis, E.; Kontoes, C.; El-Khayat, M.M. Earth-Observation-Based Estimation and Forecasting of Particulate Matter Impact on Solar Energy in Egypt. Remote Sens. 2018, 10, 1870. [Google Scholar] [CrossRef]
- Greek Renewable Energy Market Outlook 2023–2024. WATTCROP. Available online: https://wattcrop.com/wp-content/uploads/2024/07/Greek-Renewable-Energy-Market-Outlook-2024.pdf (accessed on 8 November 2024).
- What Is the Carbon Footprint of Solar Panels? Solar.com. Available online: https://www.solar.com/learn/what-is-the-carbon-footprint-of-solar-panels/ (accessed on 26 November 2024).
- Regions of Greece. From Wikipedia, the Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Regions_of_Greece (accessed on 15 August 2024).
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Bais, A.F.; Lagouvardos, K.; Kotroni, V.; Keramitsoglou, I.; Kiranoudis, C. Estimation of the Solar Energy Potential in Greece Using Satellite and Ground-Based Observations. In Perspectives on Atmospheric Sciences. Springer Atmospheric Sciences; Karacostas, T., Bais, A., Nastos, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Kambezidis, H.D. Annual and Seasonal Trends of Solar Radiation in Athens, Greece. J. Sol. Energy Res. Updates 2018, 5, 14–24. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Radiation Climate of Greece. Climate 2021, 9, 183. [Google Scholar] [CrossRef]
- Eleftheratos, K.; Raptis, I.-P.; Kouklaki, D.; Kazadzis, S.; Fountoulakis, I.; Psiloglou, B.E.; Papachristopoulou, K.; Founda, D.; Benetatos, C.; Kazantzidis, A.; et al. The ASPIRE Project: Atmospheric Parameters Affecting Solar Irradiance and Solar Energy in Athens, Greece—Overview and Results. Environ. Sci. Proc. 2023, 26, 46. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Mirasgedis, S.; Sarafidis, Y.; Giannakopoulos, C.; Varotsos, K.V.; Gakis, N. Climate Change Impacts on the Energy System of a Climate-Vulnerable Mediterranean Country (Greece). Atmosphere 2024, 15, 286. [Google Scholar] [CrossRef]
- Devasthale, A.; Andersson, S.; Engström, E.; Kaspar, F.; Trentmann, J.; Duguay-Tetzlaff, A.; Meirink, J.F.; Kjellström, E.; Landelius, T.; Thomas, M.A.; et al. Leveraging the satellite-based climate data record CLARA-A3 to understand trends and climate regimes relevant for solar energy applications over Europe. EGUsphere 2024. [Google Scholar] [CrossRef]
- Surface Radiation Data Set—Heliosat (SARAH)—Edition 3. Available online: https://wui.cmsaf.eu/safira/action/viewDoiDetails?acronym=SARAH_V003 (accessed on 18 May 2025).
- Masselot, P.; Mistry, M.N.; Rao, S.; Huber, V.; Monteiro, A.; Samoli, E.; Stafoggia, M.; De’dOnato, F.; Garcia-Leon, D.; Ciscar, J.-C.; et al. Estimating future heat-related and cold-related mortality under climate change, demographic and adaptation scenarios in 854 European cities. Nat. Med. 2025, 31, 1294–1302. [Google Scholar] [CrossRef]
- IPCC Sixth Assessment Report. Impacts, Adaptation and Vulnerability. Cross-Chapter Paper 4: Mediterranean Region. Available online: https://www.ipcc.ch/report/ar6/wg2/chapter/ccp4/ (accessed on 10 January 2025).
- Greek PV Market Statistics for 2023 (Updated: 19 February 2024). Hellenic Association of Photovoltaic Companies (HELAPCO). Available online: https://helapco.gr/xoorigle/2024/02/pv-stats_greece_2023_eng.pdf (accessed on 28 October 2024).
- Greece Adds 1.5 GW of New Solar in January–September Period. pv Magazine. Available online: https://www.pv-magazine.com/2024/09/30/greece-added-1-5-gw-of-new-solar-in-january-september-period/ (accessed on 28 October 2024).
- Greece Installs 400 MW of Net-Metered Solar in 2024. pv Magazine—Photovoltaics Markets and Technology. Available online: https://www.pv-magazine.com/2025/01/31/greece-adds-400-mw-of-solar-under-net-metering-in-2024/ (accessed on 10 February 2025).
- Capacity of the Largest Solar Photovoltaic Farms in Operation in Greece as of February 2024 (in Megawatts). Statista. Available online: https://www.statista.com/statistics/1454410/solar-energy-farms-by-capacity-greece/ (accessed on 10 February 2025).
- Pfeifroth, U.; Drücke, J.; Kothe, S.; Trentmann, J.; Schröder, M.; Hollmann, R. SARAH-3—Satellite-Based Climate Data Records of Surface Solar Radiation. Earth Syst. Sci. Data 2024, 16, 5243–5265. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; Taylor, M.; Raptis, P.I.; Keramitsoglou, I.; Kiranoudis, C.; Bais, A.F. Assessment of surface solar irradiance derived from real-time modelling techniques and verification with ground-based measurements. Atmos. Meas. Tech. 2018, 11, 907–924. [Google Scholar] [CrossRef]
- Thomas, C.; Wey, E.; Blanc, P.; Wald, L.; Lefevre, M. Validation of HelioClim-3 version 4, HelioClim-3 version 5 and MACC-RAD using 14 BSRN stations. Energy Proced. 2016, 91, 1059–1069. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Alsuhaibany, Y.; Li, Y. Estimation of Rooftop Solar Photovoltaic (PV) Potential: A Systematic Literature Review and Guidelines for Future Research. Emergent Res. Forum (ERF) Pap. 2017, 301371801, 1–10. [Google Scholar]
- Desthieux, G.; Carneiro, C.; Camponovo, R.; Ineichen, P.; Morello, E.; Boulmier, A.; Abdennadher, N.; Dervey, S.; Ellert, C. Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2018, 4, 14. [Google Scholar] [CrossRef]
- Tapia, M.; Ramos, L.; Heinemann, D.; Zondervan, E. Power to the city: Assessing the rooftop solar photovoltaic potential in multiple cities of Ecuador. Phys. Sci. Rev. 2022, 8, 2285–2319. [Google Scholar] [CrossRef]
- Elsinga, B.; van Sark, W.; Ramaekers, L. Inverse Photovoltaic Yield Model for Global Horizontal Irradiance Reconstruction. Energy Sci. Eng. 2017, 5, 226–239. [Google Scholar] [CrossRef]
- Solar Power Modelling. Available online: https://assessingsolar.org/notebooks/solar_power_modeling.html (accessed on 27 May 2025).
- Patel, P.T.; Sukhadiya, R.; Aparnathi, R. A Review of Solar Irradiation Calculation Methods for Solar Power Plant. J. Emerg. Technol. Innov. Res. (JETIR) 2019, 6, 1241–1250. [Google Scholar]

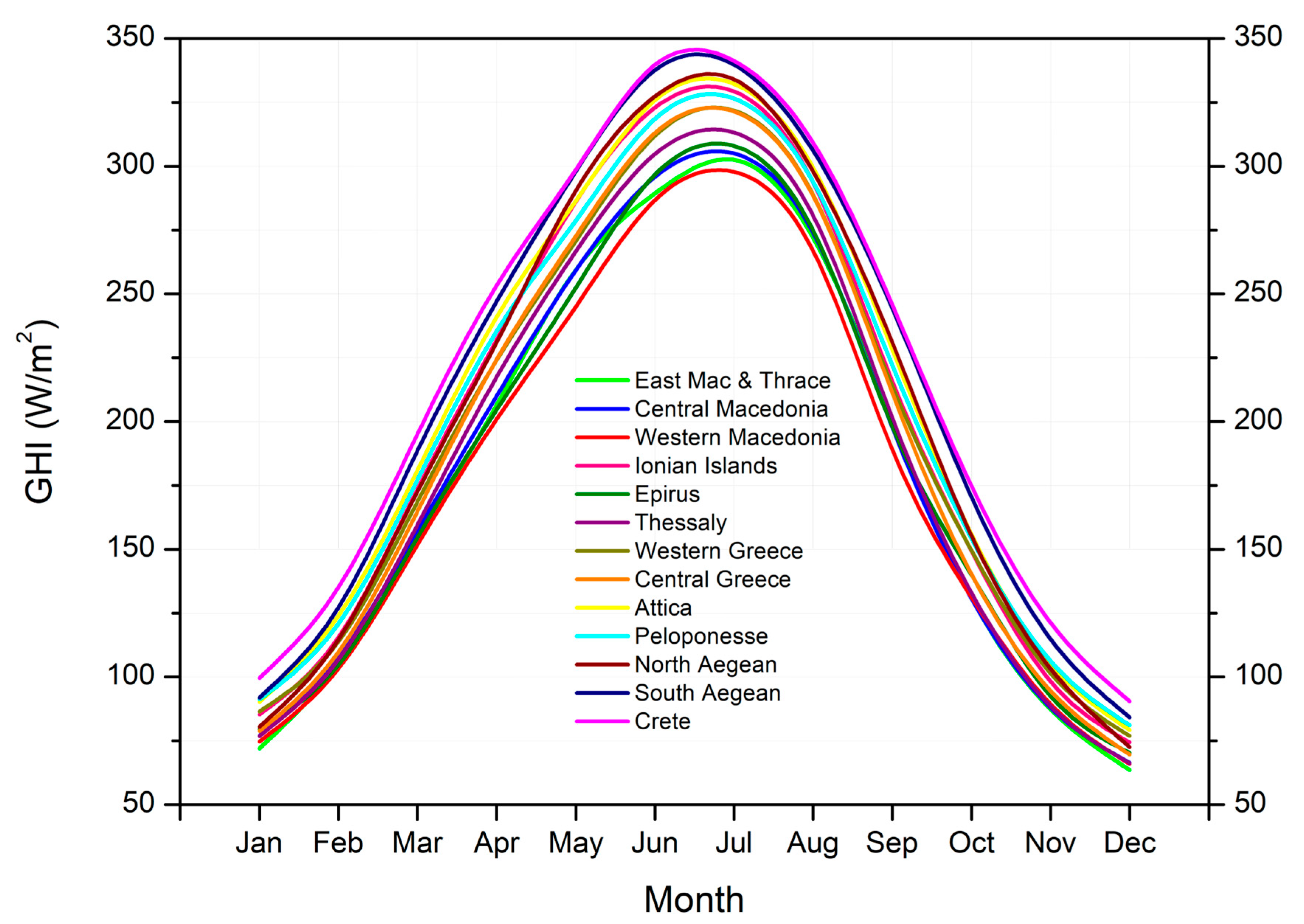
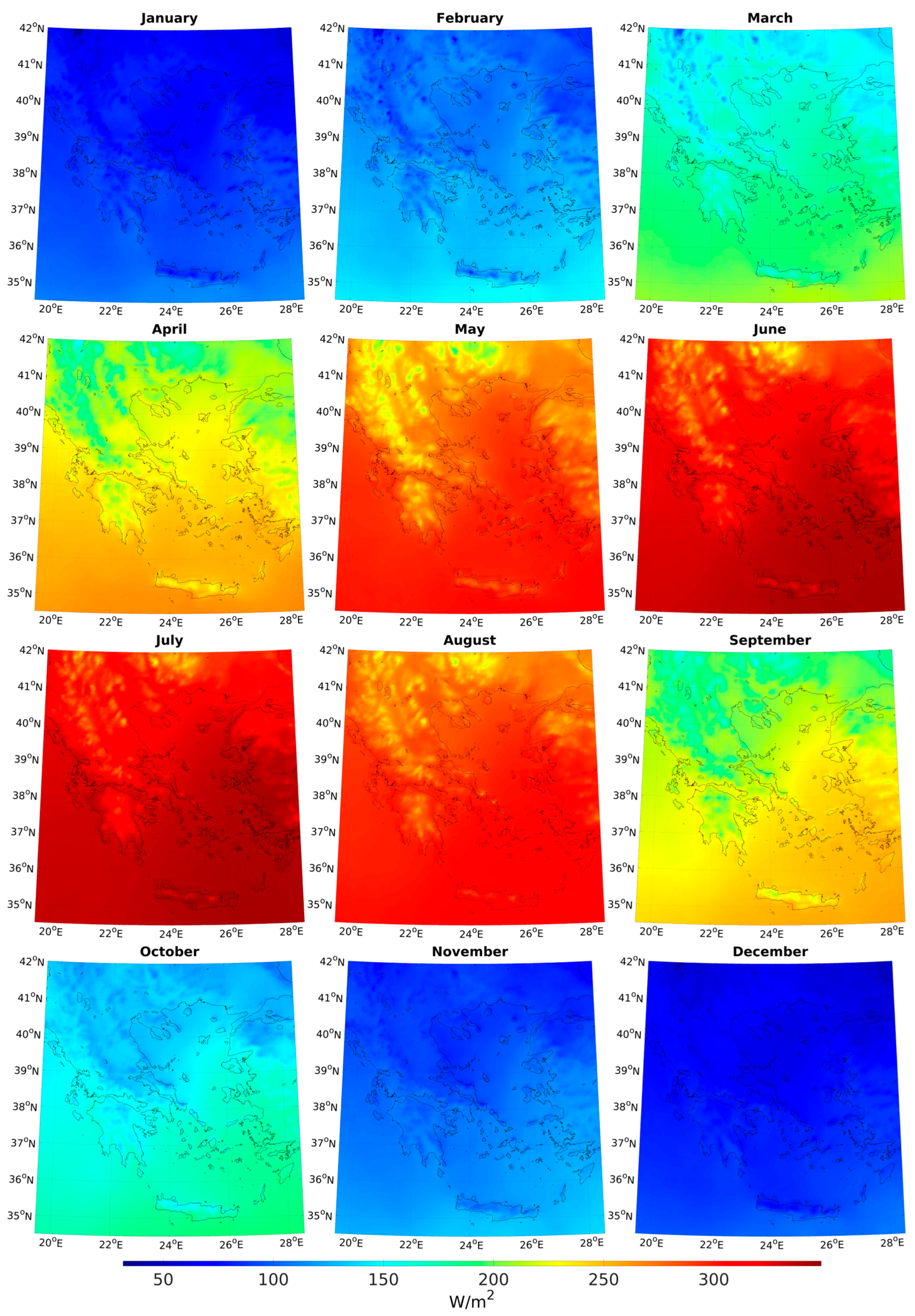
| Rate of Change in GHI (W m−2 month−1) per Greek Region | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| EastMac&Thrc | −0.04 | −0.30 | −0.52 | 1.31 | −1.04 | −1.26 | 0.05 | 0.24 | −0.25 | −0.22 | 0.22 | 0.95 |
| CentrMac | −0.15 | −0.54 | −0.60 | 1.44 | −0.79 | −0.91 | 0.05 | 0.08 | −0.38 | −0.36 | 0.27 | 1.25 |
| WestMac | −0.01 | −0.26 | −0.41 | 1.64 | −0.67 | −1.03 | 0.22 | 0.10 | −0.18 | −0.51 | 0.20 | 1.39 |
| IonianIslands | −0.17 | −0.31 | −0.26 | 1.15 | −0.58 | −0.56 | 0.18 | 0.01 | 0.16 | −0.29 | 0.26 | 1.23 |
| Epirus | −0.28 | −0.19 | −0.36 | 1.47 | −1.14 | −0.93 | 0.08 | 0.15 | 0.00 | −0.24 | 0.26 | 1.37 |
| Thessaly | −0.04 | −0.23 | −0.51 | 1.69 | −0.57 | −1.17 | 0.11 | −0.01 | −0.26 | −0.56 | 0.40 | 1.20 |
| WestGR | −0.04 | 0.10 | −0.46 | 1.52 | −0.64 | −1.10 | 0.02 | −0.01 | 0.00 | −0.75 | 0.45 | 1.26 |
| CentrGR | 0.24 | 0.10 | −0.32 | 2.05 | −0.62 | −1.52 | 0.13 | −0.05 | −0.10 | −0.63 | 0.52 | 1.01 |
| Attica | 0.38 | 0.15 | −0.07 | 1.92 | −0.64 | −1.65 | 0.09 | 0.05 | 0.12 | −0.44 | 0.57 | 0.84 |
| Peloponnese | 0.12 | 0.41 | −0.21 | 1.76 | −0.30 | −1.29 | −0.01 | −0.10 | 0.30 | −0.67 | 0.50 | 1.09 |
| NorthAegean | 0.26 | 0.01 | −0.44 | 1.86 | −0.93 | −1.51 | −0.04 | 0.08 | −0.10 | −0.13 | 0.48 | 0.73 |
| SouthAegean | 0.46 | 0.23 | −0.15 | 1.59 | −0.79 | −1.23 | −0.01 | −0.05 | −0.06 | −0.25 | 0.45 | 0.54 |
| Crete | 0.40 | 0.70 | −0.12 | 1.46 | −0.57 | −1.14 | −0.08 | −0.14 | 0.00 | −0.38 | 0.40 | 0.39 |
| Region | RoC-GHI (W m−2 Year−1) | RoC-PV (kWh Year−1) | Monetary Equivalent (EUR/kWh) | CO2 Equivalent (kg) |
|---|---|---|---|---|
| EastMac&Thrc | −0.88 | −0.96 | −0.05 | −0.67 |
| CentrMac | −0.67 | −0.73 | −0.04 | −0.51 |
| WestMac | 0.46 | 0.51 | 0.03 | 0.35 |
| Epirus | 0.17 | 0.18 | 0.01 | 0.13 |
| IonianIslands | 0.81 | 0.90 | 0.05 | 0.63 |
| Thessaly | 0.05 | 0.06 | 0.00 | 0.04 |
| WestGR | 0.34 | 0.37 | 0.02 | 0.26 |
| CentrGR | 0.80 | 0.88 | 0.05 | 0.62 |
| Attica | 1.31 | 1.44 | 0.08 | 1.00 |
| Peloponnese | 1.59 | 1.75 | 0.09 | 1.20 |
| NorthAegean | 0.27 | 0.29 | 0.02 | 0.21 |
| SouthAegean | 0.73 | 0.80 | 0.04 | 0.56 |
| Crete | 0.92 | 1.01 | 0.05 | 0.71 |
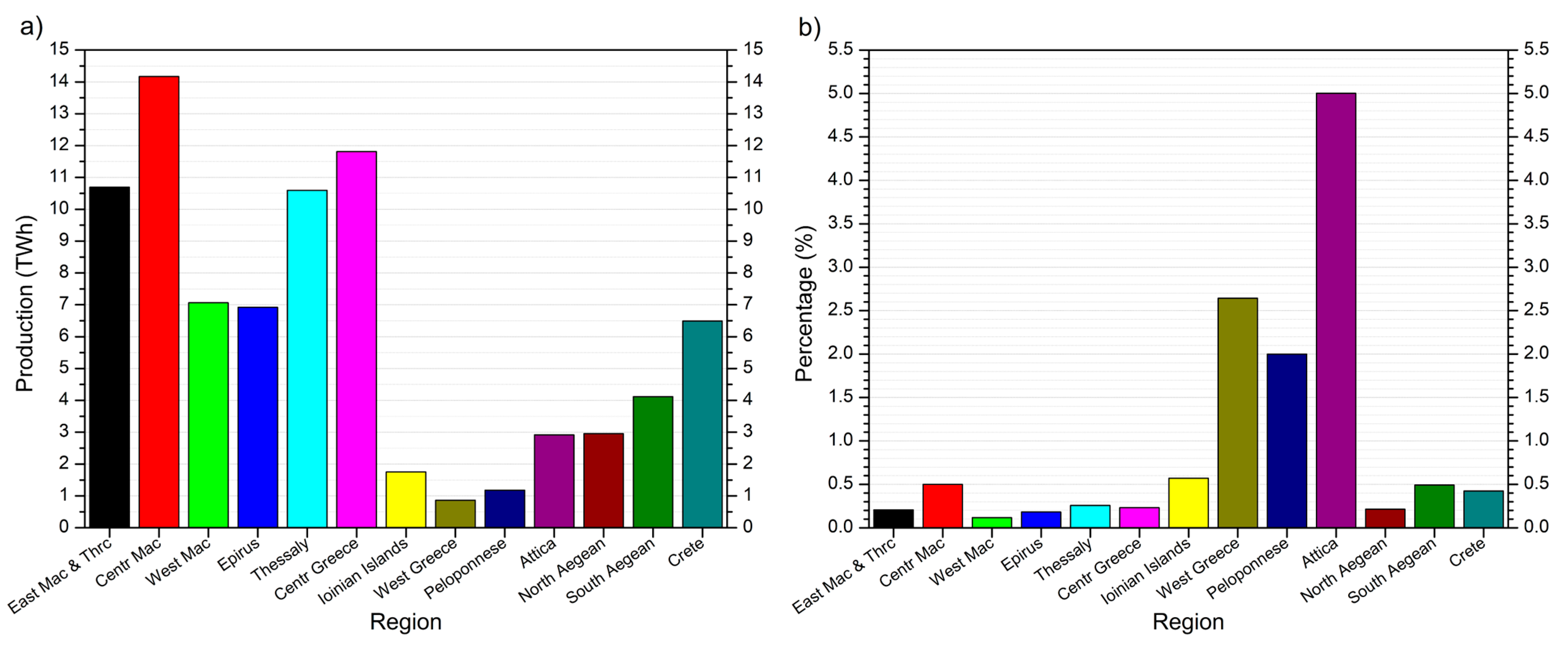
| Region | 5-Year Average Consumption (TWh) | Consumption Trend (GWh/Year) | Energy Adequacy (%) | Earnings (Million EUR) | CO2 Avoided (Mt) |
|---|---|---|---|---|---|
| EastMac&Thrc | 2.2 | −14.2 | 483.3 | 119.5 | 1.55 |
| CentrMac | 7.1 | −152.0 | 200.1 | 382.4 | 4.95 |
| WestMac | 0.8 | −22.1 | 848.2 | 45.0 | 0.58 |
| Epirus | 1.3 | −9.4 | 550.7 | 67.9 | 0.88 |
| IonianIslands | 1.0 | +15.6 | 175.2 | 54.0 | 0.70 |
| Thessaly | 2.7 | −83.3 | 388.2 | 147.4 | 1.91 |
| WestGR | 2.3 | −54.1 | 37.8 | 123.0 | 1.59 |
| CentrGR | 2.7 | −44.0 | 432.4 | 147.6 | 1.91 |
| Attica | 14.6 | −296.9 | 20.0 | 788.8 | 10.20 |
| Peloponnese | 2.4 | −30.3 | 50.0 | 127.4 | 1.65 |
| NorthAegean | 0.6 | −14.6 | 464.5 | 34.4 | 0.44 |
| SouthAegean | 2.0 | +79.1 | 203.1 | 109.5 | 1.42 |
| Crete | 2.7 | +27.4 | 235.8 | 148.7 | 1.92 |
| Region | RoC-GHI (W m−2 Year−1) | RoC-PV (kWh kWp−1 Year−1) | Consumption Trend (GWh Year−1) | 1% PV-Covered Area Energy Adequacy (%) | PV-Covered Area Percentage for Fully Meeting Demand (%) | Earnings (Million EUR | CO2 Emissions Avoided (Mt) |
|---|---|---|---|---|---|---|---|
| EastMac&Thrc | −0.88 | −0.96 | −14.2 | 483.3 | 0.21 | 119.5 | 1.55 |
| CentrMac | −0.67 | −0.73 | −152.0 | 200.1 | 0.50 | 382.4 | 4.95 |
| WestMac | 0.46 | 0.51 | −22.1 | 848.2 | 0.12 | 45.0 | 0.58 |
| Epirus | 0.17 | 0.18 | −9.4 | 550.7 | 0.18 | 67.9 | 0.88 |
| IonianIslands | 0.81 | 0.90 | +15.6 | 175.2 | 0.57 | 54.0 | 0.70 |
| Thessaly | 0.05 | 0.06 | −83.3 | 388.2 | 0.26 | 147.4 | 1.91 |
| WestGR | 0.34 | 0.37 | −54.1 | 37.8 | 2.64 | 123.0 | 1.59 |
| CentrGR | 0.80 | 0.88 | −44.0 | 432.4 | 0.23 | 147.6 | 1.91 |
| Attica | 1.31 | 1.44 | −296.9 | 20.0 | 5.00 | 788.8 | 10.20 |
| Peloponnese | 1.59 | 1.75 | −30.3 | 50.0 | 1.99 | 127.4 | 1.65 |
| NorthAegean | 0.27 | 0.29 | −14.6 | 464.5 | 0.21 | 34.4 | 0.44 |
| SouthAegean | 0.73 | 0.80 | +79.1 | 203.1 | 0.49 | 109.5 | 1.42 |
| Crete | 0.92 | 1.01 | +27.4 | 235.8 | 0.42 | 148.7 | 1.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vigkos, S.; Kosmopoulos, P.G. Mapping Solar Future Perspectives of a Climate Change Hotspot: An In-Depth Study of Greece’s Regional Solar Energy Potential, Climatic Trends Influences and Insights for Sustainable Development. Atmosphere 2025, 16, 762. https://doi.org/10.3390/atmos16070762
Vigkos S, Kosmopoulos PG. Mapping Solar Future Perspectives of a Climate Change Hotspot: An In-Depth Study of Greece’s Regional Solar Energy Potential, Climatic Trends Influences and Insights for Sustainable Development. Atmosphere. 2025; 16(7):762. https://doi.org/10.3390/atmos16070762
Chicago/Turabian StyleVigkos, Stavros, and Panagiotis G. Kosmopoulos. 2025. "Mapping Solar Future Perspectives of a Climate Change Hotspot: An In-Depth Study of Greece’s Regional Solar Energy Potential, Climatic Trends Influences and Insights for Sustainable Development" Atmosphere 16, no. 7: 762. https://doi.org/10.3390/atmos16070762
APA StyleVigkos, S., & Kosmopoulos, P. G. (2025). Mapping Solar Future Perspectives of a Climate Change Hotspot: An In-Depth Study of Greece’s Regional Solar Energy Potential, Climatic Trends Influences and Insights for Sustainable Development. Atmosphere, 16(7), 762. https://doi.org/10.3390/atmos16070762







