Prediction of Atmospheric Bioaerosol Number Concentration Based on PKO–AGA–SVM Fusion Algorithm and Fluorescence Lidar Telemetry
Abstract
1. Introduction
2. Establishment of a Prediction Model for the Number Concentration of Atmospheric Bioaerosols
2.1. Bioaerosol Fluorescence Lidar System
2.2. PKO–AGA–SVM Fusion Algorithm
2.2.1. Support Vector Machine (SVM)
2.2.2. Adaptive Genetic Algorithm (AGA)
2.2.3. Pied Kingfisher Optimizer
3. Establishment of Prediction Model Based on PKO–AGA–SVM Fusion Algorithm
3.1. Data Composition
3.2. Data Processing
3.3. Prediction Model Based on the PKO–AGA–SVM Fusion Algorithm
| PKO–AGA (PKO with Adaptive GA) Input: Popsize 30 Maxiteration 1000 LB, UB [0.1,0.001,[100,10] Dim 2 Fobj Fobj = @(c, g) cross_validation_error(c, g); Output: Best_fitness Best_position Convergence_curve Begin: BF = 8, Crest_angles = Random angle Generating the initial population X = initialization (Popsize, Dim, UB, LB) Calculate the initial fitness Fitness Determine the initial optimal solution Best_position, Best_fitness t = 1 while t <= Maxiteration: # Stage 1: PKO primary search strategy o = exp(− (t/Maxiteration)^2) Exploration/development strategy for implementing PKO generates new solutions X_1 Boundary treatment and updating of stocks # Stage 2: Symbiotic association strategies PE = Linearly decreasing predation efficiency (PEmax→PEmin) Perform symbiotic association strategy to generate new solutions X_1 Boundary treatment and updating of stocks # Phase 3: Adaptive genetic manipulation (new AGA component) GA_prob = max(0.1, 1 − (Best_fitness/max(Fitness))) for each individual i: if rand < GA_prob: Randomly select two parents parent1, parent2 # Crossover operation crossover_point = Random selection of intersections child = [parent1[1:crossover_point], parent2[crossover_point+1:end]] # Mutation operation (with 10% probability) if rand < 0.1: mutation_point = Random selection of variant dimensions child[mutation_point] = LB[mutation_point] + (UB-LB)* rand # Evaluation of offspring fitness_child = Fobj(child) # greed replacement if fitness_child < Fitness[i]: X[i] = child Fitness[i] = fitness_child # Updating the global optimum if fitness_child < Best_fitness: Best_fitness = fitness_child Best_position = child Record the convergence curve Convergence_curve[t] = Best_fitness t += 1 Returns the optimal result End |
4. Atmospheric Bioaerosol Concentration Profile Prediction Experiment
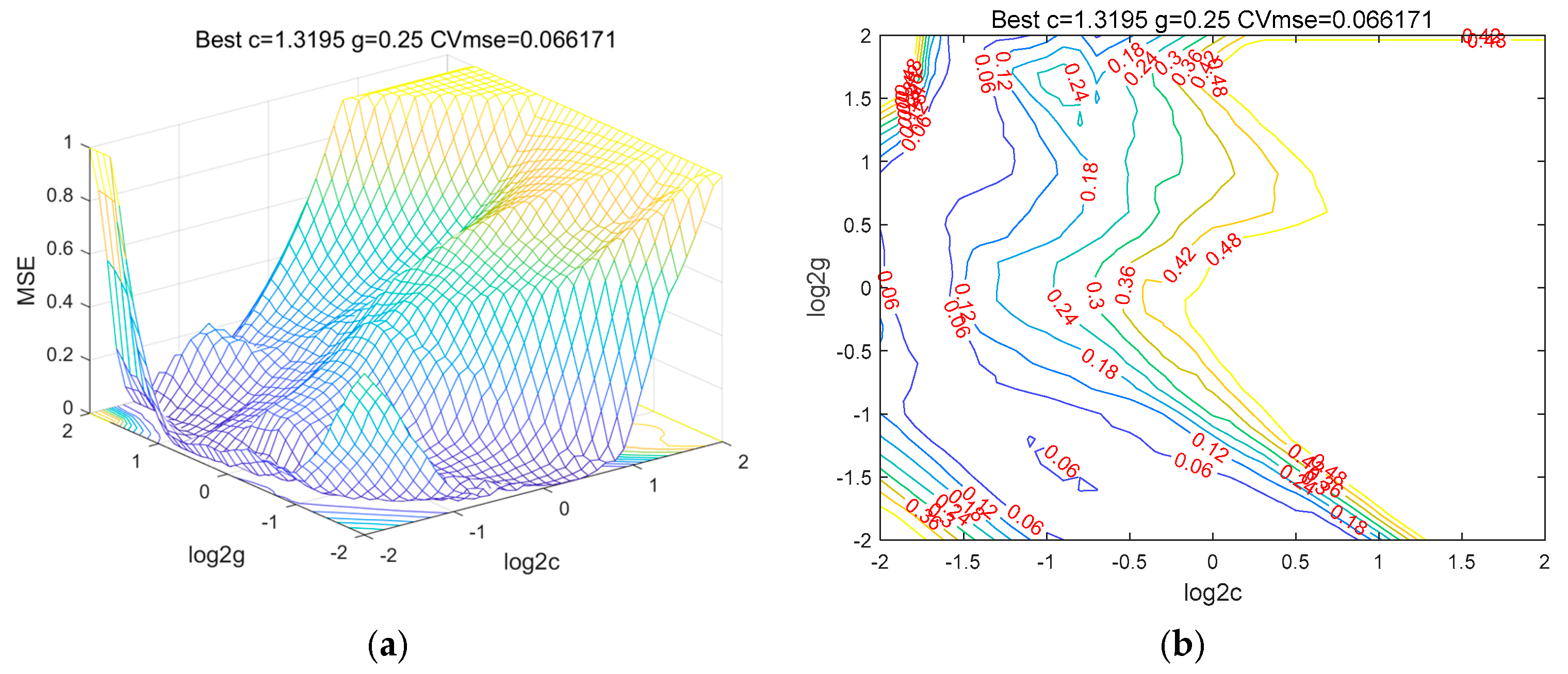
4.1. Automatic Search for Predictive Model Parameters Based on SVM
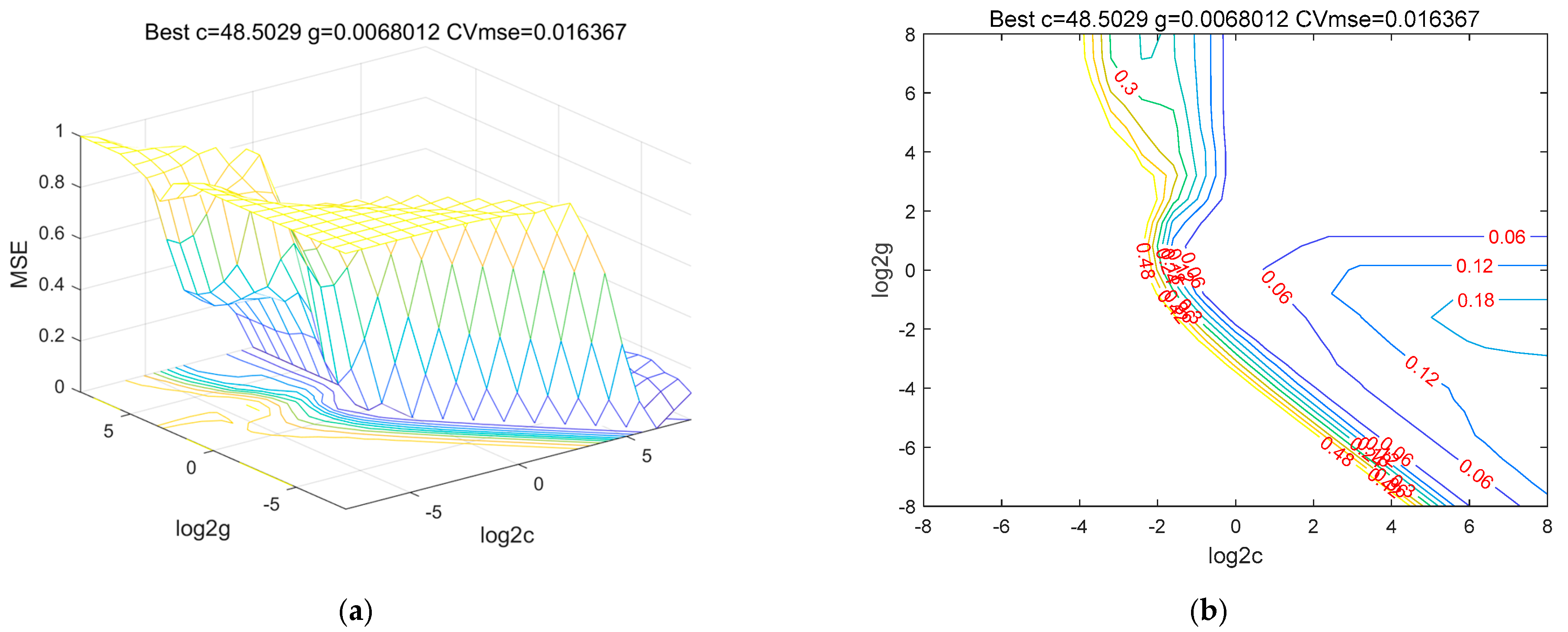
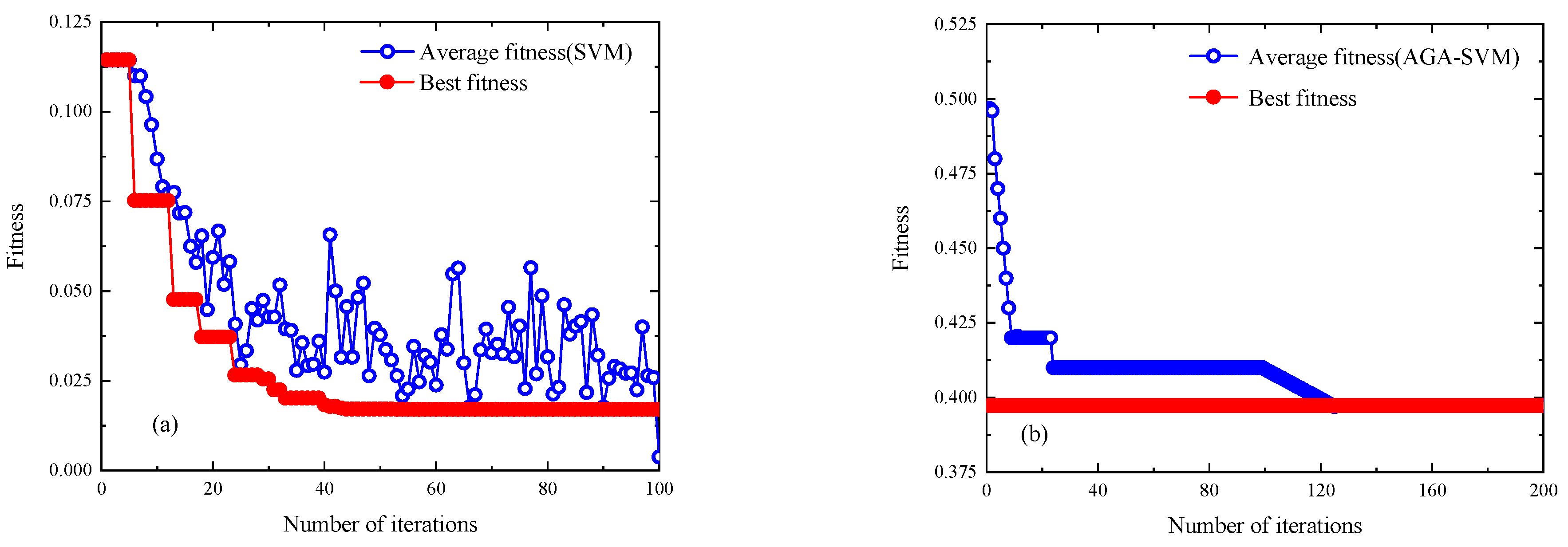
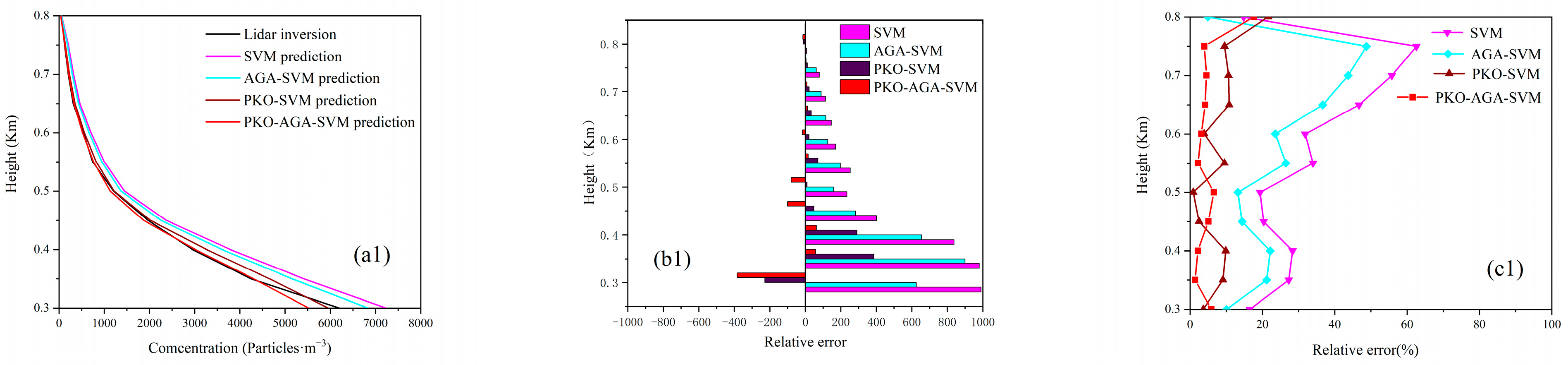
4.2. Predictive Model Optimization
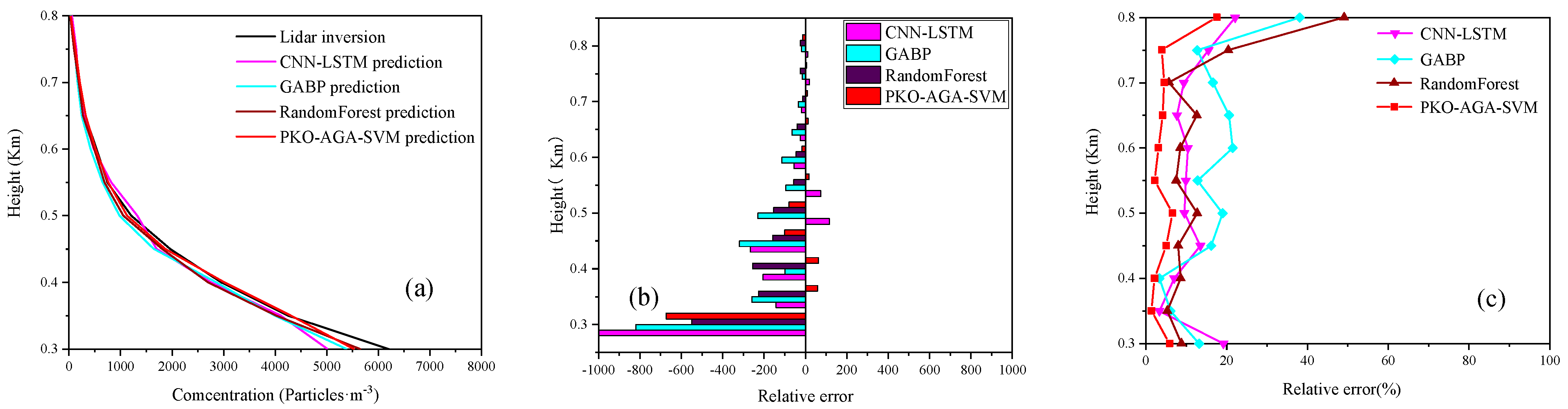
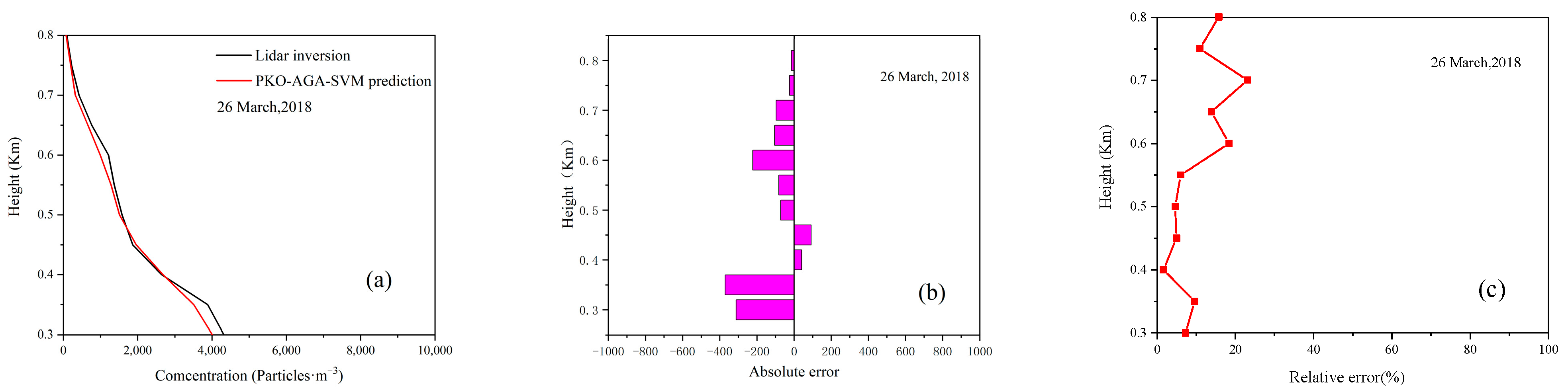
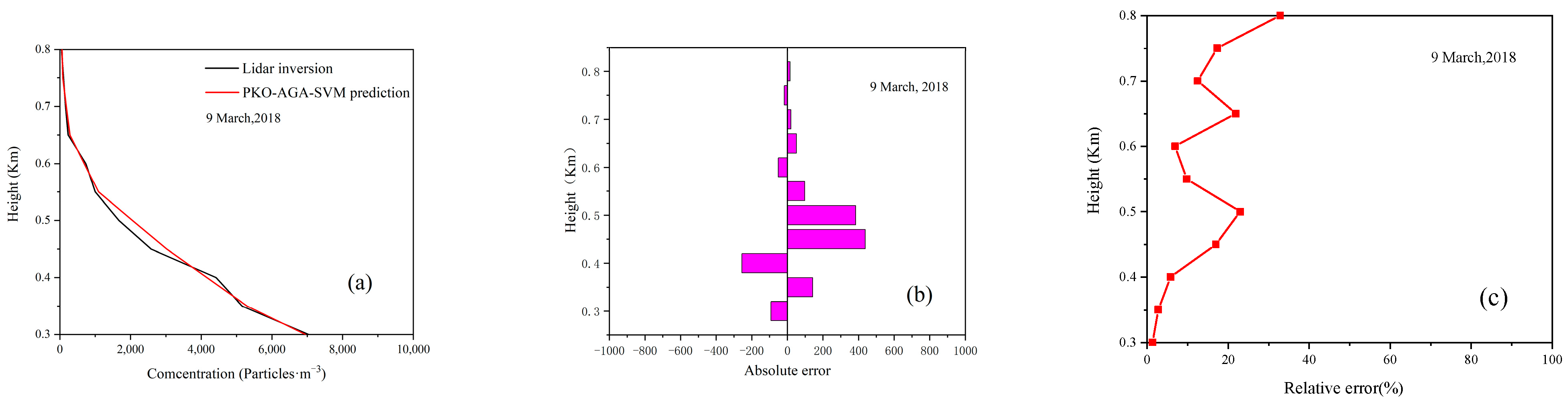
4.3. Model Prediction Accuracy Verification
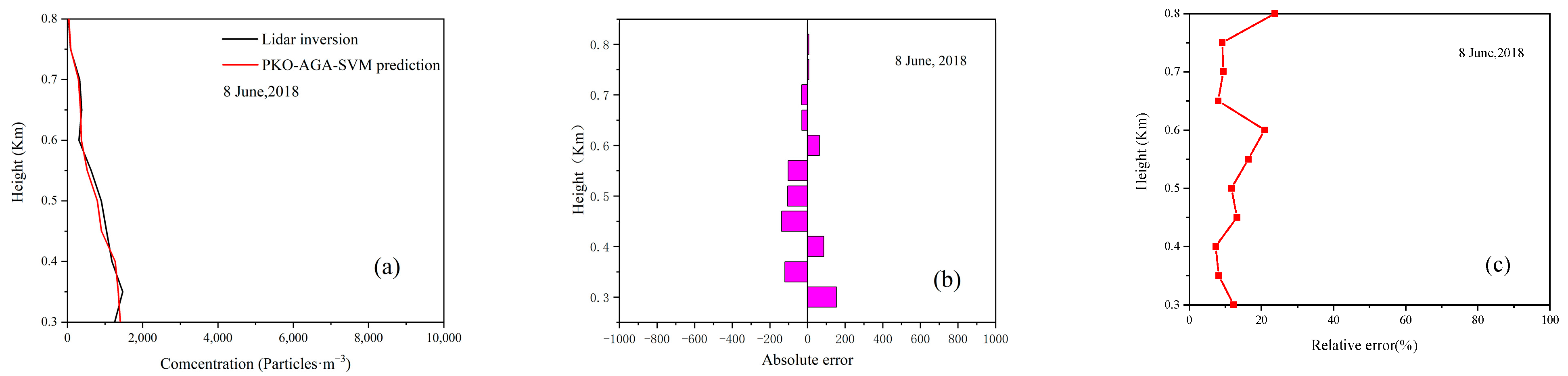
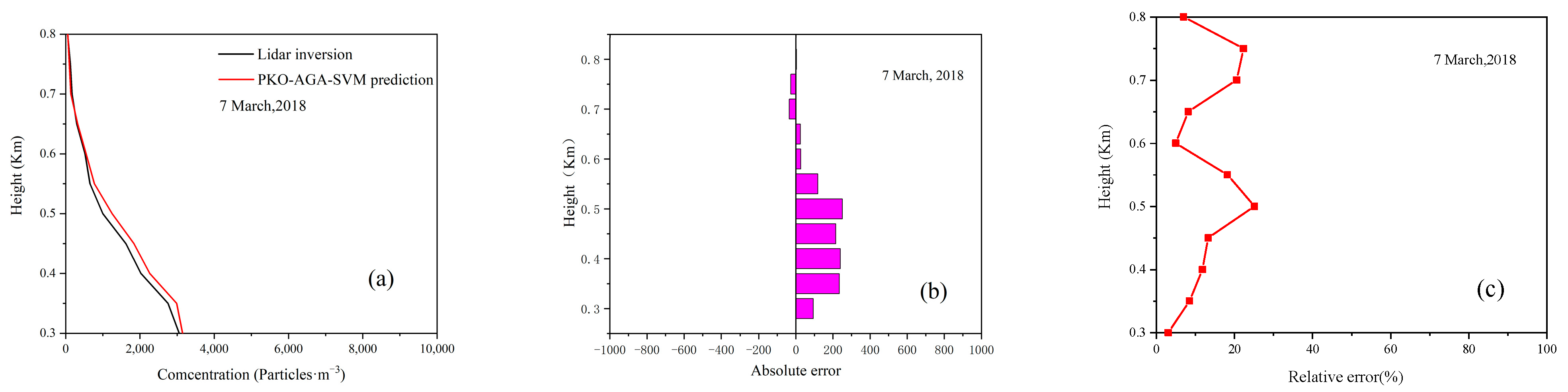
4.4. Model Prediction Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, K.S.; Lee, I.; Lee, J. Synergetic Chemo-Machaon Antimicrobial Puncturable Nanostructures for Efficient Bioaerosol Removal. Biochip J. 2024, 18, 439–452. [Google Scholar] [CrossRef]
- da Silva, J.C.R.; Lopes, M.C.d.S.; Prates, K.V.M.C.; Mantoani, M.C.; Martins, L.D. Characterization of indoor airborne particulate matter and bioaerosols in wood-fired pizzeria kitchens. Discov. Environ. 2024, 2, 107. [Google Scholar] [CrossRef]
- Nasser, N.I.; Al-Hadrawi, M.K.; Oleiwi, S.A.; Mohsin, A.A. The Diversity in Dust Fungal Spores Concentration at Four Districts of Al-Najaf Environment and their Potential Correlation with Asthma. J. Pure Appl. Microbiol. 2019, 13, 273–280. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Zhang, H.; Yao, X.; Zhou, M.; Wang, J.; He, Z.; Zhang, H.; Lou, L.; Mao, W.; et al. Effect of air pollution on the total bacteria and pathogenic bacteria in different sizes of particulate matter. Environ. Pollut. 2018, 233, 483–493. [Google Scholar] [CrossRef]
- Liggio, J.; Li, S.M. Organo sulfate formation during the uptake of pinon aldehyde on acidic sulfate aerosols. Geophys. Res. Lett. 2006, 33, 338–345. [Google Scholar] [CrossRef]
- Li, X.; Cheng, X.; Wu, W.; Wang, Q.; Tong, Z.; Zhang, X.; Deng, D.; Li, Y.; Gao, X. An improved wavelet de-noising-based back propagation neural network model to forecast the bioaerosol concentration. Aerosol Sci. Technol. 2020, 55, 352–360. [Google Scholar] [CrossRef]
- Goudarzi, G.; Birgani, Y.T.; Assarehzadegan, M.-A.; Neisi, A.; Dastoorpoor, M.; Sorooshian, A.; Yazdani, M. Prediction of airborne pollen concentrations by artificial neural network and their relationship with meteorological parameters and air pollutants. J. Environ. Health Sci. Eng. 2022, 20, 251–264. [Google Scholar] [CrossRef]
- Rao, Z.; He, T.; Hua, D.; Wang, Y.; Wang, X.; Chen, Y.; Le, J. Preliminary measurements of fluorescent aerosol number concentrations using a laser-induced fluorescence lidar. Appl. Opt. 2018, 57, 7211–7215. [Google Scholar] [CrossRef]
- Bai, Y.; Ren, P.; Feng, P.; Yan, H.; Li, W. Shift in rhizosphere and endophytic bacterial communities of tomato caused by salinity and grafting. Sci. Total Environ. 2020, 734, 139388. [Google Scholar] [CrossRef]
- Chen, Q.; Mu, Z.; Xu, L.; Wang, M.; Wang, J.; Shan, M.; Fan, X.; Song, J.; Wang, Y.; Lin, P.; et al. Triplet-State Organic Matter in Atmospheric Aerosols: Formation Characteristics and Potential Effects on Aerosol Aging. Atmos. Environ. 2021, 252, 118343. [Google Scholar] [CrossRef]
- Shoshana, O.; Baratz, A. Daytime measurements of Bioaerosol Simulants using a Hyperspectral Laser-Induced Fluorescence LIDAR for Biosphere Research. J. Environ. Chem. Eng. 2020, 8, 104392. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, H.; Ma, Y.; Zhao, P.; Zhou, H.; Li, S.; Wang, X.H. Background noise model of spaceborne photon-counting lidars over oceans and aerosol optical depth retrieval from ICESat-2 noise data. Remote Sens. Environ. 2023, 299, 113858. [Google Scholar] [CrossRef]
- Lin, B.L.; Tokai, A.; Nakanishi, J. Approaches for Establishing Predicted-No-Effect Concentrations for Population-Level Ecological Risk Assessment in the Context of Chemical Substances Management. Environ. Sci. Technol. 2005, 39, 4833. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Takimoto, M.; Tanaka, S.; Futamura, A.; Shimadera, H.; Kondo, A. Developing an Automatic Asbestos Detection Method Based on a Convolutional Neural Network and Support Vector Machine. Appl. Sci. 2024, 14, 9408. [Google Scholar] [CrossRef]
- Pratt, G.C.; Wu, C.Y.; Bock, D.; Adgate, J.L.; Ramachandran, G.; Stock, T.H.; Morandi, M.; Sexton, K. Comparing air dispersion model predictions with measured concentrations of VOCs in urban communities. Environ. Sci. Technol. 2004, 38, 1949–1959. [Google Scholar] [CrossRef]
- Karadurmus, E.; Berber, R. Dynamic Simulation and Parameter Estimation in River Streams. Environ. Technol. 2004, 25, 471–479. [Google Scholar] [CrossRef]
- Halteh, K.; AlKhoury, R.; Ziadat, S.A.; Gepp, A.; Kumar, K. Using machine learning techniques to assess the financial impact of the COVID-19 pandemic on the global aviation industry. Transp. Res. Interdiscip. Perspect. 2024, 24, 101043. [Google Scholar] [CrossRef]
- Salawu, S.; He, Y.; Lumsden, J. Approaches to automated detection of cyberbullying: A survey. IEEE Trans. Affect. Comput. 2017, 11, 3–24. [Google Scholar] [CrossRef]
- Lee, J.; Kang, S. GA based meta-modeling of BPN architecture for constrained approximate optimization. Int. J. Solids Struct. 2007, 44, 5980–5993. [Google Scholar] [CrossRef]
- Akin, P. A new hybrid approach based on genetic algorithm and support vector machine methods for hyperparameter optimization in synthetic minority over-sampling technique (SMOTE). Aims Math. 2023, 8, 9400–9415. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 2002, 24, 656–667. [Google Scholar] [CrossRef]
- Mak, K.L.; Wong, Y.S.; Wang, X.X. An Adaptive Genetic Algorithm for Manufacturing Cell Formation. Int. J. Adv. Manuf. Technol. 2000, 16, 491–497. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Siu, S.W.I.; Song, W.; Guan, S.S.-U. Adaptive Incremental Genetic Algorithm for Task Scheduling in Cloud Environments. Symmetry 2018, 10, 168. [Google Scholar] [CrossRef]
- Park, S.S.; Kim, J.H. Possible sources of two size-resolved water-soluble organic carbon fractions at a roadway site during fall season. Atmos. Environ. 2014, 94, 134–143. [Google Scholar] [CrossRef]
- Guo, H.; Ling, Z.; Cheung, K.; Wang, D.; Simpson, I.; Blake, D. Acetone in the atmosphere of Hong Kong: Abundance, sources and photochemical precursors. Atmos. Environ. 2013, 65, 80–88. [Google Scholar] [CrossRef]
- Giuliani, C.; Biggs, D.; Nguyen, T.T.; Marasco, E.; De Fanti, S.; Garagnani, P.; Le Phan, M.T.; Nguyen, V.N.; Luiselli, D.; Romeo, G. First evidence of association between past environmental exposure to dioxin and DNA methylation of CYP1A1 and IGF2 genes in present day Vietnamese population. Environ. Pollut. 2018, 242, 976–985. [Google Scholar] [CrossRef]
- Srivastava, A.N. Data Mining: Concepts, Models, Methods, and Algorithms. ASME J. Comput. Inf. Sci. Eng. 2005, 5, 394–395. [Google Scholar] [CrossRef]

| Definition | Reference Value |
|---|---|
| Pulse energy | 60 mJ |
| Field of view of the telescope | 0.5 mrad |
| Quantum efficiency of the PMT | 0.2 |
| Transmission of the receiving optical train | 0.3 |
| Filter bandwidth | 10 nm |
| Diameter of the telescope | 25 cm |
| Laser wavelength | 266 nm |
| Fluorescence wavelength | 300~460 nm |
| Pulse repetition frequency | 10 Hz |
| Detector frequency bandwidth | 5 Mz |
| Effective cross-sectional area for the fluorescence inelastic scattering | 10−12 cm2 sr−1 nm−1 |
| Reception efficiency of the entire optical system for the fluorescence wavelength | 0.3 |
| Input/Output | Input Parameter Number | Variant |
|---|---|---|
| 1 | PM2.5 | |
| 2 | PM10 | |
| 3 | CO | |
| 4 | NO2 | |
| Input | 5 | O3 |
| 6 | SO2 | |
| 7 | Temperature | |
| 8 | Humidity | |
| 9 | Wind speed | |
| Output | 1~11 | Bioaerosol concentrations at different hights |
| Serial Number | Mean Relative Error (%) | |||
|---|---|---|---|---|
| SVM | AGA–SVM | PKO–SVM | PKO–AGA–SVM | |
| 1 | 25.79 | 20.75 | 16.93 | 11.57 |
| 2 | 27.45 | 22.10 | 18.20 | 12.8 |
| 3 | 26.9 | 21.3 | 17.5 | 12.1 |
| 4 | 29.8 | 24.5 | 19.6 | 13.4 |
| 5 | 24.3 | 19.8 | 15.7 | 10.9 |
| Algorithm | Standard Deviation | Mean Values (%) | Confidence Interval (%) |
|---|---|---|---|
| SVM | 2.04 | 26.848 | 24.31–29.39 |
| AGA–SVM | 1.59 | 21.69 | 19.48–23.90 |
| PKO–SVM | 1.317 | 17.786 | 16.716–18.856 |
| PKO–AGA–SVM | 1.0078 | 12.35 | 11.106–13.594 |
| Percentage of Data | SVM (%) | AGA–SVM (%) | PKO–SVM (%) | PKO–AGA–SVM (%) |
|---|---|---|---|---|
| 100 | 25.79 | 20.75 | 16.93 | 11.57 |
| 80 | 28.15 | 22.18 | 17.82 | 12.44 |
| 60 | 31.02 | 23.95 | 19.17 | 13.61 |
| 40 | 33.35 | 24.62 | 20.01 | 14.07 |
| Times | SVM | AGA–SVM | PKO–SVM | PKO–AGA–SVM |
|---|---|---|---|---|
| 1 | 4 | 3 | 2 | 1 |
| 2 | 4 | 3 | 2 | 1 |
| 3 | 4 | 3 | 2 | 1 |
| 4 | 4 | 3 | 2 | 1 |
| 5 | 4 | 3 | 2 | 1 |
| Percentage of Data | SVM (%) | AGA–SVM (%) | PKO–SVM (%) | PKO–AGA–SVM (%) |
|---|---|---|---|---|
| Heavily polluted weather data 70%, remaining 30% | 31.5 | 25.76 | 19.55 | 13.01 |
| Lightly polluted weather data 70%, remaining 30% | 29.6 | 23.62 | 18.53 | 12.75 |
| Optimization Algorithm | Mean Relative Error (%) |
|---|---|
| PKO–AGA–SVM | 9.13 |
| CNN–LSTM | 12.4 |
| Random forest | 14.6 |
| GABP | 13.8 |
| Optimization Algorithm | Mean Relative Error (%) |
|---|---|
| SVM | 25.79 |
| AGA–SVM | 20.75 |
| PKO–SVM | 16.93 |
| PKO–AGA–SVM | 11.57 |
| Weather Conditions | Mean Relative Error (%) |
|---|---|
| Excellent | 12.75 |
| Good | 13.01 |
| Mildly polluted | 10.51 |
| Moderately pollution | 11.72 |
| Heavily polluted | 11.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, Z.; Li, Y.; Mao, J.; Zhao, H.; Gong, X. Prediction of Atmospheric Bioaerosol Number Concentration Based on PKO–AGA–SVM Fusion Algorithm and Fluorescence Lidar Telemetry. Atmosphere 2025, 16, 638. https://doi.org/10.3390/atmos16060638
Rao Z, Li Y, Mao J, Zhao H, Gong X. Prediction of Atmospheric Bioaerosol Number Concentration Based on PKO–AGA–SVM Fusion Algorithm and Fluorescence Lidar Telemetry. Atmosphere. 2025; 16(6):638. https://doi.org/10.3390/atmos16060638
Chicago/Turabian StyleRao, Zhimin, Yicheng Li, Jiandong Mao, Hu Zhao, and Xin Gong. 2025. "Prediction of Atmospheric Bioaerosol Number Concentration Based on PKO–AGA–SVM Fusion Algorithm and Fluorescence Lidar Telemetry" Atmosphere 16, no. 6: 638. https://doi.org/10.3390/atmos16060638
APA StyleRao, Z., Li, Y., Mao, J., Zhao, H., & Gong, X. (2025). Prediction of Atmospheric Bioaerosol Number Concentration Based on PKO–AGA–SVM Fusion Algorithm and Fluorescence Lidar Telemetry. Atmosphere, 16(6), 638. https://doi.org/10.3390/atmos16060638





