Improvements in Turbulent Jet Particle Dispersion Modeling and Its Validation with DNS
Abstract
1. Introduction
- Mimicking the statistical velocity fluctuations of URANS simulations via the exponential smoothing of DNS fields using real-time time averaging;
- Modifying an existing particle dispersion model by limiting the particle displacement within an eddy with respect to its size;
- Validating the particle trajectories predicted with the new model by comparing them with those of a DNS.
2. Methodology
2.1. Simulation Setup and DNS Fields
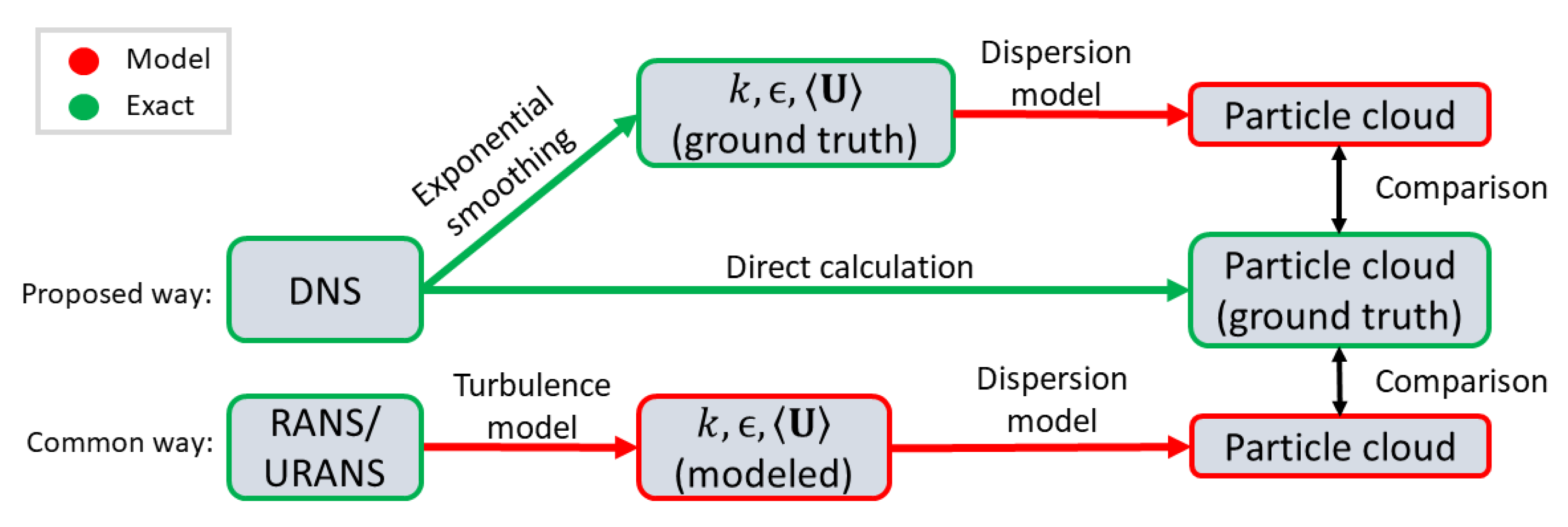
2.2. Overview of the Validation Method
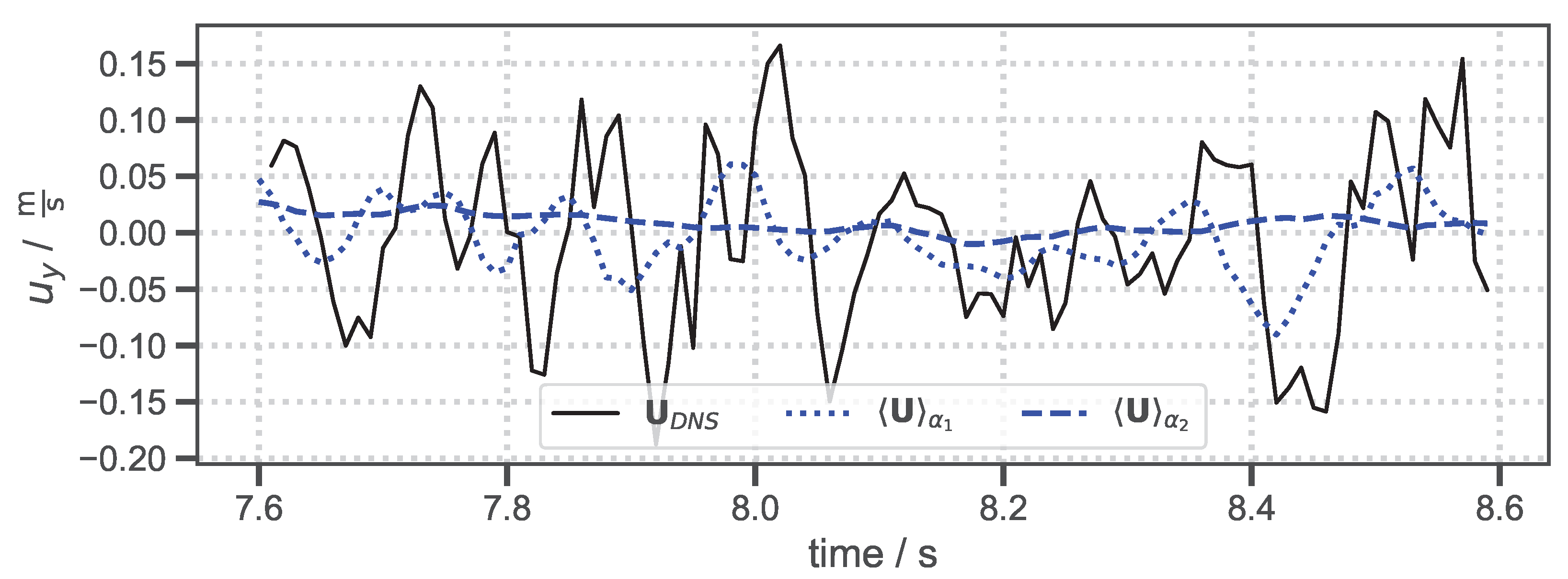
2.3. Time-Averaging of DNS Velocity Field
2.4. Particle Dynamics and Dispersion Models
New Eddy Interaction Time
2.5. Test Cases
2.6. Evaluation Methods for Particle Dispersion
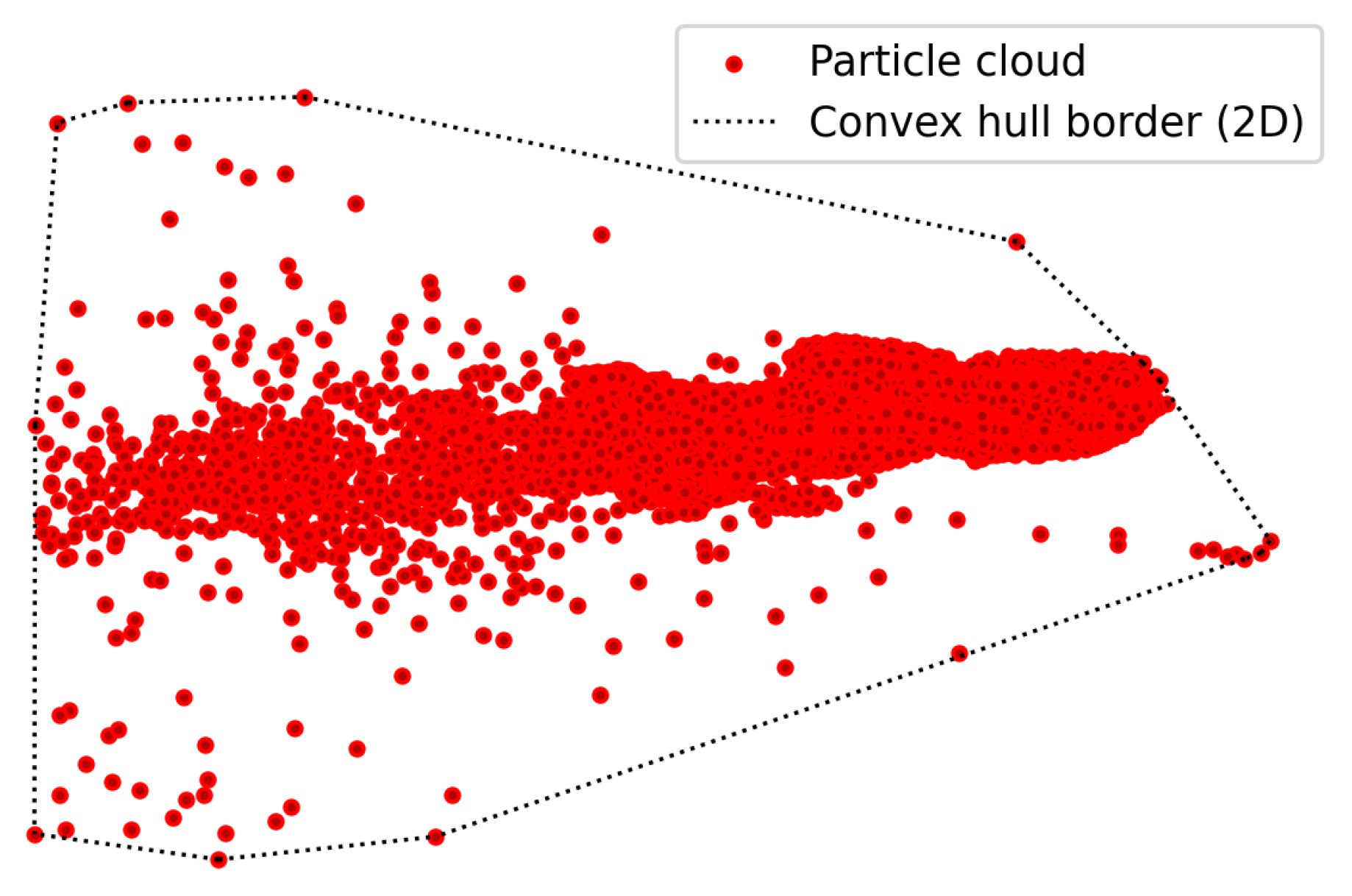
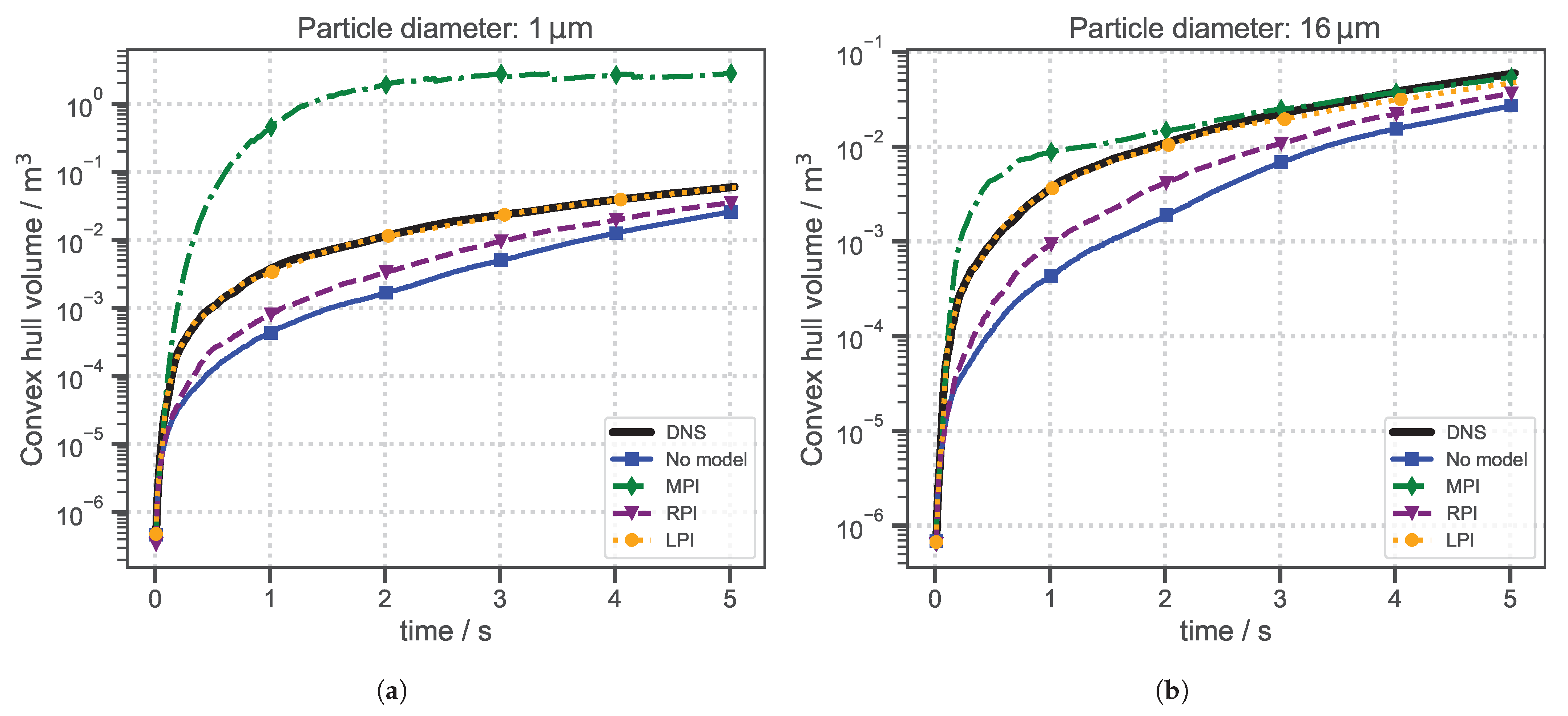
2.6.1. Convex Hull
2.6.2. Mean Square Distance
2.6.3. Particle Concentration
3. Results and Discussion
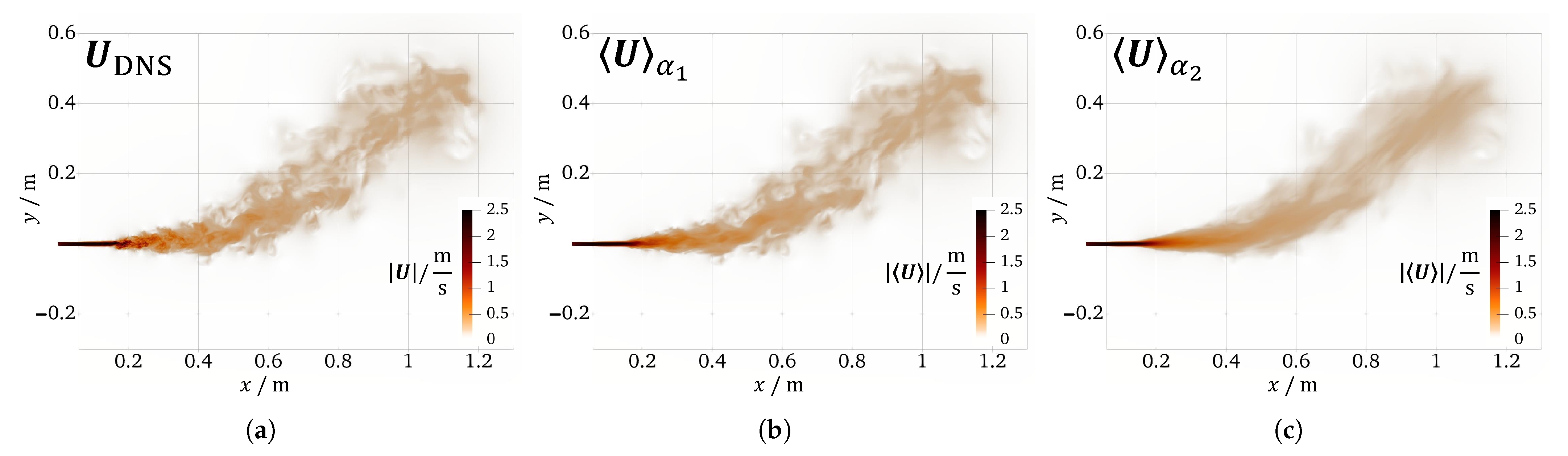
3.1. Comparison of Mean Velocity Fields
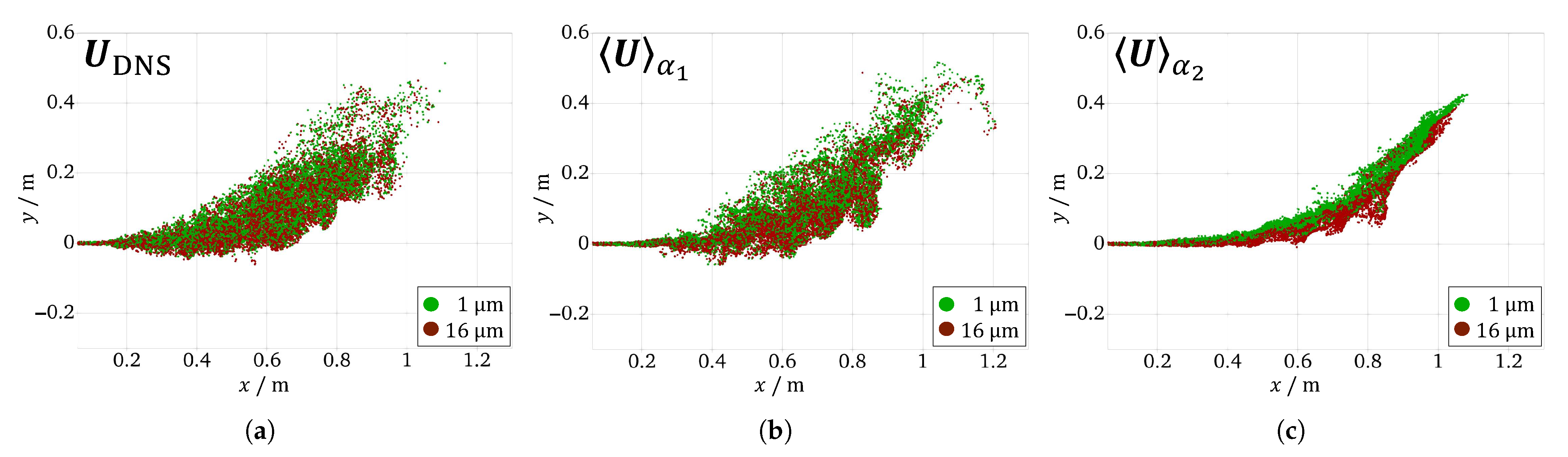
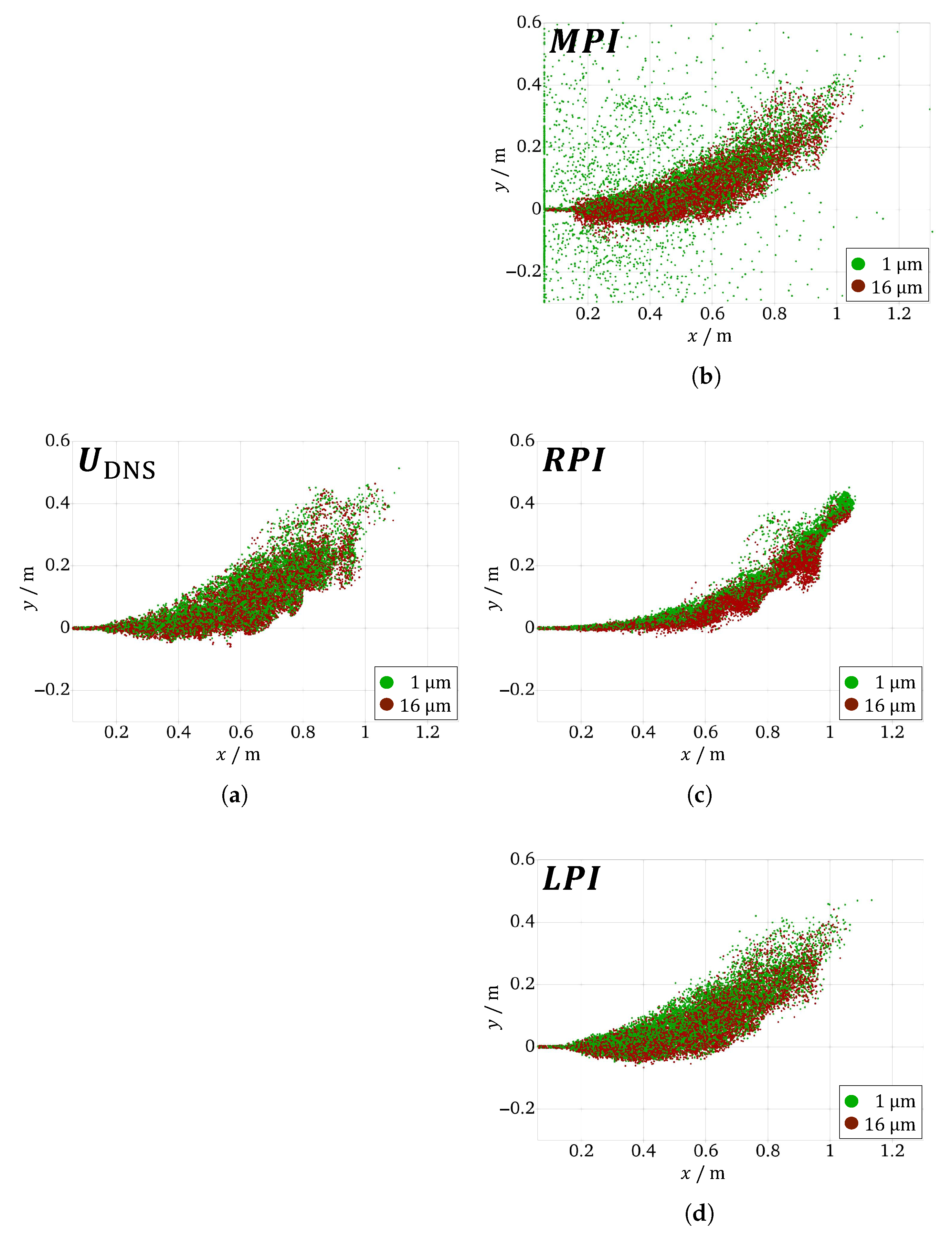
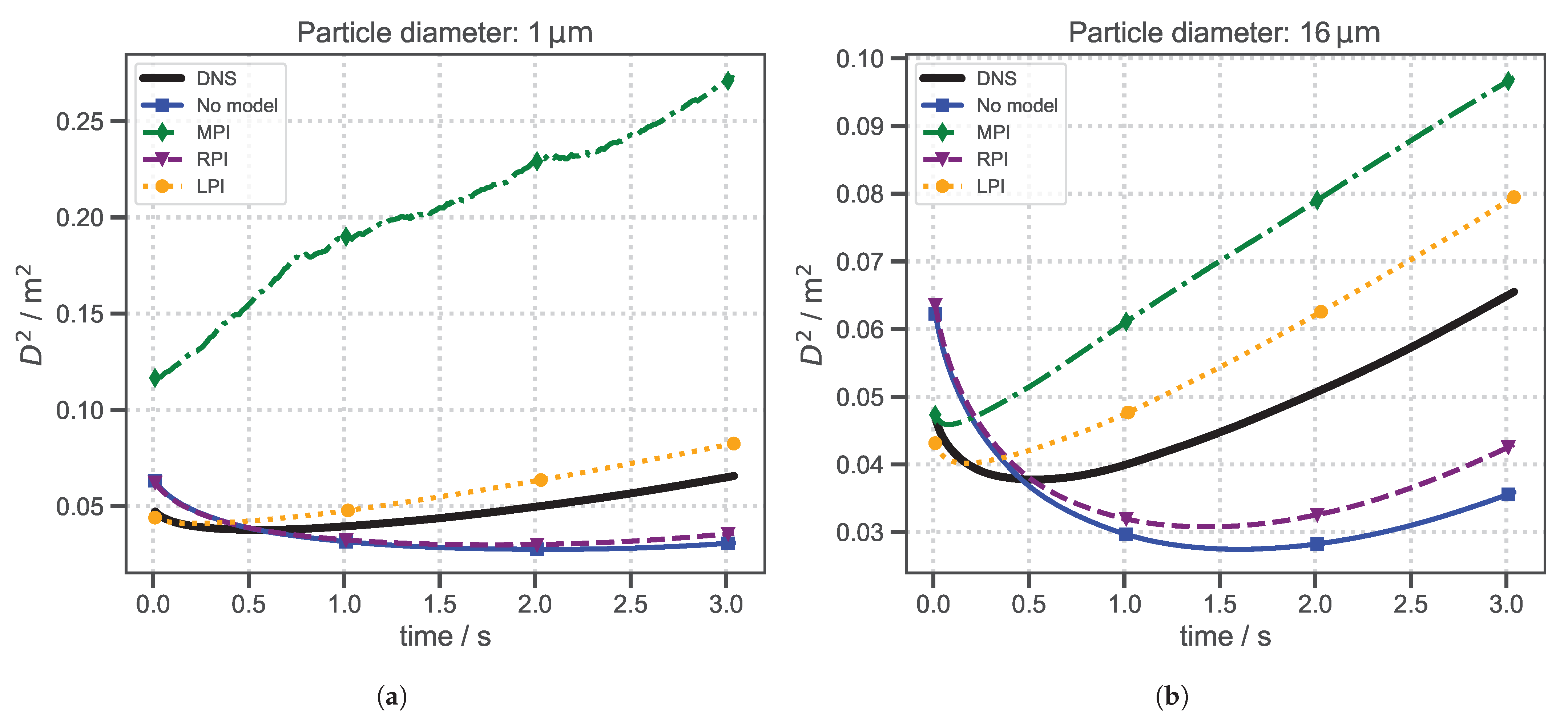
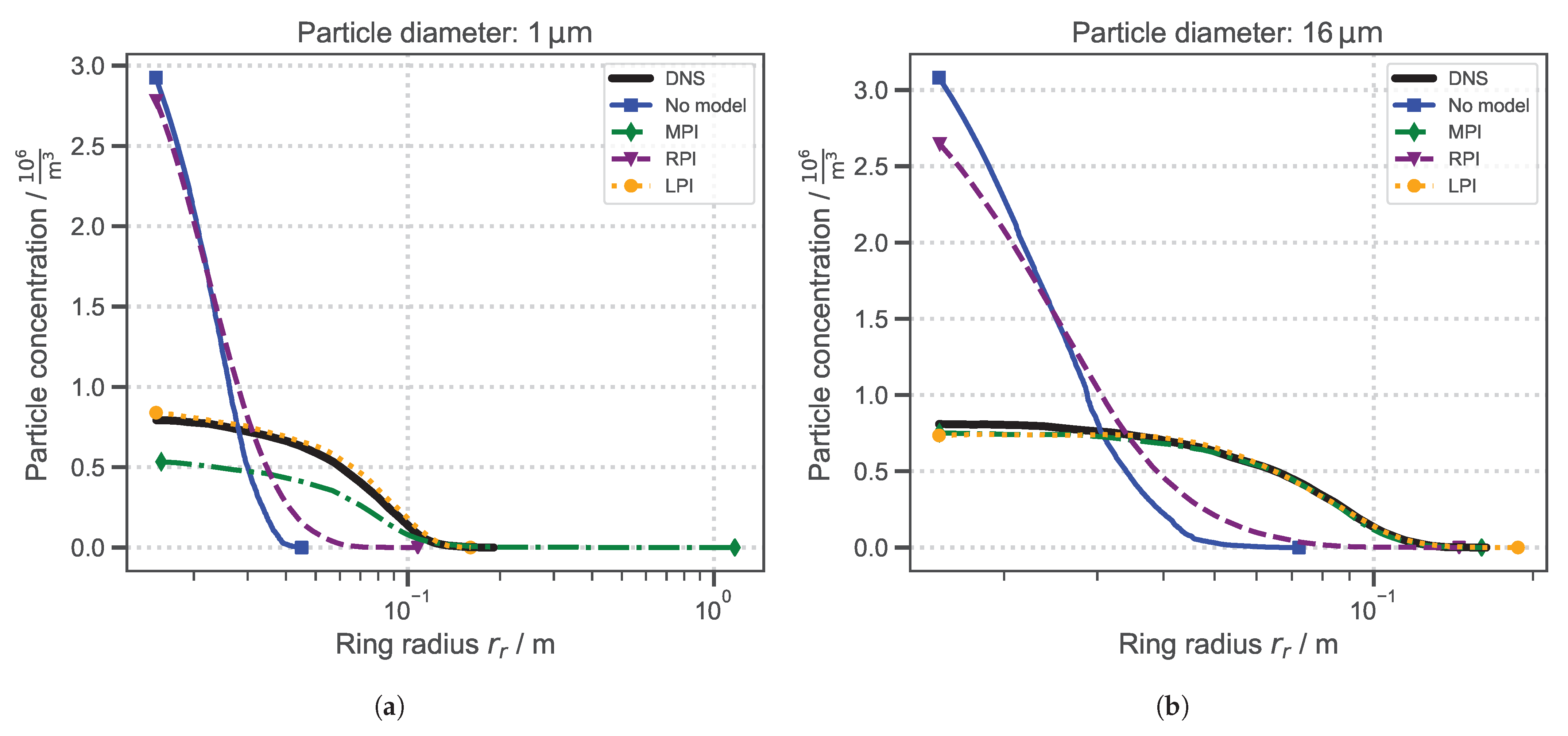
3.2. Comparison of Particle Dispersion
- Exponential smoothing is a viable, memory-efficient alternative to the conventional running average when processing DNS fields.
- Applying particle dispersion models to time-averaged DNS flow fields allows independent validation, free from secondary errors introduced by turbulence modeling or measurement uncertainty.
- The exponential smoothing approach allows us to validate arbitrary particle sizes under arbitrary flow conditions, overcoming the limitations of typical experimental setups.
- The particle dispersion model currently implemented in OpenFOAM® (MPI) performs satisfactorily for larger particles (≥16m, ). However, it shows erratic behavior for smaller diameters. This may be due to a lack of validation at low Stokes numbers—especially those relevant for virus-laden aerosols.
- The proposed model with the limited eddy interaction time (LPI) successfully suppresses erratic particle trajectories and outperforms both the randomized particle–eddy interaction time (RPI) and the mean particle–eddy interaction time (MPI) models in any of the dispersion evaluation methods applied. Due to its straightforward implementation and proven effectiveness in the turbulent jet configuration, this model could be particularly useful for researchers investigating particle-laden flows in respiratory or similar jet-like applications.
3.3. Limitations and Assumptions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dupont, S.; Brunet, Y.; Jarosz, N. Eulerian modelling of pollen dispersal over heterogeneous vegetation canopies. Agric. For. Meteorol. 2006, 141, 82–104. [Google Scholar] [CrossRef]
- Batmaz, E.; Schmeling, D.; Wagner, C. DNS–URANS comparison study on cough-induced flow and particles in a large-scale circulation. Int. J. Numer. Methods Heat Fluid Flow, 2025. [Google Scholar] [CrossRef]
- Rosti, M.E.; Cavaiola, M.; Olivieri, S.; Seminara, A.; Mazzino, A. Turbulence role in the fate of virus-containing droplets in violent expiratory events. Phys. Rev. Res. 2021, 3, 013091. [Google Scholar] [CrossRef]
- Huilier, D.G.F. An Overview of the Lagrangian Dispersion Modeling of Heavy Particles in Homogeneous Isotropic Turbulence and Considerations on Related LES Simulations. Fluids 2021, 6, 145. [Google Scholar] [CrossRef]
- API Guide: OpenFOAM® v2406. Available online: https://api.openfoam.com/2406/ (accessed on 17 March 2025).
- Zhang, X.; Tian, Z.F.; Chinnici, A.; Zhou, H.; Nathan, G.J.; Chin, R.C. Particle dispersion model for RANS simulations of particle-laden jet flows, incorporating Stokes number effects. Adv. Powder Technol. 2024, 35, 104345. [Google Scholar] [CrossRef]
- Gardner, E.S. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Gardner, E.S. Exponential smoothing: The state of the art—Part II. Int. J. Forecast. 2006, 22, 637–666. [Google Scholar] [CrossRef]
- Cahuzac, A.; Boudet, J.; Borgnat, P.; Lévêque, E. Smoothing algorithms for mean-flow extraction in large-eddy simulation of complex turbulent flows. Phys. Fluids 2010, 22, 125104. [Google Scholar] [CrossRef]
- Gray, D.D.; Giorgini, A. The validity of the boussinesq approximation for liquids and gases. Int. J. Heat Mass Transf. 1976, 19, 545–551. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical Solution of the Navier-Stokes Equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Kath, C.; Wagner, C. Highly Resolved Simulations of Turbulent Mixed Convection in a Vertical Plane Channel. New Results Numer. Exp. Fluid Mech. X 2016, 132, 515–524. [Google Scholar] [CrossRef]
- Shishkina, O.; Wagner, C. Stability conditions for the Leapfrog-Euler scheme with central spatial discretization of any order. Appl. Numer. Anal. Comput. Math. 2004, 1, 315–326. [Google Scholar] [CrossRef]
- Gupta, J.K.; Lin, C.H.; Chen, Q. Characterizing exhaled airflow from breathing and talking. Indoor Air 2010, 20, 31–39. [Google Scholar] [CrossRef]
- Dekker, E. Transition between laminar and turbulent flow in human trachea. J. Appl. Physiol. 1961, 16, 1060–1064. [Google Scholar] [CrossRef]
- Poletto, R.; Craft, T.; Revell, A. A New Divergence Free Synthetic Eddy Method for the Reproduction of Inlet Flow Conditions for LES. Flow, Turbul. Combust. 2013, 91, 519–539. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Snyder, W.H.; Lumley, J.L. Some measurements of particle velocity autocorrelation functions in a turbulent flow. J. Fluid Mech. 1971, 48, 41–71. [Google Scholar] [CrossRef]
- Amsden, A.A.; O’Rourke, P.J.; Butler, T.D. KIVA-II: A Computer Program for Chemically Reactive Flows with Sprays; Technical Report LA-11560-MS, 6228444; Los Alamos National Laboratory: Los Alamos, NM, USA, 1989. [Google Scholar] [CrossRef]
- Gosman, A.D.; Loannides, E. Aspects of Computer Simulation of Liquid-Fueled Combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- O’Rourke, P.J. Statistical properties and numerical implementation of a model for droplet dispersion in a turbulent gas. J. Comput. Phys. 1989, 83, 345–360. [Google Scholar] [CrossRef]
- Shuen, J.S.; Chen, L.D.; Faeth, G.M. Evaluation of a stochastic model of particle dispersion in a turbulent round jet. AIChE J. 1983, 29, 167–170. [Google Scholar] [CrossRef]
- Shuen, J.S.; Solomon, A.S.P.; Zhang, Q.F.; Faeth, G.M. Structure of particle-laden jets—Measurements and predictions. AIAA J. 1985, 23, 396–404. [Google Scholar] [CrossRef]
- Dehbi, A. Turbulent particle dispersion in arbitrary wall-bounded geometries: A coupled CFD-Langevin-equation based approach. Int. J. Multiph. Flow 2008, 34, 819–828. [Google Scholar] [CrossRef]
- Mito, Y.; Hanratty, T.J. Use of a Modified Langevin Equation to Describe Turbulent Dispersion of Fluid Particles in a Channel Flow. Flow Turbul. Combust. 2002, 68, 1–26. [Google Scholar] [CrossRef]
- Alsved, M.; Nygren, D.; Thuresson, S.; Fraenkel, C.J.; Medstrand, P.; Löndahl, J. Size distribution of exhaled aerosol particles containing SARS-CoV-2 RNA. Infect. Dis. 2023, 55, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Coleman, K.K.; Tay, D.J.W.; Tan, K.S.; Ong, S.W.X.; Than, T.S.; Koh, M.H.; Chin, Y.Q.; Nasir, H.; Mak, T.M.; Chu, J.J.H.; et al. Viral Load of Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) in Respiratory Aerosols Emitted by Patients With Coronavirus Disease 2019 (COVID-19) While Breathing, Talking, and Singing. Clin. Infect. Dis. Off. Publ. Infect. Dis. Soc. Am. 2022, 74, 1722–1728. [Google Scholar] [CrossRef]
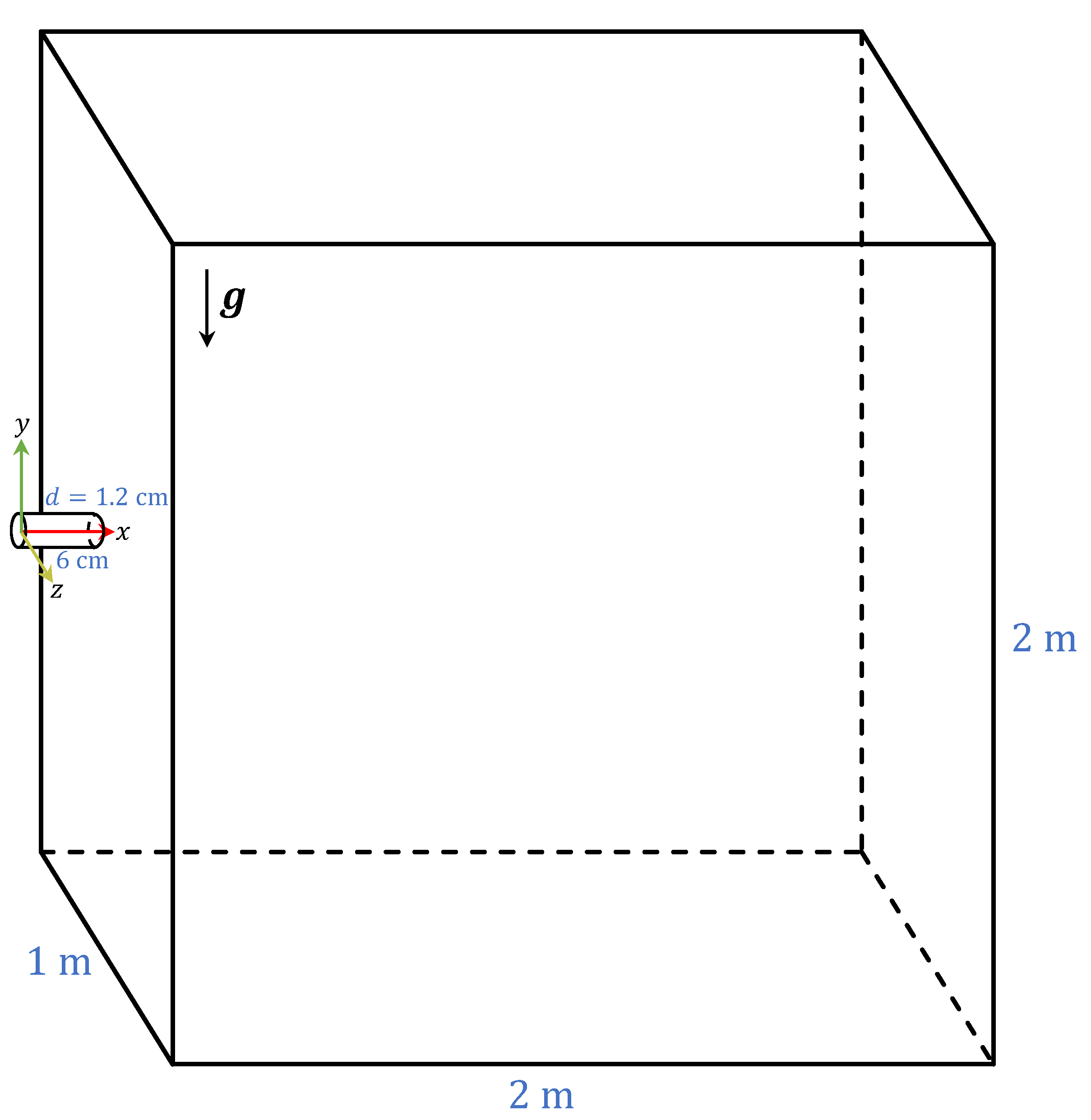



| Property | Symbol | Value |
|---|---|---|
| Ambient temperature | 20 °C | |
| Breath temperature | 34 °C | |
| Ambient vapor concentration | 0.01151 (50% RH) | |
| Breath vapor concentration | 0.04719 (90% RH) | |
| Air density | 1.204 kg m−3 | |
| Air kinematic viscosity | m2 s−1 | |
| Thermal expansion coefficient | K−1 | |
| Thermal diffusivity | m2 s−1 | |
| Vapor molar fraction expansion coefficient | 0.385 | |
| Vapor mass diffusivity | D | m2 s−1 |
| Particle density | 1000 kg m−3 |
| Label | Abbreviation | Eddy Interaction Time | Used in |
|---|---|---|---|
| Mean Particle–Eddy Interaction Time | MPI | OpenFOAM® [5] | |
| Randomized Particle–Eddy Interaction Time | RPI | Gosman and Ioannides [20] | |
| Limited Particle–Eddy Interaction Time | LPI | – |
| Particle Cloud | Velocity Field | Cut-Off Frequency | Dispersion Model | Particle–Eddy Interaction Time |
|---|---|---|---|---|
| 1 | DNS | − | − | − |
| 2 | 0.55 Hz | − | − | |
| 3 | 0.55 Hz | MPI | ||
| 4 | 0.55 Hz | RPI | ||
| 5 | 0.55 Hz | LPI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batmaz, E.; Webner, F.; Schmeling, D.; Wagner, C. Improvements in Turbulent Jet Particle Dispersion Modeling and Its Validation with DNS. Atmosphere 2025, 16, 637. https://doi.org/10.3390/atmos16060637
Batmaz E, Webner F, Schmeling D, Wagner C. Improvements in Turbulent Jet Particle Dispersion Modeling and Its Validation with DNS. Atmosphere. 2025; 16(6):637. https://doi.org/10.3390/atmos16060637
Chicago/Turabian StyleBatmaz, Ege, Florian Webner, Daniel Schmeling, and Claus Wagner. 2025. "Improvements in Turbulent Jet Particle Dispersion Modeling and Its Validation with DNS" Atmosphere 16, no. 6: 637. https://doi.org/10.3390/atmos16060637
APA StyleBatmaz, E., Webner, F., Schmeling, D., & Wagner, C. (2025). Improvements in Turbulent Jet Particle Dispersion Modeling and Its Validation with DNS. Atmosphere, 16(6), 637. https://doi.org/10.3390/atmos16060637






