Next Article in Journal
Atmospheric Photochemical Oxidation of 4-Nitroimidazole
Previous Article in Journal
Assessment of Coastal Zone Vulnerability in Context of Sea-Level Rise and Inundation Risk in Qatar
Previous Article in Special Issue
Homogenization of the Probability Distribution of Climatic Time Series: A Novel Algorithm
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 16
Issue 5
10.3390/atmos16050623
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Using Chemical Transport Model and Climatology Data as Backgrounds for Aerosol Optical Depth Spatial–Temporal Optimal Interpolation

by
Natallia Miatselskaya
*,
Andrey Bril
and
Anatoly Chaikovsky
Institute of Physics, National Academy of Sciences of Belarus, 220072 Minsk, Belarus
*
Author to whom correspondence should be addressed.
Atmosphere 2025, 16(5), 623; https://doi.org/10.3390/atmos16050623
Submission received: 17 April 2025 / Revised: 12 May 2025 / Accepted: 16 May 2025 / Published: 20 May 2025
(This article belongs to the Special Issue Data Analysis in Atmospheric Research)
Browse Figures
Review Reports Versions Notes

Abstract

:
A common approach to estimating the spatial–temporal distribution of atmospheric species properties is data assimilation. Data assimilation methods provide the best estimate of the required parameter by combining observations with appropriate prior information (background) that can include the model output, climatology data, or some other first guess. One of the relatively simple and computationally cheap data assimilation methods is optimal interpolation (OI). It estimates a value of interest through a weighted linear combination of observational data and background that is defined only once for the whole time interval of interest. Spatial–temporal OI (STOI) utilizes both spatial and temporal observational error covariance and background error covariance. This allows for filling in not only spatial, but also temporal gaps in observations. We applied STOI to daily mean aerosol optical depth (AOD) observations obtained at the European AERONET (Aerosol Robotic Network) sites with the use of the GEOS-Chem chemical transport model simulations and the AOD climatology data as backgrounds. We found that mean square errors in the estimate when using modeled data are comparable with those when using climatology data. Based on these results, we merged estimates obtained using modeled and climatology data according to their mean square errors. This allows for improving the AOD estimates in areas where observations are limited in space and time.

1. Introduction

Studying the composition of the Earth’s atmosphere is crucial for understanding climate change and predicting air quality. The state of the atmosphere is monitored using various in situ and remote sensing observations. However, there can be significant differences in data obtained using different instruments and techniques. Observations can be irregular and sparse in space, with different uncertainties. To estimate atmospheric characteristics on some regular spatial–temporal grid, data assimilation [1,2,3,4,5] is commonly applied. The goal of data assimilation is to minimize, on average, the difference between the estimate of the system state and the true system state.
Data assimilation comprises methods that merge information from different sources for obtaining the best estimate of the system state. The mathematical basis for data assimilation is the estimation theory [6,7]. In a data assimilation scheme, observations are combined with some prior information, or background, that provides a first-guess estimate. The background represents the best estimate of the true state available before observations are made. In atmospheric science, the background is often chosen to be a model output or climatology data represented on some discrete grid. The information contained in observational data is spread in space using background error correlations.
Data assimilation methods are historically divided into optimal interpolation (OI) [8,9], Kalman filtering (KF) [10,11,12], and variational three-dimensional (3D-Var) [13,14,15] and four-dimensional (4D-Var) [16,17,18] methods. Under common assumptions of linearity and Gaussian error probability distribution, 3D-Var methods differ from OI, and 4D-Var methods differ from KF only by the mathematical approach to the solution [4,5,19,20]. OI and 3D-Var methods are non-sequential. Non-sequential assimilation uses the background, which is defined only once for the whole time interval of interest. KF and 4D-Var methods are sequential. In sequential assimilation, the background is given by the model forecast, starting from the estimate at the previous time step. The background and its error variance are updated at every time step, so sequential methods, in general, provide a lower mean square error of the estimate [21]. At present, KF and 4D-Var are the main data assimilation methods used for assessment and forecasting the state of the atmosphere [22,23,24,25]. However, in sequential methods, the trajectory of the estimated system state contains discontinuities whenever a new observation is encountered [26], so these methods are not well suited for retrospective analysis. Sequential assimilation needs to be regularly fed with observations. Otherwise the system returns to the model trajectory within a relatively small time interval, and sequential methods do not provide better performance than non-sequential methods [2,27].
Among the data assimilation methods, OI is the simplest and the least computationally costly [4,11,21]. OI is one of the easiest ways to perform data assimilation. This method is rather data fusion. To produce the estimate, OI merges observations and a background, which is defined only once for the whole time interval of interest.
Being a non-sequential method, OI can benefit from the possibility of using not only spatial, but also temporal correlation. In previous studies, we developed a spatial–temporal optimal interpolation (STOI) method [28,29]. This is an extended OI method in which a time dimension is added by using correlations in time in addition to correlations in space. STOI allows for filling in not only spatial, but also temporal gaps in observations. This makes STOI particularly useful for the assimilation of temporally sparse observations. STOI is a simple-to-implement and computationally cheap method that shows accuracy comparable with other assimilation methods when using observational data with large temporal gaps. STOI is suitable for a retrospective analysis. Due to the use of temporal correlations, the system trajectory is smooth in time and provides a physically more realistic picture of a spatial–temporal distribution of atmospheric species characteristics. These are the reasons for developing STOI in the application of observations limited in space and time, such as optical remote sensing observations.
One of the important atmospheric characteristics obtained using optical remote sensing is the aerosol optical depth (AOD).
The AOD is an aerosol optical quantity that reflects the column-integrated atmospheric aerosol amount. A number of actual problems require knowing a spatial–temporal distribution of the AOD. Various atmospheric aerosol properties can be derived from AOD observations [30,31]. In the last decades, numerous studies have been dedicated to the estimation of AOD distribution using different data assimilation approaches [32,33,34,35,36,37] including OI [38,39,40]. However, only spatial OI was considered.
In [29], we showed that STOI provides an improvement in AOD estimates. The present paper is dedicated to further improvement of the STOI accuracy. The choice of the background can significantly affect the result of the estimation. In the early OI methods, the climatology data were used as backgrounds [8]. Later, the climatology data were replaced with the model output. We wondered whether the model output is much better than the climatology data when used as a background for the AOD assimilation. In the present study, we applied the STOI technique to AOD observations using chemical transport model simulations and climatology data as backgrounds. We compared the results obtained using these two categories of background, and proposed an approach to STOI that uses both modeled and climatology data as backgrounds according to their mean square errors.
The paper is organized as follows: In Section 2, we described the STOI technique, AOD observations and background fields used in the assimilation process; in Section 3, we evaluated and discussed the proposed approach to the AOD estimation; and in Section 4, we drew conclusions.

2. Materials and Methods

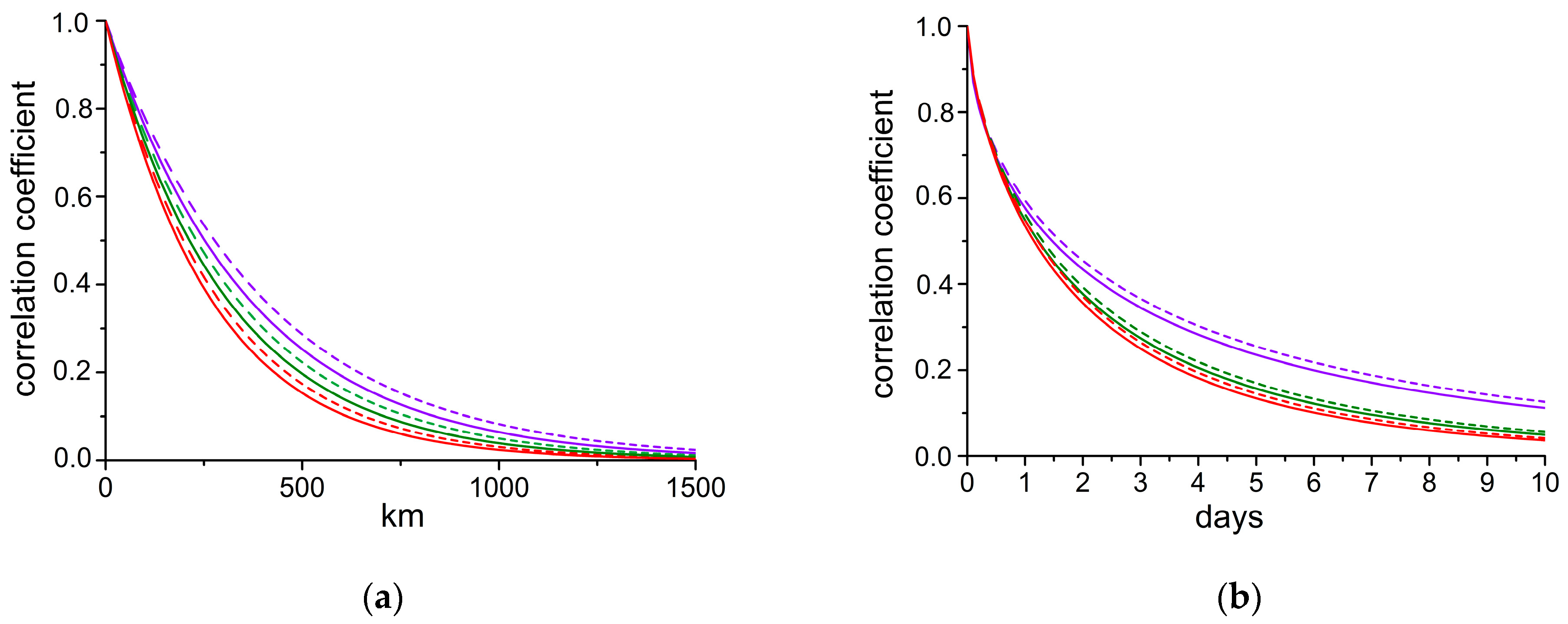
2.1. Spatial–Temporal Optimal Interpolation

The spatial–temporal optimal interpolation method is based on the classical OI. It uses common equations of the optimal estimation theory [4,20]:
x a = x b + K [ y − H ( x b ) ]
K = B H T ( H B H T + R ) − 1
where xa is a vector containing estimates of the state of the system, xb is a vector containing background values, y is a vector containing values of observations, K is a matrix containing weighting coefficients, H is an observation operator (observation model) providing the link between the observations and variables describing the state of the system, B is a covariance matrix of background errors, and R is a covariance matrix of observational errors. The matrix of weighting coefficients, K, is to be determined by minimizing the mean square error in the estimate. In OI, the estimates are obtained for each grid point independently with weighting coefficients determined at each grid point. The estimate at a particular grid point is obtained as the sum of the background value at the point of estimation, and the estimation increment (deviation of the estimate from the background). After transforming the vector of observations into the same type of variables as the background (or if observational and background variables are the same), the estimation increment is calculated as a weighted linear combination of the anomalies (deviations of the observations from the background) at the neighboring observational points. Only a limited number of observations are taken into consideration in the vicinity of the point of estimation. In the absence of observational data and outside of the background error correlation area, the background is considered to be the best estimate of a system state.
In the OI scheme, background and observational errors are assumed to be unbiased, observational errors are assumed to be uncorrelated, and background and observational errors are assumed to be mutually uncorrelated. Another common assumption is that the background error correlation is homogeneous and isotropic.
In STOI, not only observations at the time point of estimation, but also observations at the neighboring time points are used, assuming homogeneity and isotropy in time.

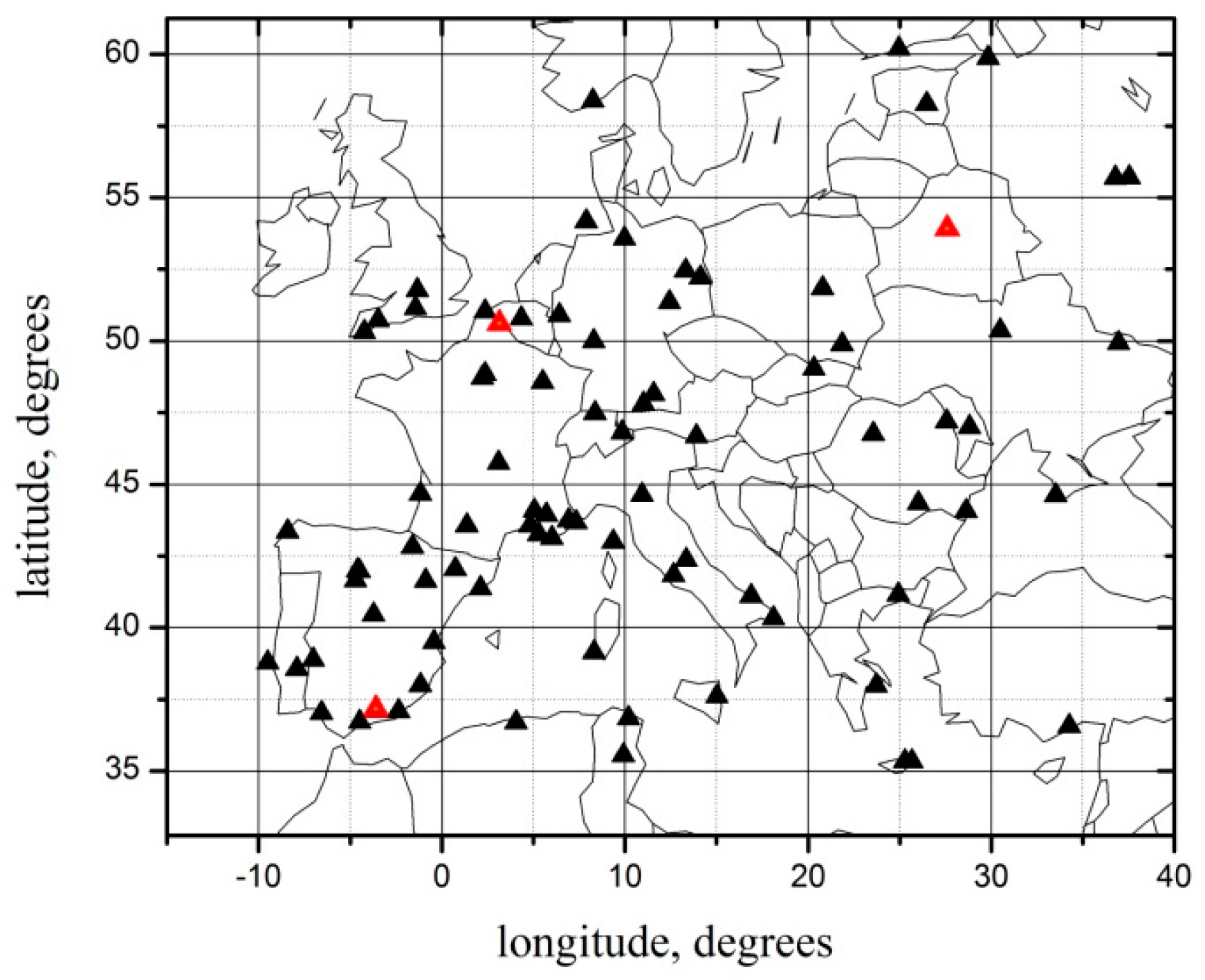
2.2. AERONET AOD Observations

We applied STOI to daily mean AOD observations from a global radiometric ground-based Aerosol Robotic Network (AERONET) [41,42,43]. AERONET utilizes Cimel multi-channel, automatic sun–sky–lunar scanning photometers, CE318, designed for automatic multispectral atmospheric photometry [44]. The measurements of direct solar, lunar, and diffused sky radiance are performed at a number of wavelengths in the range of 340–1640 nm. The AOD is derived from AERONET radiance measurements using a retrieval algorithm [45]. The AOD and other aerosol optical, microphysical, and radiative properties are displayed on the AERONET website [46]. An uncertainty of AERONET observations of the AOD is estimated to be 0.01 for wavelengths >440 nm [47,48]. We used version 3 AERONET Level 2.0 cloud-screened and quality-assured daily averaged total AOD data at wavelengths of 440, 675, and 870 nm.
We performed STOI using observations from the 86 European AERONET sites for the period of two years from 1 January 2015 to 31 December 2016. Table A1 lists the AERONET sites used in the study along with their geographic location. Figure 1 [29] illustrates the location of these sites.

2.3. Background Estimate

We used two different backgrounds: climatology data and the results of a chemical transport model simulation.

2.3.1. Climatology Data as a Background

We averaged all daily mean Level 2.0 AERONET AOD values at all of the abovementioned AERONET sites to obtain a very simplified model of the climatology background. This background is represented by only one AOD value for each wavelength for the entire European domain and entire two-year period. This approach is acceptable for initial assessment because in the assimilation scheme, only correlations of deviations from the background are taken into account and not correlations of background values themselves.

2.3.2. Model Output as a Background

We obtained a modeled background by calculations using the GEOS-Chem chemical transport model [49,50,51]. This model is continuously updated and widely used by the air quality community. GEOS-Chem simulates the evolution of more than two hundred atmospheric species including aerosols. We used version v12.1.1 of GEOS-Chem in the classical configuration (GEOS-Chem Classic) in the offline mode, in which the model is driven by archived meteorological observations from the Goddard Earth Observing System (GEOS) of the NASA Global Modeling and Assimilation Office [52]. GEOS-Chem uses the Harvard–NASA Emissions Component (HEMCO) [53] for computing atmospheric emissions from different inventories. The advection algorithm of CEOS-Chem Classic was described in [54]. The oxidant-aerosol chemistry in the troposphere and stratosphere was described in [55,56,57]. When calculating the AOD, the aerosol types in GEOS-Chem are categorized into groups according to their optical properties: sulfate–nitrate–ammonium; size fractions of mineral dust; sea salt in accumulation and coarse modes; and black carbon; organic aerosols. Aerosol optical properties are from [58,59]. The hygroscopic growth is taken into account.
GEOS-Chem allows for simulations at global and regional scales. The nested capability for CEOS-Chem Classic was implemented by the authors in [60,61,62]. The nested European domain in GEOS-Chem is 32.75° N–61.25° N, 15° W–40° E.
We simulated the daily averaged AOD at 440, 675, and 870 nm for the European domain at 0.25° latitude × 0.3125° longitude horizontal resolution and 47 vertical σ-layers up to ~80 km. For performing the nested simulation, we used boundary conditions from the global simulation at 2° latitude × 2.5° longitude horizontal resolution.

3. Results and Discussion

The AOD uncertainty obtained with a model simulation is significantly larger than that retrieved from AERONET measurements [63,64], so we assumed the AERONET AOD uncertainty to be negligible. This assumption allows for calculating background covariances using differences between the observational and background values. As the correlation structure of the background errors is assumed to be homogeneous and isotropic, the correlation function is the same for any spatial–temporal point and in any direction. We modeled spatial and temporal correlation coefficients by exponential functions on the basis of calculated spatial and temporal covariances.
Obtained spatial and temporal correlation functions for the GEOS-Chem output and climatology data as backgrounds are shown in Figure 2.
Correlation functions are almost similar for both model and climatology data errors in the AOD estimate. Correlation curves for climatology data lie slightly higher than those for the model output. Such behavior can be explained by the higher imperfection of climatology data.
To evaluate the efficiency of STOI when using model output and climatology data as backgrounds, we compared the estimates against observations that were not used in data assimilation. We chose the Lille, Minsk, and Granada AERONET sites to be excluded from the data assimilation process, the same as in our previous article [29]. We calculated the root mean square errors (RMSEs) of the estimates for the model output and climatology backgrounds. The results are presented in Table 1 (using the GEOS-Chem output as the background) and Table 2 (using climatology data as the background). The reduction in the RMSE of the estimate after STOI is shown in parentheses in the tables.
The comparison shows that the RMSE in the STOI estimate of the AOD when using modeled data as the background do not differ significantly from those when using climatology data. This indicates that the AOD calculations are prone to large errors. The difference in the RMSE is larger in Lille than in Granada because the area where the Granada site is located is rich in AERONET sites and has a large number of sunny days. Minsk shows the largest difference in the RMSE due to sparse distribution of AERONET sites in this area and the predominance of cloudy days. It is obvious that far from the spatial–temporal observation points, the background plays a more important role.
The results of the comparison of the RMSEs in Table 1 and Table 2 imply the possibility of using climatology data as the background instead of the model output for AERONET AOD assimilation. This greatly reduces the computational cost. On the basis of the obtained results, we assumed that the RMSE in the STOI estimate of the AOD can probably be decreased by using both model results and climatology data as backgrounds with weighting coefficients according to the RMSE of these fields. The second background would provide additional independent information and therefore enhance the accuracy of the estimate.
The results of merging the AOD estimates obtained using both the model output and climatology data are shown in Table 3.
It can be seen from Table 3, in comparison with Table 1 and Table 2, that using two backgrounds does not affect the results for Granada, slightly improves the results for Lille, and significantly improves the results for Minsk. This is in agreement with statements of the data assimilation theory that the background makes the main contribution to the estimate that is far from the observations.
Therefore, the proposed approach has the potential to improve the estimate of atmospheric species characteristic distribution when observations are sparse.
Further improvements will concern approaches to the construction of backgrounds. The approach to building the climatology background used in the present study is clearly crude, and in future, we plan to build a more relevant climatology background by averaging AERONET AOD data over months or seasons, and over smaller regions, applying simple interpolation to avoid sharp distinctions between regions. An improvement of the model output is also possible. Aerosol microphysical and optical properties used to compute the AOD are constantly being updated and incorporated into the GEOS-Chem model.

4. Conclusions

The main conclusions are as follows:
  • The present study confirms the capability of STOI to fill spatial and temporal gaps in observations;
  • The STOI estimates are sensitive to the choice of the background in areas with sparsely distributed observations;
  • Using both the model output and climatology data as backgrounds allows for reducing the uncertainty in the estimate in areas where observations are limited in space and time without significantly increasing the computational cost.
The proposed method can be used in atmospheric aerosol monitoring. In future, we plan to apply the developed approach to the estimation and analysis of spatial distribution and temporal variation in atmospheric species over certain regions of interest.

Author Contributions

Conceptualization, N.M. and A.C.; methodology, N.M.; software, N.M. and A.B.; validation, N.M. and A.B.; investigation, N.M.; data curation, N.M., A.B. and A.C., writing—original draft preparation, N.M.; writing—review and editing, A.B. and A.C.; visualization, N.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

AERONET data are freely available from https://aeronet.gsfc.nasa.gov (accessed on 16 April 2025). GEOS-Chem simulation and the STOI data generated in this study are freely available from http://scat.bas-net.by/~assimilation/ (accessed on 16 April 2025).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AODAerosol optical depth
OIOptimal interpolation
STOISpatial–temporal optimal interpolation
KFKalman filtering
3D-VarThree-dimensional variational
4D-VarFour-dimensional variational
AERONETAerosol Robotic Network
RMSERoot mean square error

Appendix A

Table A1. AERONET sites taken into account when performing STOI and their geographic location as presented via the AERONET website [36].
Table A1. AERONET sites taken into account when performing STOI and their geographic location as presented via the AERONET website [36].
AERONET SiteLongitudeLatitude
Lille3.142° E50.612° N
Barcelona2.112° E41.389° N
Venice12.508° E45.314° N
Xanthi24.919° E41.147° N
Ispra8.627° E45.803° N
Mainz8.3° E49.999° N
Helgoland7.887° E54.178° N
Palaiseau2.215° E48.712° N
Paris2.356° E48.847° N
Moldova28.816° E47.001° N
IMS-METU-ERDEMLI34.255° E36.565° N
Kyiv30.497° E50.364° N
Hamburg9.973° E53.568° N
Modena10.945° E44.632° N
Moscow_MSU_MO37.522° E55.707° N
Minsk27.601° E53.92° N
Rome_Tor_Vergata12.647° E41.84° N
Leipzig12.435° E51.353° N
Davos9.844° E46.813° N
Munich_University11.573° E48.148° N
Lecce_University18.111° E40.335° N
ATHENS-NOA23.718° E37.972° N
Belsk20.792° E51.837° N
Villefranche7.329° E43.684° N
Palencia4.516° W41.989° N
Carpentras5.058° E44.083° N
Toulon6.009° E43.136° N
Dunkerque2.368° E51.035° N
Evora7.911° W38.568° N
Laegeren8.364° E47.478° N
Cabo_da_Roca9.498° W38.782° N
Granada3.605° W37.164° N
Gustav_Dalen_Tower17.467° E58.594° N
OHP_OBSERVATOIRE5.71° E43.935° N
Chilbolton1.437° W51.144° N
Helsinki_Lighthouse24.926° E59.949° N
Sevastopol33.517° E44.616° N
Brussels4.35° E50.783° N
Zvenigorod36.775° E55.695° N
Porquerolles6.161° E43.001° N
Burjassot0.42° W39.507° N
Bucharest_Inoe26.028° E44.348° N
Autilla4.603° W41.997° N
Kanzelhohe_Obs13.901° E46.677° N
Ersa9.359° E43.004° N
Arcachon1.163° W44.664° N
Wytham_Woods1.332° W51.77° N
Malaga4.478° W36.715° N
Birkenes8.252° E58.388° N
Eforie28.632° E44.075° N
Huelva6.569° W37.016° N
Aubiere_LAMP3.111° E45.761° N
Frioul5.293° E43.266° N
CLUJ_UBB23.551° E46.768° N
Gloria29.36° E44.6° N
Bari_University16.884° E41.108° N
Tabernas_PSA-DLR2.358° W37.091° N
Calern_OCA6.923° E43.752° N
Montsec0.73° E42.051° N
Bure_OPE5.505° E48.562° N
Coruna8.421° W43.363° N
Madrid3.724° W40.452° N
Tizi_Ouzou4.056° E36.699° N
Iasi_LOASL27.556° E47.193° N
Zaragoza0.882° W41.633° N
FZJ-JOYCE6.413° E50.908° N
Badajoz7.011° W38.883° N
Cerro_Poyos3.487° W37.109° N
Valladolid4.706° W41.664° N
Murcia1.171° W38.001° N
MetObs_Lindenberg14.121° E52.209° N
Ben_Salem9.914° E35.551° N
CENER1.602° W42.816° N
HohenpeissenbergDWD11.012° E47.802° N
Galata_Platform28.193° E43.045° N
Tunis_Carthage10.2° E36.839° N
Carloforte8.31° E39.14° N
Exeter_MO3.475° W50.729° N
Strzyzow21.861° E49.879° N
LAQUILA_Coppito13.351° E42.368° N
Toulouse_MF1.374° E43.573° N
Martova36.953° E49.936° N
Zeebrugge-MOW13.12° E51.362° N
Peterhof29.826° E59.881° N
Finokalia-FKL25.67° E35.338° N
Berlin_FUB13.31° E52.458° N

References

  1. Lahoz, W.A. Data Assimilation; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
  2. Sandu, A.; Chai, T. Chemical Data Assimilation—An Overview. Atmosphere 2011, 2, 426–463. [Google Scholar] [CrossRef]
  3. Bocquet, M.; Elbern, H.; Eskes, H.; Hirtl, M.; Žabkar, R.; Carmichael, G.R.; Flemming, J.; Inness, A.; Pagowski, M.; Pérez Camaño, J.L.; et al. Data Assimilation in Atmospheric Chemistry Models: Current Status and Future Prospects for Coupled Chemistry Meteorology Models. Atmos. Chem. Phys. 2015, 15, 5325–5358. [Google Scholar] [CrossRef]
  4. Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
  5. Wikle, C.K.; Berliner, L.M. A Bayesian Tutorial for Data Assimilation. Phys. D Nonlinear Phenom. 2007, 230, 1–16. [Google Scholar] [CrossRef]
  6. Daley, R. Atmospheric Data Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
  7. Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
  8. Gandin, L.S. Objective Analysis of Meteorological Fields; Gidrometeorol. Izd.: Leningrad, Russia, 1963. [Google Scholar]
  9. Lorenc, A.C. A Global Three-Dimensional Multivariate Statistical Analysis Scheme. Mon. Weather Rev. 1981, 109, 701–721. [Google Scholar] [CrossRef]
  10. Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
  11. Constantinescu, E.M.; Sandu, A.; Chai, T.; Carmichael, G. Ensemble-based Chemical Data Assimilation: General Approach. Q. J. R. Meteorol. Soc. 2007, 133, 1229–1243. [Google Scholar] [CrossRef]
  12. Perrot, A.; Pannekoucke, O.; Guidard, V. Toward a Multivariate Formulation of the Parametric Kalman Filter Assimilation: Application to a Simplified Chemical Transport Model. Nonlin. Processes Geophys. 2023, 30, 139–166. [Google Scholar] [CrossRef]
  13. Sasaki, Y. An Objective Analysis Based on the Variational Method. J. Meteorol. Soc. Jpn. 1958, 36, 77–88. [Google Scholar] [CrossRef]
  14. Le Dimet, F.-X.; Talagrand, O. Variational Algorithms for Analysis and Assimilation of Meteorological Observations: Theoretical Aspects. Tellus 1986, 38A, 97–110. [Google Scholar] [CrossRef]
  15. Zang, Z.; You, W.; Ye, H.; Liang, Y.; Li, Y.; Wang, D.; Hu, Y.; Yan, P. 3DVAR Aerosol Data Assimilation and Evaluation Using Surface PM2.5, Himawari-8 AOD and CALIPSO Profile Observations in the North China. Remote Sens. 2022, 14, 4009. [Google Scholar] [CrossRef]
  16. Courtier, P.; Thepaut, J.-N.; Hollingsworth, A. A Strategy for Operational Implementation of 4D-Var, Using an Incremental Approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
  17. Carmichael, G.R.; Sandu, A.; Chai, T.; Daescu, D.N.; Constantinescu, E.M.; Tang, Y. Predicting Air Quality: Improvements through Advanced Methods to Integrate Models and Measurements. J. Comput. Phys. 2008, 227, 3540–3571. [Google Scholar] [CrossRef]
  18. Tian, X.; Zhang, H.; Feng, X.; Li, X. i4DVar: An Integral Correcting Four-Dimensional Variational Data Assimilation Method. Earth Space Sci. 2021, 8, e2021EA001767. [Google Scholar] [CrossRef]
  19. Wahba, G.; Wendelberger, J. Some New Mathematical Methods for Variational Objective Analysis Using Splines and Cross Validation. Mon. Wea. Rev. 1980, 108, 1122–1143. [Google Scholar] [CrossRef]
  20. Lorenc, A.C. Analysis Methods for Numerical Weather Prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
  21. Candiani, G.; Carnevale, C.; Finzi, G.; Pisoni, E.; Volta, M. A Comparison of Reanalysis Techniques: Applying Optimal Interpolation and Ensemble Kalman Filtering to Improve Air Quality Monitoring at Mesoscale. Sci. Total Environ. 2013, 458–460, 7–14. [Google Scholar] [CrossRef]
  22. Zhao, M.; Dai, T.; Goto, D.; Wang, H.; Shi, G. Assessing the Assimilation of Himawari-8 Observations on Aerosol Forecasts and Radiative Effects during Pollution Transport from South Asia to the Tibetan Plateau. Atmos. Chem. Phys. 2024, 24, 235–258. [Google Scholar] [CrossRef]
  23. Fang, L.; Jin, J.; Segers, A.; Liao, H.; Li, K.; Xu, B.; Han, W.; Pang, M.; Lin, H.X. A Gridded Air Quality Forecast through Fusing Site-available Machine Learning Predictions from RFSML v1.0 and Chemical Transport Model Results from GEOS-Chem v13.1.0 using the Ensemble Kalman Filter. Geosci. Model Dev. 2023, 16, 4867–4882. [Google Scholar] [CrossRef]
  24. Jin, J.; Fang, L.; Li, B.; Liao, H.; Wang, Y.; Han, W.; Li, K.; Pang, M.; Wu, X.; Lin, H.X. 4DEnVar-based Inversion System for Ammonia Emission Estimation in China through Assimilating IASI Ammonia Retrievals. Environ. Res. Lett. 2023, 18, 034005. [Google Scholar] [CrossRef]
  25. Pouyaei, A.; Mizzi, A.P.; Choi, Y.; Mousavinezhad, S.; Khorshidian, N. Downwind Ozone Changes of the 2019 Williams Flats Wildfire: Insights from WRF-Chem/DART Assimilation of OMI NO2, HCHO, and MODIS AOD Retrievals. J. Geophys. Res. Atmos. 2023, 128, e2022JD038019. [Google Scholar] [CrossRef]
  26. Khattatov, B.V.; Gille, J.C.; Lyjak, L.V.; Brasseur, G.P.; Dvortsov, V.L.; Roche, A.E.; Waters, J. Assimilation of Photochemically Active Species and a Case Analysis of UARS Data. J. Geophys. Res. 1999, 104, 18715–18737. [Google Scholar] [CrossRef]
  27. Tombette, M.; Mallet, V.; Sportisse, B. PM10 Data Assimilation over Europe with the Optimal Interpolation Method. Atmos. Chem. Phys. 2009, 9, 57–70. [Google Scholar] [CrossRef]
  28. Miatselskaya, N.S.; Bril, A.I.; Chaikovsky, A.P.; Yukhymchuk, Y.Y.; Milinevski, G.P.; Simon, A.A. Optimal Interpolation of AERONET Radiometric Network Observations for the Evaluation of the Aerosol Optical Thickness Distribution in the Eastern European Region. J. Appl. Spectrosc. 2022, 89, 296–302. [Google Scholar] [CrossRef]
  29. Miatselskaya, N.; Milinevsky, G.; Bril, A.; Chaikovsky, A.; Miskevich, A.; Yukhymchuk, Y. Application of Optimal Interpolation to Spatially and Temporally Sparse Observations of Aerosol Optical Depth. Atmosphere 2023, 14, 32. [Google Scholar] [CrossRef]
  30. Donkelaar, A.; Martin, R.V.; Park, R.J. Estimating Ground-level PM2.5 with Aerosol Optical Depth Determined from Satellite Remote Sensing. J. Geophys. Res. 2006, 111, D21201. [Google Scholar] [CrossRef]
  31. Perez-Ramirez, D.; Veselovskii, I.; Whiteman, D.N.; Suvorina, A.; Korenskiy, M.; Kolgotin, A.; Holben, B.; Dubovik, O.; Siniuk, A.; Alados-Arboledas, L. High Temporal Resolution Estimates of Columnar Aerosol Microphysical Parameters from Spectrum of Aerosol Optical Depth by Linear Estimation: Application to Long-term AERONET and Star-photometry Measurements. Atmos. Meas. Tech. 2015, 8, 3117–3133. [Google Scholar] [CrossRef]
  32. Yu, H.; Dickinson, R.E.; Chin, M.; Kaufman, Y.J.; Geogdzhayev, B.; Mishchenko, M.I. Annual Cycle of Global Distributions of Aerosol Optical Depth from Integration of MODIS Retrievals and GOCART Model Simulations. J. Geophys. Res. 2003, 108, 4128. [Google Scholar] [CrossRef]
  33. Adhikary, B.; Kulkarni, S.; Dallura, A.; Tang, Y.; Chai, T.; Leung, L.R.; Qian, Y.; Chung, C.E.; Ramanathan, V.; Carmichael, G.R. A Regional Scale Chemical Transport Modeling of Asian Aerosols with Data Assimilation of AOD Observations Using Optimal Interpolation Technique. Atmos. Environ. 2008, 42, 8600–8615. [Google Scholar] [CrossRef]
  34. Rubin, J.I.; Reid, J.S.; Hansen, J.A.; Anderson, J.L.; Holben, B.N.; Xian, P.; Westphal, D.L.; Zhang, J. Assimilation of AERONET and MODIS AOT Observations Using Variational and Ensemble Data Assimilation Methods and Its Impact on Aerosol Forecasting Skill. J. Geophys. Res.–Atmos. 2017, 122, 4967–4992. [Google Scholar] [CrossRef]
  35. Li, J.; Kahn, R.A.; Wei, J.; Carlson, B.E.; Lacis, A.A.; Li, Z.; Li, X.; Dubovik, O.; Nakajima, T. Synergy of Satellite- and Ground-based Aerosol Optical Depth Measurements using an Ensemble Kalman Filter Approach. J. Geophys. Res. Atmos. 2020, 125, e2019JD031884. [Google Scholar] [CrossRef]
  36. Huang, B.; Pagowski, M.; Trahan, S.; Martin, C.R.; Tangborn, A.; Kondragunta, S.; Kleist, D.T. JEDI-based Three-Dimensional Ensemble-Variational Data Assimilation System for Global Aerosol Forecasting at NCEP. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003232. [Google Scholar] [CrossRef]
  37. Goto, D.; Nishizawa, T.; Uchida, J.; Yumimoto, K.; Jin, Y.; Higurashi, A.; Shimizu, A.; Sugata, S.; Yashiro, H.; Hayasaki, M.; et al. Development of an Aerosol Assimilation System Using a Global Non-Hydrostatic Model, a 2-Dimensional Variational Method, and Multiple Satellite-Based Aerosol Products. J. Adv. Model. Earth Syst. 2024, 16, e2023MS004046. [Google Scholar] [CrossRef]
  38. Collins, W.D.; Rasch, P.J.; Eaton, B.E.; Khattatov, B.V.; Lamarque, J.-F.; Zender, C.S. Simulating Aerosols Using a Chemical Transport Model with Assimilation of Satellite Aerosol Retrievals: Methodology for INDOEX. J. Geophys. Res. Atmos. 2001, 106, 7313–7336. [Google Scholar] [CrossRef]
  39. Xue, Y.; Xu, H.; Guang, J.; Mei, L.; Guo, J.; Li, C.; Mikusauskas, R.; He, X. Observation of an Agricultural Biomass Burning in Central and East China Using Merged Aerosol Optical Depth Data from Multiple Satellite Missions. Int. J. Remote Sens. 2014, 35, 5971–5983. [Google Scholar] [CrossRef]
  40. Li, K.; Bai, K.; Li, Z.; Guo, J.; Chang, N.-B. Synergistic Data Fusion of Multimodal AOD and Air Quality Data for Near Real-Time Full Coverage Air Pollution Assessment. J. Environ. Manag. 2022, 302, 114121. [Google Scholar] [CrossRef]
  41. Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
  42. Holben, B.N.; Kim, J.; Sano, I.; Mukai, S.; Eck, T.F.; Giles, D.M.; Schafer, J.S.; Sinyuk, A.; Slutsker, I.; Smirnov, A. An Overview of Mesoscale Aerosol Processes, Comparisons, and Validation Studies from DRAGON Networks. Atmos. Chem. Phys. 2018, 18, 655–671. [Google Scholar] [CrossRef]
  43. Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 Database—Automated Near-Real-Time Quality Control Algorithm with Improved Cloud Screening for Sun Photometer Aerosol Optical Depth (AOD) Measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef]
  44. Cimel Electronique. Available online: https://www.cimel.fr/ (accessed on 10 April 2025).
  45. Dubovik, O.; King, M.D. A Flexible Inversion Algorithm for Retrieval of Aerosol Optical Properties from Sun and Sky Radiance Measurements. J. Geophys. Res. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
  46. NASA, Goddard Spase Flight Center; AERONET; Aerosol Robotic Network. Available online: https://aeronet.gsfc.nasa.gov/ (accessed on 16 April 2025).
  47. Eck, T.F.; Holben, B.N.; Reid, J.S.; Dubovik, O.; Smirnov, A.; O’Neill, N.T.; Slutsker, I.; Kinne, S. Wavelength Dependence of the Optical Depth of Biomass Burning, Urban and Desert Dust Aerosols. J. Geophys. Res. 1999, 104, 31333–31349. [Google Scholar] [CrossRef]
  48. Holben, B.N.; Tanre, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.; Chatenet, B.; Lavenue, F.; et al. An Emerging Ground-Based Aerosol Climatology: Aerosol Optical Depth from AERONET. J. Geophys. Res. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
  49. GEOS-Chem. Available online: https://geoschem.github.io (accessed on 10 April 2025).
  50. Bey, I.; Jacob, D.J.; Yantosca, R.M.; Logan, J.A.; Field, B.D.; Fiore, A.M.; Li, Q.; Liu, H.Y.; Mickley, L.J.; Schultz, M.G. Global Modeling of Tropospheric Chemistry with Assimilated Meteorology: Model Description and Evaluation. J. Geophys. Res. 2001, 106, 23073–23096. [Google Scholar] [CrossRef]
  51. Park, R.J.; Jacob, D.J.; Field, B.D.; Yantosca, R.M.; Chin, M. Natural and Transboundary Pollution Influences on Sulfate-Nitrate-Ammonium Aerosols in the United States: Implications for Policy. J. Geophys. Res. 2004, 109, D15204. [Google Scholar] [CrossRef]
  52. NASA, Goddard Space Flight Center; Global Modeling and Assimilation Office; GEOS Systems. Available online: https://gmao.gsfc.nasa.gov/GEOS_systems/ (accessed on 16 April 2025).
  53. Keller, C.A.; Long, M.S.; Yantosca, R.M.; Da Silva, A.M.; Pawson, S.; Jacob, D.J. HEMCO v1.0: A Versatile, ESMF-Compliant Component for Calculating Emissions in Atmospheric Models. Geosci. Model Dev. 2014, 7, 1409–1417. [Google Scholar] [CrossRef]
  54. Lin, S.-J.; Rood, R.B. Multidimensional Flux Form Semi-Lagrangian Transport Schemes. Mon. Weather Rev. 1996, 124, 2046–2070. [Google Scholar] [CrossRef]
  55. Sherwen, T.; Schmidt, J.A.; Evans, M.J.; Carpenter, L.J.; Grossmann, K.; Eastham, S.D.; Jacob, D.J.; Dix, B.; Koenig, T.K.; Sinreich, R.; et al. Global Impacts of Tropospheric Halogens (Cl, Br, I) on Oxidants and Composition in GEOS-Chem. Atmos. Chem. Phys. 2016, 16, 12239–12271. [Google Scholar] [CrossRef]
  56. Travis, K.R.; Jacob, D.J.; Fisher, J.A.; Kim, P.S.; Marais, E.A.; Zhu, L.; Yu, K.; Miller, C.C.; Yantosca, R.M.; Sulprizio, M.P.; et al. Why Do Models Overestimate Surface Ozone in the Southeast United States? Atmos. Chem. Phys. 2016, 16, 13561–13577. [Google Scholar] [CrossRef]
  57. Eastham, S.D.; Weisenstein, D.K.; Barrett, S.R.H. Development and Evaluation of the Unified Tropospheric–Stratospheric Chemistry Extension (UCX) for the Global Chemistry-Transport Model GEOS-Chem. Atmos. Environ. 2014, 89, 52–63. [Google Scholar] [CrossRef]
  58. Latimer, R.N.C.; Martin, R.V. Interpretation of Measured Aerosol Mass Scattering Efficiency over North America Using a Chemical Transport Model. Atmos. Chem. Phys. 2019, 19, 2635–2653. [Google Scholar] [CrossRef]
  59. Ridley, D.A.; Heald, C.L.; Ford, B. North African Dust Export and Deposition: A Satellite and Model Perspective. J. Geophys. Res. 2012, 117, D02202. [Google Scholar] [CrossRef]
  60. Wang, Y.X.; Mcelroy, M.B.; Jacob, D.J.; Yantosca, R.M. A Nested Grid Formulation for Chemical Transport over Asia: Applications to CO. J. Geophys. Res. Atmos. 2004, 109, D22307. [Google Scholar] [CrossRef]
  61. Zhang, L.; Liu, L.; Zhao, Y.; Gong, S.; Zhang, Z.; Henze, D.K.; Capps, S.L.; Fu, T.-M.; Zhang, Q.; Wang, Y. Source Attribution of Particulate Matter Pollution over North China with the Adjoint Method. Environ. Res. Lett. 2015, 10, 084011. [Google Scholar] [CrossRef]
  62. Kim, P.S.; Jacob, D.J.; Fisher, J.A.; Travis, K.; Yu, K.; Zhu, L.; Yantosca, R.M.; Sulprizio, M.P.; Jimenez, J.L.; Campuzano-Jost, P.; et al. Sources, Seasonality, and Trends of Southeast US Aerosol: An Integrated Analysis of Surface, Aircraft, and Satellite Observations with the GEOS-Chem Model. Atmos. Chem. Phys. 2015, 15, 10411–10433. [Google Scholar] [CrossRef]
  63. Li, S.; Garay, M.J.; Chen, L.; Rees, E.; Liu, Y. Comparison of GEOS-Chem Aerosol Optical Depth with AERONET and MISR Data over the Contiguous United States. J. Geophys. Res. 2013, 118, 11228–11241. [Google Scholar] [CrossRef]
  64. Curci, G.; Hogrefe, C.; Bianconi, R.; Im, U.; Balzarini, A.; Baró, R.; Brunner, D.; Forkel, R.; Giordano, L.; Hirtl, M.; et al. Uncertainties of Simulated Aerosol Optical Properties Induced by Assumptions on Aerosol Physical and Chemical Properties: An AQMEII-2 Perspective. Atmos. Environ. 2015, 115, 541–552. [Google Scholar] [CrossRef]
Atmosphere 16 00623 g001
Figure 1. Location of the Aerosol Robotic Network (AERONET) sites. Black triangles mark the sites considered in the assimilation scheme. Red triangles mark the sites chosen for the validation. Figure taken from [29].
Figure 1. Location of the Aerosol Robotic Network (AERONET) sites. Black triangles mark the sites considered in the assimilation scheme. Red triangles mark the sites chosen for the validation. Figure taken from [29].
Atmosphere 16 00623 g001
Atmosphere 16 00623 g002
Figure 2. (a) Spatial and (b) temporal correlation coefficients at 440 (violet lines), 675 (green), and 870 (red) nm for GEOS-Chem output as background (solid lines) and climatology data as background (dashed lines).
Figure 2. (a) Spatial and (b) temporal correlation coefficients at 440 (violet lines), 675 (green), and 870 (red) nm for GEOS-Chem output as background (solid lines) and climatology data as background (dashed lines).
Atmosphere 16 00623 g002
Table 1. Root mean square errors (RMSEs) of the aerosol optical depth (AOD) calculated using GEOS-Chem and assimilated using spatial–temporal optimal interpolation (STOI) with GEOS-Chem output as background (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Table 1. Root mean square errors (RMSEs) of the aerosol optical depth (AOD) calculated using GEOS-Chem and assimilated using spatial–temporal optimal interpolation (STOI) with GEOS-Chem output as background (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Wavelength
nm		GranadaLilleMinsk
GEOS-ChemSTOIGEOS-ChemSTOIGEOS-ChemSTOI
4400.1420.064 (55%)0.1160.094 (19%)0.1300.103 (21%)
6750.1280.048 (62%)0.0890.077 (14%) 0.0740.070 (7%)
8700.1250.046 (63%)0.0810.070 (13%)0.0550.059 (−7%)
Table 2. RMSE of AOD calculated using GEOS-Chem and assimilated using STOI with climatology data as background (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Table 2. RMSE of AOD calculated using GEOS-Chem and assimilated using STOI with climatology data as background (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Wavelength
nm		GranadaLilleMinsk
GEOS-ChemSTOIGEOS-ChemSTOIGEOS-ChemSTOI
4400.1420.064 (55%)0.1160.101 (13%)0.1300.128 (1%)
6750.1280.048 (63%)0.0890.079 (10%)0.0740.069 (8%)
8700.1250.045 (64%)0.0810.071 (12%)0.0550.047 (14%)
Table 3. RMSE of AOD calculated using GEOS-Chem and assimilated using STOI with both GEOS-Chem output and climatology data as backgrounds (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Table 3. RMSE of AOD calculated using GEOS-Chem and assimilated using STOI with both GEOS-Chem output and climatology data as backgrounds (the reduction in RMSE of the estimate after STOI is shown in parentheses).
Wavelength
nm		GranadaLilleMinsk
GEOS-ChemSTOIGEOS-ChemSTOIGEOS-ChemSTOI
4400.1420.063 (56%)0.1160.095 (18%)0.1300.103 (20%)
6750.1280.047 (63%)0.0890.077 (14%)0.0740.060 (20%)
8700.1250.045 (64%)0.0810.070 (13%)0.0550.044 (19%)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Miatselskaya, N.; Bril, A.; Chaikovsky, A. Using Chemical Transport Model and Climatology Data as Backgrounds for Aerosol Optical Depth Spatial–Temporal Optimal Interpolation. Atmosphere 2025, 16, 623. https://doi.org/10.3390/atmos16050623

AMA Style

Miatselskaya N, Bril A, Chaikovsky A. Using Chemical Transport Model and Climatology Data as Backgrounds for Aerosol Optical Depth Spatial–Temporal Optimal Interpolation. Atmosphere. 2025; 16(5):623. https://doi.org/10.3390/atmos16050623

Chicago/Turabian Style

Miatselskaya, Natallia, Andrey Bril, and Anatoly Chaikovsky. 2025. "Using Chemical Transport Model and Climatology Data as Backgrounds for Aerosol Optical Depth Spatial–Temporal Optimal Interpolation" Atmosphere 16, no. 5: 623. https://doi.org/10.3390/atmos16050623

APA Style

Miatselskaya, N., Bril, A., & Chaikovsky, A. (2025). Using Chemical Transport Model and Climatology Data as Backgrounds for Aerosol Optical Depth Spatial–Temporal Optimal Interpolation. Atmosphere, 16(5), 623. https://doi.org/10.3390/atmos16050623

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop