The Development and Application of a Three-Dimensional Corona Discharge Numerical Model Considering the Thunderstorm Electric Field Polarity Reversal Process
Abstract
1. Introduction
2. Establishment and Verification of Model
2.1. The Establishment of the Model
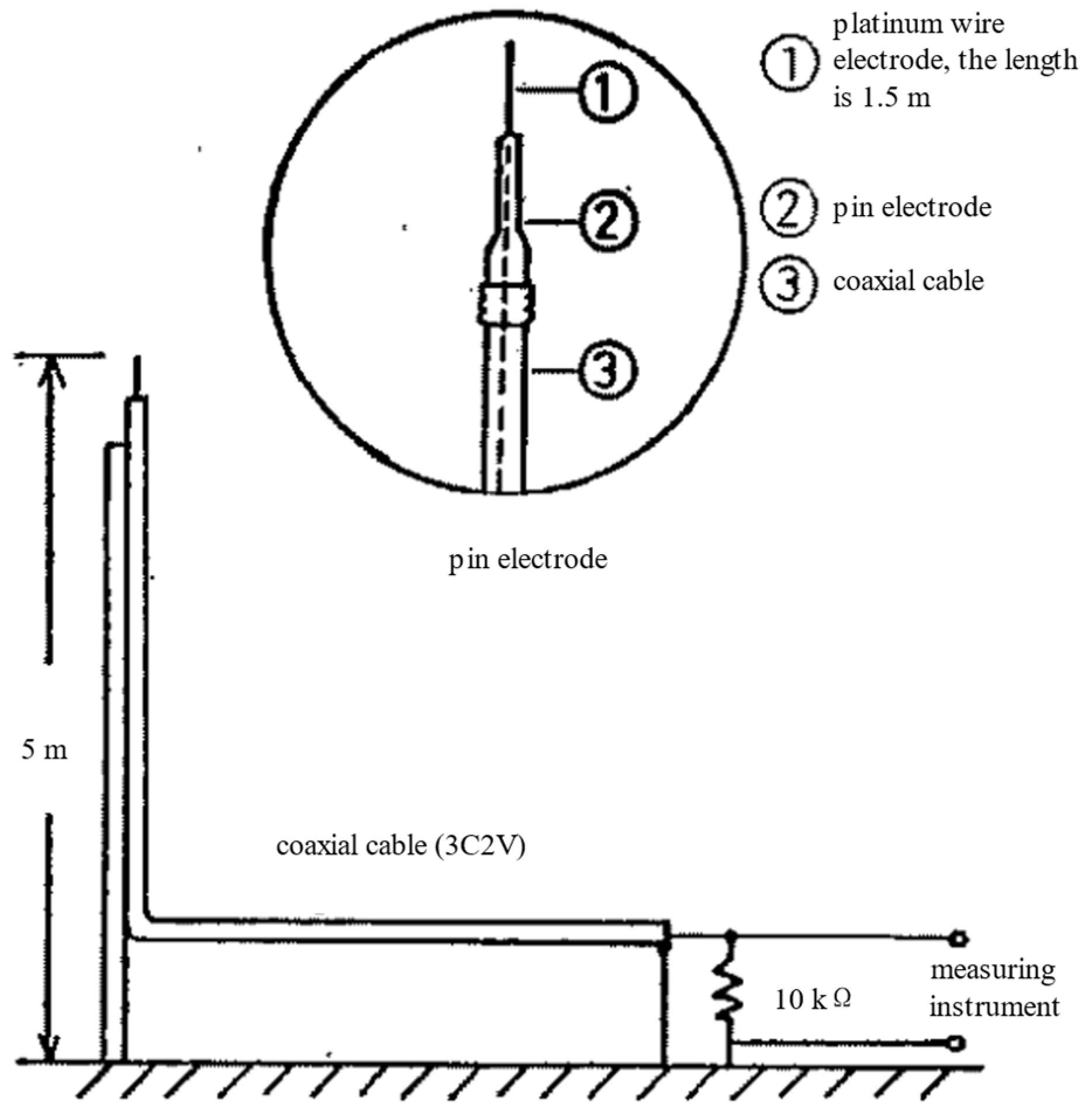
2.2. Model Validation
3. Model Application
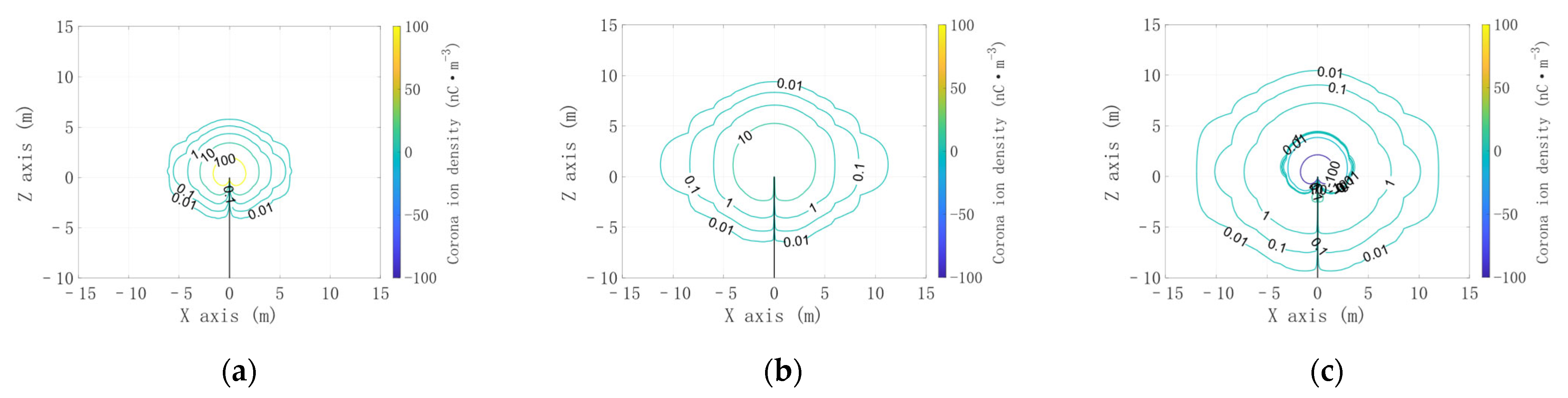
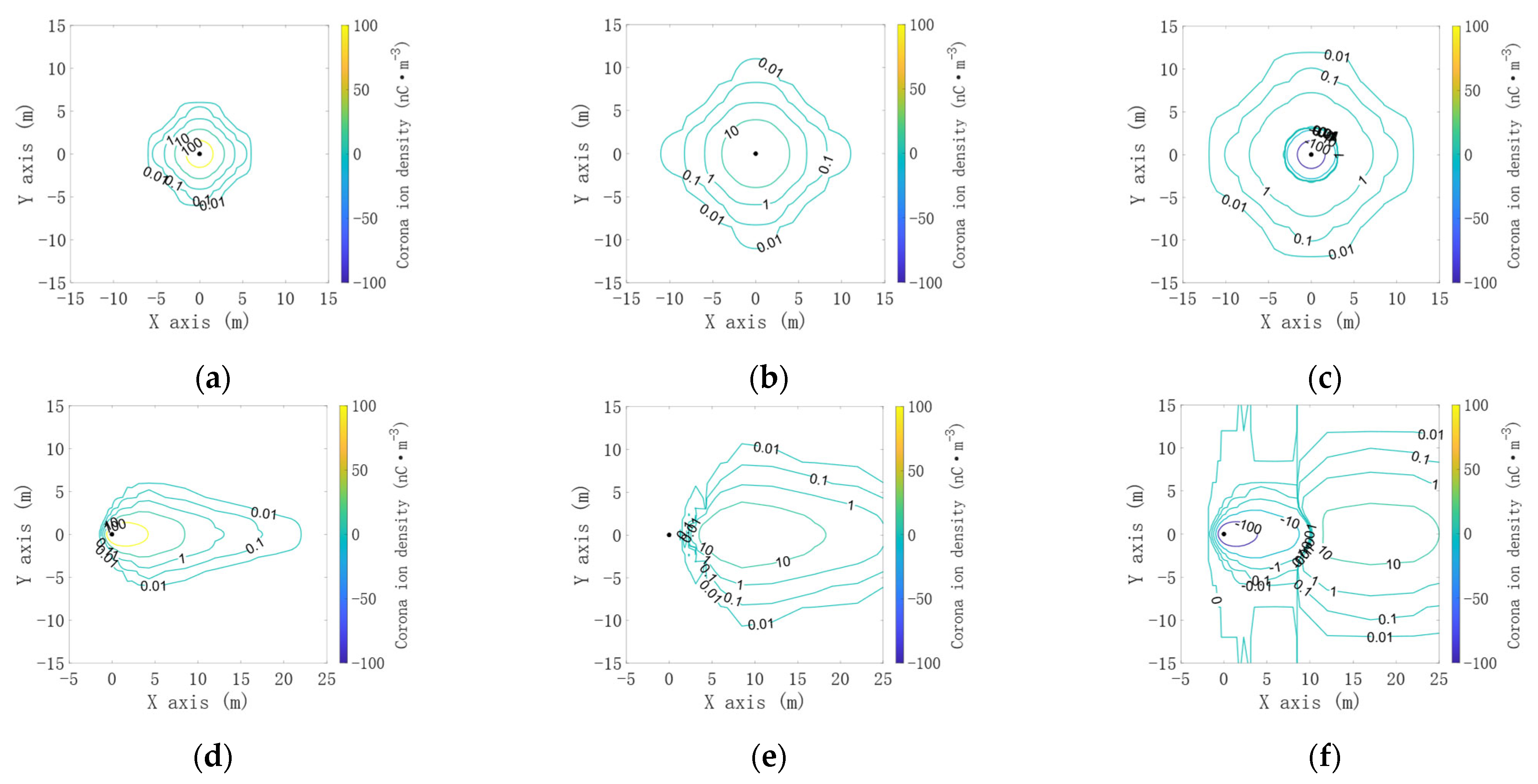
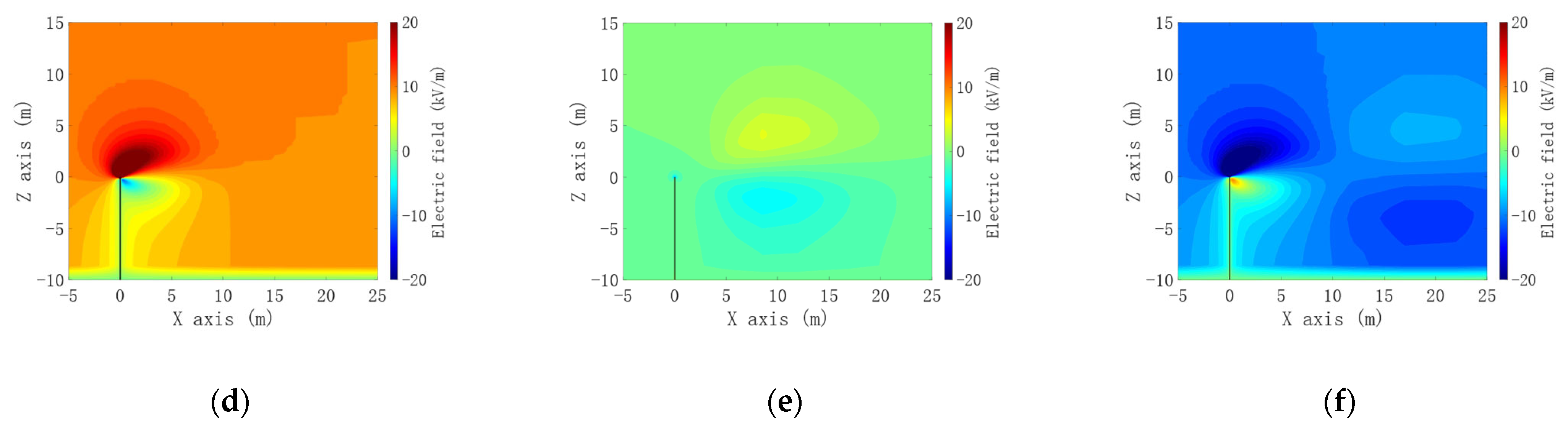
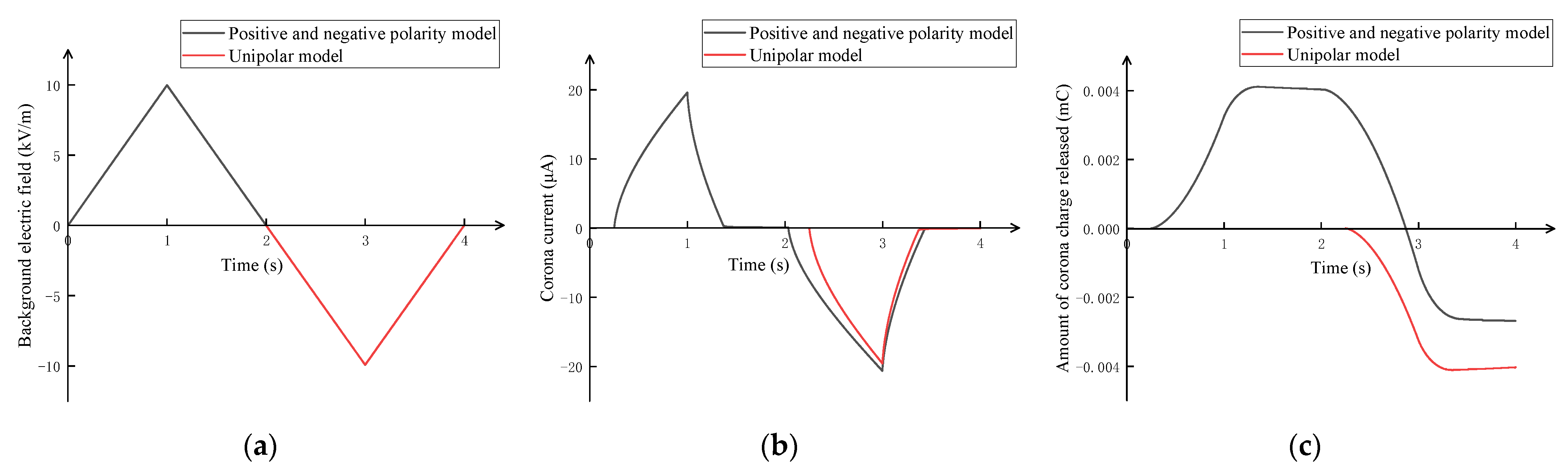
3.1. Comparison of Positive and Negative Corona Discharge Model and Unipolar Corona Discharge Model
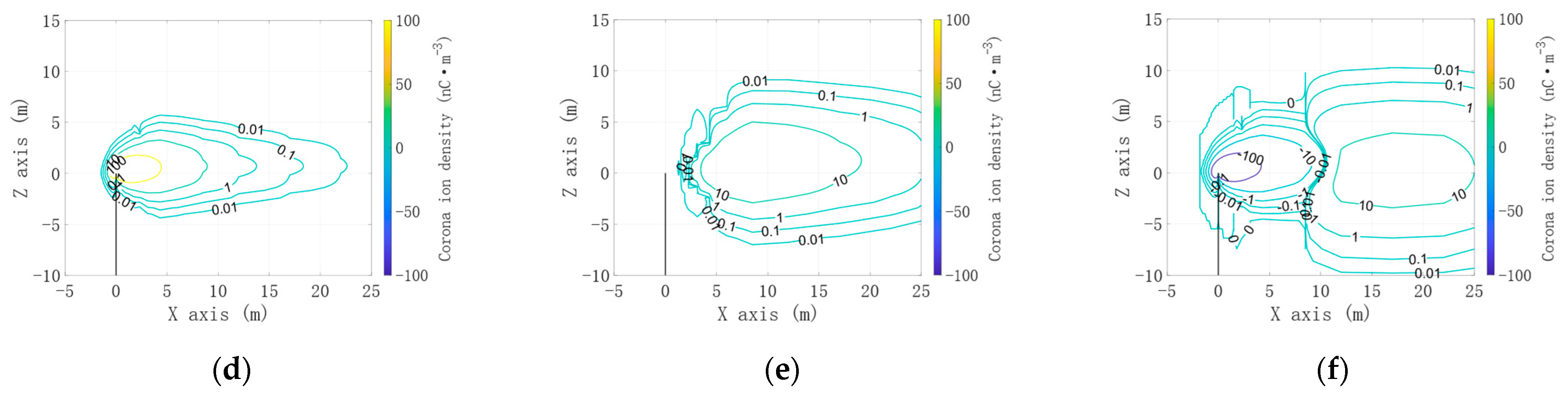
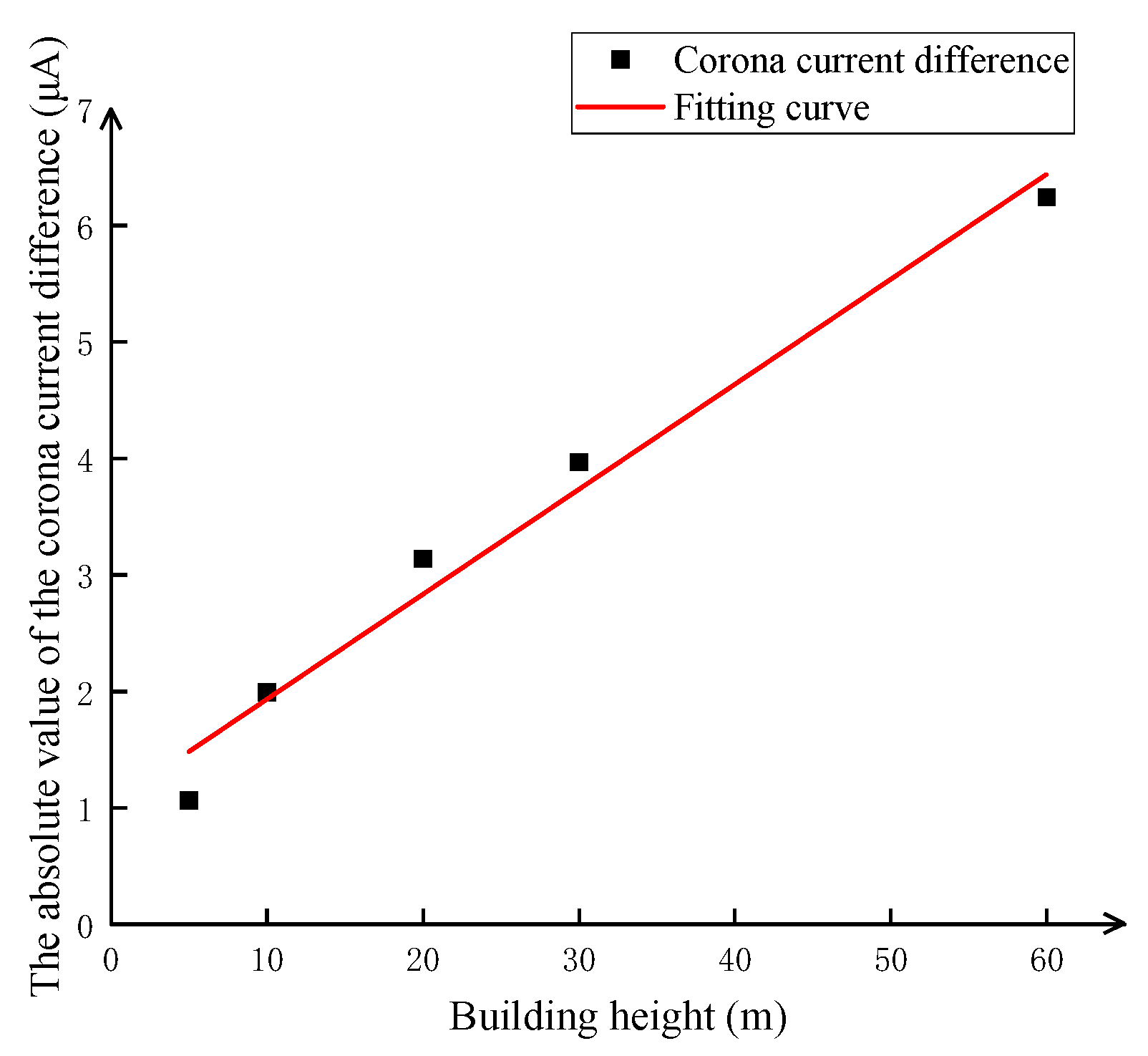
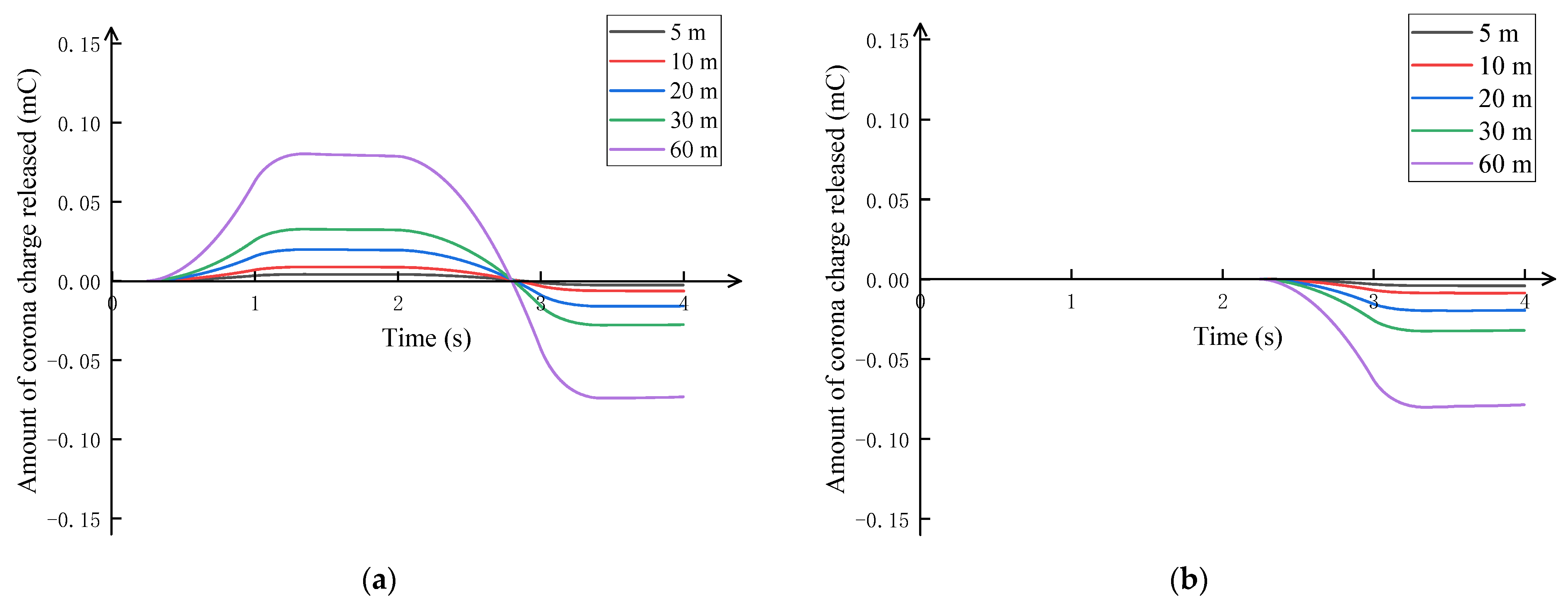
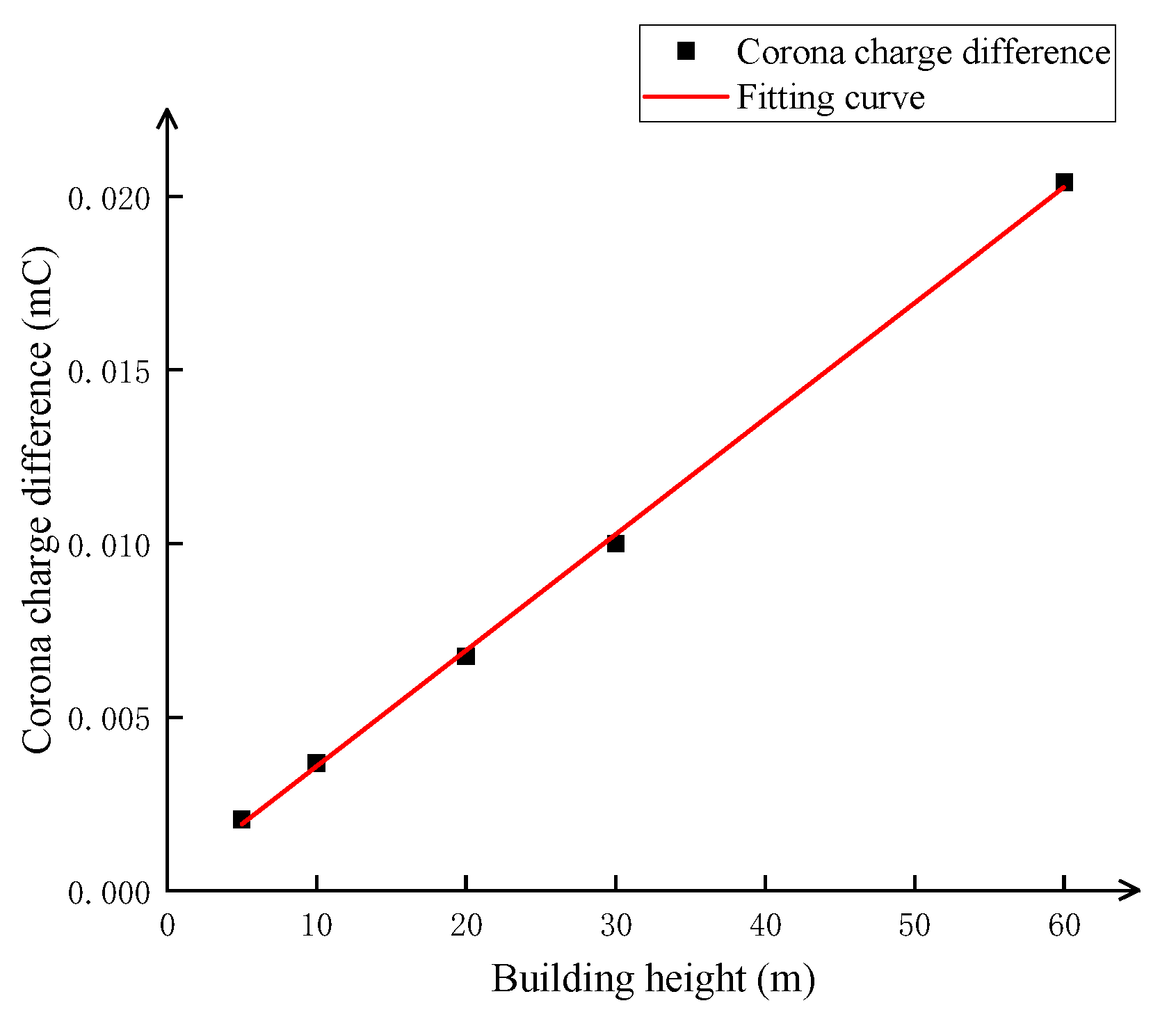
3.2. Comparison of Positive and Negative Corona Discharge Models and Unipolar Corona Discharge Models at Different Building Heights
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Townsend, J.S. Electricity in gases. J. Rőntgen Soc. 1915, 11, 87. [Google Scholar] [CrossRef]
- Moreau, E.; Audier, P.; Benard, N. Ionic wind produced by positive and negative corona discharges in air. J. Electrost. 2018, 93, 85–96. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Meng, J. Lightning detection technology development and data application. J. Appl. Meteor. 2006, 17, 10. [Google Scholar]
- Mokrov, M.S.; Raizer, Y.P. Development of a positive corona from a long grounded wire in a growing thunderstorm field. J. Phys. D Appl. Phys. 2013, 46, 5202. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhou, B.Q. Lightning law and lightning protection design analysis of super high-rise buildings. Guangdong Meteor. 2019, 41, 70–72. [Google Scholar]
- Moore, C.B.; Rison, W. Lightning rod improvement studies. J. Appl. Meteor. 2000, 39, 593–609. [Google Scholar] [CrossRef][Green Version]
- Zipse, D.W. Lightning protection systems: Advantages and disadvantages. IEEE Trans. Ind. Appl. 1994, 30, 1351–1361. [Google Scholar] [CrossRef]
- Qie, X. Lightning Physics; Science Press: Beijing, China, 2013. [Google Scholar]
- Chen, S.S. Simulation Study on Corona Space Charge Distribution Characteristics of UHV DC Transmission Lines During Thunderstorms. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Zeng, F.H.; Guo, F.X. Formation mechanism of positive charge region at the bottom of thunderstorm clouds over inland plateau of China. Sci. Tech. Eng. 2019, 19, 25–33. [Google Scholar]
- Tan, Y.; Guo, X. Influence on simulation accuracy of atmospheric electric field around a building by space resolution. Atmos. Res. 2014, 138, 301–307. [Google Scholar] [CrossRef]
- Tan, Y.B.; Liang, Z.W. Numerical simulation of the effect of lower positive charge region in thunderstorms on different types of lightning. Sci. China Earth Sci. 2014, 57, 2125–2134. [Google Scholar] [CrossRef]
- Luo, H. Study on Corona Discharge Characteristics of Metal Tip. Master’s Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2021. [Google Scholar]
- Tian, Y. Study on the Microscopic Physical Process of AC and DC Corona Discharge. Master’s Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2017. [Google Scholar]
- Higashiyama, Y. Characteristics of discharge current from a needle electrode and its application to detection of a thundercloud approach. Electr. Eng. Jpn. 1979, 99, 411–418. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M. The effect of coronae on leader initiation and development under thunderstorm conditions and in long air gaps. J. Phys. D Appl. Phys. 2001, 34, 3256–3266. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M. Corona discharge at the tip of a tall object in the electric field of a thundercloud. Plasma Phys. Rep. 2002, 28, 953–964. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M. Initiation and development of first lightning leader: The effects of coronae and position of lightning origin. Atmos. Res. 2005, 76, 307–329. [Google Scholar] [CrossRef]
- Bazelyan, E.M.; Raizer, Y.P. The effect of space charge produced by corona at ground level on lightning attachment to high objects. Atmos. Res. 2015, 153, 74–86. [Google Scholar] [CrossRef]
- Becerra, M. Glow corona generation and streamer inception at the tip of grounded objects during thunderstorms: Revisited. J. Phys. D Appl. Phys. 2013, 46, 135205. [Google Scholar] [CrossRef]
- Guo, X.F.; Zhang, Q.L. Establishment and application of corona discharge model with asymmetric structure. Sci. Tech. Eng. 2018, 18, 13–20. [Google Scholar]
- Guo, X.F.; Ji, Z.Y. Research on the influence of lightning rod tip shape on corona discharge. Compu. D. Eng. 2022, 50, 2802. [Google Scholar]
- Qie, X.S. Numerical simulation of temporal and spatial evolution of corona discharge ions at the natural tip of the ground under thunderstorms. J. Geophys. 1996, S1, 43–51. [Google Scholar]
- Becerra, M.; Cooray, V. Effect of the space charge layer created by corona at ground level on the inception of upward lightning leaders from tall towers. J. Geophys. Res. Atmos. 2007, 112, D12. [Google Scholar] [CrossRef]
- Soula, S.; Chauzy, S. Multilevel measurement of the electric field underneath a thundercloud: 2. Dynamical evolution of a ground space charge layer. J. Geophys. Res. Atmos. 1991, 96, 22327–22336. [Google Scholar] [CrossRef]
- Guo, F.X.; Zhang, Y.J. Correlation between thunderstorm cloud electrical activity and microphysical field characteristics in the Northwest Inland Plateau. J. Atmos. Sci. 2012, 35, 205–213. [Google Scholar]
- Bazelyan, E.M.; Raizer, Y.P. Corona processes and lightning attachment: The effect of wind during thunderstorms. Atmos. Res. 2009, 94, 436–447. [Google Scholar] [CrossRef]
- Zou, Y.; He, J.; He, H. Effect of wind on the distribution of the corona discharge ionized field generated from grounded wire during thunderstorms. In Proceedings of the International Conference on Lightning Protection, New York, NY, USA, 11–18 October 2014. [Google Scholar]
- Guo, X.F.; Ji, Z.Y. 3D corona discharge model and its use in the presence of wind during a thunderstorm. Front. Environ. Sci. 2022, 10, 2–8. [Google Scholar] [CrossRef]
- Guo, X.F.; Zhang, L. Development and application of three-dimensional corona discharge model. Sci. Tech. Eng. 2024, 24, 3997–4004. [Google Scholar]
- Peek, F.W. Dielectric Phenomena in High Voltage Engineering; McGraw-Hill Book Company: London, UK, 1920. [Google Scholar]
- Cristina, S.; Dinelli, G. Numerical computation of corona space charge and VI characteristic in DC electrostatic precipitators. IEEE Trans. Ind. Appl. 1991, 27, 147–153. [Google Scholar] [CrossRef]
- Caron, A.; Dascalescu, L. Numerical modeling of combined corona-electrostatic fields. J. Electrostat. 2004, 61, 43–55. [Google Scholar] [CrossRef]
- Nouri, H.; Zebboudj, Y. Analysis of positive corona in wire-to-plate electrostatic precipitator. Eur. Phys. J. Appl. Phys. 2010, 49, 11001. [Google Scholar] [CrossRef]
- Yan, M.H. Numerical calculation of space charge layer distribution due to metal tip discharge under thunderstorms. Atmos. Sci. 1986, 10, 80–87. [Google Scholar]
- Johnson, H.; Graham, M. High Speed Digital Design: A Handbook of Black Magic; Pearson Education India: Hoboken, NJ, USA, 1993. [Google Scholar]
- Mekious, M.; Megherbi, M. Active electrode material influence on the characteristics of corona discharge reactor at atmospheric pressure. Russ. Elect. Eng. 2022, 93, 277–283. [Google Scholar] [CrossRef]
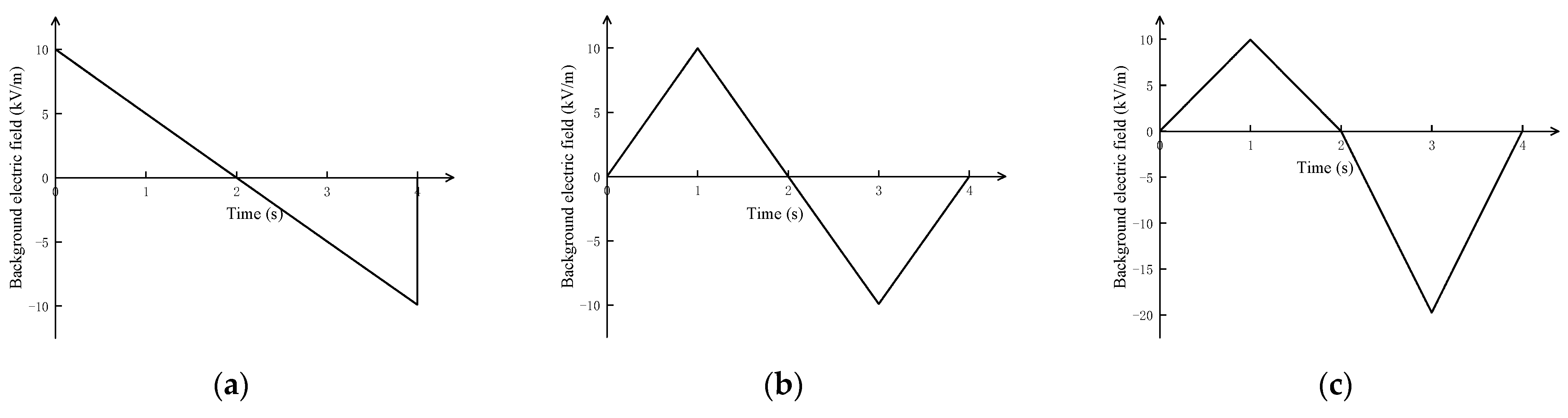



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wu, B.; Guo, X.; Zhao, N.; Zhang, H.; Zhao, Y.; Zheng, Y. The Development and Application of a Three-Dimensional Corona Discharge Numerical Model Considering the Thunderstorm Electric Field Polarity Reversal Process. Atmosphere 2025, 16, 612. https://doi.org/10.3390/atmos16050612
Wang Z, Wu B, Guo X, Zhao N, Zhang H, Zhao Y, Zheng Y. The Development and Application of a Three-Dimensional Corona Discharge Numerical Model Considering the Thunderstorm Electric Field Polarity Reversal Process. Atmosphere. 2025; 16(5):612. https://doi.org/10.3390/atmos16050612
Chicago/Turabian StyleWang, Zhaoxia, Bin Wu, Xiufeng Guo, Nian Zhao, He Zhang, Yubin Zhao, and Yuhang Zheng. 2025. "The Development and Application of a Three-Dimensional Corona Discharge Numerical Model Considering the Thunderstorm Electric Field Polarity Reversal Process" Atmosphere 16, no. 5: 612. https://doi.org/10.3390/atmos16050612
APA StyleWang, Z., Wu, B., Guo, X., Zhao, N., Zhang, H., Zhao, Y., & Zheng, Y. (2025). The Development and Application of a Three-Dimensional Corona Discharge Numerical Model Considering the Thunderstorm Electric Field Polarity Reversal Process. Atmosphere, 16(5), 612. https://doi.org/10.3390/atmos16050612





