Automatic Detection of Whistler Waves in the Top-Side Ionosphere: The WhISPER Technique
Abstract
1. Introduction
2. Data and Methods
2.1. Search Coil Magnetometer
2.2. Electric Field Detector
2.3. Geomagnetic Activity Data
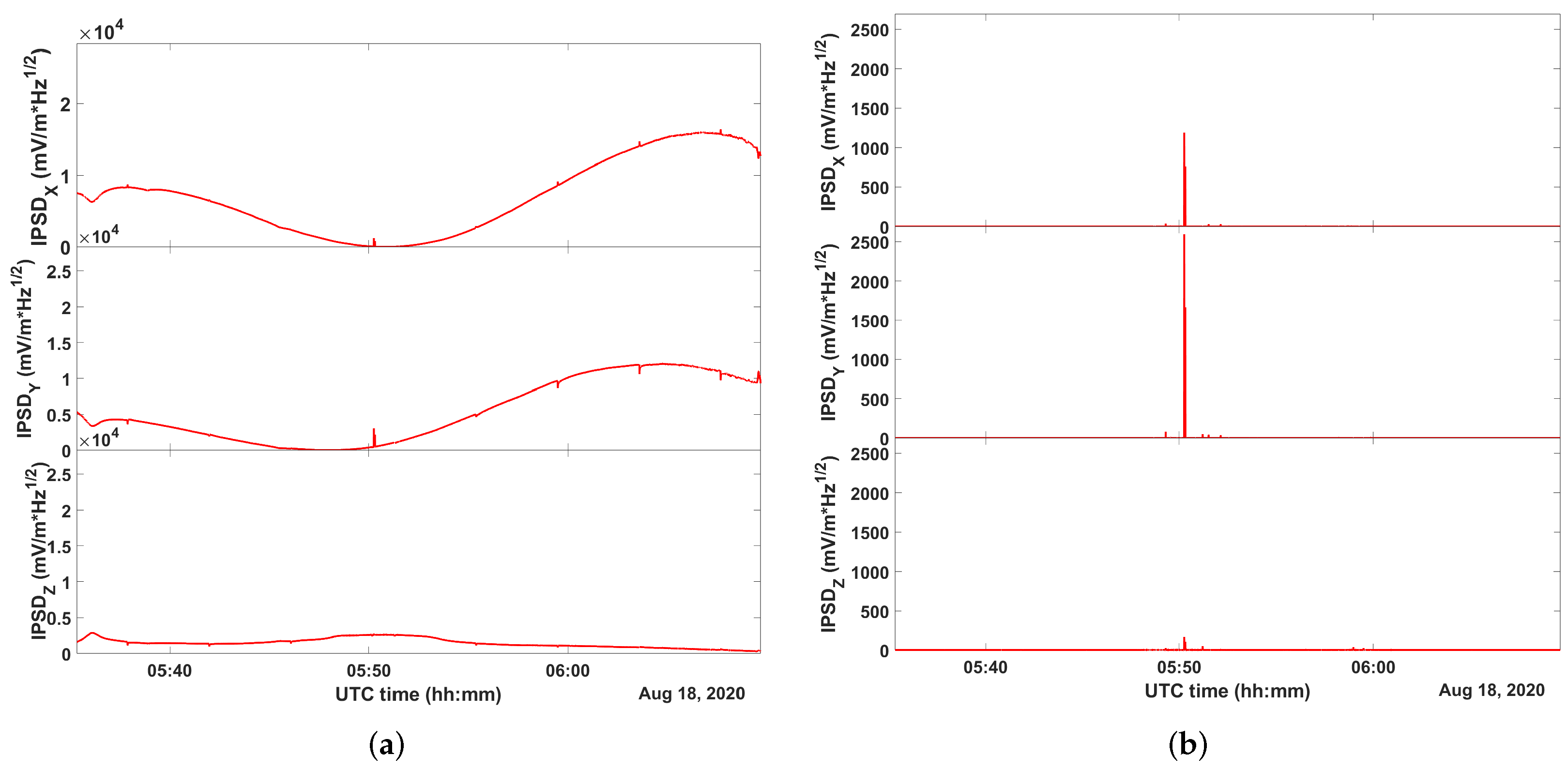
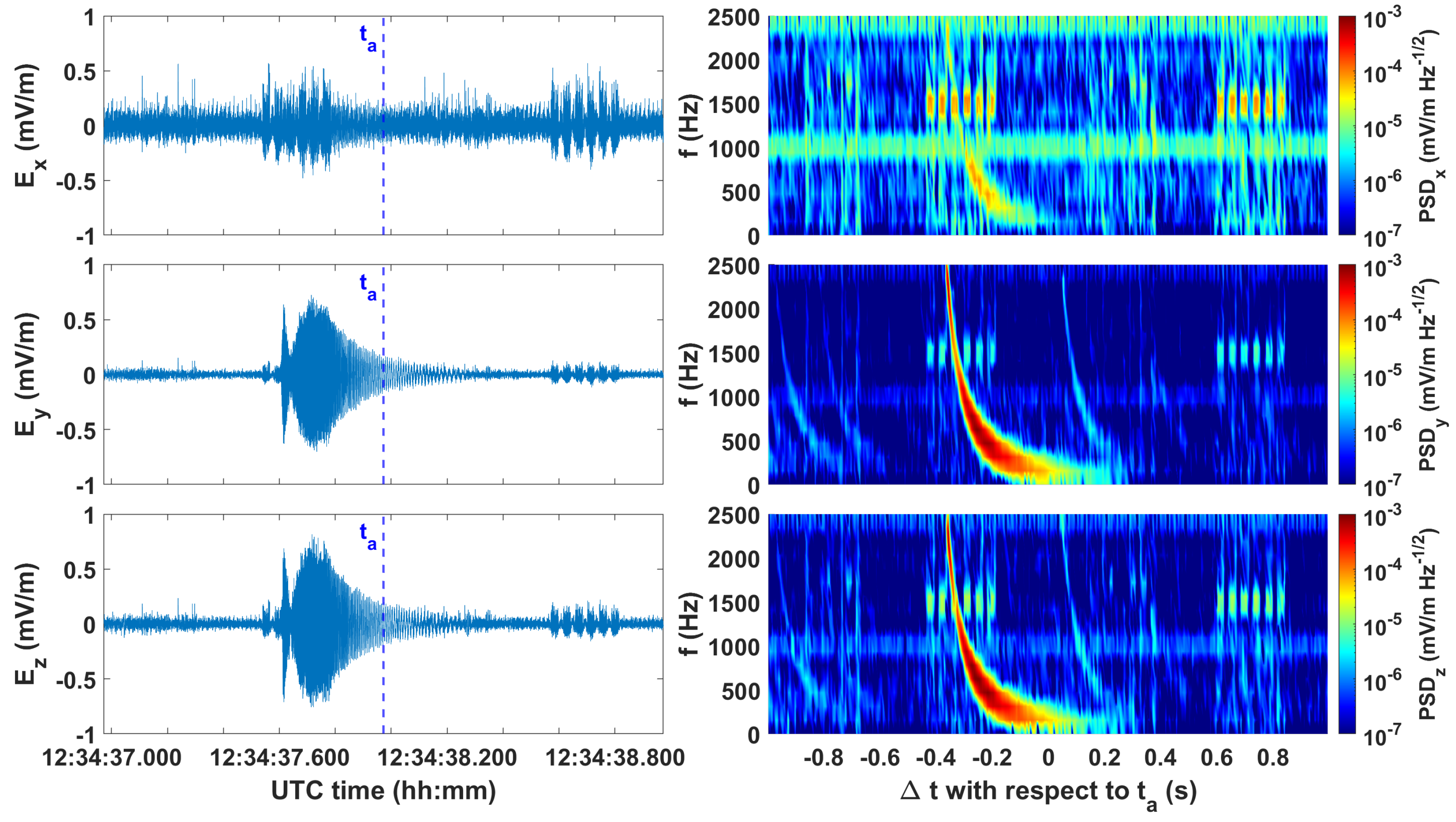
2.4. Detection Algorithm
2.5. Selection Thresholds
- peak amplitude: [];
- peak prominence: , which is a measure of how much the peak stands out relative to other peaks [];
- peak prominence-to-amplitude ratio: R [dimensionless];
- peak width: W, expressed as a multiple of the temporal window (TW) employed for SCM PSD calculations (400 ms).
- > ;
- > ;
- > ;
- W < · TW.
- P (actual positive): spectrograms visually classified as containing whistler waves;
- N (actual negative): spectrograms visually classified as not containing whistler waves;
- TP (true positive): events confirmed as whistlers by the visual inspection and correctly classified as whistlers by WhISPER;
- FN (false negative): events confirmed as whistlers by the visual inspection but incorrectly classified as non-whistlers by WhISPER;
- FP (false positive): events confirmed as non-whistlers by the visual inspection but incorrectly classified as whistlers by WhISPER;
- TN (true negative): events confirmed as non-whistlers by the visual inspection and correctly classified as non-whistlers by WhISPER.
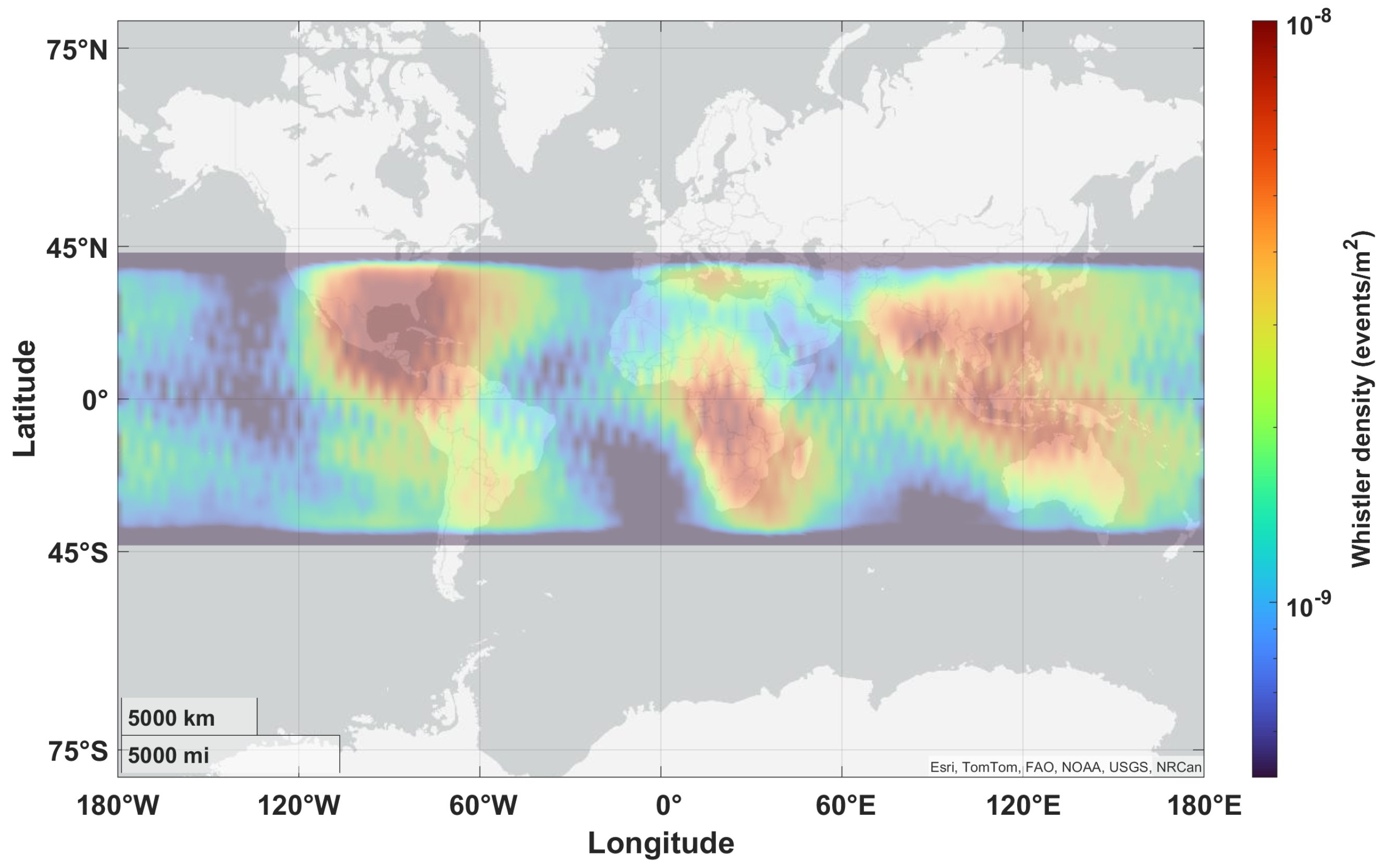
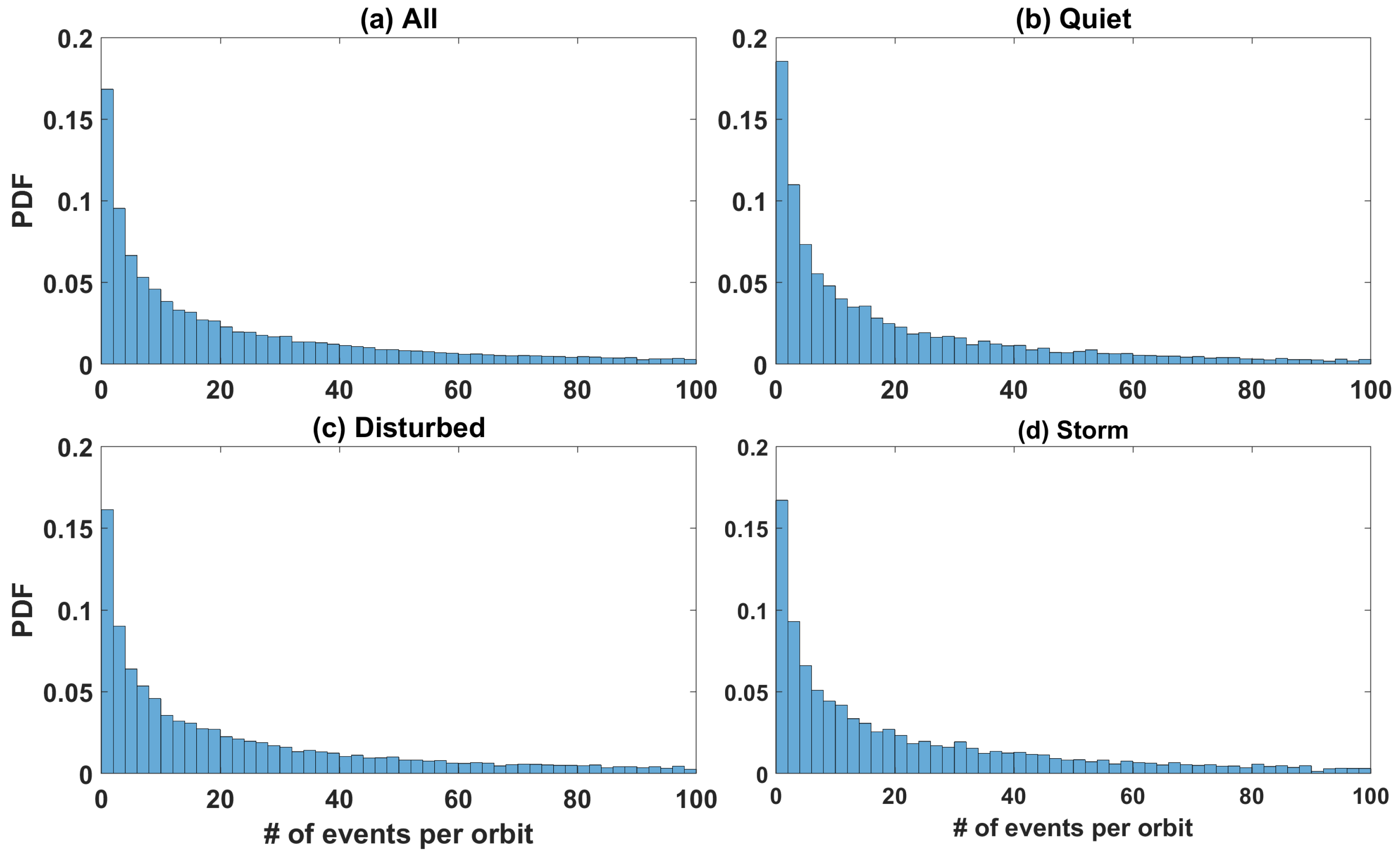
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AWD | Automatic Whistler Detector |
| ASI | Italian Space Agency |
| CNN | Convolutional Neural Network |
| CNSA | China National Space Administration |
| CSES | China Seismo-Electromagnetic Satellite |
| DFT | Discrete Fourier Transform |
| EFD | Electric Field Detector |
| ELF | Extreme Low Frequency |
| GOR | GNSS Occultation Receiver |
| HEPD | High-Energy Particle Detector |
| HEPP | High-Energy Particle Package |
| HPM | High Precision Magnetometer |
| IPSD | Integrated Power Spectral Density |
| LAP | Langumir Probe |
| LEO | Low Earth Orbit |
| PAP | Plasma Analyser Package |
| PLHR | Power Line Harmonic Radiation |
| PSD | Power Spectral Density |
| SCM | Search Coil Magnetometer |
| SR | Schumann Resonances |
| SAA | South Atlantic Anomaly |
| SNR | Signal-to-Noise Ratio |
| STFT | Short-Time Fourier Transform |
| TBB | Tri-Band Beacon |
| TW | Temporal Window |
| VLF | Very Low Frequency |
| WhISPER | Whistler Identification by Spectral Power Estimation and Recognition |
References
- Storey, L. An investigation of whistling atmospherics. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1953, 246, 113–141. [Google Scholar]
- Helliwell, R.; Crary, J.; Pope, J.; Smith, R. The “nose” whistler—A new high-latitude phenomenon. J. Geophys. Res. 1956, 61, 139–142. [Google Scholar] [CrossRef]
- Smith, R.; Helliwell, R.; Yabroff, I. A theory of trapping of whistlers in field-aligned columns of enhanced ionization. J. Geophys. Res. 1960, 65, 815–823. [Google Scholar] [CrossRef]
- Carpenter, D.L. Electron-density variations in the magnetosphere deduced from whistler data. J. Geophys. Res. 1962, 67, 3345–3360. [Google Scholar] [CrossRef]
- Park, C. Some features of plasma distribution in the plasmasphere deduced from Antarctic whistlers. J. Geophys. Res. 1974, 79, 169–173. [Google Scholar] [CrossRef]
- Tarcsai, G.; Szemeredy, P.; Hegymegi, L. Average electron density profiles in the plasmasphere between L = 1.4 and 3.2 deduced from whistlers. J. Atmos. Terr. Phys. 1988, 50, 607–611. [Google Scholar] [CrossRef]
- Park, C.G. Whistler observations of the interchange of ionization between the ionosphere and the protonosphere. J. Geophys. Res. (1896-1977) 1970, 75, 4249–4260. [Google Scholar] [CrossRef]
- Carpenter, D.L. Whistler evidence of a ‘knee’ in the magnetospheric ionization density profile. J. Geophys. Res. 1963, 68, 1675–1682. [Google Scholar] [CrossRef]
- Carpenter, D.; Anderson, R. An ISEE/whistler model of equatorial electron density in the magnetosphere. J. Geophys. Res. Space Phys. 1992, 97, 1097–1108. [Google Scholar] [CrossRef]
- Horne, R.B.; Thorne, R.M.; Glauert, S.A.; Albert, J.M.; Meredith, N.P.; Anderson, R.R. Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. Space Phys. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Thorne, R.; Li, W.; Ni, B.; Ma, Q.; Bortnik, J.; Chen, L.; Baker, D.; Spence, H.E.; Reeves, G.; Henderson, M.; et al. Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 2013, 504, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Shen, X.C.; Ma, Q.; Capannolo, L.; Shi, R.; Redmon, R.; Rodriguez, J.; Reeves, G.; Kletzing, C.; Kurth, W.; et al. Quantification of energetic electron precipitation driven by plume whistler mode waves, plasmaspheric hiss, and exohiss. Geophys. Res. Lett. 2019, 46, 3615–3624. [Google Scholar] [CrossRef]
- Ma, Q.; Li, W.; Zhang, X.J.; Bortnik, J.; Shen, X.C.; Connor, H.; Boyd, A.; Kurth, W.; Hospodarsky, G.; Claudepierre, S.; et al. Global survey of electron precipitation due to hiss waves in the Earth’s plasmasphere and plumes. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029644. [Google Scholar] [CrossRef]
- Thorne, R.; Horne, R.; Meredith, N. Comment on “On the origin of whistler mode radiation in the plasmasphere” by Green et al. J. Geophys. Res.-ALL Ser. 2006, 111, A09210. [Google Scholar] [CrossRef]
- Záhlava, J.; Němec, F.; Santolík, O.; Kolmašová, I.; Hospodarsky, G.; Parrot, M.; Kurth, W.; Kletzing, C. Lightning contribution to overall whistler mode wave intensities in the plasmasphere. Geophys. Res. Lett. 2019, 46, 8607–8616. [Google Scholar] [CrossRef]
- Gołkowski, M.; Harid, V.; Hosseini, P. Review of controlled excitation of non-linear wave-particle interactions in the magnetosphere. Front. Astron. Space Sci. 2019, 6, 2. [Google Scholar] [CrossRef]
- Hwang, J.A.; Lee, D.Y.; Lyons, L.; Smith, A.; Zou, S.; Min, K.; Kim, K.H.; Moon, Y.J.; Park, Y. Statistical significance of association between whistler-mode chorus enhancements and enhanced convection periods during high-speed streams. J. Geophys. Res. Space Phys. 2007, 112, A09213. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, J.; Cao, J.; Liu, Y.; Huang, J.; Li, B.; Wang, Q.; Zhang, Z.; Zhao, Z.; Han, Y.; et al. Spaceborne Algorithm for Recognizing Lightning Whistler Recorded by an Electric Field Detector Onboard the CSES Satellite. Atmosphere 2023, 14, 1633. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, J.; Yuan, J.; Hu, R.; Peng, X.; Chen, A.; Shen, X. Lightning-generated Whistlers recognition for accurate disaster monitoring in China and its surrounding areas based on a homologous dual-feature information enhancement framework. Remote Sens. Environ. 2024, 304, 114021. [Google Scholar] [CrossRef]
- Harid, V.; Liu, C.; Pang, Y.; Alvina, A.J.; Golkowski, M.; Hosseini, P.; Cohen, M. Automated large-scale extraction of whistlers using mask-scoring regional convolutional neural network. Geophys. Res. Lett. 2021, 48, e2021GL093819. [Google Scholar] [CrossRef]
- Barbarino, G.; Cicone, A. Stabilization and variations to the adaptive local iterative filtering algorithm: The fast resampled iterative filtering method. Numer. Math. 2024, 156, 395–433. [Google Scholar] [CrossRef]
- Lichtenberger, J.; Ferencz, C.; Bodnár, L.; Hamar, D.; Steinbach, P. Automatic whistler detector and analyzer system: Automatic whistler detector. J. Geophys. Res. Space Phys. 2008, 113, A12201. [Google Scholar] [CrossRef]
- Suarjaya, I.M.A.D.; Putri, D.P.S.; Tanaka, Y.; Purnama, F.; Bayupati, I.P.A.; Linawati; Kasahara, Y.; Matsuda, S.; Miyoshi, Y.; Shinohara, I. Deep Learning Model Size Performance Evaluation for Lightning Whistler Detection on Arase Satellite Dataset. Remote Sens. 2024, 16, 4264. [Google Scholar] [CrossRef]
- Záhlava, J.; Němec, F.; Pinçon, J.L.; Santolík, O.; Kolmašová, I.; Parrot, M. Whistler influence on the overall very low frequency wave intensity in the upper ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 5648–5660. [Google Scholar] [CrossRef]
- Bernard, L. A new nose extension method for whistlers. J. Atmos. Terr. Phys. 1973, 35, 871–880. [Google Scholar] [CrossRef]
- Stanford. The Stanford VLF Group Automated Detection of Whistlers for the TARANIS Spacecraft. Overview of the Project. Available online: https://vlfstanford.ku.edu.tr (accessed on 8 September 2024).
- Dharma, K.S.; Bayupati, I.; Buana, P.W. Automatic Lightning Whistler Detection Using Connected Component Labeling Method. J. Theor. Appl. Inf. Technol. 2014, 66, 638–645. [Google Scholar]
- Ali Ahmad, U.; Kasahara, Y.; Matsuda, S.; Ozaki, M.; Goto, Y. Automatic detection of lightning whistlers observed by the plasma wave experiment onboard the Arase satellite using the OpenCV library. Remote Sens. 2019, 11, 1785. [Google Scholar] [CrossRef]
- Konan, O.J.; Mishra, A.K.; Lotz, S. Machine learning techniques to detect and characterise whistler radio waves. arXiv 2020, arXiv:2002.01244. [Google Scholar]
- Ran, Z.; Lu, C.; Hu, Y.; Yang, D.; Sun, X.; Zhima, Z. Automatic Detection of Quasi-Periodic Emissions from Satellite Observations by Using DETR Method. Remote Sens. 2024, 16, 2850. [Google Scholar] [CrossRef]
- Picozza, P.; Battiston, R.; Ambrosi, G.; Bartocci, S.; Basara, L.; Burger, W.; Campana, D.; Carfora, L.; Casolino, M.; Castellini, G.; et al. Scientific goals and in-orbit performance of the high-energy particle detector on board the CSES. Astrophys. J. Suppl. Ser. 2019, 243, 16. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The state-of-the-art of the China Seismo-Electromagnetic Satellite mission. Sci. China Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Cao, J.; Zeng, L.; Zhan, F.; Wang, Z.; Wang, Y.; Chen, Y.; Meng, Q.; Ji, Z.; Wang, P.; Liu, Z.; et al. The electromagnetic wave experiment for CSES mission: Search coil magnetometer. Sci. China Technol. Sci. 2018, 61, 653–658. [Google Scholar] [CrossRef]
- Walker, A. The theory of whistler propagation. Rev. Geophys. 1976, 14, 629–638. [Google Scholar] [CrossRef]
- Diego, P.; Huang, J.; Piersanti, M.; Badoni, D.; Zeren, Z.; Yan, R.; Rebustini, G.; Ammendola, R.; Candidi, M.; Guan, Y.B.; et al. The Electric Field Detector on Board the China Seismo Electromagnetic Satellite—In-Orbit Results and Validation. Instruments 2021, 5, 1. [Google Scholar] [CrossRef]
- Huang, J.; Lei, J.; Li, S.; Zeren, Z.; Li, C.; Zhu, X.; Yu, W. The Electric Field Detector (EFD) onboard the ZH-1 satellite and first observational results. Earth Planet. Phys. 2018, 2, 469–478. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Tsurutani, B.T. Geomagnetic storms: Historical perspective to modern view. Geosci. Lett. 2016, 3, 1–11. [Google Scholar] [CrossRef]
- Iyemori, T. Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J. Geomagn. Geoelectr. 1990, 42, 1249–1265. [Google Scholar] [CrossRef]
- Recchiuti, D.; D’Angelo, G.; Papini, E.; Diego, P.; Cicone, A.; Parmentier, A.; Ubertini, P.; Battiston, R.; Piersanti, M. Detection of electromagnetic anomalies over seismic regions during two strong (MW > 5) earthquakes. Front. Earth Sci. 2023, 11, 1152343. [Google Scholar] [CrossRef]
- King, J.; Papitashvili, N. Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. Space Phys. 2005, 110, A02104. [Google Scholar] [CrossRef]
- Svenningsson, I.; Yordanova, E.; Khotyaintsev, Y.V.; André, M.; Cozzani, G.; Steinvall, K. Whistler waves in the quasi-parallel and quasi-perpendicular magnetosheath. J. Geophys. Res. Space Phys. 2024, 129, e2024JA032661. [Google Scholar] [CrossRef]
- Sentman, D.D. Schumann resonances. In Handbook of Atmospheric Electrodynamics; CRC Press: Boca Raton, FL, USA, 2017; Volume I, pp. 267–295. [Google Scholar]
- Karslı, H.; Dondurur, D. A mean-based filter to remove power line harmonic noise from seismic reflection data. J. Appl. Geophys. 2018, 153, 90–99. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Park, S.A.; Falkowski, B.J.; Lakhina, G.S.; Pickett, J.S.; Bortnik, J.; Hospodarsky, G.; Santolik, O.; Parrot, M.; Henri, P.; et al. Plasmaspheric hiss: Coherent and intense. J. Geophys. Res. Space Phys. 2018, 123, 10-009. [Google Scholar] [CrossRef]
- Malaspina, D.M.; Ripoll, J.F.; Chu, X.; Hospodarsky, G.; Wygant, J. Variation in plasmaspheric hiss wave power with plasma density. Geophys. Res. Lett. 2018, 45, 9417–9426. [Google Scholar] [CrossRef]
- Zhima, Z.; Zhou, B.; Zhao, S.; Wang, Q.; Huang, J.; Zeng, L.; Lei, J.; Chen, Y.; Li, C.; Yang, D.; et al. Cross-calibration on the electromagnetic field detection payloads of the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2022, 65, 1415–1426. [Google Scholar] [CrossRef]
- Yang, D.; Zhima, Z.; Wang, Q.; Huang, J.; Wang, X.; Zhang, Z.; Zhao, S.; Guo, F.; Cheng, W.; Lu, H.; et al. Stability validation on the VLF waveform data of the China-Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2022, 65, 3069–3078. [Google Scholar] [CrossRef]
- Collier, A.B.; Delport, B.; Hughes, A.R.; Lichtenberger, J.; Steinbach, P.; Öster, J.; Rodger, C. Correlation between global lightning and whistlers observed at Tihany, Hungary. J. Geophys. Res. Space Phys. 2009, 114, A07210. [Google Scholar] [CrossRef]
- Collier, A.; Hughes, A.R.W.; Lichtenberger, J.; Steinbach, P. Seasonal and diurnal variation of lightning activity over southern Africa and correlation with European whistler observations. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2006; Volume 24, pp. 529–542. [Google Scholar]
- Collier, A.B.; Lichtenberger, J.; Clilverd, M.A.; Rodger, C.; Steinbach, P. Source region for whistlers detected at Rothera, Antarctica. J. Geophys. Res. Space Phys. 2011, 116, A03219. [Google Scholar] [CrossRef]
- Kaplan, J.O.; Lau, K.H.K. World wide lightning location network (WWLLN) global lightning climatology (WGLC) and time series, 2022 update. Earth Syst. Sci. Data 2022, 14, 5665–5670. [Google Scholar] [CrossRef]
- Bitzer, P.M. Global distribution and properties of continuing current in lightning. J. Geophys. Res. Atmos. 2017, 122, 1033–1041. [Google Scholar] [CrossRef]
- Rodger, C.; Werner, S.; Brundell, J.B.; Lay, E.H.; Thomson, N.R.; Holzworth, R.H.; Dowden, R. Detection efficiency of the VLF World-Wide Lightning Location Network (WWLLN): Initial case study. In Annales Geophysicae; Copernicus GmbH: Göttingen, Germany, 2006; Volume 24, pp. 3197–3214. [Google Scholar]
- Delport, B.; Collier, A.; Steinbach, J.L.P.; Parrot, M. Correlating fractional hop whistlers detected on DEMETER with WWLLN lightning. In Proceedings of the 56th Annual Conference of the South African Institute of Physics, Pretoria, South Africa, 4–8 July 2011. [Google Scholar]
- Němec, F.; Santolík, O.; Hospodarsky, G.; Hajoš, M.; Demekhov, A.; Kurth, W.; Parrot, M.; Hartley, D. Whistler mode quasiperiodic emissions: Contrasting Van Allen Probes and DEMETER occurrence rates. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027918. [Google Scholar] [CrossRef]
- Holle, R.L.; Cummins, K.L.; Brooks, W.A. Seasonal, monthly, and weekly distributions of NLDN and GLD360 cloud-to-ground lightning. Mon. Weather Rev. 2016, 144, 2855–2870. [Google Scholar] [CrossRef]
- Dowdy, A.J.; Kuleshov, Y. Climatology of lightning activity in Australia: Spatial and seasonal variability. Aust. Meteorol. Oceanogr. J. 2014, 64, 103–108. [Google Scholar] [CrossRef]
- Helliwell, R.A. Whistlers and Related Ionospheric Phenomena; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Laaspere, T.; Morgan, M.; Johnson, W. Some results of five years of whistler observations from Labrador to Antarctica. Proc. IEEE 1963, 51, 554–568. [Google Scholar] [CrossRef]
- Kumar, S.; Anil, D.; Kishore, A.; Ramachandran, V. Whistlers observed at low-latitude ground-based VLF facility in Fiji. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1366–1376. [Google Scholar] [CrossRef]
- Sonwalkar, V.; Carpenter, D.; Bell, T.; Spasojević, M.; Inan, U.; Li, J.; Chen, X.; Venkatasubramanian, A.; Harikumar, J.; Benson, R.; et al. Diagnostics of magnetospheric electron density and irregularities at altitudes< 5000 km using whistler and Z mode echoes from radio sounding on the IMAGE satellite. J. Geophys. Res. Space Phys. 2004, 109, A11212. [Google Scholar]
- Zhang, H.; Zhong, Z.; Lu, J.; Wang, M.; Yi, Y.; Tang, R.; Deng, X. Statistical Properties of Whistler-mode Waves in the Dayside Terrestrial Space: MMS Observations. Astrophys. J. 2024, 969, 14. [Google Scholar] [CrossRef]
- Fiser, J.; Chum, J.; Diendorfer, G.; Parrot, M.; Santolík, O. Whistler intensities above thunderstorms. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2010; Volume 28, pp. 37–46. [Google Scholar]
- Coïsson, P.; Hulot, G.; Vigneron, P.; Deram, P.; Léger, J.M.; Jager, T. 0+ whistlers in the ELF band recorded by Swarm satellites used to reconstruct the ionosphere below the satellite height. In Proceedings of the Geophysical Research Abstracts, EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019; Volume 21. [Google Scholar]






| Band | Sampling Frequency (Hz) | Frequency Range (Hz) |
|---|---|---|
| ULF | 1024 | 10–200 |
| ELF | 200–2200 | |
| VLF | – |
| Band | Sampling Frequency (Hz) | Frequency Range (Hz) |
|---|---|---|
| ULF | 125 | –16 |
| ELF | 6–2200 | |
| VLF | – | |
| HF | – |
| ⋄ | (TW) | |||
|---|---|---|---|---|
| Set 1 | 0.29 | 0.25 | 0.5 | 2 |
| Set 2 | 0.9 | 0.6 | 0.65 | 2 |
| Set 3 | 0.1 | 0.05 | 0.3 | 3 |
| Total Population P + N = 1346 | Set 1 | Set 2 | Set 3 | |||
|---|---|---|---|---|---|---|
| P 1232 | TP 1180 | FN 52 | TP 453 | FN 779 | TP 1232 | FN 0 |
| N 114 | FP 7 | TN 107 | FP 4 | TN 110 | FP 113 | TN 1 |
| Metrics | Set 1 | Set 2 | Set 3 |
|---|---|---|---|
| Accuracy | 0.96 | 0.42 | 0.92 |
| True Positive Rate | 0.96 | 0.37 | 1 |
| False Negative Rate | 0.04 | 0.63 | 0 |
| False Positive Rate | 0.06 | 0.04 | 0.99 |
| True Negative Rate | 0.94 | 0.96 | 0.01 |
| Positive Predictive Value | 0.99 | 0.99 | 0.92 |
| False Omission Rate | 0.33 | 0.88 | 0 |
| False Discovery Rate | 0.01 | 0.01 | 0.08 |
| Negative Predicted Value | 0.67 | 0.12 | 1 |
|
score | 0.98 | 0.54 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Recchiuti, D.; Battiston, R.; D’Angelo, G.; Papini, E.; Neubüser, C.; Burger, W.J.; Piersanti, M. Automatic Detection of Whistler Waves in the Top-Side Ionosphere: The WhISPER Technique. Atmosphere 2025, 16, 522. https://doi.org/10.3390/atmos16050522
Recchiuti D, Battiston R, D’Angelo G, Papini E, Neubüser C, Burger WJ, Piersanti M. Automatic Detection of Whistler Waves in the Top-Side Ionosphere: The WhISPER Technique. Atmosphere. 2025; 16(5):522. https://doi.org/10.3390/atmos16050522
Chicago/Turabian StyleRecchiuti, Dario, Roberto Battiston, Giulia D’Angelo, Emanuele Papini, Coralie Neubüser, William Jerome Burger, and Mirko Piersanti. 2025. "Automatic Detection of Whistler Waves in the Top-Side Ionosphere: The WhISPER Technique" Atmosphere 16, no. 5: 522. https://doi.org/10.3390/atmos16050522
APA StyleRecchiuti, D., Battiston, R., D’Angelo, G., Papini, E., Neubüser, C., Burger, W. J., & Piersanti, M. (2025). Automatic Detection of Whistler Waves in the Top-Side Ionosphere: The WhISPER Technique. Atmosphere, 16(5), 522. https://doi.org/10.3390/atmos16050522












