Abstract
Forecasting thunderstorms, along with their intensity and phenomenon, is still one of the most challenging tasks in modern weather forecasting. One of the methods for this prediction is based on the indices of convective instability in the atmosphere. For the first time, we analysed the values and trends of 23 stability indices on days when hail occurred. From 2005 to 2020, the most frequently observed hailstones had a diameter between 13 and 20 mm, which accounted for 35.8% of all hail days, which was 826. Huge hailstones with a greater than 50 mm diameter were observed on only two days. Eight of the 23 stability indices show a monotonically decreasing (Showalter Index, Lifted Index, Lifted Index using the virtual temperature, and Humidity Index) or increasing trend (K Index, Convective Available Potential Energy for the most unstable air parcel and for mixing layer, and Convective Available Potential Energy in the layer between air temperatures −10 and −30 °C). These trends indicate that the environment is becoming increasingly favourable for the formation of thunderstorms. However, this potential does not appear to be fully realised, as the frequency of severe and large hail (with diameters of 21 mm or more) has not increased during the period studied.
1. Introduction
Hail is defined as precipitation in the form of transparent or partly or completely opaque ice particles with a diameter of 5 mm or more. Smaller particles of translucent ice that are usually spherical and sometimes have conical tips, with diameters smaller than 5 mm, are called small hail [1]. Hail causes considerable damage to property in Serbia during the warm season. It almost always forms in cumulonimbus clouds. According to the recognised model of the thunderstorm clouds [2], there is a region in these clouds where hail embryos form and a zone where hail grows. The first is located at the front of the main updraft region relative to the direction of movement of the thunderstorm and the second is a region of stronger updrafts situated within the high vertical velocity zone between −10 and −30 °C. Hail forms in the regions containing supercooled cloud droplets and ice embryos. Sufficiently strong updrafts are also required to support growing hailstones. Hailstones grow when hail embryos collide with supercooled cloud droplets, which immediately freeze partially or completely on their surface after an impact. If all of the supercooled water on the surface of the hailstone freezes, this is referred to as dry growth. In wet growth, some of the supercooled water remains unfrozen and fills the air spaces on the hailstones before it freezes. The signature of these types of growth is visible as multiple layers of hailstones. The hail embryo will grow into a large hailstone if there is enough available supercooled water that it can collect. However, if there is a large number of hail embryos competing for the available supercooled water, the resulting hailstones will be smaller. Larger hailstones cause more damage than smaller ones due to their greater kinetic energy.
It is difficult to predict exactly when and where hail will occur. Stability indices or convective parameters assess the stability of the atmosphere and the ability to develop thunderstorm activity and extreme weather. They are calculated from the state of the atmosphere before the development of a thunderstorm, including convective instability and the availability of moisture at low altitudes, which are among the most important atmospheric factors for hail-prone thunderstorms. Meteorologists use these indices to identify areas where conditions are favourable for the development of thunderstorms. The index forecast quality may sometimes exceeds the skills of numerical weather models [3]. They can be used as predictors of the probability of occurrence and intensity of thunderstorms.
The purpose of these indices is to represent conditional, latent, or potential instability in the atmosphere. A layer of air is considered conditionally unstable if the environmental lapse rate lies between the dry and wet adiabatic lapse rate curves on a thermodynamic diagram. Indices that capture this condition include the Vertical Totals (VT) and the Boyden Index (BI).
In contrast, a layer is classified as latently unstable if the actual lapse rate above the level of free convection is lower than the wet adiabatic lapse rate. The Convective Available Potential Energy (CAPE), Lifted Index (LI), and Showalter Index (SI) are used to represent these conditions. Potential instability refers to a condition in the air layer where the potential temperature decreases with height. This study did not consider specific indices that describe these conditions, such as the KO index and the potential instability index. Instead, we focused on the total totals (TT) and the K Index (KI), which are combinations of these three concepts. The Severe Weather Threat Index (SWEAT) and the Bulk Richardson Number (BRN) incorporate information on wind shear and speed.
In addition to the instability, three environmental conditions are necessary for thunderstorm formation: high humidity in the boundary layer, trigger mechanisms initiating the lifting of an air parcel, and wind shear. Therefore, we calculated the bulk wind shear in the 0–6 km layer, an important factor for hail formation (BSHR06). We also evaluated the Convective Available Potential Energy calculated in three ways (CAPE, MLCAPE and MUCAPE). CAPE is calculated using the mean potential and dew point temperature in the lowest 50 hPa and the temperature corresponding to that potential temperature; the air parcel is released from the middle level of the layer. The other two are for the mixing layer and the most unstable air parcel. Additionally, we assessed the storm-relative helicity in the first 3 km of the atmosphere (SREH03), which helps identify environments conducive to hail production, particularly those favourable for supercell development. We analysed a total of 23 indices, with detailed definitions available in Appendix A and acronyms in Table 1.

Table 1.
Convective indices and their acronyms.
Numerous studies have investigated the effectiveness of stability indices for short-term predictions of thunderstorms [4,5,6,7,8]. The values of these stability indices, which indicate an atmosphere conducive to thunderstorm development, vary from one region to another. There is a noticeable lack of studies that focus on the use of stability indices for predicting thunderstorm clouds in Serbia in the short term. Vujović et al. [8] assessed the effectiveness of various stability indices derived from radiosonde observations specifically for short-term thunderstorm forecasting in the Belgrade region, which is the capital of Serbia. They proposed optimal threshold values for five different stability indices (BI, KI, LI, SI, and TT) as well as dew point temperature (td) and water vapour mixing ratio (mr) on the surface.
The values of convective indices can vary significantly from one observation to another due to minor changes in wind patterns and low-level moisture. As a result, the convective indices derived from a sounding profile are highly dependent on the specific time and location of the observation. Therefore, these indices may not accurately reflect the overall environmental conditions.
This research analyses a comprehensive set of 23 stability indices for the Belgrade region in Serbia during hail events, intending to find some of their tendencies, if there are any. The indices are analysed for the six subdivided hailstone sizes. A particular focus is paid to the index values corresponding to instances of larger hailstones. The air temperature and humidity at various heights were analysed to determine if any significant changes occurred, which can lead us to the answer “what was the atmospheric environment that generated large hail events?”.
Serbia has been chosen as a study area due to its frequent hailfall during the warm part of the year (April to October), particularly in summer [9]. As a result, a hail suppression system has been gradually developed over the past decades. This research aims to analyse the behaviour of stability indices in Serbia during the observed period 2005–2020 and seeks to improve the operational efficiency of the hail suppression system.
2. Data and Method
We collected two types of data for this study. One is data from radiosonde measurements, that are regularly carried out at the meteorological station in Belgrade—Košutnjak, Serbia (φ = 44°46′ N, λ = 20°25′ E, h = 203 a.m.s.l.). This station is under the authority of the Republic Hydrometeorological Institute of Serbia (RHMZ). For this study, we used radiosonde data from the upper air sounding open archive on the University of Wyoming website (http://weather.uwyo.edu/upperair/sounding.html, accessed on 24 November 2024). As 96.9% of all thunderstorms in the 35 years (1975–2009) in the Belgrade region occurred in a warm part of the year [10], we collected radiosonde data for sixteen consecutive years, from 2005 to 2020, at 12 UTC for the warm part of the year. These data differ very little from the data for the period when hail suppression is in effect in Serbia, from 15 April to 15 October, because there are negligible hail occurrences in the first half of April and the second half of October. The radiosondes from 12 UTC should describe the pre-convective atmosphere well because 95.9% of all hail events in Serbia were recorded between 12:00 and 24:00 local time [9]. The advantage of this approach is that it relies on direct measurements of the atmosphere. However, a key disadvantage is that it reflects the state of the upper atmosphere at a single point, which is then used to represent a larger area. The atmospheric sounding should capture the same air mass that could lead to the development of a thunderstorm with hail. A pertinent question arises: how close must the sounding be to accurately represent the environment where a thunderstorm with hail is likely to occur? This environment is, in its nature, horizontally inhomogeneous and exhibits significant temporal variability, meaning it can change notably between the time of the sounding and the occurrence of the event. To address this, we followed the proximity condition for severe storms established by Brooks et al. [11]. They proposed a spatial proximity limit of 160 km to ensure a sufficiently large dataset. Dessens et al. [12] also utilised this same proximity condition. The implicit assumption behind the application of proximity soundings is that, given the same environmental conditions, similar weather patterns would occur anywhere in the world. It seems reasonable to believe that the fundamental physics of the atmosphere remains consistent across different locations with inevitable local influences. Therefore, we accept that upper air soundings represent the meteorological conditions in an area located within 160 km of Košutnjak, as a compromise between the representativeness of the sounding measurements and the number of proximity soundings that would result for each hazard type.
We developed a Fortran program to read data from radiosonde measurements, and used and calculated various stability indices that were considered to be predictors for expected thunderstorm development. To help monitor the analysis results, it is important to note that higher values of the Boyden Index (BI), K Index (KI), Total Totals Index (TT), Convective Available Potential Energy (CAPE), Bulk Richardson Number (BRN), SWEAT index, vertical wind shear (WSH), 0–6 km bulk shear (BSHR06), bulk storm-relative helicity in the lower 1 and 3 km (SREH01, SREH03), and Significant Hail Parameter (SHIP) indicate a greater likelihood of thunderstorm occurrence. Conversely, lower values of the Lifted Index (LI), Humidity Index (HI), and Showalter Index (SI) suggest an increased potential for thunderstorms.
The second dataset contains information on hail precipitation. Hail is a small-scale meteorological phenomenon. It typically affects a small area, usually only a few square km [13]. Since the distance between the first-order meteorological stations is large (from 20 to 100 km), as is the distance between climatological stations, it very often happens that these stations do not register the occurrence of hail, although there are reports that there was hail in their vicinity. The most reliable hail data source is the densest network for observing hail, the Rocket Launch Station (RLS) system. Since the late 1960s, Serbia has developed a hail suppression system that has been continuously improved. Today, this system includes 13 radar centres equipped with S-band radars, a large number of RLS, a radio communication system consisting of repeaters and radios, and an operational and methodological centre in Belgrade [14]. On average, around 1600 RLSs are active each year [9], creating a very dense network of observation points. An active RLS is defined here as one that is in operation for at least three months during the hail suppression season. Outside of this period, hail rarely falls in Serbia, with 99.6% of occurrences recorded during the warm part of the year from 2002 to 2015 [9].
Trained personnel work at every RLS. When they report hail, they simultaneously code the predominant size of the hailstones according to an established procedure. They compare the size of the observed hailstones with some objects with known sizes. During this, it is possible that there is a slight overestimation of the hail size [15]. However, no significant mistakes appear to have been made here, and this type of data was used in analyses [16]. These data are very valuable because they enable the observation of hail that would otherwise not be recorded. It is also high-quality data, as the RHMZ subjects all this data to strict quality control [9]. In the practice of the RHMZ, there are eight classes of hailstones. The sizes of hailstones according to coding and their diameter are given in Table 2 according to [17]. Following the accepted proximity condition, we collected reports on the hailfall and hailstone size from 1300 RLS.

Table 2.
Diameter of hailstones according to coding of the Republic Hydrometeorological Institute of Serbia [17], p. 60.
In addition to hail, the observers also document cases of rain, sleet, hail, small hail, thunder, and high winds, as well as the intensity and duration of the individual events. We disposed of the data on hail days and hailstone sizes for the period 2005–2020 from the 1300 RLSs whose distance from Košutnjak is less than 160 km. Figure 1 shows the region of the study with the included limits of validity of the sounding.
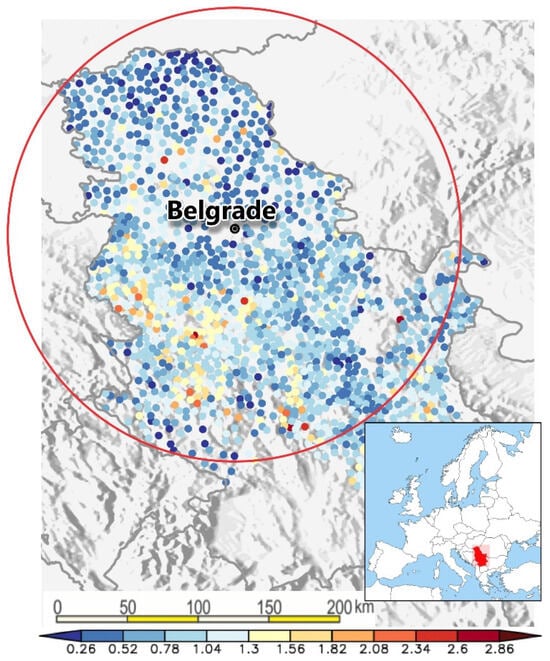
Figure 1.
Study area. Circle represents limits of validity of sounding. Dots represent RLSs whose data are used in study. Colours represent average annual number of hail days per RLS in Serbia [9].
A hail day was defined as a day when at least one RLS recorded a hail. If the hail was observed by two or more RLS, the largest reported hailstone size was coded (the size parameter is named code).
We used the Mann–Kendall test to statistically assess if there is a monotonic upward or downward trend of the stability indices over time [18,19]. This test is widely used in atmospheric sciences as it is non-parametric [9,20,21,22]. This means that the random variable does not require a normal distribution, as is the case with the residuals in linear regression. A monotonic upward trend means that the variable increases consistently over time, but the trend may or may not be linear. We calculated the magnitude of the trend using Sen’s slope [23]. The null hypothesis was that there is no monotonic trend in the data, while the alternative hypothesis was that a trend exists.
3. Results and Discussion
3.1. Descriptive Statistics of Stability Indices
The statistical analysis usually begins with descriptive statistics. In the reporting period, 889 hail days were recorded (nearly 15% of all days in 2005–2020). Not all of these days could be compared with measured soundings, because in some years there were no soundings at 12 UTC, but only at 00 UTC. In addition, some soundings were unsuccessful; they were unfinished (had incomplete humidity, air temperature, or wind data), so the stability indices could not be calculated. We obtained 3178 days with measured soundings at 12 UTC for the warm part of the years 2005–2020. This means that measured soundings cover 92.8% of the days in the warm period of the years 2005–2020. There were 826 hail days from 2005 to 2020 with the corresponding soundings. That is 92.9% of the data for all recorded days with hailstorms.
The average values of the 23 stability indices for different hailstone sizes, recorded on days when hail fell during the warm half of the year, are presented in Table 3. Stability indices are utilised to predict the likelihood of thunderstorms developing in the atmosphere, indicating the potential for extreme weather conditions. While these indices only reflect the conditions during observation, they remain useful for assessing the short-term potential for thunderstorm development in the atmosphere [22,24]. Feldmann et al. [25] used the stability indices calculated from radiosoundings to all thunderstorm classes occurring within the 2 h before or 12 h after a sounding. Descriptive statistics of all listed stability indices for all days, regardless of whether there was hail or not, for all days when hail fell and for different hailstone sizes are given in Appendix B.

Table 3.
Average values of stability indices for different hailstone sizes for hail days in 2005–2020. The definitions of the indices are given in Appendix A. Bolded numbers indicate a greater potential for thunderstorms to form.
The literature suggests the threshold of different stability indices. For example, when SI is ≤1, thunderstorms are likely, and when its values are in the range 1 < SI < 3, thunderstorms are possible [8]. In other words, the lower the values of the SI index, the higher the probability of a thunderstorm forming. On all days when hail was observed, the mean SI index values were less than 0.08 °C for each hailstone size. The lowest value of −7.57 °C was recorded for walnut-sized hailstones (code = 4). A lower value of LI and HI also gives a greater probability of the occurrence of a more intensive thunderstorm. The mean LI values for our data are all very low; the lowest value was recorded for days when hailstones with the size of a pigeon’s egg were observed (code = 5), regardless of whether the index was calculated using air temperature (LI) or virtual air temperature (LIv). Although they have proven to be good, these two indices still have the limitation of considering air temperature and humidity at altitudes below about 5500 m, so they do not give a state of the entire atmosphere.
The SWEAT estimates the potential for extreme weather by combining several meteorological parameters into a single index (dew point temperature at 850 hPa, instability, i.e., TT index, wind speeds at 850 and 500 hPa, and warm air advection in that layer of the atmosphere). The highest mean value was recorded for the largest hailstones with the size of a chicken egg (code = 6). The mean values of the KI are all above 20 °C, and the highest value of 29.56 °C was calculated for code = 6.
The mean values of the TT index are all nearly 50 °C, indicating that even severe thunderstorms are possible. The highest value of 50.85 °C was recorded on days when the observed hail was sized a pigeon egg (code = 5). CAPE calculated for different air parcels has the highest mean values for code = 5, with the highest value of 5433.2 J kg−1 for MUCAPE. The lowest mean absolute value of convective inhibition (CIN, CINv) in an absolute sense is for walnut-sized hailstones (code = 6). BRN has the highest mean value for code = 0, and BI for code = 6 (96.84). The HI has the lowest mean value for code = 2 (23.51 °C). BSHR06 mean values increase as the hail size increases; the largest value is 20.41 m s−1 for code = 6. Its largest value of 21.8 m s−1 is for one of two days with a reported gigantic hailstone of code.
The mean values of the stability indices for all days, regardless of whether hail occurred, as well as for days when hail of any size fell during the hail protection period (15 April to 15 October), are presented in Table 4. Comparing the stability index values for these two scenarios is useful. It is observed that the mean values of the LI and SI are significantly lower on days when hail fell compared to all days. Conversely, the mean values of the KI and TT are higher on days with hail. Additionally, the mean values of CAPE, CAPEv, and BRN are significantly greater on days with hail compared to all days. The mean values for MLCAPE and MLCAPE1030 are about three times greater in days when hail was recorded. Interestingly, the mean values of indices BSHR06 and WSH are slightly greater on all days than on the days when hail was observed.

Table 4.
Mean values of stability indices for all days, regardless of whether hail fell or not, and for days when hail of any size fell. The larger number in the pair is bolded.
Figure 2 illustrates the evaluation of various stability indices across different hail sizes. There is considerable overlap among the smallest hail sizes (codes 0 to 3) for BSHR06 and WSH. Storm Relative Helicity (SREH) utilises storm-relative environmental winds to calculate a relative horizontal helicity contribution, which is useful for forecasting mesocyclones. SREH01 and SREH06 show overlap across all hail sizes: there is little if any index value spacing among all hail sizes. Instability within the hail growth zone and the region typically nearly below can be explored by analysing CAPE1030, MUCAPE1030, and MLCAPE1030. These indices exhibit a tendency to occupy different parameter spaces as hail size increases, suggesting that they could be effective in distinguishing between hail sizes. One of the newer indices that incorporates multiple factors favourable for hail formation—such as humidity, instability, and wind shear—is the Significant Hail Parameter (SHIP). Its values range from 0 to 4. If the pre-storm environment has a SHIP value greater than 1, there is a possibility of significant hailstones with diameters larger than 5 cm forming. Additionally, SHIP effectively differentiates between larger and smaller sizes of hail, as evidenced by the varying values depicted for different hailstone sizes in Figure 1.
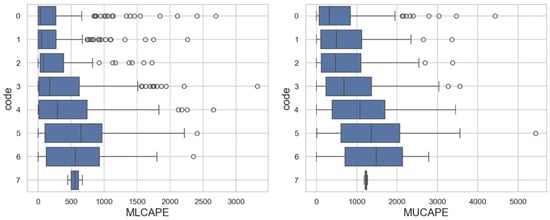
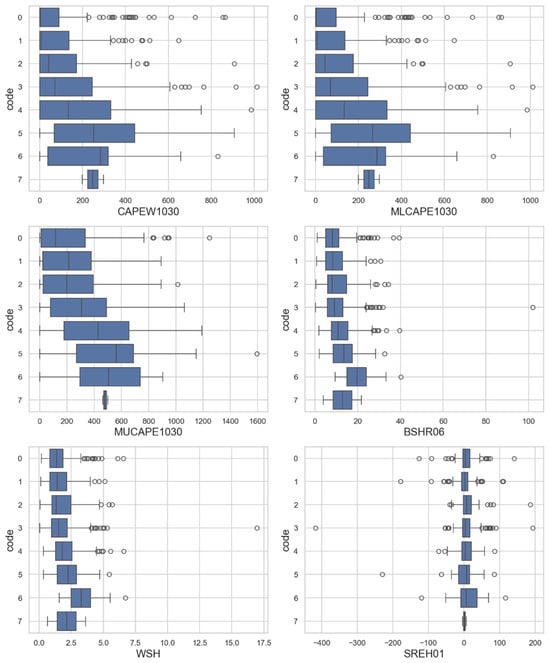
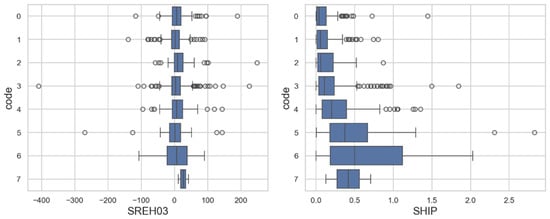
Figure 2.
Box and whiskers plots of magnitude of stability indices for each hail size. Boxes denote 25th to 75th percentiles, with the line representing the median value. Thin horizontal lines (whiskers) extend to the farthest data point lying within 1.5 times the interquartile range from the box. Flier points are those past the end of the whiskers.
3.2. Hail Distribution by Size
The distribution of hail days according to specific hailstone sizes is shown in Table 3. In the 16 years from 2005 to 2020, hailstones larger than a chicken egg (code = 7) were only recorded on 2 days, which corresponds to 0.2% of the total number. Hailstones with the size of a chicken’s egg (code = 6) were the second least representing size, occurring on only 16 days, or 1.9% of the total of 826 days recorded. The most frequently observed size was hazelnut-sized hailstones (code = 3), which occurred on 35.8% of the hail days. Small hail was recorded on 18.0% of days, while hailstones with the size of a corn kernel (code = 1) were recorded on 16.9% of days. Hailstones with a diameter equivalent to that of a walnut (code = 4) accounted for 14.8% of the observations. Overall, large hailstones (the size of a walnut or larger) were observed on 20.4% of days, while gigantic hailstones (the size of a pigeon egg or larger) occurred on 5.9% of days.
3.3. Daily and Monthly Values of CAPE and LI Indices
The CAPE and LI indices are commonly used in meteorology to predict the likelihood of thunderstorms. Lower LI values indicate a greater difference between the observed temperature at 500 hPa and the temperature of an air parcel that has been pseudo-adiabatically lifted at this level from its original level, which corresponds to higher CAPE values. We examined the values of these indices on days when different hailstone sizes were observed. The highest daily value for CAPE of 3190.6 J kg−1 was calculated for code = 3. The smaller the values of LI are, the greater the likelihood of stronger thunderstorms forming, and therefore hail. The lowest values of LI = −8.4 °C were calculated for code = 2 and code = 4.
Scatter plots can quickly highlight intriguing patterns within the data. The relationship observed between CAPE and LI during the three summer months (June, July, and August) in the analysed period follows a fifth-degree polynomial (see Figure 3). The coefficient of determination is notably high, with an R2 value of 0.868. It shows how well a model fits the data and indicates the proportion of variance in the dependent variable that the model explains. When the LI is greater than zero, CAPE tends to remain close to zero. However, as LI values drop below zero, CAPE increases rapidly.
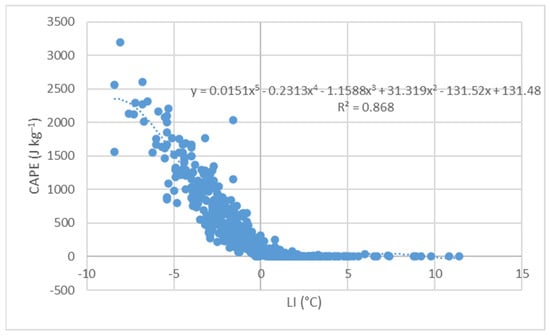
Figure 3.
Scatter plot for CAPE and LI for three summer months (June, July, and August) for hail days in the period 2005–2020.
The thunderstorms in Serbia most commonly occur during the warm part of the year. The highest daily CAPE value, indicating the greatest potential for cumulonimbus cloud development, was recorded in June at 3190 J kg−1. In contrast, the lowest maximum CAPE value was found in April at 574.7 J kg−1. The lowest LI value, which indicates the highest potential for thunderstorm formation, was observed in June and August, −8.41 °C. Meanwhile, the largest negative LI value of −2.59 °C was recorded in April. Figure 4 illustrates the difference between the values of CAPE and LI in the hail days in the most stable (April) and the most unstable month (June) during the warm half of the year.
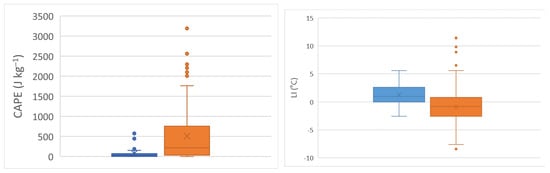
Figure 4.
Box and whiskers plots of daily values of CAPE (J kg−1) and LI (°C) for hail days for April (blue) and June (orange) during 2005–2020.
3.4. Thresholds of the Stability Indices
Various stability indices have different threshold values that apply to different regions around the world. Vujović et al. [8] evaluated various stability parameters derived from radiosonde measurements for short-term forecasting of thunderstorm clouds and proposed optimal thresholds for the Belgrade region. First, they performed the Rank Sum Score (RSS) method, which determined that the best results were obtained by the LI, KI, SI, BI, and TT indices. In addition, the highest RSS values were obtained by the water vapour mixing ratio and dew point temperature. They then performed a threshold test for these indices and meteorological variables to find their optimal values. The index values that had the best forecast scores were taken as optimal thresholds and their values are given in Table 5. mr is the water vapour mixing ratio measured at ground level, at a height of 2 m. Their results were obtained from ten years of radiosonde measurements in 2001–2010. Hail is possible only from cumulonimbus (i.e., thunderclouds). We have extended the radiosonde dataset by an additional ten years. Therefore, we were curious about how many days these thresholds were reached in our dataset, which contains records of all days on which hail of all sizes was recorded (826 days).

Table 5.
Stability indices threshold values (i.e., critical values) and frequency of days that satisfied threshold values in total number of hail days (“All codes”) and days with different hailstone sizes for the dataset of 2005–2020. Bolded are values above 80%.
The results for all values of the code parameter, i.e., for all hailstone sizes, are given in Table 5, third column. According to the results, the thresholds that are best determined are for the LI, SI, and TT indices. The TT index showed the best performance, accounting for 84.4% of the total number of hail days across all individual hailstone sizes. It was closely followed by the LI index, which represented 83.1%. High shares in the total number of days with hail are also given for SI (80.4%) and KI (76.5%). This again confirms that latent instability, embodied in LI and SI, and potential instability (TT, KI) are very important conditions for the occurrence of hail-bearing clouds. It should be emphasized here that there is no magic value of any index that, when overcome, can be used to predict hail (or the occurrence of thunderstorms) in the short term with 100% certainty.
As we can see in Table 3, of all hailstone sizes, those with the size of a hazelnut (code = 3) were recorded most frequently, accounting for 35.8% of the occurrences. For these days, the threshold values for the KI, LI, SI, and TT indices were well-defined in over 80% of cases, which is, by forecasters’ experience, the threshold that indicates good predictability (see Table 5). This pattern was also true for days on which hailstones of all sizes except code = 1 were recorded. In general, as the size of the hailstones increased, the frequency of days on which the threshold values were reached also increased. All four indices showed particularly significant results for code = 5, which corresponds to hailstones with the size of a pigeon egg, with values of up to 93.8% for the LI index and 90.6% for the other three indices. The threshold value for the water vapour mixing ratio provided the least favourable results, which was to be expected as this measurement only refers to the shallow air layer. In contrast, the stability indices provide information about the conditions of the atmosphere in deeper layers, which are crucial for the formation of thunderclouds. Nevertheless, the water vapour mixing ratio with a frequency of 93.8% showed a significant predictive potential for the largest hailstones (code = 6). While the frequency of all parameters listed in Table 5 was 100% for code = 7, we did not present this result because the largest hailstones were observed only on two days in the entire period.
3.5. Trends of the Stability Indices
The Mann–Kendall test for the mean annual values of the stability indices from 2005 to 2020 is conducted and the results are listed in Table 6. We have shortened the analysis period by three years to analyse trends and linear regressions for the years 2005 to 2020 due to the limited data available. Eight of the twenty-three indices have a monotonic trend (consistently increasing or decreasing): SI, LI, Liv, and HI have a decreasing monotonic trend, and KI, CAPE, MLCAPE, and MLCAPE1030 have a monotonic increasing trend. Sen’s slope for SI and LI is −0.144 °C year−1 and −0.095 °C year−1, respectively. The listed trends of all stability indices indicate that, over 16 years, the environment shows an increasing suitability for the formation of thunderstorms.

Table 6.
Trend and Sen’s slope for the average annual stability index values in 2005–2020 for hail days. Z is the Mann–Kendall test statistic.
These indices are calculated using the air temperature and humidity at different levels. Are there trends in the meteorological variables based on which the stability indices are calculated? The answer to this question is Table 7, which shows the trend analysis of air temperature (t), relative humidity (rh), dew point temperature (td), and water vapour mixing ratio (mr) at different heights (2 m, 850 hPa, 700 hPa, 500 hPa, and 300 hPa). The temperature, the dew point temperature, and the water vapour mixing ratio at the ground level do not show a monotonic trend. However, it is interesting that the temperature and water vapour mixing ratio show a statistically significant increasing trend on all significant isobaric levels (850, 700, 500, and 300 hPa), roughly representing the heights from 1500 m to 9000 m. The monotonic trend could not be detected in the mean mixing ratio in the mixed layer (MLMR).

Table 7.
Trend and Sen’s slope for average annual values of meteorological variables in 2005–2020 for hail days. Z is the Mann–Kendall test statistic. Bolded are trends with significance level of 0.01.
To determine whether the frequency of occurrence of days with stability index values above the threshold for the Belgrade area has changed, we performed a linear regression analysis of the number of these days from 2005 to 2020. Although a threshold for CAPE has not been established for the Belgrade area, we calculated a linear regression for the number of hail days when the CAPE value exceeded 500 J kg⁻1, indicating strong convective activity [16]. The results are shown in Figure 5. There is an increase in KI, TT, and BI, from which it can be concluded that the atmosphere is more favourable for the formation of thunderstorms. The opposite is true for the indices whose lower values indicate a higher probability of thunderstorm formation (SI, LI, and CAPE), which increase. However, this increase/decrease is not statistically significant for any of these indices. That confirms the p-value and t-statistic, which are shown in Figure 4. Based on the available data, no recognisable trends could be identified for the indices. Furthermore, the Mann–Kendall test was conducted on these data, revealing the absence of monotonic trends.
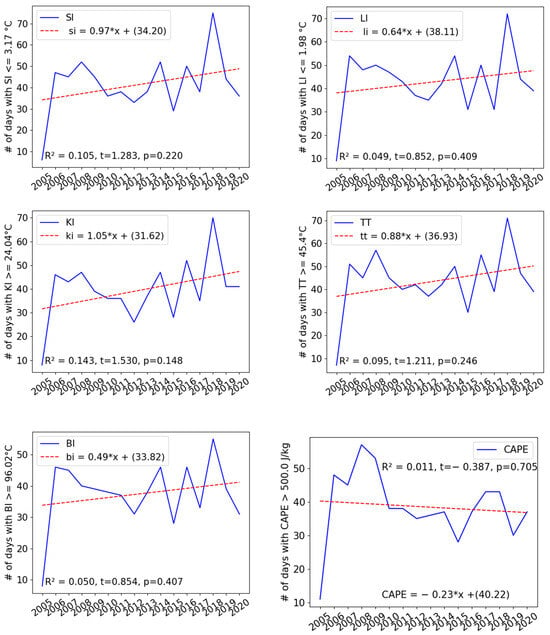
Figure 5.
Number of hail days with fulfilled conditions regarding stability indices thresholds with belonging linear regressions from 2005 to 2020. R2, t, and p are the coefficient of determination, t-statistic, and p-value, respectively.
3.6. Temporal Variability of Stability Indices on Severe Hail Days
Wells et al. [16] defined severe or large hail as hailstones with a diameter greater than 20 mm. In our analysis, we considered hail days with hailstones with a diameter greater than 21 mm categorised as codes four, five, six, and seven. We examined whether there were noticeable changes in the stability index values on days when severe hail occurred, given the potential damage it could cause. Of all analysed indices, only the HI showed a consistent decreasing trend, with Sen’s slope measuring −0.777 °C per year (Z = −2.704, α = 0.01), indicating a higher probability of thunderstorms. Therefore, the stability indices data from the 16 years (2005–2020) reveal no increased likelihood of severe hail occurrences, as the trends do not support atmospheric conditions that facilitate the formation of thunderstorms.
We analysed whether there were significant changes in the number of days with monitored severe or large hail. The hail days meeting threshold conditions regarding the stability indices for severe and large hail with a diameter ≥ 21 mm from 2005 to 2020 are given in Figure 6. There is no significant decreasing or increasing trend in the number of hail days with met threshold of the indices, which is confirmed by the t-statistics and p-values shown in each subfigure. We also analysed this data using the Mann–Kendall test, which did not reveal any trends. Therefore, we cannot conclude that days with fulfilled threshold criteria for stability indices for severe and large hail occur more frequently.
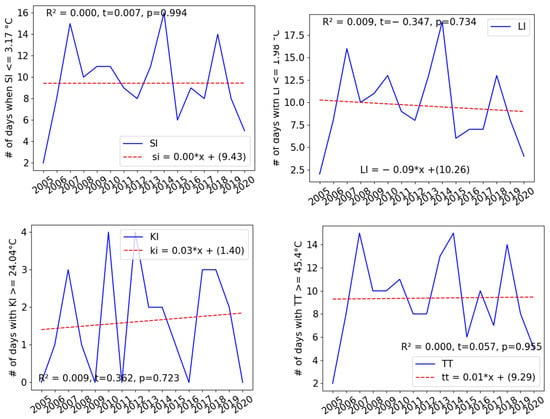
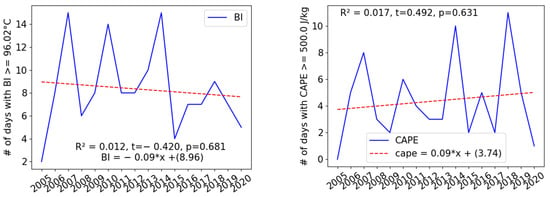
Figure 6.
Number of hail days meeting threshold conditions regarding stability indices for severe and large hail with a diameter > 21 mm corresponds to hailstone codes of 4, 5, 6, and 7 from 2005 to 2020. Corresponding linear regressions are also shown. R2, t, and p are coefficient of determination, t-statistic, and p-value, respectively.
The number of hail days with severe or strong hail (code = 4, 5, 6, or 7) was 172, which makes 20.8% of all days with hail. Wells et al. [16] stated that 17% of reports included a hail event-maximum size code for the United Kingdom. According to the linear regression equation, the number of hail days with a hail diameter in the range of 21 to 30 mm (code = 4) increases slightly over time, namely by 0.6 days in 16 years (Figure 7). However, due to the large p-value (p = 0.794), this is not a statistically significant trend. The coefficient of determination is small, R2 = 0.005. The slope of the linear regression for a number of days with hailstones of a diameter of 31–35 mm (code = 5) is zero, and the p-value indicates that it is not statistically significant. The days with the largest hail with a diameter of 36–50 mm (code = 6) decrease: the slope is −0.08, and R2 = 0.099. The p-value of 0.234 indicates that it is not a statistically significant decrease. The Mann–Kendall test shows no monotonic trends for days with this extreme hail precipitation. Therefore, we cannot conclude that the number of days with severe and strong hail increases with the years in the analysed period 2005–2020. This is consistent with the results of [16], who analysed data from a different geographical area (United Kingdom) and a longer period than our data. They concluded that there is no evidence of a long-term increase in hail reporting rates in the period 1979–2022. The conclusion may be that hail has a high interannual variability in different parts of Europe.
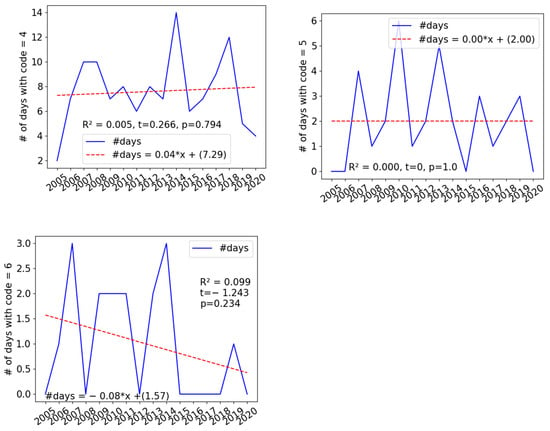
Figure 7.
Number of hail days when codes four, five, and six were reported from 2005 to 2020. Corresponding linear regressions are also shown. R2, t, and p are the coefficient of determination, t-statistic, and p-value, respectively.
4. Discussion
For the first time, the values of the stability indices for hail days were analysed for the region of Belgrade. Descriptive statistics of stability indices for hail days with different hailstone sizes are compiled. We are unaware of any similar research for our broader region, so we cannot compare the results.
The representative area of the sounding validity of 160 km can apply to Serbia. A similar proximity sounding distance of 150 km was used for Central Europe [26], and 167 km [27], 185 km [28], and 200 km [29] for the United States.
A special contribution of this paper is the analysis of the trends of stability indices for hail days with observed severe and large hailstones (i.e., hailstones larger than 21 mm, according to the definition of [16]). The previously established threshold values of the stability indices [8] were confirmed to be well-defined on a larger sample of data. When investigating the pre-convective environment on days with thunderstorms in southwest Germany, the authors of [5] concluded that for the prediction of severe thunderstorms associated with hail damage, the best results were achieved for the LI threshold of −2.07 °C with a prediction probability of 80. Our analysis confirms the success of this index, with the threshold for our study region being significantly higher: 1.98 °C, and a prediction probability of 83.1% for all hail days, up to 100% for days with hailstones with code = 6.
The data of the stability indices from 16 years show that their tendencies do not speak in favour of atmospheric conditions that favour the formation of thunderstorms. Only eight of twenty-three indices show a monotonically decreasing (SI, LI, LIv, HI) or increasing trend (KI, CAPE, MLCAPE, MLCAPE1030). Accordingly, the environment appears to be more favourable for the formation of thunderstorms in the years studied. Similarly, the authors of [22] analysed the trends of the synoptic fields of geopotential height at 500 hPa, sea level pressure, and lapse rate between 850 and 500 hPa for the period 1948 and 2015, and found a tendency towards more favourable conditions for hail development in southern Europe during the hail season. They noted the strengthening of the gradient between the ridge over the western Mediterranean and the troughs circulating over the North Atlantic, together with an increase in the thermal instability of the air mass over the western Mediterranean. However, this finding does not necessarily mean that the frequency of hail days should increase. It should take into account the processes that could act in the opposite direction, for example, the melting of hail [12]. That would be our next research topic.
According to the authors of [26], the annual number of reports of large and very large hail in Europe shows a steep increase in the 30 years between 1989 and 2018. This conclusion is based on the reports of large hail submitted to the European Severe Weather Database. Our results do not support this. We do not show an increase in days with large and severe hail based on reliable data of observed hail precipitation from a dense network of RLSs.
Jonson and Sugden [7] claimed that there is considerable overlap between the three larger hail groups (44 to 89 mm) in BSHR06. In our analysis, the overlap is between the smallest hail sizes with codes zero to three (up to 20 mm). MUCAPE1030 and MLCAPE1030 could be effective in discriminating hail sizes. The same conclusion was drawn by Jonson and Sugden [7].
5. Conclusions
The 23 stability indices were analysed in the warm part of the years 2005–2020. CAPE values calculated for different parcels are nearly three times higher on hail days compared to all other days.
TT and LI showed the best performance for all hail sizes with a frequency of successful prediction of 84.4% and 83.1%, respectively. This means that potential instability (TT) and latent instability (LI) are the most important conditions for hail formation. This is especially true for larger hailstones. The number of days on which the stability index thresholds were reached increases with increasing hail size, with the largest numbers for hailstones over 31 mm. The water vapour mixing ratio, the air temperature, and the dew point temperature at the surface showed no trend. At altitudes between 1500 and 9000 m (850–300 hPa), we detected an increasing monotonic trend for air temperature and water vapour mixing ratio.
There has been no increase in the frequency of days with extreme hailstones. Therefore, we cannot conclude that days with large hailstones have become more common in recent times. Interestingly, we also do not observe a consistent trend in the stability indices for days with large and severe hailstones.
What clearly distinguishes smaller hailstones from large and severe hailstones is the potential instability in the mixed layer and within the hail growth zone, especially between −10 and −30 °C (MLCAPE, MUCAPE, MLCAPE1030, MUCAPE1030). The composite parameter SHIP also effectively distinguishes between large and small hail.
Author Contributions
D.V.: Conceptualisation, Methodology, Software, Investigation, Writing—Original Draft, Visualisation, Supervision. V.V.: Conceptualisation, Investigation, Software, Writing—Original Draft. A.Z.: Investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Science Fund of the Republic of Serbia, No. 7389, Project “Extreme weather events in Serbia—analysis, modelling and impacts”—EXTREMES.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
All authors confirm informed consent. All authors confirm consent to publish. All authors whose names appear on the submission approved the version to be published and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors have no interests that are directly, or indirectly related to the work submitted for publication to disclose. The authors report there are no competing interests to declare.
Appendix A
Definitions of the stability indices:
The Lifted Index (LI) is defined as the difference between the observed temperature at 500 hPa and the temperature of an air parcel that has been pseudo-adiabatically lifted from its original level defined by the average pressure, temperature and dew point in the lowest 500 m of air to 500 hPa: (°C). It serves as a measure of atmospheric stability between the surface (z = 0) and 500 hPa (approximately 5500 m). When LI is greater than 0, the atmosphere is considered stable. Conversely, lower values of LI (particularly more negative numbers) indicate a higher likelihood of thunderstorms and an increased risk of severe weather. The main difference between the LI and the SI lies in the initial level from which the air parcel is lifted.
The Lifted Index calculated using the virtual temperature instead of the actual ones is LIv (°C).
The Showalter Index (SI, °C) is calculated by taking the difference between the air temperature at the 500 hPa level and the temperature of an air parcel that is lifted from the 850 hPa level to the 500 hPa level. This parcel is first lifted dry adiabatically until it reaches saturation, and then it continues to rise wet adiabatically: . A greater negative value of the SI indicates a higher probability of a storm event. The main difference between the SI and the LI lies in the initial level from which the air parcel is lifted. It is important to note that if the humidity at the 850 hPa level is low, the SI may underestimate the likelihood of a storm event.
The Total Totals Index (TT, °C) is calculated by summing the difference between air temperature and dew-point temperature at 850 hPa and 500 hPa:
TT = (T850 − T500) + (Td850 − T500)
The larger TT is, the more likely it is that a thunderstorm will develop.
The Severe Weather Threat Index (SWEAT) evaluates the potential for severe weather by combining kinematic and thermodynamic variables: low-level moisture (Td850), instability (TT), wind speed at 850 hPa and 500 hPa and warm advection (veering between 850 and 500 hPa). It is utilised to assess the severe weather potential. It is calculated via an expression:
where u850 and u500 are wind speeds in m s−1 and S is the shear term, actually the sine of the angle between 500 and 850 hPa wind direction. The larger the value of SWEAT, the greater the chance of a thunderstorm developing.
SWEAT = 12Td850 + 20(TT − 49) + u850 + 2u500 +125(S + 0.2),
The K index (KI) is defined based on the temperature and dew point temperature at different altitudes (i.e., pressures):
KI = (T850 − T500) + Td850 − (T700 − Td700)
The KI (°C) increases when static stability decreases in the layer between 850 and 500 hPa, when there is an increase in moisture at 850 hPa, and when relative humidity rises at 700 hPa. As we can see from the above equation, KI increases with the decreasing static stability in the layer 850–500 hPa, increasing moisture at 850 hPa and increasing relative humidity at 700 hPa.
Convective Available Potential Energy (CAPE, J kg−1) measures the work done by the upward buoyancy force on an air parcel as it is lifted from its initial level to its final equilibrium level:
is the gas constant for dry air, p is the air pressure, and Tp and T are the temperatures of the air parcel and environment, respectively. Large values of CAPE indicate a suitable environment for the formation of thunderstorms. is the level from which the air parcel is lifted, and depending on it a few CAPE values are defined. When a rising air parcel originates near the surface, it is referred to as surface-based CAPE or SBCAPE. This measure is particularly useful for mid-afternoon pre-storm soundings. To improve the estimation of atmospheric boundary conditions, the conditions are averaged over the lowest 50 hPa. This average, which serves as the initial conditions for the rising air parcel, represents the conditions of the mean layer or mixed layer. Mean Layer CAPE or MLCAPE uses an air parcel with a uniformly mixed equivalent potential temperature in the lowest 50 hPa (almost 500 m). This 50 hPa layer was chosen compared to the more common 100 hPa layer to better represent the shallow moisture layers with thicknesses less than 500 m thick [7]. If the thicker air layer were used, this shallow moisture layer would mix with the drier air, resulting in lower CAPE values.
To determine the best initial altitude of the air parcel, one can select the altitude within the lowest 50 hPa that corresponds to the highest CAPE value; this is called the Most Unstable CAPE (MUCAPE). This index has been useful during elevated instability.
Hail-growth zone occurs in the layer between −10 and −30 °C. All kind of CAPE was calculated for this layer, separately.
Convective Available Potential Energy using virtual temperature (CAPEv, J kg−1) is calculated similarly to CAPE. However, it utilizes the virtual temperatures of the air parcel and the environment instead of the actual temperatures (Tp and T).
Convective Inhibition (CIN, J kg−1) refers to the amount of work the environment must perform on a parcel of air to elevate it to the level of free convection, overcoming the effects of negative buoyancy. The processes that enable this include daytime heating causing convection, air convergence at low levels, and forcing uplifts (atmospheric fronts, mountains). A smaller CIN value means that less forced lift is required. It indicates the region of negative energy on the sounding where the temperature of the parcel is lower than that of the surrounding environmental air.
Convective Inhibition calculated using virtual air temperature rather than the actual temperature is CINv (J kg−1).
The Bulk Richardson Number (BRN) is a non-dimensional ratio that compares Convective Available Potential Energy (CAPE) to a measure of vertical wind shear in the atmosphere. It is calculated using the formula:
where U represents the magnitude of the wind shear. When the BRN is less than 45, it indicates conditions that may allow for the formation of supercell clouds. Higher BRN values suggest a greater likelihood of developing simple and multicellular cloud systems.
Boyden Index (BI) is the difference between the thickness at 1000 hPa and 700 hPa, minus 200 from the temperature at 700 hPa (Z is the geopotential height at the indicated pressure level):
BI = 0.1 × (Z700 − Z1000) − T700 − 200
The larger the BI value, the larger the possibility of a thunderstorm forming.
Humidity Index (HI, °C) combines measures of saturation at standard pressure levels of 850, 700, and 500 hPa:
The smaller the HI value, the larger the possibility of a thunderstorm forming.
Storm Relative Helicity (SREH, m2 s−2) uses storm-relative ambient winds to obtain a relative horizontal helicity contribution. SREH from 0–3 km AGL (SREH03) distinguish well between supercells and non-supercells, which means they can help to detect large hail. SREH from 0–1 km AGL (SREH01) is used rather to discriminate tornadic against non-tornadic supercells.
Bulk shear from 0 to 6 km (BSHR06) is deep-layer shear that strongly influences convective organisation. The rough threshold for supercell development is 20 m s−1.
All indices are summarised in Table A1.
Appendix B

Table A1.
Descriptive statistics of stability indices for all days (April–October, 2005–2020), regardless of whether hail has fallen or not.
Table A1.
Descriptive statistics of stability indices for all days (April–October, 2005–2020), regardless of whether hail has fallen or not.
| All Days | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 3.87 | 3.67 | 3.50 | 108.17 | 17.12 | 43.00 | 126.15 | 145.42 | −33.32 | −25.75 | 73.72 | 95.22 | 32.38 |
| SE | 0.5 | 0.1 | 0.1 | 1.3 | 0.6 | 0.5 | 5.8 | 6.4 | 1.3 | 1.1 | 15.3 | 0.1 | 0.3 |
| Median | 3.9 | 3.1 | 2.9 | 102.1 | 22.2 | 45.0 | 0.0 | 1.1 | 0.0 | 0.0 | 0.1 | 95.7 | 29.2 |
| Mode | 3.2 | −0.1 | 3.5 | 33.0 | 23.3 | 45.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 96.5 | 44.0 |
| SD | 25.5 | 4.6 | 4.7 | 75.0 | 34.3 | 27.1 | 327.6 | 358.7 | 75.8 | 60.6 | 864.8 | 3.4 | 19.1 |
| SV | 650.6 | 21.1 | 22.2 | 5630.2 | 1175.1 | 733.5 | 107,295.1 | 128,634.4 | 5743.9 | 3675.9 | 747,884.5 | 11.6 | 366.5 |
| Kurtosis | 1504.0 | 0.4 | 0.3 | 73.9 | 727.6 | 1378.9 | 18.5 | 17.0 | 17.3 | 24.4 | 874.7 | 10.1 | 1.7 |
| Skewness | −38.3 | 0.6 | 0.5 | −4.5 | −24.7 | −35.9 | 3.9 | 3.8 | −3.6 | −4.2 | 27.9 | −1.5 | 1.0 |
| Range | 1021.1 | 33.2 | 33.8 | 1480.0 | 1044.0 | 1062.2 | 3190.6 | 3449.2 | 734.2 | 682.7 | 30,782.3 | 57.3 | 145.0 |
| Minimum | −999.0 | −8.4 | −9.0 | −999.0 | −999.0 | −999.0 | 0.0 | 0.0 | −734.2 | −682.7 | −999.0 | 65.7 | 0.0 |
| Maximum | 22.1 | 24.8 | 24.8 | 481.0 | 45.0 | 63.2 | 3190.6 | 3449.2 | 0.0 | 0.0 | 29,783.3 | 123.0 | 145.0 |
| Sum | 12,286.3 | 11,679.1 | 11,114.6 | 343,769.1 | 54,402.3 | 136,662.1 | 400,901.6 | 462,149.1 | −105,900.9 | −81,827.0 | 234,267.7 | 302,614.4 | 102,909.4 |
| Count | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 | 3178 |
| CL (95.0%) | 0.9 | 0.2 | 0.2 | 2.6 | 1.2 | 0.9 | 11.4 | 12.5 | 2.6 | 2.1 | 30.1 | 0.1 | 0.7 |
SE—standard error, SD—standard deviation, SV—sample variance, CL—confidence level.

Table A2.
Descriptive statistics of stability indices for all hail days, regardless of hailstone size (April–October, 2005–2020).
Table A2.
Descriptive statistics of stability indices for all hail days, regardless of hailstone size (April–October, 2005–2020).
| All Codes | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.04 | −0.27 | −0.54 | 143.48 | 26.04 | 47.26 | 345.95 | 391.91 | −59.31 | −45.05 | 148.10 | 96.48 | 25.96 |
| SE | 1.2 | 0.1 | 0.1 | 2.7 | 1.3 | 1.3 | 17.0 | 18.4 | 2.8 | 2.3 | 38.5 | 0.1 | 0.5 |
| Median | 1.3 | −0.2 | −0.5 | 136.0 | 28.3 | 48.7 | 117.5 | 151.8 | −28.9 | −19.3 | 13.0 | 97.2 | 23.0 |
| Mode | 0.9 | −0.1 | 0.4 | 29.1 | 30.1 | 46.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 97.5 | 31.0 |
| SD | 34.9 | 2.7 | 2.8 | 77.8 | 36.4 | 36.6 | 489.3 | 528.9 | 80.9 | 67.0 | 1105.3 | 3.7 | 14.0 |
| SV | 1217.6 | 7.5 | 8.1 | 6053.8 | 1322.7 | 1342.4 | 239,456.4 | 279,714.0 | 6540.1 | 4495.3 | 1,221,682.6 | 13.6 | 197.2 |
| Kurtosis | 817.4 | 1.5 | 1.4 | 56.5 | 767.4 | 808.8 | 4.3 | 4.0 | 8.2 | 11.1 | 629.6 | 18.0 | 1.2 |
| Skewness | −28.5 | 0.5 | 0.4 | −3.2 | −27.2 | −28.3 | 2.0 | 1.9 | −2.4 | −2.8 | 23.8 | −2.3 | 1.0 |
| Range | 1011.0 | 19.8 | 20.2 | 1480.0 | 1044.0 | 1062.2 | 3190.6 | 3449.2 | 642.5 | 575.0 | 30,782.3 | 57.3 | 89.0 |
| Minimum | −999.0 | −8.4 | −9.0 | −999.0 | −999.0 | −999.0 | 0.0 | 0.0 | −642.5 | −575.0 | −999.0 | 65.7 | 0.0 |
| Maximum | 12.0 | 11.4 | 11.2 | 481.0 | 45.0 | 63.2 | 3190.6 | 3449.2 | 0.0 | 0.0 | 29783.3 | 123.0 | 89.0 |
| Sum | 29.5 | −225.1 | −446.5 | 118,513.8 | 21,510.5 | 39,033.9 | 285,751.5 | 323,720.5 | −48,991.5 | −37,213.6 | 122,328.5 | 79,692.9 | 21,439.3 |
| Count | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 | 826 |
| CL (95.0%) | 2.4 | 0.2 | 0.2 | 5.3 | 2.5 | 2.5 | 33.4 | 36.1 | 5.5 | 4.6 | 75.5 | 0.3 | 1.0 |

Table A3.
Descriptive statistics of stability indices for all days when small hail was observed (April–October, 2005–2020).
Table A3.
Descriptive statistics of stability indices for all days when small hail was observed (April–October, 2005–2020).
| Code = 0 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2.1 | 0.64 | 0.41 | 123.4 | 25.32 | 47.59 | 239.71 | 275.37 | −41.73 | −30.57 | 345.06 | 96.13 | 25.91 | 254.13 | 600.77 | 92.06 | 92.1 | 210.72 | 9.53 | 1.59 | 7.21 | 9.59 | 0.1 |
| SE | 0.2 | 0.2 | 0.2 | 5 | 0.7 | 0.3 | 37.1 | 40.2 | 5.3 | 4.1 | 204.6 | 0.4 | 1.3 | 39 | 62.6 | 14.1 | 14.1 | 20.8 | 0.6 | 0.1 | 2.1 | 2.5 | 0 |
| Median | 2 | 0.6 | 0.4 | 126.1 | 26.5 | 48 | 34.8 | 64.4 | −8.3 | −7.5 | 7.9 | 96.5 | 23 | 37.9 | 308.9 | 3.5 | 3.5 | 108 | 8.2 | 1.4 | 4 | 6.4 | 0 |
| Mode | 3.8 | 1.4 | 0.4 | 134.6 | 22.7 | 48.6 | 0 | 0 | 0 | 0 | 0 | 97.9 | 16.7 | 0 | 0 | 0 | 0 | 0 | 8.6 | 0.6 | 1.6 | −5.7 | 0 |
| SD | 2.6 | 2.9 | 3 | 61 | 8 | 3.9 | 453 | 491.1 | 65.1 | 50 | 2497.6 | 4.7 | 15.4 | 476.5 | 764.3 | 172.2 | 172.2 | 254.4 | 6.7 | 1.1 | 26.1 | 30.7 | 0.2 |
| SV | 6.8 | 8.3 | 8.9 | 3715.3 | 64.1 | 15.5 | 205,240.40 | 241,146.90 | 4236.4 | 2502.1 | ########## | 22.3 | 237.6 | 227,044.90 | 584,202.50 | 29,667.20 | 29,654.30 | 64,695.40 | 45.3 | 1.3 | 679 | 942.7 | 0 |
| Kurtosis | 1.8 | 1.4 | 1.3 | 4.5 | 4.7 | 4.6 | 9.2 | 8.9 | 6.9 | 10.8 | 133 | 19.4 | 1.1 | 8.7 | 5.3 | 6 | 6 | 2 | 4.2 | 4.1 | 9.8 | 9.2 | 29.7 |
| Skewness | 0.1 | 0.5 | 0.4 | 1.3 | −1.6 | −1.2 | 2.9 | 2.8 | −2.4 | −2.8 | 11.3 | −0.9 | 1 | 2.8 | 2.1 | 2.4 | 2.4 | 1.5 | 1.8 | 1.8 | 0 | 1.4 | 4.4 |
| Range | 18.9 | 16.6 | 17.5 | 431.5 | 46.1 | 31.5 | 2600.3 | 2807.7 | 379 | 328.4 | 29,783.25 | 57.3 | 83.5 | 2692.3 | 4427.7 | 865 | 864.9 | 1245.4 | 38.3 | 6.4 | 267.3 | 305.6 | 1.4 |
| Minimum | −6.9 | −6.8 | −7.6 | 7.8 | −7.5 | 27 | 0 | 0 | −379 | −328.4 | 0 | 65.7 | 1.5 | 0 | 0 | 0 | 0 | 0 | 1.1 | 0.2 | −126.0 | −116.6 | 0 |
| Maximum | 12 | 9.8 | 9.9 | 439.3 | 38.6 | 58.5 | 2600.3 | 2807.7 | 0 | 0 | 29,783.25 | 123 | 85 | 2692.3 | 4427.7 | 865 | 864.9 | 1245.4 | 39.4 | 6.6 | 141.3 | 189 | 1.445 |
| Sum | 312.8 | 95 | 61.2 | 18,386.90 | 3772 | 7090.9 | 35,716.30 | 41,029.80 | −6218.3 | −4554.7 | 51,414.06 | 14,323.20 | 3860.1 | 37,864.80 | 89,514.40 | 13,717.40 | 13,723.00 | 31,397.10 | 1419.4 | 236.3 | 1073.8 | 1428.9 | 14.9 |
| Count | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 | 149 |
| CL (95.0%) | 0.4 | 0.5 | 0.5 | 9.9 | 1.3 | 0.6 | 73.3 | 79.5 | 10.5 | 8.1 | 404.3 | 0.8 | 2.5 | 77.1 | 123.7 | 27.9 | 27.9 | 41.2 | 1.1 | 0.2 | 4.2 | 5 | 0 |

Table A4.
Descriptive statistics of stability indices for all days when corn kernel-sized hail fell (April–October, 2005–2020).
Table A4.
Descriptive statistics of stability indices for all days when corn kernel-sized hail fell (April–October, 2005–2020).
| Code = 1 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | Hail g | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.97 | 0.56 | 0.31 | 123.33 | 25.69 | 47.76 | 228.35 | 265.08 | −46.23 | −33.99 | 99.06 | 96.07 | 27.28 | 239.17 | 666.74 | 83.75 | 83.75 | 232.58 | 9.96 | 1.66 | 0.76 | 1.16 | 0.116 |
| SE | 0.2 | 0.2 | 0.2 | 4.4 | 0.5 | 0.3 | 31.5 | 34.4 | 7.3 | 6.2 | 30 | 0.3 | 1.2 | 33 | 56.1 | 11.3 | 11.2 | 18.1 | 0.5 | 0.1 | 2.4 | 2.6 | 0 |
| Median | 2 | 0.6 | 0.4 | 119.6 | 26.3 | 48.1 | 45.8 | 71.5 | −14.9 | −8.4 | 11.8 | 96.8 | 24.8 | 48.9 | 488.2 | 6.5 | 6.4 | 206.7 | 8.5 | 1.4 | 2.5 | 2.8 | 0.1 |
| Mode | 3.2 | 0.8 | 0.4 | 47.5 | 24.1 | 49.5 | 0 | 0 | 0 | 0 | 0 | 96.4 | 51 | 0 | 0 | 0 | 0 | 0 | 2.1 | 0.3 | 0.8 | 3.1 | 0 |
| SD | 2.2 | 2.5 | 2.6 | 51.7 | 6.1 | 3.3 | 372.5 | 407 | 86.2 | 73.8 | 354.6 | 3.8 | 14.4 | 390.2 | 663.5 | 133.2 | 133 | 213.9 | 6.4 | 1.1 | 27.9 | 30.8 | 0.2 |
| SV | 4.7 | 6.2 | 6.6 | 2669.5 | 37.4 | 10.9 | 138,787.40 | 165,662.80 | 7432.2 | 5440.8 | 125,762.10 | 14.8 | 206.3 | 152,263.80 | 440,166.10 | 17,735.30 | 17,680.20 | 45,762.40 | 41.3 | 1.1 | 778.6 | 950.1 | 0 |
| Kurtosis | 1 | 1.2 | 1 | 3.2 | 1.4 | 1.1 | 7.4 | 6.3 | 24 | 30.4 | 41.5 | 16.7 | −0.4 | 6.9 | 1.4 | 3 | 3 | −0.1 | 0.1 | 0.1 | 14.9 | 3.7 | 4.6 |
| Skewness | 0.1 | 0.6 | 0.5 | 1.1 | −0.8 | −0.7 | 2.5 | 2.3 | −4.3 | −5.0 | 6.2 | −3.6 | 0.6 | 2.4 | 1.2 | 1.8 | 1.8 | 0.7 | 0.8 | 0.8 | −1.4 | −0.7 | 2.1 |
| Range | 13.6 | 15.4 | 15.6 | 327.2 | 34.3 | 17.2 | 2204.4 | 2349.8 | 642.5 | 575 | 2961.7 | 30 | 61.8 | 2264 | 3359.7 | 647.9 | 645.9 | 893 | 30 | 5 | 289.6 | 230.7 | 0.8 |
| Minimum | −5.3 | −5.3 | −5.7 | 29.1 | 5.5 | 37.4 | 0 | 0 | −642.5 | −575.0 | 0 | 71.4 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0.8 | 0.1 | −178.7 | −139.5 | 0 |
| Maximum | 8.3 | 10.1 | 9.9 | 356.3 | 39.8 | 54.6 | 2204.4 | 2349.8 | 0 | 0 | 2961.7 | 101.4 | 62 | 2264 | 3359.7 | 647.9 | 645.9 | 893 | 30.8 | 5.1 | 110.9 | 91.2 | 0.804 |
| Sum | 275.1 | 78 | 43.8 | 17,265.50 | 3596.2 | 6686.8 | 31,968.60 | 37,110.60 | −6472.2 | −4759.0 | 13,868.40 | 13,449.60 | 3819 | 33,484.20 | 93,343.00 | 11,725.20 | 11,725.50 | 32,560.90 | 1394.9 | 232.2 | 106.4 | 161.9 | 16.3 |
| Count | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 | 140 |
| CL (95.0%) | 0.4 | 0.4 | 0.4 | 8.6 | 1 | 0.6 | 62.3 | 68 | 14.4 | 12.3 | 59.3 | 0.6 | 2.4 | 65.2 | 110.9 | 22.3 | 22.2 | 35.7 | 1.1 | 0.2 | 4.7 | 5.2 | 0 |

Table A5.
Descriptive statistics of stability indices for all days when bean-sized hail fell (April–October, 2005–2020).
Table A5.
Descriptive statistics of stability indices for all days when bean-sized hail fell (April–October, 2005–2020).
| Code = 2 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.38 | −0.12 | −0.36 | 142.91 | 27.22 | 48.73 | 261.62 | 302.41 | −41.46 | −30.11 | 130.33 | 96.58 | 23.51 | 276.75 | 702.99 | 105.31 | 105.49 | 249.37 | 10.62 | 1.77 | 12.89 | 16.71 | 0.133 |
| SE | 0.3 | 0.3 | 0.3 | 8.1 | 0.9 | 0.4 | 47.3 | 51.4 | 6.5 | 5.4 | 60.9 | 0.4 | 1.5 | 49.8 | 90.4 | 19.8 | 19.8 | 30.3 | 0.9 | 0.2 | 3.7 | 4.8 | 0 |
| Median | 1.4 | −0.1 | −0.2 | 137.1 | 27.8 | 48.8 | 67.8 | 109.6 | −23.4 | −14.4 | 9.8 | 96.9 | 20.2 | 78.4 | 434.9 | 41.6 | 43.6 | 194.1 | 8 | 1.3 | 7.4 | 9 | 0.1 |
| Mode | 1.8 | 0 | −0.2 | #N/A | 24.1 | 49.6 | 0 | 0 | 0 | 0 | 0 | 96.8 | 11.1 | 0 | 0 | 0 | 0 | 0 | 6 | #N/A | 40.6 | 9.4 | 0 |
| SD | 2.5 | 2.2 | 2.2 | 67 | 7.1 | 3.5 | 392.7 | 426.9 | 53.7 | 44.7 | 506.1 | 3 | 12.6 | 413.8 | 751.2 | 164.3 | 164.2 | 251.4 | 7.7 | 1.3 | 30.9 | 39.6 | 0.2 |
| SV | 6.1 | 4.6 | 5.1 | 4485.9 | 50 | 12 | 154,175.90 | 182,261.00 | 2887.3 | 2001 | 256,117.30 | 9 | 159.3 | 171,268.30 | 564,354.30 | 26,984.10 | 26,950.00 | 63,211.80 | 59.8 | 1.7 | 954.9 | 1565.6 | 0 |
| Kurtosis | 4.7 | 2 | 2 | 8.9 | 2 | 3.8 | 3.8 | 3.7 | 4.3 | 5.6 | 60.7 | 12.2 | 0.7 | 3.6 | 2.1 | 8 | 7.9 | 0.5 | 1.2 | 1.2 | 14.1 | 17 | 4.9 |
| Skewness | −0.9 | −0.7 | −0.8 | 2.2 | −0.9 | 0.6 | 2.1 | 2 | −2.0 | −2.4 | 7.6 | −2.7 | 0.8 | 2.1 | 1.5 | 2.5 | 2.5 | 1.1 | 1.3 | 1.3 | 2.8 | 3.2 | 2 |
| Range | 16.3 | 12.2 | 12.8 | 439.8 | 39.1 | 22.6 | 1623.6 | 1834.4 | 249.8 | 195.9 | 4147.8 | 22 | 59 | 1724.2 | 3373.9 | 908 | 906.5 | 1013.3 | 33.9 | 5.6 | 226.1 | 306.3 | 0.9 |
| Minimum | −9.5 | −8.4 | −9.0 | 41.2 | 5.9 | 40.6 | 0 | 0 | −249.8 | −195.9 | 0 | 80.6 | 1 | 0 | 0 | 0 | 0 | 0 | 0.4 | 0.1 | −40.0 | −58.0 | 0 |
| Maximum | 6.8 | 3.8 | 3.8 | 481 | 45 | 63.2 | 1623.6 | 1834.4 | 0 | 0 | 4147.8 | 102.6 | 60 | 1724.2 | 3373.9 | 908 | 906.5 | 1013.3 | 34.3 | 5.7 | 186.1 | 248.3 | 0.869 |
| Sum | 95.3 | −8.2 | −25.1 | 9860.8 | 1878 | 3362.7 | 18,051.90 | 20,866.10 | −2860.4 | −2077.3 | 8993.1 | 6663.9 | 1621.9 | 19,095.50 | 48,506.10 | 7266.4 | 7278.7 | 17,206.80 | 732.6 | 122 | 889.7 | 1152.9 | 9.2 |
| Count | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 | 69 |
| CL (95.0%) | 0.6 | 0.5 | 0.5 | 16.1 | 1.7 | 0.8 | 94.3 | 102.6 | 12.9 | 10.7 | 121.6 | 0.7 | 3 | 99.4 | 180.5 | 39.5 | 39.4 | 60.4 | 1.9 | 0.3 | 7.4 | 9.5 | 0 |

Table A6.
Descriptive statistics of stability indices for all days when hazelnut-sized hail fell (April–October, 2005–2020).
Table A6.
Descriptive statistics of stability indices for all days when hazelnut-sized hail fell (April–October, 2005–2020).
| Code = 3 | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 386.50 | 892.95 | 149.24 | 149.47 | 320.52 | 10.43 | 1.74 | 5.73 | 5.45 | 0.179 |
| SE | 29.7 | 46.0 | 11.0 | 11.0 | 15.2 | 0.5 | 0.1 | 2.0 | 2.3 | 0.0 |
| Median | 176.0 | 682.5 | 71.7 | 72.3 | 294.1 | 9.2 | 1.5 | 3.9 | 3.1 | 0.1 |
| Mode | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.8 | 1.6 | 2.2 | 8.3 | 0.0 |
| SD | 511.1 | 791.8 | 190.0 | 189.7 | 262.3 | 8.1 | 1.3 | 34.0 | 39.6 | 0.2 |
| SV | 261,216.6 | 626,882.5 | 36,095.9 | 36,000.4 | 68,782.0 | 64.9 | 1.8 | 1156.7 | 1564.8 | 0.1 |
| Kurtosis | 4.2 | 0.2 | 2.1 | 2.1 | −0.4 | 55.7 | 55.7 | 83.8 | 43.8 | 14.1 |
| Skewness | 1.8 | 0.9 | 1.5 | 1.5 | 0.6 | 5.3 | 5.3 | −5.8 | −3.1 | 3.1 |
| Range | 3321.6 | 3547.1 | 1013.2 | 1011.4 | 1063.6 | 101.6 | 16.9 | 610.6 | 633.0 | 1.8 |
| Minimum | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 0.0 | −417.3 | −408.6 | 0.0 |
| Maximum | 3321.6 | 3547.1 | 1013.2 | 1011.4 | 1063.6 | 101.9 | 17.0 | 193.3 | 224.4 | 1.845 |
| Sum | 114,404.3 | 264,314.5 | 44,174.6 | 44,242.0 | 94,874.4 | 3087.0 | 513.8 | 1696.2 | 1614.4 | 53.1 |
| Count | 296 | 296 | 296 | 296 | 296 | 296 | 296 | 296 | 296 | 296 |
| CL (95.0%) | 58.5 | 90.6 | 21.7 | 21.7 | 30.0 | 0.9 | 0.2 | 3.9 | 4.5 | 0.0 |

Table A7.
Descriptive statistics of stability indices for all days when walnut-sized hail fell (April–October, 2005–2020).
Table A7.
Descriptive statistics of stability indices for all days when walnut-sized hail fell (April–October, 2005–2020).
| Code = 4 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | −7.57 | −1.06 | −1.36 | 148.26 | 20.13 | 40.4 | 456.01 | 509.01 | −88.41 | −70.94 | 94.35 | 96.54 | 26.32 | 470.53 | 1112.93 | 196.16 | 196.37 | 417.87 | 12.68 | 2.11 | 7.53 | 10.86 | 0.288 |
| SE | 8.2 | 0.3 | 0.3 | 11.5 | 8.4 | 8.6 | 47.5 | 51 | 9.2 | 7.9 | 32.8 | 0.3 | 1.3 | 49.4 | 72 | 18.8 | 18.8 | 25.4 | 0.6 | 0.1 | 2.2 | 3 | 0 |
| Median | 0.3 | −1.4 | −1.7 | 150.7 | 29.2 | 49 | 286.5 | 319.9 | −53.3 | −37.7 | 20.9 | 97.5 | 22.6 | 293.4 | 1078.7 | 133.6 | 133.7 | 428.9 | 10.9 | 1.8 | 3.9 | 6.2 | 0.2 |
| Mode | 0.3 | −2.9 | −4.3 | 373.6 | 28.3 | 48.6 | 0 | 0 | 0 | 0 | 0 | 97.7 | 31 | 0 | 0 | 0 | 0 | 0 | 7.1 | 1.2 | 3.7 | −9.3 | 0 |
| SD | 90.5 | 2.9 | 3 | 126.8 | 93.2 | 95 | 525 | 563.1 | 102.2 | 87 | 362.2 | 3.4 | 14.1 | 546 | 794.8 | 208.1 | 207.9 | 280.2 | 7.1 | 1.2 | 24.7 | 33.5 | 0.3 |
| SV | 8197.1 | 8.4 | 8.9 | 16,082.90 | 8692.1 | 9018.1 | 275,676.50 | 317,073.50 | 10,436.10 | 7565.5 | 131,202.70 | 11.5 | 197.6 | 298,167.40 | 631,695.20 | 43,325.40 | 43,238.30 | 78,517.10 | 50.9 | 1.4 | 611.7 | 1122.4 | 0.1 |
| Kurtosis | 121.8 | 1.8 | 1.7 | 55.5 | 120.9 | 121.6 | 2.8 | 2.5 | 2.4 | 3.2 | 45.6 | 3.6 | 0.9 | 2.9 | −0.6 | 1 | 1 | −0.9 | 1.4 | 1.4 | 0.9 | 2.8 | 2.9 |
| Skewness | −11.0 | 0.8 | 0.7 | −6.0 | −11.0 | −11.0 | 1.6 | 1.5 | −1.6 | −1.7 | 6 | −1.9 | 1.1 | 1.6 | 0.3 | 1.1 | 1.1 | 0 | 1.2 | 1.2 | 0.2 | 0.6 | 1.7 |
| Range | 1009 | 19.2 | 19.6 | 1372.6 | 1037.5 | 1060 | 2560.9 | 2734.6 | 452.6 | 451.1 | 4036.9 | 18.2 | 70.3 | 2656.3 | 3453.2 | 986 | 985.3 | 1191.1 | 37.6 | 6.3 | 157.3 | 239 | 1.4 |
| Minimum | −999.0 | −8.4 | −9.0 | −999.0 | −999.0 | −999.0 | 0 | 0 | −452.6 | −451.1 | −999.0 | 84 | 0.7 | 0 | 0 | 0 | 0 | 0 | 1.9 | 0.3 | −71.5 | −96.1 | 0 |
| Maximum | 10 | 10.8 | 10.6 | 373.6 | 38.5 | 61 | 2560.9 | 2734.6 | 0 | 0 | 3037.9 | 102.2 | 71 | 2656.3 | 3453.2 | 986 | 985.3 | 1191.1 | 39.5 | 6.6 | 85.8 | 142.9 | 1.351 |
| Sum | −923.7 | −129.1 | −165.6 | 18,087.60 | 2456.1 | 4928.6 | 55,632.80 | 62,099.70 | −10,786.5 | −8655.2 | 11,510.60 | 11,778.10 | 3211.6 | 57,405.10 | 135,777.60 | 23,931.70 | 23,956.70 | 50,980.50 | 1547 | 257.5 | 918.7 | 1324.7 | 35.2 |
| Count | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 | 122 |
| CL (95.0%) | 16.2 | 0.5 | 0.5 | 22.7 | 16.7 | 17 | 94.1 | 100.9 | 18.3 | 15.6 | 64.9 | 0.6 | 2.5 | 97.9 | 142.5 | 37.3 | 37.3 | 50.2 | 1.3 | 0.2 | 4.4 | 6 | 0.1 |

Table A8.
Descriptive statistics of stability indices for all days when pigeon egg-sized hail fell (April–October, 2005–2020).
Table A8.
Descriptive statistics of stability indices for all days when pigeon egg-sized hail fell (April–October, 2005–2020).
| Code = 5 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | −0.42 | −2.37 | −2.71 | 198.48 | 29.54 | 50.85 | 704.43 | 774.05 | −78.61 | −61.33 | 57.27 | 96.38 | 26.38 | 736.62 | 1512.31 | 292.85 | 294.32 | 532.39 | 13.68 | 2.28 | −0.01 | −1.49 | 0.549 |
| SE | 0.5 | 0.5 | 0.5 | 14 | 1.2 | 0.7 | 123.2 | 132.2 | 14.6 | 11.1 | 19.1 | 0.8 | 2.9 | 127.8 | 214 | 46.5 | 46.4 | 64.2 | 1.2 | 0.2 | 8.9 | 11.9 | 0.1 |
| Median | −0.2 | −2.3 | −2.8 | 211.6 | 30.5 | 51.1 | 613.7 | 698.7 | −56.4 | −40.9 | 20.2 | 97.5 | 22.8 | 649.8 | 1361 | 250.9 | 266.1 | 562.6 | 13.6 | 2.3 | 7.5 | 1.5 | 0.4 |
| Mode | 0.4 | −1.9 | −3.2 | 114.5 | 31.9 | 52.6 | 0 | #N/A | 0 | 0 | #N/A | 98.7 | 35 | 0 | #N/A | 0 | 0 | #N/A | #N/A | #N/A | 10.3 | #N/A | 0.6 |
| SD | 2.7 | 2.8 | 2.9 | 79.3 | 6.8 | 3.8 | 697.1 | 747.7 | 82.4 | 63 | 107.8 | 4.5 | 16.7 | 722.9 | 1210.8 | 263.1 | 262.7 | 363.3 | 6.7 | 1.1 | 50.3 | 67.1 | 0.6 |
| SV | 7.2 | 7.7 | 8.5 | 6287.7 | 46.1 | 14.3 | 485,905.60 | 559,082.90 | 6781.5 | 3973.9 | 11,631.50 | 20.7 | 278.3 | 522,556.30 | ########## | 69,200.50 | 68,994.70 | 131,952.10 | 44.3 | 1.2 | 2527.2 | 4501.8 | 0.4 |
| Kurtosis | −0.8 | −0.3 | −0.3 | −1.0 | 10.4 | −0.8 | 0.1 | 0.1 | 1.2 | 0.7 | 9.7 | 2.8 | 2.5 | 0.1 | 2.2 | −0.3 | −0.3 | 1.1 | 1.1 | 1.1 | 14.4 | 8.5 | 5.9 |
| Skewness | 0.1 | 0.1 | 0.1 | 0.1 | −2.6 | −0.2 | 1 | 1 | −1.3 | −1.2 | 3 | −0.9 | 1.4 | 1 | 1.2 | 0.8 | 0.7 | 0.6 | 0.9 | 0.9 | −3.1 | −1.8 | 2.3 |
| Range | 10.8 | 11.4 | 12.1 | 298.5 | 39.9 | 13.8 | 2296 | 2494.3 | 296 | 211.9 | 500.3 | 25 | 76.4 | 2406.5 | 5421.5 | 907.8 | 907.9 | 1596 | 30.6 | 5.1 | 315 | 412.3 | 2.8 |
| Minimum | −5.7 | −7.3 | −8.0 | 48.6 | 0.5 | 43.2 | 0 | 0.1 | −296.0 | −211.9 | 0 | 83.3 | 4.6 | 0 | 11.7 | 0 | 0 | 0 | 2.1 | 0.3 | −230.0 | −269.6 | 0 |
| Maximum | 5.1 | 4.1 | 4.1 | 347.1 | 40.4 | 57 | 2296 | 2494.4 | 0 | 0 | 500.3 | 108.3 | 81 | 2406.5 | 5433.2 | 907.8 | 907.9 | 1596 | 32.7 | 5.5 | 85 | 142.7 | 2.828 |
| Sum | −13.5 | −75.9 | −86.8 | 6351.2 | 945.3 | 1627.3 | 22,541.70 | 24,769.70 | −2515.5 | −1962.7 | 1832.7 | 3084.1 | 844 | 23,571.80 | 48,393.90 | 9371.2 | 9418.2 | 17,036.40 | 437.7 | 72.9 | −0.4 | −47.7 | 17.6 |
| Count | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 |
| CL (95.0%) | 1 | 1 | 1 | 28.6 | 2.4 | 1.4 | 251.3 | 269.6 | 29.7 | 22.7 | 38.9 | 1.6 | 6 | 260.6 | 436.5 | 94.8 | 94.7 | 131 | 2.4 | 0.4 | 18.1 | 24.2 | 0.2 |

Table A9.
Descriptive statistics of stability indices for all days when chicken egg-sized hail fell (April–October, 2005–2020).
Table A9.
Descriptive statistics of stability indices for all days when chicken egg-sized hail fell (April–October, 2005–2020).
| Code = 6 | SI | LI | Liv | SWEAT | KI | TT | CAPE | CAPEv | CIN | CINv | BRN | BI | HI | MLCAPE | MUCAPE | CAPEW1030 | MLCAPE1030 | MUCAPE1030 | BSHR06 | WSH | SREH01 | SREH03 | SHIP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.75 | −1.75 | −2.14 | 202.64 | 29.56 | 48 | 638.86 | 713.39 | −101.59 | −75.83 | 19.63 | 96.84 | 30.37 | 678.31 | 1430.19 | 258.74 | 260.17 | 496.17 | 20.41 | 3.4 | 9.32 | 0.09 | 0.707 |
| SE | 0.6 | 0.5 | 0.6 | 19.1 | 1.3 | 0.8 | 163 | 173.7 | 20.9 | 17.5 | 6.9 | 0.8 | 3.1 | 168.4 | 224.9 | 61 | 60.9 | 73.9 | 2.1 | 0.3 | 13.4 | 13.6 | 0.1 |
| Median | 1 | −1.9 | −2.4 | 189 | 29 | 48 | 520.8 | 581.3 | −87.9 | −57.6 | 9.2 | 97.5 | 29.6 | 560.9 | 1481.9 | 282.5 | 286.3 | 504.7 | 19.7 | 3.3 | 6.8 | 6.7 | 0.5 |
| Mode | 0.6 | #N/A | −2.5 | #N/A | 29 | #N/A | 0 | 0 | #N/A | #N/A | 0 | 98 | #N/A | #N/A | #N/A | 0 | 0 | #N/A | #N/A | #N/A | #N/A | #N/A | #N/A |
| SD | 2.5 | 2.2 | 2.3 | 76.2 | 5.1 | 3.4 | 651.9 | 694.8 | 83.7 | 70 | 27.7 | 3.3 | 12.3 | 673.6 | 899.8 | 244.1 | 243.8 | 295.5 | 8.2 | 1.4 | 53.6 | 54.3 | 0.6 |
| SV | 6.1 | 4.7 | 5.4 | 5807.8 | 25.7 | 11.5 | 424,950.40 | 482,758.00 | 7007 | 4906.4 | 765.7 | 11.1 | 150.8 | 453,793.90 | 809,634.20 | 59,590.40 | 59,428.20 | 87,332.40 | 67.2 | 1.9 | 2871.4 | 2944.4 | 0.4 |
| Kurtosis | 3.6 | 0.6 | 0.6 | 0 | 1.6 | 1.6 | 1.5 | 1.2 | 2.9 | 2.1 | 4 | 12.9 | −1.0 | 1.3 | −1.2 | 0.6 | 0.6 | −1.1 | 1.1 | 1.1 | 1.6 | −0.2 | −0.2 |
| Skewness | −1.2 | −0.8 | −0.7 | 0.8 | 0.4 | 0.7 | 1.3 | 1.2 | −1.4 | −1.4 | 2 | −3.4 | −0.1 | 1.2 | −0.1 | 0.9 | 0.9 | −0.3 | 0.9 | 0.9 | −0.5 | −0.5 | 0.7 |
| Range | 11 | 7.9 | 8.5 | 253.7 | 22.1 | 14 | 2270 | 2418.8 | 331.4 | 261.7 | 98.8 | 14.4 | 38.2 | 2349.7 | 2784.1 | 829.9 | 828.1 | 905.3 | 30.8 | 5.1 | 235.5 | 196.9 | 2 |
| Minimum | −6.2 | −6.8 | −7.5 | 105.4 | 19.3 | 42.4 | 0 | 0 | −331.4 | −261.7 | 0 | 84.9 | 10.8 | 0 | 1.1 | 0 | 0 | 0 | 9.4 | 1.6 | −119.3 | −106.6 | 0 |
| Maximum | 4.8 | 1.1 | 1 | 359.1 | 41.4 | 56.4 | 2270 | 2418.8 | 0 | 0 | 98.8 | 99.3 | 49 | 2349.7 | 2785.2 | 829.9 | 828.1 | 905.3 | 40.2 | 6.7 | 116.2 | 90.3 | 2.027 |
| Sum | 12 | −28.0 | −34.3 | 3242.3 | 472.9 | 768 | 10,221.70 | 11,414.20 | −1625.5 | −1213.2 | 314.1 | 1549.5 | 485.9 | 10,852.90 | 22,883.10 | 4139.9 | 4162.7 | 7938.7 | 326.6 | 54.4 | 149.1 | 1.5 | 11.3 |
| Count | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| CL (95.0%) | 1.3 | 1.2 | 1.2 | 40.6 | 2.7 | 1.8 | 347.4 | 370.2 | 44.6 | 37.3 | 14.7 | 1.8 | 6.5 | 359 | 479.5 | 130.1 | 129.9 | 157.5 | 4.4 | 0.7 | 28.6 | 28.9 | 0.3 |
References
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Springer: Cham, The Netherlands, 2010; p. 954. [Google Scholar] [CrossRef]
- Young, K.C. Microphysical Processes in Clouds; Oxford University Press: New York, NY, USA, 1993; p. 427. ISBN 0-19-507563-3. [Google Scholar]
- Holtslag, M.C.; Steeneveld, G.J.; Holtslag, A.A.M. Fog forecasting: “old fashioned” semi-empirical methods from radio sounding observations versus “modern” numerical models. In Proceedings of the 5th International Conference on Fog, Fog Collection and Dew (FOGDEW2010), Münster, Germany, 25–30 July 2010; Available online: http://meetingorganizer.copernicus.org/FOGDEW2010/FOGDEW2010-69.pdf (accessed on 29 December 2024).
- Sanchez, J.L.; Fraile, R.; De la Fuente, M.T.; Marcos, J.L. Discriminant analysis applied to the forecasting of thunderstorms. Meteorol. Atmos. Phys. 1998, 68, 187–195. [Google Scholar] [CrossRef]
- Kunz, M. The skill of convective parameters and indices to predict isolated and severe thunderstorms. Nat. Hazard Earth Syst. 2007, 7, 327–342. [Google Scholar] [CrossRef]
- Jayakrishnan, P.R.; Babu, C.A. Assessment of convective activity using stability indices as inferred from radiosonde and MODIS data. Atmos. Clim. Sci. 2014, 4, 122–130. [Google Scholar] [CrossRef]
- Johnson, A.W.; ESugden, K. Evaluation of sounding-derived thermodynamic wind-related parameters associated with large hail events. E-J. Severe Storms Meteor. 2014, 9, 1–42. [Google Scholar] [CrossRef]
- Vujović, D.; Paskota, M.; Todorović, N.; Vučković, V. Evaluation of the stability indices for the thunderstorm forecasting in the region of Belgrade, Serbia. Atmos. Res. 2015, 161–162, 143–152. [Google Scholar] [CrossRef]
- Nađ, J.; Vujović, D.; Vučković, V. Hail characteristics in Serbia based on data obtained from the network of hail suppression system stations. Int. J. Climatol. 2021, 41, 6556–6572. [Google Scholar] [CrossRef]
- Todorović, N.; Vujović, D. Analysis of frequency of thunder and lightning in the Belgrade area in Serbia in the period 1975–2009. In Proceedings of the 8th European Conference on Applied Climatology (ECAC), Zurich, Switzerland, 13–17 September 2010; pp. 13–17. [Google Scholar]
- Brooks, H.E.; Doswell, C.A., III; Cooper, J. On the environments of tornadic and non-tornadic mesocyclones. Weather Forecast. 1994, 9, 606–618. [Google Scholar] [CrossRef]
- Dessens, J.; Berthet, C.; Sanchez, J.L. Change in hailstone size distributions with an increase in the melting level height. Atmosph. Res. 2015, 158–159, 245–253. [Google Scholar] [CrossRef]
- Potapov, E.; Burundukov, G.; Garaba, I.; Petrov, V. Hail modification in the Republic of Moldova. Russ. Meteorol. Hydrol. 2007, 32, 360–365. [Google Scholar] [CrossRef]
- Vujović, D.; Vučinić, Z.; Babić, Z. 40 years of hail suppression in Serbia. In Proceedings of the 9th WMO Scientific Conference on Weather Modification and Weather Modification Workshop, Antalya, Turkey, 22–24 October 2007. [Google Scholar]
- Webb, J.D.C.; Elsom, D.M.; Meaden, G.T. Severe hailstorms in Britain and Ireland, a climatological survey and hazard assessment. Atmos. Res. 2009, 93, 587–606. [Google Scholar] [CrossRef]
- Wells, H.M.; Hillier, J.; Garry, F.K.; Dunstone, N.; Clark, M.R.; Kahraman, A.; Chen, H. Climatology and convective mode of severe hail in United Kingdom. Atmos. Res. 2024, 309, 107569. [Google Scholar] [CrossRef]
- Radovanović Bulić, R.; Bulić, I.; Hrkalović, D. The spectrum of hail and small hail sizes in 15-day periods of the hail suppression season in the period 1984-1997. In Proceedings of the Conference “Meteorological Data—A national Treasure”, 66–71, Vrnjacka Banja, Serbian, 25–28 October 1999. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1970. [Google Scholar]
- Romanić, Đ.; Ćurić, M.; Jovičić, I.; Lompar, M. Long-term trends of the ‘Koshava’ wind during the period 1949–2010. Int. J. Climatol. 2015, 35, 288–302. [Google Scholar] [CrossRef]
- Vujović, D.; Milić-Petrović, B. Analysis of bulk precipitation chemistry in Serbia for the period from 1982 to 2010. J. Atmos. Chem. 2016, 73, 101–118. [Google Scholar] [CrossRef]
- Sanchez, J.L.; Merino, A.; Melcon, P.; Garcia-Ortega, E.; Fernandez-Gonzalez, S.; Berthet, C.; Dessens, J. Are meteorological conditions favouring hail precipitation change in southern Europe? Analysis of the period 1948–2015. Atmos. Res. 2017, 198, 1–10. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall's tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kulikov, M.Y.; Belikovich, M.V.; Skaluga, N.K.; Shatalina, M.V.; Dementyeva, S.O.; Ryskin, V.G.; Shvetsov, A.A.; Krasiljnikov, A.A.; Serov, E.A.; Feigin, A.M. Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data. Remote Sens. 2020, 12, 604. [Google Scholar] [CrossRef]
- Feldmann, M.; Hering, A.; Gabella, M.; Berne, A. Hailstorms and rainstorms versus supercells—A regional analysis of convective storm types in the Alpine region. npj Clim. Atmos. Sci. 2023, 6, 19. [Google Scholar] [CrossRef]
- Pučik, T.; Castellano, C.; Groenemeijer, P.; Kuhne, T. Large hail incidence and its economic impacts across Europe. Mon. Weather Rev. 2019, 147, 3901–3916. [Google Scholar] [CrossRef]
- Evans, J.S.; Doswell, C.A., III. Examination of derecho environments using proximity soundings. Weather Forecast. 2001, 16, 329–342. [Google Scholar] [CrossRef]
- Craven, J.P.; Brooks, H.E. Baseline climatology of sounding derived parameters associated with deep, moist convection. Natl. Wea. Dig. 2004, 28, 13–24. [Google Scholar]
- Cohen, A.E.; Coniglio, M.C.; SF, C.; Corfidi, S.J. Discrimination of mesoscale convective system environments using sounding observations. Weather Forecast. 2007, 22, 1045–1062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).