Modeling Short-Term Drought for SPEI in Mainland China Using the XGBoost Model
Abstract
1. Introduction
2. Data and Methods
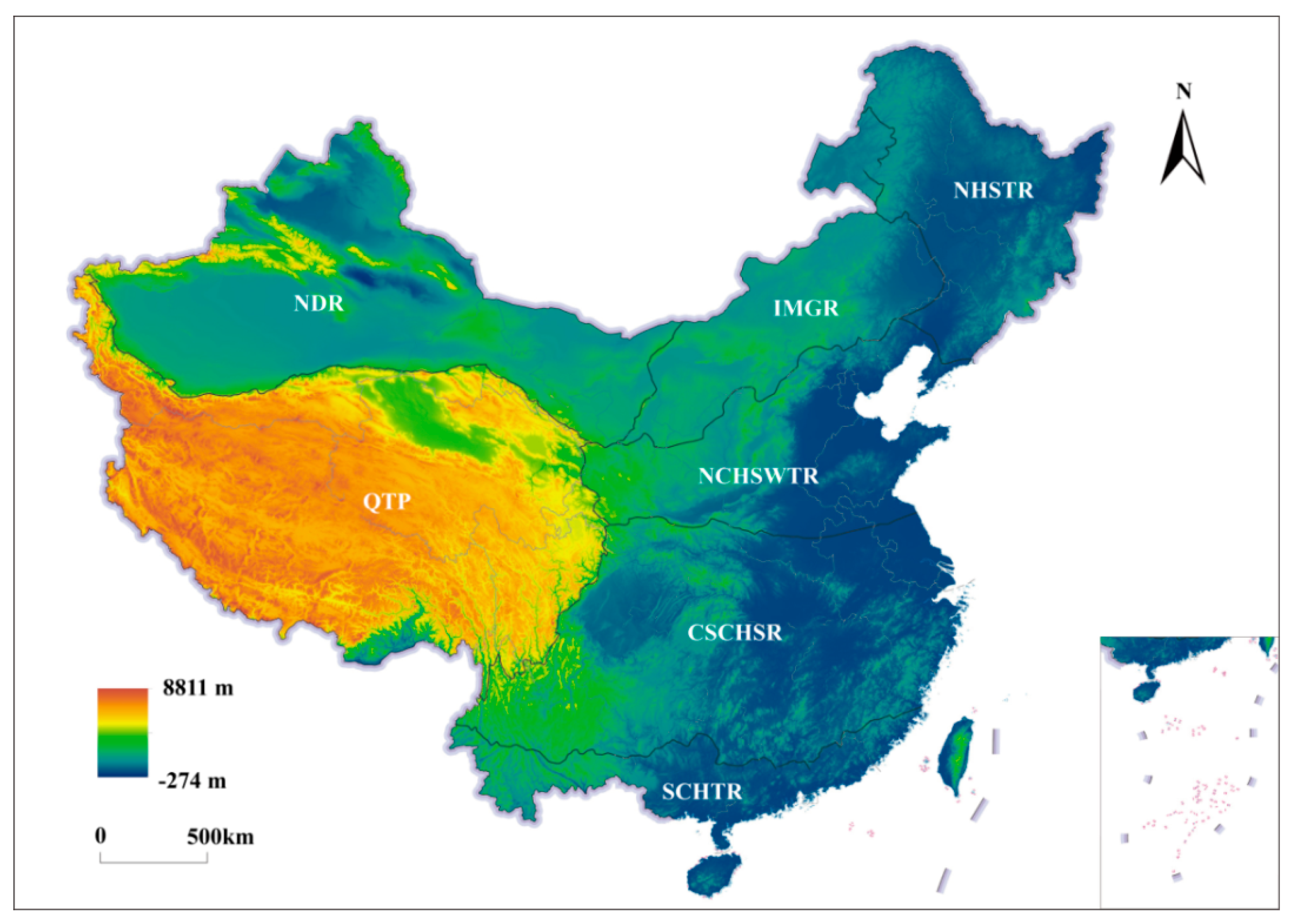
2.1. Study Area and Data Sources
2.2. Model Construction and Accuracy Assessment
2.2.1. Pearson Correlation Analysis
2.2.2. XGBoost Architecture
2.2.3. Hybrid Coding Particle Swarm Optimization
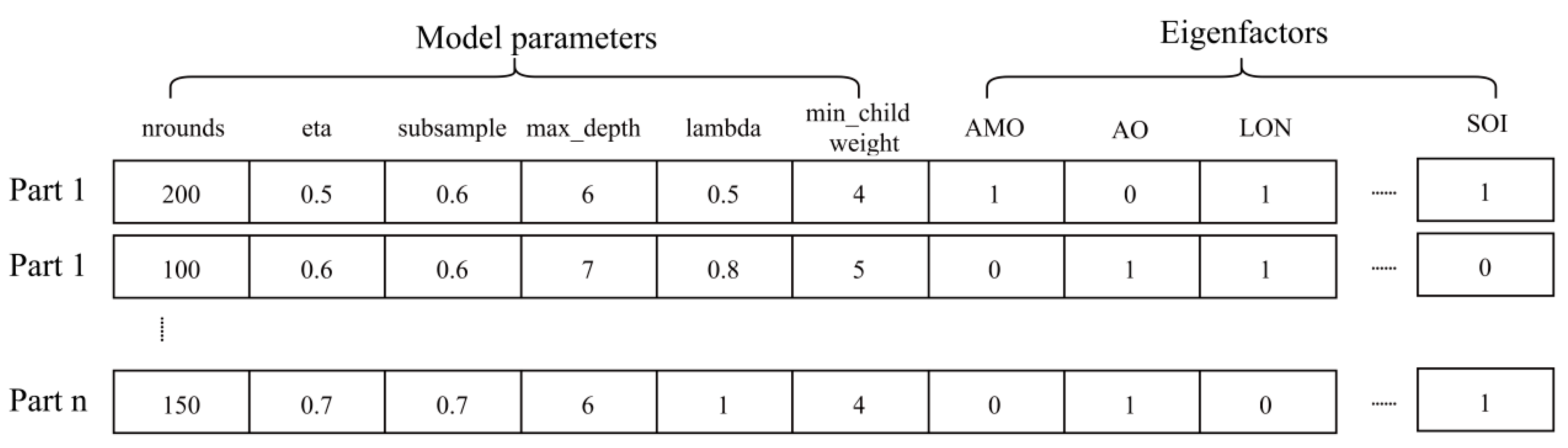
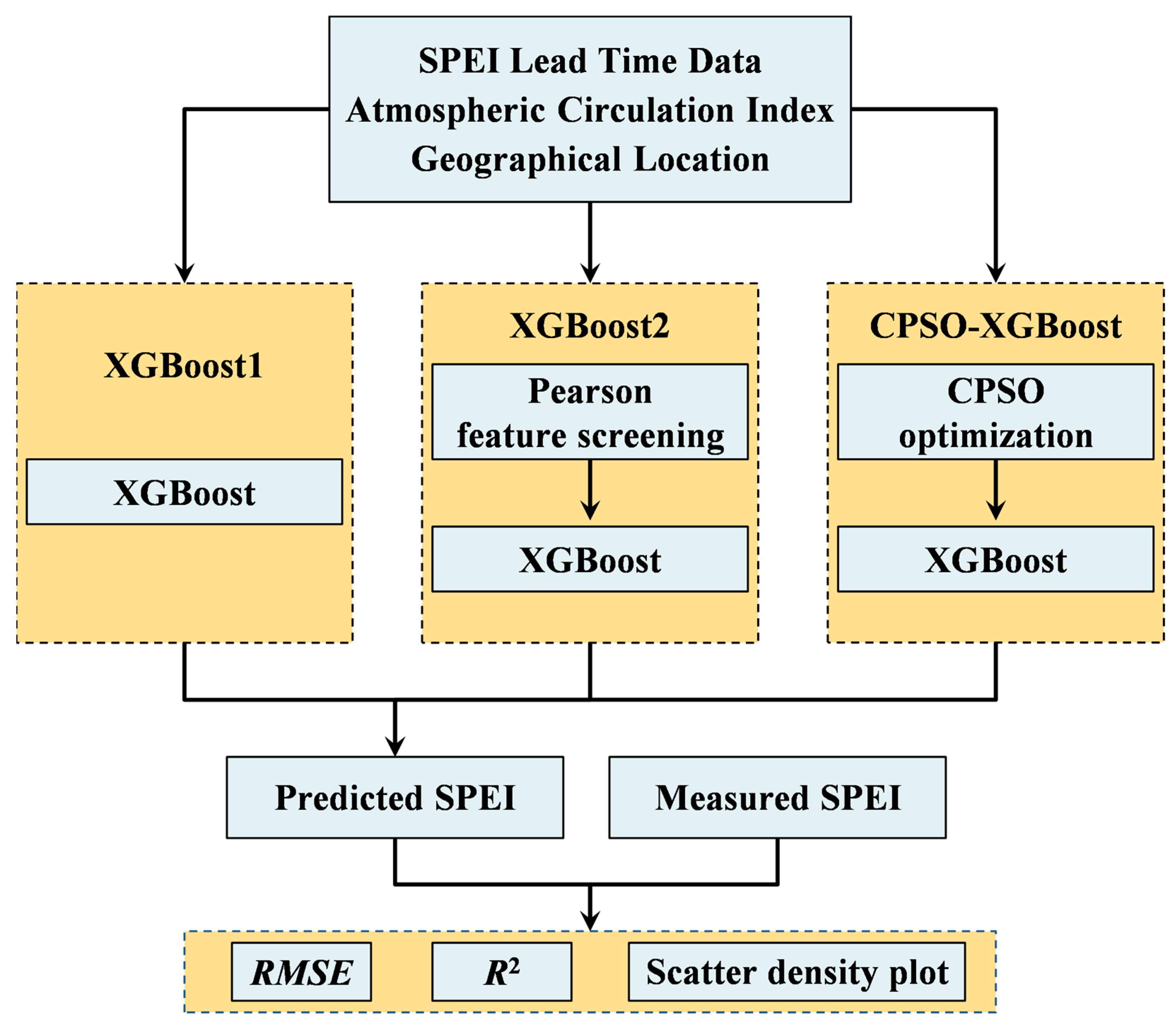
2.2.4. Predictive Model Architecture
2.2.5. Predictive Model Evaluation
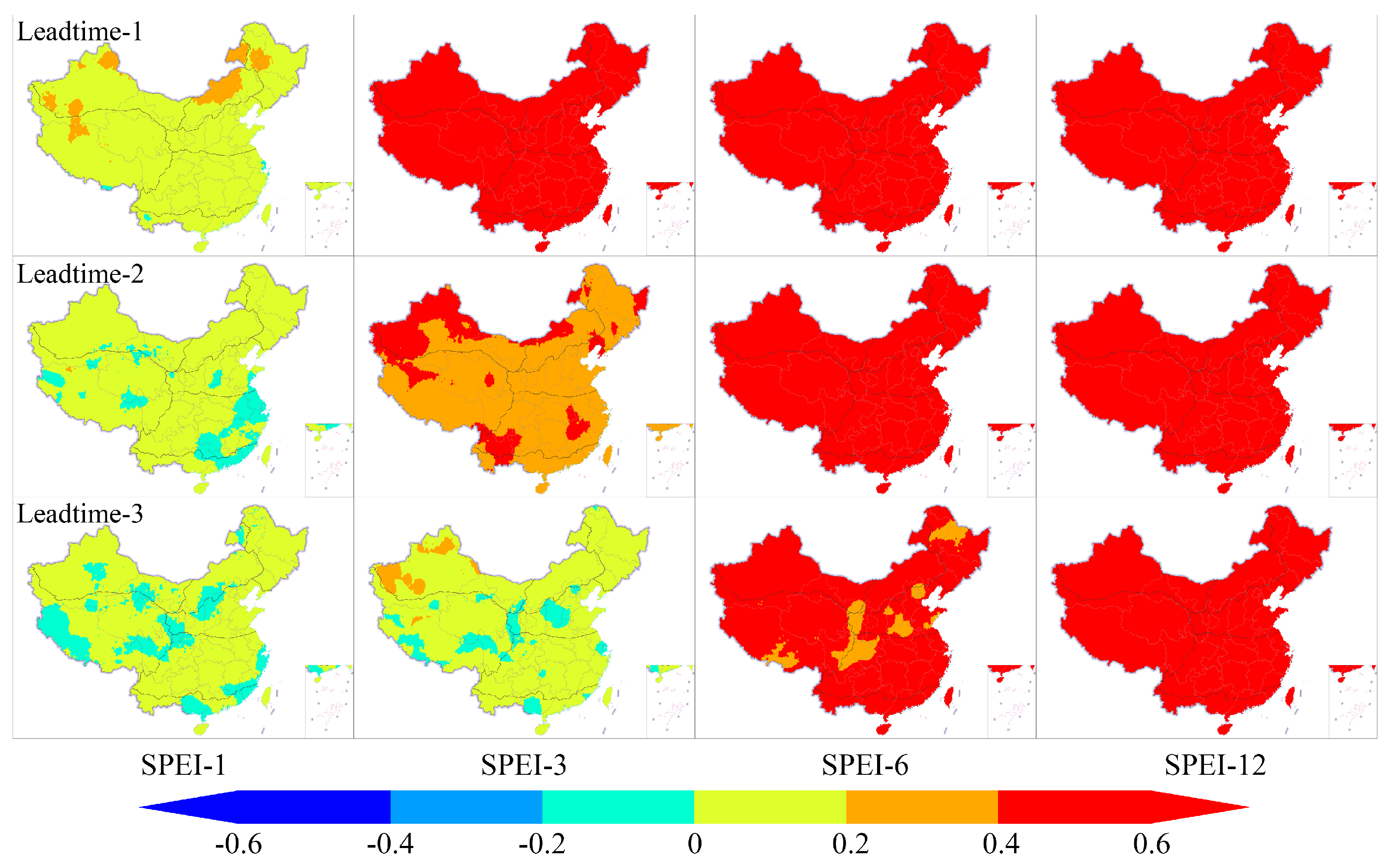
3. Results
3.1. Short-Term Drought Prediction of SPEI in Mainland China Using the XGBoost1 Model
3.2. Short-Term Drought Prediction of SPEI in Mainland China Using the XGBoost2 Model
3.2.1. Extraction of Pearson Eigen Factors
3.2.2. Simulation Results of the Model
3.3. Short-Term Drought Prediction of SPEI in Mainland China Using the CPSO-XGBoost Model
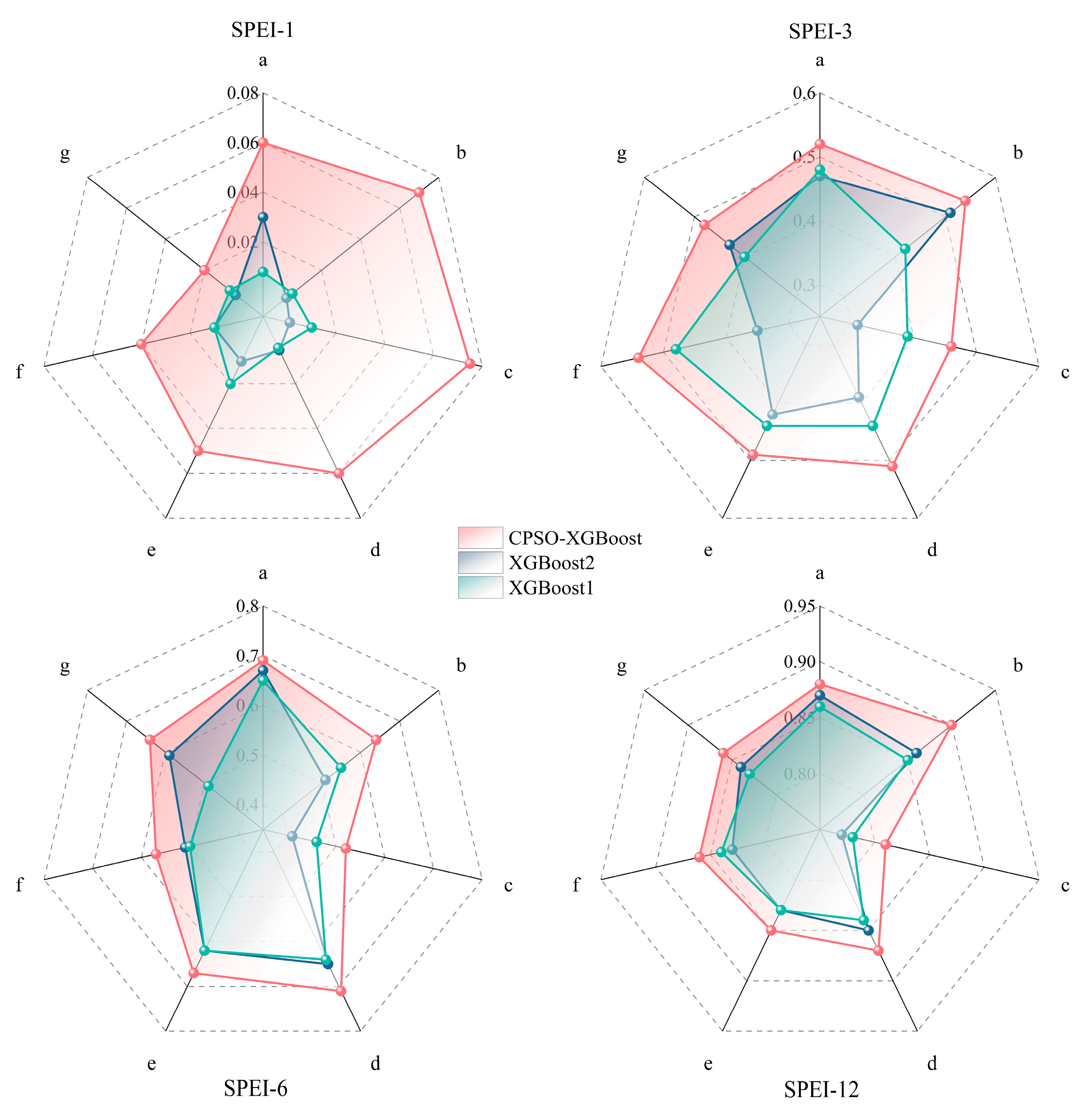
3.4. Comparative Analysis of Model Simulation Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPEI | Standardized Precipitation Evapotranspiration Index |
| SPEI-1 | Standardized Precipitation Evapotranspiration Index at 1-month timescale |
| SPEI-3 | Standardized Precipitation Evapotranspiration Index at 3-month timescale |
| SPEI-6 | Standardized Precipitation Evapotranspiration Index at 6-month timescale |
| SPEI-12 | Standardized Precipitation Evapotranspiration Index at 12-month timescale |
| Leadtime-1 | 1-month forecast lead time |
| Leadtime-2 | 2-month forecast lead time |
| Leadtime-3 | 3-month forecast lead time |
| AMO | Atlantic Multidecadal Oscillation |
| DMI | Indian Ocean Dipole Mode Index |
| AO | Arctic Oscillation |
| ESPI | El Niño–Southern Oscillation Precipitation Index |
| NAO | North Atlantic Oscillation |
| MEI | Multivariate ENSO Index |
| Niño1+2 | Average Sea Surface Temperature Anomaly in Niño1 and Niño2 Regions |
| Niño3.4 | Average Sea Surface Temperature Anomaly in the Overlap of Niño3 and Niño4 Regions |
| Niño3 | Average Sea Surface Temperature Anomaly in Niño3 Region |
| Niño4 | Average Sea Surface Temperature Anomaly in Niño4 Region |
| ONI | Oceanic Niño Index |
| PDO | Pacific Decadal Oscillation |
| SOI | Southern Oscillation Index |
| TPI(IPO) | Tripole Index of Interdecadal Pacific Oscillation |
| R2 | Coefficient of Determination |
| RMSE | Root Mean Squared Error |
| XGBoost | Extreme Gradient Boosting |
| CPSO | Coding Particle Swarm Optimization |
| BPSO | Binary Particle Swarm Optimization |
| PSO | Particle Swarm Optimization |
| CPSO-XGBoost | Chaotic Particle Swarm Optimization eXtreme Gradient Boosting |
| NDR | Northwest Desert Region |
| IMGR | Inner Mongolia Grassland Region |
| NHSTR | Northeast Humid and Semi-Humid Temperate Region |
| QTP | Qinghai-Tibet Plateau |
| NCHSWTR | North China Humid and Semi-Humid Warm Temperate Region |
| CSCHSR | Central-South China Humid Subtropical Region |
| SCHTR | South China Humid Tropical Region |
| NDI | New Drought Index |
References
- Wang, X.Y.; Li, J.; Xing, L.T. Comparative agricultural drought monitoring based on three machine learning methods. Arid Zone Res. 2022, 39, 322–332. [Google Scholar]
- Wang, Y.; Wang, L.; Lu, X.; Zhang, J.; Wang, Z.; Sha, S.; Hu, D.; Yang, Y.; Yan, P.; Li, Y. Analysis of the characteristics and causes of drought in China in the first half of 2023. J. Arid Meteorol. 2023, 41, 884. [Google Scholar]
- Zhang, R.; Chen, Z.Y.; Xu, L.J.; Ou, C.Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yao, Y.; Li, Y.; Huang, J.; Ma, Z.; Wang, Z.; Wang, S.; Wang, Y.; Zhang, Y. Progress and prospect on the study of causes and variation regularity of droughts in China. Acta Meteorol. Sin. 2020, 78, 500–521. [Google Scholar] [CrossRef]
- Achite, M.; Jehanzaib, M.; Elshaboury, N.; Kim, T.W. Evaluation of Machine Learning Techniques for Hydrological Drought Modeling: A Case Study of the Wadi Ouahrane Basin in Algeria. Water 2022, 14, 431. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C.X. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Milevski, I.; Aleksova, B.; Lukić, T.; Dragićević, S.; Valjarević, A. Multi-Hazard Modeling of Erosion and Landslide Susceptibility at the National Scale in the Case of North Macedonia. Open Geosci. 2024, 16, 20220718. [Google Scholar] [CrossRef]
- Valjarević, A.; Morar, C.; Brasanac-Bosanac, L.; Cirkovic-Mitrovic, T.; Djekic, T.; Mihajlović, M.; Kaplan, G. Sustainable Land Use in Moldova: GIS & Remote Sensing of Forests and Crops. Land Use Policy 2025, 152, 107515. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle swarm optimisation: A historical review up to the current developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review and comparison of genetic algorithm and particle swarm optimization in the optimal power flow problem. Energies 2023, 16, 1152. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, W.; Xu, L.; Zhangzhong, L.; Zhang, G.; Shan, F. A PSO-XGBoost model for estimating daily reference evapotranspiration in the solar greenhouse. Intell. Autom. Soft Comput. 2020, 26, 989–1003. [Google Scholar] [CrossRef]
- Jia, H.J.; Li, X.H.; Wang, L.; Xue, Y.; Lin, H. Remote sensing drought monitoring and assessment in southwestern China based on machine learning. Plateau Meteorol. 2022, 41, 1572–1582. [Google Scholar]
- Kumar, S.; Tian, D. Causal Discovery Analysis Reveals Global Sources of Predictability for Regional Flash Droughts. Water Resour. Res. 2024, 60, e2024WR038391. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.; Nguyen, T.T.; Liu, J.; Wu, T.; Lee, E.; Tu, X.M. Partial least squares regression and principal component analysis: Similarity and differences between two popular variable reduction approaches. Gen. Psychiatry 2022, 35, e100662. [Google Scholar] [CrossRef]
- Jiang, J.; Atkinson, P.M.; Chen, C.; Cao, Q.; Tian, Y.; Zhu, Y.; Liu, X.; Cao, W. Combining UAV and Sentinel-2 satellite multi-spectral images to diagnose crop growth and N status in winter wheat at the county scale. Field Crop. Res. 2023, 294, 108860. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Chakraborty, S.; Behera, M.D. Winter wheat yield prediction in the conterminous United States using solar-induced chlorophyll fluorescence data and XGBoost and random forest algorithm. Ecol. Inform. 2023, 77, 102194. [Google Scholar] [CrossRef]
- Yang, J.; Tian, Y.; Wu, C.H. Air quality prediction and ranking assessment based on bootstrap-XGBoost algorithm and ordinal classification models. Atmosphere 2024, 15, 925. [Google Scholar] [CrossRef]
- Lyu, Y.; Yong, B. A Novel Double Machine Learning Strategy for Producing High-Precision Multi-Source Merging Precipitation Estimates over the Tibetan Plateau. Water Resour. Res. 2024, 60, e2023WR035643. [Google Scholar] [CrossRef]
- Dong, J.; Zeng, W.; Wu, L.; Huang, J.; Gaiser, T.; Srivastava, A.K. Enhancing short-term forecasting of daily precipitation using numerical weather prediction bias correcting with XGBoost in different regions of China. Eng. Appl. Artif. Intell. 2023, 117, 105579. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; IEEE: New York, NY, USA, 1995; pp. 39–43. [Google Scholar]
- Xiujia, C.; Guanghua, Y.; Jian, G.; Ningning, M.; Zihao, W. Application of WNN-PSO model in drought prediction at crop growth stages: A case study of spring maize in semi-arid regions of northern China. Comput. Electron. Agric. 2022, 199, 107155. [Google Scholar] [CrossRef]
- Wang, Z.; Cui, G.; Liu, X.; Zheng, K.; Lu, Z.; Li, H.; Wang, G.; An, Z. Greening of the Qinghai–Tibet Plateau and Its Response to Climate Variations along Elevation Gradients. Remote Sens. 2021, 13, 3712. [Google Scholar] [CrossRef]
- Qolomany, B.; Maabreh, M.; Al-Fuqaha, A.; Gupta, A.; Benhaddou, D. Parameters optimization of deep learning models using particle swarm optimization. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; IEEE: New York, NY, USA, 2017; pp. 1285–1290. [Google Scholar]
- Fan, Y.; Zhang, Y.; Guo, B.; Luo, X.; Peng, Q.; Jin, Z. A hybrid sparrow search algorithm of the hyperparameter optimization in deep learning. Mathematics 2022, 10, 3019. [Google Scholar] [CrossRef]
- Li, A.D.; Xue, B.; Zhang, M. Improved binary particle swarm optimization for feature selection with new initialization and search space reduction strategies. Appl. Soft Comput. 2021, 106, 107302. [Google Scholar]
- Zhou, G.; Gao, J.; Zuo, D.; Li, J.; Li, R. MSXFGP: Combining improved sparrow search algorithm with XGBoost for enhanced genomic prediction. BMC Bioinform. 2023, 24, 384. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Piao, J.; Cai, Q.; Chen, S.; Xue, X.; Ma, T. Synergistic Effects of High Atmospheric and Soil Dryness on Record-Breaking Decreases in Vegetation Productivity over Southwest China in 2023. NPJ Clim. Atmos. Sci. 2025, 8, 6. [Google Scholar]
- Jiang, L.; Chen, Y.D.; Li, J.; Liu, C. Amplification of Soil Moisture Deficit and High Temperature in a Drought-Heatwave Co-Occurrence in Southwestern China. Nat. Hazards 2022, 111, 641–660. [Google Scholar] [CrossRef]
- Sundararajan, K.; Srinivasan, K. A Synergistic Optimization Algorithm with Attribute and Instance Weighting Approach for Effective Drought Prediction in Tamil Nadu. Sustainability 2024, 16, 2936. [Google Scholar] [CrossRef]
- Sundararajan, K.; Srinivasan, K.; Kaliappan, J. Improving Meteorological Drought Prediction in Tamil Nadu through Weighted Dataset Construction and Multi-Objective Optimization. IEEE Access 2024, 12, 96878–96892. [Google Scholar]
- Katipoğlu, O.M.; Ertugay, N.; Elshaboury, N.; Aktürk, G.; Kartal, V.; Pande, C.B. A Novel Metaheuristic Optimization and Soft Computing Techniques for Improved Hydrological Drought Forecasting. Phys. Chem. Earth A/B/C 2024, 135, 103646. [Google Scholar]
- Zhang, C.; Long, D.; Zhang, Y.; Anderson, M.C.; Kustas, W.P.; Yang, Y. A Decadal (2008–2017) Daily Evapotranspiration Data Set of 1 km Spatial Resolution and Spatial Completeness across the North China Plain Using TSEB and Data Fusion. Remote Sens. Environ. 2021, 262, 112519. [Google Scholar]
- Ghilain, N. Continental Scale Monitoring of Subdaily and Daily Evapotranspiration Enhanced by the Assimilation of Surface Soil Moisture Derived from Thermal Infrared Geostationary Data. In Satellite Soil Moisture Retrieval; Elsevier: Amsterdam, The Netherlands, 2016; pp. 309–332. [Google Scholar]
- Wang, C.C.; Kuo, P.H.; Chen, G.Y. Machine learning prediction of turning precision using optimized XGBoost model. Appl. Sci. 2022, 12, 7739. [Google Scholar] [CrossRef]
- He, B.; Wang, H.; Guo, L.; Liu, J. Global Analysis of Ecosystem Evapotranspiration Response to Precipitation Deficits. J. Geophys. Res. Atmos. 2017, 122, 13–308. [Google Scholar]
- Ratnasingam, S.; Muñoz-Lopez, J. Distance correlation-based feature selection in random forest. Entropy 2023, 25, 1250. [Google Scholar] [CrossRef]
- Han, D.; Li, H.; Fu, X. Reflective distributed denial of service detection: A novel model utilizing binary particle swarm optimization—Simulated annealing for feature selection and gray wolf optimization-optimized LightGBM algorithm. Sensors 2024, 24, 6179. [Google Scholar] [CrossRef]
- Lavate, S.; Joshi, A.A.; Shinde, T.S. Enhancing the convergence speed and accuracy of particle swarm optimizers through adaptive learning. In Proceedings of the 2022 International Conference on Emerging Smart Computing and Informatics (ESCI), Pune, India, 4–5 March 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Wang, W.; Zhu, Y.; Xu, R.; Liu, J. Drought Severity Change in China during 1961–2012 Indicated by SPI and SPEI. Nat. Hazards 2015, 75, 2437–2451. [Google Scholar]
- Chen, X.; Mo, X.; Zhang, Y.; Sun, Z.; Liu, Y.; Hu, S.; Liu, S. Drought Detection and Assessment with Solar-Induced Chlorophyll Fluorescence in Summer Maize Growth Period over North China Plain. Ecol. Indic. 2019, 104, 347–356. [Google Scholar]
- Bonacci, O.; Žaknić-Ćatović, A.; Roje-Bonacci, T. Prominent Increase in Air Temperatures on Two Small Mediterranean Islands, Lastovo and Lošinj, Since 1998 and Its Effect on the Frequency of Extreme Droughts. Water 2024, 16, 3175. [Google Scholar] [CrossRef]
- Bonacci, O.; Bonacci, D.; Roje-Bonacci, T.; Vrsalović, A. Proposal of a New Method for Drought Analysis. J. Hydrol. Hydromech. 2023, 71, 100–110. [Google Scholar]
- Xia, Y.; Jiang, S.; Meng, L.; Ju, X. XGBoost-B-GHM: An ensemble model with feature selection and GHM loss function optimization for credit scoring. Systems 2024, 12, 254. [Google Scholar] [CrossRef]

| Index | Full Name | Period (Year) |
|---|---|---|
| AMO | Atlantic Multidecadal Oscillation | 1856–2022 |
| DMI | Indian Ocean Dipole Mode Index | 1870–2022 |
| AO | Arctic Oscillation | 1950–2022 |
| ESPI | El Niño–Southern Oscillation Precipitation Index | 1979–2022 |
| NAO | North Atlantic Oscillation | 1950–2022 |
| MEI | Multivariate ENSO Index | 1979–2022 |
| Niño1+2 | Average Sea Surface Temperature Anomaly in Niño1 and Niño2 Regions | 1950–2022 |
| Niño3.4 | Average Sea Surface Temperature Anomaly in the Overlap of Niño3 and Niño4 Regions | |
| Niño3 | Average Sea Surface Temperature Anomaly in Niño3 Region | |
| Niño4 | Average Sea Surface Temperature Anomaly in Niño4 Region | |
| ONI | Oceanic Niño Index | |
| PDO | Pacific Decadal Oscillation | 1900–2022 |
| SOI | Southern Oscillation Index | 1948–2022 |
| TPI(IPO) | Tripole Index of Interdecadal Pacific Oscillation | 1854–2021 |
| Time Scales | SPEI-1 | SPEI-3 | SPEI-6 | SPEI-12 |
|---|---|---|---|---|
| NDR | Latitude, Longitude, Leadtime-1 | AMO, DMI, PDO, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, Niño3, Niño4, PDO, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| IMGR | AO, Longitude, Latitude, Leadtime-1 | DMI, Longitude, Latitude, Leadtime-1, Leadtime-2 | DMI, Niño3.4, Niño3, Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| NHSTR | AO, Longitude, Latitude, Leadtime-1 | Leadtime-1, Leadtime-2 | SOI, Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| NHSTR | AO, Longitude, Latitude | DMI, Longitude, Latitude, Leadtime-1, Leadtime-2 | DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| QTP | AMO, AO, Longitude, Latitude, Leadtime-1, Leadtime-2 | AMO, DMI, ESPI, MEI, Niño3, ONI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| CSCHSR | AO, ESPI, MEI, Niño1+2, Niño3.4, Niño3, ONI, SOI, TPI(IPO), Longitude, Latitude | AO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, DMI, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
| SCHTR | ESPI, MEI, Niño3.4, Niño3, ONI, TPI(IPO), Longitude, Latitude | AO, ESPI, MEI, Niño1+2, Niño3.4, Niño3, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2 | ESPI, MEI, Niño1+2, Niño3.4, Niño3, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 | AMO, ESPI, MEI, Niño1+2, Niño3.4, Niño3, Niño4, ONI, PDO, SOI, TPI(IPO), Longitude, Latitude, Leadtime-1, Leadtime-2, Leadtime-3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Gao, Q.; Wu, L.; Rao, Z.; Wang, Z.; Zhang, X.; Yao, F.; Sun, J. Modeling Short-Term Drought for SPEI in Mainland China Using the XGBoost Model. Atmosphere 2025, 16, 419. https://doi.org/10.3390/atmos16040419
Zeng F, Gao Q, Wu L, Rao Z, Wang Z, Zhang X, Yao F, Sun J. Modeling Short-Term Drought for SPEI in Mainland China Using the XGBoost Model. Atmosphere. 2025; 16(4):419. https://doi.org/10.3390/atmos16040419
Chicago/Turabian StyleZeng, Fanchao, Qing Gao, Lifeng Wu, Zhilong Rao, Zihan Wang, Xinjian Zhang, Fuqi Yao, and Jinwei Sun. 2025. "Modeling Short-Term Drought for SPEI in Mainland China Using the XGBoost Model" Atmosphere 16, no. 4: 419. https://doi.org/10.3390/atmos16040419
APA StyleZeng, F., Gao, Q., Wu, L., Rao, Z., Wang, Z., Zhang, X., Yao, F., & Sun, J. (2025). Modeling Short-Term Drought for SPEI in Mainland China Using the XGBoost Model. Atmosphere, 16(4), 419. https://doi.org/10.3390/atmos16040419






