Atmospheric Energetics of Three Contrasting West African Monsoon Seasons as Simulated by a Regional Climate Model
Abstract
1. Introduction
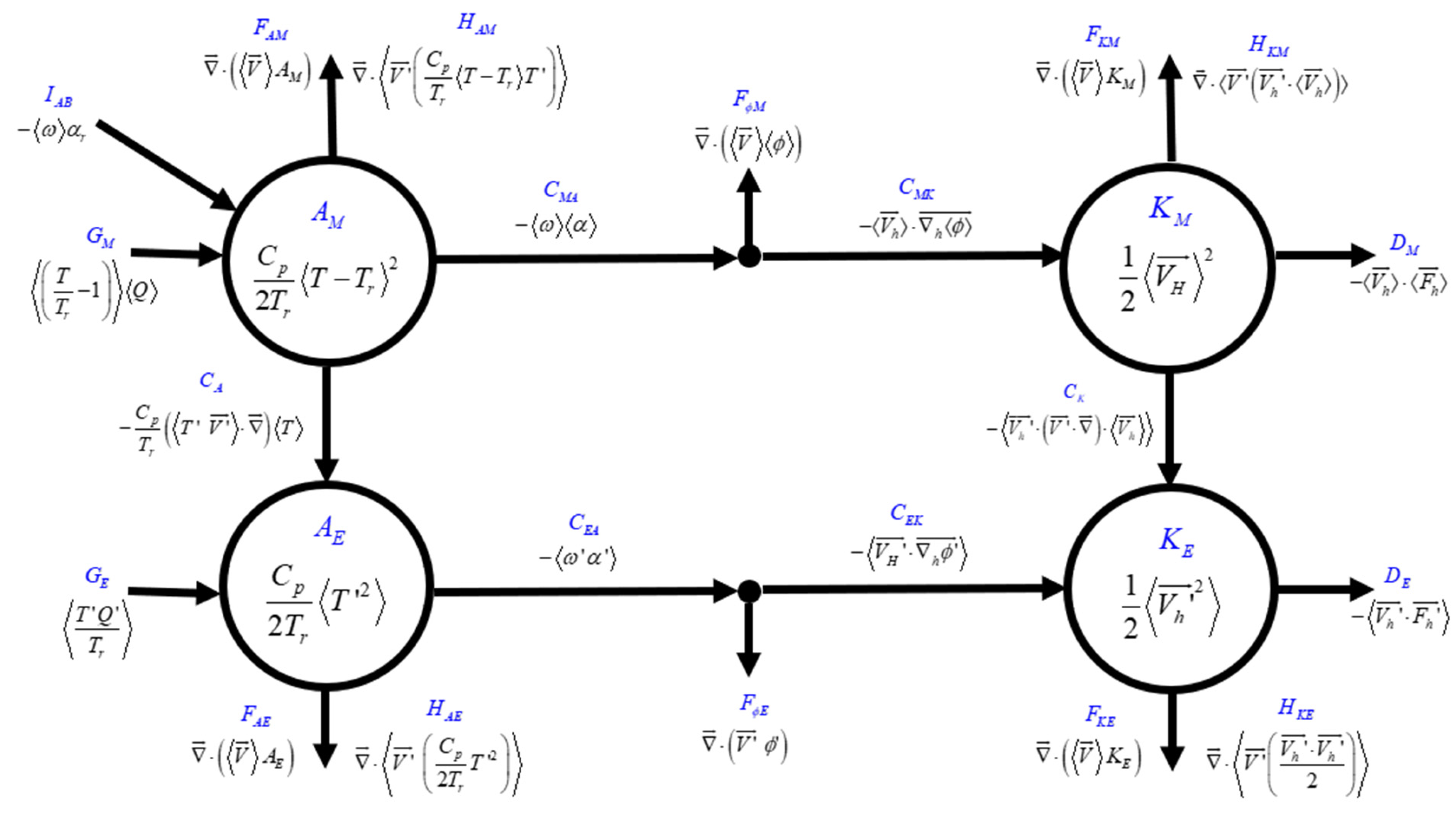
2. Methodology for the Computation of an Atmospheric Energy Cycle Suitable for Climate Studies
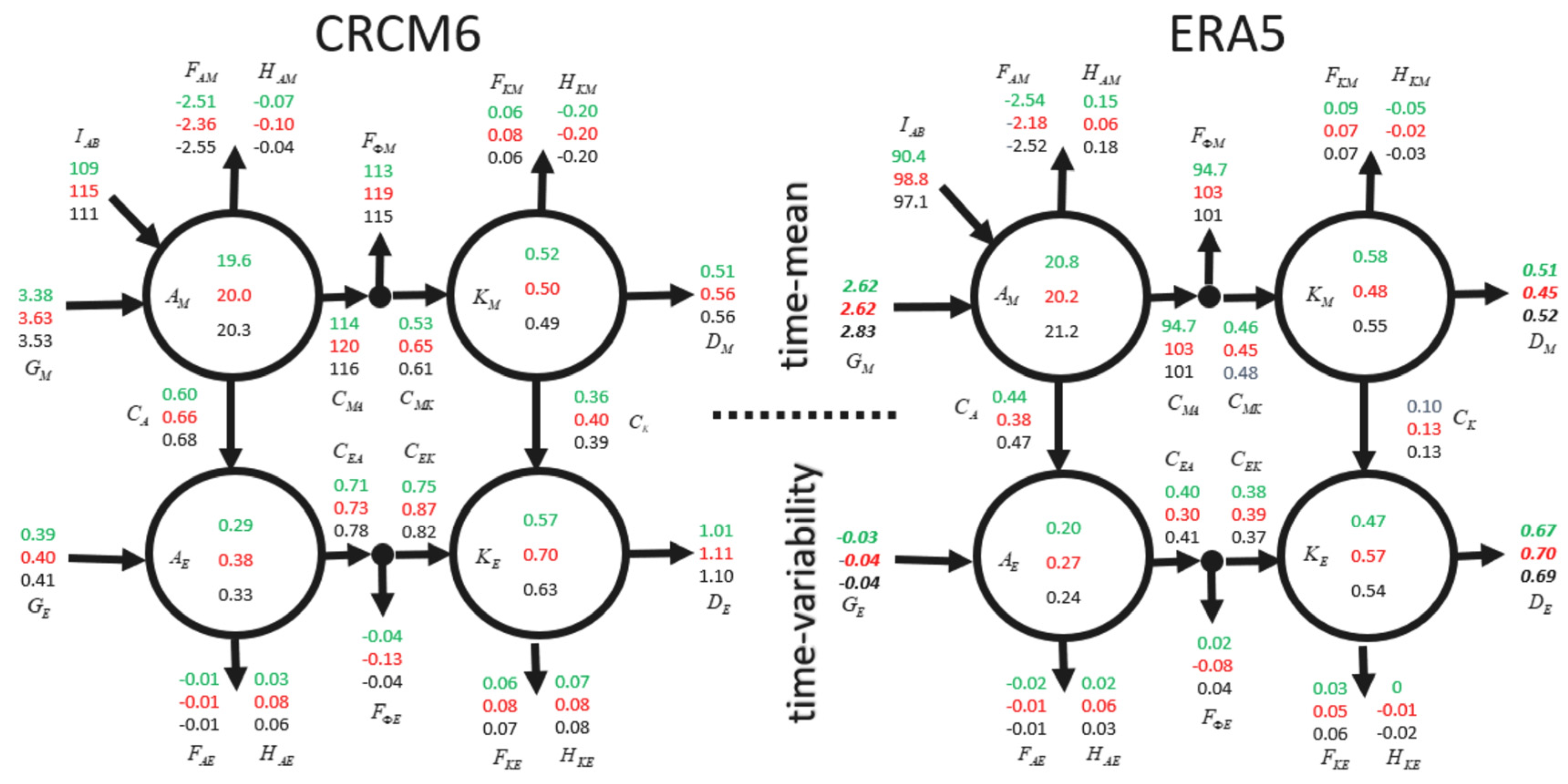
- Boundary flux terms starting with capital letters F or H represent the transport of the energy reservoirs by the time-mean and the time-variability wind (FAM, HAM, FKM, HKM, FAE, HAE, FKE, HKE).
- Conversion terms starting with the capital letter C (CA, CK, CMA, CMK, CEA, and CEK) represent the conversion of energy from one reservoir to another. In regional energy budgets, the presence of lateral boundaries affects the direct conversion from one reservoir to another. As discussed in NLN24, the presence of zero-sum nodes between the available energy and kinetic energy reservoirs implies that the fluxes into kinetic energy CMK and CEK differ from the fluxes from available enthalpy CMA and CEA. IAB is also a conversion term resulting from the splitting of the available enthalpy into temperature- and pressure-dependent components.
- Generation and dissipation terms start with capital letters G and D (GM, GE, DM, and DE), respectively. Generation terms are, in general, the main sources of the generation of available enthalpy, while dissipative terms are the main sinks of kinetic energy in the atmosphere.
3. Simulation Configuration and Climate Overview
3.1. Simulation Configuration
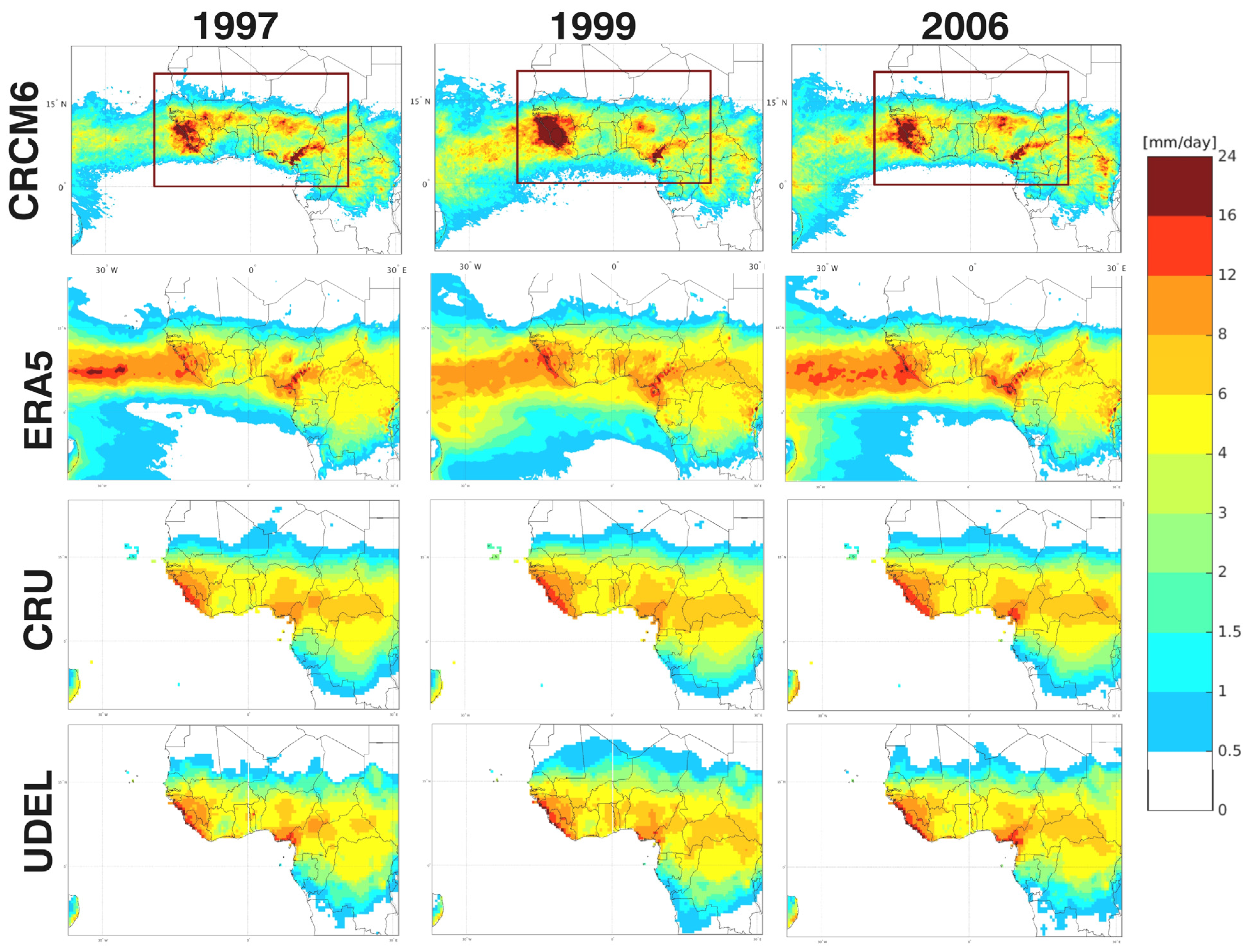
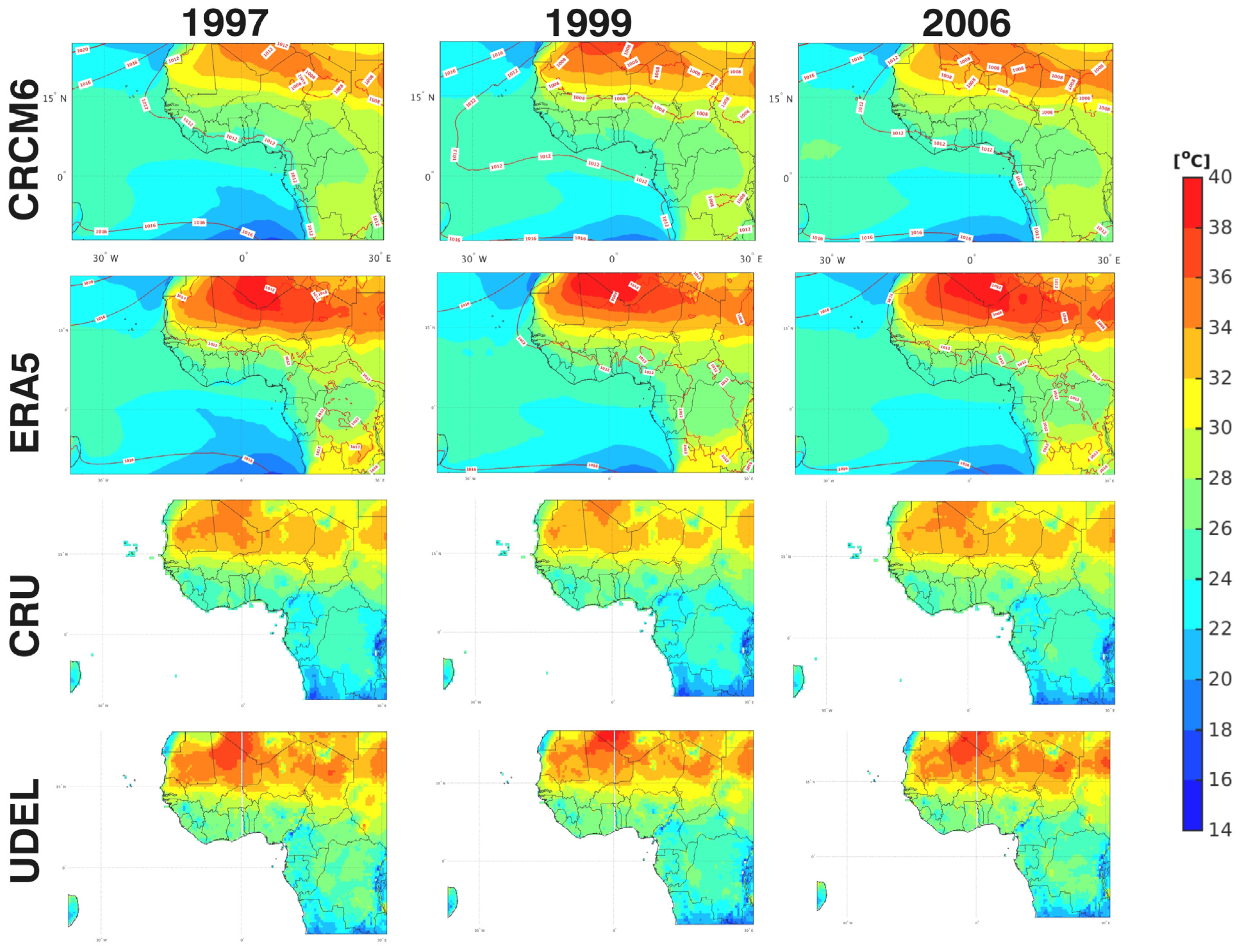
3.2. West African Climate Overview
4. West Africa Energy Budget
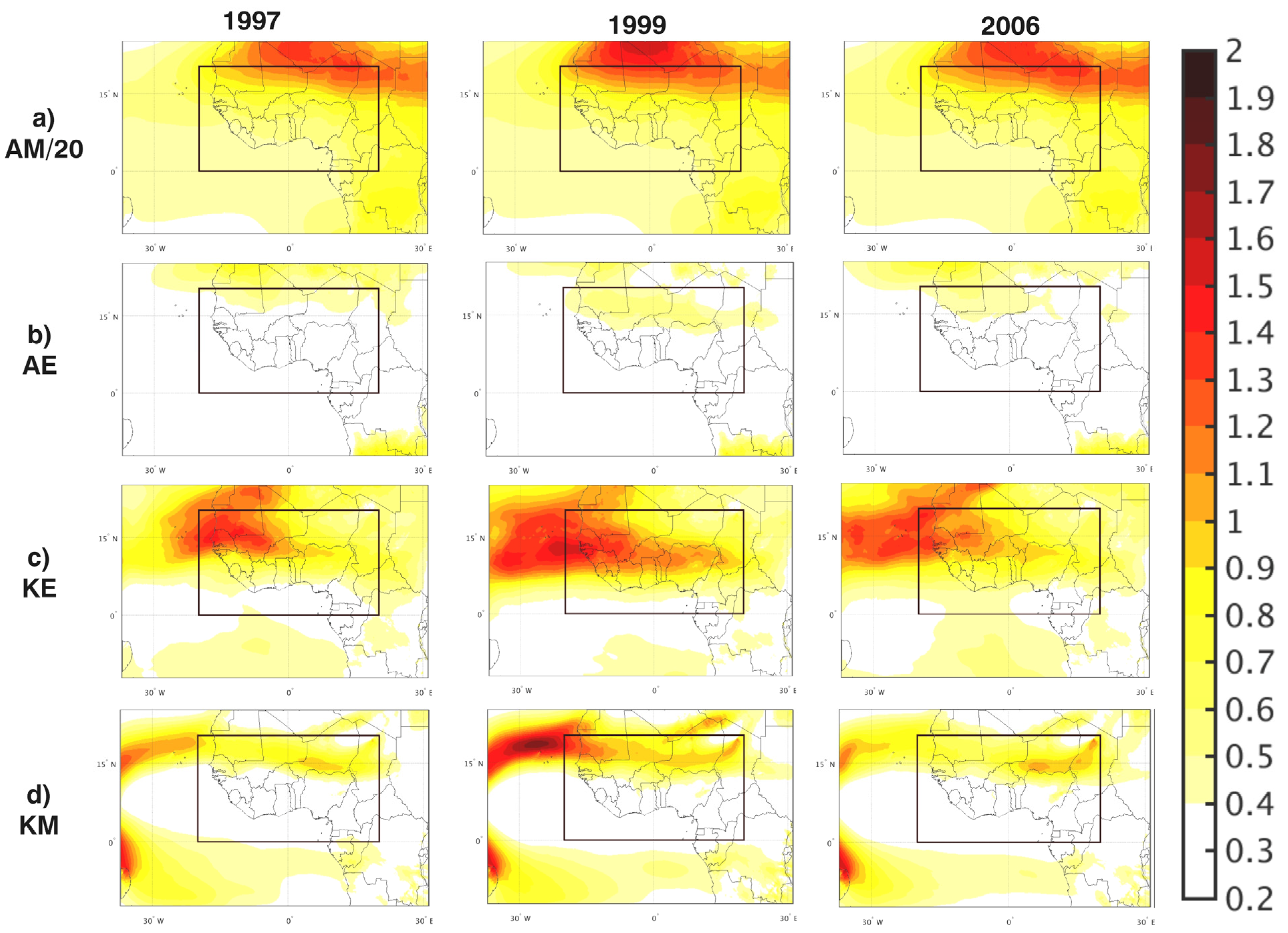
4.1. Analysis of Energy Reservoirs AM, AE, KM, and KE
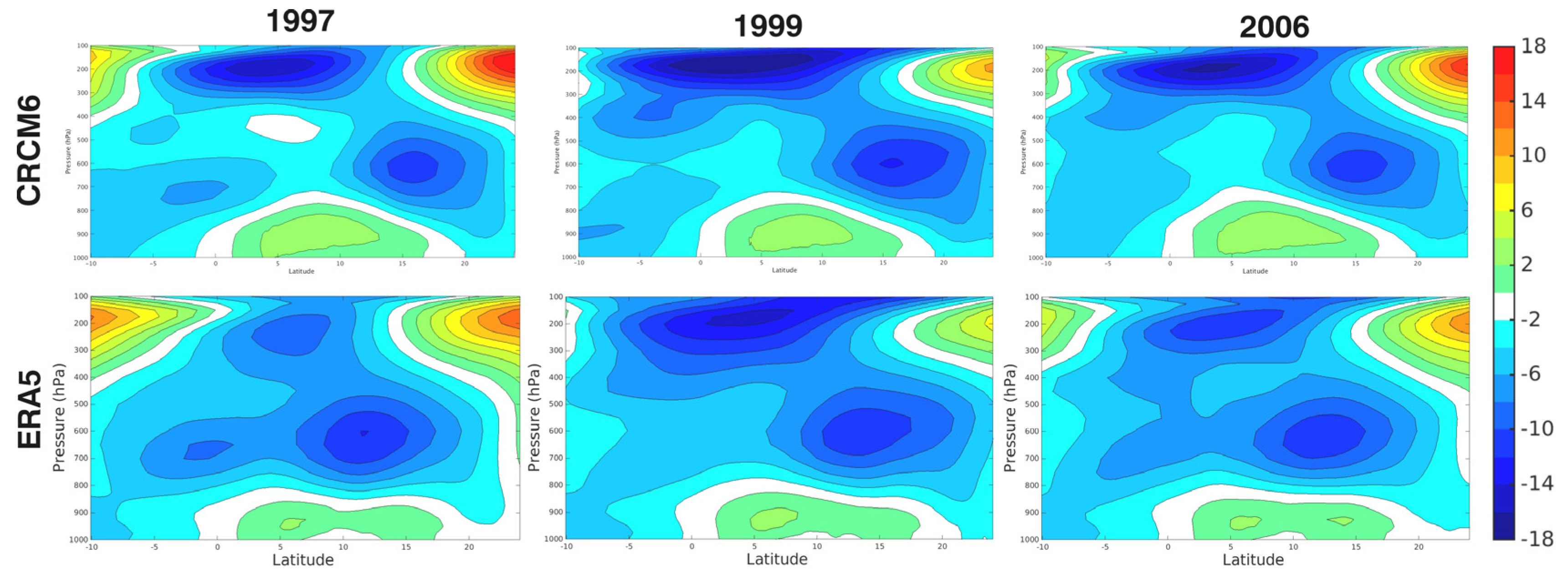
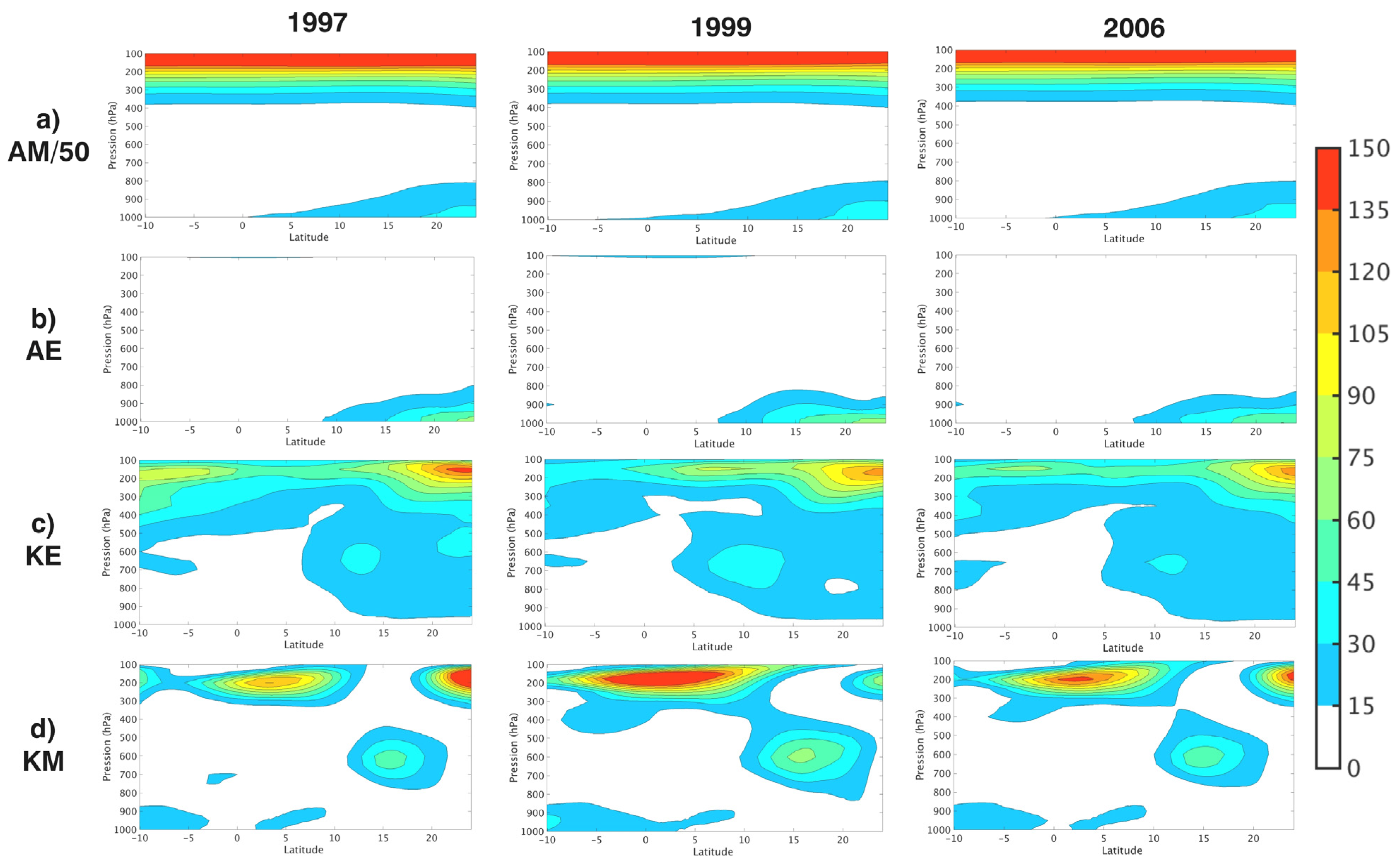
4.1.1. AM
4.1.2. AE
4.1.3. KE
4.1.4. KM
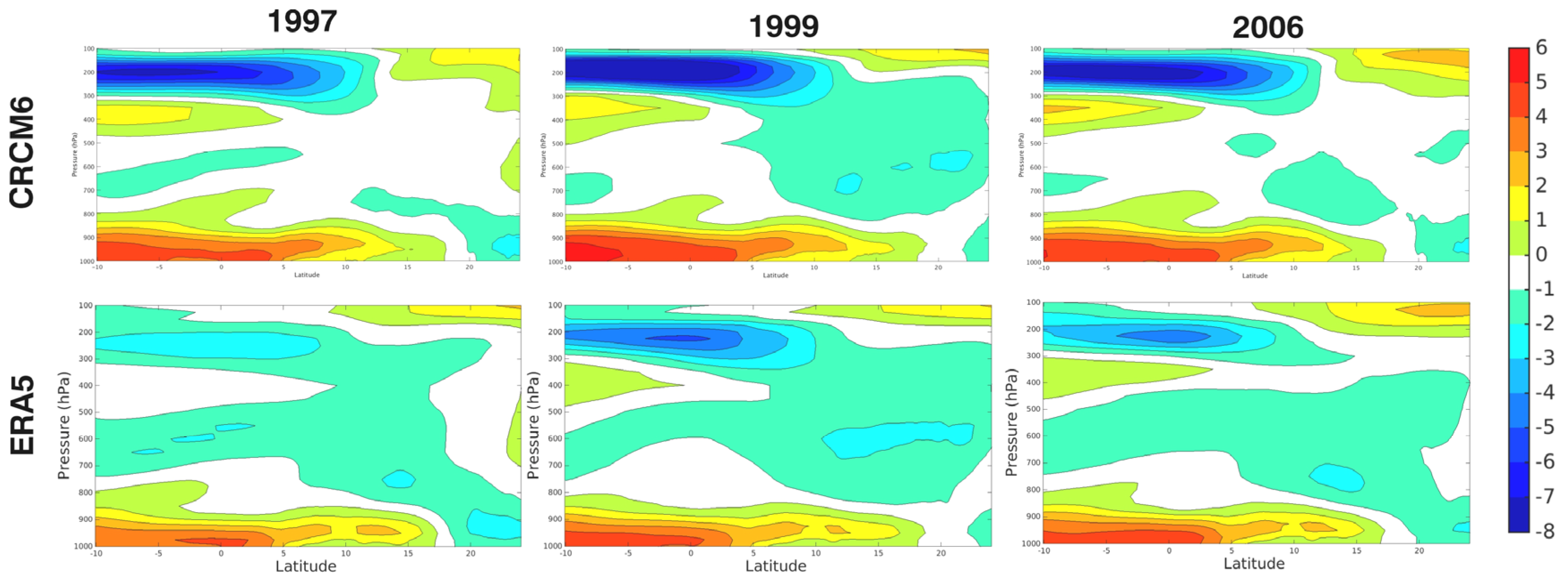
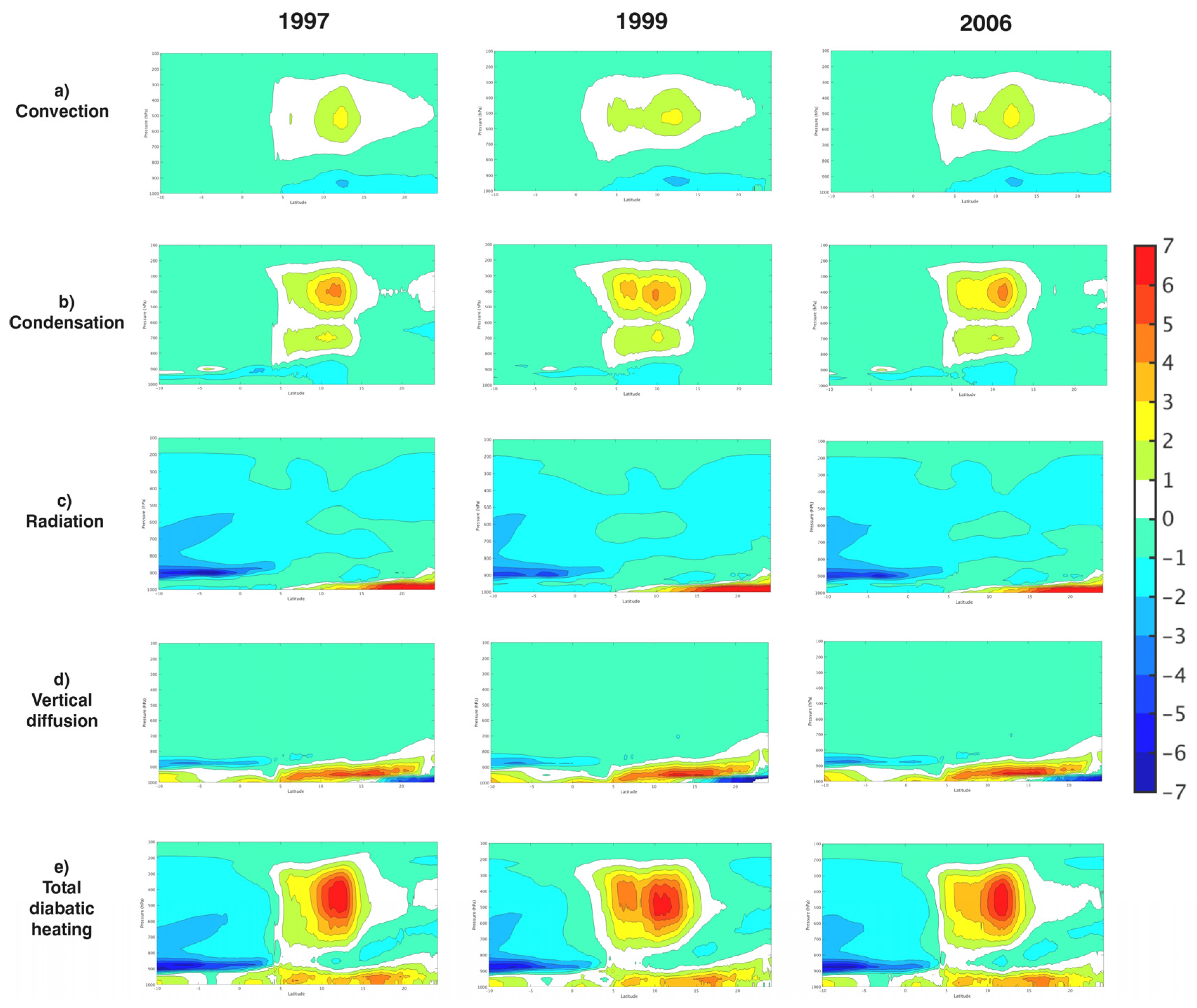
4.2. Conversion Terms
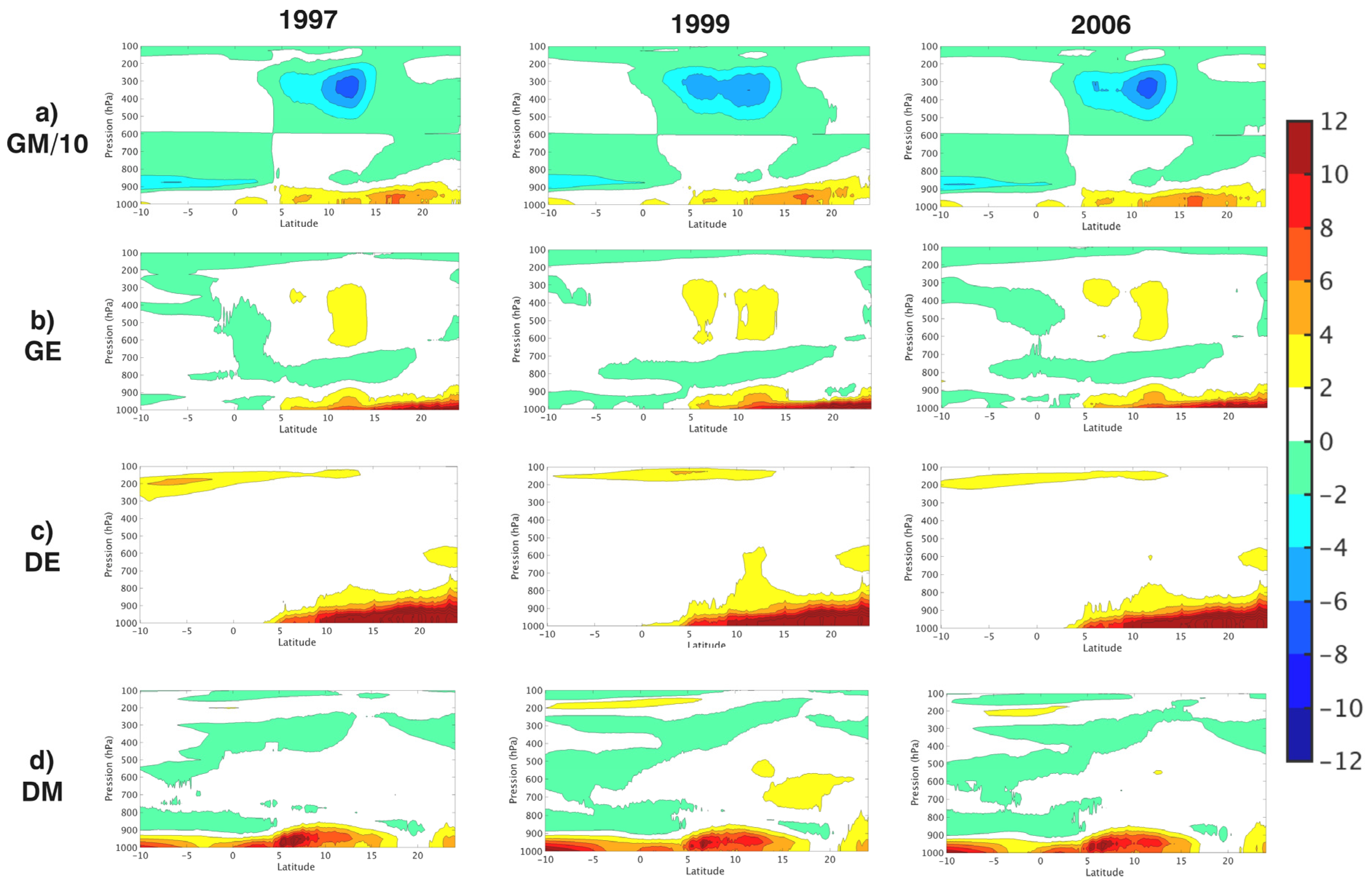
4.3. Energy Generation and Dissipation Terms
4.4. Boundaries Fluxes Terms
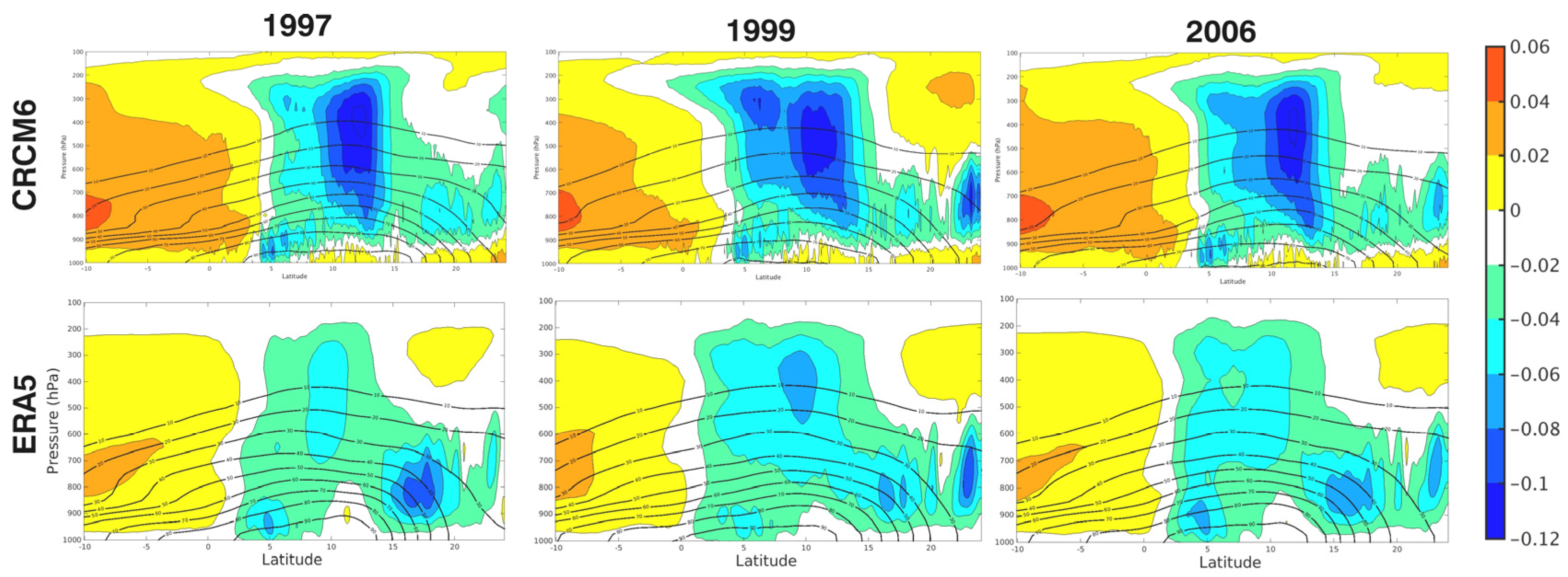
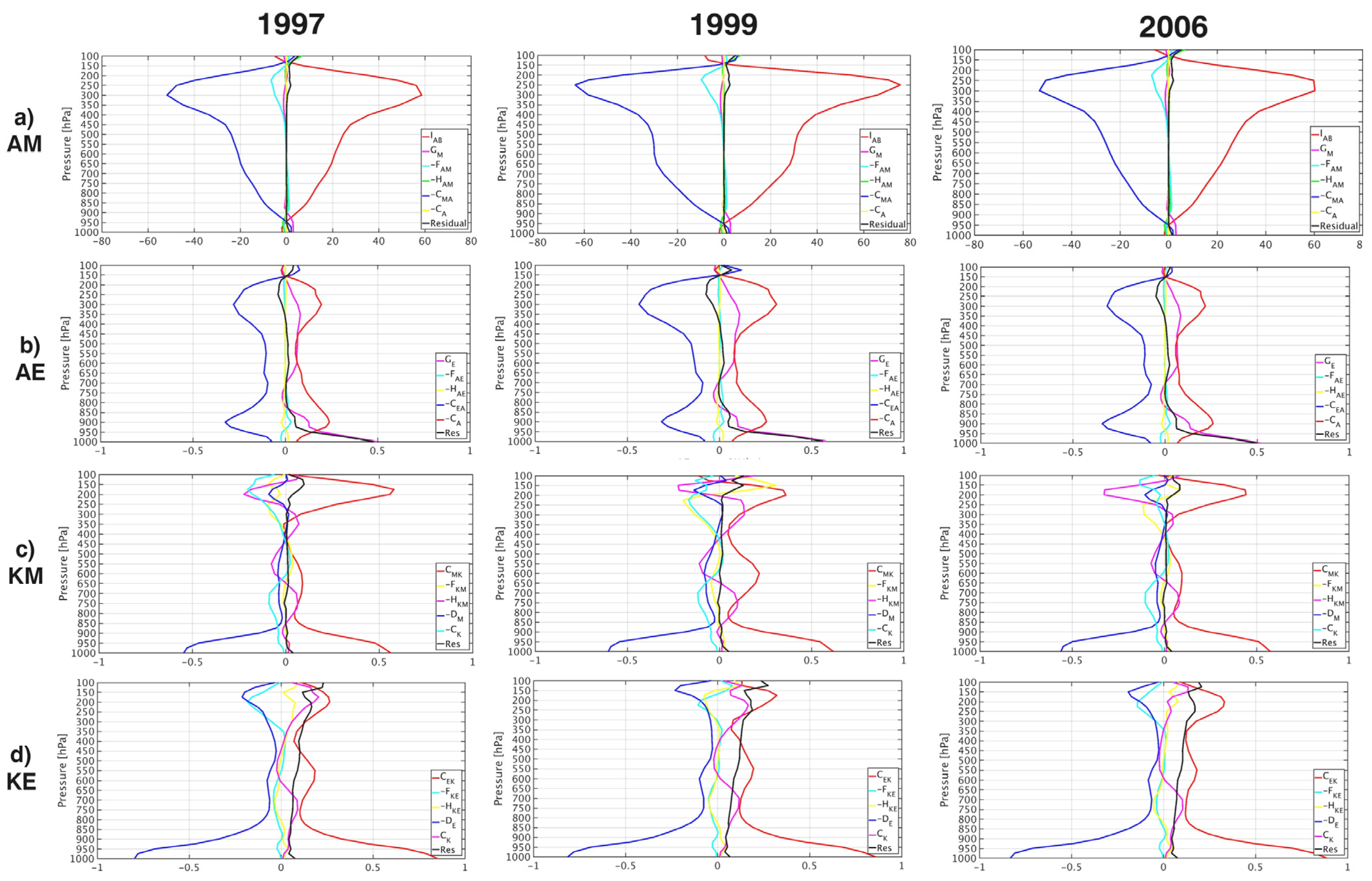
4.5. Vertical Profiles
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Link Between CE and CA’s Vertical Component
References
- Gowing, J.W. Food security for sub-Saharan Africa: Does water scarcity limit the options? Land Use Water Resour. Res. 2003, 3. [Google Scholar] [CrossRef]
- Redelsperger, J.-L.; Thorncroft, C.D.; Diedhiou, A.; Lebel, T.; Parker, D.J.; Polcher, J. African Monsoon Multidisciplinary Analysis: An international research project and field campaign. Bull. Am. Meteorol. Soc. 2006, 87, 1739–1746. [Google Scholar] [CrossRef]
- Lebel, T.; Parker, D.J.; Flamant, C.; Bourlès, B.; Marticorena, B.; Mougin, E.; Peugeot, C.; Diedhiou, A.; Haywood, J.; Ngamini, J.-B. The AMMA field campaigns: Multiscale and multidisciplinary observations in the West African region. Q. J. R. Meteorol. Soc. 2010, 136, 8–33. [Google Scholar] [CrossRef]
- Hourdin, F.; Musat, I.; Guichard, F.s.; Ruti, P.M.; Favot, F.; Filiberti, M.-A.; Pham, M.; Grandpeix, J.-Y.; Polcher, J.; Marquet, P. AMMA-model intercomparison project. Bull. Am. Meteorol. Soc. 2010, 91, 95–104. [Google Scholar] [CrossRef]
- Boone, A.; De Rosnay, P.; Balsamo, G.; Beljaars, A.; Chopin, F.; Decharme, B.; Delire, C.; Ducharne, A.; Gascoin, S.; Grippa, M. The AMMA land surface model intercomparison project (ALMIP). Bull. Am. Meteorol. Soc. 2009, 90, 1865–1880. [Google Scholar] [CrossRef]
- Xue, Y.; De Sales, F.; Lau, W.-M.; Boone, A.; Feng, J.; Dirmeyer, P.; Guo, Z.; Kim, K.-M.; Kitoh, A.; Kumar, V. Intercomparison and analyses of the climatology of the West African Monsoon in the West African Monsoon Modeling and Evaluation project (WAMME) first model intercomparison experiment. Clim. Dyn. 2010, 35, 3–27. [Google Scholar] [CrossRef]
- Hernández-Díaz, L.; Laprise, R.; Sushama, L.; Martynov, A.; Winger, K.; Dugas, B. Climate simulation over CORDEX Africa domain using the fifth-generation Canadian Regional Climate Model (CRCM5). Clim. Dyn. 2013, 40, 1415–1433. [Google Scholar] [CrossRef]
- Lorenz, E.N. Available potential energy and the maintenance of the general. Tellus 1955, 7, 157–167. [Google Scholar] [CrossRef]
- Li, L.; Ingersoll, A.P.; Jiang, X.; Feldman, D.; Yung, Y.L. Lorenz energy cycle of the global atmosphere based on reanalysis datasets. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Ngueto, Y.F.; Laprise, R.; Nikiéma, O. A Detailed Limited-Area Atmospheric Energy Cycle for Climate and Weather Studies. Atmosphere 2024, 15, 87. [Google Scholar] [CrossRef]
- Nikiéma, O.; Laprise, R. An approximate energy cycle for inter-member variability in ensemble simulations of a regional climate model. Clim. Dyn. 2013, 41, 831–852. [Google Scholar]
- Thorncroft, C.; Hoskins, B. An idealized study of African easterly waves. II: A nonlinear view. Q. J. R. Meteorol. Soc. 1994, 120, 983–1015. [Google Scholar] [CrossRef]
- Kebe, I.; Diallo, I.; Sylla, M.B.; De Sales, F.; Diedhiou, A. Late 21st century projected changes in the relationship between precipitation, African easterly jet, and African easterly waves. Atmosphere 2020, 11, 353. [Google Scholar] [CrossRef]
- Lorenz, E.N. Energy and numerical weather prediction. Tellus 1960, 12, 364–373. [Google Scholar]
- Roberge, F.; Di Luca, A.; Laprise, R.; Lucas-Picher, P.; Thériault, J. Spatial spin-up of precipitation in limited-area convection-permitting simulations over North America using the CRCM6/GEM5. 0 model. Geosci. Model Dev. 2024, 17, 1497–1510. [Google Scholar]
- McTaggart-Cowan, R.; Vaillancourt, P.; Zadra, A.; Chamberland, S.; Charron, M.; Corvec, S.; Milbrandt, J.; Paquin-Ricard, D.; Patoine, A.; Roch, M. Modernization of atmospheric physics parameterization in Canadian NWP. J. Adv. Model. Earth Syst. 2019, 11, 3593–3635. [Google Scholar]
- Laprise, R. The Euler equations of motion with hydrostatic pressure as an independent variable. Mon. Weather Rev. 1992, 120, 197–207. [Google Scholar]
- Milbrandt, J.; Morrison, H. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part III: Introduction of multiple free categories. J. Atmos. Sci. 2016, 73, 975–995. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar]
- Hernández-Díaz, L.; Laprise, R.; Nikiéma, O.; Winger, K. 3-Step dynamical downscaling with empirical correction of sea-surface conditions: Application to a CORDEX Africa simulation. Clim. Dyn. 2017, 48, 2215–2233. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [PubMed]
- Matsuura, K.; Willmott, C. University of Delaware Terrestrial Precipitation; NOAA ESRL: Boulder, CO, USA, 2018. [Google Scholar]
- Sultan, B.; Janicot, S.; Diedhiou, A. The West African monsoon dynamics. Part I: Documentation of intraseasonal variability. J. Clim. 2003, 16, 3389–3406. [Google Scholar]
- Lavaysse, C.; Flamant, C.; Janicot, S.; Parker, D.J.; Lafore, J.-P.; Sultan, B.; Pelon, J. Seasonal evolution of the West African heat low: A climatological perspective. Clim. Dyn. 2009, 33, 313–330. [Google Scholar]
- Parker, D.J.; Thorncroft, C.D.; Burton, R.R.; Diongue-Niang, A. Analysis of the African easterly jet, using aircraft observations from the JET2000 experiment. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2005, 131, 1461–1482. [Google Scholar]
- Cook, K.H. Generation of the African easterly jet and its role in determining West African precipitation. J. Clim. 1999, 12, 1165–1184. [Google Scholar] [CrossRef]
- Lemburg, A.; Bader, J.; Claussen, M. Sahel rainfall–tropical easterly jet relationship on synoptic to intraseasonal time scales. Mon. Weather Rev. 2019, 147, 1733–1752. [Google Scholar]
- Clément, M.; Nikiéma, O.; Laprise, R. Limited-area atmospheric energetics: Illustration on a simulation of the CRCM5 over eastern North America for December 2004. Clim. Dyn. 2017, 48, 2797–2818. [Google Scholar]
- Lavaysse, C.; Flamant, C.; Janicot, S.; Knippertz, P. Links between African easterly waves, midlatitude circulation and intraseasonal pulsations of the West African heat low. Q. J. R. Meteorol. Soc. 2010, 136, 141–158. [Google Scholar]
- Mekonnen, A.; Thorncroft, C.D.; Aiyyer, A.R. Analysis of convection and its association with African easterly waves. J. Clim. 2006, 19, 5405–5421. [Google Scholar]
- Nicholson, S.E. The intensity, location and structure of the tropical rainbelt over west Africa as factors in interannual variability. Int. J. Climatol. A J. R. Meteorol. Soc. 2008, 28, 1775–1785. [Google Scholar]
- Thorncroft, C.D.; Nguyen, H.; Zhang, C.; Peyrillé, P. Annual cycle of the West African monsoon: Regional circulations and associated water vapour transport. Q. J. R. Meteorol. Soc. 2011, 137, 129–147. [Google Scholar] [CrossRef]
- Shekhar, R.; Boos, W.R. Weakening and shifting of the Saharan shallow meridional circulation during wet years of the West African monsoon. J. Clim. 2017, 30, 7399–7422. [Google Scholar] [CrossRef]
- Lavaysse, C.; Flamant, C.; Evan, A.; Janicot, S.; Gaetani, M. Recent climatological trend of the Saharan heat low and its impact on the West African climate. Clim. Dyn. 2016, 47, 3479–3498. [Google Scholar] [CrossRef]
- Nicholson, S.E. A revised picture of the structure of the “monsoon” and land ITCZ over West Africa. Clim. Dyn. 2009, 32, 1155–1171. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngueto, Y.; Laprise, R.; Nikiéma, O. Atmospheric Energetics of Three Contrasting West African Monsoon Seasons as Simulated by a Regional Climate Model. Atmosphere 2025, 16, 405. https://doi.org/10.3390/atmos16040405
Ngueto Y, Laprise R, Nikiéma O. Atmospheric Energetics of Three Contrasting West African Monsoon Seasons as Simulated by a Regional Climate Model. Atmosphere. 2025; 16(4):405. https://doi.org/10.3390/atmos16040405
Chicago/Turabian StyleNgueto, Yves, René Laprise, and Oumarou Nikiéma. 2025. "Atmospheric Energetics of Three Contrasting West African Monsoon Seasons as Simulated by a Regional Climate Model" Atmosphere 16, no. 4: 405. https://doi.org/10.3390/atmos16040405
APA StyleNgueto, Y., Laprise, R., & Nikiéma, O. (2025). Atmospheric Energetics of Three Contrasting West African Monsoon Seasons as Simulated by a Regional Climate Model. Atmosphere, 16(4), 405. https://doi.org/10.3390/atmos16040405



