Study of Thermodynamic Horizontal Structure of the Middle and Upper Atmosphere Based on Atmospheric Detection Lidar Networks
Abstract
1. Introduction
2. Methods
2.1. Lidar System
2.2. Lidar Network
2.3. Lidar Network Data Processing—3DVAR Method
3. Results and Discussion
3.1. Assimilation Data
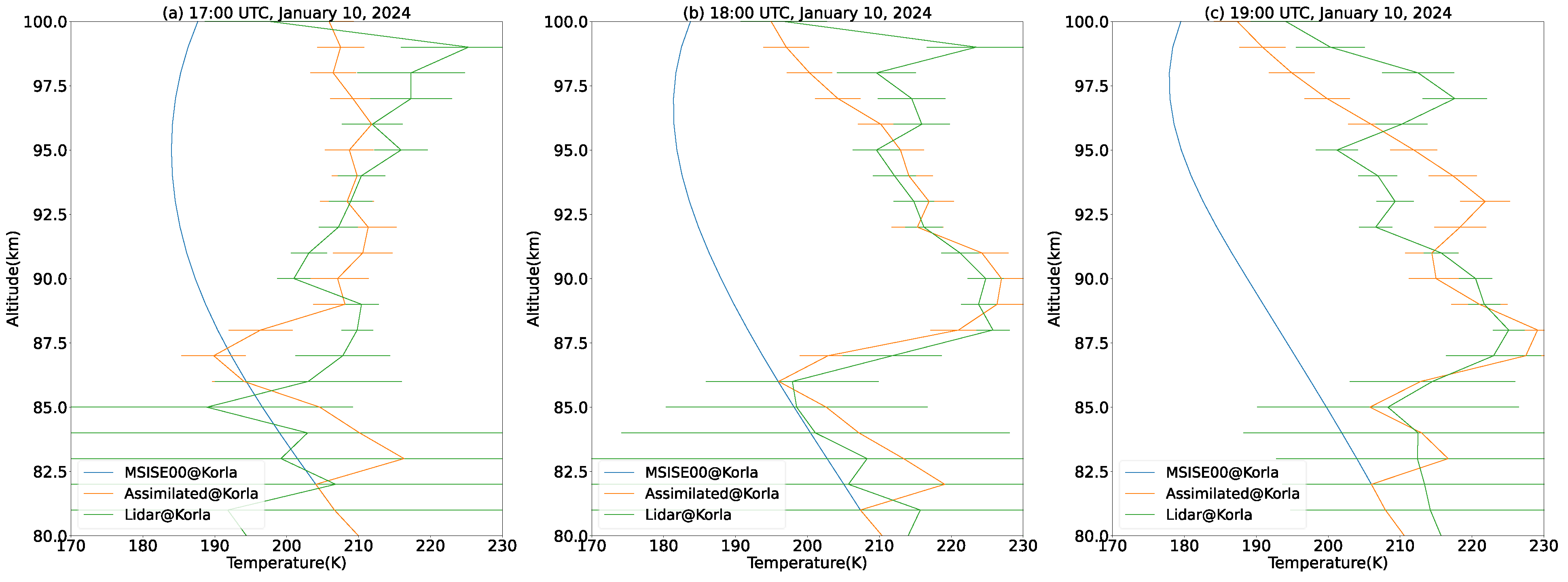
3.2. Validation of the 3DVAR Data Assimilation Method
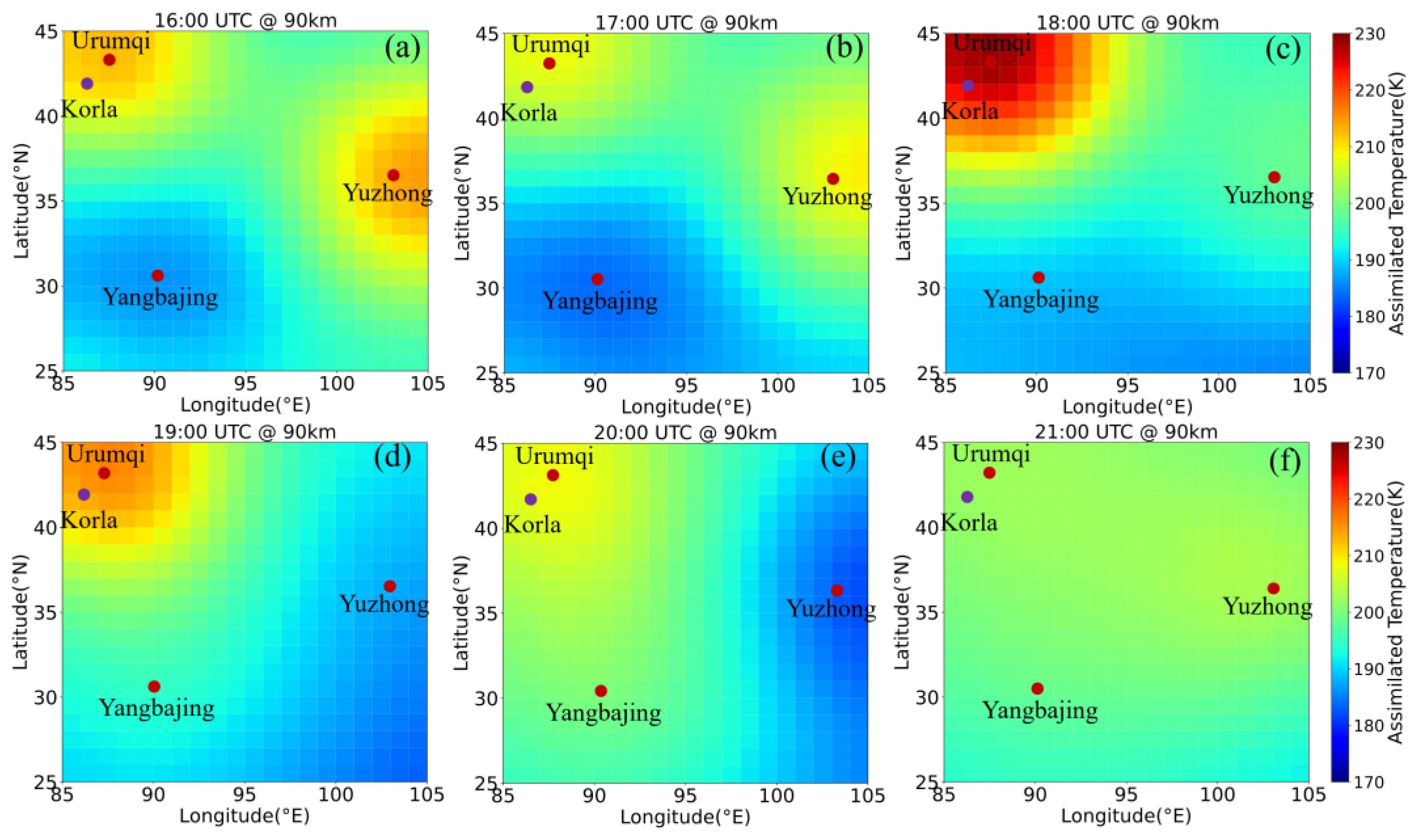
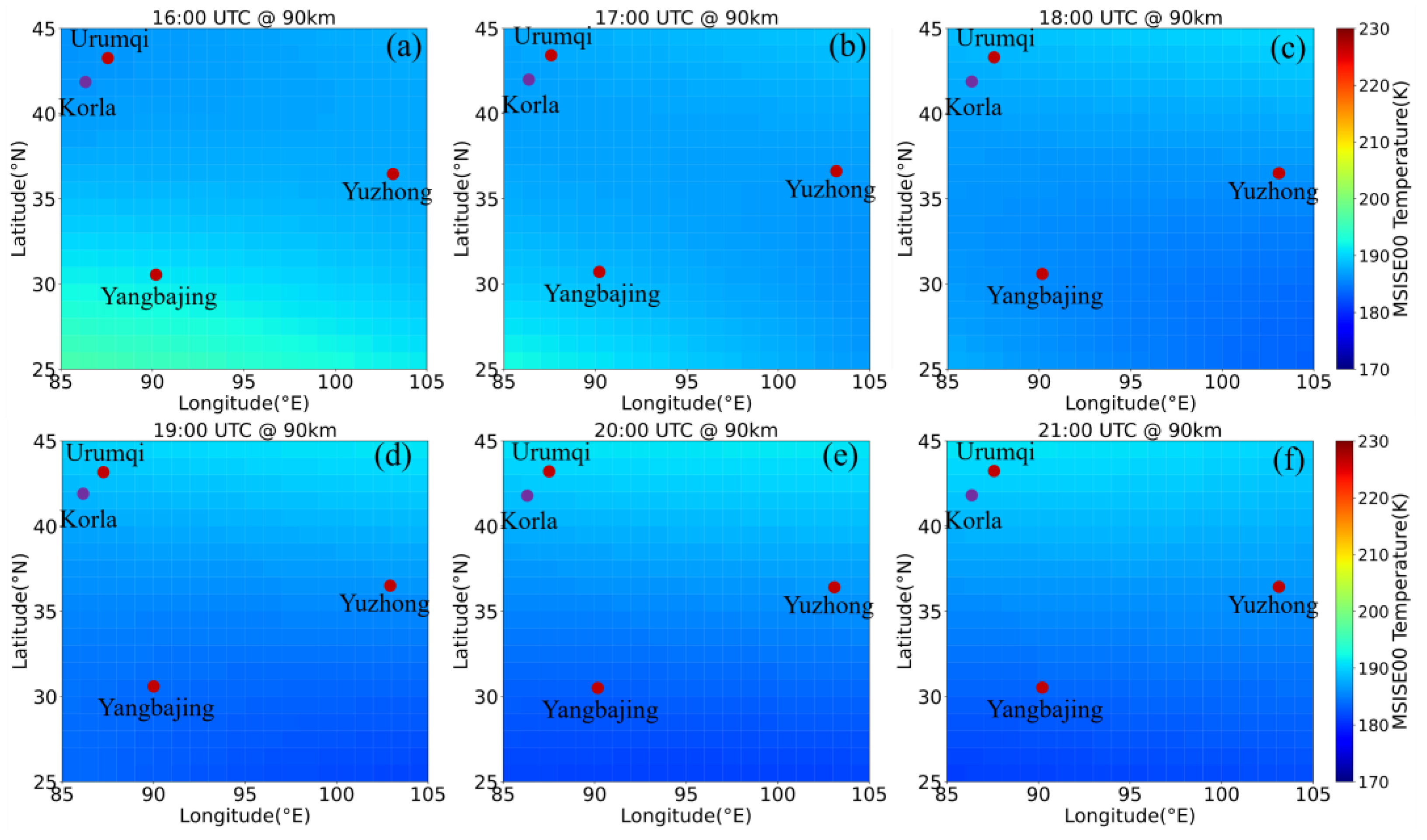
3.3. Thermodynamic Horizontal Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daren, L.; Fan, Y.; Jiyao, X. Advances in studies of the middle and upper atmosphere and their coupling with the lower atmosphere. Adv. Atmos. Sci. 2004, 21, 361–368. [Google Scholar] [CrossRef]
- Smith, A.K. Global Dynamics of the MLT. Surv. Geophys. 2012, 33, 1177–1230. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Vincent, R.A. The dynamics of the mesosphere and lower thermosphere: A brief review. Prog. Earth Planet. Sci. 2015, 2, 4. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Reid, I.M.; Murphy, D.J.; Hall, C.M.; Tsutsumi, M.; Ning, B.; Li, G.; Vincent, R.A.; Chen, J.; et al. Climatology of the mesopause relative density using a global distribution of meteor radars. Atmos. Chem. Phys. 2019, 19, 7567–7581. [Google Scholar] [CrossRef]
- Xu, J.; Liu, H.L.; Yuan, W.; Smith, A.K.; Roble, R.G.; Mertens, C.J.; Russell, J.M.; Mlynczak, M.G. Mesopause structure from Thermosphere, Ionosphere, Mesosphere, Energetics, and Dynamics (TIMED)/Sounding of the Atmosphere Using Broadband Emission Radiometry (SABER) observations. J. Geophys. Res. Atmos. 2007, 112, D09102. [Google Scholar] [CrossRef]
- Gardner, C.S. Sodium resonance fluorescence lidar applications in atmospheric science and astronomy. Proc. IEEE 1989, 77, 408–418. [Google Scholar] [CrossRef]
- Alpers, M.; Eixmann, R.; Fricke-Begemann, C.; Gerding, M.; Hoeffner, J. Temperature lidar measurements from 1 to 105 km altitude using resonance, Rayleigh, and Rotational Raman scattering. Atmos. Chem. Phys. 2004, 4, 793. [Google Scholar]
- Arnold, K.S.; She, C.Y. Metal fluorescence lidar (light detection and ranging) and the middle atmosphere. Contemp. Phys. 2003, 44, 35–49. [Google Scholar] [CrossRef]
- Cheng, X.; Gong, S.; Li, F.; Dai, Y.; Song, J.; Wang, J.; Li, F. 24 h continuous observation of sodium layer over Wuhan by lidar. Sci. China Ser. G Phys. Mech. Astron. 2007, 50, 287–293. [Google Scholar] [CrossRef]
- She, C.Y.; Sherman, J.; Yuan, T.; Williams, B.P.; Arnold, K.; Kawahara, T.D.; Li, T.; Xu, L.F.; Vance, J.D.; Acott, P.; et al. The first 80-hour continuous lidar campaign for simultaneous observation of mesopause region temperature and wind. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Chane-Ming, F.; Molinaro, F.; Leveau, J.; Keckhut, P.; Hauchecorne, A. Analysis of gravity waves in the tropical middle atmosphere over La Reunion Island (21°S, 55°E) with lidar using wavelet techniques. Ann. Geophys. 2000, 18, 485–498. [Google Scholar] [CrossRef][Green Version]
- Chanin, M.L.; Hauchecorne, A. Lidar observation of gravity and tidal waves in the stratosphere and mesosphere. J. Geophys. Res. Ocean. 1981, 86, 9715–9721. [Google Scholar] [CrossRef]
- Collins, R.L.; Senft, D.C.; Gardner, C.S. Lidar measurements of the middle atmosphere at South Pole. Rev. Can. Phys. 1991, 69, 1076–1086. [Google Scholar] [CrossRef]
- Gardner, C.S.; Voelz, D.G.; Sechrist, C.F.; Segal, A.C. Lidar studies of the nighttime sodium layer over Urbana, Illinois: 1. Seasonal and nocturnal variations. J. Geophys. Res. Space Phys. 1986, 91, 13659–13673. [Google Scholar] [CrossRef]
- Gardner, C.S.; Kane, T.J.; Hecht, J.H.; Walterscheid, R.L.; Yee, J.H.; Niciejewski, R.J.; Lowe, R.P.; Turnbull, D.N. Formation characteristics of sporadic Na layers observed simultaneously by lidar and airglow instruments during ALOHA-90. Geophys. Res. Lett. 1991, 18, 1369–1372. [Google Scholar] [CrossRef]
- Chau, J.L.; Urco, J.M.; Vierinen, J.P.; Volz, R.A.; Clahsen, M.; Pfeffer, N.; Trautner, J. Novel specular meteor radar systems using coherent MIMO techniques to study the mesosphere and lower thermosphere. Atmos. Meas. Tech. 2019, 12, 2113–2127. [Google Scholar] [CrossRef]
- Zherebtsov, G.A.; Chaikovsky, A.; Ivanov, A.; Balin, Y.; Elnikov, A.; Tulinov, G.; Plusnin, I.; Bukin, O.; Chen, B.; Matvienko, G.G. Lidar network CIS-LiNet for monitoring aerosol and ozone in CIS regions. In Proceedings of the Twelfth Joint International Symposium on Atmospheric and Ocean Optics/Atmospheric Physics, Tomsk, Russia, 27–30 June 2005; pp. 833–841. [Google Scholar]
- Sugimoto, N.; Matsui, I.; Shimizu, A.; Nishizawa, T. Lidar Network for Monitoring Asian Dust and Air Pollution Aerosols. In Proceedings of the IGARSS 2008, Boston, MA, USA, 7–11 July 2008; Volume 2, p. II-573. [Google Scholar] [CrossRef]
- Huang, Z.; Dong, Q.; Chen, B.; Wang, T.; Bi, J.; Zhou, T.; Alam, K.; Shi, J.; Zhang, S. Method for retrieving range-resolved aerosol microphysical properties from polarization lidar measurements. Opt. Express 2023, 31, 7599–7616. [Google Scholar] [CrossRef]
- Wang, C. Development of the Chinese Meridian Project. Chin. J. Space Sci. 2010, 30, 382–384. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Z.; Xu, J. Introduction to Chinese Meridian Project-Phase II. Chin. J. Space Sci. 2020, 40, 718–722. [Google Scholar] [CrossRef]
- Yang, Y.; Li, F.; Cheng, X.; Yang, G.; Lyu, D.; Lin, X.; Liu, L.; Fang, X.; Zheng, J.; Du, L.; et al. Lidar Network for Temperature and Wind Measurements in the Mesosphere and Lower Thermosphere Region. Space Weather 2024, 22, e2024SW003981. [Google Scholar] [CrossRef]
- Li, T.; Ban, C.; Fang, X.; Li, J.; Wu, Z.; Feng, W.; Plane, J.M.C.; Xiong, J.; Marsh, D.R.; Mills, M.J.; et al. Climatology of mesopause region nocturnal temperature, zonal wind and sodium density observed by sodium lidar over Hefei, China (32° N, 117° E). Atmos. Chem. Phys. 2018, 18, 11683–11695. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suarez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Courtier, P.; Thépaut, J.N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Chao, Y.; Li, Z.; McWilliams, J.C.; Ide, K. A Three-Dimensional Variational Data Assimilation Scheme for the Regional Ocean Modeling System. J. Atmos. Ocean. Technol. 2008, 25, 2074–2090. [Google Scholar] [CrossRef]
- Wang, D.; You, W.; Zang, Z.; Pan, X.; He, H.; Liang, Y. A three-dimensional variational data assimilation system for a size-resolved aerosol model: Implementation and application for particulate matter and gaseous pollutant forecasts across China. Sci. China Earth Sci. 2020, 63, 1366–1380. [Google Scholar] [CrossRef]
- Lahoz, W.A.; Errera, Q.; Swinbank, R.; Fonteyn, D. Data assimilation of stratospheric constituents: A review. Atmos. Chem. Phys. 2007, 7, 5745–5773. [Google Scholar] [CrossRef]
- Pfrommer, T.; Hickson, P.; She, C.Y. A large-aperture sodium fluorescence lidar with very high resolution for mesopause dynamics and adaptive optics studies. Geophys. Res. Lett. 2009, 36, L15831. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, Y.; Xu, X.; You, W.; Zang, Z.; Gao, L.; Chen, Y.; Su, D.; Yan, P. Lidar data assimilation method based on CRTM and WRF-Chem models and its application in PM2.5 forecasts in Beijing. Sci. Total Environ. 2019, 682, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Talagrand, O. Assimilation of Observations, an Introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar] [CrossRef]
- Vadas, S.L.; Fritts, D.C. Thermospheric responses to gravity waves: Influences of increasing viscosity and thermal diffusivity. J. Geophys. Res. Atmos. 2005, 110, D15103. [Google Scholar] [CrossRef]
- Clemesha, B.; Simonich, D.; Batista, P. Mesopause region temperature structure observed by sodium resonance lidar. J. Atmos. Sol. Terr. Phys. 2010, 72, 740–744. [Google Scholar] [CrossRef]
- Becker, E. Dynamical Control of the Middle Atmosphere. Space Sci. Rev. 2011, 168, 283–314. [Google Scholar] [CrossRef]
- Forbes, J.M. Tidal and Planetary Waves. In The Upper Mesosphere and Lower Thermosphere: A Review of Experiment and Theory; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 1995; pp. 67–87. [Google Scholar] [CrossRef]
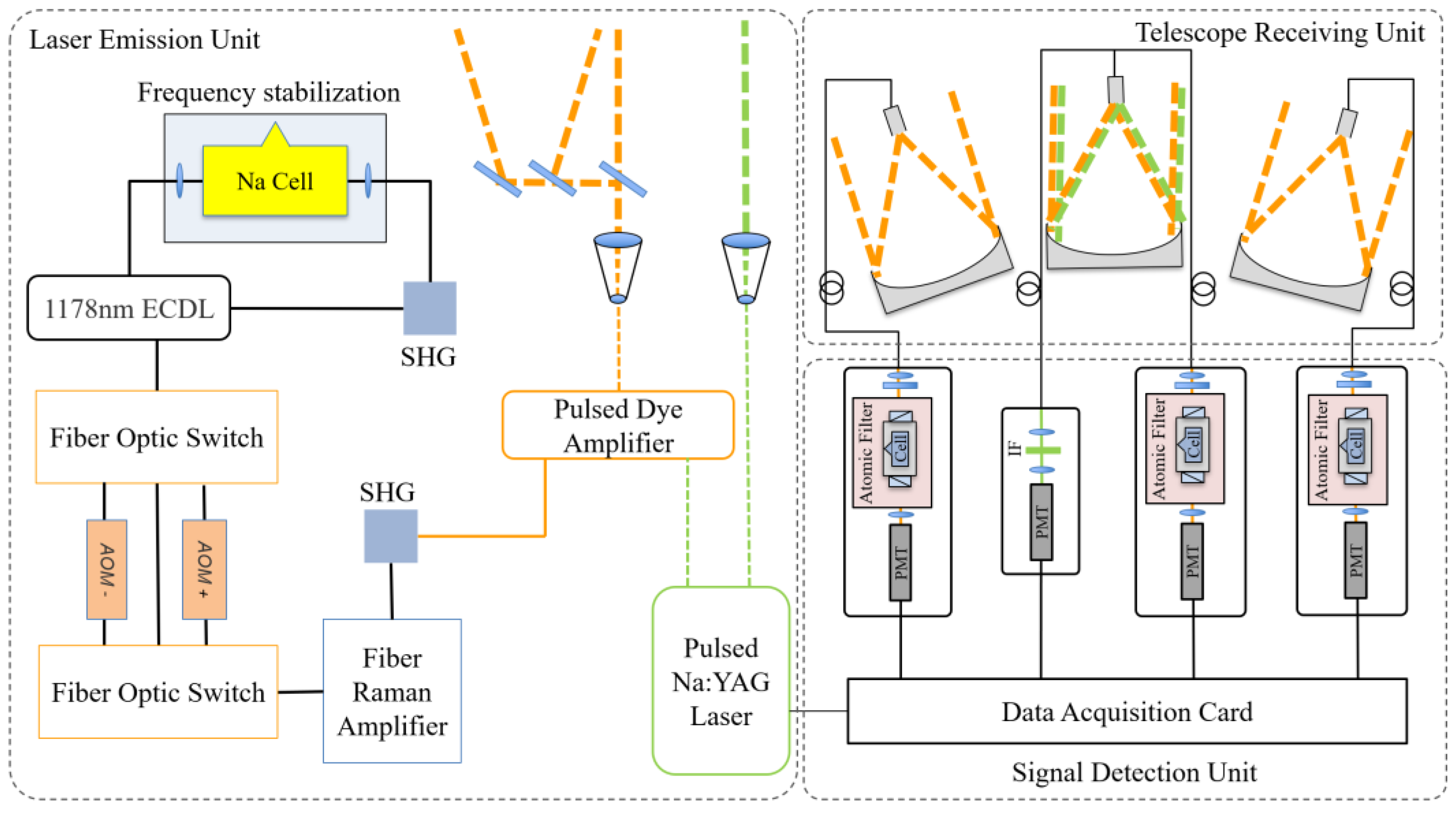
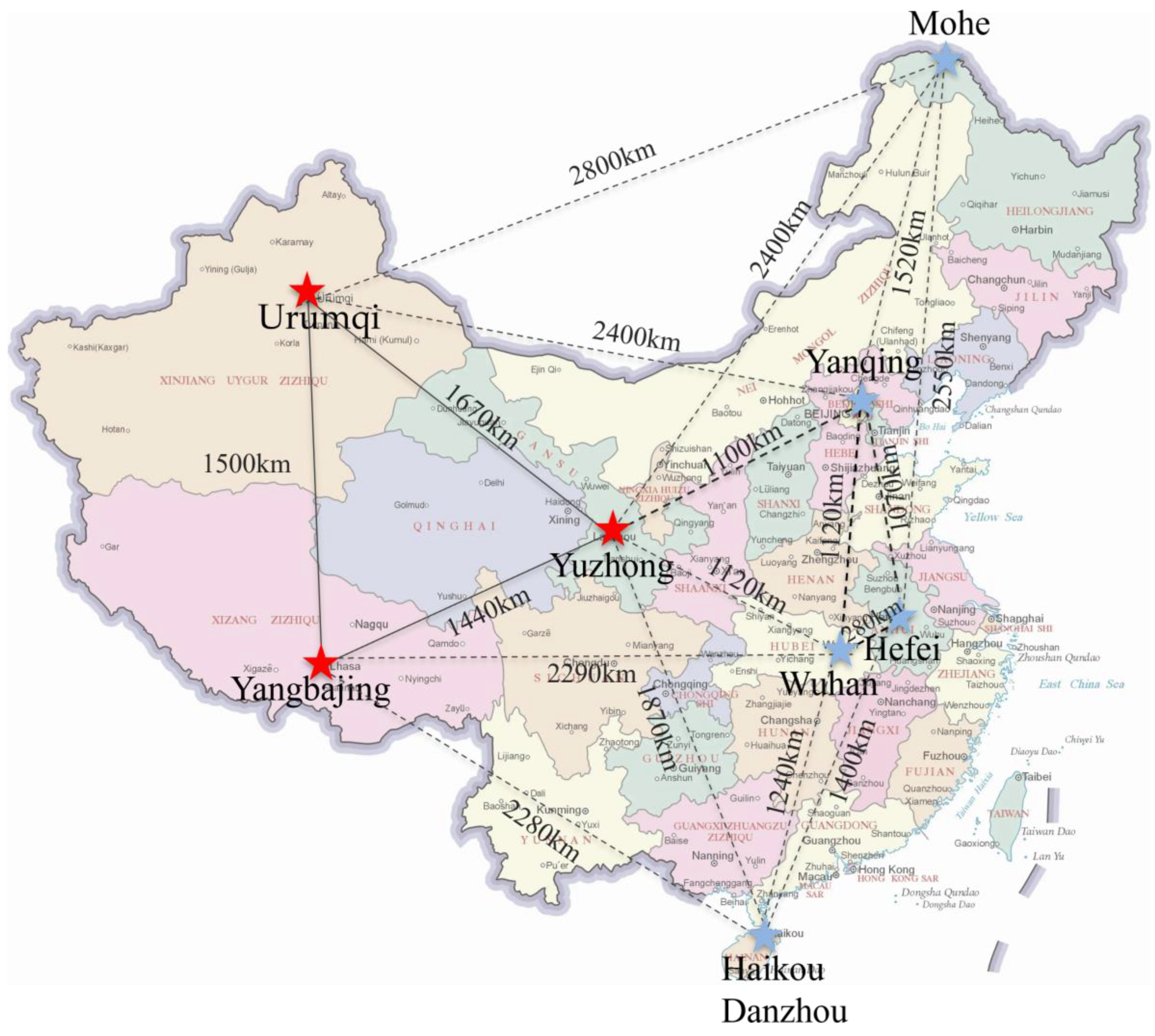
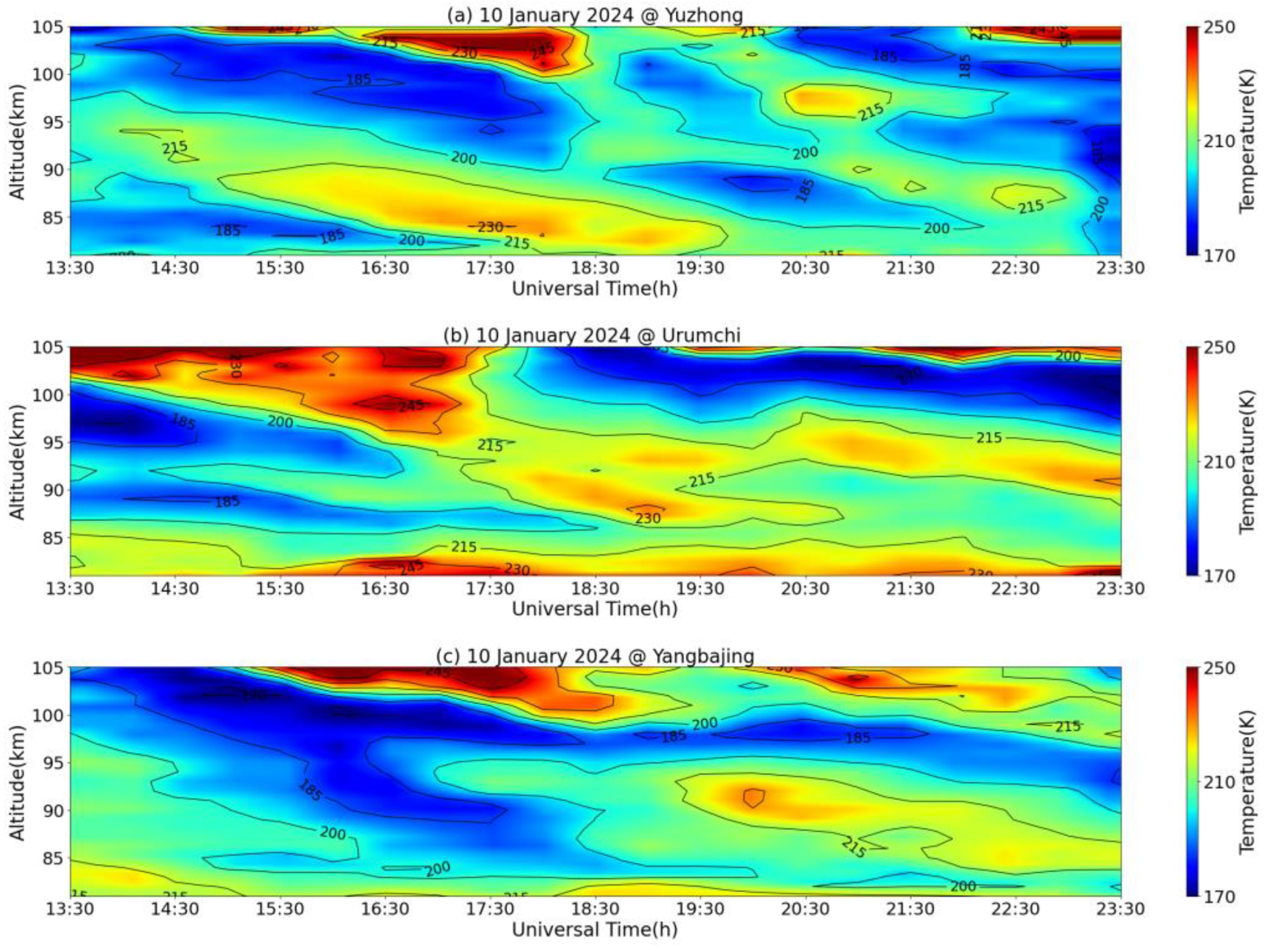
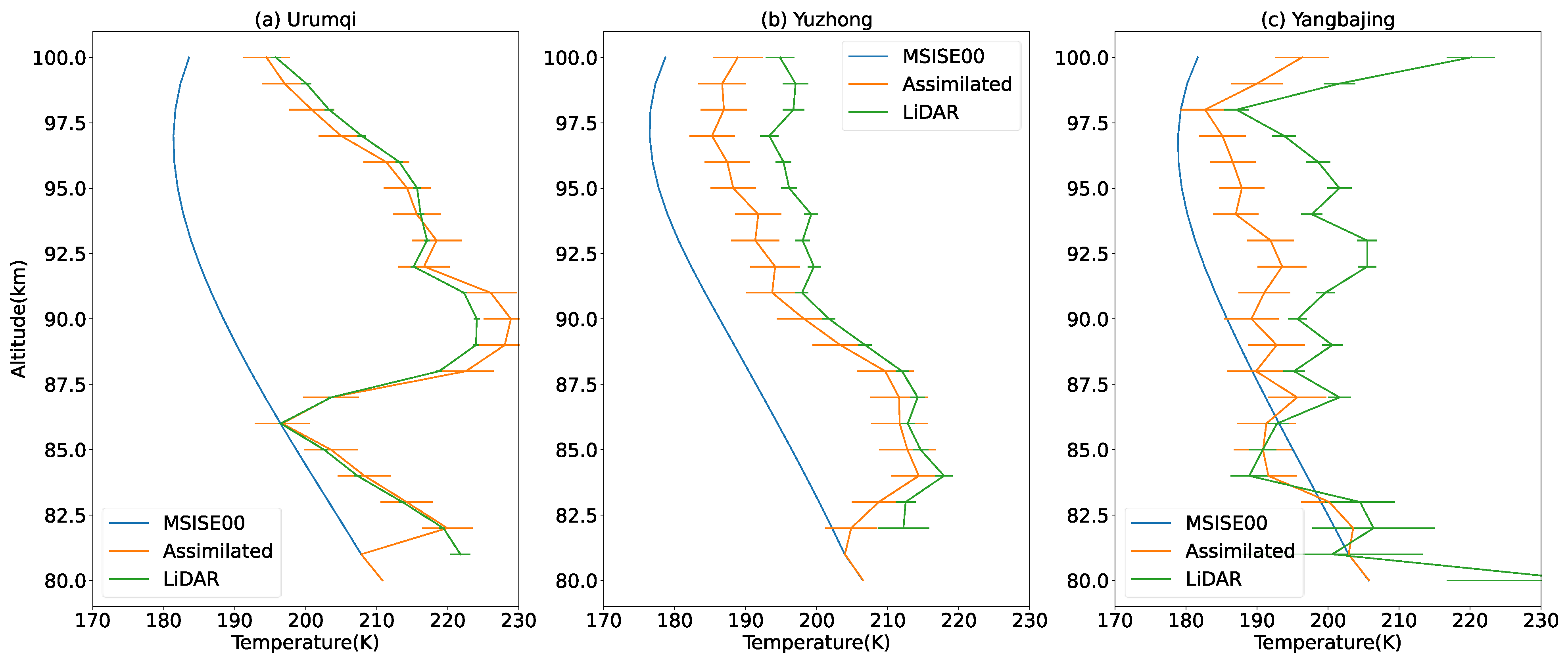


| Urumqi | Yuzhong | Yangbajing | |
|---|---|---|---|
| Longitude | 87.10° E | 104.15° E | 90.50° E |
| Latitude | 43.28° N | 35.95° N | 30.10° N |
| Altitude | 2080 m | 1965 m | 4287 m |
| Wavelength | 589 nm, 532 nm | 589 nm, 532 nm | 589 nm, 532 nm |
| Temporal Resolution | 1 min | 1 min | 1 min |
| Spatial Resolution | 30.72 m | 30.72 m | 30.72 m |
| 16:00–17:00 | 17:00–18:00 | 18:00–19:00 | 19:00–20:00 | 20:00–21:00 | 21:00–22:00 | Average | ||
|---|---|---|---|---|---|---|---|---|
| Urumqi | MSISE-Lidar(K) | 26.12 | 26.55 | 24.41 | 25.12 | 24.85 | 27.30 | 25.73 |
| 3DVAR-Lidar(K) | 12.00 | 13.82 | 3.88 | 5.07 | 6.83 | 8.82 | 8.40 | |
| Yuzhong | MSISE-Lidar(K) | 18.18 | 17.19 | 17.81 | 16.40 | 20.97 | 22.86 | 18.90 |
| 3DVAR-Lidar(K) | 5.72 | 2.57 | 6.06 | 7.19 | 11.92 | 11.12 | 7.43 | |
| Yangbajing | MSISE-Lidar(K) | 3.81 | 9.43 | 17.30 | 23.64 | 30.24 | 26.93 | 18.56 |
| 3DVAR-Lidar(K) | 3.77 | 5.61 | 11.57 | 14.33 | 19.82 | 17.51 | 12.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, L.; Yang, Y.; Liu, L.; Lin, X.; Zheng, J.; Wang, W.; Liang, J.; Xia, Y.; Wang, J.; Ji, K.; et al. Study of Thermodynamic Horizontal Structure of the Middle and Upper Atmosphere Based on Atmospheric Detection Lidar Networks. Atmosphere 2025, 16, 401. https://doi.org/10.3390/atmos16040401
Ren L, Yang Y, Liu L, Lin X, Zheng J, Wang W, Liang J, Xia Y, Wang J, Ji K, et al. Study of Thermodynamic Horizontal Structure of the Middle and Upper Atmosphere Based on Atmospheric Detection Lidar Networks. Atmosphere. 2025; 16(4):401. https://doi.org/10.3390/atmos16040401
Chicago/Turabian StyleRen, Liting, Yong Yang, Linmei Liu, Xin Lin, Jinzhou Zheng, Wei Wang, Jiaming Liang, Yuan Xia, Jiqin Wang, Kaijie Ji, and et al. 2025. "Study of Thermodynamic Horizontal Structure of the Middle and Upper Atmosphere Based on Atmospheric Detection Lidar Networks" Atmosphere 16, no. 4: 401. https://doi.org/10.3390/atmos16040401
APA StyleRen, L., Yang, Y., Liu, L., Lin, X., Zheng, J., Wang, W., Liang, J., Xia, Y., Wang, J., Ji, K., Chen, Z., Zhang, Y., Cheng, X., & Li, F. (2025). Study of Thermodynamic Horizontal Structure of the Middle and Upper Atmosphere Based on Atmospheric Detection Lidar Networks. Atmosphere, 16(4), 401. https://doi.org/10.3390/atmos16040401








