Abstract
Using chaos theory, maximum entropies are calculated for 108 time series, each consisting of 28,463 hourly data of urban meteorology and pollutants. The series were measured with standardized and certified instruments (EPA) in six locations at different heights and in three periods (2010/2013, 2017/2020, and 2019/2022) in a basin geomorphology. Each urban meteorology series corresponds to relative humidity (RH), temperature (T), and wind speed magnitude (WS), and each pollutant series corresponds to 10 µm particulate matter (PM10), 2.5 µm particulate matter (PM2.5), and carbon monoxide (CO). These pollutants are in the top three places of presence in the studied geomorphology and in incidence in population diseases. From the calculated entropies, a quotient is constructed between the entropies of each of the first two urban meteorology variables (RH and T) and the sum of maximum entropies of the time series of anthropogenic pollutants, demonstrating the gradual decay in time of the quotient that is dominated by the maximum entropies of the pollutants. The latter leads to a more excited and warm boundary layer, due to thermal transfers, which makes it more unpredictable, increasing its capacity to contain water. It is verified that the diffusion is anomalous with alpha < 1 and that the contamination has a high probability, using a heavy-tailed probability function, of causing extreme events by influencing urban meteorology.
1. Introduction
Various investigations address meteorology and atmospheric pollution from the perspective of chaos theory. From the point of view of meteorology, in [1], it is indicated that atmospheric flows, which are a case of turbulent fluid flows, show fractal fluctuations on all space–time scales, from the turbulence scale of mm/sec to climatic scales of thousands of kilometers/years [1]. Fractal fluctuations show a form of inverse power law, meaning long-range correlations described as dynamical systems having critical points as an attractor in their time evolution (self-organized criticality), and are present in dynamical systems in nature. These systems are revealed with sensitive dependence on the initial condition (deterministic chaos) in restricted precision computer elaborations of nonlinear mathematical models of real-world dynamical systems [1]. While the self-similar nature of atmospheric flows has been analyzed for some time, the correct physical mechanism has not yet been identified. Basic physical concepts of nonlinear dynamics and chaos need to be developed and incorporated into classical meteorology for more realistic predictive models of weather and climate [1]. On the other hand, outdoor air pollution has a high impact on human health. This drives the search for a better understanding of the dynamics and statistics of measured air pollution concentrations, including temporal variations in observed concentrations and spatial heterogeneities. Analysis of extensive measured data from Europe [2] resulted in the construction of probability density functions (PDFs) of air pollution concentrations which were shown to be highly dependent on spatial location and pollutant type [2]. Thus, time-series data from 3544 different monitoring sites showed that the PDFs of nitric oxide (NO), nitrogen dioxide (NO2), and particulate matter (PM10 and PM2.5) concentrations exhibit generally heavy tails. These are approximated asymptotically by q-exponential distributions for a given entropic index q and width parameter (λ). The power law parameter (q) and width parameter (λ) vary widely for different spatial locations. Data analysis allows in [2] to construct a map showing the relevance of q and λ in a given region. The resulting spatial patterns can be correlated with properties of the regional geography. Results are also obtained for typical time scales associated with dynamic behavior. Another study [3] analyzed the definition, consequences, and applications of an entropy, called Sq, that generalizes the usual Boltzmann–Gibbs entropy SBG (S1 = SBG), the basis of usual statistical mechanics, which is known to be applicable whenever ergodicity is satisfied at the microscopic dynamical level. Such an entropy Sq is based on the notion of q-exponential and exhibits properties that are not shared by other available alternative generalizations of SBG. The thermodynamics arising in this way is generically non-extensive [3]. This approximation describes very well a vast class of natural and artificial systems that are not ergodic or close to it [4].
The study presented here includes concepts and ideas indicated above, but it is carried out on a basin geomorphology and is based on measurements to which the chaos theory is applied [1]. This gives rise to the basic question that guides the authors (Pacheco et al) in this article: is it possible, based exclusively on measurements, with data records (using calibrated, certified, and standardized instruments according to EPA), in the form of time series, with variables to be measured without boundary condition restrictions, to reveal that the nature of the processes that have been incubated is chaotic, thus favoring entropic, dynamic, anomalous subdiffusion and heavy-tailed statistics?
For this purpose, the measuring instruments were located at a height between 4 and 10 m (from the ground) depending on the communes. Each commune was treated, in a first approximation, as an island up to a radius of 5 km. Each of the three measurement periods covered 3.25 years, and the measurement periods were 2010/2013, 2017/2020, and 2019/2022. In each of the six commons studied, three urban meteorological variables (temperature (T), wind speed magnitude (WS), and relative humidity (RH)) and three atmospheric pollutant variables (10 µm particulate matter (PM10), 2.5 µm particulate matter (PM2.5), and carbon monoxide (CO)) were measured as hourly time series. This gives a total of 36 time series containing 1,024,668 data for each period. In total, 3,074,004 data were involved in the three periods. The measurement area corresponds to 641 km2 and is subject to increasing processes of intensive high-rise construction, population growth that currently borders on 7,500,000 (data recording area), polluting vehicles, built-up area, reduction of agricultural areas and green areas, drought, low relative humidity, piping and channeling of water courses, etc. Through chaos theory, the chaotic parameters are calculated for each time series: λ (Lyapunov coefficient) > 0, 0 < DC (correlation dimension) < 5, SK (Kolmogorov entropy) > 0, 0.5 < H (Hurst coefficient) < 1, LZ (Lempel–Ziv complexity) > 0, D (fractal dimension) > 0, <ΔI> (information loss) < 0, demonstrating that the 108 time series are chaotic. From the Kolmogorov entropy, calculated for the time series, the quotient is constructed between the sum of the Kolmogorov entropies of the relative humidity (of each commune and for each period) and the sum of the Kolmogorov entropies of the pollutants (of each commune and for each period), SK,RH/SK,P (same procedure for temperature), which allows us to show the following in a relatively simple way:
- The interactive decay, as the periods advance toward the present, of the quotient. This decay is compatible with what has been observed (of the relative humidity with respect to the pollutants and of the temperature with respect to the thermal flow of the pollutants).
- The presence of entropic dynamic
- The manifestation and permanence of a subdiffusive phenomenon in the studied basin.
- The presence of statistics of extreme events through the heavy-tail analysis.
1.1. Basic Concepts
1.1.1. Water in the Atmosphere
Although the amount of water contained in the atmosphere (in the form of vapor, clouds and small ice crystals) constitutes a minimal part of the amount existing on the planet, of the order of 0.001%, its importance is vital: it participates in temperature regulation processes, in the water cycle, in climatic phenomena, and even in natural disasters [5]. This very small proportion of water in the atmosphere is at the center of the processes that determine climate, the hydrological cycle, atmospheric chemistry, and the development of life. The main form of atmospheric water is water vapor, and the quantity of this content in the air is called humidity. Although not as visible as liquid or solid forms (clouds, fog, rain, snow, and hail), water vapor is always present in the atmosphere, even in deserts.
The behavior of water in the atmosphere; what its quantity depends on; when and where it will fall; whether it will manifest itself as rain, snow, or frost; and whether there will be too little or too much, are issues that have always concerned humans. Over time, progress has been made in its study, although it has also introduced greater complexities, such as air pollution, changes in land use, and water catchment areas, to name a few.
The troposphere is the lower part of the atmosphere (from 0 to approximately 12 km), where climate and life develop. It contains three-quarters of the mass of the atmosphere and around 99% of atmospheric water; its depth varies with latitude and the season of the year. Solar energy does not heat this layer appreciably, so its heating is due to radiation coming from the Earth’s surface. Its temperature therefore decreases with height, approximately 6.5 °C per kilometer [6], corresponding to the thermal gradient of the standard atmosphere in a static state. Deviations from this value cause thermal convection.
1.1.2. Atmospheric Composition
Although the concentration of water vapor in the atmosphere is highly variable spatially and temporally, its average proportion in a mixed volume of air is of the order of 1 percent, so it can be considered the third most abundant gas in the atmosphere. Dry air [7] is composed of nitrogen (78.08%), oxygen (20.88%), and argon (0.93%). About 0.1% of the total volume corresponds to other greenhouse gases, such as carbon dioxide, methane, nitrous oxide, and ozone. The atmosphere also contains aerosols (small solid and liquid particles in suspension) that interact with solar and terrestrial radiation, depending on their spatial location, chemical composition, and concentration. In addition, half of atmospheric water, present in its liquid and solid phases, is concentrated in the first two kilometers of altitude. This article, when analyzing water in the atmosphere, will refer to that which is present in the troposphere and in the boundary layer in particular (from 1 to 2 km).
When the vapor entering the atmosphere reaches the saturation point of the air (that is, when it contains all the water vapor that it can contain at that temperature), the excess molecules condense, forming droplets (dew, rain, and fog) or ice crystals. Evaporation and condensation are continuous processes that generate and redistribute heat, transporting it and transforming it all the time between vapor, liquid, and ice crystals, depending on the temperature and pressure of the air. The higher the temperature of the air, the greater its capacity to contain water vapor. Hence, the concept of relative humidity serves to indicate, in percentage, the amount of water vapor that a portion of air contains, in relation to what it can contain given its temperature. A relative humidity of 100 percent indicates that that portion of air cannot contain more vapor. If the temperature of the air drops, the amount of vapor that it can contain decreases, and all the excess will condense. If the temperature of the saturated air increases, its capacity to contain water vapor will increase and the relative humidity will decrease.
Since the atmosphere is a small reservoir of water compared to oceans and continents, transfer to other reservoirs must be rapid. The turnover time of all atmospheric water is estimated to be about ten days [8,9]. Compared to the 10-year atmospheric lifetime of methane and the more than 50 years of carbon dioxide, the short average life of water does not allow for a more homogeneous mixture, resulting in an uneven global distribution.
1.1.3. Pollution
Some gases penetrate the drops, changing the characteristics of rainwater. This is the case of acid rain, which negatively impacts the sites where it falls, contaminating lakes and other ecosystems and damaging buildings [10,11,12,13]. The gases involved in these reactions are the product of human activity, mainly sulfuric acid and nitric acid.
Pollution also has climatic effects, since the excess of anthropogenic aerosols (produced by man), which act as condensation nuclei, causes an increase in the number of drops formed. This results in an increase in the albedo of the cloud, as well as the formation of smaller drops (less influenced by gravity), thus decreasing the possibility of rain and increasing the lifetime of the cloud.
1.1.4. Climate Change and Atmospheric Water
Water in the atmosphere plays a very active role in climate: it participates in the entry and exit of energy, the redistribution of heat in the atmosphere, and the movement of water between distant regions. Any spatial or temporal modification of the water content in the atmosphere results in a change in the conditions of the Earth’s surface. Droughts, floods, hurricanes, and tornadoes are related to the amount of water in the atmosphere and its behavior, hence the interest in any signal that may indicate long-term changes [13,14,15,16]. Global data from the last 30 years show an increase in precipitable water throughout the world except in a portion of Canada, where it decreased. It is not unusual for temperature increases to result in increases in evaporation; but all the consequences that this can have when combining situations such as greater cloud formation with smaller droplets that do not precipitate are not clear. The change in rainfall patterns in different regions has consequences for the economy and the lives of many people.
1.1.5. Relative Humidity (RH)
Intensive variables are those whose value does not depend on the size or quantity of matter in the system (they have the same value for a system as for each of its parts considered as subsystems of the same), as is the case of temperature and pressure. In thermodynamics, a system is said to be in thermodynamic equilibrium when the intensive variables that describe its state do not vary over time. If the system is not isolated, thermodynamic equilibrium is defined in relation to its surroundings.
Relative humidity (RH or Φ) is the ratio of the partial pressure of water vapor (pH20) in the mixture to the equilibrium vapor pressure of water () at a given temperature. Relative humidity depends on the temperature and pressure of the system of interest [17,18,19,20,21]. The same amount of water vapor produces a higher relative humidity in cold air than in warm air. One parameter of the relationship is the dew point. The correspondence between the pressures on a flat surface of pure water at a given temperature is written as follows:
RH is usually expressed as a percentage; a higher percentage means that the air–water mixture is more humid. At 100% relative humidity, the air is saturated, cannot hold more vapor, and, as noted, is at its dew point. Pollutants transfer thermal energy to the water vapor system of the atmosphere, adjacent to the ground, and which has a certain RH. H2O molecules have the energy to disperse toward volumes of lower thermal energy, decreasing their diffusion possibilities and favoring their concentration. The polluting system can cause a decrease in relative humidity, contributing to aridity in a basin morphology. In this geomorphology, pollutants experience a subdiffusive process, since their concentration grows steadily over time due to the permanent contribution of heat from human activity (anthropogenic causes), which stabilizes a drying dynamic. Due to conservation of mass, water vapor cannot disappear; the concentration and rehydration of geographies and fragments of atmospheric layers become chaotic and unpredictable; and its emergence can generate high-risk events.
If the temperature of the saturated air increases, due to the effect of the thermal transfer of the same pollutants, its capacity to contain water vapor will increase and the relative humidity will decrease. From a dynamic perspective, if the entropic forces due to pollutants are greater than those of urban meteorology and RH in particular, they can favor an increase in environmental dryness. When considering the forces of an entropic nature (2) originated by the entropy surface, S (x, y, z; Figure 1) [22,23,24,25], we have the following:
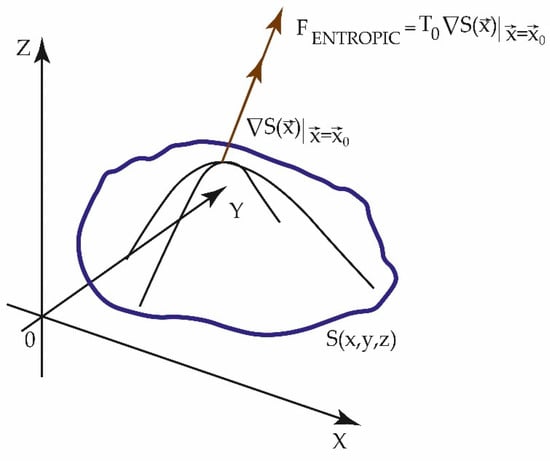
Figure 1.
Representation of an entropy surface, S (x, y, z), which has maxima of entropy of time series that can be measurements of urban meteorological variables or of pollutants in different locations. From S(x,y,z) the entropic forces, we can calculate the .
The pressure is p = F/A, so then it is possible to write using (2), following the notation of (1), and we obtain the following expression:
Expression that gives a relationship between relative humidity and the gradient of the entropic surface. Assuming that the process occurs in a spherical volume, with the operator ∇ only having radial dependence (r), we obtain the following:
which indicates for RH a dependence, considering the assumptions indicated, on the Kolmogorov-type entropies [26,27,28,29,30].
As a note, if we perform the calculation, we obtain the following:
where is the entropic force associated with relative humidity, and is the entropic force associated with pollutants
If the volume fraction of the vapor is saturated, at dew point, its entropy is minimal. It will experience a phase transition releasing heat. Under standard atmospheric conditions (ideal). As the contaminant system increasingly invades the boundary layer of the atmosphere with sufficient energy to affect it, the atmospheric air is more likely to expand, there is more space to contain water vapor. This phenomenon is not static in time, it is extremely dynamic, the entropic layers are very variable, very rough. The entropic force is very variable. This increases the low predictability of the events. What formula states is that an entropic force of urban meteorology is related to the entropic force of pollutants (and vice versa) and to CK. Equilibria have been lost and the systems, which have entered into irreversible processes, are complex, connected and chaotic. Equation (4) is a very crude approximation of the current processes in the atmosphere. But it is possible to show from the entropy ratio the turbulence and disorder of the interactive systems.
1.1.6. Thermodynamic Aspects Associated with Relative Humidity
Thermodynamic Principles
RH is a thermodynamically controlled property of air. Thermodynamics provides substance to psychometry [31], the study of the transformations of air necessary for its use in a multitude of fields: food preservation in chambers, air conditioning of premises, drying processes and drug manufacturing, metrology, explosive atmospheres, environments in computer rooms, textile industry, clean rooms, etc. [32,33].
There are four laws of thermodynamics, which govern the behavior of energy and matter and are basic to understanding the behavior of air when it reaches saturation and a relative humidity of 100% [34].
The first law of thermodynamics states the conservation of energy in the context of thermodynamics and indicates that if work (W) is performed on a system or it exchanges heat (Q) with another, the internal energy (U) of the system will change. This law is important to understand the exchange of energy that occurs in the atmosphere when the air reaches saturation.
The second law of thermodynamics states that in every irreversible process, the entropy of the universe increases: Isolated systems, when evolving, tend to become disordered, never ordered. Entropy is a measure of the disorder or randomness of a system. When the air is saturated with humidity, any addition of humidity will result in the condensation of water vapor into liquid water, which will release latent heat and increase the entropy of the system.
The Gibbs free energy equation [G] describes the relationship between changes in enthalpy, H, entropy, S, and temperature, T of a system, as dG = dH − TdS.
If the variation is: less than 0, the reaction is spontaneous.
greater than 0, the reaction is not spontaneous (that is, work needs to be performed for it to happen).
is equal to 0, the reaction is in equilibrium.
As the relative humidity of the air reaches 100%, which occurs at the dew point temperature, the moist air reaches its maximum because the specific volume of the air increases with its moisture content. This causes the Gibbs free energy of the system to reach its minimum value, leading to a state of equilibrium.
Latent Heat
This is the amount of energy required for a substance to change phase, from solid to liquid (heat of fusion) and from liquid to gas (heat of vaporization) [6]. It should be noted that this energy in the form of heat is invested in the phase change and not in an increase in temperature. Air is saturated in a given volume when it can no longer support water vapor. Any excess beyond this point results in phenomena such as dew, rain, fog.
When a phase change occurs (i.e., when a substance passes from one region of its phase diagram to another), Figure 2:
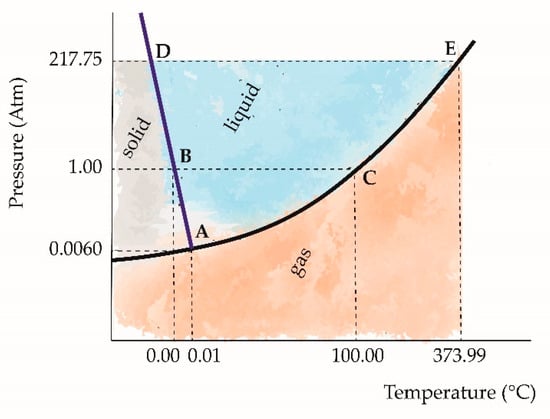
Figure 2.
Phase diagram of water. A: triple point; B: melting point; C: boiling point; D: critical pressure; E: critical point.
The entropy of that substance changes, even if its temperature remains the same. A substance in solid phase has a low entropy; in liquid phase, a medium entropy; in gas phase, a high entropy. The entropy of fusion increases when a substance melts. This is almost always positive, since the degree of disorder increases in the transition from an organized crystalline solid to the disorganized structure of a liquid; the only known exception is Helium. It is denoted as ΔS fusion and usually expressed in J mol−1 K−1.
2. Materials and Methods
2.1. Study Area
The city of Santiago is located at 33.5° S and 70.8° W. It contains a population of 8,420,000 inhabitants, representing 40% of the total population of the country, on a surface of approximately 641 km2. It is located in the middle of the country, at a height of about 520 m.a.s.l. The altitude above sea level increases from west to east. It is surrounded by two mountain chains: the Andes and the Coastal Mountain range. Its climate is Mediterranean (Figure 3). The driest and warmest months are from December to February, historically reaching maximum temperatures of around 35 °C in the shade (air temperature in the sun); however, these temperatures are currently exceeded. Given its topography and the dominant meteorological conditions, there is, in general, a strong horizontal and vertical dispersion of pollutants generated by an important number of sources in the city (heating, vehicles, industries, etc.), especially during fall (20 March–21 June) and winter (21 June–23 September). The emissions have a tendency to increase given the also increasing population density, which implies an increase in fixed and mobile sources. In addition, the number of vehicles has increased rapidly in recent years.
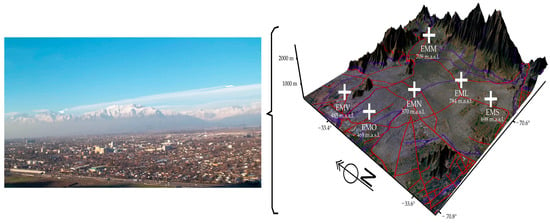
Figure 3.
Santiago de Chile is located in a basin geomorphology.
2.2. Kolmogorov Entropy
Using the Chaos Data Analyzer (CDA) program [35,36], 108 time series (each with 28,463 data) were processed, representing a total of 3,074,004 data points, corresponding to variables of temperature (T), wind speed magnitude (WS), relative humidity (RH), concentration of particulate matter of 10 μm (PM10) and 2.5 μm (PM2.5), and carbon monoxide (CO). For the series to be chaotic, the fundamental parameters to be calculated must satisfy the following:
λ (Lyapunov coefficient) > 0, 0 < DC (correlation dimension) < 5, SK (Kolmogorov entropy) > 0, 0.5 < H (Hurst coefficient) < 1, LZ (Lempel–Ziv complexity) > 0, D (fractal dimension) > 0, <ΔI> (information loss) < 0.
It is common that in the ordered pairs that make up the data sequence of the time series, there are missing measurement discrepancies. This happens, for example, due to an electrical fault, a defect in the measuring equipment, etc. The missing data in a series were completed using the Kriging technique [37] (this is indicated in the flowchart in Figure 4). Figure 4 is a flowchart showing the process followed to apply chaotic analysis software (CDA) [36] to time series.
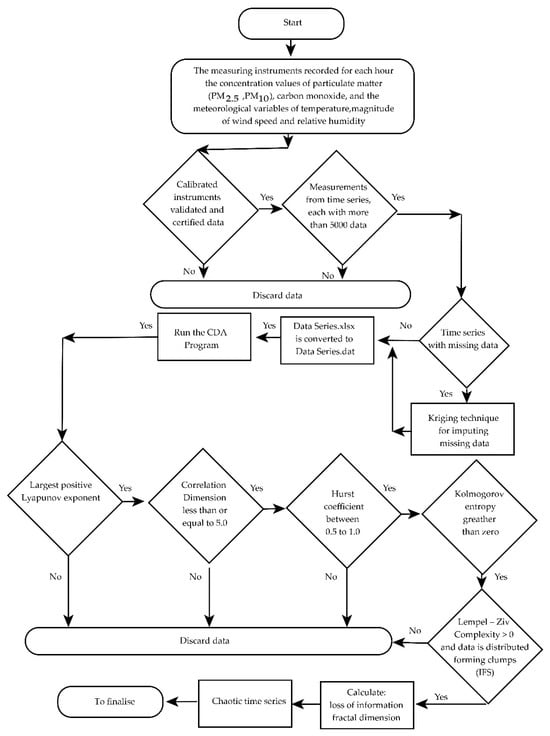
Figure 4.
All time series meet the conditions to be described as chaotic, so they form two chaotic systems [35,36,38,39,40,41,42,43,44,45,46,47]: the urban meteorology system (T, WS, and RH) and the pollutant system (PM10, PM2.5, and CO). The results of the calculations are in Table A1, Table A2 and Table A3 of Appendix A.
3. Results
3.1. Temperatures
The ability of air to hold water vapor depends entirely on its temperature. As air temperature changes, the ability to hold moisture increases or decreases, thus affecting relative humidity. Table 1 is a comparative chart, by measurement periods, of temperature and relative humidity.

Table 1.
Average total temperature and relative humidity by commune and periods. La Florida, EML, masl: 784 m. Las Condes, EMM, masl: 709 m. Santiago Parque O’Higgins, EMN, masl: 570 m. Pudahuel, EMO, masl: 469 m. Puente Alto, EMS, masl: 698 m. Quilicura, EMV, masl: 485 m.
According to Table 1, two periods, 2010–2013 and 2017–2020, show an increase in the average temperature and a decrease in relative humidity. This is consistent with what was previously stated: if the temperature of saturated air increases, its capacity to contain water vapor will increase and relative humidity will decrease. The period of 2019–2022 contains the most complex moment of the coronavirus pandemic and a strong confinement of the population with a drastic decrease in activity (transport, industries, etc.). This favored a decrease in temperature and an improvement in relative humidity, as shown in Table 1. It is possible to interpret this period, considering that in 2023 Santiago de Chile fell to sixth place as the warmest since 1950 (2023 was the warmest year since 1961), with a large accumulation of water vapor in the boundary layer, with a decrease in relative humidity and discounting phenomena such as El Niño, as a preamble to a relatively rainier 2024.
Based on the Hurst coefficients (H) and the fractal dimension (D) (Appendix A), H decreases for T and for HR, and D increases for T and HR, indicating a greater complexity and less predictability of future climatic events. They suggest that a system sensitive to initial conditions is being created for the coming years, which may lead to a rainier year (as occurred in Chile in 2024). Table 2 allows us to visualize the decline in persistence (H = Hurst exponent) of both the polluting system and the urban meteorology system with an increase (2019–2022), in general, of the fractal dimension (D).

Table 2.
Values of the Hurst exponent (H) and fractal dimension (D) for all the variables of interest, the study commons, and the three periods (2010–2013, 2017–2020, and 2019–2022).
Persistence decreases, and complexity increases; thus, the system moves away from regularity and becomes more complex and unpredictable. The average temperature of each of the six study communes in each of the measurement periods is as follows: 2010/2013: = 15.64 °C, 2017/2020: = 16.20 °C, 2019/2022: 15.51 °C.
Using Equation (23) from [48] allows us to calculate the effect of chemical reactions (), thermal radiation (R), and heat dissipation through shear stress (), summarized in the general formula , which applies to each commune and is therefore subindicated with a C:
where w is the vertical component of the wind. The average of for each series of 28,463 data measured by commune as follows:
for the period 2019–2022 (Table 3):

Table 3.
Variation in in 2019/2022.
From Table 4 and its eighth column, the average temperature value is obtained, 15.47 °C, which is in the order of the average temperature values arising from the time series () of the six communes (2019/2022 period), comparing them as follows:

Table 4.
Summary of according to locality (commune), height (referred to sea level), average temperature, and the increase in temperature per period. The values in columns 6, 7, and 8 were approximated. The values in columns 1–4 and 6–7 were extracted from [48].
The analysis according to , an indicator of human and natural activities, shows that human activities decrease significantly if there is a drop in temperature.
3.2. Entropies
Table 5 contains the calculation of the entropy for time series of relative humidity and pollutants (PM10, PM2.5, and CO). There are 72 series, each containing 28,463 hourly data, spread over three measurement periods: 2010/2013, 2017/2020, and 2019/2022.

Table 5.
SK Summary for pollutants and relative humidity in Santiago, Chile, for 2010/2013, 2017/20230, and 2019/2022 periods (Appendix A).
Table 5 allows the construction of Table 6, which contains the quotients between the maximum entropies of relative humidity and the sum of the maximum entropies of the pollutants, by commune, for the 3 measurement periods:

Table 6.
Santiago, Chile, comparative table of entropies quotients SK,RH/SK,P, 2010/2013, 2017/20230, 2019/2022 Period).
From Table 6, Figure 5 is constructed. Figure 5 shows the decay, according to the periods studied, of the quotient between the maximum entropy of relative humidity and the maximum entropies of the pollutants symbolically, SK,HR/SK,P.
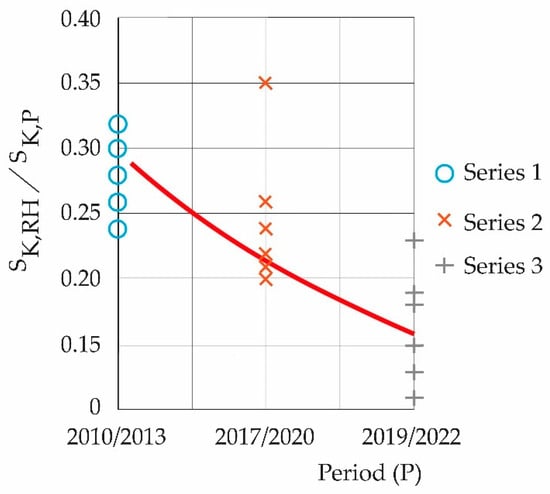
Figure 5.
Decay of the SK,HR ratio with SK,P.
The influence of the maximum entropy of pollutants on the maximum entropy of the ambient temperature time series is increasing as the periods progress toward the present. This thermodynamically affects the atmosphere, making it warmer and giving it a greater capacity to contain water because, if (heating of the atmosphere due to the effect of pollutants), fractions of the atmosphere in the boundary layer expand, , according to the simplified model in Figure 6:
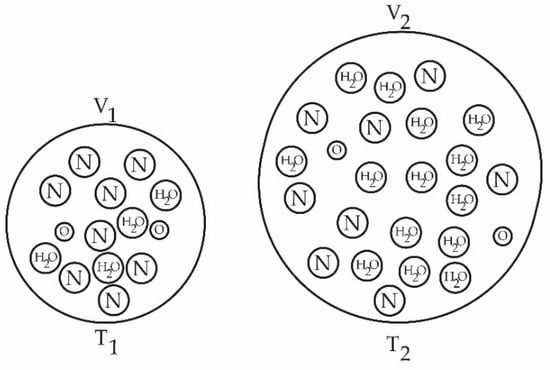
Figure 6.
Simplified representation of the increase in water vapor retention by the atmosphere as the temperature rises (T2 > T1).
There is dependence on the initial conditions of the systems (HR, T, WS, and pollutants) due to the high variability of human activity that makes them unpredictable. The warming of the atmosphere becomes chaotic in its location, and it is persistent and increasing. If, at some point, the appropriate temperature and pressure scenario occurs, the localized water discharge from the atmosphere can reach very high and risky levels. Figure 6 shows how relative humidity decreases as the measurement periods progress toward the present time due to a polluted environment that promotes environmental dryness.
Table 7 allows the construction of Table 8, which contains the quotients between the maximum entropies of Temperature and the sum of the maximum entropies of the pollutants, by commune, for the 3 measurement periods:

Table 7.
SK summary for pollutants and temperature for Santiago, Chile, for 2010/2013, 2017/20230, and 2019/2022 periods (Appendix A).

Table 8.
Santiago, Chile, comparative table of entropies, SK,T/SK,P, for 2010/2013, and 2017/2020, 2019/2022 periods).
Figure 7 shows the decay, according to the periods studied, of the quotient between the maximum entropy of the temperature and the maximum entropies of the pollutants symbolically, SK,T/SK,P. Pollutants generate the highest thermal flows, affecting the thermodynamics of the boundary layer.
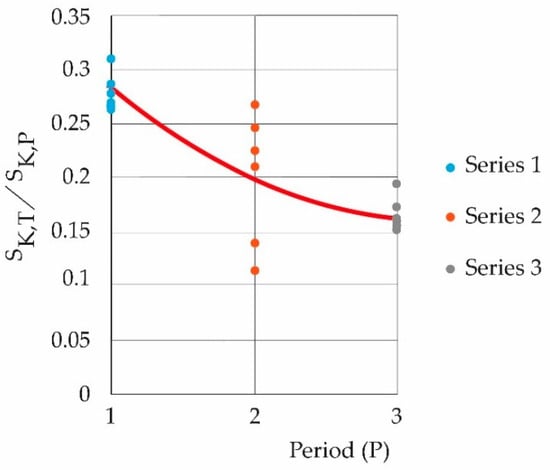
Figure 7.
Decay of maximum temperature entropies due to the effect of maximum entropies of pollutants; the dominant thermal effect is carried by the latter.
From Table 6, Figure 8, Figure 9 and Figure 10 were constructed, showing the areas of influence of the pollutants with respect to relative humidity: red indicates the strong dominance of pollution, and green indicates the enhanced activity of relative humidity. The data were recorded in the city of Santiago de Chile, which is located in a basin geomorphology and correspond to measurements carried out in six communes, located at different heights, in the periods of 2010/2013, 2017/2020, and 2019/2022.
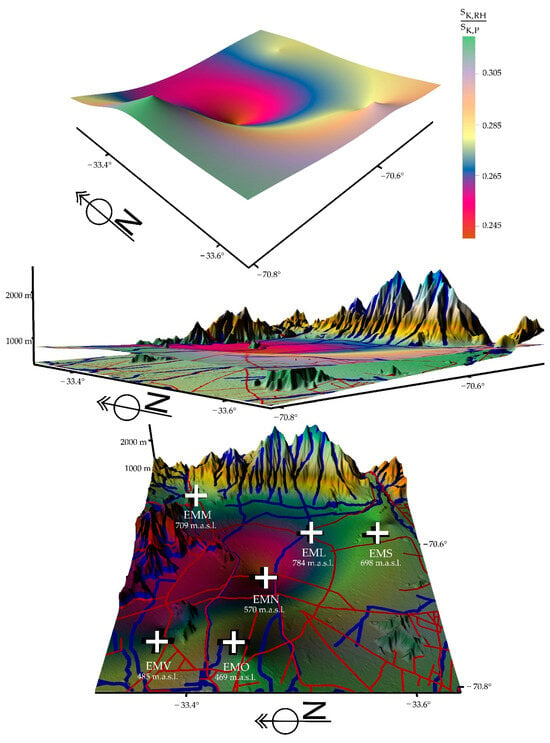
Figure 8.
Depiction for the period 2010/2013 showing that there is a higher percentage presence, according to geographic area, of relative humidity (green color). Santiago de Chile is a city that is in a basin geomorphology that exacerbates the problem of pollution.
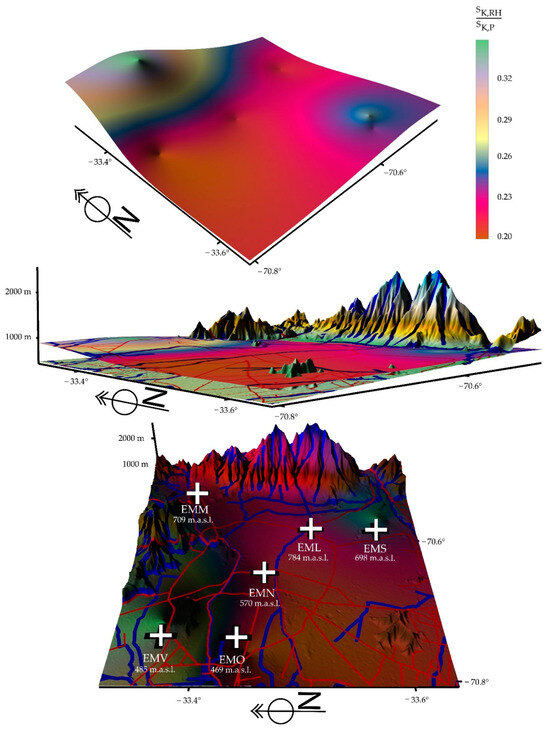
Figure 9.
Depictions show, for the period 2017/2020, a large percentage decline in relative humidity (green color) in the geographic area studied and which corresponds to the basin geomorphology in which the city of Santiago is located. The presence of atmospheric pollution is dominant.
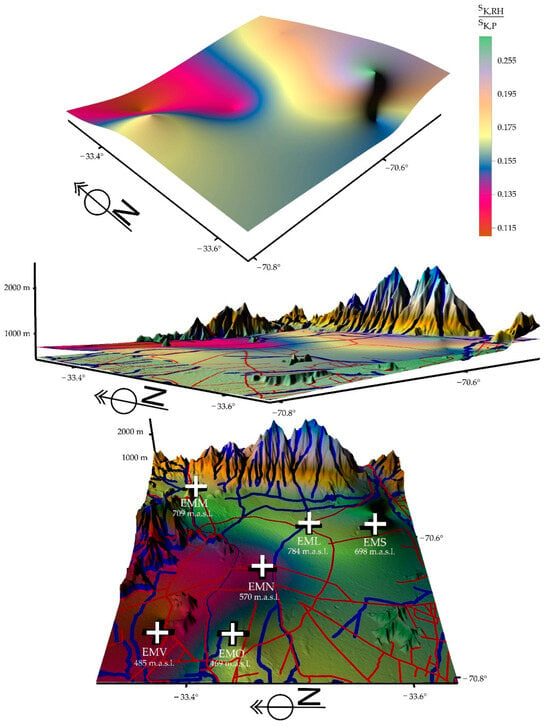
Figure 10.
Depictions of a certain return of relative humidity in a wide geographic sector (green color) in the basin geomorphology of the city of Santiago for the period of 2019/2022. This return occurs during the reduction of activities, in all orders of things, and the confinement of the population due to the coronavirus pandemic.
Gibbs free energy under thermodynamic equilibrium condition [49]:
dG = dH − TdS = 0,
dH = TdS/:dt,
For each species, MV represents the meteorological variables, P represents the pollutants, and is the average temperature of each commune for the measurement period.
3.3. Thermal Fluxes
From the perspective, in a first approximation, of the results extracted from Tables 6 and 7 and Equations (29) and (30) of [48], the total flux in K/h weighting for both urban meteorology and pollutants gives 788.2 K/h (Δ = (δQ/dt)P − (δQ/dt)MV(K/h)) 43.54 K/h) for the 2010/2013 period, 765.9 K/h (Δ = 103.3572 K/h) for the 2017/2020 period, and 478.1 K/h (Δ = 112.3636 K/h) for the 2019/2022 period, according to Table 9.

Table 9.
Average temperature for the measurement period 2019–2022 and the difference between temporary heat variation between pollutants and meteorological variables using equation (30 of [48]). The last row are average values.
Figure 11 shows the trend of the average value Δ according to the three study periods:
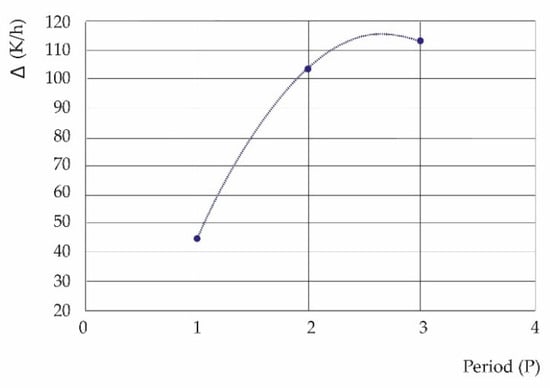
Figure 11.
The curve represents the difference between the thermal fluxes of pollutants and meteorological variables for the three study periods, 1:2010/2013, 2:2017/2020, and 3:2019/2022. It shows a break in the upward trend of Δ toward 2023, (A fitting function between Δ and P is given by Δ = −25.405 P2 + 136.03 P − 67.088; R2 = 1).
The Meteorological Directorate of Chile indicates that 2003–2013 was the driest decade of the last 150 years, with the inclusion of period 1 of Figure 11.
The year 2020 was considerably rainier than 2019; however, it maintained the deficit trend of around 40% compared to a normal year. As of June 2021, the precipitation trend looks similar to that of 2019. It includes period 2.
Despite winter precipitation, 2022 closed as one of the 10 driest years ever recorded; it includes period 3.
Period 3 (until 2022) announces a break in the upward trend of Δ beyond period 3. The Meteorological Directorate of Chile confirmed that 2023 was one of the rainiest in the last 15 years, where some stations far exceeded the amounts expected for a normal year. At the end of 2024, precipitation is more normal. Even so, the precipitation deficit in Chile takes over many localities in the country. According to the data released by the Meteorological Directorate of Chile, only three stations have a surplus greater than 20%.
According to Table 9 and Figure 11, the effect of heat flux on the boundary layer of each species (pollutants and meteorological variables) decays according to periods. Tables 6 and 7 of [48] show that, for each species, the magnitudes of their thermal fluxes are in high orders, resulting in narrow differences that result from a more polluted environmental context and that favors higher temperatures due to greater thermal transfers. In Table 9, the magnitudes of the thermal fluxes (δQ/dt) are in the lower orders, less excited, compared to those of the periods 2010/2013 and 2017/2020, but result in higher differences (Δ). These fluxes are referred to as less excited levels that are compatible with a downward shift of the thermal fluxes of urban meteorology, a less excited atmosphere. There is less energy per species to perform work. Thus, for the period 2019/2022, urban meteorology once again gains some importance (EMS and EMO localities) compared to the period of 2017/2020, which may be due to the severe lockdown due to the coronavirus pandemic. This confirms the relevance of the initial conditions and the context in which the thermal flows develop, which is characteristic of a chaotic system.
3.4. Anomalous Diffusion
Physical and biological systems have now been discovered in which the mean square displacement of the diffusing substance grows with time in the form < r2 (t) > ∝ t α, where the value of the exponent divides the processes diffusive in two different regimes: superdiffusion for α > 1 and subdiffusion for α < 1, particular cases of the so-called anomalous diffusion, Figure 12 [17]:
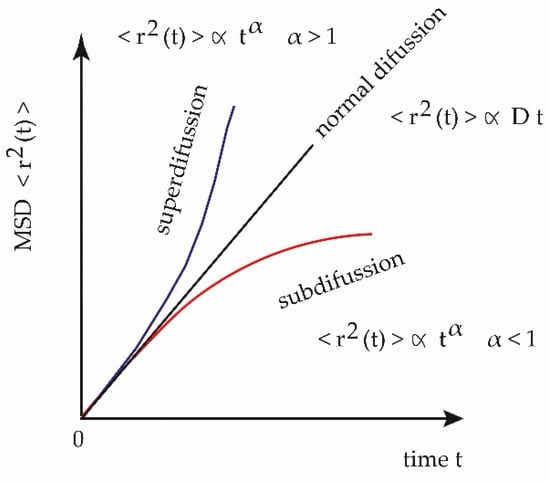
Figure 12.
Mean square displacement of anomalous and normal diffusion.
Anomalous diffusion, like normal diffusion, is studied and applied not only in the physical sciences. It is used in various complex systems, such as the internal structure of living cells, the process carried out by various species to search for and find food, etc.
The quadratic diffusive variance associated with the displacement of the urban meteorology variables from the atmosphere to the interior of the boundary layer, close to the ground, is dependent on the interaction between the entropies of the urban meteorology variables and the entropies of the pollutants according to the CK quotient. In basin geomorphology, the entropic forces of the pollutants are dominant and hinder diffusion (anomalous sub diffusion with α < 1), according to Table 7 and Table 8, with MV = RH or MV = T.
The Fréchet distribution is a special case of extreme value distribution or heavy-tailed distribution [50,51]. The distribution function that represents it is as follows:
where β > 0 is the shape parameter. The generalization includes a location parameter, n, and a scale parameter, s > 0, leaving us with the following:
In heavy-tailed distributions, there is a higher probability of extreme events compared to more commonly observed distributions, such as the Gaussian or normal distribution. One of the fundamental concepts in heavy-tailed distributions is power law behavior, as occurs with the mean value of the squared variance of the position. Power law distributions are present between the probability density function and the variable of interest:
We will now separately consider one of the six monitoring stations of the study, EML, since the treatment for the others is similar. The approach can be carried out from two perspectives:
- 1.
- 0 < c′K = SK,RH/SK,P <
Figure 13 is the heavy-tailed probability distribution with a domain of variables such that it assumes that the greatest influence on the system, according to the different periods of the study, is exerted by the entropy of relative humidity, the lowest probability is in the period 2019/2022 and then 2017/2020, and, finally, the highest probability is in the period of 2010/2013:
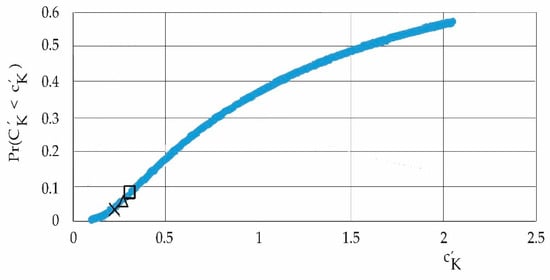
Figure 13.
Declining probability by period: X: 2019/2022, Δ: 2017/2020, and □: 2010/2013.
- 2.
- 0 ≤ 1/c′K = SK,P/SK,RH <
Figure 14 is the heavy-tail probability distribution with a domain of variables such that it assumes that the greatest influence on the system, according to the different periods of the study, is exerted by the entropy of the pollutants; the lowest probability is in the period 2010/2013, and then 2017/2020 and 2019/2022.
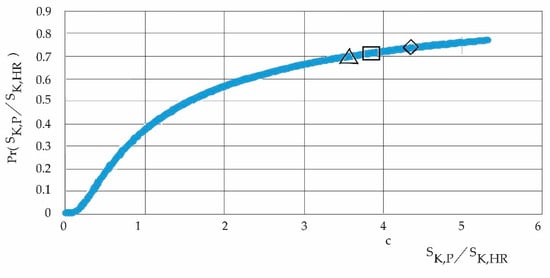
Figure 14.
Ascending probability according to periods Δ: 2010/2013, □: 2017/2020, and ◊: 2019/2022.
Figure 15 is the heavy-tailed probability density function (15) with a domain of variables such that it assumes that the least influence on the system, according to the different periods of the study, is exerted by relative humidity; and the lowest probability is in the period 2019/2022, and then 2017/2020 and 2010/2013.
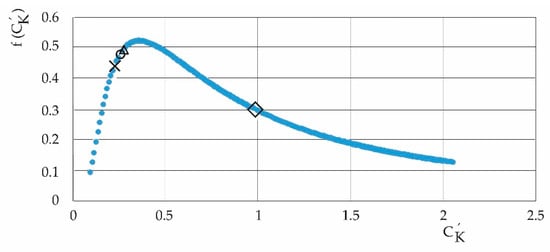
Figure 15.
Probability density function (Equation (15), with x = , Δ: 2010/2013; o: 2017/2020; x: 2019/2022; = SK,RH/SK,P. It denotes the lower domain in the current periods of relative humidity due to the influence of pollutants.
4. Discussion
The first three methods applied (Section 3.1, Section 3.2 and Section 3.3) have a common denominator and that is that their fundamental concepts are in thermodynamics: temperature, heat, thermal flows, entropy, and enthalpy. The study of heavy-tail probabilities is included in Section 3.4 because the domain of definition of the probability function makes use of the entropies ratio of relative humidity and the pollutants in this study, a ratio that is directly related to anomalous subdiffusion (α < 1).
Everyone agrees that a warmer atmosphere, basically due to human activity, allows the boundary layer to retain more water, breaking historical regularities [49,52,53], as follows from Figure 6 and Figure 7. The heavy-tail probability study establishes that this extreme condition has the highest probability of occurrence. Likewise, extreme health events such as the coronavirus pandemic, which forced a very strong reduction in human activities and a forced confinement of the population, produced an improvement in the thermal condition of the boundary layer.
From the perspective of a heat wave, this corresponds to a continuous period of extremely high temperature for a specific region. The heat wave is measured in relation to the average temperature considered in the study region. As there is no standardized definition of a heat wave [54,55,56], the meteorological agencies of each country have their own definitions in relation to what they estimate is a heat wave. The initial conditions generated by human activity in a basin geomorphology include the following [22,48]:
Air pollution,
Urban densification,
High albedo construction materials,
Changing of soil roughness due to high-rise buildings,
Thermal islands,
Expansion of cities into agricultural areas,
Concrete piping or channeling of natural waterways and river tributaries, thus reducing the contribution to relative humidity,
Consistent and permanent reduction of tree vegetation, etc.
From this perspective, an atmosphere with low relative humidity and strong air pollution dominance affects the indicator, which can be indicated in the geographic areas where the initial conditions that would mark the effect of a heat wave are found. Furthermore, heat waves can influence epidemiological events [57]. From the perspective of hydroclimatic volatility (sudden, large, and/or frequent transitions between very dry and very humid conditions) [58], its evolution is expected with anthropogenic warming. According to the standardized precipitation evapotranspiration index, sudden transitions at a global level have increased on average since the mid-twentieth century.
Evidence links these increases primarily to thermodynamics, namely the increasing water vapor holding capacity and potential evaporative demand of the atmosphere. Increased hydroclimatic volatility will amplify hazards associated with rapid shifts between wet and dry states (including flash floods, wildfires, landslides, and disease outbreaks) and could accelerate a shift in water management toward joint management of drought and flood risks.
5. Conclusions
After processing 108 time series of urban meteorology (T, WS, and RH) and atmospheric pollutants (PM10, PM2.5, CO), with each series consisting of 28,463 hourly data, using chaos theory software, it was shown that all series had their fundamental chaotic parameters in the appropriate ranges, confirming the chaotic nature of all series. From one of the parameters of each time series, the Kolmogorov entropy, the quotient between the sum of the Kolmogorov entropies of the relative humidity (and another quotient with the temperature, of each commune and for each period), and the sum of the Kolmogorov entropies of the pollutants (of each commune and for each period), SK,RH/SK,P, (for the case of temperature SK,T/SK,P) was constructed, which allows us to discover the following in a relatively simple way:
- The interactive decay, as the periods advance toward the present, of the quotient. This decay is compatible with what has been observed (of the relative humidity with respect to the pollutants and of the temperature with respect to the thermal flow of the pollutants).
- The presence of entropic dynamics associated with relative humidity and temperature, of lesser magnitude than those caused by pollutants.
- The manifestation and permanence of a subdiffusive phenomenon in the studied basin.
- The presence of statistics of extreme events through the heavy-tail analysis.
In the context of the boundary layer and in measurements with instruments whose location does not exceed 10 m from the ground surface, the natural place of most human activities, the limitations of the applied procedure are as follows:
- In the number of pollutants considered, although they are most significant in the geomorphology of the studied basin;
- In which it is necessary to consider a fourth period of measurements of 3.25 years (2025/2028), which is currently being carried out, together with new measurements, in the same studied communities, using ultrasonic anemometers with the purpose of measuring the vertical component of the wind and the sonic temperature and carrying out comparative studies, during the interperiod, of thermal flows;
- Analyze the mountainous and coastal geomorphologies where the authors [22] have already carried out a follow-up showing that, in a first approximation, they seem to favor anomalous superdiffusion and heavy-tailed extreme events to the benefit of urban meteorology.
Author Contributions
Conceptualization, P.P.; methodology, P.P.; software, P.P., E.M., G.N., and S.P.; validation, P.P., E.M., and G.N.; formal analysis, P.P.; investigation, P.P.; resources, P.P., E.M., G.N., and S.P.; data curation, P.P., E.M., and G.N.; writing—original draft preparation, P.P. and E.M.; writing—review and editing, P.P.; visualization, P.P., E.M., G.N., and S.P.; supervision, P.P.; project administration, P.P.; funding acquisition, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
Project supported by the Competition for Research Regular Projects, year 2024, code LPR23-15, Universidad Tecnológica Metropolitana. This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data were obtained from the public network for online monitoring of air pollutant concentration and meteorological variables. The network is distributed throughout all of Chile, without access restrictions. It is the responsibility of SINCA, the National Air Quality Information System, dependent on the Environment Ministry of Chile. The data for the two study periods are available for free use on the WEB page: URL: https://sinca.mma.gob.cl, accessed on 11 January 2024.
Acknowledgments
To the Research Directorate of the Universidad Tecnológica Metropolitana that made possible the progress of this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The appendix presents the three tables containing the values of the chaotic parameters calculated in six communes in the three measurement periods.

Table A1.
Chaotic parameters of three pollution variables and three meteorological variables in six monitoring stations (Santiago, Chile, 2010/2013 period) [48].
Table A1.
Chaotic parameters of three pollution variables and three meteorological variables in six monitoring stations (Santiago, Chile, 2010/2013 period) [48].
| Parameters Station | PM10 (µg/m3) | PM2.5 (µg/m3) | CO (ppm) | Temperature (°C) | RH (%) | WS (m/s) |
|---|---|---|---|---|---|---|
| EML | ||||||
| λ | 0.491 | 0.603 | 0.514 | 0.440 | 0.613 | 0.777 |
| Dc | 4.149 | 4.226 | 3.950 | 2.683 | 3.135 | 4.470 |
| H | 0.967 | 0.973 | 0.959 | 0.989 | 0.991 | 0.976 |
| SK (1/h) | 0.520 | 0.465 | 0.557 | 0.409 | 0.425 | 0.500 |
| EMM | ||||||
| λ | 0.302 | 0.585 | 0.630 | 0.460 | 0.713 | 0.892 |
| Dc | 3.877 | 3.966 | 4.719 | 3.128 | 3.507 | 4.285 |
| H | 0.972 | 0.977 | 0.981 | 0.991 | 0.990 | 0.980 |
| SK (1/h) | 0.441 | 0.528 | 0.581 | 0.409 | 0.427 | 0.616 |
| EMN | ||||||
| λ | 0.576 | 0.467 | 0.323 | 0.501 | 0.679 | 0.734 |
| Dc | 3.952 | 4.019 | 4.332 | 2.951 | 3.496 | 4.239 |
| H | 0.972 | 0.974 | 0.953 | 0.989 | 0.991 | 0.968 |
| SK (1/h) | 0.463 | 0.545 | 0.523 | 0.426 | 0.366 | 0.470 |
| EMO | ||||||
| λ | 0.467 | 0.289 | 0.229 | 0.453 | 0.689 | 0.855 |
| Dc | 3.785 | 4.085 | 4.640 | 2.801 | 3.194 | 4.053 |
| H | 0.965 | 0.955 | 0.937 | 0.992 | 0.989 | 0.968 |
| SK (1/h) | 0.522 | 0.428 | 0.260 | 0.375 | 0.382 | 0.440 |
| EMS | ||||||
| λ | 0.421 | 0.542 | 0.439 | 0.489 | 0.725 | 0.880 |
| Dc | 4.133 | 4.012 | 4.686 | 3.171 | 3.697 | 4.250 |
| H | 0.969 | 0.973 | 0.953 | 0.990 | 0.992 | 0.957 |
| SK (1/h) | 0.452 | 0.531 | 0.394 | 0.395 | 0.416 | 0.478 |
| EMV | ||||||
| λ | 0.561 | 0.295 | 0.296 | 0.495 | 0.746 | 0.836 |
| Dc | 3.788 | 3.788 | 4.631 | 3.155 | 3.249 | 3.584 |
| H | 0.967 | 0.970 | 0.952 | 0.989 | 0.989 | 0.956 |
| SK (1/h) | 0.552 | 0.538 | 0.341 | 0.384 | 0.370 | 0.448 |

Table A2.
Parameters for chaos study of three pollution variables and three meteorological variables in six monitoring stations (Santiago, Chile, 2017–2020 period) [48].
Table A2.
Parameters for chaos study of three pollution variables and three meteorological variables in six monitoring stations (Santiago, Chile, 2017–2020 period) [48].
| Parameters Station | PM10 (µg/m3) | PM2.5 (µg/m3) | CO (ppm) | Temperature (°C) | HR (%) | WV (m/s) |
|---|---|---|---|---|---|---|
| EML | ||||||
| λ | 0.550 | 0.235 | 0.026 | 0.205 | 0.064 | 0.935 |
| Dc | 3.451 | 1.364 | 0.580 | 2.290 | 2.029 | 3.697 |
| H | 0.922 | 0.963 | 0.933 | 0.915 | 0.942 | 0.975 |
| SK (1/h) | 0.295 | 0.596 | 0.686 | 0.355 | 0.414 | 0.515 |
| EMM | ||||||
| λ | 0.383 | 0.614 | 0.013 | 0.184 | 0.067 | 0.937 |
| Dc | 2.530 | 1.215 | 1.254 | 2.102 | 2.203 | 3.729 |
| H | 0.906 | 0.983 | 0.933 | 0.917 | 0.941 | 0.976 |
| SK (1/h) | 0.514 | 0.400 | 0.492 | 0.377 | 0.309 | 0.519 |
| EMN | ||||||
| λ | 0.621 | 0.292 | 0.033 | 0.223 | 0.092 | 0.917 |
| Dc | 2.948 | 1.276 | 2.277 | 2.280 | 2.095 | 3.735 |
| H | 0.929 | 0.960 | 0.933 | 0.916 | 0.942 | 0.973 |
| SK (1/h) | 0.242 | 0.825 | 0.412 | 0.366 | 0.308 | 0.471 |
| EMO | ||||||
| λ | 0.550 | 0.332 | 0.046 | 0.189 | 0.081 | 0.928 |
| Dc | 2.659 | 1.284 | 2.334 | 1.611 | 2.010 | 2.755 |
| H | 0.936 | 0.925 | 0.933 | 0.919 | 0.942 | 0.974 |
| SK (1/h) | 0.819 | 0.424 | 0.387 | 0.184 | 0.330 | 0.479 |
| EMS | ||||||
| λ | 0.597 | 0.279 | 0.030 | 0.228 | 0.063 | 0.933 |
| Dc | 3.535 | 1.396 | 3.302 | 2.300 | 2.306 | 3.004 |
| H | 0.921 | 0.975 | 0.933 | 0.915 | 0.942 | 0.976 |
| SK (1/h) | 0.898 | 0.422 | 0.382 | 0.357 | 0.404 | 0.489 |
| EMV | ||||||
| λ | 0.516 | 0.304 | 0.031 | 0.170 | 0.065 | 0.915 |
| Dc | 1.148 | 1.419 | 2.149 | 1.577 | 1.947 | 2.355 |
| H | 0.931 | 0.966 | 0.933 | 0.919 | 0.942 | 0.975 |
| SK (1/h) | 0.267 | 0.463 | 0.490 | 0.171 | 0.428 | 0.395 |

Table A3.
Parameters for chaos study of three pollution variables and three meteorological ones in six monitoring stations (Santiago, Chile, 2019/2022 period) [52].
Table A3.
Parameters for chaos study of three pollution variables and three meteorological ones in six monitoring stations (Santiago, Chile, 2019/2022 period) [52].
| Parameters Station | PM10 (µg/m3) | PM2.5 (µg/m3) | CO (ppm) | Temperature (°C) | HR (%) | WV(m/s) |
|---|---|---|---|---|---|---|
| EML | ||||||
| λ | 0.716 | 0.246 | 0.025 | 0.191 | 0.167 | 0.314 |
| Dc | 1.067 | 1.306 | 2.089 | 1.632 | 2.465 | 1.991 |
| H | 0.930 | 0.946 | 0.933 | 0.920 | 0.934 | 0.942 |
| SK (1/h) | 0.257 | 0.367 | 0.382 | 0.175 | 0.229 | 0.275 |
| EMM | ||||||
| λ | 0.561 | 0.345 | 0.011 | 0.220 | 0.203 | 0.339 |
| Dc | 0.984 | 1.531 | 2.156 | 1.923 | 2.691 | 1.986 |
| H | 0.914 | 0.969 | 0.933 | 0.916 | 0.935 | 0.942 |
| SK (1/h) | 0.247 | 0.360 | 0.333 | 0.182 | 0.180 | 0.278 |
| EMN | ||||||
| λ | 0.727 | 0.242 | 0.026 | 0.184 | 0.060 | 0.328 |
| Dc | 0.978 | 1.421 | 2.053 | 1.626 | 2.752 | 1.997 |
| H | 0.934 | 0.947 | 0.933 | 0.921 | 0.908 | 0.941 |
| SK (1/h) | 0.409 | 0.385 | 0.333 | 0.172 | 0.148 | 0.283 |
| EMO | ||||||
| λ | 0.540 | 0.332 | 0.015 | 0.222 | 0.256 | 0.347 |
| Dc | 0.973 | 1.354 | 2.095 | 1.821 | 2.499 | 2.019 |
| H | 0.940 | 0.920 | 0.933 | 0.918 | 0.936 | 0.941 |
| SK (1/h) | 0.388 | 0.400 | 0.329 | 0.180 | 0.205 | 0.283 |
| EMS | ||||||
| λ | 0.747 | 0.257 | 0.021 | 0.194 | 0.104 | 0.349 |
| Dc | 0.940 | 1.232 | 1.883 | 1.662 | 2.770 | 2.005 |
| H | 0.930 | 0.964 | 0.933 | 0.919 | 0.930 | 0.942 |
| SK (1/h) | 0.280 | 0.346 | 0.404 | 0.168 | 0.149 | 0.290 |
| EMV | ||||||
| λ | 0.574 | 0.241 | 0.580 | 0.161 | 0.714 | 0.080 |
| Dc | 0.945 | 1.432 | 2.127 | 1.559 | 2.704 | 1.939 |
| H | 0.930 | 0.938 | 0.933 | 0.920 | 0.934 | 0.940 |
| SK (1/h) | 0.252 | 0.415 | 0.285 | 0.153 | 0.100 | 0.351 |
Appendix B. [17]
Suppose there is a Kolmogorov entropy that fluctuates, but in infinitesimal amounts at different times for which, approximately, there is a Lyapunov exponent such that the separation between two phase space trajectories is maximum (maximum diffusion), as the figure shows:
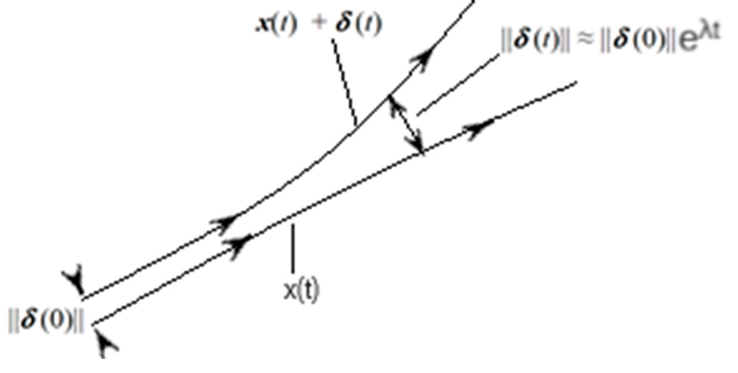

If y , they are separations between two trajectories of pollutants (P) and urban meteorology (MV) in very short times.
and
Considering a and b in a time, t″, we obtain
According to
using the assumption of very small times, such that , we obtain the following:
If the maximum spacing between phase space trajectories for the contaminant system is assumed to be linear in time, :
Then, the square root of the arithmetic mean of the squares of displacements in the direction x is as follows:
In basin geomorphology, the entropic forces of the pollutants are dominant and hinder diffusion (anomalous sub diffusion with α < 1). Data can be extracted from Table A1, Table A2 and Table A3. In the studied basin geomorphology, the anomalous subdiffusion of contamination manifests itself as a ponding.
References
- Selvam, A.M. Nonlinear Dynamics and Chaos: Applications in Meteorology and Atmospheric Physics. In Self-Organized Criticality and Predictability in Atmospheric Flows; Springer Atmospheric Sciences; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- He, H.; Schäfer, B.; Beck, C. Spatial analysis of tails of air pollution PDFs in Europe. arXiv 2024. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Maximum Entropy Principle in statistical inference: Case for non-Shannonian entropies. Phys. Rev. Lett. 2019, 22, 120601. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. arXiv 2003. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C. 0.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Quante, M.; Matthias, V. Water in the Earth’s atmosphere. J. Phys. IV France 2006, 139, 37–61. [Google Scholar] [CrossRef]
- Stull, R.B. Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands; London, UK, 1988; p. 666. [Google Scholar]
- Schlesinger, W.H.; Bernhardt, E.S. The Atmosphere. In Biogeochemistry; Academic Press: Cambridge, MA, USA, 2020; pp. 51–97. [Google Scholar] [CrossRef]
- Meran, G.; Siehlow, M.; von Hirschhausen, C. Water Availability: A Hydrological View. In The Economics of Water; Springer Water; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Shiklomanov, I.A. World fresh water resources. In Water in Crisis: A Guide to the World’s Fresh Water Resources; Gleick, P.H., Ed.; Oxford University Press: New York, NY, USA, 1990; pp. 13–24. [Google Scholar]
- Wang, R.; Cui, K.; Sheu, H.L.; Wang, L.C.; Liu, X. Effects of Precipitation on the Air Quality Index, PM2.5 Levels and on the Dry Deposition of PCDD/Fs in the Ambient Air. Aerosol Air Qual. Res. 2023, 23, 220417. [Google Scholar] [CrossRef]
- Pacheco, P.R.; Salini, G.A.; Mera, E.M. Entropía y neguentropía: Una aproximación al proceso de difusión de contaminantes y su sostenibilidad. Rev. Int. Contam. Ambient. 2021, 37, 167–185. [Google Scholar] [CrossRef]
- Abbass, K.; Qasim, M.Z.; Song, H.; Murshed, M.; Mahmood, H.; Younis, I. A review of the global climate change impacts, adaptation, and sustainable mitigation measures. Environ. Sci. Pollut. Res. 2022, 29, 42539–42559. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Arnell, N.W. Climate change and global water resources. Glob. Environ. Change 1999, 91, S31–S49. [Google Scholar] [CrossRef]
- Patel, V.K.; Kuttippurath, J. Increase in Tropospheric Water Vapor Amplifies Global Warming and Climate Change. Ocean Land Atmos Res. 2023, 2, 0015. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X. (Eds.) Climate Change 2001: The Scientific Basis, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change (IPCC); Cambridge University Press: Cambridge, UK, 2002; p. 944. [Google Scholar]
- Davis, R.E.; McGregor, G.R.; Enfield, K.B. Humidity: A review and primer on atmospheric moisture and human health. Environ. Res. 2016, 144, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Guarnieri, G.; Olivieri, B.; Senna, G.; Vianello, A. Relative Humidity and Its Impact on the Immune System and Infections. Int. J. Mol. Sci. 2023, 24, 9456. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Xu, J.; Liao, L.; Yu, Y.; Liu, W.; Zhou, J.; Ding, Y. Indicators for evaluating trends of air humidification in arid regions under circumstance of climate change: Relative humidity (RH) vs. Actual water vapour pressure (ea). Ecol. Indic. 2021, 121, 107043. [Google Scholar] [CrossRef]
- Peixoto, J.; Oort, A.H. 1996: The Climatology of Relative Humidity in the Atmosphere. J. Clim. 1996, 9, 3443–3463. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Navarro, G.; Parodi, C. Urban Meteorology, Pollutants, Geomorphology, Fractality, and Anomalous Diffusion. Fractal Fract. 2024, 8, 204. [Google Scholar] [CrossRef]
- Verlinde, E. On the Origin of Gravity and the Laws of Newton. arXiv 2010. [Google Scholar] [CrossRef]
- Peterson, M.A. Analogy between thermodynamics and mechanics. Am. J. Phys. 1979, 47, 488. [Google Scholar] [CrossRef]
- Baldiotti, M.C.; Fresneda, R.; Molina, C. A Hamiltonian approach to Thermodynamics. Ann. Phys. 2016, 373, 245–256. [Google Scholar] [CrossRef]
- Mao, Y.; Li, Y.; Yuan, X.; Kosonen, R. Characterization of the maximum entropy change in the process of drying materials based on a heat pump. Therm. Sci. Eng. Prog. 2024, 47, 102292, ISSN 2451-9049. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Simpson, J. An Equation for Moist Entropy in a Precipitating and Icy Atmosphere. J. Atmos. Sci. 2005, 62, 4293–4309. [Google Scholar] [CrossRef]
- Pikeroen, Q.; Paillard, D.; Watrin, K. A radiative–convective model computing precipitation with the maximum entropy production hypothesis. Geosci. Model Dev. 2024, 17, 3801–3814. [Google Scholar] [CrossRef]
- Li, J.; Chylek, P. Atmospheric Entropy. Part I: Climate Dissipation Structure. J. Clim. 2012, 25, 3173–3190. [Google Scholar] [CrossRef]
- Kleidon, A. Entropy Production by Evapotranspiration and its Geographic Variation. Soil Water Res. 2008, 3, S89–S94. [Google Scholar] [CrossRef]
- Alahmer, A.; Omar, M.A.; Mayyas, A.; Dongri, S. Effect of relative humidity and temperature control on in-cabin thermal comfort state: Thermodynamic and psychometric analyses. Appl. Therm. Eng. 2011, 31, 2636–2644. [Google Scholar] [CrossRef]
- Boregowda, S.C.; Choate, R.E.; Handy, R. Entropy Generation Analysis of Human Thermal Stress Responses. Int. Sch. Res. Netw. ISRN Thermodyn. 2012, 2012, 830103. [Google Scholar] [CrossRef]
- Mendoza, V.; Pazos, M.; Garduño, R.; Mendoza, B. Thermodynamics of climate change between cloud cover, atmospheric temperature and humidity. Sci. Rep. 2021, 11, 21244. [Google Scholar] [CrossRef]
- London, J.A. Study of the Atmospheric Heat Balance; New York University: New York, NY, USA, 1957. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis, 1st ed.; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Sprott, J.C. Chaos Data Analyzer Software. The Professional Version 2.1, 1998, Madison Wisconsin, USA. Available online: http://sprott.physics.wisc.edu/cda.htm (accessed on 12 November 2024).
- Pacheco, P.; Mera, E.; Salini, G. Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory. Sustainability 2022, 14, 2845. [Google Scholar] [CrossRef]
- Shiozawa, K.; Tokuda, I.S. Estimating Kolmogorov–Sinai entropy from time series of high-dimensional complex systems. Phys. Lett. A 2024, 510, 129531. [Google Scholar] [CrossRef]
- Farmer, J.D. Chaotic attractors of an infinite dimensional dynamical system. Phys. D 1982, 4, 366–393. [Google Scholar] [CrossRef]
- Farmer, J.D.; Otto, E.; Yorke, J.A. The dimension of chaotic attractors. Phys. D 1983, 7, 153–180. [Google Scholar] [CrossRef]
- Farmer, J.D. Information Dimension and the Probabilistic Structure of Chaos. Z. Für Naturforschung A 1982, 37, 1304–1326. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On Entropy per unit Time as a Metric Invariant of Automorphisms. Dokl. Akad. Nauk. SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the concept of entropy of a dynamical system. Dolk. Akad. Nauk. SSSR 1959, 124, 768. [Google Scholar]
- Pesin, Y. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar] [CrossRef]
- Ruelle, D. Thermodynamic Formalism; Addison-Wesley-Longman: Reading, MA, USA, 1978. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Fuentes, V. Intensive Urbanization, Urban Meteorology and Air Pollutants: Effects on the Temperature of a City in a Basin Geography. Int. J. Environ. Res. Public Health 2023, 20, 3941. [Google Scholar] [CrossRef]
- Middelburg, J.J. The Gibbs Free Energy. In Thermodynamics and Equilibria in Earth System Sciences: An Introduction; SpringerBriefs in Earth System Sciences; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann. Société Pol. Math. Crac. 1927, 6, 93–116. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E. Evolution over Time of Urban Thermal Conditions of a City Immersed in a Basin Geography and Mitigation. Atmosphere 2023, 14, 777. [Google Scholar] [CrossRef]
- Cuthbert, M.O.; Rau, G.C.; Ekström, M.; O’carroll, D.M.; Bates, A.J. Global climate-driven trade-offs between the water retention and cooling benefits of urban greening. Nat. Commun. 2022, 13, 518. [Google Scholar] [CrossRef]
- Bolan, S.; Padhye, L.P.; Jasemizad, T.; Govarthanan, M.; Karmegam, N.; Wijesekara, H.; Amarasiri, D.; Hou, D.; Zhou, P.; Biswal, B.K.; et al. Impacts of climate change on the fate of contaminants through extreme weather events. Sci. Total Environ. 2024, 909, 168388. [Google Scholar] [CrossRef] [PubMed]
- Russo, S.; Sillmann, J.; Sterl, A. Humid heat waves at different warming levels. Sci. Rep. 2017, 7, 7477. [Google Scholar] [CrossRef]
- Robinson, P.J. On the Definition of a Heat Wave. J. Appl. Meteor. Climatol. 2001, 40, 762–775. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Navarro, G. The Effects of Lockdown, Urban Meteorology, Pollutants, and Anomalous Diffusion on the SARS-CoV-2 Pandemic in Santiago de Chile. Atmosphere 2024, 15, 414. [Google Scholar] [CrossRef]
- Swain, D.L.; Prein, A.F.; Abatzoglou, J.T.; Albano, C.M.; Brunner, M.; Diffenbaugh, N.S.; Singh, D.; Skinner, C.B.; Touma, D. Hydroclimate volatility on a warming Earth. Nat. Rev. Earth Environ. 2025, 6, 35–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).