Role of Position of Pacific Subtropical High in Deciding Path of Tropical Storms
Abstract
1. Introduction
2. Materials and Methods
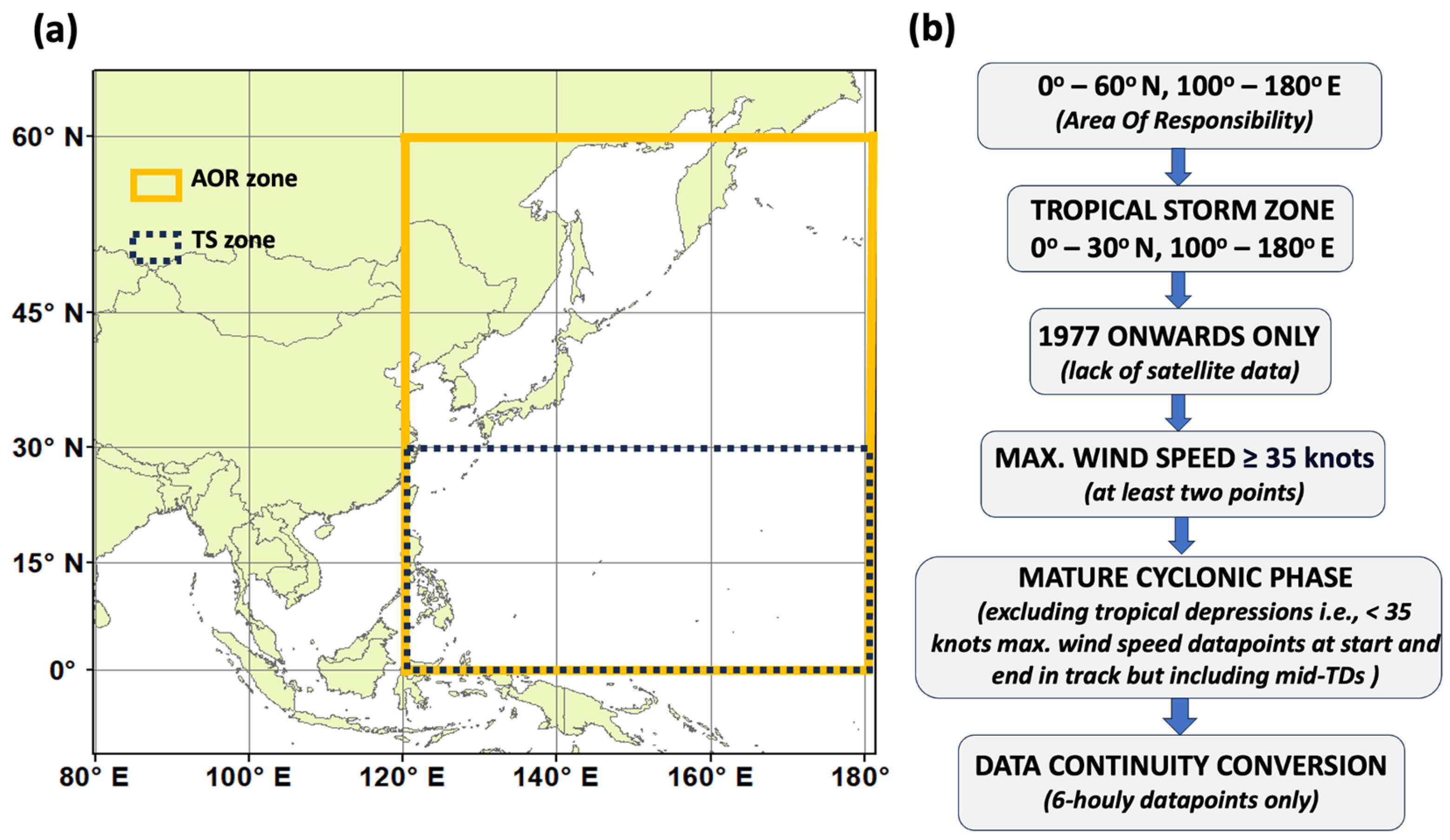
2.1. Data Source
2.2. Data Sorting
2.3. Sinuosity Index
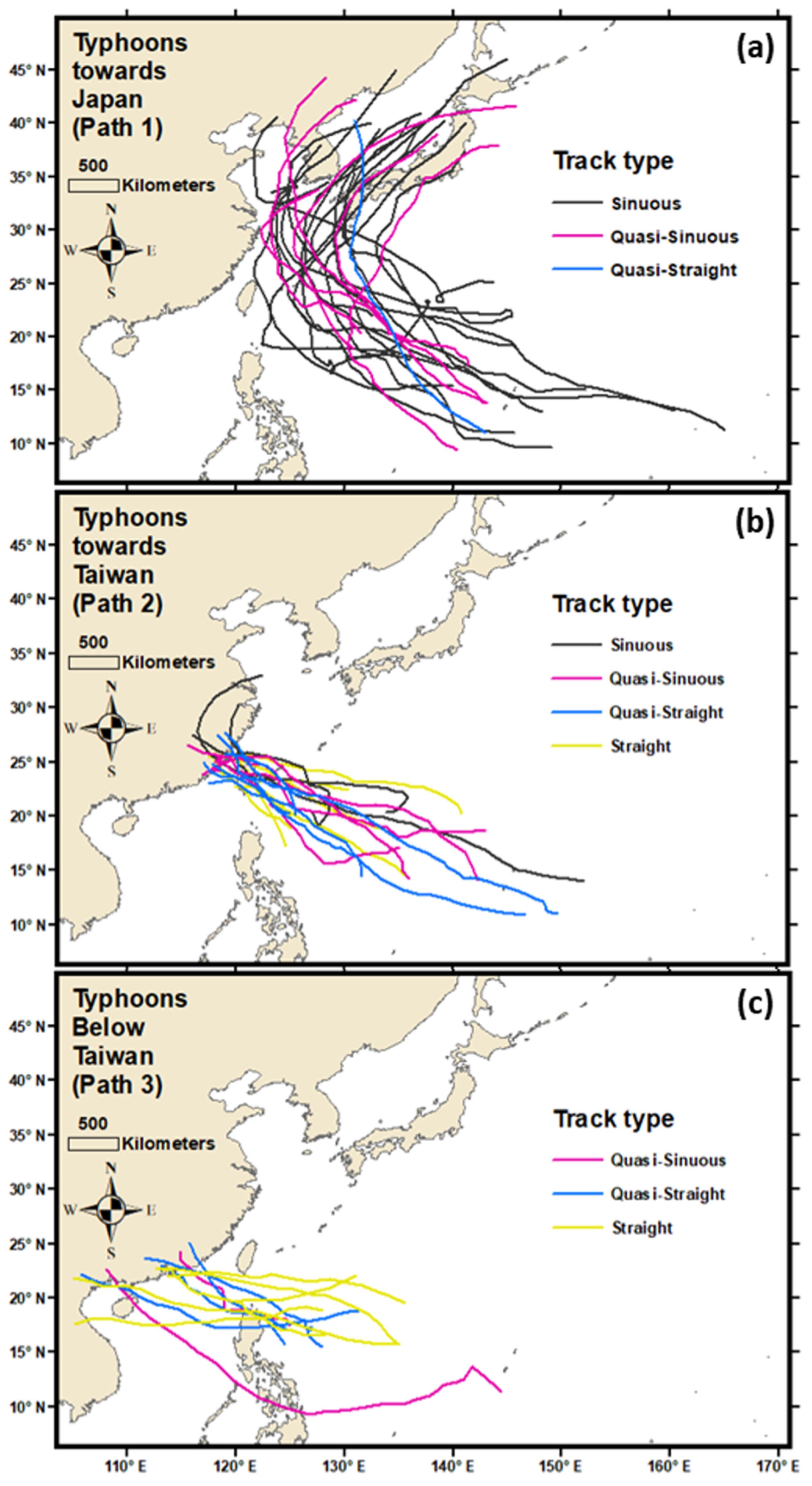
2.4. Technique for Detecting TSs Following Three Different Paths
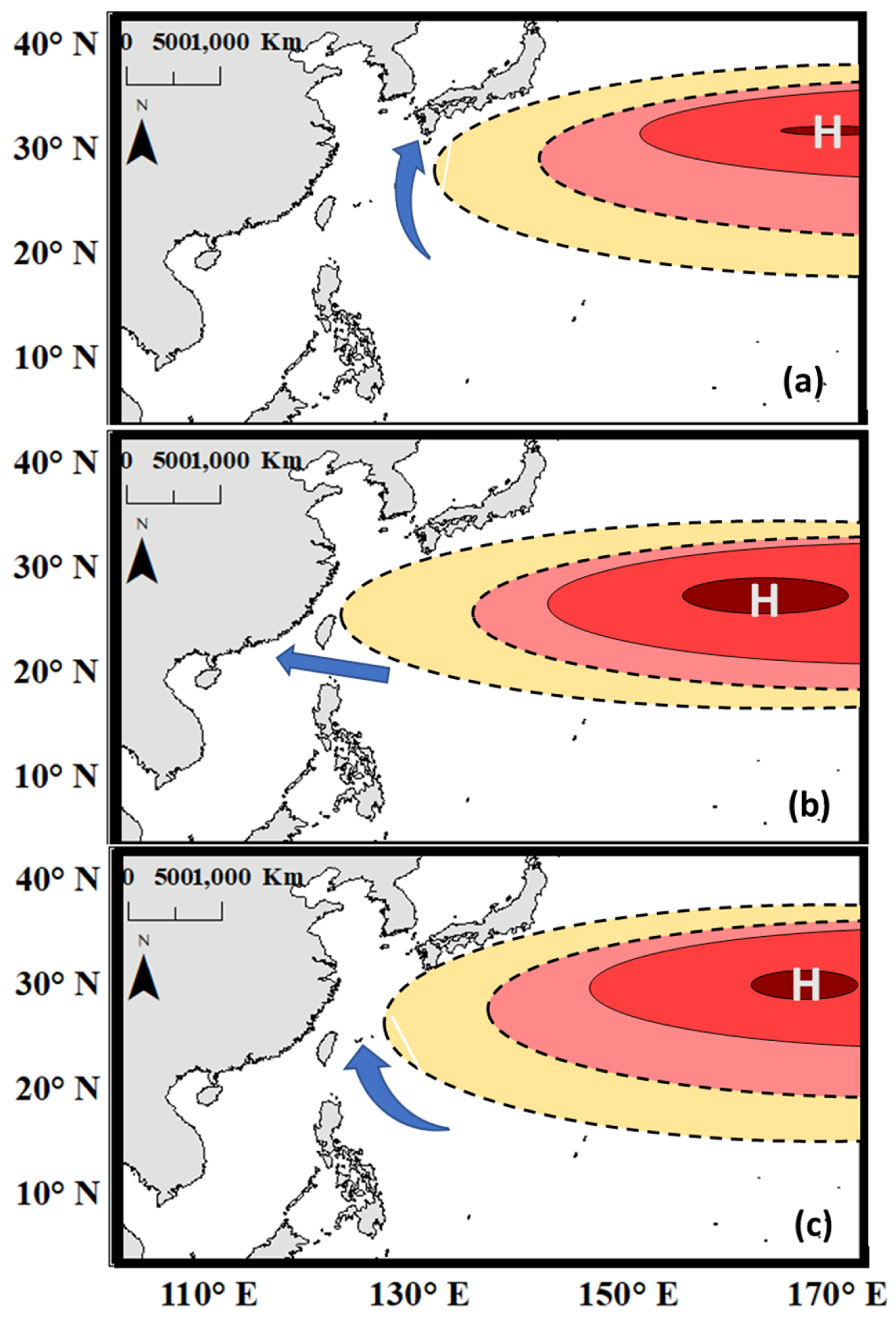
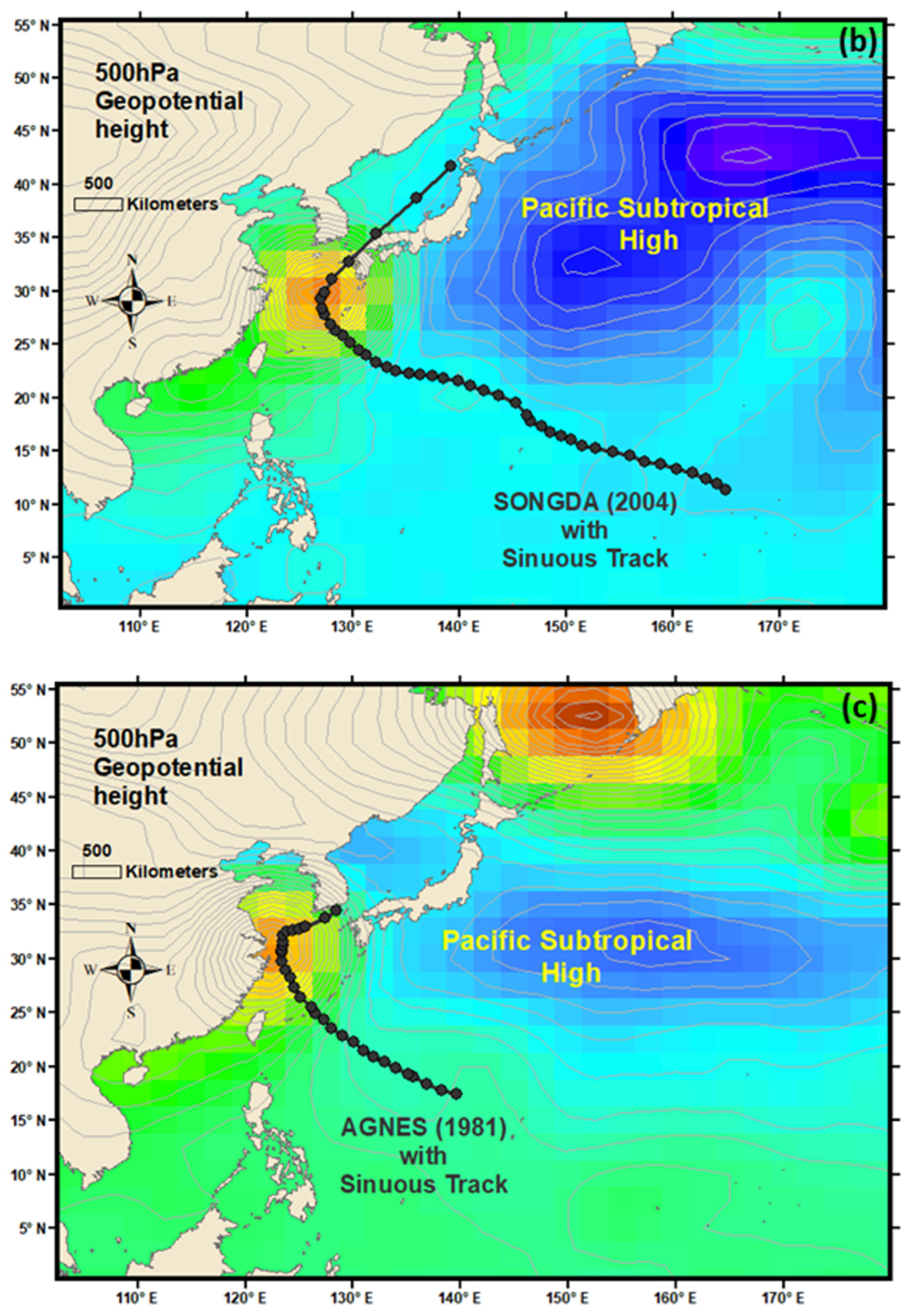
2.5. Detection of the Pacific Subtropical High
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TS | Tropical Storm |
| PSH | Pacific subtropical high |
| NWP | Northwest Pacific |
| SI | Sinuosity Index |
| IBTrACS | International Best Track Archive for Climate Stewardship |
| SCS | South China Sea |
| BoB | Bay of Bengal |
| NOAA | National Oceanic and Atmospheric Administration |
| STY | Super typhoon |
| RSMC | Regional Specialized Meteorological Center |
| JMA | Japan Meteorological Agency |
| AOR | Area of Responsibility |
References
- IPCC. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007—The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007; p. 996. Available online: https://www.ipcc.ch/pdf/assessment-report/ar4/wg2/ar4_wg2_full_report.pdf (accessed on 26 October 2018).
- NOAA. Hurricane Research Division Report. Available online: http://www.aoml.noaa.gov/hrd/tcfaq/E25.html (accessed on 26 October 2018).
- Pandey, R.S.; Liou, Y.A. Decadal Behaviors of Tropical Storm Tracks in the Northwest Pacific Ocean. Atmos. Res. 2020, 246, 105143. [Google Scholar] [CrossRef]
- Pandey, R.S. Statistical analysis of environmental parameters on the occurrences of tropical cyclones and earthquakes: An example from West North Pacific region. Mar. Geophys. Res. 2022, 43, 44. [Google Scholar] [CrossRef]
- Pandey, R.S.; Liou, Y.A. Yearly, 5-Yearly, and Decadal Sea Surface Temperature (SST) and SST Anomaly (SSTA) Data Averaged over the Whole Typhoon Season (May–November) over the Entire Global Ocean, North Pacific Ocean, Philippine Sea, South China Sea, and Eastern China Sea; Mendeley Data V1; National Central University Center for Space and Remote Sensing Research: Taoyuan, Taiwan, 2020. [Google Scholar] [CrossRef]
- Pandey, R.S.; Liou, Y.A. Typhoon Strength Rising in the Past Four Decades. Weather Clim. Extrem. 2022, 36, 100446. [Google Scholar] [CrossRef]
- Hornyak, T. Typhoons Getting Stronger, Making Landfall More Often. Eos 2020, 101. [Google Scholar] [CrossRef]
- Pandey, R.S.; Liou, Y.A.; Liu, J.C. Season-Dependent Variability and Influential Environmental Factors of Super-Typhoons in the Northwest Pacific Basin During 2013–2017. Weather Clim. Extrem. 2021, 31, 100307. [Google Scholar] [CrossRef]
- Kornei, K. Storms Interact but Rarely Merge into Bigger Tempests. Eos 2020, 101. [Google Scholar] [CrossRef]
- Sangomla, A. Perfect Storm: What Is the Fujiwhara Effect? Down to Earth. Available online: https://www.downtoearth.org.in/news/world/perfect-storm-what-is-the-fujiwhara-effect--85337 (accessed on 28 November 2022).
- Liou, Y.A.; Pandey, R.S. Interactions Between Typhoons Parma and Melor (2009) in Northwest Pacific Ocean. Weather Clim. Extrem. 2020, 29, 100272. [Google Scholar] [CrossRef]
- Pandey, R.S. A Comparative Analysis of a Global and a Regional Model on the tropical cyclone track forecast. Nat. Hazards 2024. [Google Scholar] [CrossRef]
- Terry, J.P.; Gienko, G. Developing a New Sinuosity Index for Cyclone Tracks in the Tropical South Pacific. Nat. Hazards 2011, 59, 1161–1174. [Google Scholar] [CrossRef]
- Nakazawa, T.; Rajendran, K. Relationship Between Tropospheric Circulation over the Western North Pacific and Tropical Cyclone Approach/Landfall on Japan. J. Meteorol. Soc. Jpn. 2007, 85, 101–114. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; Lee, S.K.; Atlas, R. Impact of the Atlantic Warm Pool on United States Landfalling Hurricanes. Geophys. Res. Lett. 2011, 38, L19702. [Google Scholar] [CrossRef]
- Knaff, J.A. Revisiting the Maximum Intensity of Recurving Tropical Cyclones. Int. J. Climatol. 2009, 29, 827–837. [Google Scholar] [CrossRef]
- Wu, L.; Wang, B. Assessing Impacts of Global Warming on Tropical Cyclone Tracks. J. Clim. 2004, 17, 1686–1698. [Google Scholar] [CrossRef]
- Hong, C.C.; Lee, M.Y.; Hsu, H.H.; Lin, N.H.; Tsuang, B.J. Tropical SST Forcing on the Anomalous WNP Subtropical High During July–August 2010 and the Record-High SST in the Tropical Atlantic. Clim. Dyn. 2015, 45, 633–650. [Google Scholar] [CrossRef]
- Hung, C.W.; Shih, M.F.; Lin, T.Y. The Climatological Analysis of Typhoon Tracks, Steering Flow, and the Pacific Subtropical High in the Vicinity of Taiwan and the Western North Pacific. Atmosphere 2020, 11, 543. [Google Scholar] [CrossRef]
- Song, J.J.; Wang, Y.; Wu, L. Trend Discrepancies Among Three Best Track Data Sets of Western North Pacific Tropical Cyclones. J. Geophys. Res. 2010, 115, D12128. [Google Scholar] [CrossRef]
- Schreck, C.J.; Knapp, K.R.; Kossin, J.P. The Impact of Best Track Discrepancies on Global Tropical Cyclone Climatologies Using IBTrACS. Mon. Weather Rev. 2014, 142, 3881–3899. [Google Scholar] [CrossRef]
- Dvorak, V.F. A Technique for the Analysis and Forecasting of Tropical Cyclone Intensities from Satellite Pictures. NOAA Tech. Memo. NESS 1972, 36, 15. [Google Scholar]
- Dvorak, V.F. A Technique for the Analysis and Forecasting of Tropical Cyclone Intensities from Satellite Pictures. NOAA Tech. Memo. NESS 1973, 45, 19. [Google Scholar]
- Vincenty, T. Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations. Surv. Rev. 1975, 22, 88–93. [Google Scholar] [CrossRef]
- Morioka, Y.; Yamagata, T.; Behera, S.K. Structure and Maintenance Mechanisms of the Mascarene High in Austral Winter. Int. J. Climatol. 2021, 41, 1–15. [Google Scholar]
- Xulu, N.G.; Chikoore, H.; Bopape, M.-J.M.; Nethengwe, N.S. Climatology of the Mascarene High and Its Influence on Weather and Climate over Southern Africa. Climate 2020, 8, 86. [Google Scholar] [CrossRef]
- Jury, M.R. Climate-Weather Interactions Modulating Tropical Cyclones over the Mascarene Islands 2000–2024. Meteorol. Atmos. Phys. 2025, 137, 14. [Google Scholar] [CrossRef]
- Miyamoto, A.; Nakamura, H.; Miyasaka, T.; Kosaka, Y. Wintertime Weakening of Low-Cloud Impacts on the Subtropical High in the South Indian Ocean. J. Clim. 2022, 35, 323–334. [Google Scholar] [CrossRef]

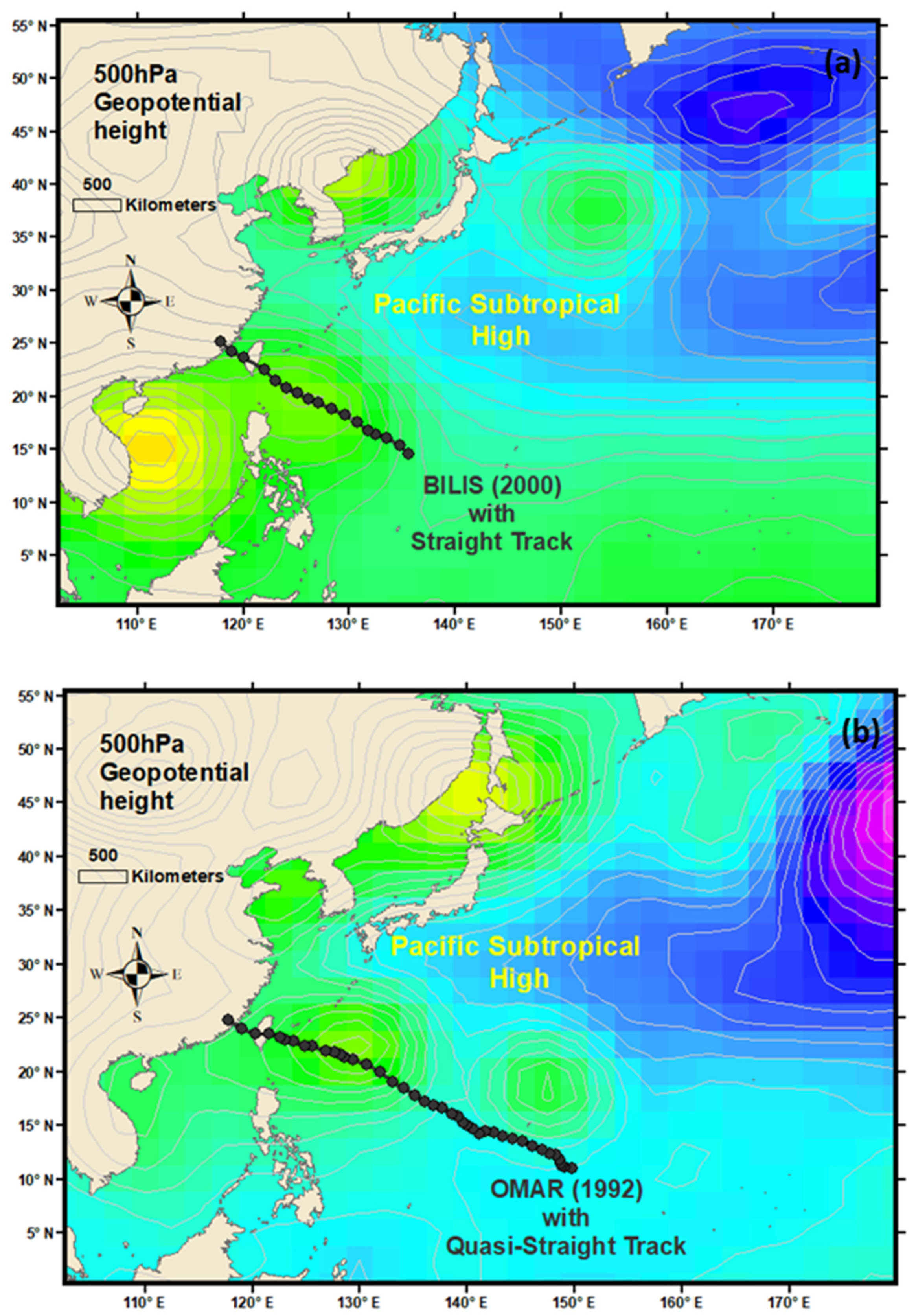
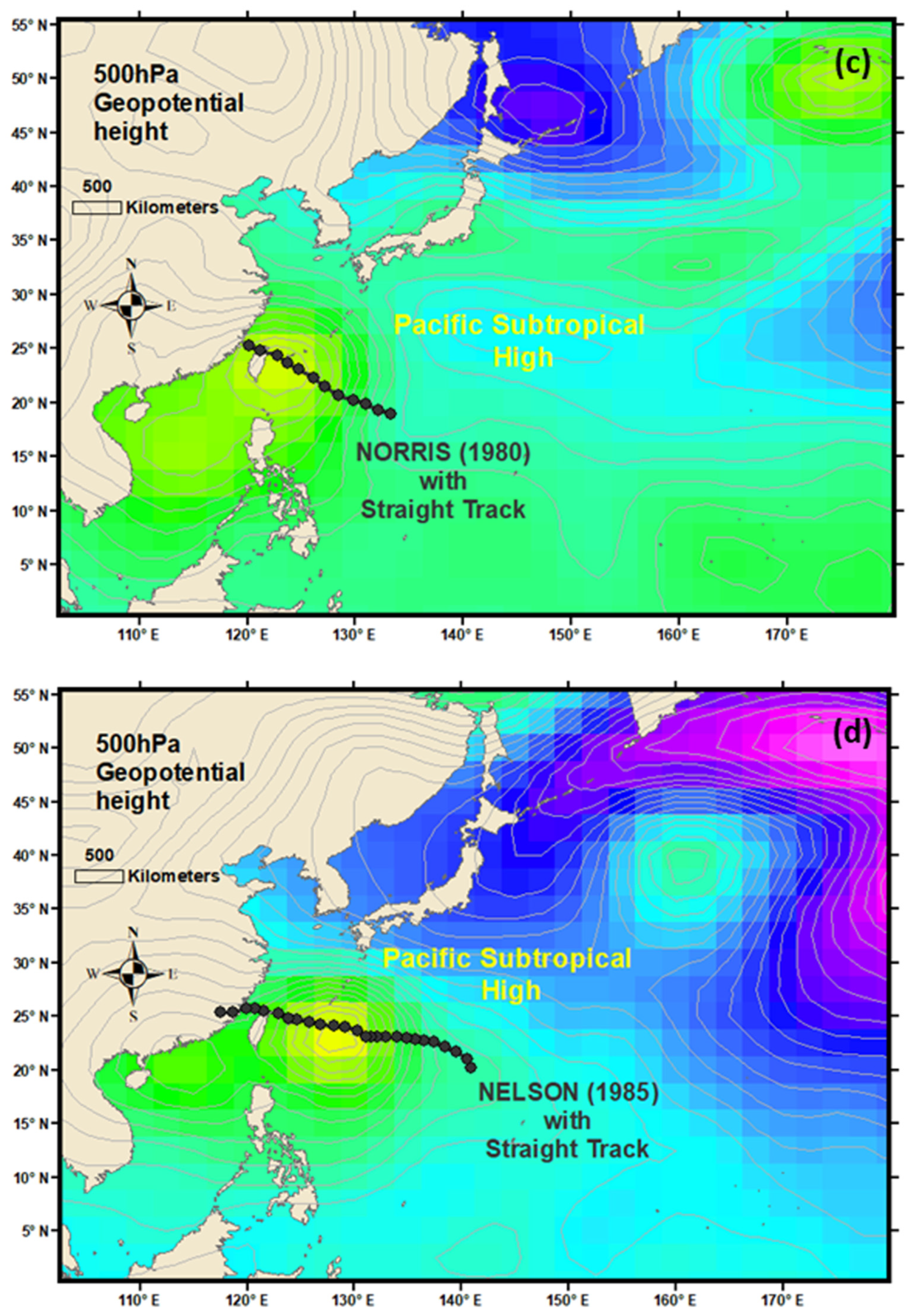
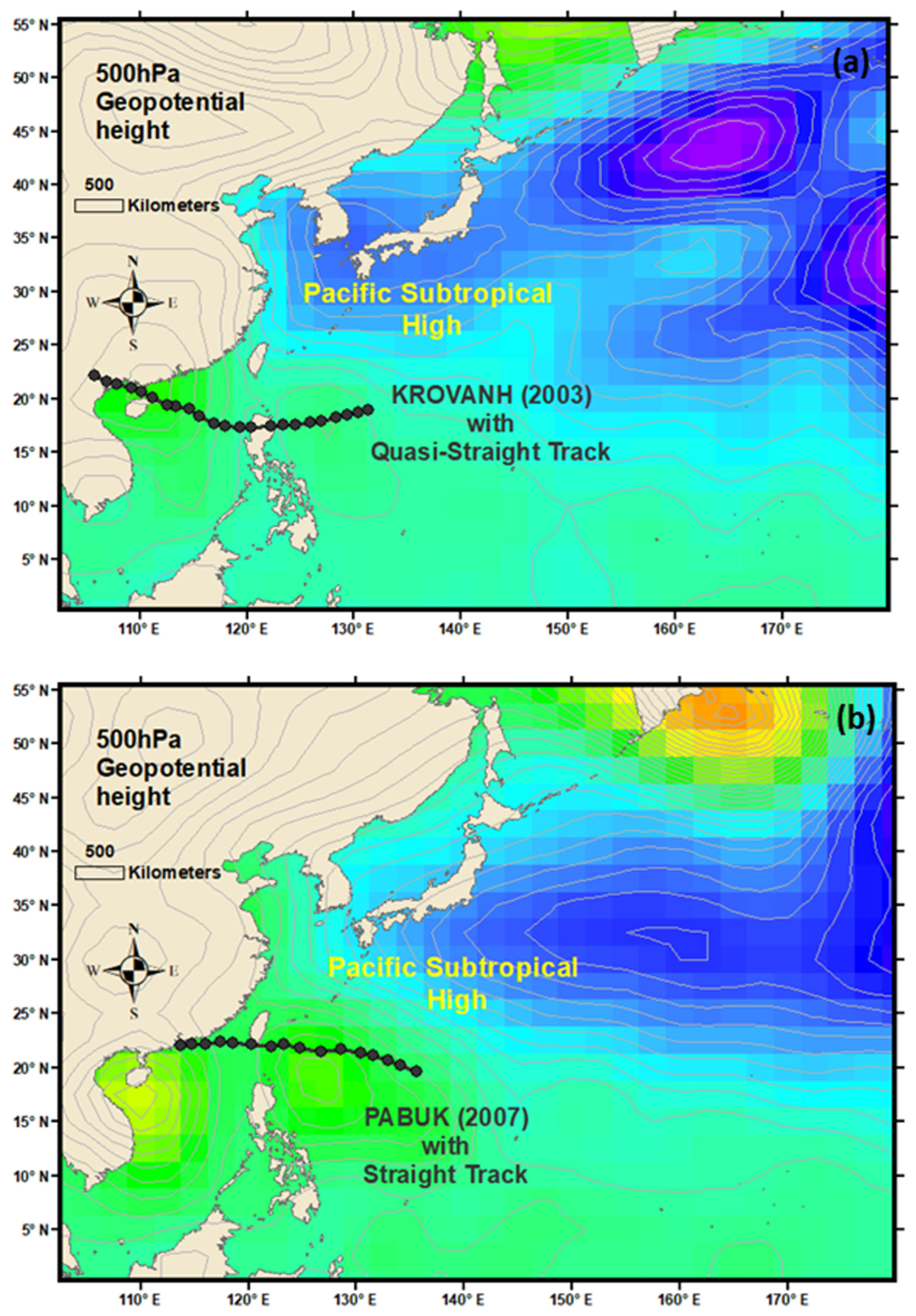
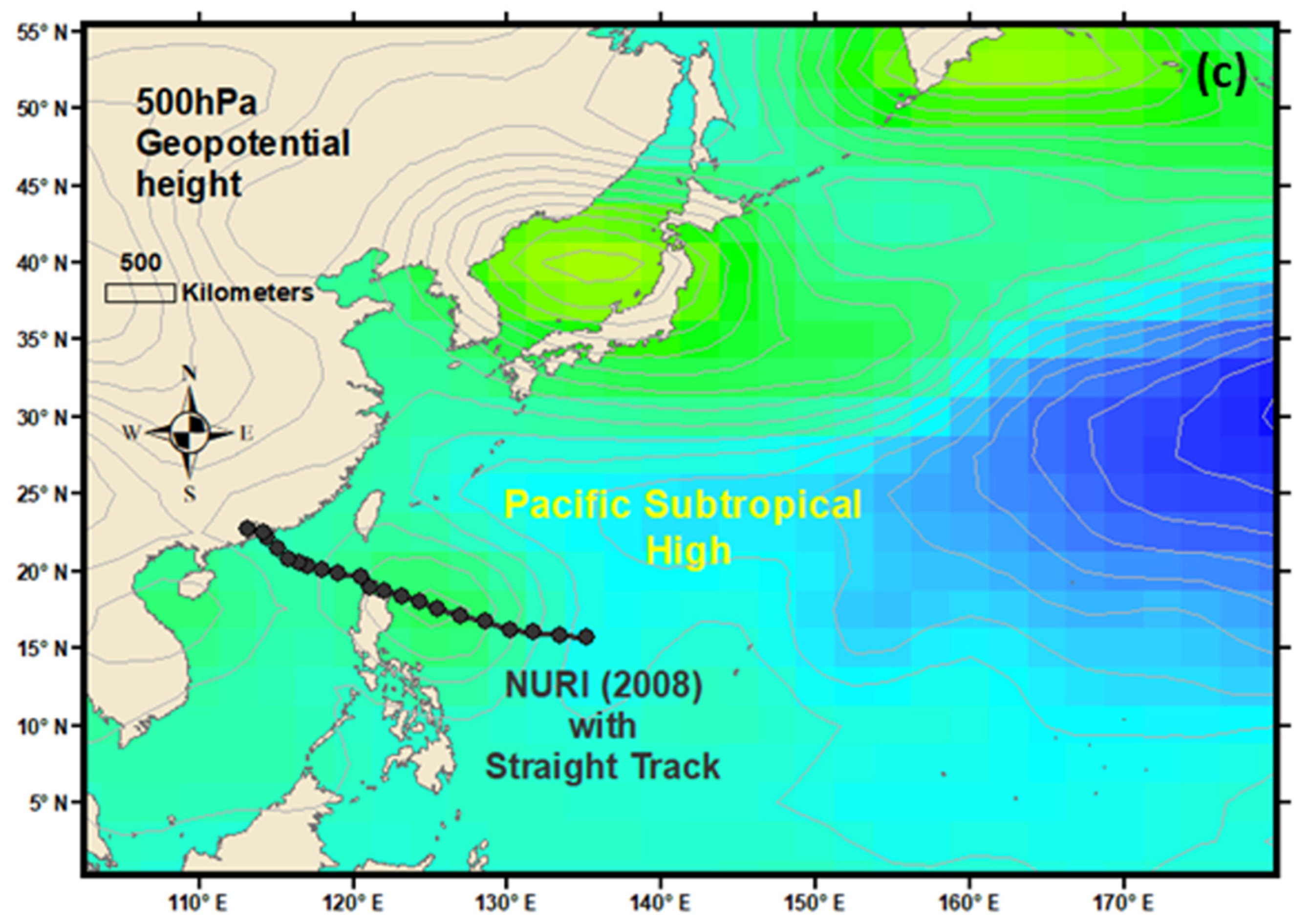
| Year | TS Name | Track Type | Turning Day/Time | Path | Sinuosity Value | Sinuosity Index |
|---|---|---|---|---|---|---|
| 1979 | IRVING | Sn | 15-08-79 18:00 | Towards Japan (Path 1) | 1.53 | 8.11 |
| 1979 | JUDY | QSn | 22-08-79 6:00 | Towards Japan (Path 1) | 1.33 | 6.91 |
| 1980 | NORRIS | St | 27-08-80 0:00 | Towards Taiwan (Path 2) | 1.01 | 2.01 |
| 1981 | AGNES | Sn | 1/9/1981 0:00 | Towards Japan (Path 1) | 1.39 | 7.32 |
| 1982 | DOT | QSt | 12/8/1982 6:00 | Towards Taiwan (Path 2) | 1.04 | 3.44 |
| 1982 | ELLIS | QSt | 23-08-82 6:00 | Towards Japan (Path 1) | 1.09 | 4.43 |
| 1983 | ABBY | QSn | 10/8/1983 0:00 | Towards Japan (Path 1) | 1.33 | 6.9 |
| 1983 | CARMEN | St | 14-08-83 12:00 | Towards Below Taiwan (Path 3) | 1.02 | 2.62 |
| 1984 | FREDA | QSt | 7/8/1984 0:00 | Towards Taiwan (Path 2) | 1.04 | 3.46 |
| 1984 | HOLLY | Sn | 20-08-84 0:00 | Towards Japan (Path 1) | 1.35 | 7.03 |
| 1984 | IKE | QSn | 31-08-84 12:00 | Towards Below Taiwan (Path 3) | 1.16 | 5.47 |
| 1984 | JUNE | QSn | 28-08-84 12:00 | Towards Below Taiwan (Path 3) | 1.15 | 5.29 |
| 1985 | NELSON | St | 21-08-85 18:00 | Towards Taiwan (Path 2) | 1.03 | 3.23 |
| 1986 | VERA | Sn | 27-08-86 6:00 | Towards Japan (Path 1) | 2.68 | 11.9 |
| 1987 | DINAH | Sn | 29-08-87 12:00 | Towards Japan (Path 1) | 1.37 | 7.18 |
| 1990 | BECKY | St | 25-08-90 6:00 | Towards Below Taiwan (Path 3) | 1.02 | 2.65 |
| 1990 | YANCY | QSn | 17-08-90 12:00 | Towards Taiwan (Path 2) | 1.25 | 6.29 |
| 1992 | JANIS | QSn | 7/8/1992 12:00 | Towards Japan (Path 1) | 1.33 | 6.89 |
| 1992 | OMAR | QSt | 2/9/1992 0:00 | Towards Taiwan (Path 2) | 1.05 | 3.63 |
| 1992 | POLLY | QSt | 28-08-92 0:00 | Towards Taiwan (Path 2) | 1.05 | 3.62 |
| 1993 | ROBYN | Sn | 9/8/1993 6:00 | Towards Japan (Path 1) | 1.36 | 7.11 |
| 1993 | YANCY | Sn | 1/9/1993 12:00 | Towards Japan (Path 1) | 1.49 | 7.9 |
| 1994 | CAITLIN | QSt | 2/8/1994 18:00 | Towards Taiwan (Path 2) | 1.04 | 3.47 |
| 1994 | DOUG | Sn | 8/8/1994 6:00 | Towards Japan (Path 1) | 1.47 | 7.75 |
| 1994 | ELLIE | Sn | 15-08-94 18:00 | Towards Japan (Path 1) | 1.43 | 7.53 |
| 1995 | KENT | QSt | 29-08-95 6:00 | Towards Below Taiwan (Path 3) | 1.11 | 4.81 |
| 1997 | AMBER | QSt | 28-08-97 0:00 | Towards Taiwan (Path 2) | 1.07 | 4.03 |
| 1998 | OTTO | St | 3/8/1998 6:00 | Towards Taiwan (Path 2) | 1.03 | 2.94 |
| 1999 | SAM | QSt | 20-08-99 0:00 | Towards Below Taiwan (Path 3) | 1.05 | 3.64 |
| 2000 | BILIS | St | 21-08-00 12:00 | Towards Taiwan (Path 2) | 1.01 | 2.38 |
| 2000 | PRAPIROON | QSn | 27-08-00 6:00 | Towards Japan (Path 1) | 1.31 | 6.74 |
| 2001 | PABUK | Sn | 20-08-01 0:00 | Towards Japan (Path 1) | 1.53 | 8.1 |
| 2003 | DUJUAN | St | 31-08-03 18:00 | Towards Below Taiwan (Path 3) | 1.03 | 2.93 |
| 2003 | ETAU | Sn | 7/8/2003 0:00 | Towards Japan (Path 1) | 1.35 | 7.08 |
| 2003 | KROVANH | QSt | 21-08-03 18:00 | Towards Below Taiwan (Path 3) | 1.05 | 3.79 |
| 2003 | MORAKOT | St | 2/8/2003 18:00 | Towards Taiwan (Path 2) | 1.02 | 2.85 |
| 2004 | AERE | QSn | 23-08-04 12:00 | Towards Taiwan (Path 2) | 1.13 | 5 |
| 2004 | CHABA | Sn | 29-08-04 18:00 | Towards Japan (Path 1) | 1.53 | 8.11 |
| 2004 | MEGI | QSn | 18-08-04 0:00 | Towards Japan (Path 1) | 1.28 | 6.54 |
| 2004 | SONGDA | Sn | 6/9/2004 6:00 | Towards Japan (Path 1) | 1.53 | 8.11 |
| 2005 | NABI | Sn | 6/9/2005 0:00 | Towards Japan (Path 1) | 1.56 | 8.22 |
| 2005 | SANVU | QSt | 11/8/200512:00 | Towards Below Taiwan (Path 3) | 1.05 | 3.72 |
| 2005 | TALIM | QSt | 28-08-05 18:00 | Towards Taiwan (Path 2) | 1.06 | 3.83 |
| 2006 | BOPHA | St | 8/8/2006 12:00 | Towards Taiwan (Path 2) | 1.02 | 2.69 |
| 2007 | PABUK | St | 6/8/2007 18:00 | Towards Below Taiwan (Path 3) | 1.02 | 2.48 |
| 2007 | SEPAT | QSn | 15-08-07 0:00 | Towards Taiwan (Path 2) | 1.16 | 5.47 |
| 2007 | WUTIP | St | 8/8/2007 6:00 | Towards Taiwan (Path 2) | 1 | 1.61 |
| 2008 | NURI | St | 19-08-08 6:00 | Towards Below Taiwan (Path 3) | 1.03 | 3.24 |
| 2009 | MORAKOT | Sn | 7/8/2009 6:00 | Towards Taiwan (Path 2) | 1.51 | 7.97 |
| 2010 | KOMPASU | Sn | 1/9/2010 6:00 | Towards Japan (Path 1) | 1.35 | 7.07 |
| 2012 | BOLAVEN | QSn | 25-08-12 0:00 | Towards Japan (Path 1) | 1.23 | 6.1 |
| 2012 | KAI-TAK | St | 14-08-12 0:00 | Towards Below Taiwan (Path 3) | 1.02 | 2.81 |
| 2013 | TRAMI | Sn | 20-08-13 18:00 | Towards Taiwan (Path 2) | 1.46 | 7.72 |
| 2015 | GONI | Sn | 21-08-15 12:00 | Towards Japan (Path 1) | 1.63 | 8.59 |
| 2015 | SOUDELOR | Sn | 6/8/2015 0:00 | Towards Taiwan (Path 2) | 1.37 | 7.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, R.S. Role of Position of Pacific Subtropical High in Deciding Path of Tropical Storms. Atmosphere 2025, 16, 322. https://doi.org/10.3390/atmos16030322
Pandey RS. Role of Position of Pacific Subtropical High in Deciding Path of Tropical Storms. Atmosphere. 2025; 16(3):322. https://doi.org/10.3390/atmos16030322
Chicago/Turabian StylePandey, Ravi Shankar. 2025. "Role of Position of Pacific Subtropical High in Deciding Path of Tropical Storms" Atmosphere 16, no. 3: 322. https://doi.org/10.3390/atmos16030322
APA StylePandey, R. S. (2025). Role of Position of Pacific Subtropical High in Deciding Path of Tropical Storms. Atmosphere, 16(3), 322. https://doi.org/10.3390/atmos16030322





