Significance of Cloud Microphysics and Cumulus Parameterization Schemes in Simulating an Extreme Flood-Producing Precipitation Event in the Central Himalaya
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Description
2.2. Description of Cloud Microphysics Schemes
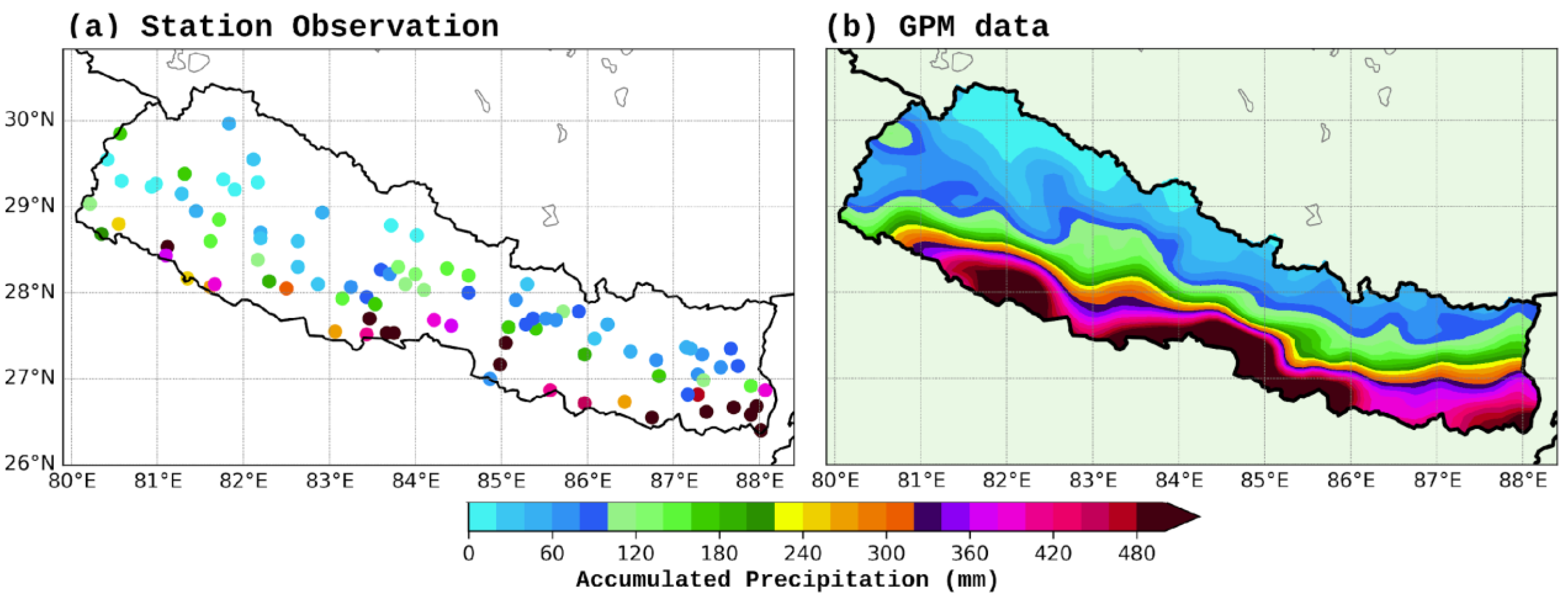
2.3. Station and Satellite Observation
2.4. Model Evaluation
2.4.1. Percentage Bias (PBIAS)
2.4.2. Normalized Root Mean Square Error
2.4.3. Coefficient of Determination (R2)
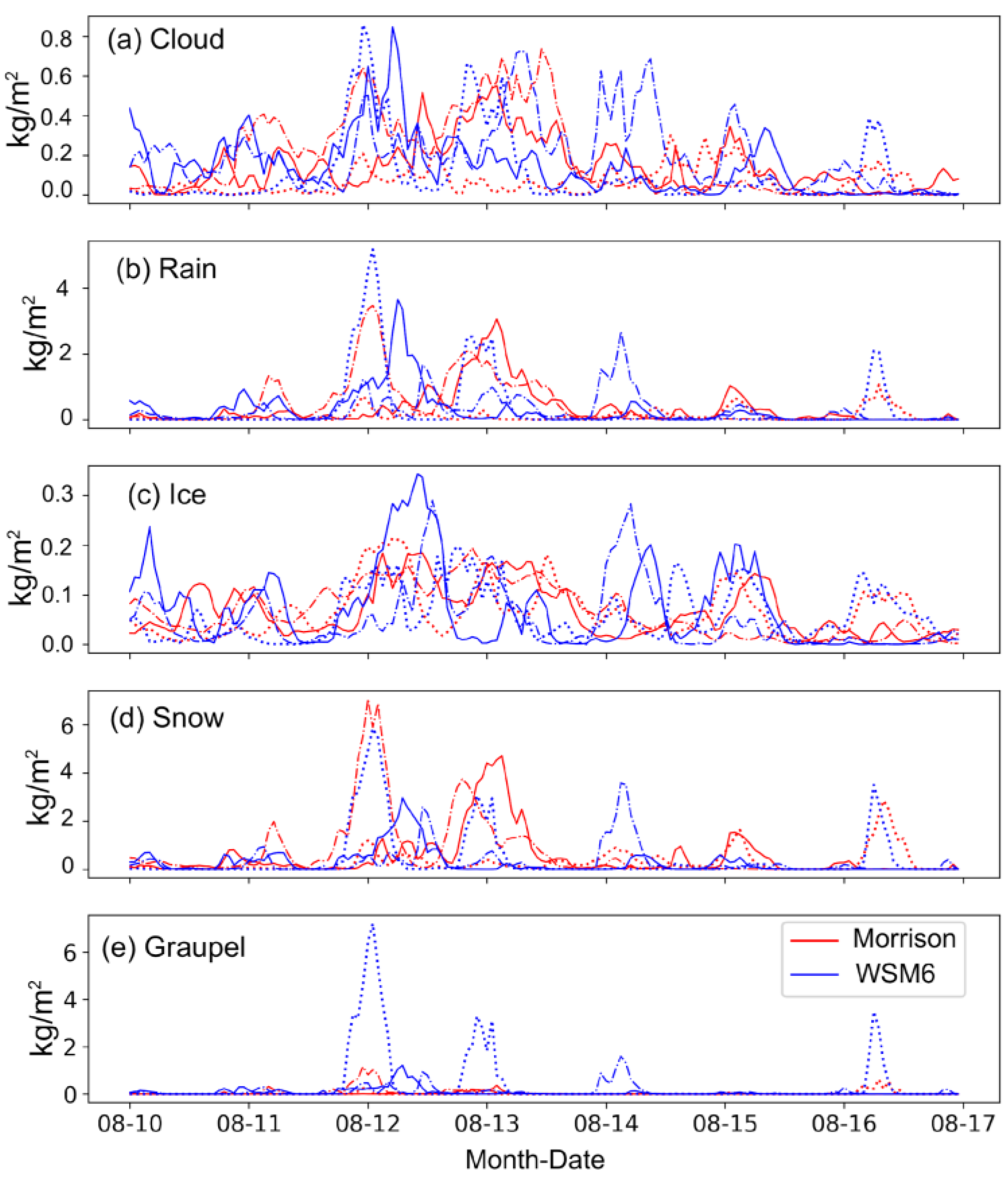
2.5. Column Density of Hydrometeors
3. Results
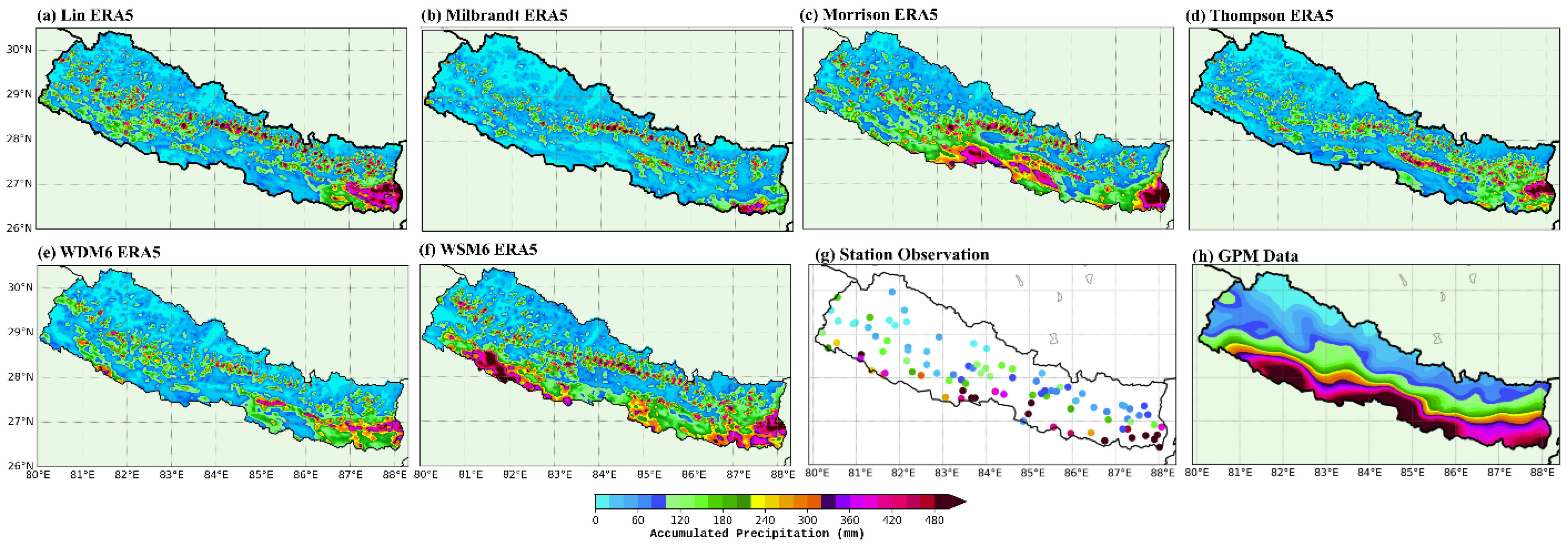
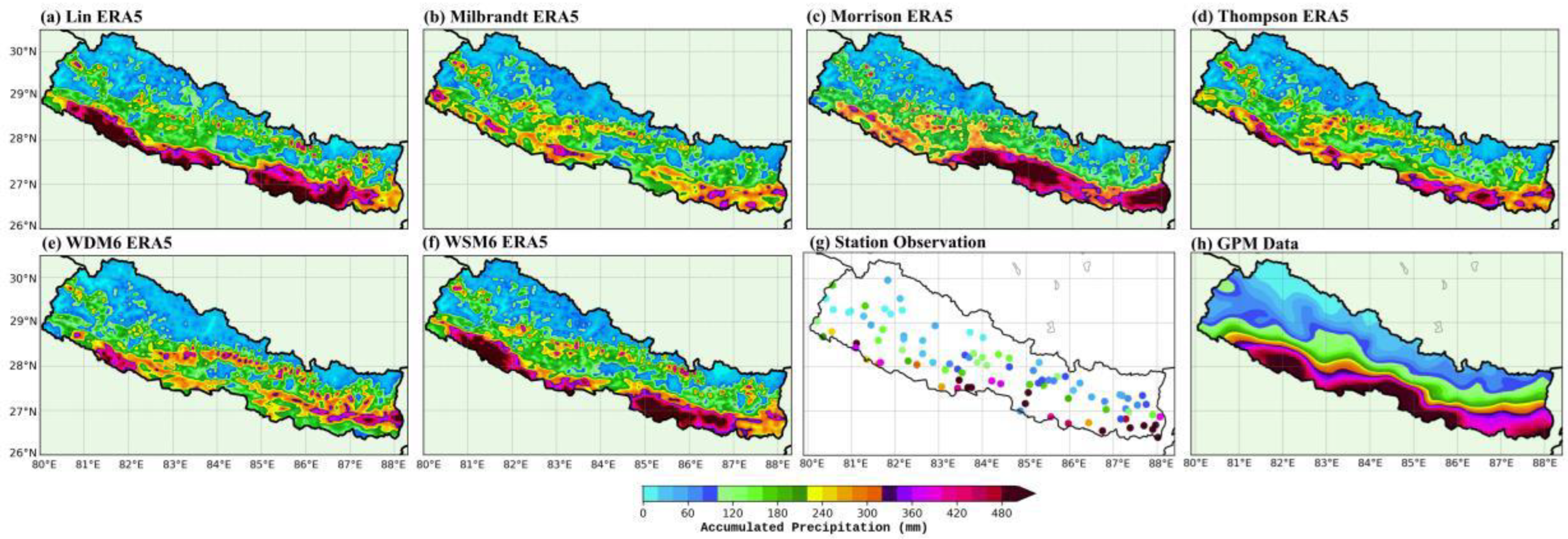
3.1. Simulations with Cumulus Parameterization off
3.2. Simulations with Cumulus Parameterization Turned on
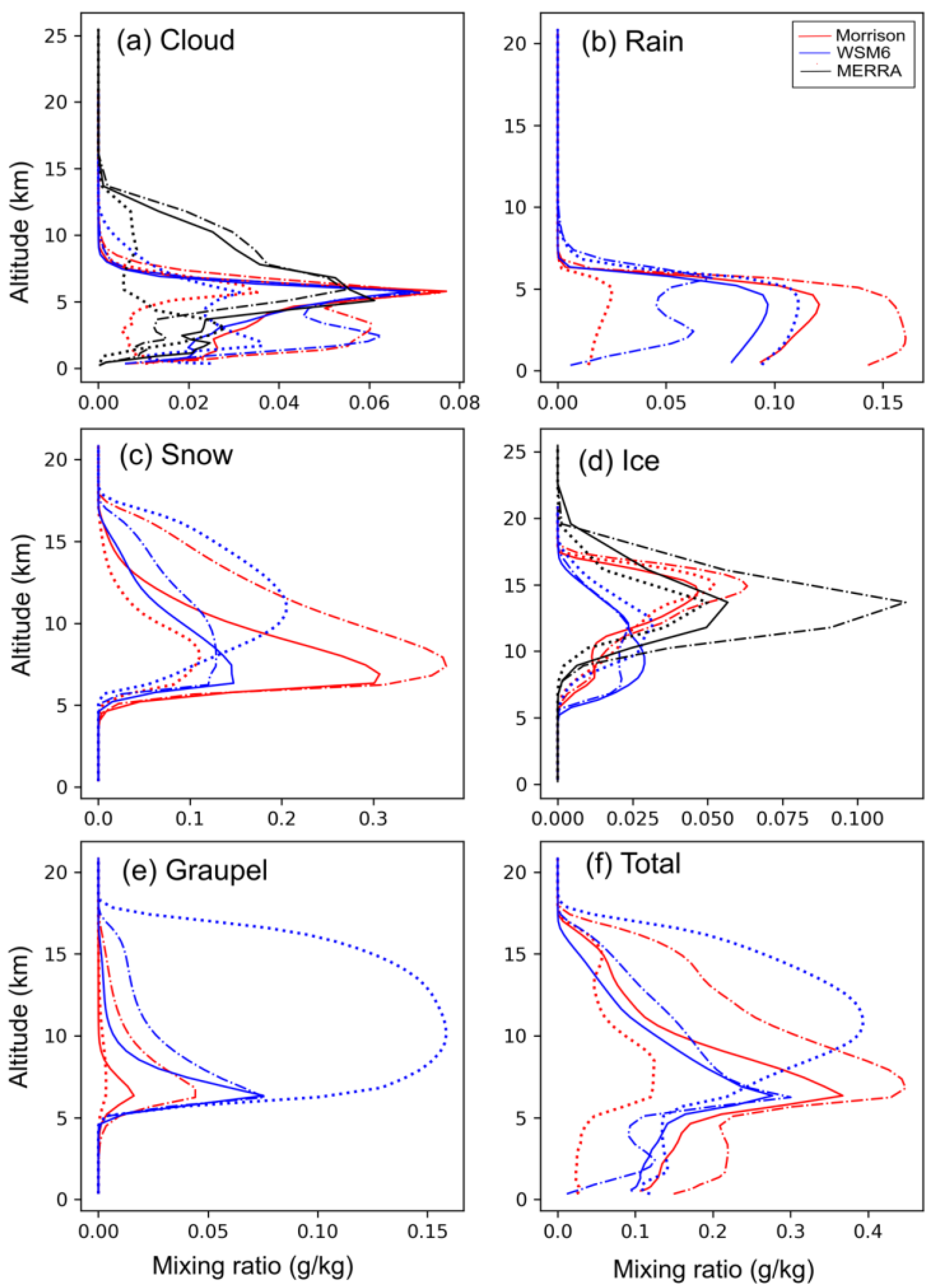
3.3. Cloud Microphysics
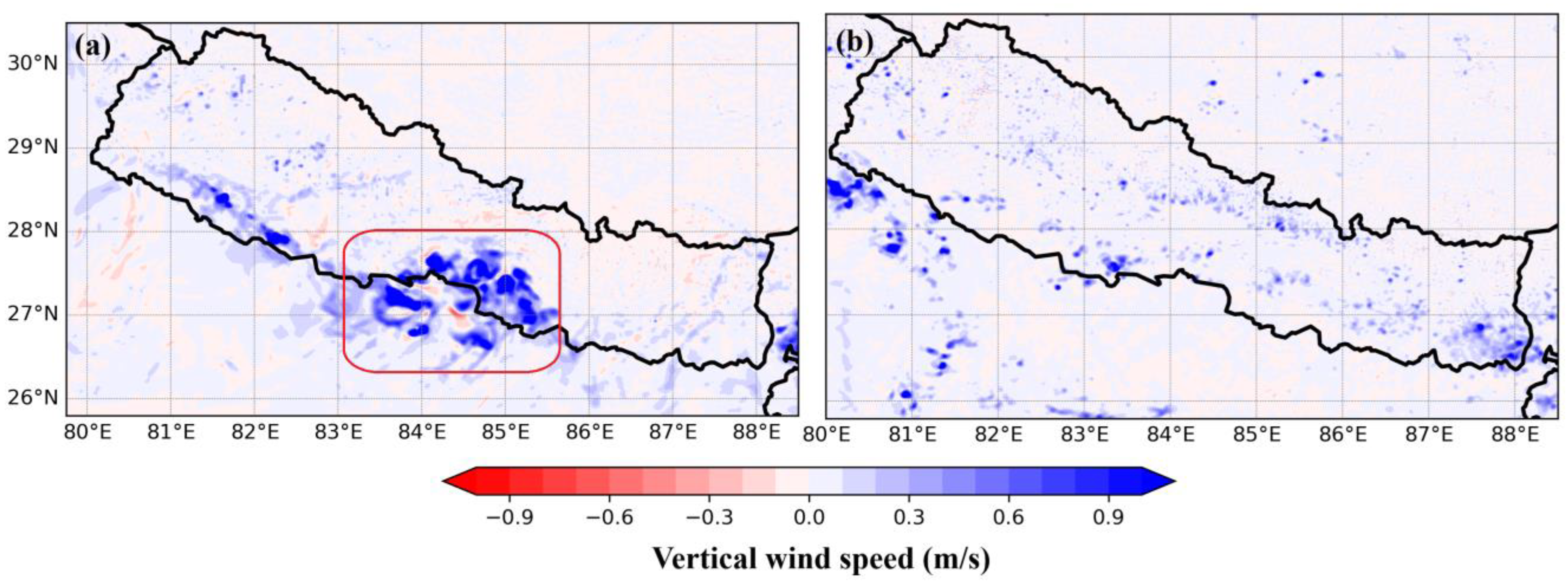
3.4. Role of Cumulus Scheme in Triggering Convection
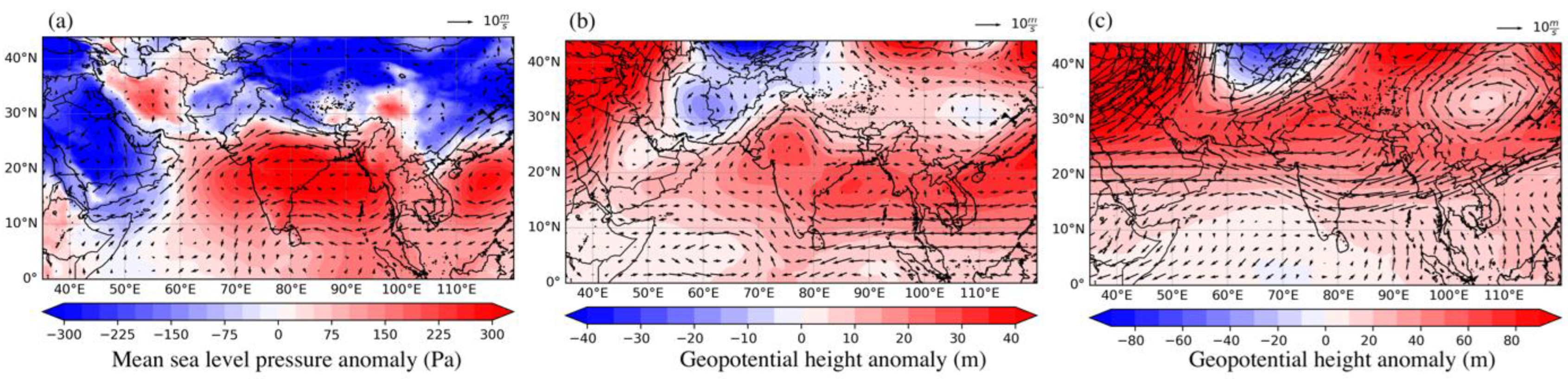
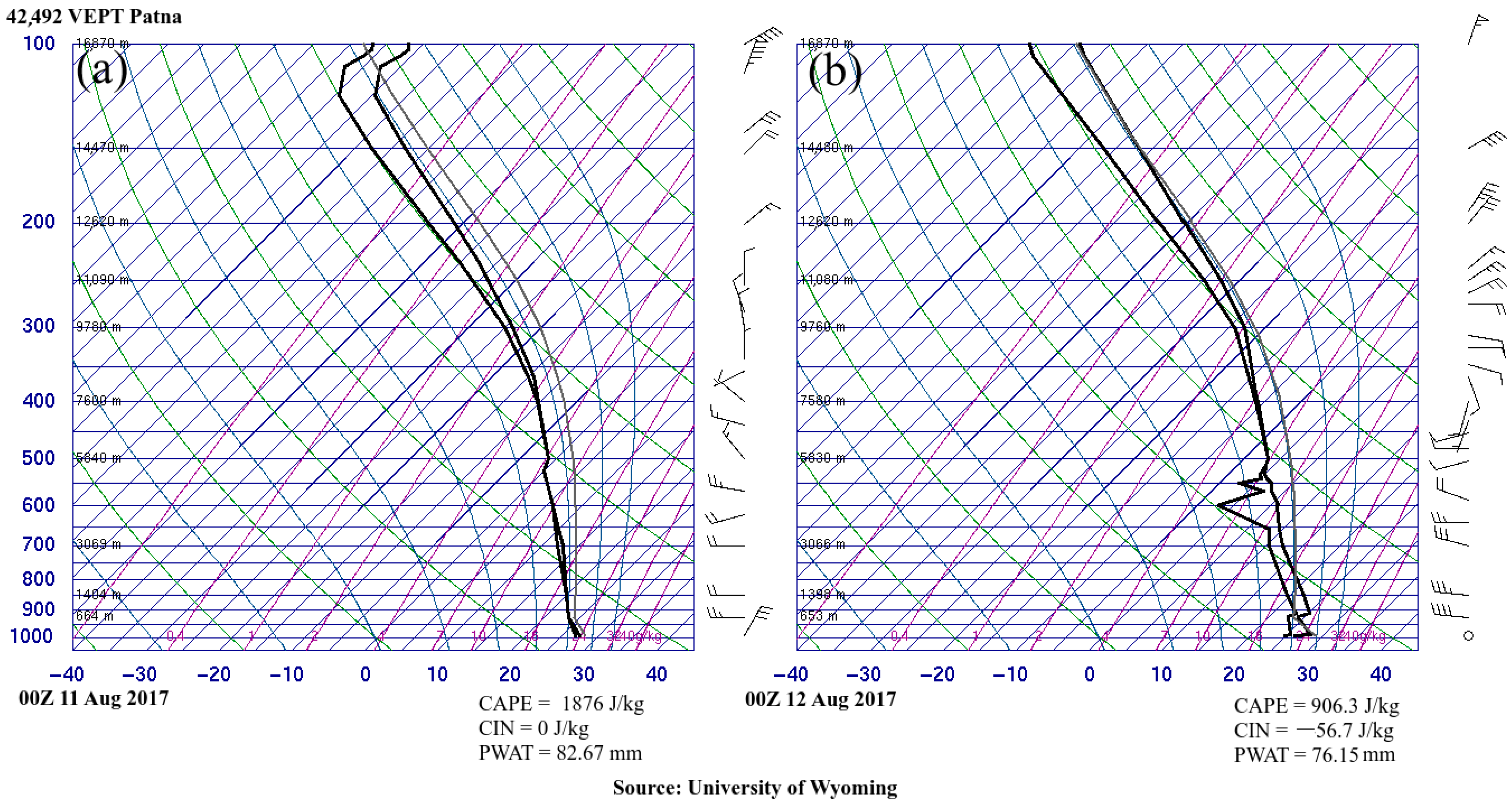
3.5. Synoptic Conditions Surrounding the Event
4. Discussion
Limitations of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karki, R.; ul Hasson, S.; Gerlitz, L.; Schickhoff, U.; Scholten, T.; Böhner, J. Quantifying the Added Value of Convection-Permitting Climate Simulations in Complex Terrain: A Systematic Evaluation of WRF over the Himalayas. Earth Syst. Dyn. 2017, 8, 507–528. [Google Scholar] [CrossRef]
- Bonekamp, P.N.J.; Collier, E.; Immerzeel, W.W. The Impact of Spatial Resolution, Land Use, and Spinup Time on Resolving Spatial Precipitation Patterns in the Himalayas. J. Hydrometeorol. 2018, 19, 1565–1581. [Google Scholar] [CrossRef]
- Barros, A.P.; Lang, T.J. Monitoring the Monsoon in the Himalayas: Observations in Central Nepal, June 2001. Mon. Weather Rev. 2003, 131, 1408–1427. [Google Scholar] [CrossRef]
- Lang, T.J.; Barros, A.P. Winter Storms in the Central Himalayas. J. Meteorol. Soc. Jpn. 2004, 82, 829–844. [Google Scholar] [CrossRef]
- Karki, R.; ul Hasson, S.; Gerlitz, L.; Talchabhadel, R.; Schenk, E.; Schickhoff, U.; Scholten, T.; Böhner, J. WRF-Based Simulation of an Extreme Precipitation Event over the Central Himalayas: Atmospheric Mechanisms and Their Representation by Microphysics Parameterization Schemes. Atmos. Res. 2018, 214, 21–35. [Google Scholar] [CrossRef]
- Orr, A.; Listowski, C.; Couttet, M.; Collier, E.; Immerzeel, W.; Deb, P.; Bannister, D. Sensitivity of Simulated Summer Monsoonal Precipitation in Langtang Valley, Himalaya, to Cloud Microphysics Schemes in WRF. J. Geophys. Res. Atmos. 2017, 122, 6298–6318. [Google Scholar] [CrossRef]
- Chawla, I.; Osuri, K.K.; Mujumdar, P.P.; Niyogi, D. Assessment of the Weather Research and Forecasting (WRF) Model for Simulation of Extreme Rainfall Events in the Upper Ganga Basin. Hydrol. Earth Syst. Sci. 2018, 22, 1095–1117. [Google Scholar] [CrossRef]
- Bonekamp, P.N.J.; de Kok, R.J.; Collier, E.; Immerzeel, W.W. Contrasting Meteorological Drivers of the Glacier Mass Balance Between the Karakoram and Central Himalaya. Front. Earth Sci. 2019, 7, 107. [Google Scholar] [CrossRef]
- Collier, E.; Immerzeel, W.W. High-Resolution Modeling of Atmospheric Dynamics in the Nepalese Himalaya. J. Geophys. Res. Atmos. 2015, 120, 9882–9896. [Google Scholar] [CrossRef]
- Tiwari, U.; Bush, A.B.G. A Relationship Between Ural-Siberian Blocking and Himalayan Weather Anomalies. Earth Space Sci. 2019, 6, 1633–1651. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Wang, W.; Huang, X.-Y.; Duda, M. A Description of the Advanced Research WRF Version 3; NCAR/TN-475+STR; University Corporation for Atmospheric Research (UCAR); National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2008; p. 1002 KB. [Google Scholar]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk Parameterization of the Snow Field in a Cloud Model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Palash, W.; Akanda, A.S.; Islam, S. The Record 2017 Flood in South Asia: State of Prediction and Performance of a Data-Driven Requisitely Simple Forecast Model. J. Hydrol. 2020, 589, 125190. [Google Scholar] [CrossRef]
- MoHA Nepal Disaster Report, 2017: The Road to Sendai; Government of Nepal: Kathmandu, Nepal, 2018.
- NPC Nepal Flood 2017: Post Flood Recovery Needs Assessment; Government of Nepal: Kathmandu, Nepal, 2017.
- Deng, A.; Stauffer, D.R. On Improving 4-Km Mesoscale Model Simulations. J. Appl. Meteorol. Climatol. 2006, 45, 361–381. [Google Scholar] [CrossRef]
- Gallus, W.A.; Harrold, M.A. Challenges in Numerical Weather Prediction of the 10 August 2020 Midwestern Derecho: Examples from the FV3-LAM. Weather. Forecast. 2023, 38, 1429–1445. [Google Scholar] [CrossRef]
- Amirudin, A.A.; Salimun, E.; Zuhairi, M.; Tangang, F.; Juneng, L.; Mohd, M.S.F.; Chung, J.X. The Importance of Cumulus Parameterization and Resolution in Simulating Rainfall over Peninsular Malaysia. Atmosphere 2022, 13, 1557. [Google Scholar] [CrossRef]
- Kotroni, V.; Lagouvardos, K. Evaluation of MM5 High-Resolution Real-Time Forecasts over the Urban Area of Athens, Greece. J. Appl. Meteorol. Climatol. 2004, 43, 1666–1678. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. Climatol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An Improved Mellor–Yamada Level-3 Model: Its Numerical Stability and Application to a Regional Prediction of Advection Fog. Bound.-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-Scale Measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather. Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Hong, S.-Y. Hongandlim-JKMS-2006. J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Lim, K.-S.S.; Hong, S.-Y. Development of an Effective Double-Moment Cloud Microphysics Scheme with Prognostic Cloud Condensation Nuclei (CCN) for Weather and Climate Models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Morrison, H.; Gettelman, A. A New Two-Moment Bulk Stratiform Cloud Microphysics Scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and Numerical Tests. J. Clim. 2008, 21, 3642–3659. [Google Scholar] [CrossRef]
- Morrison, H.; Curry, J.A.; Khvorostyanov, V.I. A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, K.; Hsu, R.; Joyce, R.; Xie, P. Integrated Multi-SatellitE Retrievals for GPM (IMERG), Version 4.4. NASA’s Precipitation Processing Center. Available online: https://gpm.nasa.gov/data/imerg (accessed on 31 March 2015).
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A Preliminary Assessment of GPM-Based Multi-Satellite Precipitation Estimates over a Monsoon Dominated Region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Sharma, S.; Chen, Y.; Zhou, X.; Yang, K.; Li, X.; Niu, X.; Hu, X.; Khadka, N. Evaluation of GPM-Era Satellite Precipitation Products on the Southern Slopes of the Central Himalayas Against Rain Gauge Data. Remote Sens. 2020, 12, 1836. [Google Scholar] [CrossRef]
- Field, P.R.; Broz̆ková, R.; Chen, M.; Dudhia, J.; Lac, C.; Hara, T.; Honnert, R.; Olson, J.; Siebesma, P.; de Roode, S.; et al. Exploring the Convective Grey Zone with Regional Simulations of a Cold Air Outbreak. Q. J. R. Meteorol. Soc. 2017, 143, 2537–2555. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, UK, 2023; ISBN 978-1-00-915789-6. [Google Scholar]




| Domain Configuration | |
| Horizontal grid spacing | 15 and 3 km |
| Vertical levels | 50 |
| Model top pressure | 50 hPa |
| Model Physics | |
| Radiation | Community Atmospheric Model |
| Cumulus | Kain–Fritsch [20] |
| Planetary boundary layer | MYNN level 2.5 [21] |
| Atmospheric surface layer | Revised MM5 [22] |
| Land surface model | NOAH-MP [23] |
| Dynamics | |
| Top boundary condition | Rayleigh damping |
| Diffusion | Calculated in physical space |
| Lateral Boundaries | |
| Forcing | ERA5 (31 km × 31 km) |
| Microphysics | Characteristics |
|---|---|
| Lin et al. scheme (Lin) [12] | Single-moment scheme with ice, snow, and graupel processes Six classes of moisture variables: water vapour, cloud water, rain, cloud ice, snow, and graupel |
| WRF Single-Moment 6-class scheme (WSM6) [25] | Single-moment scheme with ice, snow, and graupel processes Six classes of moisture variables scheme like Lin Sedimentation of precipitating particles is computed with a Lagrangian scheme |
| WRF Double-Moment 6-class scheme (WDM6) [26] | Double-moment scheme with ice, snow, and graupel processes Six classes of moisture variables like Lin and WSM6 Sedimentation of precipitation particle computed by a Lagrangian scheme Suitable for cloud and cloud condensation nuclei (CCN) for warm rain processes |
| New Thompson et al. scheme (Thompson) [27] | Double-moment bulk microphysics scheme for cloud ice and rain processes, while single-moment for cloud water, snow, and graupel processes |
| Morrison double-moment scheme (Morrison) [28,29] | Double-moment bulk microphysics scheme with ice, snow, and graupel processes |
| Milbrandt–Yau Double-Moment 7-class scheme (Milbrandt) [30] | Double-moment microphysics scheme with 12 prognostic variables (besides water vapour) Computes graupel and hail separately |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, U.; Bush, A.B.G. Significance of Cloud Microphysics and Cumulus Parameterization Schemes in Simulating an Extreme Flood-Producing Precipitation Event in the Central Himalaya. Atmosphere 2025, 16, 298. https://doi.org/10.3390/atmos16030298
Tiwari U, Bush ABG. Significance of Cloud Microphysics and Cumulus Parameterization Schemes in Simulating an Extreme Flood-Producing Precipitation Event in the Central Himalaya. Atmosphere. 2025; 16(3):298. https://doi.org/10.3390/atmos16030298
Chicago/Turabian StyleTiwari, Ujjwal, and Andrew B. G. Bush. 2025. "Significance of Cloud Microphysics and Cumulus Parameterization Schemes in Simulating an Extreme Flood-Producing Precipitation Event in the Central Himalaya" Atmosphere 16, no. 3: 298. https://doi.org/10.3390/atmos16030298
APA StyleTiwari, U., & Bush, A. B. G. (2025). Significance of Cloud Microphysics and Cumulus Parameterization Schemes in Simulating an Extreme Flood-Producing Precipitation Event in the Central Himalaya. Atmosphere, 16(3), 298. https://doi.org/10.3390/atmos16030298





