The Sensitivity of Heatwave Climatology to Input Gridded Datasets: A Case Study of Ukraine
Abstract
1. Introduction
2. Materials and Methods
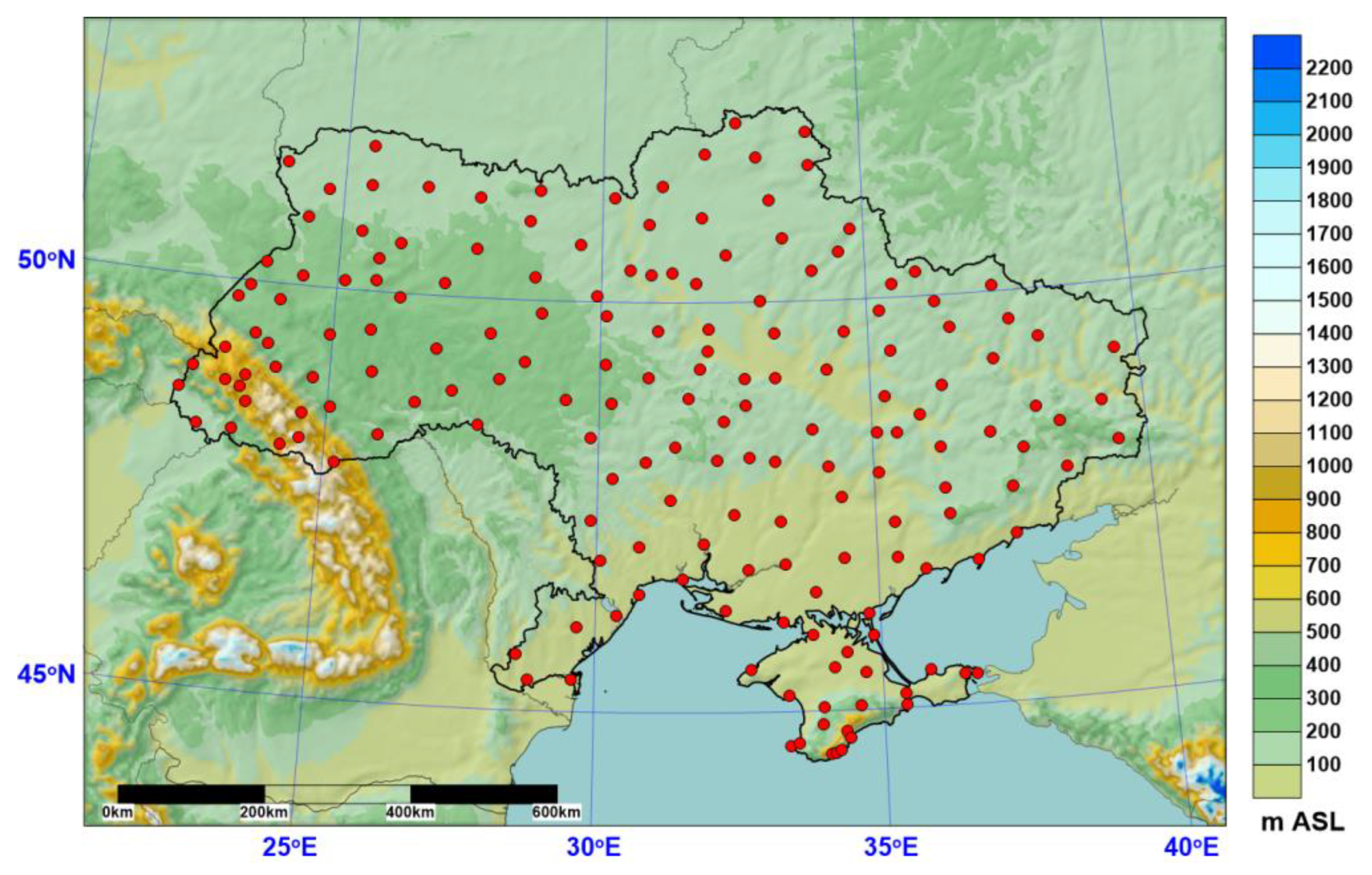
2.1. Domain and Reference Station Data
2.2. Gridded Datasets Used for HW Metric Calculations
2.3. Heatwave Calculation Methodology
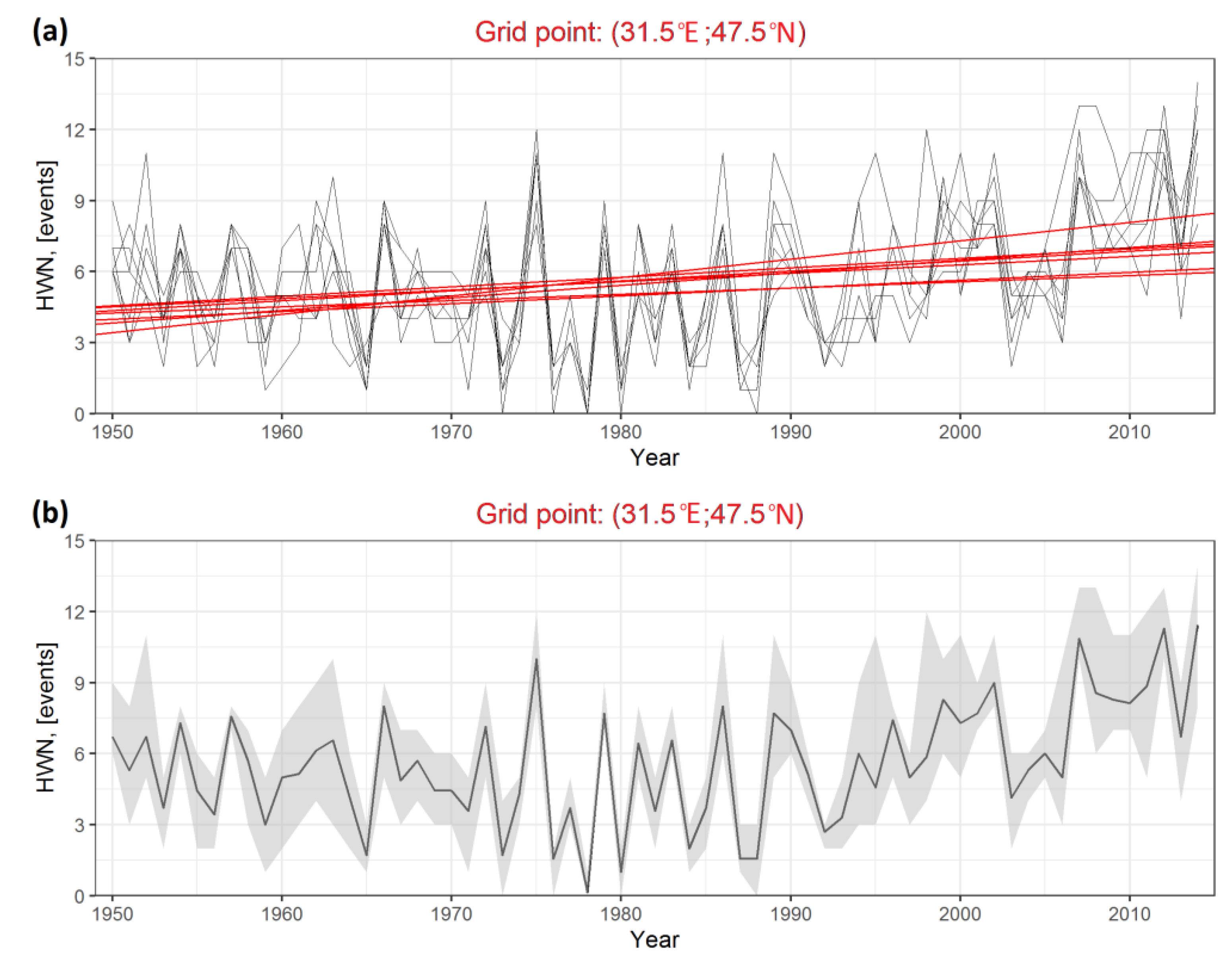
2.4. Quantification of the Sensitivity of HW Metrics to Input Gridded Datasets and Their Comparison with Station-Based Calculations
3. Results and Discussion
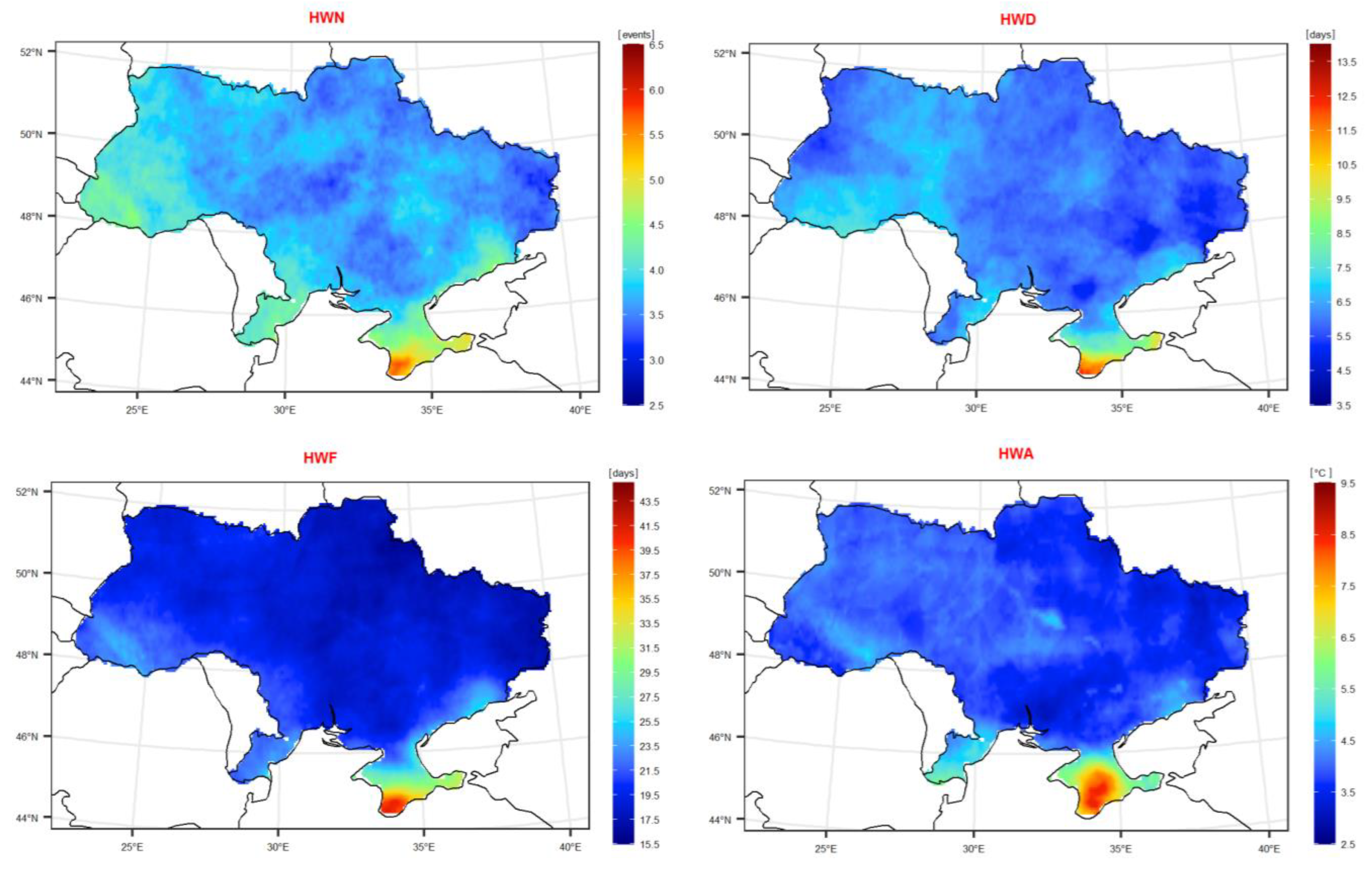
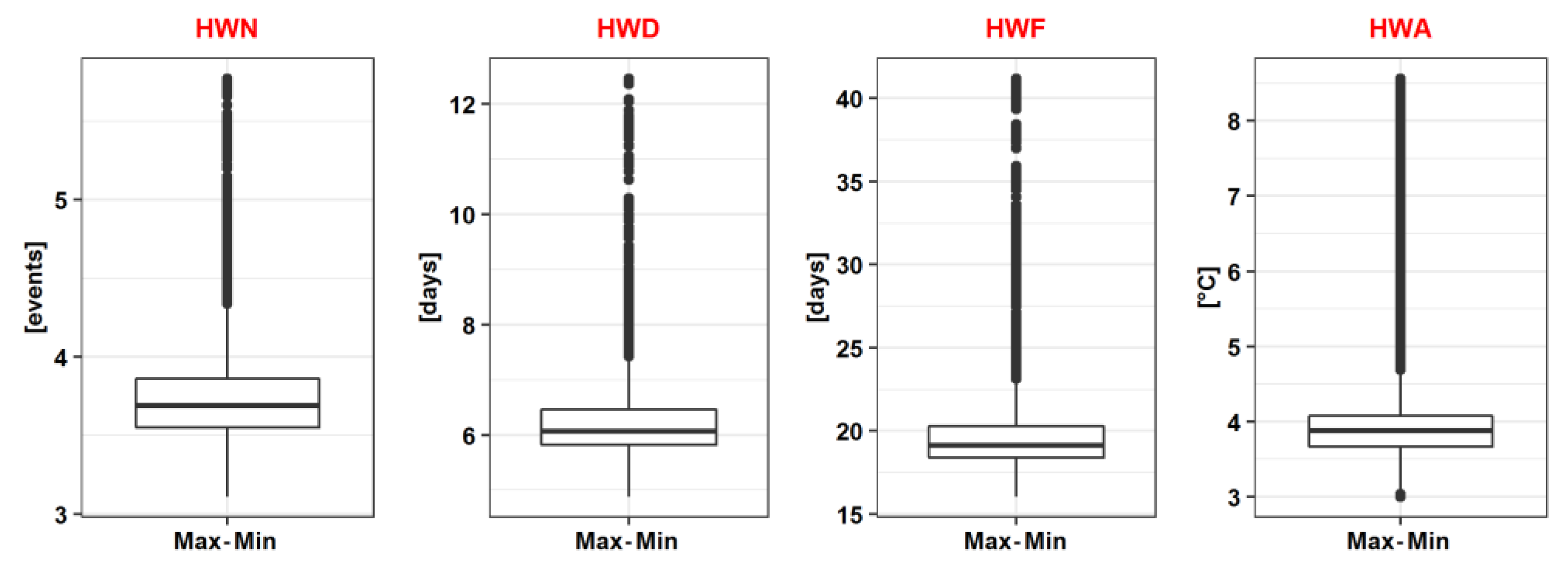
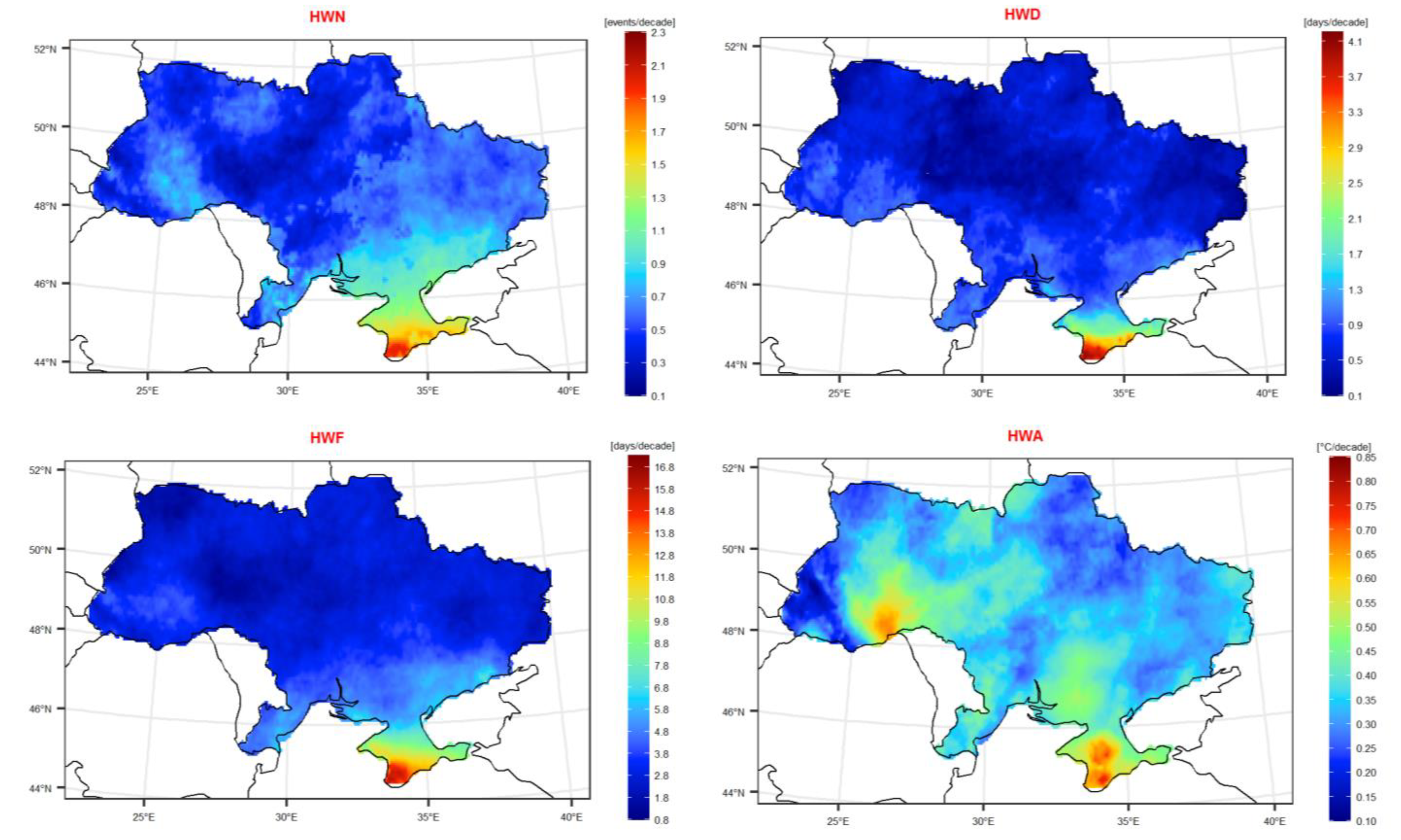
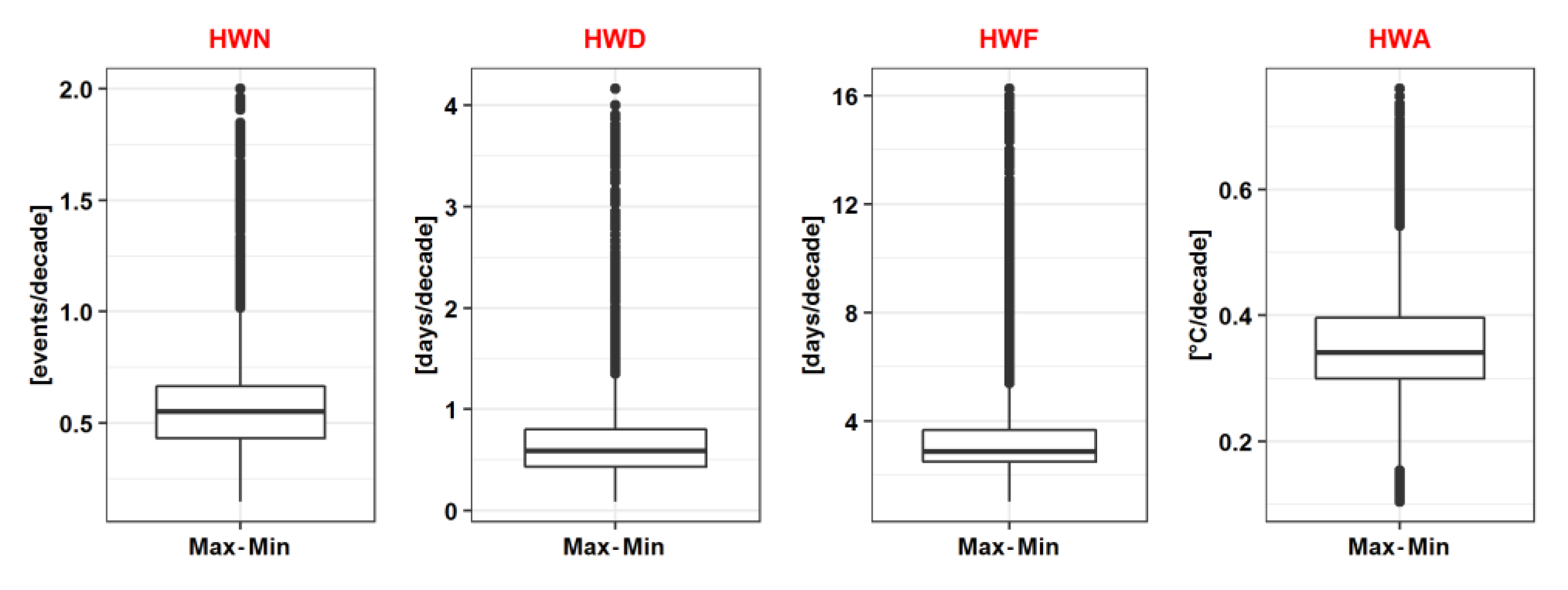
3.1. Absolute HW Metrics Sensitivity/Uncertainty Quantification
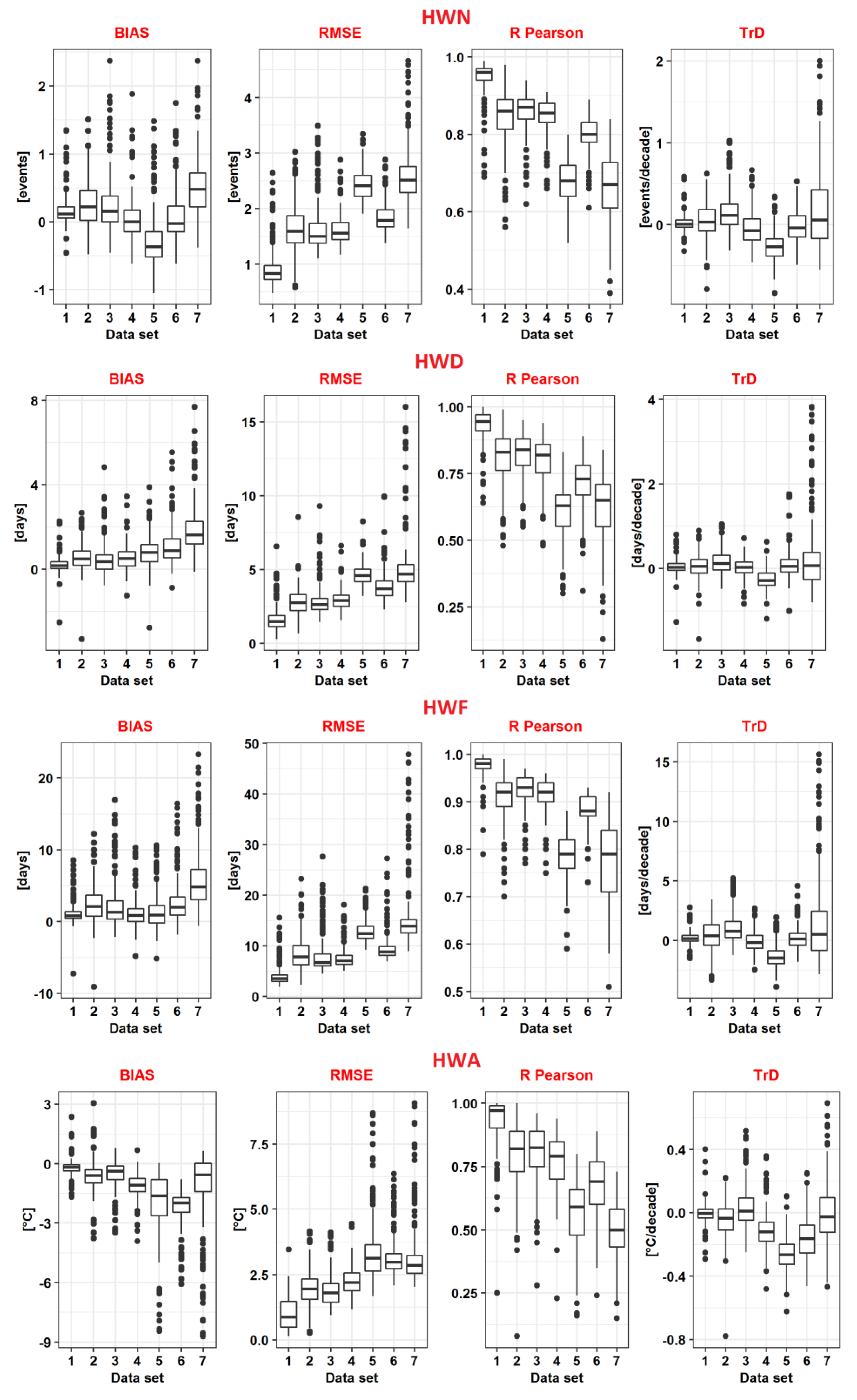
3.2. Verification of HW Metrics Against the Reference Station Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perkins, S.E.; Alexander, L.V. On the measurement of heat waves. J. Clim. 2013, 26, 4500–4517. [Google Scholar] [CrossRef]
- Campbell, S.; Remenyi, T.A.; White, C.J.; Johnston, F.H. Heatwave and health impact research: A global review. Health Place 2018, 53, 210–218. [Google Scholar] [CrossRef]
- Perkins-Kirkpatrick, S.E.; Lewis, S.C. Increasing trends in regional heatwaves. Nat. Commun. 2020, 11, 3357. [Google Scholar] [CrossRef] [PubMed]
- Yadav, N.; Rajendra, K.; Awasthi, A.; Singh, C.; Bhushan, B. Systematic exploration of heat wave impact on mortality and urban heat island: A review from 2000 to 2022. Urban Clim. 2023, 51, 101622. [Google Scholar] [CrossRef]
- Shevchenko, O.; Lee, H.; Snizhko, S.; Mayer, H. Long-term analysis of heat waves in Ukraine. Int. J. Climatol. 2014, 34, 1642–1650. [Google Scholar] [CrossRef]
- Spinoni, J.; Lakatos, M.; Szentimrey, T.; Bihari, Z.; Szalai, S.; Vogt, J.; Antofie, T. Heat and cold waves trends in the Carpathian Region from 1961 to 2010. Int. J. Climatol. 2015, 35, 4197–4209. [Google Scholar] [CrossRef]
- Lhotka, O.; Kyselý, J. The 2021 European heat wave in the context of past major heat waves. Earth Space Sci. 2022, 9, e2022EA002567. [Google Scholar] [CrossRef]
- Serrano-Notivoli, R.; Lemus-Canovas, M.; Barrao, S.; Sarricolea, P.; Meseguer-Ruiz, O.; Tejedor, E. Heat and cold waves in mainland Spain: Origins, characteristics, and trends. Weather Clim. Extrem. 2022, 37, 100471. [Google Scholar] [CrossRef]
- Cimolai, C.; Aguilar, E. Assessing Argentina’s heatwave dynamics (1950–2022): A comprehensive analysis of temporal and spatial variability using ERA5-LAND. Theor. Appl. Climatol. 2024, 155, 4925–4940. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Molina, M.O.; Sánchez, E.; Gutiérrez, C. Future heat waves over the Mediterranean from an Euro-CORDEX regional climate model ensemble. Sci. Rep. 2020, 10, 8801. [Google Scholar] [CrossRef] [PubMed]
- Ramarao, M.V.S.; Arunachalam, S.; Sánchez, B.N.; Schinasi, L.H.; Bakhtsiyarava, M.; Caiaffa, W.T.; Dronova, I.; O’neill, M.S.; Avila-Palencia, I.; Gouveia, N.; et al. Projected changes in heatwaves over Central and South America using high-resolution regional climate simulations. Sci. Rep. 2024, 14, 23145. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, A.; Zhang, T.; Pan, P.; Ren, Y. Projected increase in heatwaves under 1.5 and 2.0 °C warming levels will increase the socio-economic exposure across China by the late 21st century. Atmosphere 2024, 15, 900. [Google Scholar] [CrossRef]
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. WMO Guidelines on Climate Metadata and Homogenization; WCDMP No. 53, WMO-TD No. 1186; WMO: Geneva, Switzerland, 2003; p. 55. [Google Scholar]
- Amou, M.; Gyilbag, A.; Demelash, T.; Xu, Y. Heatwaves in Kenya 1987–2016: Facts from CHIRTS High Resolution Satellite Remotely Sensed and Station Blended Temperature Dataset. Atmosphere 2021, 12, 37. [Google Scholar] [CrossRef]
- Oliveira, A.; Lopes, A.; Correia, E. Annual summaries dataset of Heatwaves in Europe, as defined by the Excess Heat Factor. Data Brief 2022, 4, 108511. [Google Scholar] [CrossRef] [PubMed]
- Becker, F.N.; Fink, A.H.; Bissolli, P.; Pinto, J.G. Towards a more comprehensive assessment of the intensity of historical European heat waves (1979–2019). Atmos. Sci. Lett. 2022, 23, e1120. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M.; Matos, J.P. ERA5-Land reanalysis temperature data addressing heatwaves in Portugal. In INCREaSE 2023. Advances in Sustainability Science and Technology; Semião, J.F.L.C., Sousa, N.M.S., da Cruz, R.M.S., Prates, G.N.D., Eds.; Springer: Cham, Switzerland, 2023; pp. 81–94. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M.; Moreira Freitas, L.M.; Gharbia, S. Addressing the spatiotemporal patterns of heatwaves in Portugal with a validated ERA5-Land dataset (1980–2021). Water 2023, 15, 3102. [Google Scholar] [CrossRef]
- Labban, A.; Morsy, M.; Abdeldym, A.; Abdel Basset, H.; Al-Mutairi, M. Assessment of changes in heatwave aspects over Saudi Arabia during the last four decades. Atmosphere 2023, 14, 1667. [Google Scholar] [CrossRef]
- Fiddes, J.; Gruber, S. TopoSCALE v.1.0: Downscaling gridded climate data in complex terrain. Geosci. Model Dev. 2014, 7, 387–405. [Google Scholar] [CrossRef]
- Frustaci, G.; Pilati, S.; Lavecchia, C.; Montoli, E.M. High-Resolution Gridded Air Temperature Data for the Urban Environment: The Milan Data Set. Forecasting 2022, 4, 238–261. [Google Scholar] [CrossRef]
- Sterl, A. On the (In)Homogeneity of Reanalysis Products. J. Clim. 2004, 17, 3866–3873. [Google Scholar] [CrossRef]
- Ferguson, C.R.; Villarini, G. An evaluation of the statistical homogeneity of the Twentieth Century Reanalysis. Clim. Dyn. 2014, 42, 2841–2866. [Google Scholar] [CrossRef]
- Coughlan de Perez, E.; Arrighi, J.; Marunye, J. Challenging the universality of heatwave definitions: Gridded temperature discrepancies across climate regions. Clim. Change 2023, 176, 167. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, X.; Cleverly, J.; Huete, A.; Zhang, H.; Yu, Q. Heat wave tracker: A multi-method, multi-source heat wave measurement toolkit based on Google Earth Engine. Environ. Model. Softw. 2022, 147, 105255. [Google Scholar] [CrossRef]
- Velikou, K.; Lazoglou, G.; Tolika, K.; Anagnostopoulou, C. Reliability of the ERA5 in replicating mean and extreme temperatures across Europe. Water 2022, 14, 543. [Google Scholar] [CrossRef]
- Sidău, M.R.; Croitoru, A.-E.; Alexandru, D.-E. Comparative Analysis between Daily Extreme Temperature and Precipitation Values Derived from Observations and Gridded Datasets in North-Western Romania. Atmosphere 2021, 12, 361. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Donat, M.G.; Alexander, L.V. Comparing extremes indices in recent observational and reanalysis products. Front. Clim. 2022, 4, 989505. [Google Scholar] [CrossRef]
- Lipinsky, V.M.; Dyachuk, V.A.; Babichenko, V.M. (Eds.) Climate of Ukraine; Vydavnytstvo Raevskogo: Kyiv, Ukraine, 2003; p. 343. ISBN 966-7016-18-8. (In Ukrainian) [Google Scholar]
- Skrynyk, O.Y.; Sidenko, V.; Aguilar, E.; Guijarro, J.; Skrynyk, O.A.; Palamarchuk, L.; Oshurok, D.; Osypov, V.; Osadchyi, V. Data quality control and homogenization of daily precipitation and air temperature (mean, max and min) time series of Ukraine. Int. J. Climatol. 2023, 43, 4166–4182. [Google Scholar] [CrossRef]
- Osadchyi, V.; Skrynyk, O.Y.; Sidenko, V.; Aguilar, E.; Guijarro, J.; Szentimrey, T.; Skrynyk, O.A.; Palamarchuk, L.; Oshurok, D.; Kravchenko, I.; et al. Gridded data of daily atmospheric precipitation and minimum, mean and maximum air temperature for Ukraine, 1946–2020. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. [Google Scholar] [CrossRef]
- Aguilar, E. INDECIS Quality Control Software and Manual: INQC, Beta Version. 2019. Available online: http://www.indecis.eu/docs/Deliverables/Deliverable_3.1.a.pdf (accessed on 30 November 2024).
- Guijarro, J.A. Homogenization of Climatic Series with Climatol. Version 4.0.7. Guide. 2023. Available online: https://www.climatol.eu/climatol4.1.2-en.pdf (accessed on 30 November 2024).
- ClimUAd: Ukrainian Gridded Daily Air Temperature (Min, Max, Mean) and Atmospheric Precipitation Data (1946–2020). Available online: https://www.uhmi.org.ua/data_repo/ClimUAd_Ukrainian_gridded_daily (accessed on 30 November 2024). [CrossRef]
- Cornes, R.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An ensemble version of the E-OBS temperature and precipitation datasets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
- Slivinski, L.C.; Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Giese, B.S.; McColl, C.; Allan, R.; Yin, X.; Vose, R.; Titchner, H.; et al. Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteorol. Soc. 2019, 145, 2876–2908. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–470. [Google Scholar] [CrossRef]
- Szentimrey, T.; Bihari, Z. Manual of Interpolation Software MISHv1.03; Hungarian Meteorological Service: Budapest, Hungary, 2014. [Google Scholar]
- Schulzweida, U.; Climate Data Operators (CDO). Max-Plank Institute for Meteorology. 2023. Available online: https://code.mpimet.mpg.de/projects/cdo (accessed on 30 November 2024).
- Tong, S.; Wang, X.Y.; Barnett, A.G. Assessment of heat-related health impacts in Brisbane, Australia: Comparison of different heatwave definitions. PLoS ONE 2010, 5, e12155. [Google Scholar] [CrossRef] [PubMed]
- Perkins, S.E. A review on the scientific understanding of heatwaves—Their measurement, driving mechanisms, and changes at the global scale. Atmos. Res. 2015, 164–165, 242–267. [Google Scholar] [CrossRef]
- Awasthi, A.; Vishwakarma, K.; Pattnayak, K.C. Retrospection of heatwave and heat index. Theor. Appl. Climatol. 2022, 147, 589–604. [Google Scholar] [CrossRef] [PubMed]
- McGregor, G. Heatwaves, Cause, Consequences and Responses; Springer Nature: Cham, Switzerland, 2024; ISBN 978-3-031-69906-1. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Smit, A.J. heatwaveR: A central algorithm for the detection of heatwaves and cold-spells. J. Open Source Softw. 2017, 3, 1821. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Elsevier Academic Press: Cambridge, MA, USA, 2006; p. 627. ISBN 978-0-12-751966-1. [Google Scholar]

| # | Name | Temporal Coverage | Spatial Resolution, lon × lat | Reference |
|---|---|---|---|---|
| 1 | ClimUAd | 1946–2020 | 0.1° × 0.1° | [32,35] |
| 2 | E-OBS | 1950 to present | 0.1° × 0.1° | [36] |
| 3 | ERA5 | 1940 to present | 0.25° × 0.25° | [37] |
| 4 | ERA5-Land | 1950 to present | 0.1° × 0.1° | [38] |
| 5 | 20CRV2c | 1850–2014 | 2° × 2° | [39] |
| 6 | 20CRV3 | 1806–2015 | 1° × 1° | [39,40] |
| 7 | NCEP-NCAR R1 | 1948 to present | 2.5° × 2.5° | [41] |
| HW Metric | Verification Statistic | Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| ClimUAd | E-OBS | ERA5 | ERA5-Land | 20CRV2c | 20CRV3 | NCEP-NCAR R1 | ||
| HWN, [events] | BIAS | 0.16 | 0.26 | 0.25 | 0.05 | −0.29 | 0.07 | 0.49 |
| RMSE | 0.92 | 1.64 | 1.63 | 1.64 | 2.44 | 1.85 | 2.61 | |
| R Pearson | 0.95 | 0.85 | 0.86 | 0.84 | 0.68 | 0.80 | 0.66 | |
| TrD | 0.02 | 0.03 | 0.14 | −0.05 | −0.26 | −0.03 | 0.20 | |
| HWD, [days] | BIAS | 0.23 | 0.58 | 0.50 | 0.53 | 0.83 | 1.11 | 1.86 |
| RMSE | 1.62 | 2.83 | 2.89 | 2.97 | 4.63 | 3.89 | 5.22 | |
| R Pearson | 0.93 | 0.81 | 0.82 | 0.80 | 0.61 | 0.71 | 0.62 | |
| TrD | 0.04 | 0.06 | 0.16 | 0.02 | −0.27 | 0.08 | 0.26 | |
| HWF, [days] | BIAS | 1.12 | 2.45 | 2.24 | 1.18 | 1.49 | 2.87 | 5.76 |
| RMSE | 4.04 | 8.52 | 8.21 | 7.60 | 13.08 | 9.82 | 15.81 | |
| R Pearson | 0.97 | 0.91 | 0.92 | 0.91 | 0.78 | 0.88 | 0.77 | |
| TrD | 0.17 | 0.39 | 0.99 | −0.14 | −1.37 | 0.16 | 1.56 | |
| HWA, [°C] | BIAS | −0.19 | −0.64 | −0.55 | −1.13 | −1.98 | −2.29 | −1.14 |
| RMSE | 0.97 | 1.95 | 1.89 | 2.25 | 3.41 | 3.20 | 3.25 | |
| R Pearson | 0.93 | 0.80 | 0.81 | 0.77 | 0.56 | 0.68 | 0.49 | |
| TrD | −0.01 | −0.05 | 0.03 | −0.10 | −0.26 | −0.16 | 0.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skrynyk, O.; Aguilar, E.; Cimolai, C. The Sensitivity of Heatwave Climatology to Input Gridded Datasets: A Case Study of Ukraine. Atmosphere 2025, 16, 289. https://doi.org/10.3390/atmos16030289
Skrynyk O, Aguilar E, Cimolai C. The Sensitivity of Heatwave Climatology to Input Gridded Datasets: A Case Study of Ukraine. Atmosphere. 2025; 16(3):289. https://doi.org/10.3390/atmos16030289
Chicago/Turabian StyleSkrynyk, Oleg, Enric Aguilar, and Caterina Cimolai. 2025. "The Sensitivity of Heatwave Climatology to Input Gridded Datasets: A Case Study of Ukraine" Atmosphere 16, no. 3: 289. https://doi.org/10.3390/atmos16030289
APA StyleSkrynyk, O., Aguilar, E., & Cimolai, C. (2025). The Sensitivity of Heatwave Climatology to Input Gridded Datasets: A Case Study of Ukraine. Atmosphere, 16(3), 289. https://doi.org/10.3390/atmos16030289






