Optimizing the Architecture of a Quantum–Classical Hybrid Machine Learning Model for Forecasting Ozone Concentrations: Air Quality Management Tool for Houston, Texas
Abstract
1. Introduction
- Proposing a novel air quality forecasting tool based on quantum machine learning.
- Addressing the information gap regarding using hybrid QML models for air quality modeling.
- Assessing distinct topologies for the hybrid approach; several configurations for the QML architecture must be investigated, including different preprocessing techniques for normalization.
- Validating the proposed approach for predicting ozone concentrations in the atmosphere up to 6 h ahead.
2. Methodology
2.1. Important Quantum Mechanics Concepts
2.1.1. Superposition
2.1.2. Measurement of a Quantum System
2.1.3. Entanglement
2.1.4. Interference
2.2. Quantum Computing
2.3. Quantum Neural Networks
2.3.1. Feature Map
2.3.2. Ansatz
2.3.3. Ansatz Optimization Strategy
2.3.4. Measurement
2.3.5. On the Use of Simulated Quantum Circuits
2.4. Graph-Based Deep Learning
2.5. Validation Study Site and Database
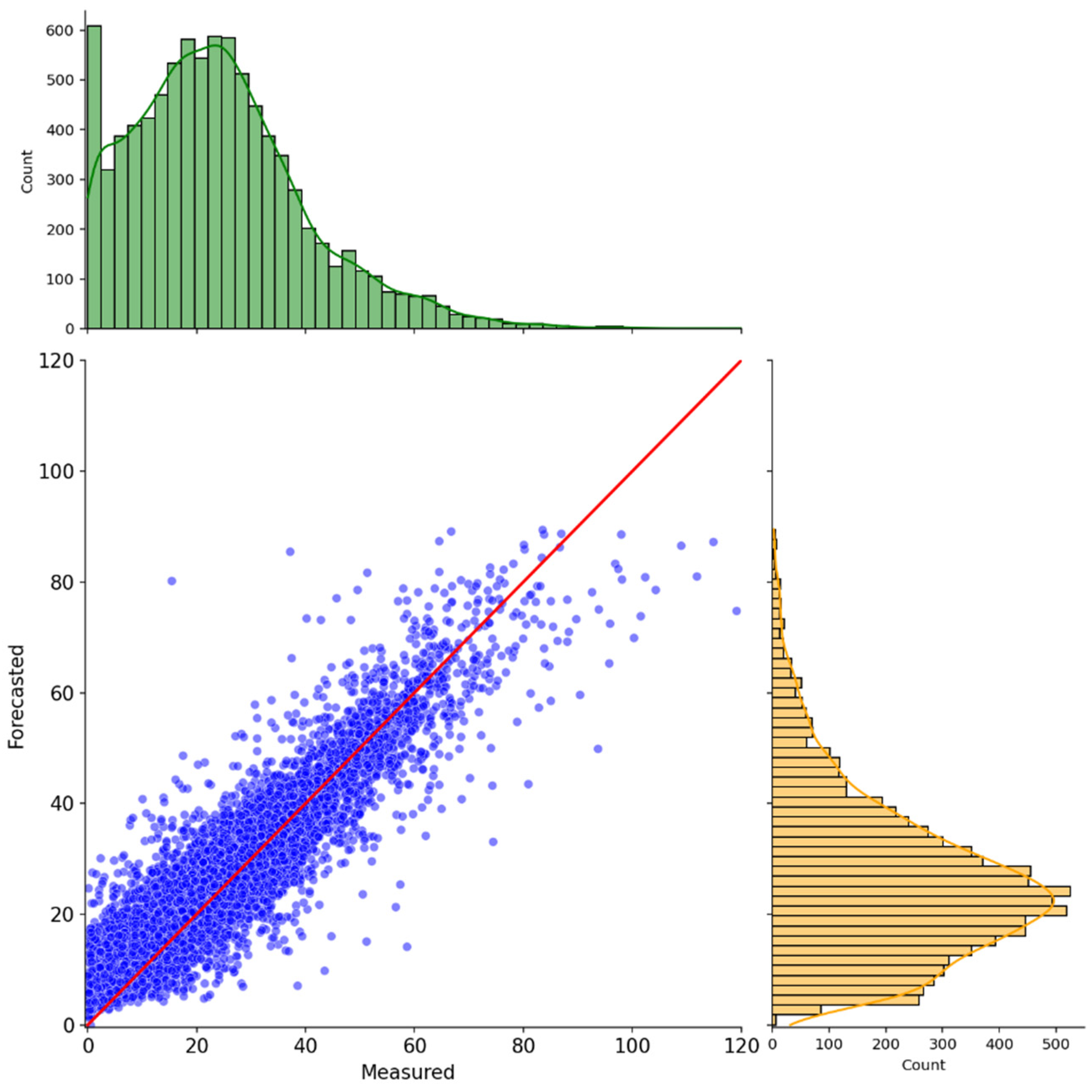
2.6. Data Normalization
3. Results
3.1. The Initial Hybrid GNN-SAGE-QNN Architecture
3.2. Topological Investigation of the Dense Layer of the GNN-SAGE-QNN Model
3.3. Investigation of the Normalization Approach and Ansatz Repetitions
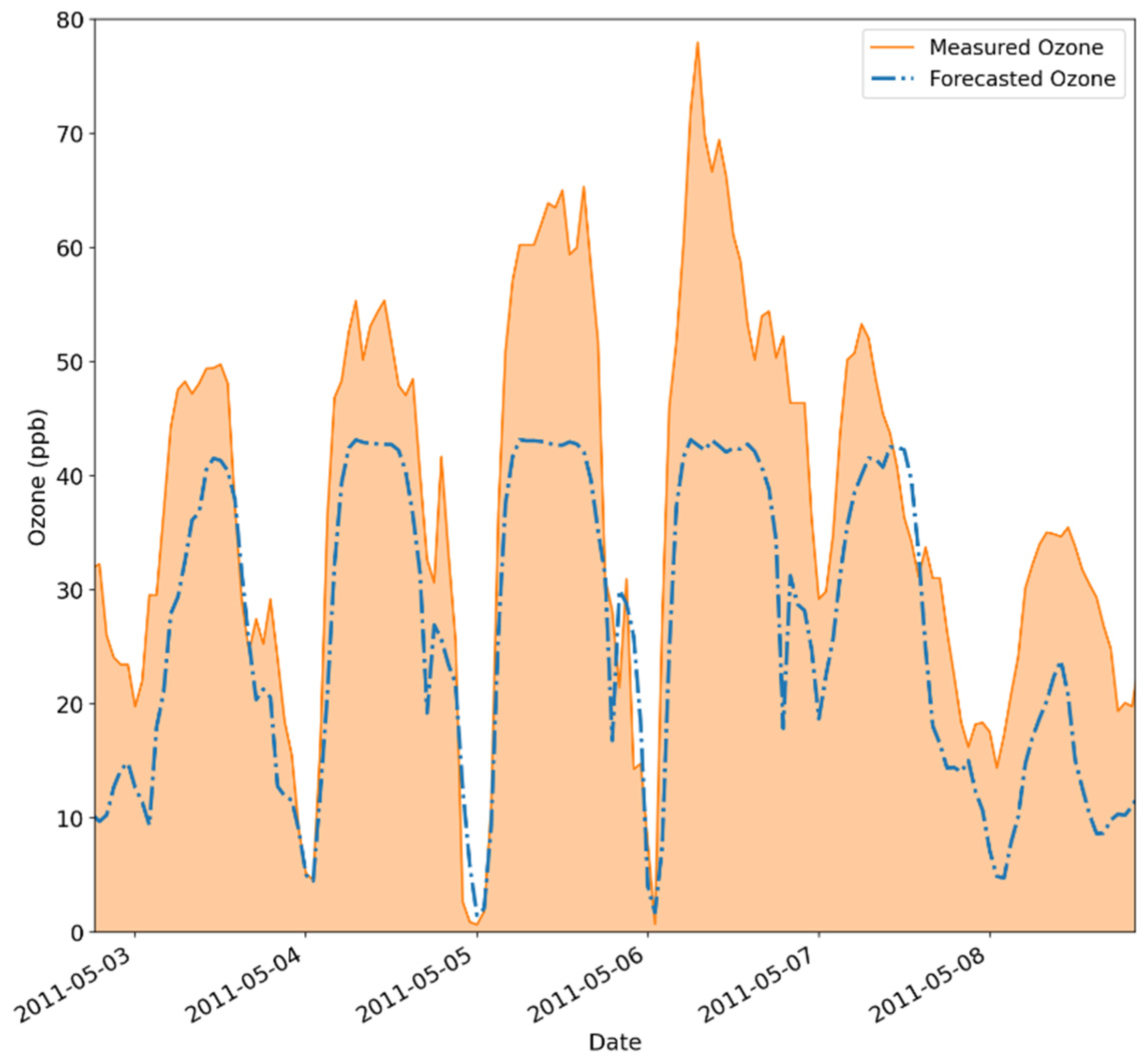
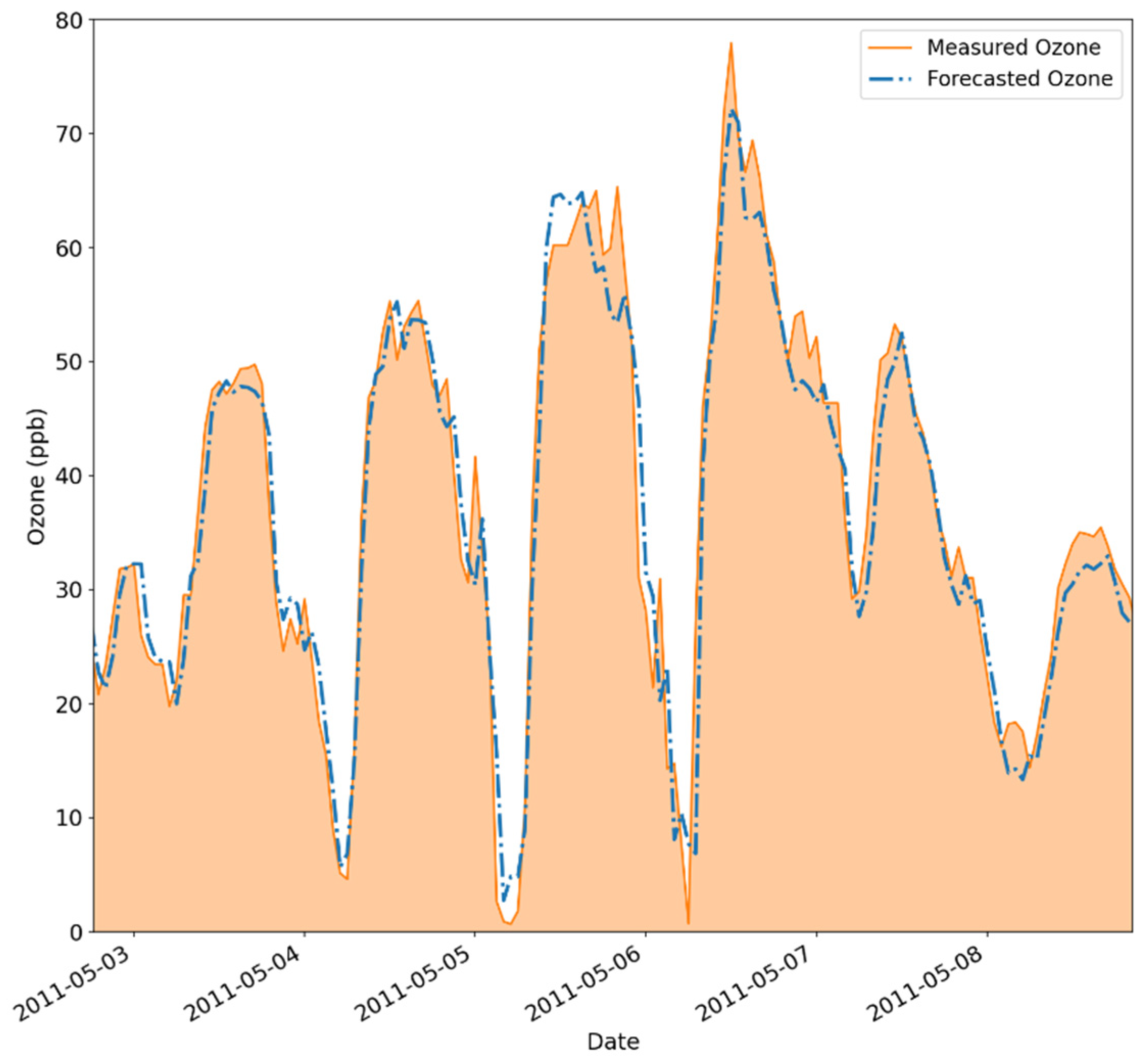
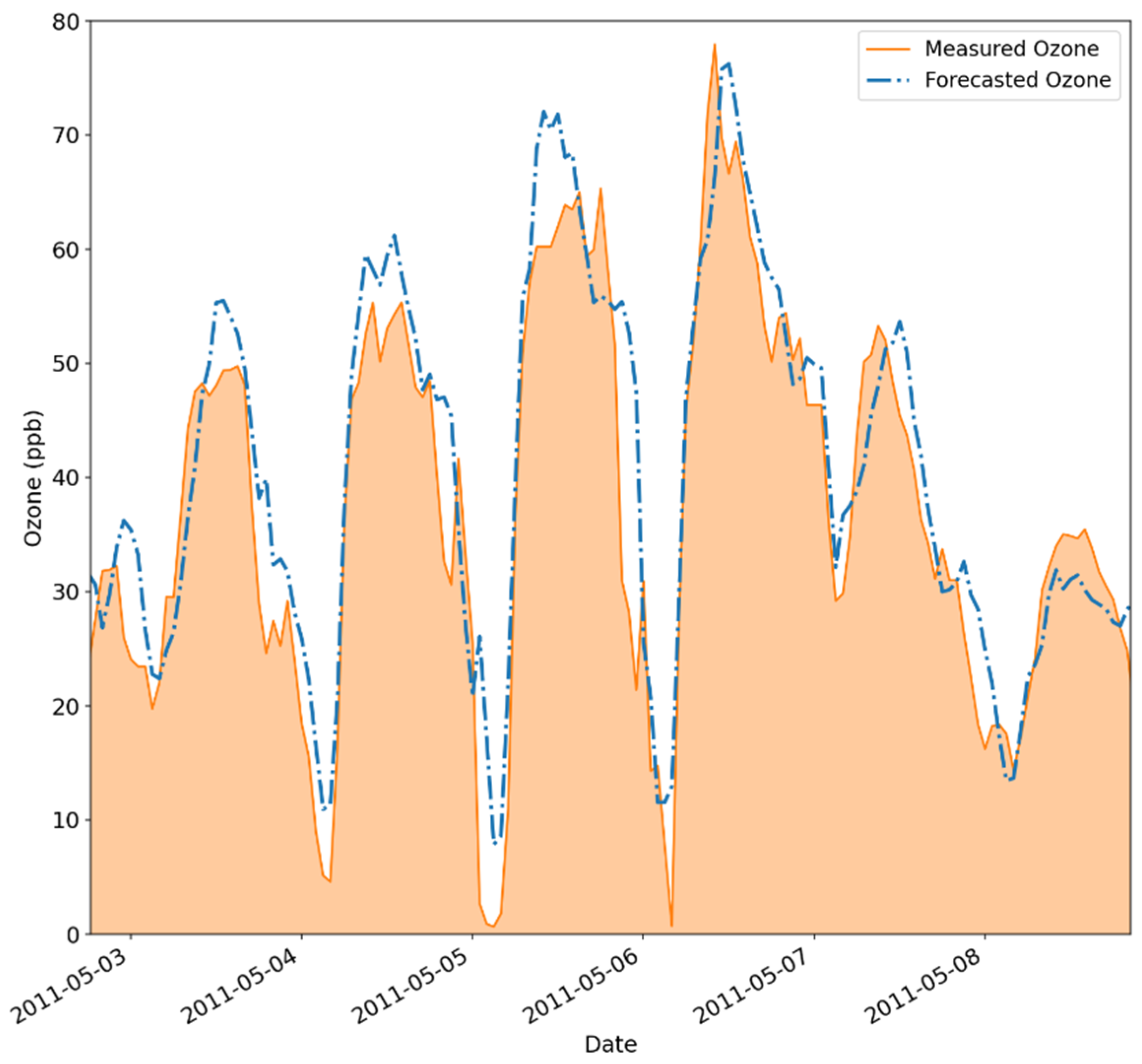
3.4. Ozone Forecasting Results for 1, 3, and 6 h Ahead
4. Discussion
4.1. QML Results in the Current NISQ Era
4.2. Influence of Ansatz and Data Normalization
4.3. Comparison with Quantum Models Found in the Literature
4.4. Comparison with Classical Models Found in the Literature
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carneiro, F.O.M.; Moura, L.F.M.; Costa Rocha, P.A.; Pontes Lima, R.J.; Ismail, K.A.R. Application and Analysis of the Moving Mesh Algorithm AMI in a Small Scale HAWT: Validation with Field Test’s Results against the Frozen Rotor Approach. Energy 2019, 171, 819–829. [Google Scholar] [CrossRef]
- Vidal Bezerra, F.D.; Pinto Marinho, F.; Costa Rocha, P.A.; Oliveira Santos, V.; Van Griensven Thé, J.; Gharabaghi, B. Machine Learning Dynamic Ensemble Methods for Solar Irradiance and Wind Speed Predictions. Atmosphere 2023, 14, 1635. [Google Scholar] [CrossRef]
- Verma, P.; Verma, R.; Mallet, M.; Sisodiya, S.; Zare, A.; Dwivedi, G.; Ristovski, Z. Assessment of Human and Meteorological Influences on PM10 Concentrations: Insights from Machine Learning Algorithms. Atmos. Pollut. Res. 2024, 15, 102123. [Google Scholar] [CrossRef]
- Liao, M.; Braunstein, Z.; Rao, X. Sex Differences in Particulate Air Pollution-Related Cardiovascular Diseases: A Review of Human and Animal Evidence. Sci. Total Environ. 2023, 884, 163803. [Google Scholar] [CrossRef] [PubMed]
- Sierra-Vargas, M.P.; Montero-Vargas, J.M.; Debray-García, Y.; Vizuet-de-Rueda, J.C.; Loaeza-Román, A.; Terán, L.M. Oxidative Stress and Air Pollution: Its Impact on Chronic Respiratory Diseases. Int. J. Mol. Sci. 2023, 24, 853. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.-Y.; Cheng, Y.-H.; Dejchanchaiwong, R. Insight into Secondary Inorganic Aerosol (SIA) Production Enhanced by Domestic Ozone Using a Machine Learning Technique. Atmos. Environ. 2024, 316, 120194. [Google Scholar] [CrossRef]
- Xie, Y.; Zhou, M.; Hunt, K.M.R.; Mauzerall, D.L. Recent PM2.5 Air Quality Improvements in India Benefited from Meteorological Variation. Nat. Sustain. 2024, 7, 983–993. [Google Scholar] [CrossRef]
- Shindell, D.; Faluvegi, G.; Nagamoto, E.; Parsons, L.; Zhang, Y. Reductions in Premature Deaths from Heat and Particulate Matter Air Pollution in South Asia, China, and the United States under Decarbonization. Proc. Natl. Acad. Sci. USA 2024, 121, e2312832120. [Google Scholar] [CrossRef]
- Ghaffarpasand, O.; Okure, D.; Green, P.; Sayyahi, S.; Adong, P.; Sserunjogi, R.; Bainomugisha, E.; Pope, F.D. The Impact of Urban Mobility on Air Pollution in Kampala, an Exemplar Sub-Saharan African City. Atmos. Pollut. Res. 2024, 15, 102057. [Google Scholar] [CrossRef]
- Roy, R.; Braathen, N.A. The Rising Cost of Ambient Air Pollution Thus Far in the 21st Century: Results from the BRIICS and the OECD Countries; OECD: Paris, France, 2017. [Google Scholar]
- Tran, H.M.; Tsai, F.-J.; Lee, Y.-L.; Chang, J.-H.; Chang, L.-T.; Chang, T.-Y.; Chung, K.F.; Kuo, H.-P.; Lee, K.-Y.; Chuang, K.-J.; et al. The Impact of Air Pollution on Respiratory Diseases in an Era of Climate Change: A Review of the Current Evidence. Sci. Total Environ. 2023, 898, 166340. [Google Scholar] [CrossRef]
- Ma, M.; Liu, M.; Song, X.; Liu, M.; Fan, W.; Wang, Y.; Xing, H.; Meng, F.; Lv, Y. Spatiotemporal Patterns and Quantitative Analysis of Influencing Factors of PM2.5 and O3 Pollution in the North China Plain. Atmos. Pollut. Res. 2024, 15, 101950. [Google Scholar] [CrossRef]
- Steinebach, Y. Instrument Choice, Implementation Structures, and the Effectiveness of Environmental Policies: A Cross-National Analysis. Regul. Gov. 2022, 16, 225–242. [Google Scholar] [CrossRef]
- Tang, J.-H.; Pan, S.-R.; Li, L.; Chan, P.-W. A Machine Learning-Based Method for Identifying the Meteorological Field Potentially Inducing Ozone Pollution. Atmos. Environ. 2023, 312, 120047. [Google Scholar] [CrossRef]
- Zafra-Pérez, A.; Medina-García, J.; Boente, C.; Gómez-Galán, J.A.; Sánchez De La Campa, A.; De La Rosa, J.D. Designing a Low-Cost Wireless Sensor Network for Particulate Matter Monitoring: Implementation, Calibration, and Field-Test. Atmos. Pollut. Res. 2024, 15, 102208. [Google Scholar] [CrossRef]
- Sayeed, A.; Choi, Y.; Jung, J.; Lops, Y.; Eslami, E.; Salman, A.K. A Deep Convolutional Neural Network Model for Improving WRF Simulations. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 750–760. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; He, Q.; Chen, X.; Huang, J.; Zhang, M. Estimating Ground-Level High-Resolution Ozone Concentration across China Using a Stacked Machine-Learning Method. Atmos. Pollut. Res. 2024, 15, 102114. [Google Scholar] [CrossRef]
- Liu, Y.; Geng, X.; Smargiassi, A.; Fournier, M.; Gamage, S.M.; Zalzal, J.; Yamanouchi, S.; Torbatian, S.; Minet, L.; Hatzopoulou, M.; et al. Changes in Industrial Air Pollution and the Onset of Childhood Asthma in Quebec, Canada. Environ. Res. 2024, 243, 117831. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Stanier, C.O.; Carmichael, G.R.; Gao, M. Ozone, Nitrogen Dioxide, and PM2.5 Estimation from Observation-Model Machine Learning Fusion over S. Korea: Influence of Observation Density, Chemical Transport Model Resolution, and Geostationary Remotely Sensed AOD. Atmos. Environ. 2024, 331, 120603. [Google Scholar] [CrossRef]
- Yang, W.; Wu, Q.; Li, J.; Chen, X.; Du, H.; Wang, Z.; Li, D.; Tang, X.; Sun, Y.; Ye, Z.; et al. Predictions of Air Quality and Challenges for Eliminating Air Pollution during the 2022 Olympic Winter Games. Atmos. Res. 2024, 300, 107225. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Shi, J.; Ma, J.; Liu, X.; Han, D.; Gao, H.; Huang, T. Predicting Ozone Formation in Petrochemical Industrialized Lanzhou City by Interpretable Ensemble Machine Learning. Environ. Pollut. 2022, 318, 120798. [Google Scholar] [CrossRef] [PubMed]
- Rocha, P.A.C.; Santos, V.O. Global Horizontal and Direct Normal Solar Irradiance Modeling by the Machine Learning Methods XGBoost and Deep Neural Networks with CNN-LSTM Layers: A Case Study Using the GOES-16 Satellite Imagery. Int. J. Energy Environ. Eng. 2022, 13, 1271–1286. [Google Scholar] [CrossRef]
- Friberg, M.D.; Zhai, X.; Holmes, H.A.; Chang, H.H.; Strickland, M.J.; Sarnat, S.E.; Tolbert, P.E.; Russell, A.G.; Mulholland, J.A. Method for Fusing Observational Data and Chemical Transport Model Simulations To Estimate Spatiotemporally Resolved Ambient Air Pollution. Environ. Sci. Technol. 2016, 50, 3695–3705. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-03561-3. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Salah Eddine, S.; Drissi, L.B.; Mejjad, N.; Mabrouki, J.; Romanov, A.A. Machine Learning Models Application for Spatiotemporal Patterns of Particulate Matter Prediction and Forecasting over Morocco in North of Africa. Atmos. Pollut. Res. 2024, 15, 102239. [Google Scholar] [CrossRef]
- Luo, R.; Wang, J.; Gates, I. Estimating Air Methane and Total Hydrocarbon Concentrations in Alberta, Canada Using Machine Learning. Atmos. Pollut. Res. 2024, 15, 101984. [Google Scholar] [CrossRef]
- De La Cruz Libardi, A.; Masselot, P.; Schneider, R.; Nightingale, E.; Milojevic, A.; Vanoli, J.; Mistry, M.N.; Gasparrini, A. High Resolution Mapping of Nitrogen Dioxide and Particulate Matter in Great Britain (2003–2021) with Multi-Stage Data Reconstruction and Ensemble Machine Learning Methods. Atmos. Pollut. Res. 2024, 15, 102284. [Google Scholar] [CrossRef] [PubMed]
- Nouayti, A.; Berriban, I.; Chham, E.; Azahra, M.; Satti, H.; Drissi El-Bouzaidi, M.; Yerrou, R.; Arectout, A.; Ziani, H.; El Bardouni, T.; et al. Utilizing Innovative Input Data and ANN Modeling to Predict Atmospheric Gross Beta Radioactivity in Spain. Atmos. Pollut. Res. 2024, 15, 102264. [Google Scholar] [CrossRef]
- Costa Rocha, P.A.; Oliveira Santos, V.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Application of Graph Neural Networks to Forecast Urban Flood Events: The Case Study of the 2013 Flood of the Bow River, Calgary, Canada. Int. J. River Basin Manag. 2024, 1–18. [Google Scholar] [CrossRef]
- Ren, K.; Chen, K.; Jin, C.; Li, X.; Yu, Y.; Lin, Y. TEMDI: A Temporal Enhanced Multisource Data Integration Model for Accurate PM2.5 Concentration Forecasting. Atmos. Pollut. Res. 2024, 15, 102269. [Google Scholar] [CrossRef]
- Lei, T.M.T.; Ng, S.C.W.; Siu, S.W.I. Application of ANN, XGBoost, and Other ML Methods to Forecast Air Quality in Macau. Sustainability 2023, 15, 5341. [Google Scholar] [CrossRef]
- Al-Eidi, S.; Amsaad, F.; Darwish, O.; Tashtoush, Y.; Alqahtani, A.; Niveshitha, N. Comparative Analysis Study for Air Quality Prediction in Smart Cities Using Regression Techniques. IEEE Access 2023, 11, 115140–115149. [Google Scholar] [CrossRef]
- Ketu, S. Spatial Air Quality Index and Air Pollutant Concentration Prediction Using Linear Regression Based Recursive Feature Elimination with Random Forest Regression (RFERF): A Case Study in India. Nat. Hazards 2022, 114, 2109–2138. [Google Scholar] [CrossRef]
- Zhou, Z.; Qiu, C.; Zhang, Y. A Comparative Analysis of Linear Regression, Neural Networks and Random Forest Regression for Predicting Air Ozone Employing Soft Sensor Models. Sci. Rep. 2023, 13, 22420. [Google Scholar] [CrossRef]
- He, Z.; Guo, Q.; Wang, Z.; Li, X. Prediction of Monthly PM2.5 Concentration in Liaocheng in China Employing Artificial Neural Network. Atmosphere 2022, 13, 1221. [Google Scholar] [CrossRef]
- Ren, L.; An, F.; Su, M.; Liu, J. Exposure Assessment of Traffic-Related Air Pollution Based on CFD and BP Neural Network and Artificial Intelligence Prediction of Optimal Route in an Urban Area. Buildings 2022, 12, 1227. [Google Scholar] [CrossRef]
- Maltare, N.N.; Vahora, S. Air Quality Index Prediction Using Machine Learning for Ahmedabad City. Digit. Chem. Eng. 2023, 7, 100093. [Google Scholar] [CrossRef]
- Imam, M.; Adam, S.; Dev, S.; Nesa, N. Air Quality Monitoring Using Statistical Learning Models for Sustainable Environment. Intell. Syst. Appl. 2024, 22, 200333. [Google Scholar] [CrossRef]
- Zhen, L.; Chen, B.; Wang, L.; Yang, L.; Xu, W.; Huang, R.-J. Data Imbalance Causes Underestimation of High Ozone Pollution in Machine Learning Models: A Weighted Support Vector Regression Solution. Atmos. Environ. 2025, 343, 120952. [Google Scholar] [CrossRef]
- Salman, A.K.; Choi, Y.; Singh, D.; Kayastha, S.G.; Dimri, R.; Park, J. Temporal CNN-Based 72-h Ozone Forecasting in South Korea: Explainability and Uncertainty Quantification. Atmos. Environ. 2025, 343, 120987. [Google Scholar] [CrossRef]
- Aarthi, C.; Ramya, V.J.; Falkowski-Gilski, P.; Divakarachari, P.B. Balanced Spider Monkey Optimization with Bi-LSTM for Sustainable Air Quality Prediction. Sustainability 2023, 15, 1637. [Google Scholar] [CrossRef]
- Nguyen, H.A.D.; Ha, Q.P.; Duc, H.; Azzi, M.; Jiang, N.; Barthelemy, X.; Riley, M. Long Short-Term Memory Bayesian Neural Network for Air Pollution Forecast. IEEE Access 2023, 11, 35710–35725. [Google Scholar] [CrossRef]
- Jia, T.; Cheng, G.; Chen, Z.; Yang, J.; Li, Y. Forecasting Urban Air Pollution Using Multi-Site Spatiotemporal Data Fusion Method (Geo-BiLSTMA). Atmos. Pollut. Res. 2024, 15, 102107. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, C.; Wang, D.; Liu, H. A Novel Deep Learning Model Integrating CNN and GRU to Predict Particulate Matter Concentrations. Process Saf. Environ. Prot. 2023, 173, 604–613. [Google Scholar] [CrossRef]
- Lu, Y.; Li, K. Multistation Collaborative Prediction of Air Pollutants Based on the CNN-BiLSTM Model. Environ. Sci. Pollut. Res. 2023, 30, 92417–92435. [Google Scholar] [CrossRef] [PubMed]
- Rabie, R.; Asghari, M.; Nosrati, H.; Emami Niri, M.; Karimi, S. Spatially Resolved Air Quality Index Prediction in Megacities with a CNN-Bi-LSTM Hybrid Framework. Sustain. Cities Soc. 2024, 109, 105537. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Yang, Y. Air Pollution Measurement Based on Hybrid Convolutional Neural Network with Spatial-and-Channel Attention Mechanism. Expert Syst. Appl. 2023, 233, 120921. [Google Scholar] [CrossRef]
- Li, W.; Jiang, X. Prediction of Air Pollutant Concentrations Based on TCN-BiLSTM-DMAttention with STL Decomposition. Sci. Rep. 2023, 13, 4665. [Google Scholar] [CrossRef] [PubMed]
- Elbaz, K.; Shaban, W.M.; Zhou, A.; Shen, S.-L. Real Time Image-Based Air Quality Forecasts Using a 3D-CNN Approach with an Attention Mechanism. Chemosphere 2023, 333, 138867. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.; Hu, Q.; Zhang, T. EKLT: Kolmogorov-Arnold Attention-Driven LSTM with Transformer Model for River Water Level Prediction. J. Hydrol. 2025, 649, 132430. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Spatiotemporal Air Pollution Forecasting in Houston-TX: A Case Study for Ozone Using Deep Graph Neural Networks. Atmosphere 2023, 14, 308. [Google Scholar] [CrossRef]
- Jin, X.-B.; Wang, Z.-Y.; Kong, J.-L.; Bai, Y.-T.; Su, T.-L.; Ma, H.-J.; Chakrabarti, P. Deep Spatio-Temporal Graph Network with Self-Optimization for Air Quality Prediction. Entropy 2023, 25, 247. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, S.; Chen, Y.; He, L.; Ren, Y.; Zhang, Z.; Li, J.; Zhang, S. Air Quality Forecasting Using a Spatiotemporal Hybrid Deep Learning Model Based on VMD–GAT–BiLSTM. Sci. Rep. 2024, 14, 17841. [Google Scholar] [CrossRef] [PubMed]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Sachdeva, N.; Harnett, G.S.; Maity, S.; Marsh, S.; Wang, Y.; Winick, A.; Dougherty, R.; Canuto, D.; Chong, Y.Q.; Hush, M.; et al. Quantum Optimization Using a 127-Qubit Gate-Model IBM Quantum Computer Can Outperform Quantum Annealers for Nontrivial Binary Optimization Problems. arXiv 2024, arXiv:2406.01743. [Google Scholar]
- Klusch, M.; Lässig, J.; Müssig, D.; Macaluso, A.; Wilhelm, F.K. Quantum Artificial Intelligence: A Brief Survey. KI Künstl. Intell. 2024. [Google Scholar] [CrossRef]
- Cerezo, M.; Verdon, G.; Huang, H.-Y.; Cincio, L.; Coles, P.J. Challenges and Opportunities in Quantum Machine Learning. Nat. Comput. Sci. 2022, 2, 567–576. [Google Scholar] [CrossRef]
- Thakkar, S.; Kazdaghli, S.; Mathur, N.; Kerenidis, I.; Ferreira–Martins, A.J.; Brito, S. Improved Financial Forecasting via Quantum Machine Learning. Quantum Mach. Intell. 2024, 6, 27. [Google Scholar] [CrossRef]
- Bhasin, N.K.; Kadyan, S.; Santosh, K.; HP, R.; Changala, R.; Bala, B.K. Enhancing Quantum Machine Learning Algorithms for Optimized Financial Portfolio Management. In Proceedings of the 2024 Third International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamil Nadu, India, 14–16 March 2024; pp. 1–7. [Google Scholar]
- Avramouli, M.; Savvas, I.K.; Vasilaki, A.; Garani, G. Unlocking the Potential of Quantum Machine Learning to Advance Drug Discovery. Electronics 2023, 12, 2402. [Google Scholar] [CrossRef]
- Sagingalieva, A.; Kordzanganeh, M.; Kenbayev, N.; Kosichkina, D.; Tomashuk, T.; Melnikov, A. Hybrid Quantum Neural Network for Drug Response Prediction. Cancers 2023, 15, 2705. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, M.P.; Herrera, L.B.; Hostaš, J.; Calaminici, P.; Köster, A.M.; Tchagang, A.; Salahub, D.R. QMLMaterial─A Quantum Machine Learning Software for Material Design and Discovery. J. Chem. Theory Comput. 2023, 19, 5999–6010. [Google Scholar] [CrossRef] [PubMed]
- Rosyid, M.R.; Mawaddah, L.; Santosa, A.P.; Akrom, M.; Rustad, S.; Dipojono, H.K. Implementation of Quantum Machine Learning in Predicting Corrosion Inhibition Efficiency of Expired Drugs. Mater. Today Commun. 2024, 40, 109830. [Google Scholar] [CrossRef]
- Gohel, P.; Joshi, M. Quantum Time Series Forecasting. In Proceedings of the Sixteenth International Conference on Machine Vision (ICMV 2023), Yerevan, Armenia, 15–18 November 2024; Osten, W., Ed.; SPIE: Yerevan, Armenia, 2024; p. 39. [Google Scholar]
- Oliveira Santos, V.; Marinho, F.P.; Costa Rocha, P.A.; Thé, J.V.G.; Gharabaghi, B. Application of Quantum Neural Network for Solar Irradiance Forecasting: A Case Study Using the Folsom Dataset, California. Energies 2024, 17, 3580. [Google Scholar] [CrossRef]
- Dong, Y.; Li, F.; Zhu, T.; Yan, R. Air Quality Prediction Based on Quantum Activation Function Optimized Hybrid Quantum Classical Neural Network. Front. Phys. 2024, 12, 1412664. [Google Scholar] [CrossRef]
- Farooq, O.; Shahid, M.; Arshad, S.; Altaf, A.; Iqbal, F.; Vera, Y.A.M.; Flores, M.A.L.; Ashraf, I. An Enhanced Approach for Predicting Air Pollution Using Quantum Support Vector Machine. Sci. Rep. 2024, 14, 19521. [Google Scholar] [CrossRef] [PubMed]
- Tsoukalas, M.Z.; Stratogiannis, D.G.; Dritsas, L.; Papadakis, A. Hybrid Quantum and Classical Machine Learning Classification for IoT-Based Air Quality Monitoring. In Proceedings of the 2024 10th International Conference on Automation, Robotics and Applications (ICARA), Athens, Greece, 22–24 February 2024; pp. 546–550. [Google Scholar]
- Khan, M.A.-Z.; Al-Karaki, J.; Omar, M. Predicting Water Quality Using Quantum Machine Learning: The Case of the Umgeni Catchment (U20A) Study Region. arXiv 2024, arXiv:2411.18141v1. [Google Scholar]
- Nammouchi, A.; Kassler, A.; Theorachis, A. Quantum Machine Learning in Climate Change and Sustainability: A Review. arXiv 2023, arXiv:2310.09162. [Google Scholar] [CrossRef]
- Rahman, S.M.; Alkhalaf, O.H.; Alam, M.S.; Tiwari, S.P.; Shafiullah, M.; Al-Judaibi, S.M.; Al-Ismail, F.S. Climate Change Through Quantum Lens: Computing and Machine Learning. Earth Syst. Environ. 2024, 8, 705–722. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating Physics with Computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Berberian, S.K. Introduction to Hilbert Space; American Mathematical Soc.: Providence, RI, USA, 1999; ISBN 978-0-8218-1912-8. [Google Scholar]
- Halmos, P.R. Introduction to Hilbert Space and the Theory of Spectral Multiplicity: Second Edition; Courier Dover Publications: Garden City, NY, USA, 2017; ISBN 978-0-486-81733-0. [Google Scholar]
- Fleisch, D.A. A Student’s Guide to the Schrödinger Equation; Cambridge University Press: Cambridge, UK, 2020; ISBN 978-1-108-83473-5. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th anniversary ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2010; ISBN 978-1-107-00217-3. [Google Scholar]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press: Oxford, UK, 2007; ISBN 978-0-19-857000-4. [Google Scholar]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Shankar, R. Principles of Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1994; ISBN 978-0-306-44790-7. [Google Scholar]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC ’96, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Sutor, R.S. Dancing with Qubits: How Quantum Computing Works and How It May Change the World; Expert insight; Packt: Birmingham, UK; Mumbai, India, 2019; ISBN 978-1-83882-736-6. [Google Scholar]
- Lee, D.P.Y.; Ji, D.H.; Cheng, D.R. Quantum Computing and Information: A Scaffolding Approach; Polaris QCI Publishing: Albany, NY, USA, 2024; ISBN 978-1-961880-03-0. [Google Scholar]
- Griffiths, D.J. Introduction to Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-107-17986-8. [Google Scholar]
- Schuld, M.; Petruccione, F. Machine Learning with Quantum Computers; Springer Nature: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-030-83098-4. [Google Scholar]
- Schuld, M.; Killoran, N. Quantum Machine Learning in Feature Hilbert Spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Mengoni, R.; Di Pierro, A. Kernel Methods in Quantum Machine Learning. Quantum Mach. Intell. 2019, 1, 65–71. [Google Scholar] [CrossRef]
- Combarro, E.F.; Gonzalez-Castillo, S.; Meglio, A.D. A Practical Guide to Quantum Machine Learning and Quantum Optimization: Hands-on Approach to Modern Quantum Algorithms; Packt Publishing Ltd.: Birmingham, UK, 2023; ISBN 978-1-80461-830-1. [Google Scholar]
- Sushmit, M.M.; Mahbubul, I.M. Forecasting Solar Irradiance with Hybrid Classical–Quantum Models: A Comprehensive Evaluation of Deep Learning and Quantum-Enhanced Techniques. Energy Convers. Manag. 2023, 294, 117555. [Google Scholar] [CrossRef]
- IBM Quantum Documentation TwoLocal. Available online: https://docs.quantum.ibm.com/api/qiskit/qiskit.circuit.library.TwoLocal (accessed on 12 June 2024).
- Dalvand, Z.; Hajarian, M. Solving Generalized Inverse Eigenvalue Problems via L-BFGS-B Method. Inverse Probl. Sci. Eng. 2020, 28, 1719–1746. [Google Scholar] [CrossRef]
- Wilson, M.; Stromswold, R.; Wudarski, F.; Hadfield, S.; Tubman, N.M.; Rieffel, E.G. Optimizing Quantum Heuristics with Meta-Learning. Quantum Mach. Intell. 2021, 3, 13. [Google Scholar] [CrossRef]
- Zheng, L.; Li, D.; Xu, J.; Xia, Z.; Hao, H.; Chen, Z. A Twenty-Years Remote Sensing Study Reveals Changes to Alpine Pastures under Asymmetric Climate Warming. ISPRS J. Photogramm. Remote Sens. 2022, 190, 69–78. [Google Scholar] [CrossRef]
- Bergholm, V.; Izaac, J.; Schuld, M.; Gogolin, C.; Ahmed, S.; Ajith, V.; Alam, M.S.; Alonso-Linaje, G.; AkashNarayanan, B.; Asadi, A.; et al. PennyLane: Automatic Differentiation of Hybrid Quantum-Classical Computations. arXiv 2022, arXiv:1811.04968. [Google Scholar]
- Javadi-Abhari, A.; Treinish, M.; Krsulich, K.; Wood, C.J.; Lishman, J.; Gacon, J.; Martiel, S.; Nation, P.D.; Bishop, L.S.; Cross, A.W.; et al. Quantum Computing with Qiskit. arXiv 2024, arXiv:2405.08810. [Google Scholar]
- Correa-Jullian, C.; Cofre-Martel, S.; San Martin, G.; Lopez Droguett, E.; De Novaes Pires Leite, G.; Costa, A. Exploring Quantum Machine Learning and Feature Reduction Techniques for Wind Turbine Pitch Fault Detection. Energies 2022, 15, 2792. [Google Scholar] [CrossRef]
- Jing, H.; Li, Y.; Brandsema, M.J.; Chen, Y.; Yue, M. HHL Algorithm with Mapping Function and Enhanced Sampling for Model Predictive Control in Microgrids. Appl. Energy 2024, 361, 122878. [Google Scholar] [CrossRef]
- Labonne, M. Hands-On Graph Neural Networks Using Python: Practical Techniques and Architectures for Building Powerful Graph and Deep Learning Apps with PyTorch; Packt Publishing Ltd.: Birmingham, UK, 2023; ISBN 1-80461-070-4. [Google Scholar]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River. Water 2023, 15, 1827. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Costa Rocha, P.A.; Thé, J.V.G.; Gharabaghi, B. Graph-Based Deep Learning Model for Forecasting Chloride Concentration in Urban Streams to Protect Salt-Vulnerable Areas. Environments 2023, 10, 157. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Spatiotemporal Analysis of Bidimensional Wind Speed Forecasting: Development and Thorough Assessment of LSTM and Ensemble Graph Neural Networks on the Dutch Database. Energy 2023, 278, 127852. [Google Scholar] [CrossRef]
- Owusu-Mfum, S.; Hudson, M.D.; Osborne, P.E.; Roberts, T.J.; Zapata-Restrepo, L.M.; Williams, I.D. Atmospheric Pollution in Port Cities. Atmosphere 2023, 14, 1135. [Google Scholar] [CrossRef]
- Pan, S.; Roy, A.; Choi, Y.; Eslami, E.; Thomas, S.; Jiang, X.; Gao, H.O. Potential Impacts of Electric Vehicles on Air Quality and Health Endpoints in the Greater Houston Area in 2040. Atmos. Environ. 2019, 207, 38–51. [Google Scholar] [CrossRef]
- Sadeghi, B.; Choi, Y.; Yoon, S.; Flynn, J.; Kotsakis, A.; Lee, S. The Characterization of Fine Particulate Matter Downwind of Houston: Using Integrated Factor Analysis to Identify Anthropogenic and Natural Sources. Environ. Pollut. 2020, 262, 114345. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Kyropoulou, M. Thermal Comfort and Indoor Air Quality in Higher Education: A Case Study in Houston, TX, during Mid-Season. J. Phys. Conf. Ser. 2023, 2600, 102022. [Google Scholar] [CrossRef]
- EPA, U. Green Book. Available online: https://www3.epa.gov/airquality/greenbook/jnc.html (accessed on 16 December 2022).
- Liao, D.; Wang, L.; Wang, Y.; Huang, H.; Zhuang, Z.; Choi, S.-D.; Hong, Y. Effects of Heat Waves on Ozone Pollution in a Coastal Industrial City: Meteorological Impacts and Photochemical Mechanisms. Atmos. Pollut. Res. 2024, 15, 102280. [Google Scholar] [CrossRef]
- Open Street Map OpenStreetMap. Available online: https://www.openstreetmap.org (accessed on 27 February 2024).
- QGIS Development Team QGIS Geographic Information System 2024, Accessed Public-Domain Spatial Visualization and Decision-Making Tools. Available online: https://qgis.org/ (accessed on 1 June 2024).
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022; ISBN 978-1-0981-2246-1. [Google Scholar]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning; Cambridge University Press: Cambridge, UK, 2023; ISBN 978-1-009-38943-3. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Baïle, R.; Muzy, J.F.; Poggi, P. Short-Term Forecasting of Surface Layer Wind Speed Using a Continuous Random Cascade Model. Wind Energy 2011, 14, 719–734. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A Critical Review of Wind Power Forecasting Methods—Past, Present and Future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and Trends in Solar Irradiance and PV Power Forecasting: A Preliminary Assessment and Review Using Text Mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable Spatio-Temporal Attention LSTM Model for Flood Forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water 2021, 13, 1612. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022; ISBN 978-1-009-09848-9. [Google Scholar]
- Ghojogh, B.; Crowley, M.; Karray, F.; Ghodsi, A. Elements of Dimensionality Reduction and Manifold Learning; Springer International Publishing: Cham, Switzerland, 2023; ISBN 978-3-031-10601-9. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning: With Applications in Python; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; ISBN 978-3-031-38746-3. [Google Scholar]
- Tennie, F.; Palmer, T.N. Quantum Computers for Weather and Climate Prediction: The Good, the Bad, and the Noisy. Bull. Am. Meteorol. Soc. 2023, 104, E488–E500. [Google Scholar] [CrossRef]
- Lim, H.; Kang, D.H.; Kim, J.; Pellow-Jarman, A.; McFarthing, S.; Pellow-Jarman, R.; Jeon, H.-N.; Oh, B.; Rhee, J.-K.K.; No, K.T. Fragment Molecular Orbital-Based Variational Quantum Eigensolver for Quantum Chemistry in the Age of Quantum Computing. Sci. Rep. 2024, 14, 2422. [Google Scholar] [CrossRef] [PubMed]
- Zheng, K.; Van Griensven, J.; Fraser, R. A Quantum Machine Learning Approach to Spatiotemporal Emission Modelling. Atmosphere 2023, 14, 944. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Yang, H.; Wang, Y. Intelligent Multivariable Air-Quality Forecasting System Based on Feature Selection and Modified Evolving Interval Type-2 Quantum Fuzzy Neural Network. Environ. Pollut. 2021, 274, 116429. [Google Scholar] [CrossRef]
- Yu, Y.; Hu, G.; Liu, C.; Xiong, J.; Wu, Z. Prediction of Solar Irradiance One Hour Ahead Based on Quantum Long Short-Term Memory Network. IEEE Trans. Quantum Eng. 2023, 4, 1–15. [Google Scholar] [CrossRef]
- Nevo, S.; Morin, E.; Gerzi Rosenthal, A.; Metzger, A.; Barshai, C.; Weitzner, D.; Voloshin, D.; Kratzert, F.; Elidan, G.; Dror, G.; et al. Flood Forecasting with Machine Learning Models in an Operational Framework. Hydrol. Earth Syst. Sci. 2022, 26, 4013–4032. [Google Scholar] [CrossRef]
- Hong, F.; Ji, C.; Rao, J.; Chen, C.; Sun, W. Hourly Ozone Level Prediction Based on the Characterization of Its Periodic Behavior via Deep Learning. Process Saf. Environ. Prot. 2023, 174, 28–38. [Google Scholar] [CrossRef]
- Bekkar, A.; Hssina, B.; Douzi, S.; Douzi, K. Transformer-Based Model for Multi-Horizon Forecasting Ozone in Marrakech City, Morocco. In Proceedings of the 2023 14th International Conference on Intelligent Systems: Theories and Applications (SITA), Casablanca, Morocco, 22–23 November 2023; pp. 1–8. [Google Scholar]
- Wood, D.A. Ozone Air Concentration Trend Attributes Assist Hours-Ahead Forecasts from Univariate Recorded Data Avoiding Exogenous Data Inputs. Urban Clim. 2023, 47, 101382. [Google Scholar] [CrossRef]
- Zavala-Romero, O.; Segura-Chavez, P.A.; Camacho-Gonzalez, P.; Zavala-Hidalgo, J.; Garcia, A.R.; Oropeza-Alfaro, P.; Romero-Centeno, R.; Gomez-Ramos, O. Operational Ozone Forecasting System in Mexico City: A Machine Learning Framework Integrating Forecasted Weather and Historical Ozone Data. Atmos. Environ. 2025, 344, 121017. [Google Scholar] [CrossRef]
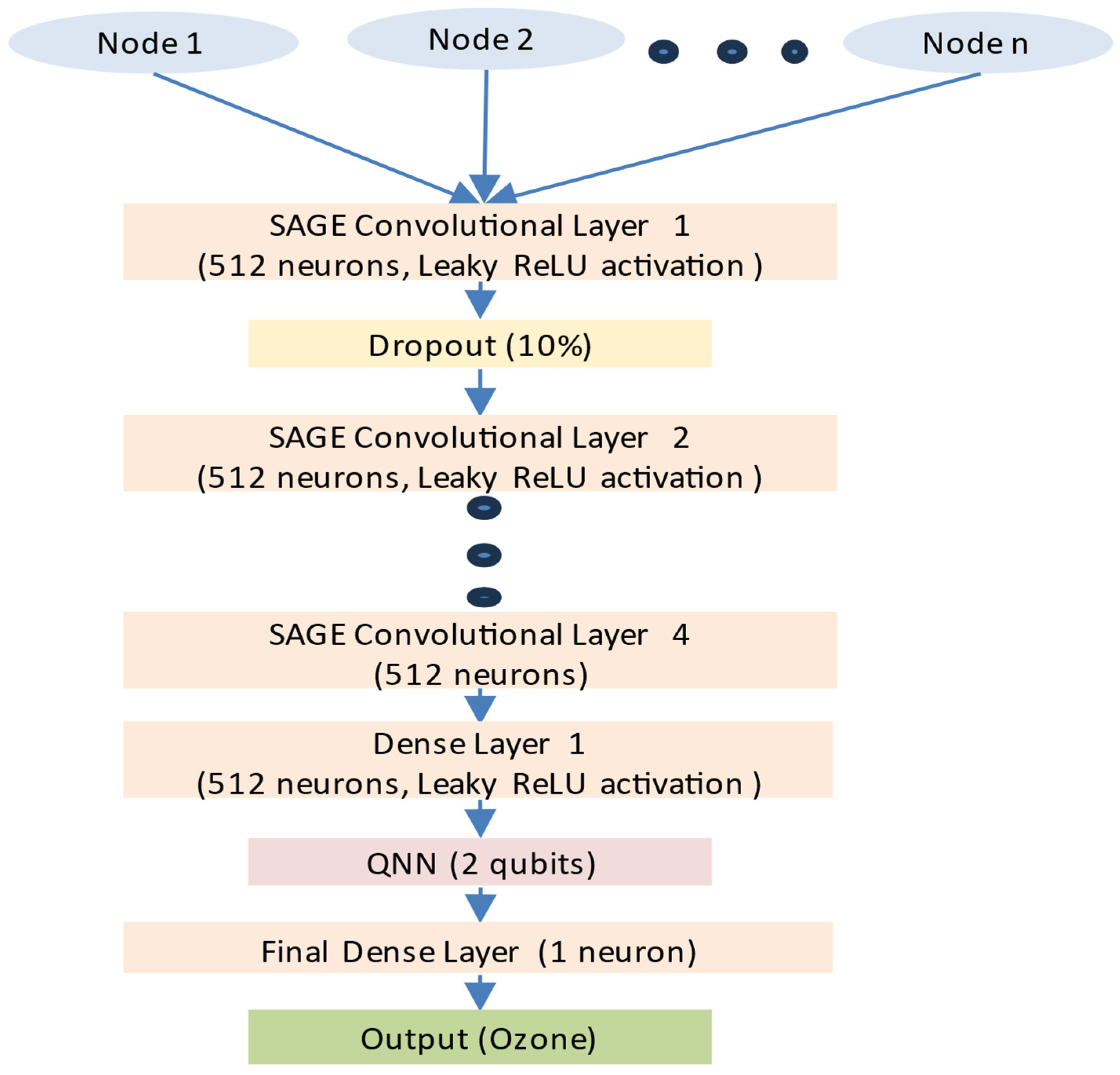
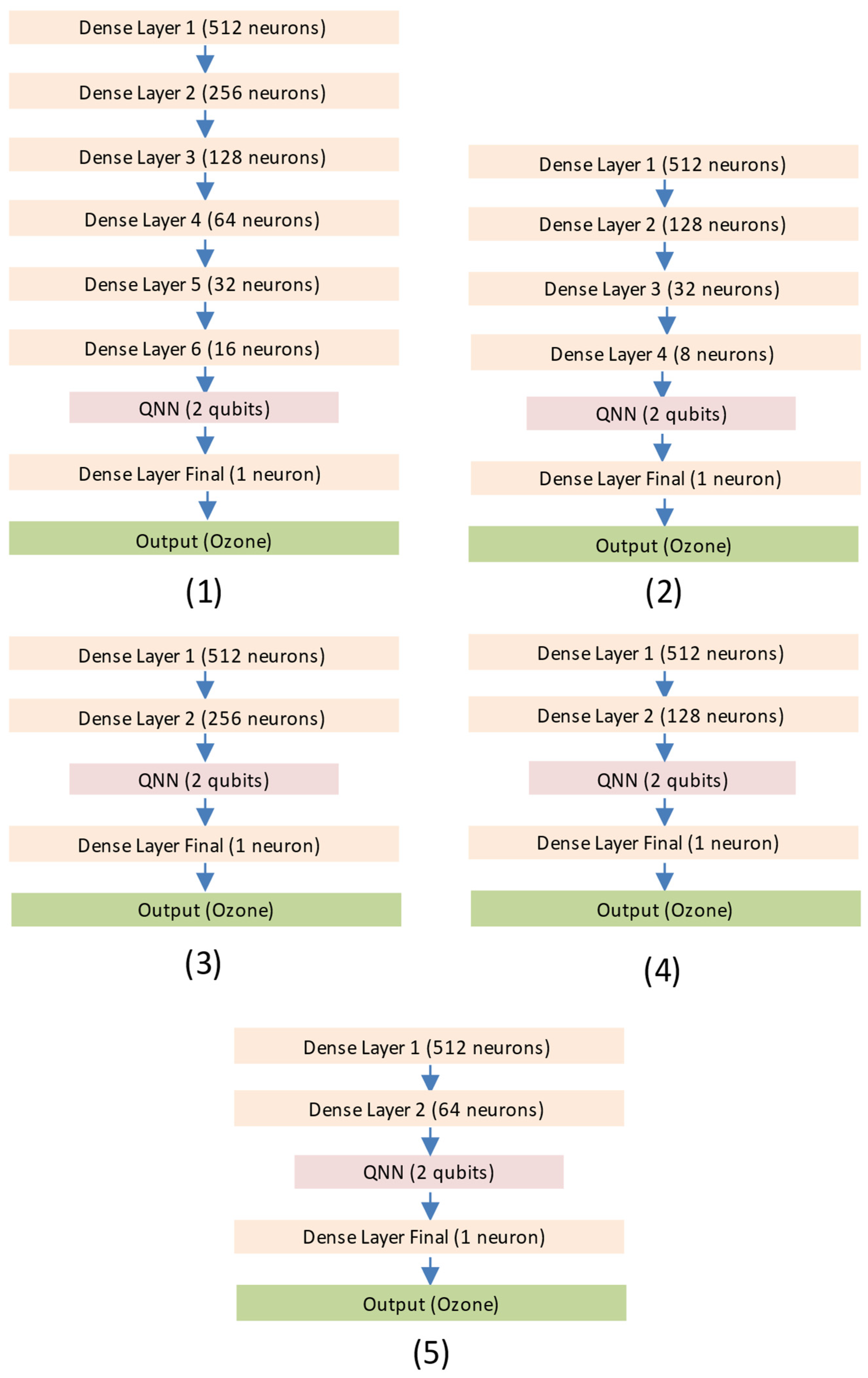
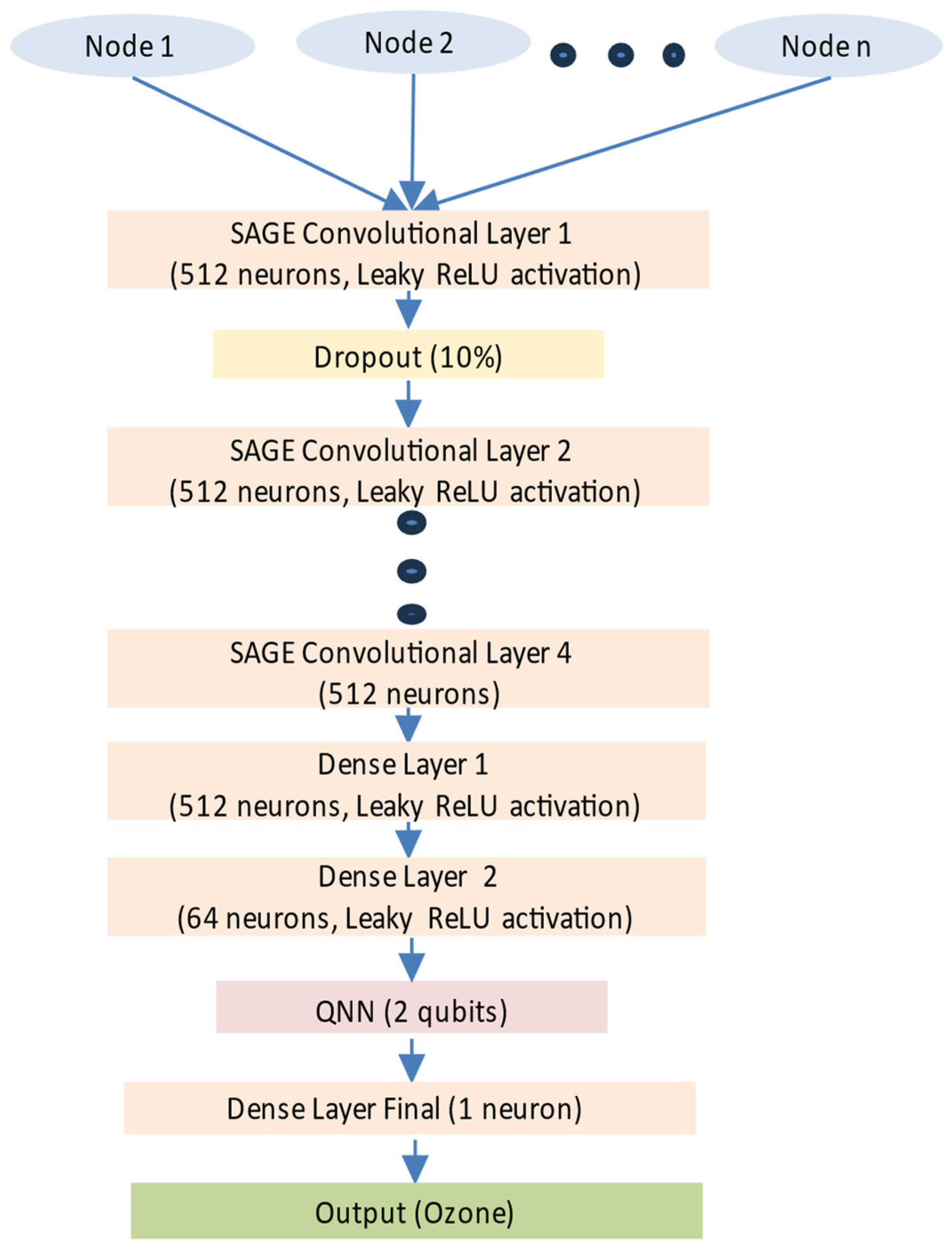
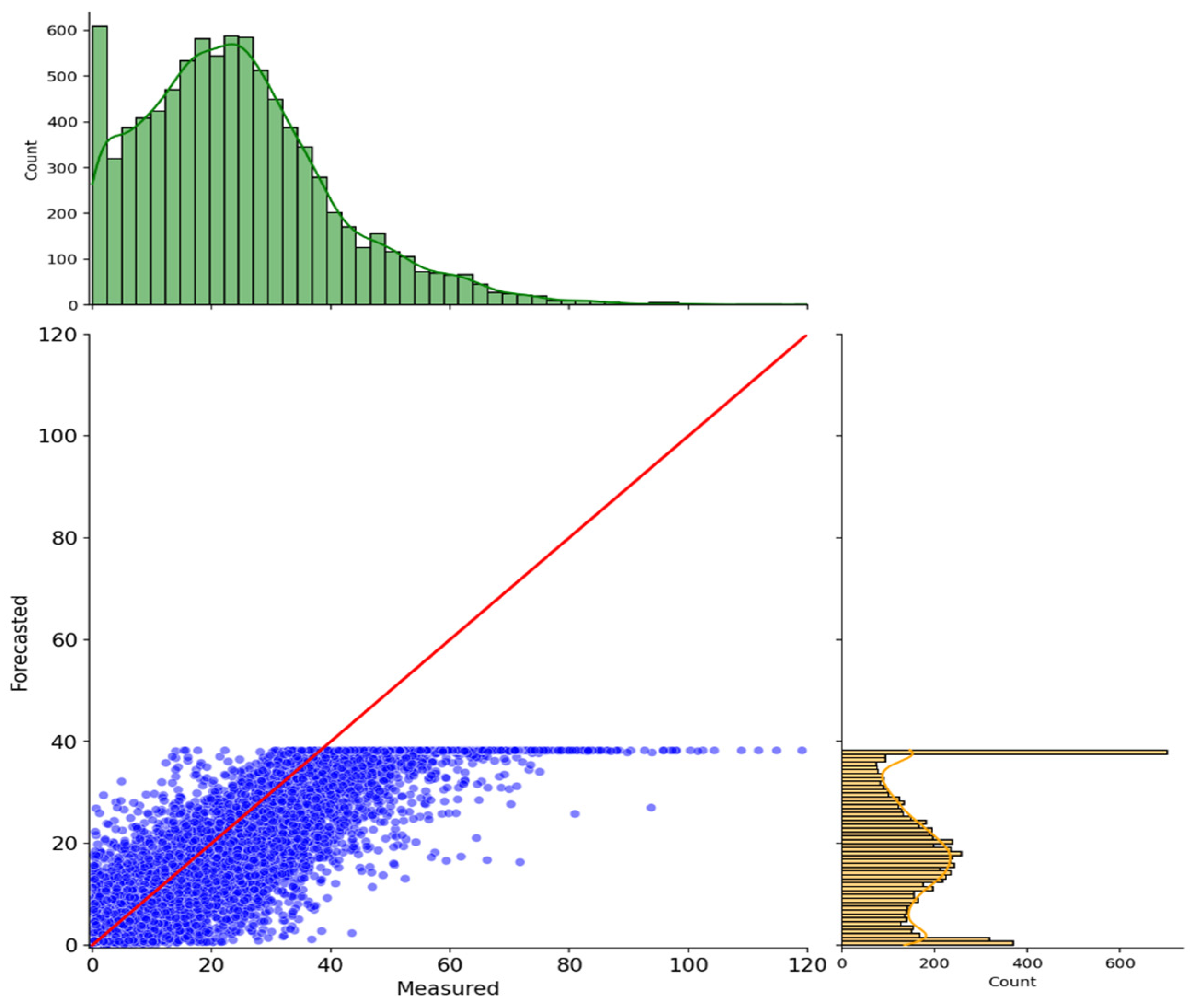
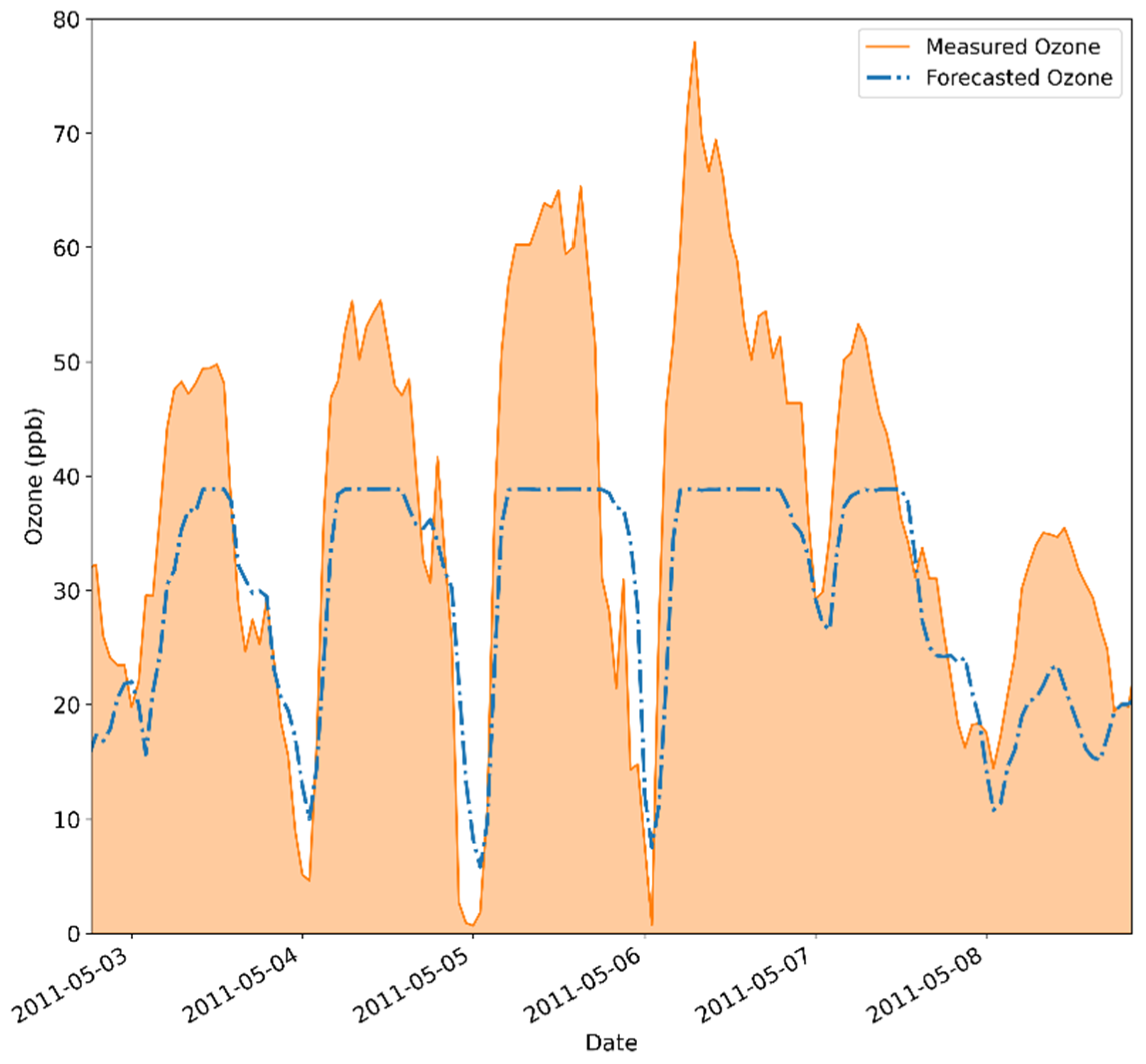
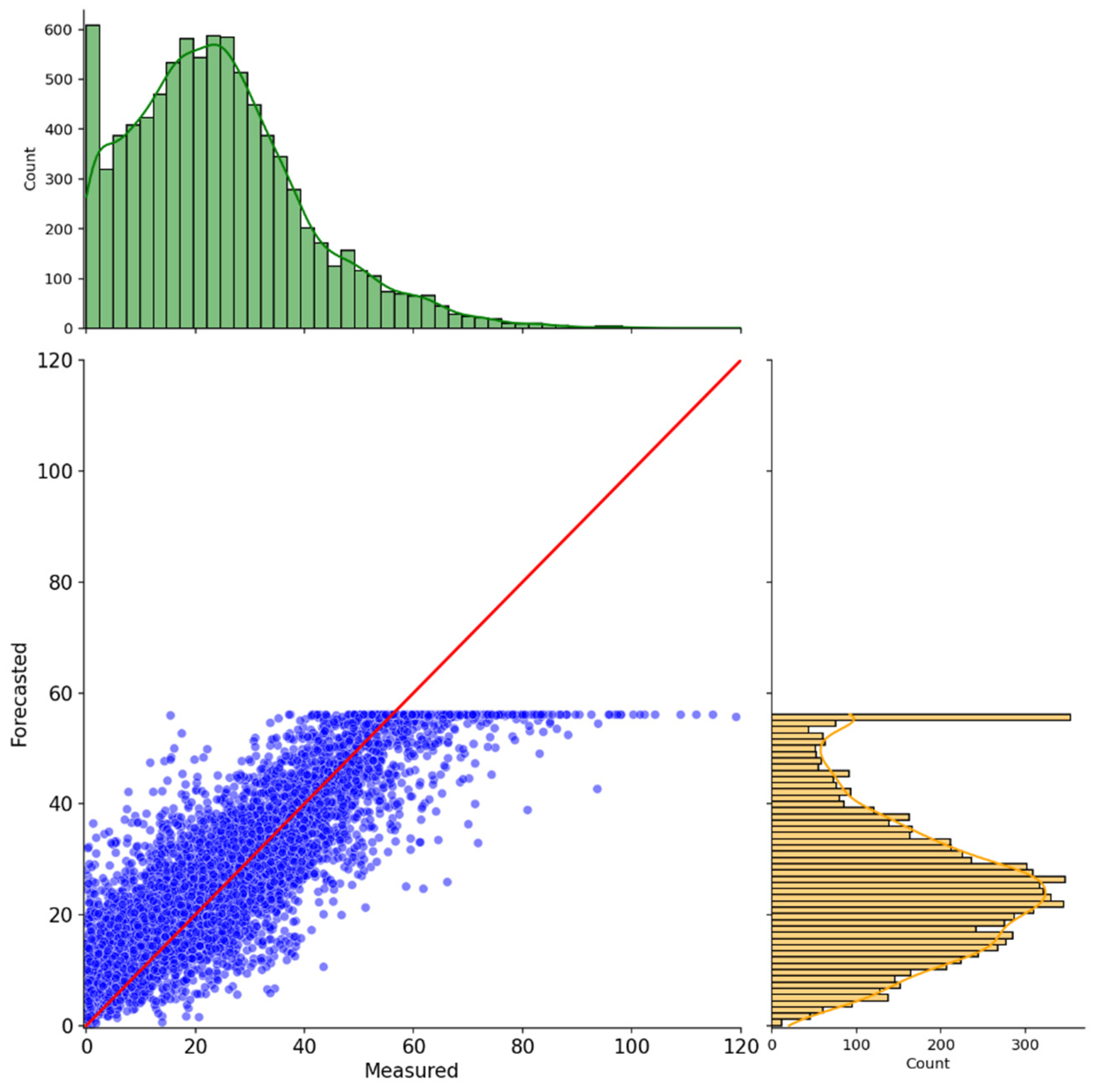

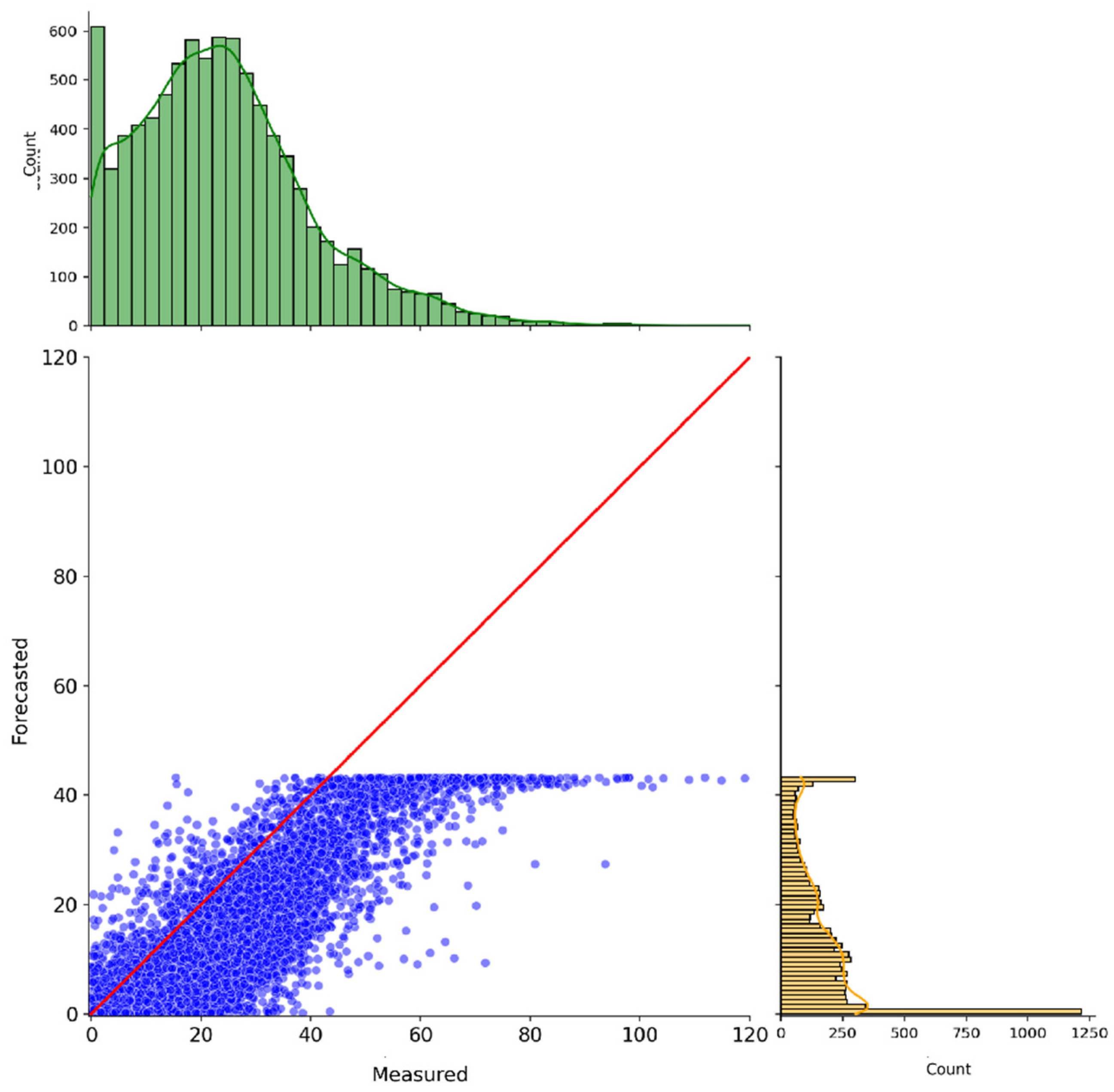

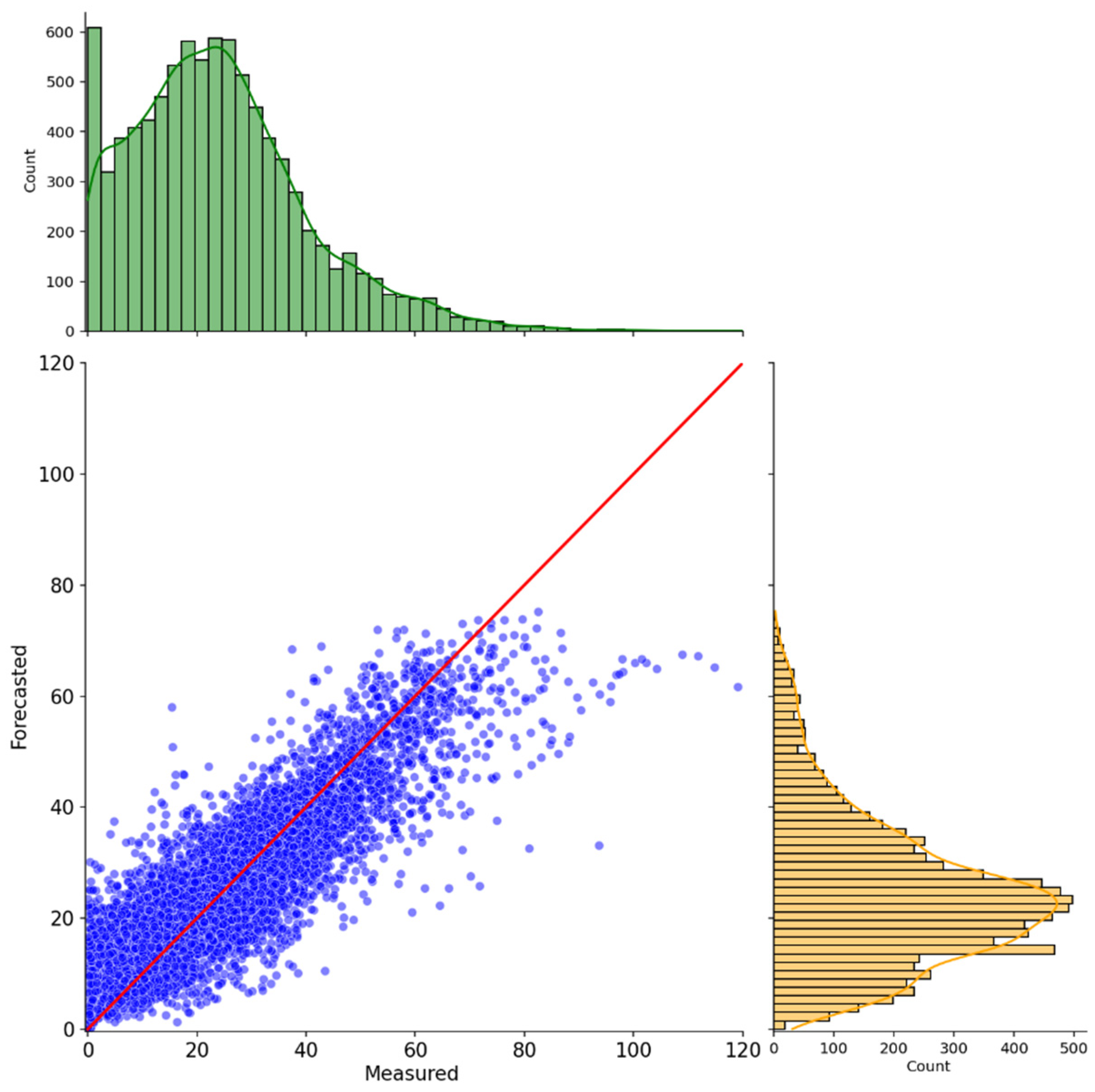
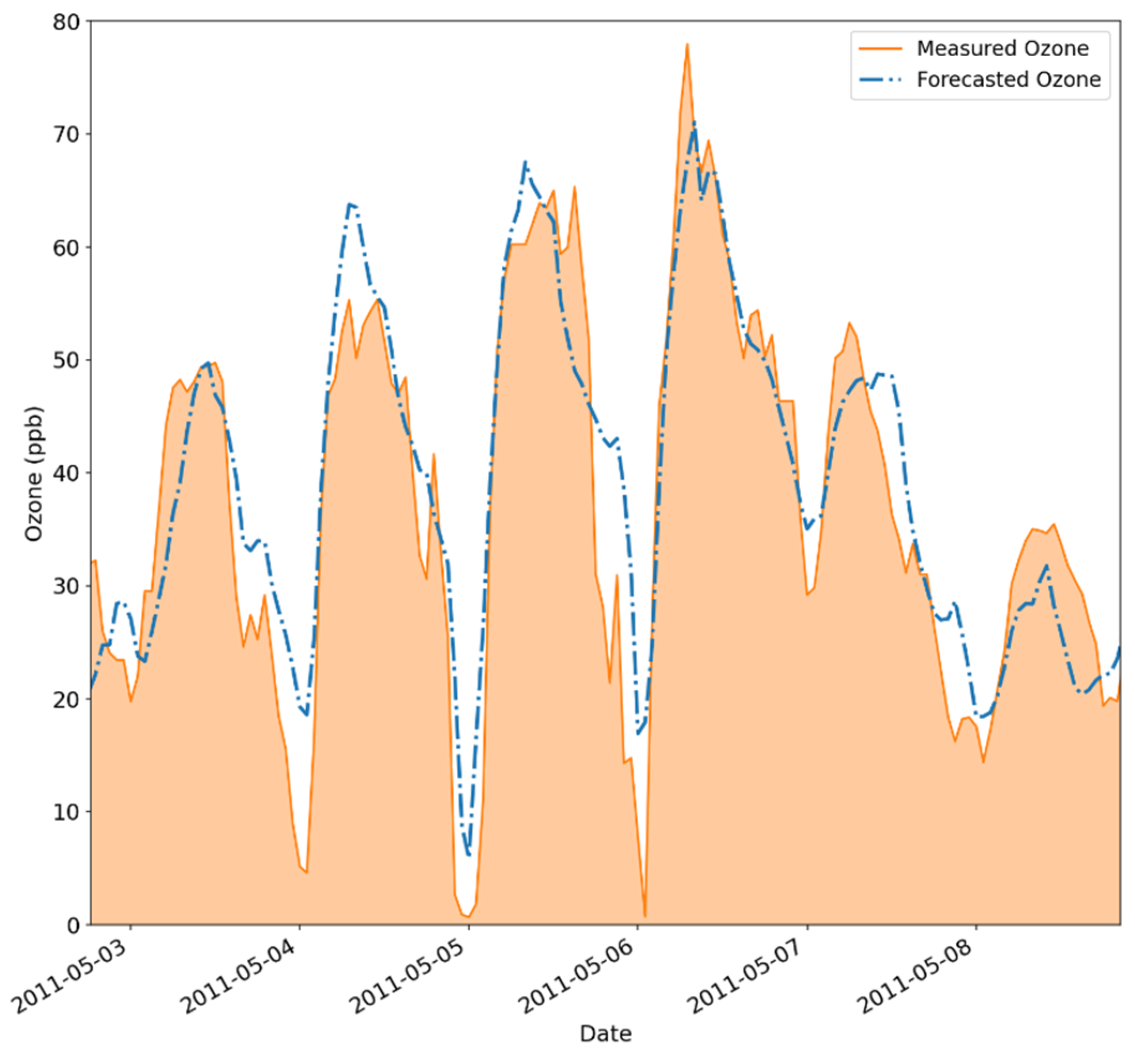
| QNN Component | Used Approach |
|---|---|
| Feature Map | Pauli Y angle encoding |
| Ansatz | TwoLocal ansatz, with linear entanglement |
| Ansatz Optimization | L-BFGS-B |
| Forecasting Window | Predictors | Time-Lag |
|---|---|---|
| 1 h |
| 4 h |
| 3 h | 2 h | |
| 6 h | 7 h |
| Forecasting Horizon | RMSE (ppb) | R2 (%) | FS (%) |
|---|---|---|---|
| 1 h | 7.61 | 78.24 | −32.53 |
| 3 h | 10.36 | 59.62 | 17.64 |
| 6 h | 9.33 | 67.18 | 50.65 |
| Approach | RMSE (ppb) | R2 (%) | FS (%) |
|---|---|---|---|
| 1 | 9.11 | 68.75 | −58.80 |
| 2 | 6.31 | 85.02 | −9.97 |
| 3 | 7.63 | 78.13 | −32.86 |
| 4 | 5.58 | 88.28 | 2.75 |
| 5 | 5.50 | 88.60 | 4.10 |
| Forecasting Horizon | RMSE (ppb) | R2 (%) | FS (%) |
|---|---|---|---|
| 1 h | 5.50 | 88.61 | 4.11 |
| 3 h | 8.10 | 75.36 | 35.66 |
| 6 h | 9.43 | 66.53 | 50.16 |
| Forecasting Horizon | Normalization | Number of Ansatz Repetition |
|---|---|---|
| 1 h | Min–max | 3 |
| 3 h | Min–max | 2 |
| 6 h | Min–max | 2 |
| Forecasting Horizon | RMSE (ppb) | R2 (%) | FS (%) |
|---|---|---|---|
| 1 h | 3.96 | 94.12 | 31.01 |
| 3 h | 6.53 | 83.94 | 48.01 |
| 6 h | 8.01 | 75.62 | 57.46 |
| Model | Metric Value | References |
|---|---|---|
| GNN-SAGE | RMSE—R2—FS 3.80 ppb—0.95%—33.70% for 1 h horizon 6.45 ppb—0.84%—48.70% for 3 h horizon 8.09 ppb—0.75%—57.10% for 6 h horizon | [52] |
| LSTM-based deep learning model | RMSE—R2 7.50 ppb—83.69% for 1 h horizon | [130] |
| Attention-based deep learning model | RMSE 2.92 ppb for 1 h horizon | [49] |
| Transformer-based deep learning model | RMSE—R2 3.99 ppb—92.20% for 1 h horizon 5.35 ppb—86.31% for 3 h horizon | [131] |
| Several classical ML models, where the SVM emerged as the best performing approach | RMSE—R2 9.24 ppb—85.00% for 1 h horizon 14.01 ppb—65.50% for 3 h horizon 17.70 ppb—45.10% for 6 h horizon | [132] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira Santos, V.; Costa Rocha, P.A.; Thé, J.V.G.; Gharabaghi, B. Optimizing the Architecture of a Quantum–Classical Hybrid Machine Learning Model for Forecasting Ozone Concentrations: Air Quality Management Tool for Houston, Texas. Atmosphere 2025, 16, 255. https://doi.org/10.3390/atmos16030255
Oliveira Santos V, Costa Rocha PA, Thé JVG, Gharabaghi B. Optimizing the Architecture of a Quantum–Classical Hybrid Machine Learning Model for Forecasting Ozone Concentrations: Air Quality Management Tool for Houston, Texas. Atmosphere. 2025; 16(3):255. https://doi.org/10.3390/atmos16030255
Chicago/Turabian StyleOliveira Santos, Victor, Paulo Alexandre Costa Rocha, Jesse Van Griensven Thé, and Bahram Gharabaghi. 2025. "Optimizing the Architecture of a Quantum–Classical Hybrid Machine Learning Model for Forecasting Ozone Concentrations: Air Quality Management Tool for Houston, Texas" Atmosphere 16, no. 3: 255. https://doi.org/10.3390/atmos16030255
APA StyleOliveira Santos, V., Costa Rocha, P. A., Thé, J. V. G., & Gharabaghi, B. (2025). Optimizing the Architecture of a Quantum–Classical Hybrid Machine Learning Model for Forecasting Ozone Concentrations: Air Quality Management Tool for Houston, Texas. Atmosphere, 16(3), 255. https://doi.org/10.3390/atmos16030255










