Dissipation Scaling with a Variable C_ϵ Coefficient in the Stable Atmospheric Boundary Layer

Abstract

This work concerns the Taylor formula for the turbulence kinetic energy dissipation rate in the stable atmospheric boundary layer. The formula relates the turbulence kinetic energy dissipation rate to statistics at large scales, namely, the turbulence kinetic energy and the integral length scale. In parameterization schemes for atmospheric turbulence, it is usually assumed that the dissipation coefficient $C_{ϵ}$ in the Taylor formula is constant. However, a series of recent theoretical works and laboratory experiments showed that $C_{ϵ}$ depends on the local Reynolds number. We calculate turbulence statistics, including the dissipation rate, the standard deviation of fluctuating velocities and integral length scales, using observational data from the MOSAiC (Multidisciplinary drifting Observatory for the Study of Arctic Climate) expedition. We show that the dissipation coefficient $C_{ϵ}$ varies considerably and is a function of the Reynolds number, however, the functional form of this dependency in the stably stratified atmospheric boundary layer is different than in previous studies.

1. Introduction

The prediction of the turbulence kinetic energy dissipation rate $ϵ$ is a key element in parameterization schemes for turbulence in the atmospheric boundary layer (ABL). The dissipation rate determines how fast the energy produced due to shear and positive buoyancy is transformed into heat at the smallest scales. These scales are on the order of millimeters in atmospheric turbulence and are difficult to measure directly. Hence, indirect methods based on the Kolmogorov assumption of equilibrium are used to estimate $ϵ$. One of them is the Taylor formula [1], the cornerstone assumption of turbulence theory, which relates the small-scale process of dissipation to statistics at large scales, namely, the characteristic velocity scale of turbulent eddies, defined as $\sigma =\sqrt{2k/3}$, where k is the turbulence kinetic energy, and the integral length scale $\mathcal{L}$:

$$ϵ=C_{ϵ}{\displaystyle \frac{{\sigma }^3}{\mathcal{L}}},$$

(1)

where $C_{ϵ}$ is the dissipation coefficient. Typically, the main focus of ABL dissipation models is on finding the appropriate expression for the length scale $\mathcal{L}$ (cf. Ref. [2] for a review). When close enough to the surface, $\mathcal{L}$ can be related to the height z and to the Obukhov length $L_O$ [3]. At higher altitudes, $\mathcal{L}$ is approximated with the use of the ratio of the geostrophic velocity and the Coriolis parameter [4], or the “center of mass” of the vertical profile of the turbulence kinetic energy [5].

In the context of atmospheric turbulence, much less attention has been paid to determining the value of the dissipation constant $C_{ϵ}$ in Equation (1). Until recently, it was commonly assumed that the dissipation coefficient $C_{ϵ}$ is constant. However, a series of recent laboratory experiments and theoretical works [6,7,8,9,10,11,12,13] showed that, under certain conditions, $C_{ϵ}$ becomes a function of the Reynolds number:

$$C_{ϵ}\propto R{e}_{\lambda }^{\alpha },$$

(2)

where $\alpha$ is a scaling coefficient, the Reynolds number is defined as $R{e}_{\lambda }=\sigma \lambda /\nu$, $\nu$ is the kinematic viscosity, and

$$\lambda =\sqrt{15{\displaystyle \frac{\nu }{ϵ}}}\sigma$$

(3)

is the Taylor microscale. Relation (2) was tested in laboratory experiments for various canonical flows. For example, it was shown by Goto and Vassilicos [9] that, in the early stages of turbulence decay, the coefficient $\alpha \approx -$1. The same scaling was observed in a region of the axisymmetric wakes and was followed by subregions of $\alpha \approx -$0.77 and $\alpha \approx -$0.5 further downstream, cf. [8]. In Ref. [12], energy dissipation scaling in uniformly sheared turbulence was considered. Therein, it was found that the scaling coefficient $\alpha \approx -$0.6 for a low Reynolds number and that the scaling was reversed to $\alpha \approx 0.5$ for a higher $R{e}_{\lambda }$ and finally became close to zero as $R{e}_{\lambda }$ further increased.

A non-constant $C_{ϵ}$ in the ABL was reported in Ref. [14] based on in situ measurements taken by instruments mounted on a helicopter platform. Turbulent boundary layer flows were investigated in the laboratory in [13,15]. Therein, a region with $\alpha \approx -$1 was found, and a small subregion with $\alpha >0$ could be identified at larger $R{e}_{\lambda }$. Finally, $\alpha$ became close to zero. In yet another work [16], the dependence of $C_{ϵ}$ on turbulence anisotropy was studied.

The above works are of particular importance for the present study, which focuses on the stable atmospheric boundary layer. Such layers form mostly overnight due to surface radiative cooling, and they also prevail in the snow-covered polar regions. Under stable stratification, the air near the surface is cooler than the air above it, inhibiting vertical mixing. Turbulence within the stably stratified boundary layer is produced by shear; however, due to the negative buoyancy flux, turbulent motions can be locally suppressed or significantly reduced [17]. The characteristic features of the stably stratified ABL are intermittency, non-stationarity and the presence of gravity wave motions [18,19]. These additional complexities make turbulence parameterization challenging.

In this work, we determined the dissipation rate, the variances of all three components of velocity and the corresponding integral length scales using observational data from the MOSAiC (Multidisciplinary drifting Observatory for the Study of Arctic Climate) expedition, available in an open database [20]. We calculated the dissipation rate coefficient $C_{ϵ}$ in Equation (1) and studied its dependence on the Reynolds number $R{e}_{\lambda }$ under varying conditions and on the stratification.

This paper is structured as follows. Section 2 presents the theory of the equilibrium energy cascade and addresses deviations from equilibrium, which result in the non-constancy of the $C_{ϵ}$ parameter. The data and methods used in this study are described in Section 3. Section 4 presents the results, followed by the discussion in Section 5.

2. Theory

The turbulence kinetic energy dissipation rate $ϵ$ is defined as

$$ϵ=2\nu ⟨s_{ij}{s}_{ij}⟩,$$

(4)

where

$$s_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i^{\prime }}{\partial x_j}}+{\displaystyle \frac{\partial u_j^{\prime }}{\partial x_i}}\right),$$

(5)

$u_i^{\prime }$ denotes the i-th component of the fluctuating velocity vector, and $⟨·⟩$ is the ensemble average operator. The energy dissipation rate is the sink term in the budget equation for the mean turbulence kinetic energy:

$$k={\displaystyle \frac{1}{2}}⟨u_i^{\prime }{u}_i^{\prime }⟩,$$

(6)

and its proper representation is key to predicting k and to computing the eddy viscosity used in many weather and climate models [21]. The direct calculation of $ϵ$ from Equation (4) is possible only if high-frequency time series, which resolve turbulence down to the smallest eddies, are available. This is usually not the case in atmospheric measurements. As an example, the MOSAiC time series used in this study have a resolution of $f_s=10$ Hz. If the mean wind speed equals $U=5$ m/s, eddies of size $l=U/f_s=0.5$ m or larger can be measured by the sensors. This is still two orders of magnitude larger than the smallest turbulence structures, which are of millimeter size.

2.1. Equilibrium Scaling

If the direct calculation of $ϵ$ from its definition is not possible, indirect methods based on the Kolmogorov hypotheses are used. According to the second hypothesis, under the assumption of local isotropy, there exists an inertial range of scales where statistics are not affected by viscosity and are uniquely determined by $ϵ$ [22]. As a consequence, the turbulence kinetic energy spectrum reads

$$E(\kappa ,t)=C_Kϵ{\left(t\right)}^{2/3}{\kappa }^{-5/3},$$

(7)

where $C_K=1.5$ is the Kolmogorov constant and $\kappa$ is the wavenumber. When analyzing time series of single components of velocity, it is more convenient to consider the one-dimensional spectra of the velocity components. Under the assumption of isotropy, they read

$$E_{\Vert }(\kappa ,t)=C_{\Vert }ϵ{\left(t\right)}^{2/3}{\kappa }^{-5/3},E_{\perp }(\kappa ,t)=C_{\perp }ϵ{\left(t\right)}^{2/3}{\kappa }^{-5/3},$$

(8)

where $E_{\Vert }$ and $E_{\perp }$ denote the one-dimensional spectra of the longitudinal (i.e., along the mean flow direction) and transverse (i.e., perpendicular to the mean flow direction) velocity components. The constants $C_{\Vert }\approx 0.5$ and $C_{\perp }\approx 0.65$. Here, a note of caution is needed, as the Kolmogorov assumptions might be violated even at small scales [16]. In spite of this, relation (7) still remains the basis of data analyses in atmospheric turbulence.

Equation (7) holds only at scales much smaller than the characteristic length scale of large eddies and much larger than the size of the smallest viscosity-affected vortices. In typical ABL turbulence parameterization schemes, the resolution is not sufficient for the direct use of Equation (8). In this case, an assumption of the Richardson–Kolmogorov equilibrium cascade is used. In this classical picture, the energy supplied at the largest scales by mechanisms of turbulence generation, such as shear and positive buoyancy, is transferred in the scale space toward the smallest structures and dissipated as heat. As a consequence, $ϵ$ is directly related to statistics at the largest scales, i.e., the characteristic velocity scale $\sigma$ and the integral length scale $\mathcal{L}$, through Equation (1). In homogeneous and isotropic turbulence, these scales are defined as

$$\sigma =\sqrt{{\displaystyle \frac{2}{3}}k},\mathcal{L}={\int }_0^{\infty }{f}_l\left(r\right)\mathrm{d}r,$$

(9)

where

$$f_l={\displaystyle \frac{⟨u_l^{\prime }(x+r,y,z,t)u_l^{\prime }(x,y,z,t)⟩}{{\sigma }_l^2}}$$

(10)

is the two-point correlation coefficient, $u_l^{\prime }$ is the fluctuation of the longitudinal velocity component, x denotes the direction of the mean flow and r is the distance between points. The standard deviation ${\sigma }_l=\sqrt{⟨u_l^{\prime 2}⟩}$.

The statistics $\mathcal{L}$, k (kinetic energy) and $ϵ$ can also be determined from the turbulence kinetic energy spectrum as follows [11]:

$$k=\int E(\kappa ,t)\mathrm{d}\kappa ,\mathcal{L}={\displaystyle \frac{3\pi }{4k}}\int {\kappa }^{-1}E(\kappa ,t)\mathrm{d}\kappa ,ϵ=2\nu \int {\kappa }^{2}E(\kappa ,t)\mathrm{d}\kappa .$$

(11)

It can be assumed that for high-Reynolds-number flows, this spectrum takes the form of (7) between wavenumbers ${\kappa }_{\mathcal{L}}$ and ${\kappa }_{\eta }$, where ${\kappa }_{\mathcal{L}}\ll {\kappa }_{\eta }$ and is zero otherwise. Here, ${\kappa }_{\eta }$ denotes the wavenumber corresponding to the smallest dissipative eddies, and ${\kappa }_{\mathcal{L}}$ corresponds to large eddies [22]. Under such assumptions and using the definitions in (11), k, $\mathcal{L}$ and $ϵ$ equal [11]

$$k\approx {\displaystyle \frac{3}{2}}{C}_K{ϵ}^{2/3}{\kappa }_{\mathcal{L}}^{-2/3},\mathcal{L}\approx {\displaystyle \frac{3\pi }{10}}{\kappa }_{\mathcal{L}}^{-1},ϵ\approx {\displaystyle \frac{3}{2}}\nu C_K{ϵ}^{2/3}{\kappa }_{\eta }^{4/3},$$

(12)

where ${\kappa }_{\eta }^{-2/3}\ll {\kappa }_{\mathcal{L}}^{-2/3}$, ${\kappa }_{\eta }^{-2/3}\ll {\kappa }_{\mathcal{L}}^{-2/3}$ and ${\kappa }_{\mathcal{L}}^{4/3}\ll {\kappa }_{\eta }^{4/3}$ are neglected. The second formula in (12) provides the relation for ${\kappa }_{\mathcal{L}}$, that is, ${\kappa }_{\mathcal{L}}=3\pi /\left(10\mathcal{L}\right)$. After substituting it into the first equation in (12), we obtain

$$ϵ\propto {\displaystyle \frac{k^{3/2}}{\mathcal{L}}},$$

(13)

which is the Taylor law in Equation (1), with the proportionality constant $C_{ϵ}=3\pi /10C_K^{-3/2}$. This shows that $C_{ϵ}$ is directly related to the inertial subrange, and hence, Equation (1) establishes a connection between energy-containing and inertial subrange eddies. An analogous relation can be derived, in the Lagrangian framework, between $C_{ϵ}$ and the Kolmogorov constant of the Lagrangian structure function [23]. The third relation in (12) provides the formula for ${\kappa }_{\eta }\propto {(ϵ/{\nu }^3)}^{1/4}$.

Equation (1) is commonly used in turbulence parameterization schemes in the ABL. However, while the turbulence kinetic energy k is available from the solution of the system of equations, the two-point correlation coefficient $f_l$ is unknown, and either an algebraic formula for the length scale $\mathcal{L}$ must be provided or a diagnostic equation for $\mathcal{L}$ should be solved. Close to the surface and in near-neutral conditions, $\mathcal{L}\propto \kappa z$ is a natural choice, where $\kappa =0.4$ is the von Kármán constant. In place of Equation (1), Mellor and Yamada [5] used

$$ϵ={\displaystyle \frac{{\sigma }^3}{Bl}}$$

(14)

where $l=\kappa z$, and B is a constant. Different values of B have been reported in the literature; e.g., $B=16.6$ was found in [5], and the value $B=24$ was used in Ref. [24]. It follows from (1) and (14) that the integral length scale

$$\mathcal{L}\approx C_{ϵ}Bl=C_{ϵ}B\kappa z.$$

(15)

In Refs. [21,25], alternative parameterization based on the vertical velocity component w was used:

$$ϵ={\displaystyle \frac{{\sigma }_w^3}{B_{w}l}}$$

(16)

where $B_w\approx 2$ and ${\sigma }_w^2=⟨w^{\prime 2}⟩$.

Further away from the surface, the characteristic length scale is believed to level off; hence, e.g., Mellor and Yamada [26] proposed a formula with the “center of mass” of the velocity variance profile

$$\mathcal{L}\propto l_0{\displaystyle \frac{\kappa z}{\kappa z+l_0}},\mathrm{where}{l}_0\propto {\displaystyle \frac{{\int }_0^{\infty }z\sigma \mathrm{d}z}{{\int }_0^{\infty }\sigma \mathrm{d}z}}.$$

(17)

In stratified flows, stability affects the length scale and should be taken into account in turbulence models. Parameterizations based on the Obukhov length $L_0$ [3] were considered in Refs. [24,25,27]:

$$\mathcal{L}=C_{ϵ}B{\displaystyle \frac{\kappa z}{1+{\alpha }_2\xi }},$$

(18)

where ${\alpha }_2=2.7$ was estimated in Ref. [24], $\xi =z/L_O$, and the Obukhov length $L_O$ is defined as

$$L_O=-{\displaystyle \frac{T_0}{\kappa g}}{\displaystyle \frac{{⟨u_l^{\prime }{w}^{\prime }⟩}^{3/2}}{⟨{\theta }^{\prime }{w}^{\prime }⟩}}$$

(19)

where $w^{\prime }$ and ${\theta }^{\prime }$ denote the fluctuations of the vertical velocity and potential temperature, respectively, g is the gravitational acceleration and $T_0$ is the reference temperature. In near-neutral conditions, $\xi =z/L_O$ is small and $\mathcal{L}$ is proportional to $\kappa z$. On the other hand, in the case of strong stratification (large $\xi$), the limit value $\mathcal{L}\to L_O$ is obtained. Alternative parameterization of the length scale based on the Richardson number was proposed in Ref. [28] and considered in [29].

In order to verify the validity of the parameterization schemes using atmospheric data, typically, the kinetic energy or vertical velocity variance is calculated from the time series, and $ϵ$ is estimated from Equation (8). Next, Equation (14) or (16) is tested with different definitions of the length scale l.

2.2. Non-Equilibrium Scaling

The assumptions behind Equation (1) are true only in fully developed, stationary and homogeneous turbulence. These criteria are not satisfied in the ABL, where the conditions may change abruptly due to changes in forcing, particularly in the stable ABL, where turbulence may locally vanish due to stratification. In this case, transiency effects become important and should be included in the parameterization schemes [30].

If turbulence is non-stationary, the dissipation coefficients $C_{ϵ}$ and B vary and become dependent on the local Reynolds number $R{e}_{\lambda }$ and the initial conditions or the global Reynolds number; see Refs. [7,9,11]. This dependence can be linked to the deviations from the Kolmogorov scaling (7). For the case of decaying turbulence, Yoshizawa [31] proposed decomposing the spectra into a Kolmogorov equilibrium part (7), further denoted by $E_0$, and the non-equilibrium correction $\tilde{E}$. This idea was further elaborated in Ref. [11], where the following form of the energy spectrum in isotropic, decaying turbulence was considered:

$$E(\kappa ,t)=E_0(\kappa ,t)+\tilde{E}(\kappa ,t)=C_K{ϵ}^{2/3}{\kappa }^{-5/3}+{\displaystyle \frac{2}{3}}{C}_K^2{ϵ}^{-2/3}{\displaystyle \frac{\mathrm{d}ϵ}{\mathrm{d}t}}{\kappa }^{-7/3}.$$

(20)

The non-equilibrium correction scales as $\tilde{E}\propto {\kappa }^{-7/3}$, and the energy spectrum $E(\kappa ,t)$ is affected by the non-equilibrium correction $\tilde{E}$ mainly at large scales, because ${\kappa }^{-7/3}$ decreases to zero faster than ${\kappa }^{-5/3}$ for large $\kappa$. At smaller scales, classical Kolmogorov equilibrium is still observed. As a result of the non-equilibrium correction, $C_{ϵ}$ is no longer constant but becomes a function of the local Reynolds number $R{e}_{\lambda }$ and the initial conditions; see the discussion in Ref. [11].

As far as the anisotropic, near-surface flows are concerned, it was shown in Ref. [32] that, also in this case, the dissipation coefficient $C_{ϵ}$ varies in time and is inversely proportional to the local Reynolds number at small $Re$. In the turbulent boundary layer considered in Ref. [13], $C_{ϵ}$ varied in the streamwise direction. The authors of Ref. [13] concluded that $C_{ϵ}$ depends on the conditions under which the dominant structures of a flow evolve. Subregions of different $\alpha$ coefficients in Equation (2) were found in Ref. [13].

It follows directly from Equations (1) and (2) that the ratio of the Taylor to the integral length scale $\lambda /\mathcal{L}$ reads

$${\displaystyle \frac{\lambda }{\mathcal{L}}}\propto {\left({\displaystyle \frac{\sigma \lambda }{\nu }}\right)}^{-\alpha }{\displaystyle \frac{\lambda ϵ}{{\sigma }^3}}\propto {\left({\displaystyle \frac{\sigma \lambda }{\nu }}\right)}^{-\alpha }{\displaystyle \frac{1}{\lambda \sigma }}\propto R{e}_{\lambda }^{-(1+\alpha )},$$

(21)

Hence, the presence of non-equilibrium scaling can be detected by investigating the dependence of both $C_{ϵ}$ and $\lambda /\mathcal{L}$ on $R{e}_{\lambda }$; see also [14]. To the best of the authors’ knowledge, the dependence of dissipation coefficients, $C_{ϵ}$ in Equation (1) and B in Equation (14) or (16), on the Reynolds number in the stable ABL has not been considered so far. Hence, this problem is the focus of our study.

2.3. Dependence of $\mathcal{L}$ on $\sigma$

In stationary near-wall turbulence under neutral conditions, the shear production is, to the leading order, balanced by the dissipation $ϵ\sim \mathcal{P}$. Using the eddy-viscosity hypothesis, the production can be expressed as $\mathcal{P}={\nu }_t{\mathcal{S}}^2$, where $\mathcal{S}=d⟨u_l⟩/dz$ is the vertical gradient of velocity and ${\nu }_t\sim \sigma \mathcal{L}$. This balance, together with Equation (1), implies

$$ϵ=C_{ϵ}{\displaystyle \frac{{\sigma }^3}{\mathcal{L}}}\propto \sigma \mathcal{L}{\mathcal{S}}^2$$

(22)

If the shear $\mathcal{S}$ and $C_{ϵ}$ remain constant, the velocity scale $\sigma$ becomes proportional to the length scale $\mathcal{L}$:

$$\mathcal{L}\propto \sigma .$$

(23)

Equation (23) is expected to hold in equilibrium, neutral turbulence close to the surface. As the second limiting case, one can consider decaying turbulence, where

$${\displaystyle \frac{\mathrm{d}k}{\mathrm{d}t}}=-ϵ$$

(24)

The common k–$ϵ$ turbulence models predict that, while k decreases with time, the integral length scale $\mathcal{L}$ increases [33]; hence, in this case,

$$\mathcal{L}\propto {\sigma }^{\beta }$$

(25)

where the coefficient $\beta <0$. In non-equilibrium decaying turbulence, the length scale may initially decrease with time and next start to increase [33]. Such tendencies were also observed in atmospheric turbulence during the decay of the convective layer [34]. Generally, the non-constancy of the $\beta$ coefficient will indicate changes in the leading-order balances in the kinetic energy equation. We can expect that $\beta$ will tend toward unity in the stationary case.

3. Data and Methods

3.1. MOSAiC Observations

The MOSAiC expedition was conducted between October 2019 and October 2020 by an international team, which involved more than 80 institutions from 20 countries [35]. Continuous observations of the surface energy budget and meteorology were performed on and around the icebreaker RV Polarstern. The icebreaker entered the Siberian sector of the Arctic in late summer 2019 under thin sea ice conditions and drifted with the natural ice drift across the polar cap toward the Atlantic during winter, reaching 88°36′ North.

A large set of measurement data was collected during the expedition by monitoring stations. This includes high-frequency observations of wind velocity and temperature at a sampling rate of 10 Hz, used in the present study. The 10 m meteorological tower was instrumented at three levels, 2, 6 and 10 m above the initial snow/ice surface, with meteorological instruments and sonic anemometers.

The processed data are archived in daily files in an open database [20]. The data has been used to test the performance of various turbulence parameterization schemes, see e.g., [36]. In this study, we used quality-controlled Level 2 data, downloaded from the database, for wind velocity and temperature from the meteorological tower. We performed analyses for the period from 1 December 2019 to 31 January 2020.

3.2. Turbulence Statistics

To estimate turbulence statistics, we used a coordinate system aligned with the mean flow direction and calculated the longitudinal, horizontal transverse and vertical velocity components $u_l$, $u_t$ and w, respectively. The processing of the data was performed using Matlab tools. We detrended the data using a 1 min moving average. This window was estimated as optimal for the stable ABL in Ref. [37]. It acts as a high-pass filter and removes part of non-turbulent, low-frequency submeso motions in the stable ABL. As discussed in Ref. [21], these motions are related to phenomena such as gravity waves, inertial oscillations and drainage flow and lead to the overprediction of the energy dissipation rate and the lack of universality of the parameterization schemes. However, as further argued in [21], high-pass filtering does not fully resolve the problem, as, often, a clear separation between small-scale turbulence and submeso motions does not exist. We note here that a larger averaging time of 10 min was used in Ref. [38], where a detailed study of the turbulence kinetic energy budget was performed. The standard deviations of velocity components ${\sigma }_l$, ${\sigma }_t$ and ${\sigma }_w$, fluxes $⟨u_l^{\prime }{w}^{\prime }⟩$, fluxes $⟨{\theta }^{\prime }{w}^{\prime }⟩$, and the two-point correlation functions and the frequency spectra were calculated with the use of detrended data and additional averaging over 20 min blocks. This longer averaging time can reduce the statistical error, which is of particular importance for $\mathcal{L}$ estimates.

We calculated the turbulence intensity, defined as $I={\sigma }_l/⟨u_l⟩$, where ${\sigma }_l$ is the standard deviation of the longitudinal velocity component. The I coefficient should be much smaller than unity for the “frozen eddy” hypothesis to be applicable. This hypothesis allows the transformation of the measured time series into spatial structures. In the case of large values of I, frequency spectra become affected, and the use of the Kolmogorov hypothesis to estimate $ϵ$ is questionable. As discussed in [39], the frozen eddy hypothesis is reliable for $I\le 0.25$. Hence, we used the threshold $0.25$ and disregarded all data with $I>0.25$.

We expect that at the highest frequencies, the frequency spectra are close to the Kolmogorov predictions, even if non-equilibrium effects are present. The results in [38] suggest that, in this range, the scaling is close to −5/3. The calculated frequency spectra were fitted to the following equilibrium form, which follows from Equation (8):

$$S\left(f\right)=C{\displaystyle \frac{⟨u_l⟩}{2\pi }}{ϵ}^{2/3}{f}^{-5/3},$$

(26)

in the range from $f=1$ Hz to $f=3$ Hz, using the least-squares algorithm. The constant $C=0.5$ for the longitudinal velocity component, and $C=0.65$ for the horizontal transverse and vertical components [40]. The energy dissipation rate was calculated from the intercept in the log–log scale; see [41] for details of the procedure. Additionally, we required that the slope in the subrange $f\in [1,3]$ Hz be −5/3 with a 10% error margin. All other data were rejected.

At smaller frequencies, the frequency spectra can deviate from the Kolmogorov equilibrium predictions, particularly under changing flow conditions. In the ABL, such deviations were observed during the decay of the ABL before sunset in [34]. In order to investigate whether changes in the slopes of the frequency spectra are related to changes in $C_{ϵ}$, we estimated the slopes using the least-squares algorithm in the interval $f\in [0.1,1]$ Hz. As the slopes also differ among velocity components, we calculated them for the frequency spectra of $u_l$, $u_t$ and w separately, and they are denoted by $a_l$, $a_t$ and $a_w$, respectively.

To compute the two-point correlation functions, we estimated the distance between points as $r=⟨u_l⟩\Delta t$. We assumed that the longitudinal two-point correlation coefficient takes approximately the exponential form

$$f\left(r\right)\approx exp\left(-{\displaystyle \frac{r}{\mathcal{L}}}\right).$$

(27)

The integral of the above exponent from 0 to ∞ is equal to the length scale $\mathcal{L}$; see Equation (9). The longitudinal length scale ${\mathcal{L}}_l$ was estimated by integrating the calculated $f\left(r\right)$ from 0 to its first zero-crossing point $r_0$:

$${\mathcal{L}}_l\approx {\int }_0^{r_0}f\left(r\right)\mathrm{d}r.$$

(28)

In the isotropic turbulence, the following relation between the longitudinal and transverse correlation coefficients holds [22]:

$$g\left(r\right)=f\left(r\right)+{\displaystyle \frac{1}{2}}r{\displaystyle \frac{\partial f\left(r\right)}{\partial r}},$$

(29)

where, in isotropic turbulence, $g\left(t\right)=g_t\left(r\right)=g_w\left(r\right)$ and

$$g_t\left(r\right)={\displaystyle \frac{⟨u_t^{\prime }(x+r,y,z,t)u_t^{\prime }(x,y,z,t)⟩}{{\sigma }_t^2}},g_w\left(r\right)={\displaystyle \frac{⟨w^{\prime }(x+r,y,z,t)w^{\prime }(x,y,z,t)⟩}{{\sigma }_w^2}}$$

(30)

Substituting (27) into (29), we obtain [14]

$$g\left(r\right)\approx exp\left(-{\displaystyle \frac{r}{\mathcal{L}}}\right)\left(1-{\displaystyle \frac{1}{2}}{\displaystyle \frac{r}{\mathcal{L}}}\right).$$

(31)

The integral of the above formula from 0 to its first zero-crossing equals approximately 0.6 $\mathcal{L}$, and we used this procedure to estimate the transverse and vertical length scales ${\mathcal{L}}_t$ and ${\mathcal{L}}_w$.

$${\mathcal{L}}_t\approx 0.6{\int }_0^{r_0}{g}_t\left(r\right)\mathrm{d}r,{\mathcal{L}}_w\approx 0.6{\int }_0^{r_0}{g}_w\left(r\right)\mathrm{d}r,$$

(32)

where $r_0$ denotes the smallest value of r where the function under the integral crosses zero.

It should be noted here that turbulence in the stable ABL is anisotropic at large scales, and formula (29) does not hold. However, we treat Equation (31) as approximations of the characteristic transverse and vertical length scales and assume that these approximations are sufficient to investigate the tendencies, while the proportionality constant might, in fact, be different from $0.6$. The predictions could possibly be improved by taking into account the anisotropy tensor [16,37]; this task is left for future work.

4. Results

Even though the data were averaged over 20 min blocks, they are still time-dependent, as the flow conditions change with time. This is visible in Figure 1, where the time series of ${\sigma }_t$, ${\mathcal{L}}_t$ and ${ϵ}_t$ at $z=10$ m for January 2020 are presented.

Figure 1. Time series of ${\sigma }_t$, ${\mathcal{L}}_t$ and ${ϵ}_t$ for January 2020.

The integral length scales ${\mathcal{L}}_l$, ${\mathcal{L}}_t$ and ${\mathcal{L}}_w$ as functions of the corresponding standard deviations of the longitudinal ${\sigma }_l$, transverse (cross-stream) ${\sigma }_t$ and vertical ${\sigma }_w$ velocity components are presented in Figure 2. As can be seen, ${\mathcal{L}}_l$ and ${\sigma }_l$ are much larger than the corresponding statistics of the horizontal transverse and vertical components, which indicates that the flow is still strongly anisotropic at $z=10$ m. Apart from the surface vicinity, the anisotropy could be caused by the presence of submeso motions, which affect mostly the horizontal components [21]. The scatter of the results is also much larger for the longitudinal component. This is to be expected, as larger length scales require larger averaging windows. On the other hand, when the averaging windows are too large, information on the time variability of the statistics is lost. We chose an averaging window of 20 min as the best compromise. It enables the calculation of the length scales of the transverse and vertical components with satisfactory accuracy.

Figure 2. Integral length scales, Equations (28) and (32), as functions of the standard deviations of velocity fluctuations estimated from the time series of the longitudinal (top plot), horizontal transverse (middle plot) and vertical components (bottom plot) measured at $z=10$ m.

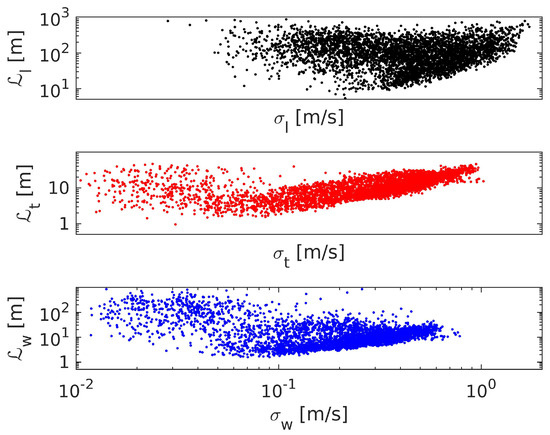
As seen in Figure 2, for large values of ${\sigma }_l$, ${\sigma }_t$ and ${\sigma }_w$, the length scales are proportional to the corresponding standard deviations, as expected for the balanced, shear-driven turbulence; see Equation (23). However, for smaller $\sigma$, subregions of inverse proportionality can be identified in all plots. They correspond to weak decaying turbulence or developing turbulence; see Equation (25). These results show that the leading-order balance of the kinetic energy equation changes over time.

We next investigated how $\sigma$ and $\mathcal{L}$ depend on the stability parameter $\xi =z/L_O$, defined in Equation (19). During the measurements, both positive and negative $\xi$ values were recorded. However, as the latter corresponds to unstable conditions, and the focus of this study is on the stable BL, we present the results only for $\xi >0$. The standard deviations presented in Figure 3 decrease with increasing $\xi$, where turbulence becomes weaker. The longitudinal component ${\sigma }_l$ is the largest, and the vertical one, ${\sigma }_w$, the smallest.

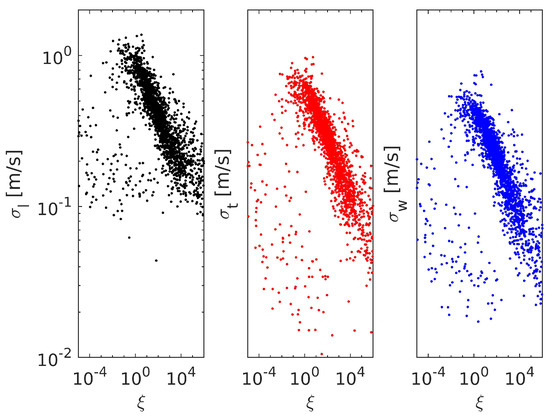
Figure 3. Standard deviations of fluctuating velocity as functions of the stability parameter $\xi =z/L_O$, estimated from the time series measured at $z=10$ m.

The integral length scales as functions of $\xi$ and the estimates that follow from Equation (18) are presented in Figure 4. The solid lines in Figure 4 are the predictions

$$\mathcal{L}\propto {\displaystyle \frac{z}{1+{\alpha }_2\xi }},$$

(33)

with ${\alpha }_2=2.7$, and the proportionality constant was set to 10 in the case of the longitudinal and 1 for the transverse and vertical components.

Figure 4. Integral length scales as functions of the stability parameter $\xi =z/L_O$, estimated from the time series of longitudinal, transverse and vertical velocity measured at $z=10$ m, Equations (28) and (32), compared with the parameterization (33) (solid line).

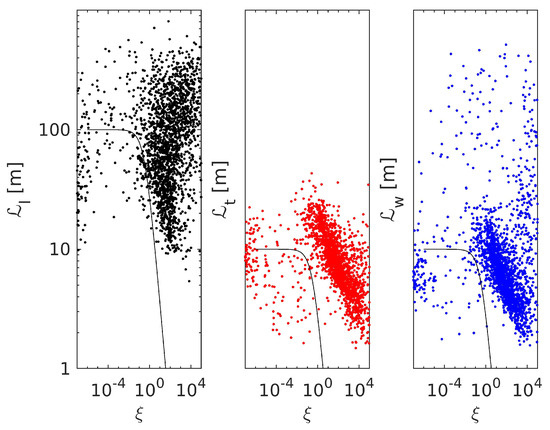
The estimates based on the longitudinal velocity components ${\mathcal{L}}_l$ are much larger than ${\mathcal{L}}_t$ and ${\mathcal{L}}_w$ and considerably scattered. The length scales decrease with increasing $\xi$, although more slowly than predicted by the parameterization schemes (33), which could be more suitable for weaker stratification.

The energy dissipation rate $ϵ$ as a function of $\xi$ is presented in Figure 5. Data for ${ϵ}_l$ are scarce due to deviations from the Kolmogorov scaling. Possibly, the range $f\in [1,3]$ was not optimal for this velocity component; in fact, for smaller f, the slopes of longitudinal spectra become closer to −5/3. However, we decided to use the same range for all three components. In contrast to standard deviations and length scales, the values of $ϵ$ estimated from the frequency spectra of the longitudinal, transverse and vertical components are comparable. This indicates that at small scales, turbulence is much closer to equilibrium for the selected data.

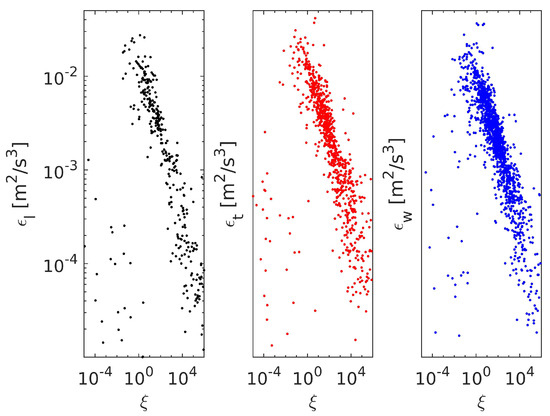
Figure 5. The energy dissipation rate $ϵ$ as a function of the stability parameter $\xi =z/L_O$ (cf. Equation (19)), estimated from the time series measured at $z=10$ m.

Having $ϵ$, $\sigma$ and $\mathcal{L}$, we next calculated the dissipation coefficient $C_{ϵ}$ from formula (1). For this, we used the longitudinal, horizontal transverse and vertical components separately; i.e., we calculated three estimates:

$$C_{ϵ}^l={ϵ}_l{\displaystyle \frac{{\mathcal{L}}_l}{{\sigma }_l^3}},C_{ϵ}^t={ϵ}_t{\displaystyle \frac{{\mathcal{L}}_t}{{\sigma }_t^3}},C_{ϵ}^w={ϵ}_w{\displaystyle \frac{{\mathcal{L}}_w}{{\sigma }_w^3}}.$$

(34)

They are presented in Figure 6 as a function of $\xi$. Even though $\sigma$, $\mathcal{L}$ and $ϵ$ depend strongly on $\xi$, there is no clear dependence of $C_{ϵ}$ on $\xi$, which could support the assumption $C_{ϵ}\approx const$. However, as will be shown further, $C_{ϵ}$ clearly depends on $R{e}_{\lambda }$. Data for $C_{ϵ}^l$ in Figure 6 are scattered, possibly due to large uncertainties in ${\mathcal{L}}_l$ estimates. $C_{ϵ}^w$ is, on average, larger than $C_{ϵ}^t$. The differences between estimates from the three velocity components might follow from the anisotropy of the flow; this dependence was analyzed in Ref. [16].

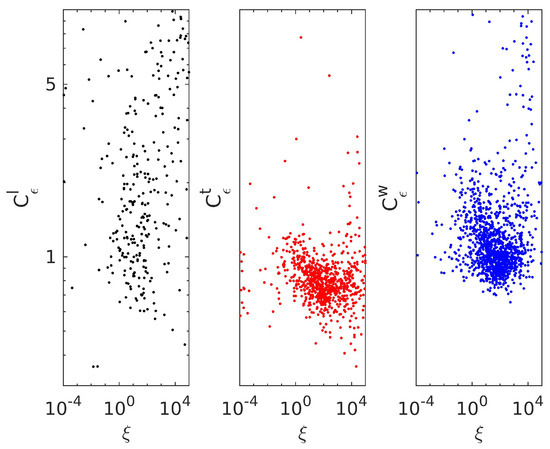
Figure 6. $C_{ϵ}$ estimated from Equation (1) as a function of the stability parameter $\xi =z/L_O$. Calculations were based on the time series of the longitudinal, horizontal transverse and vertical velocity measured at $z=10$ m.

Refs. [11,31,42] suggested that deviations from $C_{ϵ}=const$ follow from deviations from the Kolmogorov scaling at the low-wavenumber part of the spectra; see also Equation (20). To test this hypothesis, we assumed the following form of frequency spectra of the three velocity components:

$$S_l\left(f\right)\propto f^{a_l},S_t\left(f\right)\propto f^{a_t},S_w\left(f\right)\propto f^{a_w}.$$

(35)

and estimated $a_l$, $a_t$ and $a_w$ using the least-squares algorithm in the low-wavenumber interval $f\in [0.1,1]$ Hz. The results are presented in Figure 7. In the selected range of f, the scaling of the longitudinal velocity component was still close to the Kolmogorov $a_l\approx -$1.7 and hence, no dependence of $C_{ϵ}^l$ on $a_l$ was observed. Possibly, the spectra start to deviate from the equilibrium predictions at smaller f. $C_{ϵ}^t$ increases with increasing $a_t$, in line with predictions of [11,42]. Such dependence is also observed for $C_{ϵ}^w$, although it is weaker than for $C_{ϵ}^t$. $C_{ϵ}$ estimation is generally better for the transverse and vertical components, because the corresponding length scales are smaller and the averaging window of 20 min is sufficient to calculate ${\mathcal{L}}^t$ and ${\mathcal{L}}^w$ with good accuracy. Interestingly, the authors of Ref. [21] found that parameterizations of the energy dissipation rate based on the vertical velocity are more robust than parameterizations based on the turbulence kinetic energy, because the former is less affected by submeso motions. Following this idea, we further focus on the statistics of the horizontal transverse and vertical velocity components.

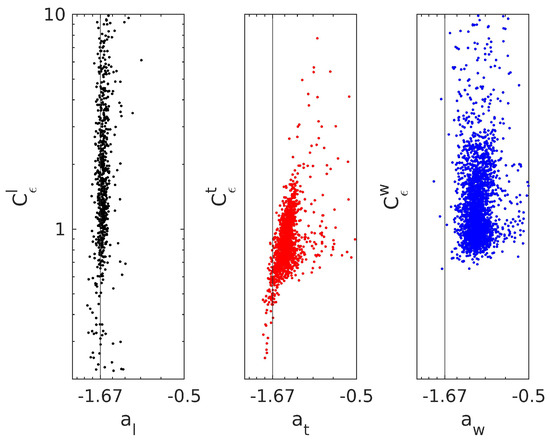
Figure 7. Slopes of frequency spectra for the interval $f\in [0.1,1]$ Hz. Calculations were based on the time series of longitudinal (left panel), horizontal transverse (middle panel) and vertical (right panel) velocity measured at $z=10$ m.

$C_{ϵ}^t$ and $C_{ϵ}^w$ as a function of the Reynolds number $R{e}_{\lambda }$ are presented in Figure 8 and Figure 9. A subregion of the classical scaling with $\alpha \approx 0$ in Equation (2) is visible only at a restricted range of $Re$. For a high $Re$, clearly $\alpha >0$.

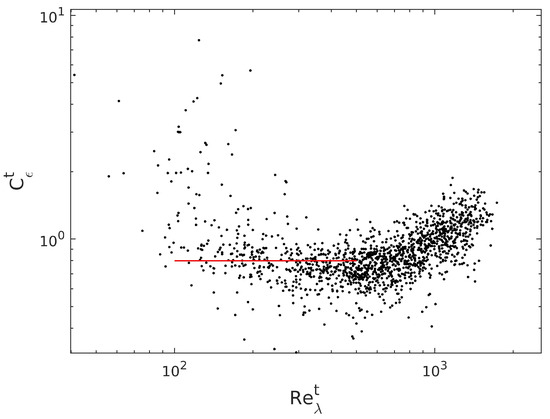
Figure 8. $C_{ϵ}^t$ as a function of the Reynolds number $R{e}_{\lambda }^t$. Classical scaling $C_{ϵ}\approx const$ is denoted by the red line.

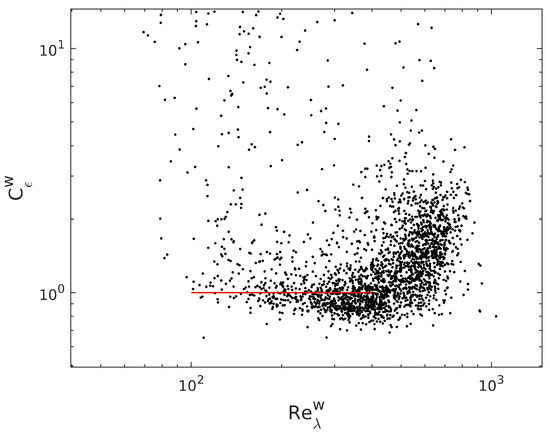
Figure 9. $C_{ϵ}^w$ as a function of the Reynolds number $R{e}_{\lambda }^w$. Classical scaling $C_{ϵ}\approx const$ is denoted by the red line.

The ratios of the length scales ${\lambda }_t/L_t$ and ${\lambda }_w/L_w$ as a function of $R{e}_{\lambda }$ are presented in Figure 10 and Figure 11. At the smallest $R{e}_{\lambda }$, the scatter of the results is considerable. The maximum of $\lambda /L$ is observed at $R{e}_{\lambda }\approx 100$; next, the ratio $\lambda /L$ decreases with increasing $R{e}_{\lambda }$. The slope also changes and becomes steeper than the −1 equilibrium prediction at the largest $R{e}_{\lambda }$.

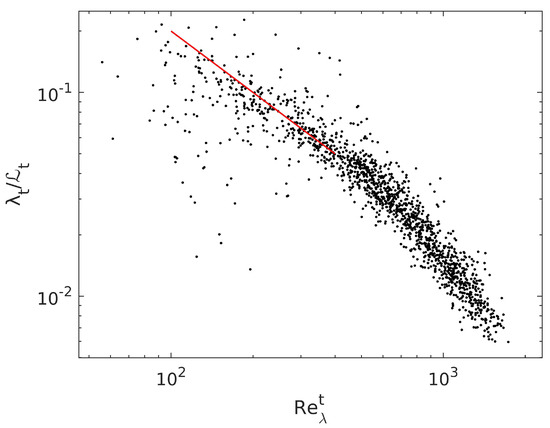
Figure 10. The ratio ${\lambda }_t/{\mathcal{L}}_t$ as a function of the Reynolds number $R{e}_{\lambda }^t$. Classical scaling ${\lambda }_t/{\mathcal{L}}_t\propto 1/R{e}_{\lambda }^t$ is denoted by the red line.

Figure 11. The ratio ${\lambda }_w/{\mathcal{L}}_w$ as a function of the Reynolds number $R{e}_{\lambda }^w$. Classical scaling ${\lambda }_w/{\mathcal{L}}_w\propto 1/R{e}_{\lambda }^w$ is denoted by the red line.

5. Discussion

In this work, we investigated the dissipation law (1) without assuming the constancy of the dissipation coefficient $C_{ϵ}$. We analyzed times series of stably stratified turbulence from the MOSAiC expedition and calculated the standard deviations of velocity components, energy dissipation rates and integral length scales. After substituting them into formula (1), we found that $C_{ϵ}$ and the ratio $\lambda /\mathcal{L}$ depend on the local Reynolds number $R{e}_{\lambda }$. This variability can easily be included in turbulence parameterization schemes for a stable ABL. The dependence $C_{ϵ}\propto R{e}_{\lambda }^{\alpha }$ was found in previous studies in various laboratory experiments [7,12,13,42] and in the ABL, above the surface layer [14]. In those previous studies, $\alpha \approx -$1 was found in certain regions of the flow, indicating the presence of non-equilibrium turbulence. We found the inverse relation between $C_{ϵ}$ and $R{e}_{\lambda }$ only at the smallest Reynolds numbers; however, the scatter of the results was too large to draw any definite conclusions. At intermediate Reynolds numbers, $R{e}_{\lambda }\in [100,400]$, the coefficient $\alpha \approx 0$, and next, it became positive; see Figure 8 and Figure 9. In contrast to previous laboratory experiments with near-wall turbulence [13], we could not identify a region where $C_{ϵ}\approx const$ at very large $Re$. This fact is intriguing and could possibly indicate that, in atmospheric turbulence, the fully developed, stationary state is never reached.