Integration of WRF-Chem Model-Based, Satellite-Based, and Ground-Based Observation Data to Predict PM2.5 Concentration by Machine Learning Approach

Abstract

Fine particulate matter (PM2.5) is a critical environmental and health concern in northern Thailand, where haze episodes are strongly influenced by biomass burning, meteorological variability, and complex topography. This study aims to (1) analyze and select input variables for PM2.5 prediction by integrating WRF-Chem outputs, satellite data, and ground observations, and (2) evaluate the predictive performance of four machine learning (ML) algorithms—Random Forest (RF), XGBoost, CNN3D, and ConvLSTM—during the 2024 haze season (January–May). The dataset included hourly PM2.5 observations from 54 stations, the WRF-Chem-simulated PM2.5 and meteorological variables, satellite-based fire data, and geographical data. To improve consistency with ground-based data, WRF-Chem PM2.5 values were bias-corrected for the training and validation phases prior to ML learning. Among Linear Regression, RF, XGBoost, Artificial Neural Network (ANN), and Convolutional Neural Network (CNN) tested for bias correction, RF achieved the best performance (R = 0.78, RMSE = 29.28 µg/m³); the RF-corrected WRF-Chem PM2.5 was then used as an input to the forecasting stage. Variable selection was supported by correlation, VIF, feature importance, and SHAP analyses. The results indicate that RF provided the most reliable predictions, achieving a correlation of R = 0.867 and the lowest RMSE of 27.6 µg/m³ when using the SHAP+VIF-selected input set (seven variables: PM2.5_lag1, PM2.5_lag24, T2, RH2, Precip, Burned Area, NDVI). Notably, RF remained the top performer, predicting PM2.5 more accurately than the other algorithms during high-pollution conditions, specifically Air Quality Index (AQI) “Unhealthy for Sensitive Groups” (high) and “Unhealthy” (very high). Taken together, RF set the performance bar across both stages, with XGBoost ranked second, whereas CNN3D and ConvLSTM performed considerably worse. These findings emphasize the effectiveness of ensemble tree-based algorithms combined with bias-corrected WRF-Chem outputs and strategic variable selection in supporting accurate hourly PM2.5 predictions for air quality management in biomass burning regions.

1. Introduction

Particulate matter with a diameter smaller than 2.5 μm (PM2.5) is an air pollutant so fine that it is invisible to the naked eye but can penetrate the human body through inhalation. These particles can travel deep into the lungs, enter the bloodstream and cause long-term effects on the cardiovascular and pulmonary systems [1]. According to the World Health Organization (WHO), PM2.5 is a major cause of premature mortality worldwide and is associated with chronic diseases and lung cancer [2]. In some regions, PM2.5 concentrations may rise to levels that pose serious risks to public health [3]. Sources of PM2.5 include both natural phenomena, such as wildfires and desert dust, and anthropogenic activities [4], and episodes intensify when the atmosphere is stable, such as weak winds, shallow boundary layers, and temperature inversions that trap pollutants near the surface [5]. In rapidly urbanizing areas, combustion processes and atmospheric chemical reactions lead to pollutant accumulation and direct health effects [6].

This problem is particularly pronounced in northern Thailand, where complex mountainous terrain surrounds many urban areas in basins and valleys [7]. Under atmospheric conditions, pollutants can become trapped, especially during the dry season when haze episodes occur regularly each year [8]. A 2024 study revealed that several provinces experienced more than 50 consecutive days of PM2.5 levels exceeding the national standard ambient air quality standard of 37.5 µg/m³, with peak hourly concentrations surpassing 200 µg/m³, a level considered extremely hazardous to health [9]. In addition to its respiratory and cardiovascular effects, PM2.5 exposure has also been associated with ocular health issues, such as conjunctival redness, tearing, and dryness, with some symptoms showing up to a twelve-fold increase in risk compared to clear-air days [10]. Biomass burning in northern Thailand, primarily driven by forest fires, constitutes the dominant form of biomass combustion in the region and occurs intensively during the dry season [11]. This emission source has been identified as a major contributor to transboundary air pollution, underscoring the strategic importance of accurate forecasting for air quality management and environmental policymaking [12].

Climate change is projected to significantly affect air quality-related meteorological conditions in Upper Northern Thailand, particularly during the haze season. Increases in the maximum temperature may enhance pollutant emissions, whereas a higher minimum temperature, together with reductions in the surface wind speed and planetary boundary layer height, are expected to weaken vertical dispersion and ventilation, creating favorable conditions for PM2.5 accumulation [13]. Meteorological variables, including wind speed, rainfall, humidity, and temperature inversions, have been shown to significantly influence spatial PM2.5 accumulation patterns in the basin topography of Chiang Mai, particularly during dry-season stagnation events [14]. Physics-based models, such as WRF-Chem, enable high-resolution simulations of atmospheric chemical processes, which are critical for understanding the formation and transport of air pollutants [15]. However, they are constrained by uncertainties in emission inventories, computational demands, and grid-related errors in complex terrains [16]. Satellite data extend spatial coverage but face issues of cloud contamination, vertical uncertainty and nonlinear relationships with ground-level PM2.5 [17]. Ground-based observations are highly accurate but spatially uneven, being concentrated in urban centers and failing to represent rural or forested emission regions [18]. Collectively, these strengths and limitations highlight the necessity of multi-source data integration to support robust and spatially consistent PM2.5 predictions.

Therefore, the concepts of data fusion and integration have gained increasing attention. For instance, Joharestani et al. employed ML models, such as RF, XGBoost, and Deep Learning, to integrate satellite-derived data, meteorological variables, and ground-based observations in Tehran [19]. Their results improved R² up to 0.81 and reduced the RMSE to 9.93 µg/m³, demonstrating the potential of multi-source integration to substantially enhance PM2.5 prediction accuracy [19]. In Thailand, particularly in the northern region, where complex terrain and multiple emission sources prevail, research of this nature remains limited, representing a critical research gap that this study seeks to address. Similarly, Feng et al. (2022) used satellite reflectance in combination with meteorological variables in hybrid models (RF, LightGBM), achieving an R² of 0.91 and reducing the RMSE to 11.6 µg/m³ compared to using AOD alone, further highlighting the benefits of multi-source data integration combined with advanced ML techniques [17].

At the same time, several studies have highlighted the limitations of physics-based models when applied in complex regions. Lyu et al. (2017) reported that although the CMAQ driven by WRF captured overall PM2.5 patterns, it still exhibited substantial biases in many areas, with accuracy depending on the grid resolution and emission inventory completeness [20]. Similarly, Dou et al. (2021) found that WRF-CMAQ failed to fully capture high-concentration pollution episodes, particularly in heavily polluted industrial areas such as the North China Plain [21]. These findings emphasize the need for complementary approaches, such as ML, which can learn complex cross-source relationships, and bias correction techniques, which can adjust model outputs to be closer to the observed values. For example, Singh et al. demonstrated that deep learning-based bias correction reduced RMSE by 25–41% and increased the Index of Agreement (IOA) above 0.70 compared with original CMAQ outputs [22]. Recent work in Chiang Mai further showed that statistical models, such as the Generalized Additive Model (GAM), incorporating environmental and temporal predictors (temperature, humidity, month, hour), significantly improved agreement with ground-based observations (R² = 0.92, RMSE = 5.08 µg/m³). Comparable performance was observed for Linear Regression (LR) (R² = 0.90, RMSE = 5.49 µg/m³) and RF when using only environmental variables (R² = 0.89, RMSE = 5.74 µg/m³), while bias correction with GAM reduced the mean absolute percentage error (MAPE) to 17% [23].

The suitability of ML algorithms largely depends on the data structure and spatiotemporal complexity. Tree-based models, such as RF and XGBoost, are well-suited for tabular data with nonlinear characteristics and provide interpretability through variable importance rankings; however, they cannot directly capture temporal sequences [19,24]. In contrast, Deep Learning models, such as Convolutional Neural Networks (CNNs), excel at extracting spatial features from satellite imagery, whereas Convolutional LSTM (ConvLSTM) integrates the strengths of CNN and LSTM to jointly capture spatial and temporal dependencies. These models are particularly effective for fine-scale daily PM2.5 forecasting, as shown by Zhang et al. (2020) and Sohrabi and Maleki (2025), who successfully combined satellite imagery and ground-based measurements to achieve accurate spatial predictions [25,26]. In contrast, basic models such as Multilayer Perceptron (MLP) and LSTM can handle temporal sequences but lack explicit spatial feature extraction, limiting their performance in complex spatiotemporal contexts. Mitreska et al. (2023) demonstrated that ConvLSTM significantly outperformed CNN-LSTM [27], while Shi et al. (2024) reported that the performance of LSTM in PM2.5 prediction decreases in regions with high spatial variability [28]. This reflects a limitation of the model in capturing complex spatial contexts, suggesting that hybrid models capable of learning multidimensional patterns may offer greater potential for both short- and long-term of PM2.5 predictions.

In this context, the present study had two primary objectives: (1) to analyze and identify suitable input variables for PM2.5 prediction by integrating WRF-Chem outputs, satellite data, and ground-based measurements; and (2) to evaluate the predictive performance of four ML algorithms—two tree-based models (RF and XGBoost) and two deep learning models (CNN and ConvLSTM)—for forecasting PM2.5 concentrations during the haze and biomass burning seasons in Chiang Mai, Thailand. The study period covered the haze season of 2024 (approximately January–May). The dataset includes ground-based PM2.5 measurements, WRF-Chem PM2.5 and meteorological variables (e.g., temperature, humidity, wind, and precipitation), geographical variables (DEM, NDVI, and LULC), and fire-related variables (hotspots and burn scars). Importantly, PM2.5 outputs from WRF-Chem were bias-corrected using ground-based observations before the ML model training. The model performance was assessed through cross-validation using different statistical indicators.

2. Data and Methods

2.1. Study Area

The study area (Figure 1) was Chiang Mai Province and its surrounding regions in northern Thailand, corresponding to Domain 3 of the WRF-Chem model. The domain is geographically located between approximately 18°30′–19°30′ N and 98°30′–99°30′ E, covering Chiang Mai as the central focus and extending into parts of the adjacent provinces, including Lamphun, Lampang, Mae Hong Son and Chiang Rai. The terrain of this area is diverse, characterized primarily by a central plain encircled by high mountains, resulting in a basin topography. These geographical features promote the accumulation of air pollutants, thereby facilitating the persistence of PM2.5, particularly during the winter and dry seasons.

2.2. Time Period

The study period was from January to May 2024, which corresponds to the haze and biomass-burning seasons in northern Thailand. This period is characterized by the highest annual accumulation of PM2.5 and represents particularly challenging conditions for air quality forecasting. The selection of this timeframe allowed for the evaluation of the performance of the models under highly variable conditions with diverse emission sources.

2.3. Data Preprocessing and Integration

This study employed multi-source datasets to enhance the spatial and temporal coverage of the PM2.5 prediction. The datasets consisted of outputs from the WRF-Chem model, satellite-derived products, and ground-based observations of air quality. Data preprocessing is a crucial step in ensuring the consistency, reliability, and suitability of datasets for machine learning (ML) model development. The details of the datasets are summarized in

Table 1. List of data and study information.

Data	Variable	Abbreviation	Unit	Period
Ground-based Observation data	PM2.5 from 54 station monitor	PM2.5_obs	µg m−3	January–May 2024 (hourly)
PM2.5 (WRF-Chem model-based data)	PM2.5 from WRF-Chem	WRF-PM2.5	µg m−3	January–May 2024 (hourly)
Meteorological (WRF-Chem model-based data)	Temperature (2 m)	T2	°C	January–May 2024 (hourly)
	Relative Humidity (2 m)	RH2	%
	Wind Speed (10 m)	WS10	m/s
	Wind Direction (10 m)	WD10	degree
	Precipitation	Precip	mm
	Planetary Boundary Layer	PBLH	m
	Ventilation Index	Venting	m2/s
Fire Variables (Satellite-based data)	Burned Area	Burned Area	ha	January–May 2024 (monthly)
	Hotspot Density	Hotspot Density	count/pixel (1 km)	January–May 2024 (daily)
Geographical (Satellite-based data)	Digital Elevation Model	DEM	m	Static
	NDVI	NDVI	unitless	January–May 2024 (16-day)
	Land Cover	Land Cover	class code	2024 (annual)

, and the main procedures are described as follows.

2.3.1. WRF-Chem Model-Based Data

The Weather Research and Forecasting model coupled with Chemistry (WRF-Chem) has been widely applied in atmospheric chemistry and air quality studies [29]. The WRF-Chem simulations were conducted using the 0.1° × 0.1° resolution EDGAR-HTAP anthropogenic emission inventory [30], while the 3BEM model [31] was applied to generate the biomass-burning emission dataset used as primary emission inputs. Both inventories provide consistent global coverage with detailed sectoral classifications and were processed to match the model’s spatial and temporal resolution prior to integration. It serves as a primary source of information for simulating pollutant dispersion and the associated meteorological conditions. The meteorological variables employed in this study are listed in Table 1 and include PM2.5 concentrations simulated by WRF-Chem (WRF-PM2.5), near-surface temperature at 2 m above ground (T2), relative humidity at 2 m (RH2), wind speed at 10 m (WS10), wind direction at 10 m (WD10), precipitation (Precip), planetary boundary layer height (PBLH), and venting index (Venting). These variables were simulated on a 99 × 99 grid with a spatial resolution of 1 km² and an hourly temporal resolution, covering the period from January to May 2024.

The WRF-Chem outputs were further downscaled to a spatial resolution of 1 km² to better represent local heterogeneity and align with the requirements for high-resolution PM2.5 forecasting. Although this downscaling process may introduce additional uncertainties and slightly reduce the statistical accuracy of the raw simulations, it provides enhanced spatial detail and ensures consistency in integrating meteorological data. In complex basin terrain, a 1 km grid helps resolve slope/valley winds and cold-air pooling that trap pollutants overnight [32,33], and it reduces spatial averaging that can smear localized hotspots at coarser grids [34]; thus, the 1 km grid serves as a common geo-temporal backbone for pixel-level fusion of station, WRF-Chem, satellite-fire, and geospatial layers used in this study [35].

2.3.2. Satellite-Based Data

Satellite-derived datasets were integrated to complement partial information related to topography, vegetation, land use, and biomass burning. Two categories of satellite-based data were used: (1) geographical data and (2) fire-related variables, each contributing to the spatiotemporal representation of PM2.5 dynamics in the study area.

• Geographical Data
  • Digital Elevation Model (DEM): Obtained from NASA’s Shuttle Radar Topography Mission (SRTM) with a resolution of 30 arc-seconds (~1 km²). DEM data provide elevation information that is critical for assessing pollutant accumulation in complex terrains [36].
  • Normalized Difference Vegetation Index (NDVI): Derived from MODIS MOD13Q1, representing vegetation greenness in the study area. The NDVI facilitates the assessment of agricultural and forest changes that influence PM2.5 distribution [37].
  • Land Use/Land Cover (LULC): Extracted from MODIS MCD12Q1, providing land classification categories such as forests, croplands, and urban areas. These data enhance the interpretation of emission sources across different land use types [38].
• Fire Variables Data
  • Burned Area: Derived from the MODIS MCD64A1 Burned Area Product, with a 1 km² spatial resolution and monthly frequency, indicating areas affected by open burning and forest fires during January–May 2024 [39].
  • Hotspot Density: Obtained from the VIIRS FIRMS product based on the Suomi NPP and NOAA-20 VIIRS sensors. With a spatial resolution of 375 m and daily temporal coverage, this dataset represents fire hotspots per pixel and is crucial for capturing biomass burning activities in regions without monitoring stations [40].

2.3.3. Ground-Based Observation Data

Ground-based air quality monitoring stations provided highly accurate point-based PM2.5 observations, which were essential for both the bias correction of the WRF-Chem outputs and the validation of the ML models. In this study, hourly PM2.5 concentrations from 54 stations within WRF-Chem Domain 3 were used, consisting of four stations operated by the Pollution Control Department of Thailand (PCD) [41] and 50 additional stations from the DustBoy Open API, which is provided by the Climate Change Data Center at Chiang Mai University (CCDC-CMU) [42]. The performance was evaluated between the PCD reference monitors and DustBoy sensors, showing strong agreement with correlation coefficients (r) of 0.89 to 0.94 and determination coefficients (R²) of 80.24–87.41%, confirming the reliability of DustBoy measurements [43].

2.3.4. Construction of Spatial and Temporal Encoding Variables

In the data preprocessing stage, spatial and temporal encoding variables were generated to enable the ML models to capture spatiotemporal patterns more effectively. The constructed variables included hour, dayofyear, hour_sin, hour_cos, dayofyear_sin, dayofyear_cos, lat_sin, lat_cos, and lon_sin. These variables enhanced the model’s ability to recognize diurnal and seasonal cycles and the spatial distribution of PM2.5 in the environment.

These variables were generated to encode cyclical temporal patterns and spatial coordinates into a format suitable for machine learning models, particularly those sensitive to input scaling and periodicity, such as tree-based and neural network (NN) algorithms. All derived spatial and temporal features were included in each variable group to enhance the representation of cyclic temporal dynamics and spatial distributions in the machine learning input space. The details of these variables are summarized in

Table 2. List of Derived Variables for Spatial and Temporal Encoding.

Variable	Description	Type	Unit/Scale	Formula
hour	Hour of the day	Temporal	0–23	Extracted from timestamp
dayofyear	Day of the year	Temporal	1–365	Extracted from timestamp
hour_sin	Sine transform of hour	Temporal (cyclic)	−1 to 1	sin (2π × hour/24)
hour_cos	Cosine transform of hour	Temporal (cyclic)	−1 to 1	cos (2π × hour/24)
dayofyear_sin	Sine transform of day of year	Temporal (cyclic)	−1 to 1	sin (2π × dayofyear/365)
dayofyear_cos	Cosine transform of day of year	Temporal (cyclic)	−1 to 1	cos (2π × dayofyear/365)
lat_sin	Sine transform of latitude	Spatial (cyclic)	−1 to 1	sin (radians (latitude))
lat_cos	Cosine transform of latitude	Spatial (cyclic)	−1 to 1	cos (radians (latitude))
lon_sin	Sine transform of longitude	Spatial (cyclic)	−1 to 1	sin (radians (longitude))
lon_cos	Cosine transform of longitude	Spatial (cyclic)	−1 to 1	cos (radians (longitude))

.

2.3.5. Construction of Lag Variables

To account for the temporal accumulation and persistence of PM2.5 pollution, a set of nine lag variables was generated: PM2.5_lag1, PM2.5_lag2, PM2.5_lag3, PM2.5_lag6, PM2.5_lag12, PM2.5_lag18, PM2.5_lag24, PM2.5_lag48, and PM2.5_lag72. The selection of these lag intervals was motivated by the characteristics of PM2.5 formation and accumulation, which are influenced by biomass burning events and meteorological conditions in the hours preceding the event. Multiple lag periods allowed the models to capture short- and long-term carryover effects, particularly at high PM2.5 concentrations. Therefore, incorporating lagged predictors facilitated the learning of complex temporal dependencies and improved the model’s ability to forecast PM2.5 concentrations over an extended horizon.

After all preprocessing steps, datasets from different sources, including WRF-Chem outputs, satellite products, and ground-based observations, were integrated using regridding and spatial interpolation techniques to harmonize the spatial and temporal frequencies. For station-based PM2.5 surfaces, we used ordinary kriging with a spherical variogram on an intermediate 1 km grid and then reprojected and bilinearly resampled the interpolated fields to the reference 1 km WRF-Chem grid. Hourly quality control requires (1) station coverage spanning the reference domain and (2) at least three stations with non-constant values; Variogram fit diagnostics were reviewed to ensure the presence of a plausible structure. For variables available only at daily or monthly frequencies, we performed temporal downscaling by replicating each daily/monthly value across all hours within its period to construct an hourly time series. These stepwise constant series were used as slowly varying covariates rather than hourly targets. To limit artifacts from replication (e.g., step effects, aliasing, phase-lag), we applied monthly standardization, added day-of-year sine/cosine terms to encode smooth seasonality, leveraged lagged PM2.5 and hourly meteorology to supply diurnal variability, and applied each product’s quality assurance and quality control masks while avoiding period-boundary edges. Regridding was applied to adjust the satellite and monitoring station data to match the 1 km² WRF-Chem grid, and spatial interpolation was employed to fill the gaps in areas without monitoring stations. This integration ensured that all datasets were consistent and suitable for subsequent machine learning modeling.

2.4. Data Preparation and Splitting

For machine learning model development, the datasets were prepared in two primary formats: tabular and sequence formats, depending on the type of model employed for the PM2.5 prediction. The data preparation process is described below.

• Tabular Format: Applied to tree-based models such as RF and XGBoost. In this format, the data were structured in a tabular form, where each column represented an input variable. These variables were selected and grouped based on the results of the variable relationship analysis [44].
• Sequence Format: Applied to sequential-based models such as Long Short-Term Memory (LSTM), CNN, and ConvLSTM. In this format, the data were organized into time-series sequences, which enabled the deep learning models to capture the temporal dependencies and dynamic variations in the data [45].

All datasets were divided into three subsets: training, validation, and test sets, which corresponded to model training, performance monitoring during training, and final evaluation, respectively. Data splitting was based on the Air Quality Index (AQI) categories defined by the PCD, which classifies air quality into five levels: very good, good, moderate, unhealthy for sensitive groups (high), and unhealthy (very high) (

Table 3. PM2.5 concentration values equivalent to the Air Quality Index.

PM2.5 (µg/m3)	Air Quality Index (AQI) Range
0–15	Very Good
15.1–25.0	Good
25.1–37.5	Moderate
37.6–75.0	High
>75.0	Very high

).

• Test set: Selected from four periods, each consisting of six consecutive days, during which AQI values fell within the unhealthy and unhealthy for sensitive groups categories.
• Validation set: Selected from periods with PM2.5 concentrations comparable to those of the test set to ensure consistency in evaluation.
• Training set: Composed of the remaining periods, covering all AQI categories to ensure the representation of diverse atmospheric conditions.

This strategy ensured that the training set encompassed the full range of AQI levels, whereas the validation and test sets specifically targeted high-pollution episodes. Such a design allowed the models to learn from diverse input conditions and be tested under the most challenging scenarios for PM2.5 forecasting. The details of the selected training, validation, and test datasets are listed in

Table 4. Train Validation and Test Dataset.

Dataset	Period	Num Day	Date Period	AQI Range
Train set	1	21	1 January 2024 00:00 to 21 January 2024 23:00	Good
	2	5	28 January 2024 00:00 to 1 February 2024 23:00	Good
	3	32	8 February 2024 00:00 to 10 March 2024 23:00	Moderate–very high
	4	16	17 March 2024 00:00 to 1 April 2024 23:00	Moderate–very high
	5	11	8 April 2024 00:00 to 18 April 2024 23:00	Moderate–very high
	6	9	1 May 2024 00:00 to 9 May 2024 23:00	Moderate–very high
	7	10	22 May 2024 00:00 to 31 May 2024 23:00	Very good–Good
Validation set	1	6	2 February 2024 00:00 to 7 February 2024 23:00	Moderate
	2	6	11 March 2024 00:00 to 16 March 2024 23:00	Very high
	3	6	25 April 2024 00:00 to 30 April 2024 23:00	High
	4	6	10 May 2024 00:00 to 15 May 2024 23:00	Good
Test set	1	4	22 January 2024 00:00 to 25 January 2024 23:00	Moderate
	2	4	2 April 2024 00:00 to 5 April 2024 23:00	Very high
	3	4	19 April 2024 00:00 to 22 April 2024 23:00	High
	4	4	16 May 2024 00:00 to 19 May 2024 23:00	Very good–Good

.

In addition, prediction experiments were designed to predict PM2.5 concentrations 24 h ahead, with evaluations conducted across four AQI categories, as defined in the test set (Table 4). Each prediction utilized the preceding three days (72 h) of data as input, followed by one day (24 h) of data for the prediction. This setup reflects the practical requirements for short-term air quality prediction and enables models to capture immediate atmospheric dynamics while being assessed under varying pollution levels. To ensure a like-for-like comparison across model families and to isolate algorithmic effects from window design, the same 72 h input → 24 h prediction window was applied to all models (RF, XGBoost, CNN3D, ConvLSTM). The 72 h look-back is sufficiently long to encompass both diurnal cycles and multi-day accumulation/dispersion that characterize high-AQI episodes yet compact enough to avoid excessive smoothing and complexity during training. Independent evidence also indicates that incorporating a multi-day context can sustain forecast skill at longer lead times in hourly PM2.5 forecasting [46]. By aligning the prediction windows with high-pollution episodes identified in the test set, the evaluation framework established a rigorous basis for examining the robustness and responsiveness of the model to rapid changes in the air quality.

2.5. Bias Correction of WRF-Chem PM2.5

After preparing all variables, the next step was to perform bias correction on the PM2.5 outputs from the WRF-Chem model to reduce discrepancies between the simulated and observed concentrations from the ground-based monitoring stations. Ground observations were used as a reference for adjusting the WRF-Chem PM2.5 values, thereby improving the accuracy and reliability of PM2.5 forecasting, particularly in areas with sparse or no monitoring data.

Following previous studies [22,23], this study evaluated multiple bias-correction approaches to assess their effectiveness in reducing model errors and improving the predictive accuracy. Bias correction was performed using the training and validation datasets, while the test set was excluded to avoid overfitting. The corrected PM2.5 values were subsequently employed as target variables for machine learning model training and were validated using an independent test set. Five algorithms were compared: Linear Regression (LR), used to adjust linear discrepancies between WRF-Chem simulations and ground observations; Artificial Neural Network (ANN), designed to capture complex and non-linear relationships; Random Forest (RF), which aggregates multiple decision trees to improve accuracy and reduce variance; Extreme Gradient Boosting (XGB), employing an iterative boosting mechanism to refine predictions; and Convolutional Neural Network (CNN), applied for spatial bias correction by learning spatial patterns from WRF-Chem outputs to adjust PM2.5 concentrations at each pixel [23].

The performance of the bias correction models was assessed using statistical indicators, including the correlation coefficient (R), coefficient of determination (R²), mean absolute error (MAE), and root mean square error (RMSE), to identify the most suitable approach for improving the WRF-Chem PM2.5 estimates [22,23].

2.6. Variable Relationship Analysis

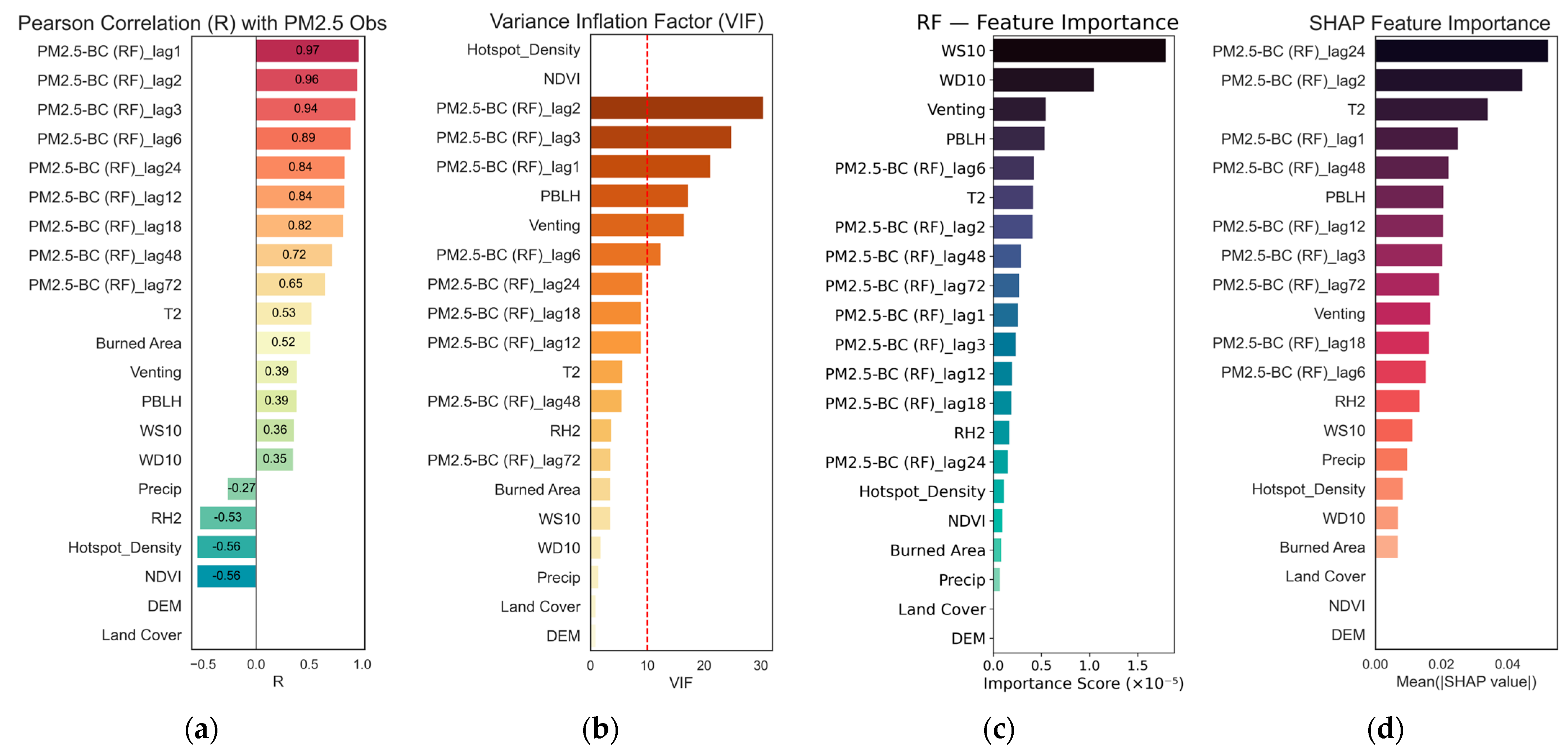
Variable Relationship Analysis is a critical step that directly influences the performance of PM2.5 forecasting models, with the objective of selecting and grouping input variables appropriately prior to their application in ML model development.

• Pearson’s Correlation Coefficient was used to assess linear relationships between variables, with |r| > 0.5 and p < 0.05 serving as the threshold for selecting moderately to strongly correlated predictors [47].
• The Variance Inflation Factor (VIF) was employed to detect multicollinearity, where variables with VIF < 5 were considered acceptable, values of 5–10 required caution, and those exceeding 10 were candidates for removal or feature consolidation [48].
• Random Forest Feature Importance evaluates variable relevance by measuring impurity reduction across decision trees, with top-ranked or above-average importance features retained to preserve model performance [49]. In this study, an impurity-based (split-based) feature importance was computed from the trained ensemble, averaged across the trees and normalized. Features were ranked and retained if they exceeded the median of the group.
• SHapley Additive exPlanations (SHAP), based on cooperative game theory, were applied to interpret the model outputs. Features with higher SHAP values were prioritized, whereas near-zero features were considered less relevant [50]. In this study, SHAP (game-theoretic attribution) was applied to the fitted tree ensemble, and the importance was summarized by the mean absolute SHAP value over the evaluation split to obtain a stable rank order. A model-specific SHAP implementation for tree ensembles was used, and rankings were interpreted jointly with correlation and VIF to mitigate collinearity.

2.7. Feature Grouping for Input Machine Learning Algorithms

Following the statistical and model-based assessments described in Section 2.6, all selected predictors were systematically organized into meaningful categories to form the input feature groups used in the machine learning (ML) model. The grouping aimed to ensure that variables with similar physical characteristics or functional roles were evaluated together, thereby facilitating model interpretability and performance comparison under different input scenarios. All sources were co-registered on a common 1 km, hourly grid to enable pixel-level fusion and consistent group comparisons.

The classification of variables was guided by both their physical relevance to PM2.5 formation and their statistical independence, as derived from previous analyses. Accordingly, all predictors were divided into four categories.

• Lag Variables, representing temporal persistence and autocorrelation of PM2.5 concentrations.
• Meteorological Variables describing atmospheric and dispersion conditions.
• Fire Variables indicating emission intensity and biomass burning activity.
• Geographical Variables represent surface and land cover characteristics that influence pollutant distribution.

Based on these categories, multiple feature groups were constructed by combining different sets of variables to test the sensitivity and robustness of the ML models. Specifically, we pre-defined six feature-comparison groups for planned evaluation on the 1 km grid: (group 1) temporal-only, (group 2) meteorology-only, (group 3) meteorology + fire, (group 4) meteorology+ geography, (group 5) All Variables (Full Set), and a compact set selected by SHAP+VIF (group 6); full variable listings appear in the results. This systematic grouping strategy provided a structured framework for examining the incremental contribution of each domain (temporal, meteorological, fire-related, and geographical) to the model’s predictive skill while maintaining parsimony and interpretability.

2.8. Machine Learning Algorithms

In this study, four ML algorithms suitable for PM2.5 forecasting were employed: Random Forest (RF), Extreme Gradient Boosting (XGBoost), Three-Dimensional Convolutional Neural Networks (CNN3D), and Convolutional Long Short-Term Memory (ConvLSTM). Each algorithm was tuned and trained using the pre-processed datasets described in the previous sections. The advantage of selecting these models lies in their ability to handle complex, high-dimensional data and learn effectively from spatiotemporal data.

2.8.1. Random Forest (RF)

Random Forest (RF) is a supervised ensemble learning technique that constructs multiple decision trees from bootstrap samples and aggregates their predictions to improve accuracy and reduce variance [51]. It is particularly suitable for tabular data without explicit temporal structures and provides transparent estimates of feature importance. Key structural hyperparameters, such as the number of trees (n_estimators), maximum depth (max_depth), splitting criteria, and minimum number of samples per leaf (min_samples_leaf), directly influenced the model’s ability to capture the complex patterns. In this study, grid search optimization was applied using the RMSE of the validation set as the primary evaluation metric. The structural hyperparameters are listed in

Table 5. Structural Hyperparameters of the Random Forest (RF) Algorithm.

Structural Hyperparameter	Value
Input shape	N, D
n_estimators	200, 400, 800
max_depth	16, 24, None
min_samples_leaf	1, 2
max_features	1.0, “sqrt”

Note: N and D denote the sample size and the number of input features, respectively.

.

2.8.2. Extreme Gradient Boosting (XGBoost)

XGBoost is a boosting algorithm that iteratively refines prediction accuracy by learning from the residual errors of prior models [52]. Its strengths lie in its computational efficiency and built-in regularization mechanisms, which reduce the overfitting. Structural hyperparameters, such as the learning rate, number of trees, tree depth, subsampling ratio, and regularization parameters, determine the model’s ability to effectively capture nonlinear relationships. In this study, XGBoost was tuned using a grid search with the RMSE as the evaluation criterion. The full configuration is presented in

Table 6. Structural Hyperparameters of the XGBoost Algorithm.

Structural Hyperparameter	Value
Input shape	N, D
n_estimators	200, 400, 800
max_depth	4, 6, 8
learning_rate	0.05, 0.1
subsample	0.8, 1.0
colsample_bytree	0.8, 1.0
min_child_weight	1, 5
reg_lambda	1.0
Output	N, 24

Note: N and D denote the sample size and the number of input features, respectively.

.

2.8.3. Three-Dimensional Convolutional Neural Network (CNN3D)

CNN3D extends conventional CNNs by incorporating the temporal axis into convolution operations, making it well-suited for dynamic environmental data, such as satellite-derived aerosol fields [53,54]. The core architectural components, including the number of filters, temporal and spatial kernel sizes, dropout rate, and dilated convolutions, shape the model’s capacity to extract long-term spatiotemporal dependencies from data. The model was trained using the MSE loss and Adam optimizer, with gradient clipping to stabilize the training. The model uses a custom CausalConv3D with kernel_size = (3, 3, 3) (time × height × width) and temporal causal padding to avoid look-ahead. Stride = 1 and “same” padding preserved the 1 km spatial resolution. Convolutions use ReLU with Glorot initialization; an in-layer dropout is available for regularization. FixedStandardize and LayerNormalization (float32) stabilized the optimization. The 3 × 3 × 3 kernels capture hour-to-hour dynamics and local spatial patterns without over-smoothing, while retaining the kilometer-scale detail needed for pollution hotspots. The hyperparameters are listed in

Table 7. Architectural Hyperparameters of the CNN3D Algorithm.

Structural Hyperparameter	Value
Input shape	72, H, W, Cx
filters	16, 24, 32, 48
depth	3, 4, 5
kt (kernel_time)	3, 5
ks (kernel_space)	3, 5
dropout	0.0, 0.1, 0.2, 0.3
lr (learning rate)	5 × ${10}^{-5}$, 1 × ${10}^{-4}$, 2 × ${10}^{-4}$
batch	1, 2
Output	24, H, W, 1

Note: H and W denote the spatial dimensions (height and width of the grid), and Cx represents the features included in the input tensor (e.g., temperature, humidity, and wind).

.

2.8.4. Convolutional Long Short-Term Memory (ConvLSTM)

ConvLSTM extends the standard LSTMs by replacing matrix multiplication with two-dimensional convolutions, thereby enabling integrated spatiotemporal learning [55]. Critical hyperparameters, such as the number of ConvLSTM layers, filter sizes, kernel dimensions, dropout rates, and normalization strategies, determine the model’s ability to capture both the temporal dependencies and spatial structures. The model was trained with MSE loss and the Adam optimizer, employing gradient clipping (clipnorm = 1.0) to prevent the gradient explosion. ConvLSTM is loaded with custom FixedStandardize and TakeLastT. 2D convolutions inside LSTM gates extract local spatial structure, while the recurrent pathway models temporal dependencies, balancing space and time. Inference enables mixed precision when supported and follows the 72→24 setup (X: N × 72 × H × W × C; Y: 24 future hours). A summary of the structural hyperparameters is presented in

Table 8. Architectural Hyperparameters of ConvLSTM Algorithm.

Structural Hyperparameter	Value
Input shape	72, H, W, Cx
filters	16, 24, 32, 48
kernel (size)	3, 5
n_layers	1, 2
dropout	0.0, 0.1, 0.2, 0.3
lr (learning rate)	$5 \times {10}^{-5}$$, 1 \times {10}^{-4}$$, 2 \times {10}^{-4}$
batch	1, 2
Output	24, H, W, 1

Note: H and W denote the spatial dimensions (height and width of the grid), and Cx represents the features included in the input tensor (e.g., temperature, humidity, and wind).

.

2.9. Model Evaluation

The performance of the machine learning models was evaluated through quantitative and spatial assessments to comprehensively capture the accuracy and reliability of PM2.5 forecasts.

2.9.1. Quantitative Evaluation

The quantitative assessment employed several statistical analyses. Pearson’s correlation coefficient (R) measures the linear association between the predicted and observed values, with values closer to 1 indicating a stronger agreement (Equation (1)) [47]. The coefficient of determination (R²) quantifies the proportion of the observed variance explained by the model, with values approaching 1 reflecting a higher predictive capability (Equation (2)) [56]. The Root Mean Squared Error (RMSE) represents the average magnitude of the prediction errors, where lower values denote greater accuracy (Equation (3)) [57]. Bias (PBIAS) evaluates the systematic deviation of predictions from observations, with positive values indicating overestimation and negative values indicating underestimation (Equation (4)). Finally, the Mean Absolute Percentage Error (MAPE) expresses the average prediction error in percentage terms, allowing meaningful comparisons across time series and forecasting methods, and can be further used to derive prediction accuracy (Equations (5) and (6)) [58].

$$\mathrm{R}={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-\overline{x}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(1)

$${\mathrm{R}}^2=1-{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\stackrel{\leftharpoonup }{y}\right)}^2}}$$

(2)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(3)

$$\mathrm{Bias}={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left({\widehat{y}}_i-y_i\right)}{{{\displaystyle \sum }}_{i=1}^n{y}_i}}\times 100\%$$

(4)

$$\mathrm{MAPE}={\displaystyle \frac{100}{n}}{\displaystyle \sum }_{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|$$

(5)

$$\mathrm{Accuracy}=100-\mathrm{MAPE}$$

(6)

where $y_i$ denotes the observed PM2.5 concentration obtained from ground-based monitoring stations, ${\widehat{y}}_i$ represents the predicted values from the machine learning model, and $\overline{y}$ is the mean of the observed values. Similarly, $x_i$ and $\overline{x}$ denote another variable and its mean, respectively, which are used in correlation-based metrics (e.g., Equation (1)). The term $n$ indicates the total number of paired samples considered in the calculation.

2.9.2. Spatial Evaluation

The spatial assessment focused on evaluating the consistency of spatial patterns. Pattern correlation methods apply the Pearson correlation coefficient (PCC) to compare the spatial distributions between the simulated and observed fields across grids, thereby assessing the linear consistency of spatial patterns (Equation (7)) [59]. In addition, the Structural Similarity Index (SSIM) was used to measure the structural resemblance between the simulated and observed maps, considering luminance, contrast, and structure. The SSIM provides a more perceptually relevant evaluation of spatial outputs than traditional error metrics, with values closer to 1 indicating a high structural similarity (Equation (8)) [60].

$$PCC={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-\overline{x}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(7)

$$SSIM\left(x,y\right)={\displaystyle \frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}}$$

(8)

where ${\mu }_x$ and ${\mu }_y$ denote the spatial means of the modeled and observed data, respectively, and ${\sigma }_x^2$ and ${\sigma }_y^2$ denote the spatial variances of both datasets. The term ${\sigma }_{xy}$ indicates the spatial covariance between the model outputs and observations. In the case of the Structural Similarity Index (SSIM), the constants $C_1$ and $C_2$ are included to stabilize the calculation when the denominator approaches zero.

2.10. Flow Chart

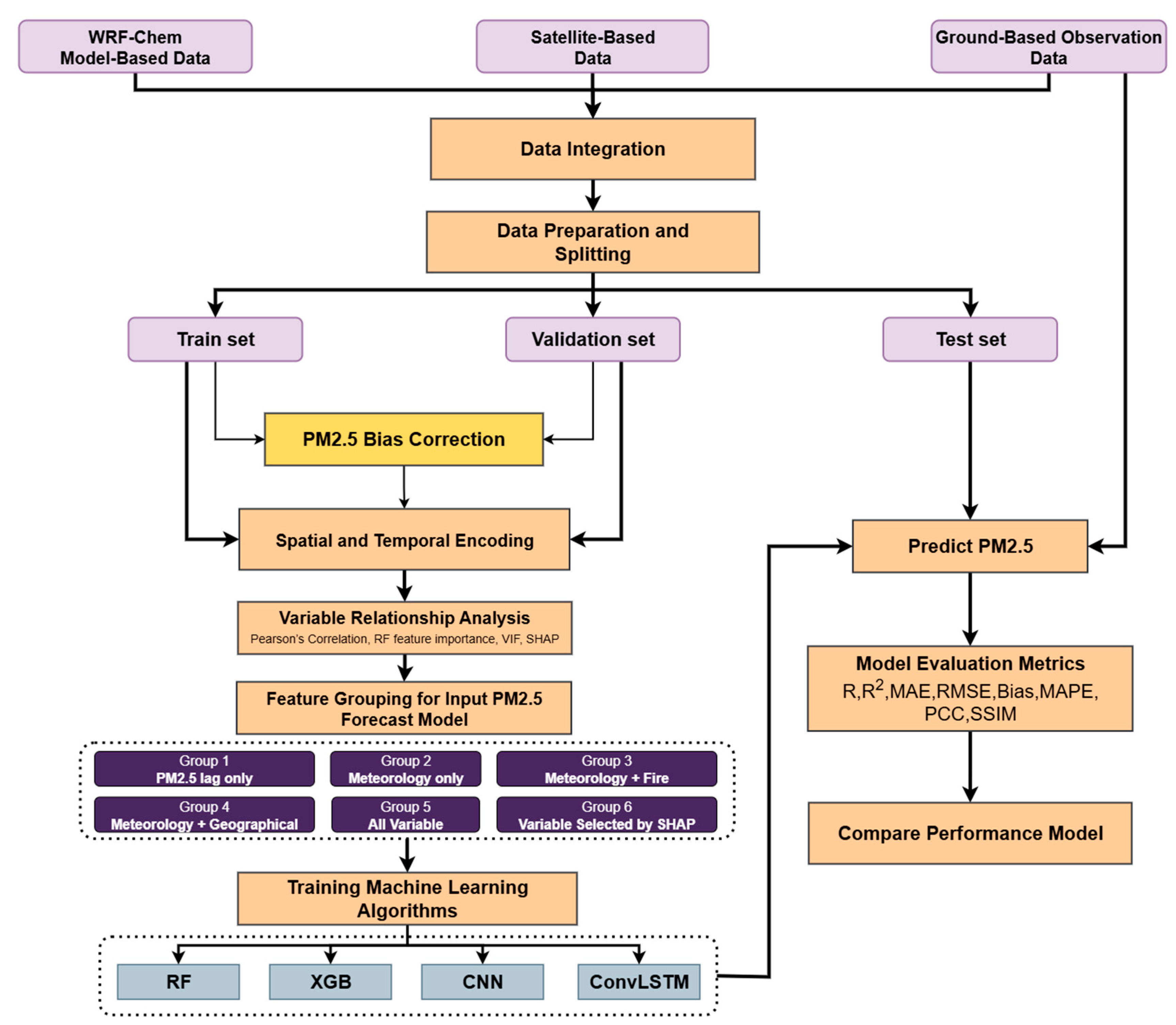
The workflow for developing and evaluating the PM2.5 forecasting models integrated multi-source datasets, including numerical model outputs from WRF-Chem (e.g., WRF-PM2.5, T2, RH2, WD10, WS10, Precipitation, PBLH), satellite-derived products (Burned Area, Hotspot Density, DEM, NDVI, Land Cover), and ground-based observations (PM2.5_obs). All datasets were preprocessed and integrated before being split into training, validation, and testing sets. Subsequently, a bias correction procedure was applied to the WRF-Chem PM2.5 outputs using multiple machine learning algorithms, including Linear Regression, Random Forest, XGBoost, and CNN, with model performance evaluated through R, R², MAE, and RMSE. After bias correction, all inputs were integrated into a unified 1 km, hourly grid to align the spatial and temporal resolutions across the numerical model outputs, satellite layers, and ground observations.

After bias correction, spatial and temporal encoding variables were generated and incorporated into a variable relationship analysis using Pearson’s correlation, VIF, and SHAP. This analysis guided the grouping of features into six categories based on variable characteristics (lag-only, meteorological-only, fire-related, geographical, and SHAP-selected). Each feature group was then used to construct forecasting models using the selected algorithms, namely, Random Forest, XGBoost, CNN3D, and ConvLSTM.

During model training and validation, the model learns a mapping from 72 h predictor sequences (meteorology, fire and geographic layers, temporal encodings, and lagged PM2.5 from the station-based observation interpolation) to the next 24 h of bias-corrected PM2.5, which serves solely as the learning target. During inference on held-out test periods, the same 72 h predictors are supplied (including lagged PM2.5 up to the forecast start time only); no future PM2.5 is used. The model then produced 24 h PM2.5 predictions that are evaluated against independent station observations, clearly separating what was predicted from how predictions were assessed and preventing temporal information leakage.

The forecasts were further evaluated using a comprehensive set of performance metrics, including R, R², MAE, RMSE, Bias, MAPE, Pattern Correlation Coefficient (PCC), and Structural Similarity Index (SSIM), to systematically compare the predictive ability of each algorithm. Overall, this workflow reflects a scientifically rigorous design that connects data acquisition, preprocessing, and bias correction with advanced modeling and final evaluation, thereby ensuring the development of high-performance hourly PM2.5 forecasting models with high accuracy and reliability (Figure 2).

3. Result

3.1. General Statistics of Data

This study utilized hourly data from 1 January to 31 May, 2024, covering 152 days (3648 h) and comprising ground-based observations from 54 monitoring stations, outputs from WRF-Chem, and satellite-based geospatial variables. Most variables contained 196,992 rows, reflecting complete hourly records across grid cells, whereas ground-based PM2.5 observations (PM2.5_obs) included only 174,734 rows, indicating occasional gaps across stations and time periods. Meteorological variables such as T2, RH2, WS10, WD10, Precipitation, PBLH, and Ventilation Index were complete and captured continuous seasonal variability, while satellite-based variables including Burned Area, Hotspot Density, DEM, NDVI, and Land Cover, although not inherently hourly, were harmonized through temporal allocation or spatial linkage to ensure consistency with the dataset. Accordingly, the descriptive statistics, namely the mean, standard deviation (Std), minimum (Min), maximum (Max), and count, are summarized in

Table 9. Summary Statistics of Model Input Variables for the Study Period (January–May 2024).

Variable	Mean	Std	Min	Max	Count
PM2.5_obs	53.24	47.23	1	663	174,734
WRF-PM2.5	20.16	97.30	6.62	19,719.11	196,992
T2	30.28	5.92	13.14	44.20	196,992
RH2	47.42	22.60	8.37	100	196,992
WS10	7.36	5.99	0.005	44.19	196,992
WD10	187.69	84.44	7.6 × 10−5	359.99	196,992
Precip	−0.08	0.59	−0.2	15.37	196,992
PBLH	655.95	813.66	26.65	4044.97	196,992
Venting	6657.47	11,609.58	0.14	95,698.12	196,992
Burned Area	41 km2/mo	35 km2/mo	5 km2/mo	93 km2/mo	5
Hotspot Density	0.43	0.09	0.24	0.85	196,992
DEM	334.71	129.18	270.58	1268.27	196,992
NDVI	0.43	0.10	0.24	0.85	196,992
Land Cover	11.87	1.82	2	13.99	196,992

Note: Burned Area values represent monthly totals of burned surface within the study domain, reported in square kilometers per month (km²/mo), derived from monthly MCD64A1 raster for January–May 2024. “Count” denotes the number of months (5 months).

to provide an overview of the dataset characteristics that support the development of the PM2.5 forecasting model.

3.2. Bias Correction Performance

The evaluation of bias correction for PM2.5 revealed that Random Forest (RF) achieved the best performance, with the highest R (0.78) and R² (0.60) and the lowest MAE (17.83 µg/m³) and RMSE (29.28 µg/m³), confirming its effectiveness in reducing errors and explaining variance. XGBoost performed comparably (R = 0.76, R² = 0.57, RMSE = 31.04), slightly less accurately, but was still highly effective in capturing nonlinear relationships. ANN and CNN achieved moderate improvements (R ~0.72–0.73; RMSE ~32–33 µg/m³), outperforming Linear Regression (LR), which had the weakest results (R = 0.57, R² = 0.32, RMSE = 39.03 µg/m³). Time series analyses from representative stations further indicated that RF and XGB most accurately tracked hourly PM2.5 trends, particularly during high-concentration episodes (r ~0.86–0.93), highlighting superior temporal consistency compared with ANN, CNN, and LR, which showed delays or deviations in their prediction. Overall, RF and XGB demonstrated the highest performance in terms of statistical accuracy and temporal agreement (

Table 10. Algorithms and Performance Metrics of Bias Correction.

Algorithms	R	R2	MAE	RMSE
LR	0.57	0.32	26.27	39.03
RF	0.78	0.60	17.83	29.28
XGB	0.76	0.57	18.86	31.04
ANN	0.73	0.53	20.16	32.41
CNN	0.72	0.52	20.42	32.87

).

3.3. Variable Analysis

Variable analysis is a critical step in identifying the role, relevance, and redundancy of variables in PM2.5 forecasting. This study applied both statistical and machine learning-based approaches. Pearson’s correlation coefficient revealed that variables such as PM2.5_lag1, PM2.5_lag24, T2, and RH2 showed moderate-to-strong correlations with PM2.5, emphasizing the influence of temporal persistence and meteorological conditions, whereas WD10 exhibited weak or insignificant associations. Variance Inflation Factor (VIF) analysis indicated severe multicollinearity for variables such as PM2.5_lag6 and PM2.5_lag12 (VIF > 10), as they were strongly correlated with PM2.5_lag1 and adjacent lags. Similarly, Venting showed high redundancy with PBLH and WS10 and was excluded to enhance model stability. The Random Forest feature importance analysis ranked PM2.5_lag1, Burned Area, and T2 as the most influential variables, reinforcing the role of both temporal and emission-related drivers, while DEM and NDVI contributed moderately to spatial representation. Finally, SHapley Additive Explanations (SHAP) provided consistent evidence, demonstrating that PM2.5_lag1, PM2.5_lag24, T2, RH2, and Burned Area exerted stable and physically meaningful effects, whereas WD10 and Venting had SHAP values close to zero, indicating minimal predictive relevance. The results are presented in Figure 3.

Although Pearson correlation and Random Forest importance offered useful screening, the final representative subset (used in Group 6) prioritized SHAP and VIF to balance predictive contribution and multicollinearity. For example, Precip and RH2 were retained despite weak or negative linear correlations because SHAP revealed marginal effects consistent with precipitation scavenging and humidity-driven particle growth. Thus, the SHAP and VIF combination emphasized physically meaningful and statistically independent predictors over purely linear associations, providing a more interpretable and robust feature basis for the grouping strategy.

3.4. Feature Grouping

As demonstrated in Section 3.3, different variables exhibited distinct contributions to PM2.5 forecasting. Lagged variables, such as PM2.5_lag1 and PM2.5_lag24, showed clear temporal relationships with current PM2.5 concentrations, whereas meteorological factors, including temperature (T2) and relative humidity (RH2), were consistently identified as influential based on both Pearson correlation and SHAP values, reflecting the role of atmospheric conditions in regulating air pollution levels. Fire-related variables, particularly Burned Area and Hotspot Density, were found to be direct drivers of PM2.5 increases, whereas geographical variables such as DEM, NDVI, and Land Cover, although less significant in tabular models (RF, XGBoost), became more relevant in image-based architectures (CNN, ConvLSTM) that are capable of capturing spatial dependencies more effectively on the common 1 km, hourly grid used for cross-source integration.

Overall, the six feature sets (

Table 11. Train Input Variable Groups for Machine Learning-based PM2.5 Predicting.

Group	Group Name	Num of Vars	Included Variables	Rationale for Selection
1	PM2.5 lag only	9	PM2.5_lag1, PM2.5_lag2, PM2.5_lag3, PM2.5_lag6, PM2.5_lag12, PM2.5_lag18, PM2.5_lag24, PM2.5_lag48, PM2.5_lag72	High correlation and SHAP.
2	Meteorology only	6	T2, RH2, Precip, WS10, WD10, PBLH	Meteorological from WRF-Chem; selected by SHAP and feature importance.
3	Meteorology + Fire	8	Group 2 + Burned Area, Hotspot Density	Fire variable; important in the biomass burning season.
4	Meteorology + Geography	9	Group 2 + DEM, NDVI, Land Cover	Geographic variables influencing the distribution and persistence of land surfaces.
5	All Variables (Full Set)	20	All variables: Group 1 + Meteorology + Fire + Geography	Benchmark set; useful to check multicollinearity.
6	Selected by SHAP and VIF	7	PM2.5_lag1, PM2.5_lag24, T2, RH2, Precip, Burned Area, NDVI	Top SHAP-ranked features with low VIF (<10).

) were configured to enable systematic comparisons across diverse input configurations: temporal-only, meteorology-augmented, fire-augmented, geography-augmented, full benchmark, and compact subsets selected for high SHAP contribution and low VIF. This design balances interpretability, redundancy reduction, and robustness across model families. Practically, we assessed each domain (temporal, meteorological, fire, and geographic) by summarizing how much its variables, in aggregate, explained the model and by examining what happens to performance when information from that domain is constrained or altered. This is not a simple collation of datasets; rather, it is an integration anchored in space and time with a clear geographic interpretation framework.

3.5. Model Performance Evaluation

3.5.1. Validation Performance

The validation results (

Table 12. Validation performance metrics (R, R², MAE, and RMSE) of the four algorithms across the six groups.

	Algorithms	Group
		1	2	3	4	5	6
R	RF	0.68	0.61	0.63	0.61	0.87	0.85
	XGBoost	0.80	0.51	0.50	0.53	0.81	0.82
	CNN3D	0.93	0.77	0.80	0.77	0.88	0.92
	ConvLSTM	0.88	0.78	0.77	0.73	0.78	0.83
R2	RF	0.29	0.27	0.29	0.27	0.60	0.68
	XGBoost	0.54	0.11	0.12	0.11	0.56	0.65
	CNN3D	0.70	0.55	0.52	0.57	0.73	0.76
	ConvLSTM	0.51	0.42	0.41	0.37	0.44	0.57
MAE	RF	36.68	25.60	25.45	25.73	17.52	14.34
	XGBoost	19.32	30.13	29.57	29.60	18.89	14.33
	CNN3D	16.02	22.33	17.97	20.80	15.16	13.98
	ConvLSTM	19.73	20.15	20.03	22.37	20.63	18.90
RMSE	RF	14.80	37.20	36.75	37.25	27.62	20.25
	XGBoost	29.60	41.08	41.01	41.10	29.00	20.97
	CNN3D	23.63	29.10	30.10	28.55	22.47	21.28
	ConvLSTM	30.35	32.86	33.23	34.41	32.45	29.43

) revealed distinct differences among the algorithms and grouped input variables. Overall, CNN3D emerged as the best-performing model, achieving the highest correlation coefficients (R) in several groups, notably in Group 1 (lag only, R = 0.93) and Group 6 (Selected by SHAP and VIF, R = 0.92), along with the highest coefficient of determination (R² = 0.76) in Group 6. These results highlight CNN3D’s superior capability to capture complex spatiotemporal structures. Furthermore, CNN3D achieved the lowest error values in many cases, with MAE = 13.98 and RMSE = 21.28 in Group 6, confirming its quantitative accuracy in both variance explanation and error reduction. The model performance across different feature groups, together with training and validation loss behavior, is illustrated in Figure 4.

In contrast, the Random Forest (RF) model exhibited consistently lower correlation values (R² mostly <0.30) but demonstrated a competitive advantage in error reduction. For example, RF achieved the lowest MAE (14.34) and RMSE (20.25) in Group 6, underscoring its robustness in minimizing quantitative errors when comprehensive variable sets were used. For Group 6, the RF configuration selected by the grid search used n_estimators = 200, max_depth = 16, min_samples_leaf = 1, and max_features = sqrt, which balanced depth-driven expressiveness with controlled feature sampling. XGBoost (XGB) provided intermediate performance, with R values ranging from 0.50 to 0.82 and a maximum R² of 0.65 in Group 6, coupled with moderate error levels (MAE ~14–30; RMSE ~21–36), indicating its strength in capturing non-linear relationships. For Group 6, the selected XGBoost setting comprised n_estimators = 200, max_depth = 4, learning_rate = 0.05, subsample = 0.8, colsample_bytree = 1.0, min_child_weight = 5.0, reg_alpha = 0, and reg_lambda = 1, favouring a conservative learning rate with appropriate regularisation and full column sampling. ConvLSTM, while producing moderate correlations (R = 0.73–0.88), consistently yielded higher RMSE (~30–34), reflecting its limited efficiency under multidimensional validation inputs.

From the perspective of variable grouping, Groups 5 (All Variables) and 6 (Selected by SHAP and VIF) consistently outperformed the other groups across most algorithms, particularly CNN3D and RF. In contrast, Groups 2 and 3 (meteorology only and Meteorology + Fire) produced relatively weaker results, implying that restricting inputs to narrower subsets may be insufficient for robust PM2.5 forecasting.

In summary, the validation assessment confirmed CNN3D as the most capable model for capturing both linear and nonlinear dependencies, particularly under the SHAP-selected and full variable sets. Meanwhile, RF—despite its lower R and R²—remains a competitive alternative owing to its strength in minimizing absolute prediction errors, highlighting the complementary advantages among the algorithms. The detailed statistical values of the correlation and error metrics for each algorithm and group are listed in Table 12.

3.5.2. Test Performance

The evaluation using the test dataset revealed clear differences between the two algorithms and the input variable groups (

Table 13. Quantitative performance summary of the four algorithms across all feature groups.

Algorithms	R	R2	MAE	RMSE	Bias	MAPE
RF	0.867 ± 0.048	0.621 ± 0.113	16.9 ± 1.0	27.6 ± 5.0	−12.2 ± 4.1	24.7 ± 1.6
XGBoost	0.817 ± 0.118	0.541 ± 0.195	18.1 ± 4.1	28.9 ± 6.3	−11.9 ± 5.0	23.7 ± 2.6
CNN3D	0.642 ± 0.257	0.141 ± 0.324	27.9 ± 8.1	38.3 ± 10.7	−16.9 ± 10.9	42.7 ± 11.2
ConvLSTM	0.794 ± 0.106	0.330 ± 0.176	22.5 ± 2.7	34.5 ± 5.1	−17.6 ± 3.5	28.7 ± 3.3

Note: Values are presented as ± standard deviation, calculated across all test samples within each variable group to reflect both the central tendency and variability of the model’s performance.

). Among the algorithms, Random Forest (RF) and XGBoost consistently achieved superior performance. RF produced the strongest agreement with observed PM2.5, achieving the highest correlation (R = 0.867 ± 0.048) and determination coefficient (R² = 0.621 ± 0.113), along with the lowest MAE (16.9 ± 1.0 µg/m³) and RMSE (27.6 ± 5.0 µg/m³). These results highlight the effectiveness of the model in explaining variance and minimizing prediction errors. The best performance from the RF model was found in the 6th group of variables with R = 0.93 and R² = 0.85 (Figure 6a,d). XGBoost performed comparably, maintaining robustness across input groups despite a slightly lower accuracy. In contrast, CNN3D and ConvLSTM exhibited weaker predictive performance, particularly CNN3D, which yielded a very low R² (0.141 ± 0.324) and a high MAPE (42.7 ± 11.2%), indicating limitations in capturing the spatiotemporal dynamics of observed PM2.5.

To substantiate the reported accuracy metrics, we assessed the statistical significance on the held-out test set by computing Pearson’s correlation between the predicted and observed hourly PM2.5 for every model and feature-group combination and reporting the associated p values. Figure 5 presents heatmaps of R, R², and RMSE with significance indicated in the caption. Overall, RF and XGBoost exhibited consistently high and statistically significant associations with lower RMSE, ConvLSTM generally attained moderate to highly significant associations, and CNN3D showed greater between-group variability with weaker associations and higher RMSE in several cases relative to the tree-based models. The contrast is most pronounced under higher-pollution conditions, where tree-based models maintain strong R and R² and comparatively low RMSE. These significance tests support the conclusions drawn from the R, R², MAE, RMSE, and MAPE values.

When comparing the input variable groups (Figure 6a–g), Group 1 (PM2.5 lag only) and Group 2 (meteorology only) showed moderate correlations but higher RMSE, suggesting limited predictive power when relying on a single type of variable. Conversely, the combined groups, such as Group 3 (Meteorology + Fire) and Group 4 (Meteorology + Geographical), improved the predictive performance, particularly with RF and XGBoost, which effectively captured nonlinear interactions. Group 5 (All Variables) demonstrated a relatively high overall performance, although the model stability was affected by multicollinearity. Group 6 (Selected by SHAP and VIF) achieved the most balanced results, reducing the number of variables while maintaining high correlation (R), determination (R²), and accuracy, with relatively low MAE, RMSE, and MAPE across most algorithms.

Spatial evaluation using the PCC and SSIM (Figure 6h,i) supports these results. Groups 6 and 5 preserved spatial consistency most effectively, particularly when modeled with RF and XGBoost, which maintained spatial agreement closest to the observed PM2.5 distribution. In contrast, CNN3D and ConvLSTM showed relatively lower PCC and SSIM across groups, suggesting that although they were designed for spatiotemporal learning, they were less effective on this dataset.

Taken together, the results show that both the algorithm and input variable grouping substantially shape prediction performance. RF and XGBoost consistently provided reliable outcomes, whereas Group 6 (Selected by SHAP and VIF) emerged as the most efficient input configuration, reducing redundancy without sacrificing accuracy. Taken together, the statistical evidence from Table 13 and the visual comparisons in Figure 6a–i demonstrate the advantages of tree-based models combined with systematically selected variables for predicting the hourly PM2.5 concentration in the study area.

3.5.3. Comparative Analysis

The comparative analysis across quantitative, temporal, and spatial dimensions highlights the strengths and limitations of each algorithm, as well as the implications of the input variable grouping.

From a quantitative perspective, RF and XGBoost consistently outperformed CNN3D and ConvLSTM, achieving higher correlations and R² values, and lower MAE and RMSE values. The scatter density plots (Figure 7) illustrate that the predictions from RF and XGBoost were concentrated around the 1:1 line, representing perfect agreement between the predicted and observed PM2.5 values. In contrast, CNN3D and ConvLSTM exhibited greater dispersion, particularly CNN3D, which systematically underestimated high PM2.5 concentrations, reflecting the challenges in capturing the variability of real data.

In terms of temporal dynamics, hourly time-series comparisons (Figure 8) confirmed that RF and XGBoost closely tracked the observed PM2.5 variations, capturing both diurnal cycles and abrupt shifts in concentration, whereas CNN3D and ConvLSTM showed temporal lag and under-prediction during high-pollution episodes. Nevertheless, model accuracy decreased during low-to-moderate AQI conditions, where PM2.5 concentrations fluctuated only slightly, making it difficult to distinguish true signals from measurement uncertainties.

From a spatial perspective, raster map comparisons (Figure 9) further revealed that RF and XGBoost effectively reproduced spatial gradients and localized hotspots, supported by higher PCC and SSIM values relative to CNN3D and ConvLSTM, which produced overly smooth fields. For illustrative purposes, we present examples from RF and XGBoost, both of which achieved comparably high performance, and CNN3D, which yielded the lowest performance, to emphasize the differences between the algorithms.

Figure 7, Figure 8 and Figure 9 demonstrate that both algorithm selection and input grouping substantially influence the predictive performance. RF and XGBoost consistently provided the most reliable results, whereas the SHAP and VIF input groups (Group 6) yielded the most balanced outcomes by reducing redundancy without compromising predictive accuracy.

4. Discussion

This study highlights the effectiveness of ML models in predicting hourly PM2.5 concentrations by integrating bias-corrected WRF-Chem model outputs, satellite-based information, and ground-based observations. Among the models tested, tree-based algorithms, particularly RF and XGBoost, demonstrated consistently high accuracies and robustness. These models were able to capture hourly variations in PM2.5 more reliably than deep learning models, particularly during high-concentration episodes. This finding is consistent with that of Chen et al. [61], who reported that RF performs well on noisy and heterogeneous datasets and extended the results of Ma et al. [62] by applying a fine-resolution (1 km) spatiotemporal framework in Northern Thailand.

Deep learning models, including CNN3D and ConvLSTM, exhibited weaker performance in this study despite their theoretical ability to capture spatiotemporal dependencies. Their instability during training and reduced generalizability under real-world conditions are consistent with the findings of Wu et al. [63]. Similarly, Qiu et al. [64] suggested that hybrid CNN-LSTM structures may offer advantages in certain contexts; the results presented here indicate that tree-based models remain more consistent when the data are incomplete, noisy, or influenced by complex topography.

The analysis of variable importance further emphasized the strong contribution of lagged PM2.5 (e.g., lag1, lag24) and meteorological drivers (T2, RH2, and wind speed/direction), consistent with Bi et al. [65], who noted the central role of temporal persistence and meteorological influences in shaping air pollution patterns in Southeast Asia. Fire-related factors, particularly burned areas, were especially relevant during high-pollution events. The Variable grouping approach applied in this study proved effective in reducing redundancy while retaining predictive skill, which supports earlier findings [61] but extends them by offering a systematic grouping strategy that facilitates fair comparison across algorithms.

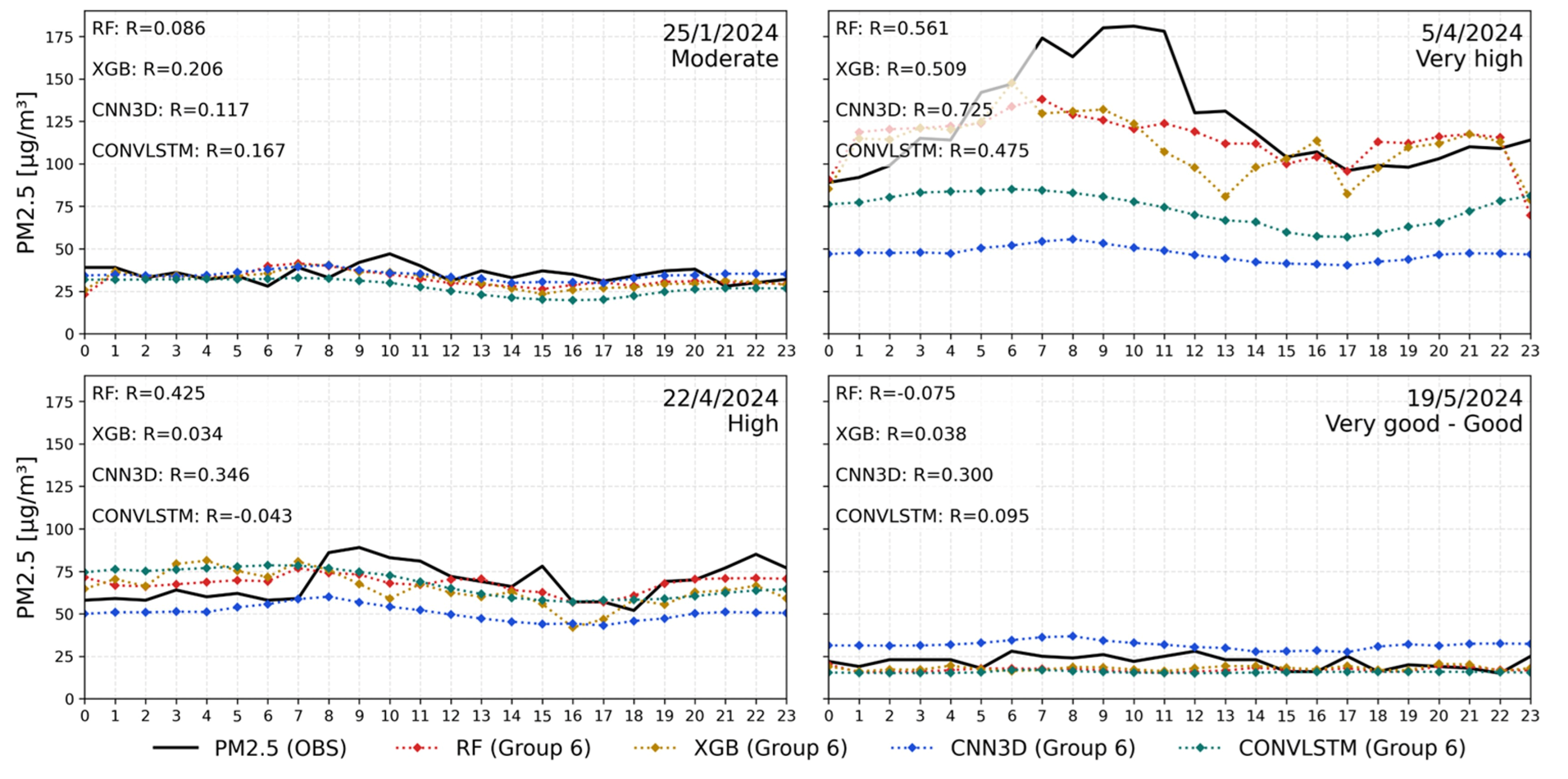
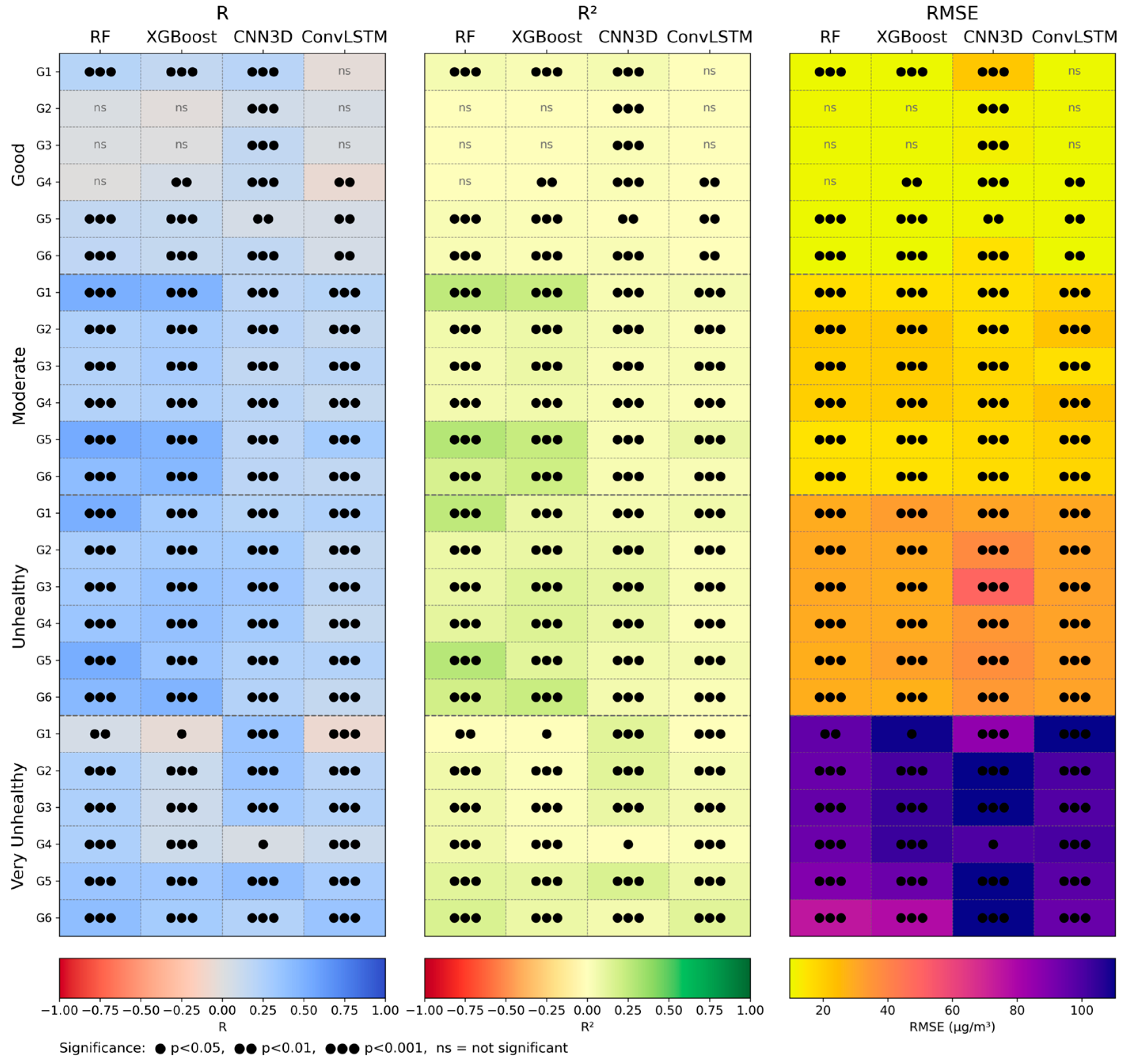
From a temporal perspective, RF and XGB successfully captured the diurnal cycles and short-term fluctuations of the observed PM2.5, demonstrating their suitability for real-time, early warning systems. Nevertheless, the performance decreased under low-to-moderate AQI conditions owing to weaker signals and lower signal-to-noise ratios, as reported by Zhang et al. [66]. At low PM2.5 levels, prediction accuracy typically declines because (1) the signal-to-noise ratio is lower and instrument/representation errors become comparable to the signal, (2) predictor–target coupling weakens (e.g., fire activity is sparse and meteorology explains less variance), and (3) variance is small so correlation-based metrics (R, R²) are mathematically bounded even when absolute errors are modest. In our AQI-stratified evaluation, models remained statistically significant but showed reduced effect sizes in the “Good” and “Moderate” ranges, consistent with these mechanisms. Practically, this suggests adopting heteroscedastic-aware training (e.g., variance-stabilizing transforms or quantile losses) and reporting AQI-stratified metrics to reflect the use-case performance under clean-air regimes. Spatially, RF and XGB maintained higher consistency with the observed PM2.5 distributions than CNN3D and ConvLSTM, indicating their suitability for regions with complex terrains, such as northern Thailand. The integration of bias-corrected WRF-Chem outputs, as emphasized by Noynoo et al. [67], plays a critical role in stabilizing predictions across both the temporal and spatial dimensions.

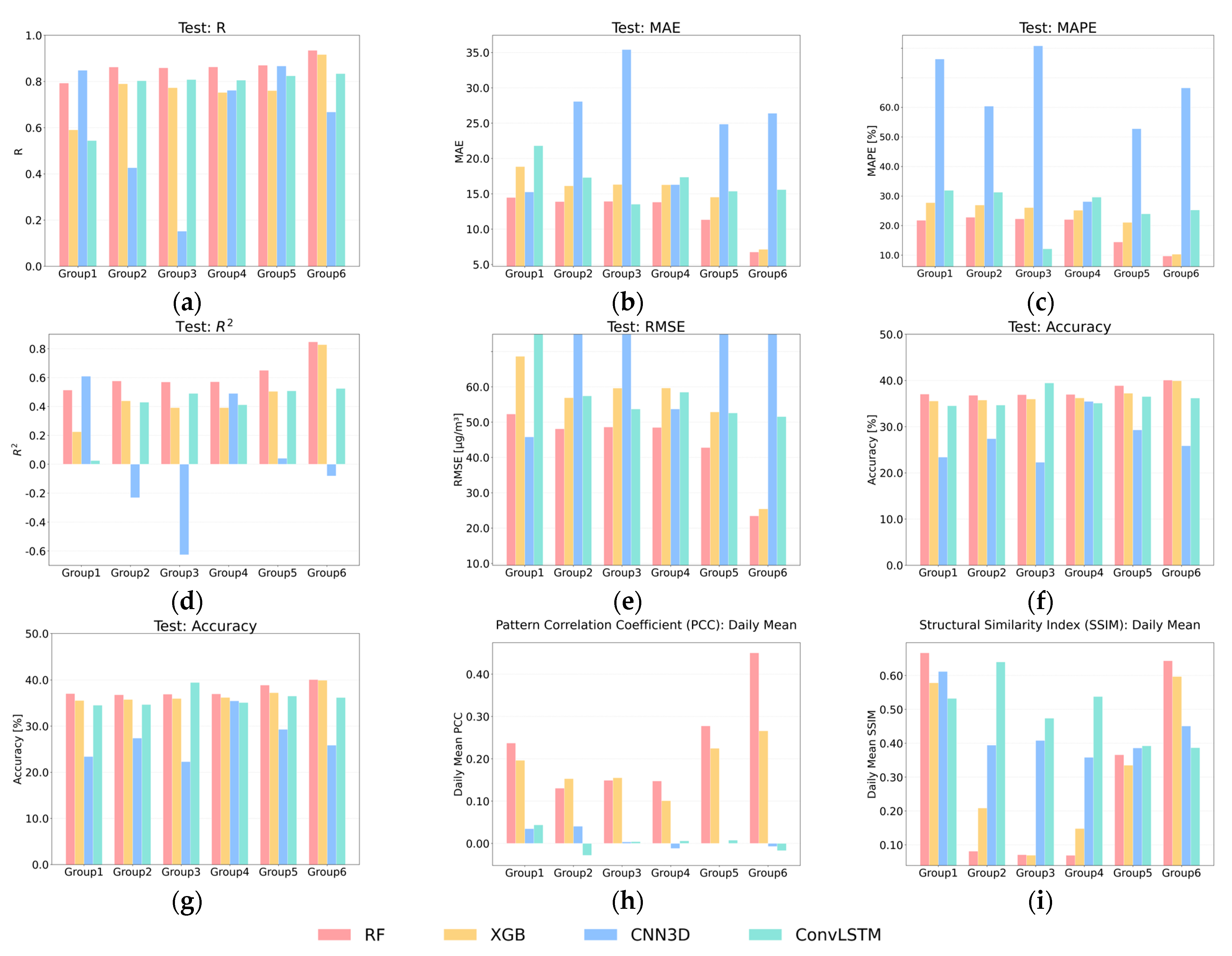
Comparative context with related works. Our Random Forest achieved R = 0.93 and R² = 0.85 in Group 6 (variables selected by SHAP and VIF), as shown in Figure 6a,d, which is above the R² = 0.81 reported by Joharestani et al. [19] for an urban domain using multisource inputs. The improvement is plausibly attributable to three design choices rather than model type alone: (1) feature curation—a disciplined SHAP+VIF screen that removed weak or redundant predictors while retaining lagged PM2.5 and key meteorology; (2) physics-informed inputs—integration of bias-corrected WRF-Chem fields that stabilize the signal and complement observations, instead of relying on AOD which did not consistently help; and (3) task framing—an hourly, fine-scale (1 km) setup with fire-related covariates suited to our biomass-burning regime, and evaluation on strictly held-out high-pollution episodes. Taken together, these choices likely increased explanatory power without inflating complexity, yielding stronger R and R² while remaining methodologically comparable to prior multisource RF studies.

Overall, while earlier studies have demonstrated the benefits of multi-source integration [62] and the strong predictive ability of tree-based models [61], this study distinguishes itself by combining both under a fine-resolution experimental framework and applying a systematic variable grouping. This approach strengthens the reliability of ML-based PM2.5 prediction and provides practical insights for operational air quality management and policy support in Southeast Asia, particularly in Thailand.

Limitations and Future Perspectives

This study has several limitations that should be considered when interpreting the results, as well as opportunities for future development that build upon these findings.

First, the spatial density and distribution of ground monitoring stations are uneven, with dense coverage in urban centers but sparse representation in rural and mountainous regions. This spatial imbalance introduces non-uniform confidence in spatial interpolation, increasing the uncertainty in areas farther from the monitoring stations. Consequently, both the bias correction and evaluation processes may be biased toward urban conditions, indicating that the reported model skill likely reflects urbanized zones more accurately than rural or topographically complex areas do. Consequently, model generalization may weaken when applied to regions with limited observational datasets.

Second, certain predictors may exert conditional importance under specific meteorological regimes. This study incorporated a comprehensive suite of meteorological, geospatial, and fire-related variables, including near-surface temperature, relative humidity, hourly precipitation, 10 m wind speed and direction, planetary boundary layer height, ventilation coefficient, burned area, hotspot density, digital elevation, land cover, temporal encodings, and lagged PM2.5—feature selection procedures inevitably reduce redundancy. However, predictors such as wind direction and the ventilation coefficient can become particularly influential under strong wind or nocturnal inversion conditions. When these variables are down-selected within specific feature groups, the fidelity of the model may decline during such events.

Third, the training dataset represented only a single haze season in Northern Thailand. This limited temporal scope constrains the model’s ability to capture interannual variability, off-season conditions, and extreme events, potentially reducing its robustness when applied in other years or in different climatological contexts. Extending the dataset to encompass multiple seasons would provide a more representative basis for training and evaluation.

Finally, computational constraints impose practical limitations. The 1 km hourly multivariable framework requires substantial computational power, memory and storage. These constraints necessitated limiting the hyperparameter search space and sensitivity analyses, preventing the exhaustive exploration of all model configurations. Despite these restrictions, the modeling system still provides a valuable benchmark for near-real-time PM2.5 prediction and a scalable foundation for future studies.

Several promising pathways for improvement are available. Expanding the temporal and spatial scopes of the training data is crucial. Incorporating multi-year haze seasons will enable the model to better represent interannual variability and long-term trends, while extending the observation network through additional ground sensors and emerging high-resolution satellite platforms can reduce spatial bias in data-sparse regions.

On the methodological front, the application of advanced deep learning architectures, such as spatial attention networks, multi-scale feature fusion, or physics-informed hybrid models, may improve the representation of atmospheric dynamics across complex terrains. Similarly, exploring ensemble learning strategies that integrate tree-based and deep learning models can balance interpretability, adaptability, and computational efficiency.

From an operational perspective, deeper integration with decision-support systems used by environmental agencies and provincial authorities is essential. Linking model outputs with real-time biomass-burning management tools, air quality dashboards, and public alert systems can transform forecast information into actionable strategies. These applications can support daily advisories, optimize the scheduling of fuel-reduction operations, and enhance surveillance during periods of elevated fire risks.

In the long term, these advancements will help transition the current research framework into a fully operational, real-time early warning, and policy support system. By combining extended datasets, improved architectures, and institutional collaboration, the modeling framework can evolve into a scalable and adaptive platform that bridges scientific modeling, environmental management, and public policy to support sustainable air quality governance across Southeast Asia.

5. Conclusions

This study demonstrated that integrating bias-corrected WRF-Chem outputs with satellite-based and ground-based observations substantially improved the accuracy of the hourly PM2.5 predictions. Among the evaluated models, tree-based algorithms, particularly RF and XGBoost, consistently outperformed deep learning architectures (CNN3D and ConvLSTM), providing more stable and reliable forecasts. Variable importance analyses confirmed the dominant influence of lagged PM2.5 and meteorological variables (e.g., T₂ and RH₂), and fire-related predictors (burned area and hotspot density) exerted substantial effects during high-pollution episodes. The systematic variable grouping approach, based on correlation, VIF, RF importance, and SHAP, effectively reduced redundancy and emphasized the most predictive features. Together, these findings highlight the value of integrating physical understanding with data-driven optimization to develop robust forecasting models suitable for air quality management in complex terrains such as northern Thailand and broader Southeast Asia.

Beyond predictive accuracy, the operational application of 24 h PM2.5 forecasts enhances their policy relevance. Forecast outputs were delivered with AQI-aligned thresholds, uncertainty ranges, and machine-readable formats (GeoTIFF/NetCDF), accessible via an hourly dashboard and API. Routine reliability summaries and calibration snapshots accompany each forecast cycle to ensure transparency and reproducibility. These products can support daily public advisories, scheduling of fuel-reduction operations, and targeted patrols or surveillance during elevated-risk periods, demonstrating how predictive analytics can be systematically integrated into biomass-burning management workflows.

Future extensions should focus on expanding the dataset to multi-year horizons to better capture the seasonal dynamics and extreme pollution events. However, this expansion must be balanced against computational demands, necessitating parallel improvements in algorithmic efficiency and infrastructure capacity to ensure optimal performance. With these advancements, the framework presented in this study offers a solid foundation for developing scalable operational PM2.5 early warning systems that bridge scientific modeling and policy implementation.