Abstract
The study aims to analyze the long-term trends of climate variables in Erzurum, Türkiye. Trend analyses were conducted on the maximum, minimum, and average temperature and total precipitation series for a 96-year period covering the period 1929–2024. Annual, seasonal, and monthly time series of the variables were illustrated along with their linear trends. Statistical analysis was conducted using the Mann–Kendall test and Sen’s innovative trend analysis methods. The Mann–Kendall test Z-statistic results were evaluated at the 90%, 95%, and 99% significance levels. Maximum temperature series show increasing trends in all months except November, December, January, and February and on the annual scale at the α = 0.01 significance level. Minimum temperature series show decreasing trends for all time periods except March and April. The average temperature variable shows no trend in the annual, summer, and winter series, increasing in spring, March, and April (α = 0.05) and decreasing in November (α = 0.1). Trend analysis of the precipitation series indicates a decreasing trend in winter snowfall, as well as in March and June precipitation. Sen’s methodology, in addition to trend indicators, offers a layered assessment opportunity for any time series, with subcategorization based on the magnitude of the data values. According to annual average values, the diurnal temperature range was determined as 11.3 °C in 1929 and 13.5 °C in 2024. Important findings have been obtained for determining sustainable resource management strategies through the monitoring of climate variables.
1. Introduction
The IPCC [1] states that climate change affects the hydrological cycle at local and global scales, causing changes in the frequency and duration of precipitation patterns and leading to extreme weather events such as floods, droughts, and temperature increases. Therefore, analyzing long-term trends in climate variables is crucial not only for monitoring and assessing climate change but also for ensuring sustainable resource management and identifying potential adaptation and mitigation strategies.
Many studies have been conducted to measure the temporal and/or spatial patterns and trends of climate variables under the perspective of climate change at the local scale. Cui et al. [2] investigated trends in air temperature and precipitation parameters recorded in the Yangtze River Basin (YRB) in China between 1960 and 2015. They used linear regression (LR) analysis, the Mann–Kendall (MK) test, and Sen’s innovative trend analysis (ITA). They found increasing trends between 0.15 and 0.23 °C in annual maximum, minimum, and average temperatures, but noted no significant trend in precipitation changes. Another study conducted on the spatial and temporal analysis of precipitation and drought conditions in southwestern Xinjiang [3], China, shows that precipitation is decreasing, and drought tendency is increasing in the study area.
Two separate studies examining temperature and precipitation records from Guwahati, Assam, India, over 50 years [4] and from Kashmir, Kashmir, over 40 years [5], reported increasing temperature trends at all stations, according to the MK and ITA tests. The annual seasonal precipitation trends are increasing in the former and decreasing in the latter. In the rainfall trend analysis based on 102 years of records of the Sindh River basin of India [6], annual and seasonal increasing trends have determined.
A study conducted for Serbia in Europe using MK and ITA trend analysis tools noted increasing trends in annual and seasonal minimum and maximum air temperature series, while no significant trends were identified in summer and winter precipitation series [7]. Similarly, studies conducted for Greece [8], Switzerland and Italy in Europe analyzed trends in climate variables, reporting a decreasing trend in spring precipitation in the Pieria region of Greece, while temperatures in Swiss [9] showed a clear upward trend. It has been shown that the annual maximum precipitation in the Campania region of Italy has no statistically significant trend at most of the recorded stations [10].
The most important common feature of the studies mentioned above, which focused on temperature and precipitation trends in specific regions of Asia and Europe, is the identification of increasing trends in temperature series. Unfortunately, some trend studies conducted in other regions of the globe have also produced similar results. For example; a study investigating the temporal trends of the maximum and minimum temperature series covering the 48 states in the USA from 1895 to 2017 found significant positive trends in both maximum and minimum temperatures [11]. A study examining annual rainfall periods in the Aguascalientes region of Central Mexico using spectral analysis found that annual rainfall has periodicities of 3, 5, 8, 13, and 21 years [12]. A study conducted a temporal and spatial analysis of temperature trends and climate change projections for a river basin in Ethiopia highlighted increasing temperature trends [13]. According to annual and monthly rainfall trends in the Sinjar Region of Iraq, positive trends were recorded in October and April, and negative trends were recorded in the other months [14]. A comprehensive study of temperature and precipitation trends and future projections in eastern and western Mazandaran Province of Iran also identified increasing trends for both parameters [15].
Similar studies to those conducted in many regions of the world to determine the temporal and/or spatial trends of climate variables have been conducted for many cities or regions in Türkiye [16,17,18,19,20,21,22]. One of the earliest studies, conducted by Türkeş in 1996 [16], determined the temporal and spatial trends of annual precipitation changes in Türkiye. Although slight decreases were detected in the area-averaged annual precipitation series, the results of the MK test indicated that the decreasing trends in the precipitation series were not statistically significant. A study analyzing precipitation and drought trends in the Aegean Region for the period 1960–2013 used records from eight stations and reported that monthly precipitation trends decreased across the region in December, January, February, and March [17]. A study on seasonal rainfall variability in the Konya Basin revealed positive winter and summer precipitation and negative spring precipitation trends in the basin between 1971 and 2020 [19]. In another study, the precipitation and temperature trends of the Antalya Basin were examined by the Frequency-Incremental Trend Analysis (F-ITA) method, and it was shown that there were increasing frequency trends in temperatures but no trend in the precipitation series [21].
In all of the studies mentioned above, the selection of temperature and precipitation (and/or drought) parameters to measure temporal and/or spatial patterns and trends in climate variables is undoubtedly no coincidence. Precipitation and temperature are the most important physical variables [4] that determine a region’s climatic conditions, water supply, floods and water scarcity [23,24], agricultural production, and food supply [25,26]. The most commonly used tools to detect temporal trends of these variables are LR, MK test, Sen’s ITA approach [2,3,4,5,6,7,8] and its other versions such as innovative polygon trend analysis (IPTA) [19,21,27,28], Spearman rho [29,30,31], wavelet analysis [32] and machine learning [23,33].
The primary objective of this article is to conduct a trend analysis of temperature and precipitation variables for the city of Erzurum, Türkiye, over a long period of 96 years, supplementing the classical MK trend detection test with the Sen’s ITA approach. The city is located at an average elevation of 2000 m above sea level, one of the highest settlements in Türkiye. The Erzurum basin’s rich groundwater and surface water resources are fed by its unique geomorphology, largely composed of mountains and plateaus, and by its harsh continental climate [34]. In the literature searches conducted during the study period, no comprehensive study examining the trends in climate variables of the region was coincided. Considering the pressure that climate change creates, especially on water resources, a comprehensive study to be conducted on the temporal trend analysis of climate variables in the province is important in terms of providing unique findings for both the scientific literature and climate change strategists.
The results obtained from the temporal trend analysis of climate variables in this city, located in northeastern Türkiye at an average elevation of 2000 m above sea level, are significant because they offer unique findings for both the literature and climate change strategists, as they have not been previously investigated.
2. Materials and Methods
2.1. Study Area and Data
Erzurum is in the north-east of Turkey and is the fourth largest city in the country with a surface area of approximately 25,000 km2. The city is located between 40°14′15″ and 42°33′35″ east longitudes and 40°54′57″ and 39°06′10″ north latitudes (Figure 1a,b). Approximately 64% of its surface morphology consists of mountains and the rest of it consists of high plateaus. It is established between 1850 and 2200 m above sea level and, due to its distance from the sea of approximately 377 km, it has climate characteristics of dry and hot summers and long and cold winters. According to the Köppen–Geiger climate classification, the Dfb climate type prevails in the city [35]. According to long-term (1929–2024) statistics, the average daily sunshine duration is 7.0 h, and the average annual temperature, average number of rainy days, and average precipitation are recorded as 5.8 °C, 121.8, and 430.9 mm, respectively [36].
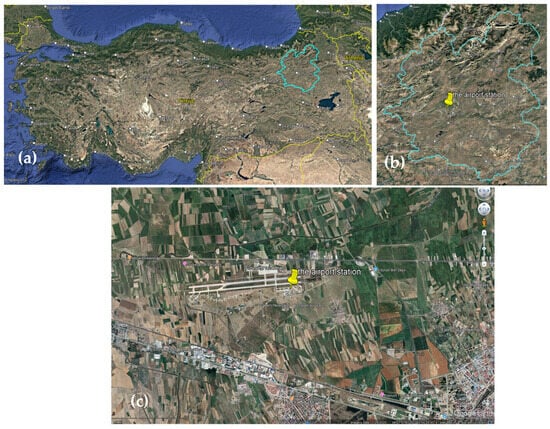
Figure 1.
(a) The geographical location of the study area (area surrounded by blue) (b) The location of the meteorological station marked with a yellow pin (c) View of the meteorological station from an eye height of approximately 12 km.
After a long and cold winter, melting snow is the most important source of water for the city’s surface and groundwater resources. Approximately 72% of the water sourced from groundwater (80.21 million m3/year) is used for agricultural irrigation, and 0.02% (2.60 million m3/year) for industrial activities. The remainder is allocated for drinking and livestock farming. 820 MW of electricity is generated from 30 hydroelectric power plants with a total installed capacity of 2500 GWh on the water resources [37].
In this study, daily maximum temperature (Tmax,°C), minimum temperature (Tmin,°C), and total precipitation (PREP, mm) values covering the 96-year long period between 1 January 1929, and 31 December 2024, were obtained from the records of the Erzurum Airport Station (station id: 17096) of the General Directorate of Meteorology [38]. The latitude and longitude information of the station (Figure 1b,c) located at an altitude of 1758 m are stated as 39.95 and 41.19, respectively [39]. This station was chosen because it has the oldest meteorological records in the city. The area where the station is located is close to the airport and the station is approximately 8.5 km from the city center and also 3.5 km from the nearest residential area.
Firstly, quality controls were performed on the data and missing data were completed. There are only 38 missing data points from each of the maximum and minimum temperature data provided by the station, and 26 missing data points from the total daily precipitation data. Missing values, corresponding to 0.07% and 0.1% of the total number of data points (35,063), were filled in using the arithmetic mean of the values before and after the missing value [40]. This method can provide reliable estimates in cases where spatial variability of the meteorological variable is absent [41].
Daily data were converted to monthly, seasonal and annual values by averaging for Tmax and Tmin and taking total precipitation values for PREP. Seasons in the study were defined as follows: spring (March–May), summer (June–August), autumn (September–November), and winter (December–February). Average temperatures were calculated from the average of minimum and maximum temperatures [Tmean = (Tmax + Tmin)/2] [42,43].
2.2. Run Homogeneity Test
Before trend analysis, homogeneity tests were conducted separately for monthly, seasonal and annual [44] average data. As in many studies investigating trend analysis in time and precipitation series for homogeneity, Refs. [28,45,46,47,48] the run homogeneity test [49] was used. The Run (Swed-Eisenhart) test can be used to test two hypotheses: assuming the data to be examined come from the same population (H0) and are independent (H1), or vice versa. A time series with a total number of data points N is generally truncated at the median value, and the number of data points below (Ni) and above (Nj) this level is determined. The run test statistic, Zr, is calculated using Equation (1), where r is the number of runs.
If the Zr value is less than the critical z value of the two-sided hypothesis test, the H0 hypothesis, which indicates that the time series under study is statistically significantly homogeneous, is accepted. Otherwise, it is rejected, and therefore, the H1 hypothesis, which indicates that the series is not homogeneous, is accepted.
2.3. Mann–Kendall (MK) Test
This nonparametric statistical method, proposed by Mann [50] and revised by Kendall [51], is used to identify trends in time series of hydrological and climatic variables. While it effectively detects increasing or decreasing monotonic trends in the series, it does not provide information about whether the trend is linear. The test statistic S, given by Equation (2), is positive, indicating an increasing trend, negative, indicating a decreasing trend, and equal to 0 when no trend is present.
where n is the data length and xi and xj represent the data values at time i and j, respectively. The variance of S, Var(S), can be calculated as follows:
In Equation (4), p is the number of connected groups and ti is the number of repetitions of the data set. The Z statistic or Standard Normal Variable used to evaluate the significance of the trend is calculated using the following Equation (5):
The calculated Z statistic is evaluated by comparing it with the critical z value in the standard normal table for the determined significance level (α). If the absolute Z value is greater than the critical z value, the trend is statistically significant, and the H0 hypothesis is rejected. H0, the initial hypothesis, and H1, the alternative hypothesis, are constructed as follows:
Hypothesis 1.
H0: “There is no trend in the series”.
Hypothesis 2.
H1: “There is a trend in the series”.
In this study, the evaluations were made based on significance levels of 90%, 95%, and 99% (α = 0.10, α = 0.05, and α = 0.01, respectively). α = 0.05 is a generally accepted significance level that balances reliability. α = 0.01 indicates a stronger significance level, which also reduces false positives, and α = 0.1 indicates a lower significance level, which can identify weak trends. Since the dataset had a sample size of more than 50 (35,063) and a high slope (≥0.01), no pre-whitening was applied to the data before testing [52].
2.4. Sen’s Innovative Trend Analysis (ITA)
According to the method developed by Şen [53], whose deterministic background is explained in detail [54], the time series is initially divided into two equal parts. The first half-series can be represented as xi (i = 1, 2, …, n/2) and the second half-series as xj (j = n/2 + 1, n/2 + 2, …, n). Each half-series is sorted from smallest to largest, and the second half-series is plotted against the first half-series as a scatter plot in a Cartesian coordinate system. The position of the scatter plot relative to a 45° line (1:1 line) inserted into the coordinate plane can be used to evaluate the trend of the time series. According to the graph presented in Figure 2, it is possible to identify five different trends in the time series: monotonic increase (or decrease), non-monotonic increase (or decrease), and trendless.
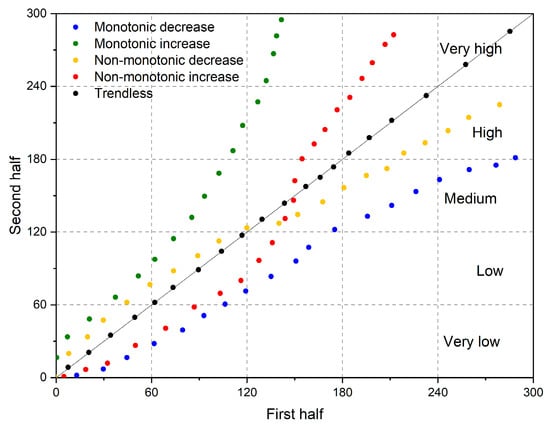
Figure 2.
Illustration of trend regions [55].
The plot area can be divided into an appropriate number of main grids and categorized as “very low (VL)”, “low (L)”, “medium (M)”, “high (H)” and “very high (VH)”. This approach can help visualize and evaluate smaller-scale trend changes in the series. The ordering starts from the origin (“very low”) and progresses sequentially toward the positive end of the y-axis. Therefore, stronger trend effects emerge as one moves to the up the scatterplot. For further reading, see Şen’s studies [53,54,55].
In the analysis, Sen’s slope can be calculated as given in Equation (6). In the equation, and are equal to the arithmetic mean of the first and second half series, respectively.
In this study, MK test, Sen’s slope and related statistics for monthly, seasonal, and annual series were calculated using R command. Data quality control and editing was done via MS Office 365 Excel, and data visualization was done using Origin 2024.
3. Results
Daily values of temperature (Tmax, Tmin, Tmean) and total precipitation (PREP) variables for Erzurum over the long period from 1929 to 2024 were converted to monthly values. According to the results of the run homogeneity test applied to the data series, all series are homogeneous. The homogeneity test results and descriptive statistics for the monthly values are presented separately in Table A1, Table A2, Table A3, Table A4 and Table A5 in Appendix A.
Annual, seasonal, and monthly trend analyses for monthly mean Tmax, Tmin, Tmean, and total precipitation were conducted separately using the MK test and Sen’s ITA approach. To ensure a combined evaluation of the results of the temporally layered analyses, the MK test results are summarized in Table 1, and the ITA results are summarized in Table 2. All of MK test and ITA results can be seen in Table A6, Table A7, Table A8 and Table A9 in the Appendix A.

Table 1.
MK trend analysis results.

Table 2.
ITA results.
Along with ITA charts, time series trends over a 96-year period and linear fit analyses for these trends are also displayed on the chart. This allows for the visualization of the variables’ temporal oscillations.
3.1. Annual Temperature and Precipitation Changes and Trend Analyses
Annual temperature and precipitation trends and their ITA plots are presented in Figure 3. The trend plots in the left column of the figure clearly show the increasing trends in monthly maximum temperatures (Figure 3a) and decreasing trends in minimum temperatures (Figure 3b). Tmax develops upwards with a linear slope of 0.024 °C/year (R2 = 0.304) over the years, while Tmin shows a downward trend with a slope of −0.027 °C/year (R2 = 0.225). When the ITA plots in the right column of the trend plots are examined, monotonically increasing and monotonically decreasing scattering profiles for Tmax and Tmin, respectively, also clearly emerge. These strong trends can also be observed in the annual MK test results in Table 1. The MK test Z statistics are 5.56 and −4.02 for Tmax and Tmin, respectively, and their absolute values are significantly higher than the critical z value of 2.575 (99% significance level). Therefore, the H0 hypothesis can be rejected for Tmax and Tmin, and it can be said that they exhibit increasing and decreasing trends, respectively. In Table 2, the Sen slope for the Tmax and Tmin series is calculated as 0.025 °C/year and −0.023 °C/year, respectively. When evaluated from the layered perspective offered by the Sen approach, both series exhibit increasing and decreasing trends, parallel to the general trends in the “VL”, “L”, “M”, “H”, and “VH” categories.
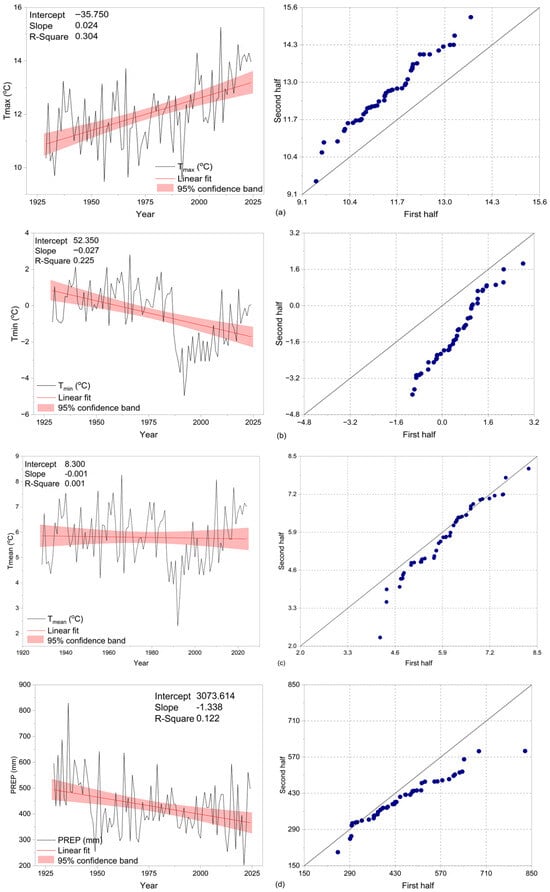
Figure 3.
The left column shows the annual trends for (a) Tmax, (°C), (b) Tmin, (°C), (c) Tmean (°C) and (d) PREP (mm) in Erzurum between 1929 and 2024. The right column shows their ITA scatter plots.
The Tmean trend trends and ITA graphs in Figure 3c show a very low decreasing trend. The slope in the annual trend graph was calculated as −0.001 °C/year (R2 = 0.001). In Table 2, Sen’s slope was also equal to this value, and decreasing trends were observed in all categories except “H.” However, according to the MK test results in Table 1, the H0: “There is no trend in the series” hypothesis cannot be rejected at any significance level (0.90, 0.95, and 0.99). The Z value of −0.190 is only slightly below the critical z value of 0.196 (α = 0.05).
For the precipitation trend graphs shown in Figure 3d, the MK test in Table 1 rejects the H0 hypothesis, and the alternative hypothesis H1, “There is a trend in the series”, is valid at a significance level of α = 0.05 (Z = −2.90). In Table 2, the Sen slope is calculated as −1.156 mm/year, and the categorical evaluation of the ITA profiles also shows decreasing trends for all categories (no data at the “VL” level). These results support the temporal trend graph profile.
3.2. Seasonal Temperature and Precipitation Changes and Trend Analyses
In the trend analysis of annual series for the period 1929–2024, the ITA profiles and MK test clearly show monotonic trends for the Tmax, Tmin, and PREP parameters, while the MK test for Tmean reveals no trend. The seasonal analysis, as well as the monthly analysis discussed in the next section, aims to identify trends at smaller time intervals.
Figure 4 presents the seasonal trends (left column) and their ITA profiles (right column) for each of the climate variables considered, presented in groups of four. The trend graphs for the Tmax time series (Figure 4a) in the left column show an upward trend in all seasons, parallel to the annual trend in Figure 3. However, the trend for the winter season is lower than for the others. In summer, the Tmax series fits a line with a slope of 0.033 °C/year with a regression coefficient of R2 = 0.344, while in winter it follows a line with a lower slope of 0.007 °C/year (R2 = 0.009). In spring and autumn, the series fits to lines with slopes of 0.035 °C/year (R2 = 0.255) and 0.024 °C/year (R2 = 0.200), respectively.
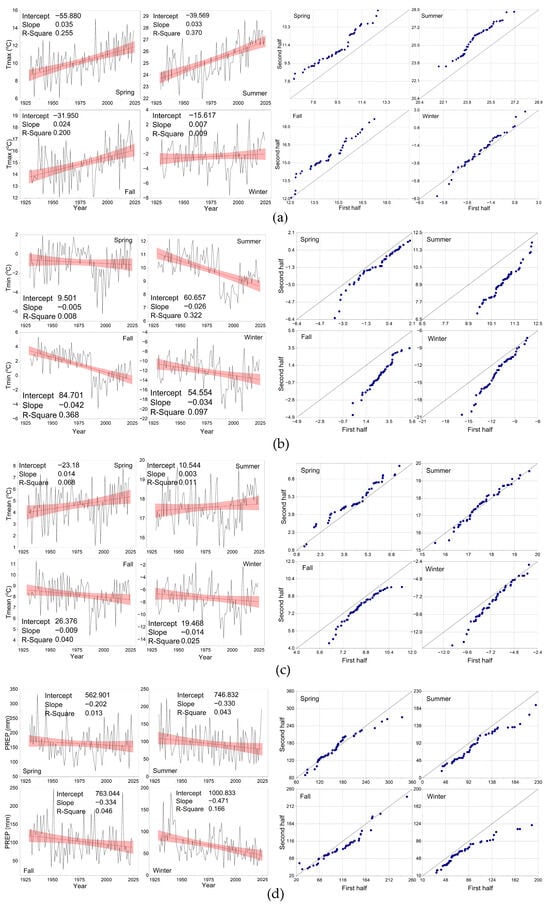
Figure 4.
The left column shows the seasonal trends (and their linear fit lines and 95% confidence bands in red) for (a) Tmax, (°C), (b) Tmin, (°C), (c) Tmean (°C) and (d) PREP (mm) in Erzurum between 1929 and 2024. The right column shows their ITA scatter plots.
The ITA profiles presented in the right column of Figure 4a, the MK test results in Table 1, and the results of Sen’s innovative approach in Table 2 support the view in the left column. According to the MK test, monthly average Tmax values in spring, summer, and autumn exhibit an increasing trend at a significance level of 99%. The MK test Z statistics for spring, summer, and autumn have values of 4.81, 6.16, and 4.47, respectively, and are significantly greater than the critical z value of 2.575 (α = 0.01). According to the innovative trend analysis approach, there is no data in the “VL” category, which has low values in spring and summer, while there are monotonic increasing trends in the other categories of these seasons and in autumn. According to the MK test Z statistics for winter (0.95), no significant trend is observed, and the H0 hypothesis is accepted. According to the ITA profile, winter exhibits a non-monotonic increasing trend, with higher values in the “H” and “VH” categories, although fewer values are present, showing an increasing trend.
Figure 4b shows the trend and ITA graphs for the Tmin series. The trend of the time series for all seasons follows a direction parallel to the annual trend, and all ITA profiles are monotonically decreasing. The slopes of the linear fit lines for all seasons except spring are greater than or close to the slope of the annual linear fit line, which is −0.027 °C/year (R2 = 0.225). The linear fit slopes of the seasonal trends in autumn and winter are −0.042 °C/year (R2 = 0.368) and −0.034 °C/year (R2 = 0.097), respectively, while this value is calculated as −0.005 °C/year (R2 = 0.008) in spring. According to the MK test results in Table 1, the decreasing trend in the Tmin series is statistically significant at the 95% significance level in winter and at the 99% significance level in summer and autumn. However, the trend in the Tmin series in spring is not statistically significant at any of the selected significance levels (α = 0.1, α = 0.05, and α = 0.001), and the H0 hypothesis cannot be rejected. Sen’s slope has values of −0.005, −0.023, −0.028, and −0.030 °C/year for spring, summer, autumn, and winter, respectively. There is no data in the “VH” category in autumn. Otherwise, there is a decreasing trend in all categories in all seasons. In spring, there is a large amount of data in the “H” and “VH” categories, where large values are present, while there is little data in the “VL” and “L” categories, where small values are present.
Figure 4c shows the trend and ITA plots for the Tmean series. The time series on the left show relatively increasing trends and positive slope values for spring and summer, while the opposite is true for autumn and winter. In the ITA scatter plots on the right, the autumn scatter plot exhibits a monotonic decreasing trend. A non-monotonic increasing trend can be observed in spring and summer, while the winter scatter plot resembles a non-monotonic decreasing trend. According to the MK test results summarized in Table 1, the spring Tmean series has a Z value of 2.45 (at an α = 0.05 significance level), indicating a significant increasing trend. In other seasons, the Ho hypothesis should be statistically accepted, and there is no trend for the Tmean. The annual MK test results for the Tmean series also revealed that there is no trend, and that the Ho hypothesis is accepted. The significant increasing trend calculated in the spring Tmean series is not valid for the Tmean series for the rest of the year.
According to the MK test, while no trend was determined in average temperatures in the annual analysis covering the period 1929–2024, seasonal analyses revealed an increasing trend in average temperatures in the spring at a 95% confidence level. When Sen’s slope values are examined in Table 2, it has a positive value (0.014, 0.005, and 0.007 °C/year) in spring, summer, and autumn, and a negative value (−0.012) in winter. This result may have been caused by the large dataset in the “VH” category in winter, i.e., the categories with the highest values. There are decreasing trends in the “VL” and “L” categories, i.e., the categories with smaller values, in spring, summer, and autumn. Consistent with the results of the MK test, there are increasing trends in the “VH” and “H” categories in spring.
One of the most striking results of the seasonal trend analyses of the selected climate variables was for monthly total precipitation. When the trend and ITA scatter plots of the PREP series shown in Figure 4d are examined, the time series are fitted with a linear slope with a negative value, parallel to the annual decreasing trend in all seasons. The ITA scatter plots show a non-monotonic decreasing trend in spring and autumn, while monotonic decreasing trends are observed in summer and winter. For the annual PREP series, the MK and ITA tests also determined decreasing trends. The MK test in Table 1 produced a Z statistic of −0.93 for the spring PREP series. According to the selected significance levels (α = 0.1, α = 0.05, and α = 0.001), this value is less than the critical z value, and therefore, the spring PREP series has no trend. According to the ITA results in Table 2, the Sen’s slope for the spring PREP series was calculated as −0.156. According to subcategorization, the spring PREP series exhibits a decreasing trend in the “VL” category, which has the lowest values, no trend in the “L” category, increasing in the “M” category, and decreasing in the “H” category. The MK test calculated decreasing trends for the summer, autumn, and winter PREP series at significance levels of α = 0.1, α = 0.05, and α = 0.001, respectively. According to the ITA approach, decreasing trends are also observed in different subcategories in summer, autumn, and winter.
One of the most striking results of the trend analyses of the PREP series, as explained above, is that important details can be revealed when trend analyses conducted on an annual scale are performed on a seasonal scale. Another important point is that the highest average precipitation in Erzurum between 1929 and 2024 occurred in spring, with 163.2 mm (Appendix A, Table A5). According to the trend analyses, there is no decrease in precipitation trends in spring.
During the study period, the lowest average precipitation in Erzurum occurred in winter, at 68.9 mm. According to MK tests, precipitation tends to decrease in winter at a 99% significance level. In cities where precipitation occurs primarily as snow during the winter season (January, February, and December), snow water may be the most significant potential recharger of groundwater resources, as opposed to rainwater runoff from asphalt and concrete pavements due to unplanned urbanization. Therefore, the decrease in winter precipitation trends is another important result of the trend analyses of the PREP series. A similar assessment can be made for the summer season. A decrease in precipitation trends during climatically dry summers (average 94.4 mm) is a potential factor that could increase the risk of drought.
3.3. Monthly Temperature and Precipitation Changes and Trend Analyses
Conducting temporal trend analyses of climate variables separately on annual, seasonal, and monthly scales provides more detailed information about the smaller time intervals of each variable. The MK test results indicate that increasing trends are statistically significant in the annual trend analyses of the Tmax series. The ITA results also reveal monotonic increasing trends across all subcategories.
The MK test for seasonal trend analyses of the Tmax series revealed no statistically significant trend in winter. Similarly, the ITA reveals increasing trends in the “H” and “VH” categories, where high values are found in winter, and decreasing or absent trends in other categories. The monthly trend analyses of the Tmax series reveal monotonic increasing trends in March, April, June, July, August, September, and October, and nonmonotonic increasing trends in the other months (Figure 5b). According to the MK test results in Table 1, in line with the seasonal trend analysis, there are no statistically significant trends in the winter months (December, January, and February), nor in November. Increasing trends were calculated at a 95% significance level in October and 99% in other months. According to the ITA results in Table 2, increasing trends are observed in all categories in March, April, June, and August, and in the “H” and/or “VH” categories during the winter months. Figure 5b shows the high values in the “VH” categories of the ITA scatter plot for February, March, October, November, and December.
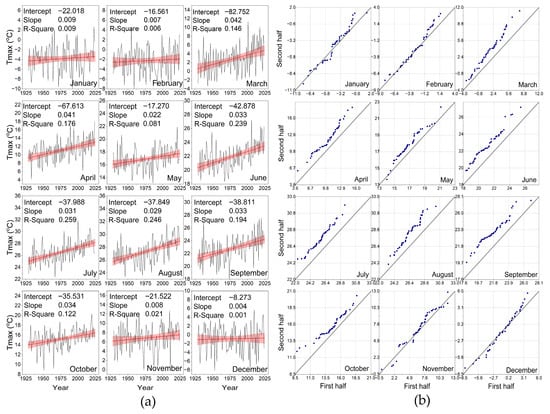
Figure 5.
The monthly trends (and their linear fit lines and 95% confidence bands in red) of Tmax (°C) (a) and ITA scatter plots for the monthly (b) in Erzurum during the period from 1929 to 2024.
The monthly trend graph for the series in Figure 5a also shows relatively flat lines in November, December, January, and February, fitting the series. The fit line with the highest slope was 0.042 °C/year (R2 = 0.146) for March, while the slope with the highest regression coefficient (R2 = 0.259) was 0.031 °C/year for July.
Table 3 was created to provide a simpler representation of the analysis results, which exhibit a more complex pattern as the annual scale progresses from a monthly scale, compared to the MK test. It can be easily seen from Table 3 that the annual increasing trends for the temporal MK trend analyses described above for the Tmax series become trendless in November and throughout the winter months as the temporal scale narrows.

Table 3.
The results of the MK test show a seasonal decreasing trend (blue), increasing trend (red), and no trend (blank).
Monthly trend and ITA scatter plots for the Tmin series are given in Figure 6. The trend profiles (Figure 6a) show negative trends similar to the trend profiles of the annual and seasonal series except for March (slope = 0.008 °C/year; R2 = 0.012). In Figure 6b, the ITA scatter profile of the March series shows a non-monotonic decreasing trend, but the strong increasing trend in the “VH” category may be the reason for the positive slope of the linear fit line in the trend profile. When the trend profiles are examined, the smallest linear fit slope was −0.007 °C/year (R2 = 0.020) for the April series, while the highest slope was 0.051 °C/year (R2 = 0.231) for the November series. Monotonic decreasing trends are observed in the ITA scatter plots for all months except January, February, and March. With the exception of the increasing trend (a small number of values) in the “VL” category of April, decreasing trends are observed for all categories of all months.
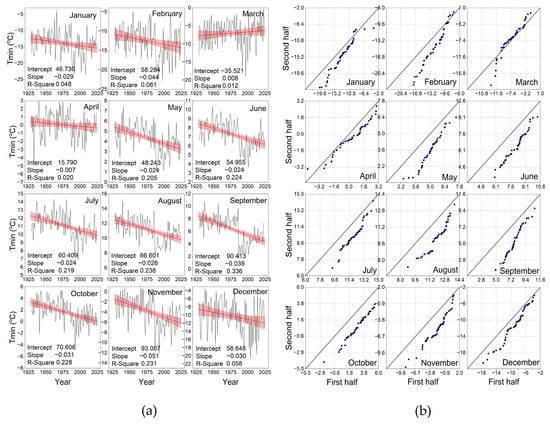
Figure 6.
The monthly trends (and their linear fit lines and 95% confidence bands in red) of Tmin (°C) (a) and ITA scatter plots for the monthly (b) in Erzurum during the period from 1929 to 2024.
An examination of the MK test results in Table 1 reveals no statistically significant trend in the March and April series. Decreasing trends were calculated at a 95% significance level for the series in January, February, and December (winter months), and at a 99% significance level for the series in the remaining months. An examination of Table 3, which summarizes the MK trend test results for the Tmin series across all time intervals, reveals that the Tmin series exhibited no trend in the spring months, March, and April, while they exhibited a decreasing trend in all other time intervals. The maximum value of the MK test statistic, S (and Z), was calculated as −1549.0 (and −4.90) for September, rejecting the H0 hypothesis and accepting the H1 hypothesis.
The trend profiles and ITA scatter plots of the monthly mean temperature series are presented in Figure 7a,b, respectively. The linear fit lines of the time series for March, April, June, July, and August have positive slopes. The fit line with the highest slope was calculated for March at 0.028 °C/year (R2 = 0.061). The fit lines of the Tmean series for the other months have negative slopes. The November fit line has the largest slope at −0.020 °C/year (R2 = 0.039).
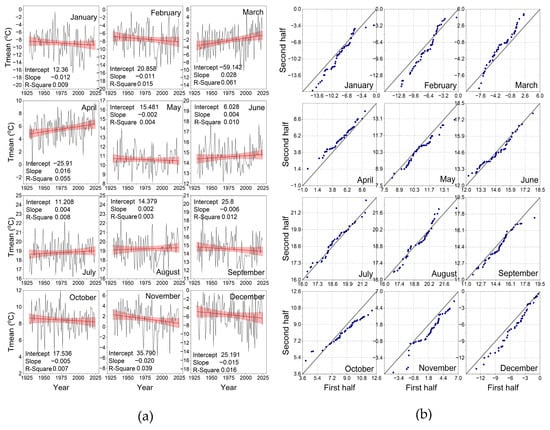
Figure 7.
The monthly trends (and their linear fit lines and 95% confidence bands in red) of Tmean (°C) (a) and ITA scatter plots for the monthly (b) in Erzurum during the period from 1929 to 2024.
An examination of the ITA scatter plots of the Tmean series reveals monotonic increasing trends in April, nonmonotonic increasing trends in March and June, and monotonic decreasing trends in November. According to the ITA approach evaluation results presented in Table 2, the November scatter profile exhibits a decreasing trend in all subcategories, and the Sen’s slope is −0.016 °C/year. For March and April, the “VL” category, which contains the smallest data values, exhibits decreasing trends and no data, respectively, while the other subcategories exhibit increasing trends. The MK statistics in Table 1 also produce results supporting these trends. The H0 hypothesis was rejected for March, April, and November. Despite the presence of increasing trends at the 95% level in March and April and decreasing trends at the 90% level in November, there is no statistically significant trend at the selected significance levels for all other months. According to the MK aggregate evaluation results for the Tmean series presented in Table 3, there are positive trends in the spring, March, and April, negative trends in November, and no trends in the other time periods.
The trend graphs and ITA scatter plots of the monthly total precipitation series are presented in Figure 8. When the trend profiles in Figure 8a are examined, the slope of the linear fit lines of the time series is negative in all months. The slope (and R2) values range between −0.218 mm/year (and R2 = 0.132) and −0.035 mm/year (and R2 = 0.001). The ITA scatter plots in Figure 8b show monotonic decreasing trends in January, February, March (with the exception of one data point above the 1:1 line), June, and September, nonmonotonic increasing trends in April, and nonmonotonic decreasing trends in the other months. Decreasing trends are observed in all categories of all months that exhibit monotonic trends, except for the “H” and “VH” categories of January and the “VH” categories of February and September, for which no data are available (Table 2).
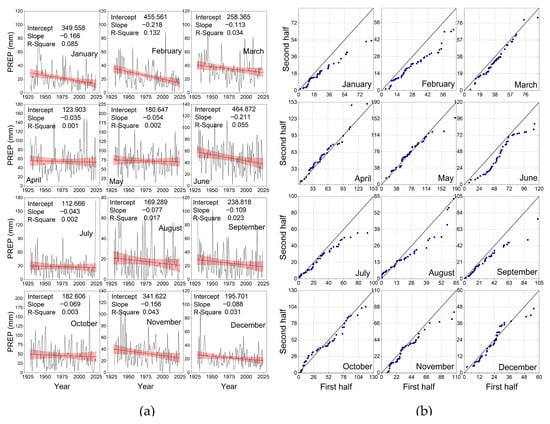
Figure 8.
The monthly trends (and their linear fit lines and 95% confidence bands in red) of PREP (mm) (a) and ITA scatter plots for the monthly (b) in Erzurum during the period from 1929 to 2024.
During the 1919–2024 period, the highest average precipitation in Erzurum occurred in the form of rain in May (73.1 mm), April (54.6 mm), and June (48.5 mm). The lowest precipitation occurred in summer rain in August (17.6 mm) and snowfall in January (21.5 mm), December (22.0 mm), and February (25.4 mm). Precipitation statistics can be found in Table A5 of Appendix A. The May ITA scatter profiles show a trendless appearance until the decreasing trend in the “H” and “VH” categories, where the highest total precipitation values are found. In April, the ITA scatter profiles show a trendless appearance until the increasing trend in the “VH” category. Table 1 shows that, according to the MK test results, there is no statistically significant trend in the PREP series in either of these months, meaning that the Ho hypothesis is accepted. In Table 1, the ITA evaluation results for June show a Sen slope of −0.216 mm/year, and there are also decreasing trends in the “VL,” “L,” “M,” and “H” categories (no data in the “VH” category). The MK test also found a decreasing slope at the 95% significance level (Z = −0.210).
Apart from the increasing trends in the “VL” category in August and the “M” category in December (no data in the “VH” category), there are decreasing slope profiles in other subcategories. However, the MK test shows no statistically significant trend for these months, while decreasing trends are found in January and February at the 95% (Z = −2.62) and 99% (Z = −3.70) significance levels, respectively. According to the same results, November precipitation tends to decrease at the 90% (Z = −1.65) significance level.
When the monthly PREP series are evaluated with the results of the annual and seasonal series, it is seen that in winter, January and It is clear that February snowfall is showing a significant downward trend. While the decrease in total precipitation in November and June in the fall is significant enough to influence seasonal trends, the decreasing trend in March precipitation in the spring is not significant enough to significantly impact seasonal statistics (Table 3).
4. Discussion
This study conducted trend analysis using monthly data for maximum, minimum, and average temperature and total precipitation variables for Erzurum over a 96-year period spanning the period 1929–2024. The Erzurum Airport Station, whose data served as the basis for this study, was chosen because it provides the oldest meteorological records in the city. Undoubtedly, the results produced in the study do not define the large surface area of the city of 25,000 km2. Daily average data from the station records were analyzed separately for each variable as annual, seasonal, and monthly time series. Analyses based on the MK trend analysis test and Sen’s ITA approach yielded significant findings.
A study conducted for western Iran, which is geographically close to the region covered in this study, identified increasing trends in the Tmax series and decreasing trends in the precipitation series [56]. Similar trends for temperature and precipitation series were found in other studies conducted in Osijek, Croatia [57], and Serbia [7].
Increasing trends in the Tmax series and decreasing trends in the Tmin series were observed at strong statistical significance levels. Essentially, temperature differences between day and night are large in continental climate conditions. Changes in this variable, known as the diurnal temperature range (DTR), are important for determining the effects of climate change [58,59]. Due to the decreasing trend in Tmin despite the increasing trend in Tmax, DTR in Erzurum is increasing. Similar results have been found in studies examining DTR changes in Europe [60] and the continental United States [61]. The most important factors causing DTR oscillations are surface shortwave and longwave radiation [60]. Factors affecting these radiations include land use [62], irrigation, urbanization [63], desertification and other climate influences [63,64,65]. Investigating the underlying causes of DTR increases in this region could be a potential research topic.
Furthermore, there were no statistically significant trends in the Tmean series, apart from increasing trends for March and April. The trendless profiles observed in most of the average temperature series can be explained by the mathematical balancing of the increase in maximum temperatures and the decrease in minimum temperatures.
Trend analyses of the total precipitation series reveal strong decreasing trends in winter snowfall and in May, the month when Erzurum receives the most precipitation. Precipitation is the primary factor feeding the region’s groundwater and surface water resources, and these results in the precipitation series may increase the risk of drought in the region. In addition to the trendless appearance of the Tmax and Tmean series in winter, the decreasing trends in the Tmin and precipitation series indicate that the magnitude of the impact of temperature on the hydrological cycle requires further investigation [4]. The decrease in total precipitation trends could be due to changes in evaporation and relative humidity rates due to changing temperature dynamics, changes in land use, and/or increases in aerosol concentrations [66]. Each of these possible causes could be considered as potential research. In addition, investigating the relationship between ERA5 reanalysis data and temperature and precipitation variability by applying clustering techniques in the region with synoptic-scale circulation is also a potential study topic.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [https://www.mgm.gov.tr/ accessed on 22 October 2025].
Acknowledgments
I would like to thank the Turkish State Meteorological Service for sharing the meteorological records of Erzurum Airport Station between 1929 and 2024. During the preparation of this manuscript/study, the author used OpenAI Graphical abstract designer, GPT-5 for the purposes of the graphical abstract. The author has reviewed and edited the output and takes full responsibility for the content of this publication.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IPCC | Intergovernmental Panel on Climate Change |
| LR | Linear regression |
| MK | Mann–Kendall |
| ITA | Innovative Trend Analysis |
| Tmax | Maximum temperature (°C) |
| Tmin | Minimum temperature (°C) |
| Tmean | Mean temperature (°C) |
| PREP | Precipitation (mm) |
| S | Mann–Kendall test statistic |
| Var(S) | Variance of S |
| R2 | Regression coefficient |
| r | Runs number of the run homogeneity test |
| n | Data length and xi and xj represent the data values at time i and j |
| N | Total number of observations in the run homogeneity test |
| Ni | Number of observations above the median in the run homogeneity test |
| Nj | Number of observations below the median in the run homogeneity test |
| Z | Normal distribution coefficient for Mann–Kendall test |
| Zr | Run homogeneity test statistics |
| z | Critical Z value from the standard normal distribution table |
| t | Time |
| xi | Data values at time i |
| xj | Data values at time j |
| Arithmetic average of the first half of the series in ITA | |
| Arithmetic average of the second half of the series in ITA | |
| i, j | ith, jth |
| VL | Very low |
| L | Low |
| M | Medium |
| H | High |
| VH | Very high |
| DTR | Diurnal Temperature Range |
Appendix A

Table A1.
The results of the runs test.
Table A1.
The results of the runs test.
| Tmax | Tmin | Precipitation | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | Nj | N | r | Zr | Hypothesis * | Ni | Nj | N | r | Zr | Hypothesis * | Ni | Nj | N | r | Zr | Hypothesis * | |
| January | 46 | 50 | 96 | 44 | −0.006 | H0 | 48 | 48 | 96 | 44 | −0.006 | H0 | 60 | 36 | 96 | 44 | 0.000 | H0 |
| February | 51 | 45 | 96 | 54 | 0.016 | H0 | 44 | 52 | 96 | 54 | 0.016 | H0 | 59 | 37 | 96 | 54 | 0.022 | H0 |
| March | 51 | 45 | 96 | 58 | 0.024 | H0 | 48 | 48 | 96 | 58 | 0.024 | H0 | 55 | 41 | 96 | 58 | 0.027 | H0 |
| April | 53 | 43 | 96 | 56 | 0.021 | H0 | 47 | 49 | 96 | 56 | 0.019 | H0 | 58 | 38 | 96 | 56 | 0.025 | H0 |
| May | 49 | 47 | 96 | 48 | 0.002 | H0 | 48 | 48 | 96 | 48 | 0.002 | H0 | 54 | 42 | 96 | 48 | 0.004 | H0 |
| June | 50 | 46 | 96 | 38 | −0.019 | H0 | 45 | 51 | 96 | 38 | −0.019 | H0 | 48 | 48 | 96 | 38 | −0.019 | H0 |
| July | 52 | 44 | 96 | 45 | −0.004 | H0 | 48 | 48 | 96 | 45 | −0.004 | H0 | 57 | 39 | 96 | 45 | −0.001 | H0 |
| August | 51 | 45 | 96 | 40 | −0.015 | H0 | 46 | 50 | 96 | 40 | −0.015 | H0 | 61 | 35 | 96 | 40 | −0.008 | H0 |
| September | 48 | 48 | 96 | 42 | −0.011 | H0 | 42 | 54 | 96 | 42 | −0.009 | H0 | 57 | 39 | 96 | 42 | −0.007 | H0 |
| October | 51 | 45 | 96 | 48 | 0.003 | H0 | 46 | 50 | 96 | 48 | 0.002 | H0 | 53 | 43 | 96 | 48 | 0.003 | H0 |
| November | 45 | 51 | 96 | 46 | −0.002 | H0 | 46 | 50 | 96 | 46 | −0.002 | H0 | 54 | 42 | 96 | 46 | −0.001 | H0 |
| December | 47 | 49 | 96 | 46 | −0.002 | H0 | 47 | 49 | 96 | 46 | −0.002 | H0 | 55 | 41 | 96 | 46 | 0.000 | H0 |
| Spring | 51 | 45 | 96 | 50 | 0.007 | H0 | 47 | 49 | 96 | 50 | 0.007 | H0 | 55 | 41 | 96 | 50 | 0.009 | H0 |
| Summer | 53 | 43 | 96 | 30 | −0.036 | H0 | 47 | 49 | 96 | 30 | −0.037 | H0 | 55 | 41 | 96 | 30 | −0.035 | H0 |
| Fall | 47 | 49 | 96 | 42 | −0.011 | H0 | 43 | 53 | 96 | 42 | −0.010 | H0 | 55 | 41 | 96 | 42 | −0.009 | H0 |
| Winter | 55 | 41 | 96 | 42 | −0.009 | H0 | 46 | 50 | 96 | 42 | −0.011 | H0 | 58 | 38 | 96 | 42 | −0.007 | H0 |
| Annual | 50 | 46 | 96 | 36 | −0.024 | H0 | 46 | 50 | 96 | 36 | −0.024 | H0 | 55 | 41 | 96 | 36 | −0.022 | H0 |
* The significance level α = 0.05 critical z = ±1.960.

Table A2.
The descriptive statistics for monthly, seasonal and annual trends of Tmax in Erzurum for the period from 1929 to 2024.
Table A2.
The descriptive statistics for monthly, seasonal and annual trends of Tmax in Erzurum for the period from 1929 to 2024.
| Min | Max | Mean | sd | |
|---|---|---|---|---|
| January | −10.0 | 2.7 | −3.8 | 2.7 |
| February | −8.0 | 4.2 | −2.2 | 2.7 |
| March | −3.3 | 11.3 | 2.7 | 3.2 |
| April | 4.1 | 18.0 | 11.1 | 2.6 |
| May | 13.2 | 21.9 | 16.9 | 1.7 |
| June | 18.4 | 27.2 | 21.9 | 1.9 |
| July | 22.4 | 31.9 | 26.6 | 1.8 |
| August | 23.3 | 31.7 | 27.3 | 1.9 |
| September | 18.1 | 27.6 | 22.7 | 2.0 |
| October | 8.8 | 20.3 | 15.2 | 2.0 |
| November | −0.1 | 12.8 | 6.9 | 2.7 |
| December | −8.1 | 5.7 | −0.9 | 3.1 |
| Spring | 6.1 | 15.0 | 10.3 | 1.8 |
| Summer | 21.8 | 28.7 | 25.3 | 1.5 |
| Fall | 12.1 | 18.7 | 14.9 | 1.5 |
| Winter | −7.7 | 2.8 | −2.3 | 1.9 |
| Annual | 9.5 | 15.3 | 12.0 | 1.2 |

Table A3.
The descriptive statistics for monthly, seasonal and annual trends of Tmin in Erzurum for the period from 1929 to 2024.
Table A3.
The descriptive statistics for monthly, seasonal and annual trends of Tmin in Erzurum for the period from 1929 to 2024.
| Min | Max | Mean | sd | |
|---|---|---|---|---|
| January | −23.4 | −3.4 | −13.9 | 3.9 |
| February | −22.9 | −4.9 | −12.5 | 4.0 |
| March | −18.8 | −0.3 | −7.0 | 3.6 |
| April | −4.5 | 3.0 | 0.1 | 1.6 |
| May | 1.2 | 7.5 | 4.3 | 1.4 |
| June | 3.7 | 10.3 | 7.3 | 1.4 |
| July | 6.9 | 14.3 | 11.1 | 1.5 |
| August | 7.3 | 15.2 | 11.2 | 1.6 |
| September | 1.5 | 10.8 | 6.4 | 2.0 |
| October | −4.1 | 5.4 | 1.7 | 2.0 |
| November | −12.1 | 0.8 | −3.8 | 2.8 |
| December | −20.5 | −3.6 | −10.2 | 4.0 |
| Spring | −6.3 | 1.9 | −0.9 | 1.6 |
| Summer | 6.9 | 12.2 | 9.9 | 1.3 |
| Fall | −4.6 | 5.4 | 1.4 | 1.9 |
| Winter | −20.5 | −5.0 | −12.2 | 3.0 |
| Annual | −5.0 | 2.8 | −0.4 | 1.6 |

Table A4.
The descriptive statistics for monthly, seasonal and annual trends of Tmean in Erzurum for the period from 1929 to 2024.
Table A4.
The descriptive statistics for monthly, seasonal and annual trends of Tmean in Erzurum for the period from 1929 to 2024.
| Min | Max | Mean | sd | |
|---|---|---|---|---|
| January | −16.7 | −0.6 | −8.9 | 3.2 |
| February | −14.9 | −0.4 | −7.4 | 3.2 |
| March | −10.2 | 5.0 | −2.1 | 3.3 |
| April | −0.2 | 9.8 | 5.6 | 1.9 |
| May | 8.2 | 14.1 | 10.6 | 1.1 |
| June | 12.2 | 17.9 | 14.6 | 1.2 |
| July | 16.2 | 22.2 | 18.8 | 1.2 |
| August | 16.7 | 22.7 | 19.3 | 1.3 |
| September | 11.5 | 18.9 | 14.6 | 1.5 |
| October | 4.0 | 12.1 | 8.5 | 1.5 |
| November | −5.7 | 6.3 | 1.5 | 2.5 |
| December | −14.0 | −0.3 | −5.6 | 3.4 |
| Spring | 1.1 | 7.9 | 4.7 | 1.5 |
| Summer | 15.4 | 19.6 | 17.6 | 0.9 |
| Fall | 4.5 | 11.3 | 8.2 | 1.3 |
| Winter | −13.8 | −1.6 | −7.3 | 2.4 |
| Annual | 2.3 | 8.3 | 5.8 | 1.1 |

Table A5.
The descriptive statistics for monthly, seasonal and annual trends of PREP in Erzurum for the period from 1929 to 2024.
Table A5.
The descriptive statistics for monthly, seasonal and annual trends of PREP in Erzurum for the period from 1929 to 2024.
| Min | Max | Mean | sd | |
|---|---|---|---|---|
| January | 1.7 | 85.6 | 21.5 | 15.9 |
| February | 1.2 | 90.0 | 25.4 | 16.7 |
| March | 1.2 | 91.2 | 35.5 | 17.1 |
| April | 8.8 | 150.2 | 54.6 | 28.9 |
| May | 12.1 | 186.9 | 73.1 | 32.8 |
| June | 2.9 | 112.6 | 48.5 | 25.1 |
| July | 0.0 | 173.6 | 28.3 | 24.8 |
| August | 0.0 | 63.0 | 17.6 | 16.5 |
| September | 0.0 | 103.1 | 24.1 | 20.0 |
| October | 0.0 | 210.8 | 46.3 | 34.8 |
| November | 0.0 | 106.7 | 32.9 | 21.0 |
| December | 2.1 | 93.4 | 22.0 | 13.8 |
| Spring | 69.7 | 333.7 | 163.2 | 49.8 |
| Summer | 18.4 | 225.2 | 94.4 | 44.5 |
| Fall | 26.4 | 249.1 | 103.3 | 43.8 |
| Winter | 17.1 | 189.5 | 68.9 | 32.2 |
| Annual | 202.4 | 829.6 | 429.9 | 106.6 |

Table A6.
Results of MK test and ITA for Tmax.
Table A6.
Results of MK test and ITA for Tmax.
| Mann–Kendall Test | ITA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | N | p | S | varS | tau | Sen’s Slope (°C/year) | 95 Percent Confidence Interval | ||
| January | 0.791 | 96 | 0.429 | 251.00 | 99,812.33 | 0.055 | 0.009 | −0.011 | 0.029 |
| February | 0.662 | 96 | 0.508 | 210.00 | 99,811.33 | 0.046 | 0.007 | −0.015 | 0.028 |
| March | 3.523 | 96 | 0.000 | 1114.00 | 99,813.33 | 0.244 | 0.044 | 0.021 | 0.069 |
| April | 3.764 | 96 | 0.000 | 1190.00 | 99,811.33 | 0.261 | 0.039 | 0.020 | 0.058 |
| May | 2.830 | 96 | 0.005 | 895.00 | 99,810.33 | 0.196 | 0.018 | 0.005 | 0.030 |
| June | 4.928 | 96 | 0.000 | 1558.00 | 99,813.33 | 0.342 | 0.033 | 0.022 | 0.046 |
| July | 5.159 | 96 | 0.000 | 1631.00 | 99,810.33 | 0.358 | 0.033 | 0.022 | 0.045 |
| August | 4.932 | 96 | 0.000 | 1559.00 | 99,812.33 | 0.342 | 0.034 | 0.021 | 0.046 |
| September | 4.406 | 96 | 0.000 | 1393.00 | 99,812.33 | 0.306 | 0.032 | 0.019 | 0.046 |
| October | 3.419 | 96 | 0.001 | 1081.00 | 99,807.67 | 0.237 | 0.023 | 0.010 | 0.038 |
| November | 1.481 | 96 | 0.139 | 469.00 | 99,812.33 | 0.103 | 0.014 | −0.005 | 0.035 |
| December | 0.149 | 96 | 0.882 | 48.00 | 99,808.67 | 0.011 | 0.002 | −0.023 | 0.027 |
| Spring | 4.808 | 96 | 0.000 | 1520.00 | 99,813.33 | 0.333 | 0.033 | 0.020 | 0.045 |
| Summer | 6.163 | 96 | 0.000 | 1948.00 | 99,813.33 | 0.427 | 0.034 | 0.025 | 0.044 |
| Fall | 4.466 | 96 | 0.000 | 1412.00 | 99,813.33 | 0.310 | 0.024 | 0.014 | 0.034 |
| Winter | 0.953 | 96 | 0.341 | 302.00 | 99,813.33 | 0.066 | 0.006 | −0.008 | 0.021 |
| Annual | 5.555 | 96 | 0.000 | 1756.00 | 99,813.33 | 0.385 | 0.025 | 0.017 | 0.033 |

Table A7.
Results of MK test and ITA for Tmin.
Table A7.
Results of MK test and ITA for Tmin.
| Mann–Kendall Test | ITA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | N | p | S | varS | tau | Sen’s Slope (°C/Year) | 95 Percent Confidence Interval | ||
| January | −1.956 | 96 | 0.050 | −619.00 | 99,812.33 | −0.136 | −0.027 | −0.054 | 0.000 |
| February | −2.080 | 96 | 0.038 | −658.00 | 99,813.33 | −0.144 | −0.034 | −0.063 | −0.002 |
| March | 1.279 | 96 | 0.201 | 405.00 | 99,812.33 | 0.089 | 0.019 | −0.008 | 0.046 |
| April | −1.605 | 96 | 0.109 | −508.00 | 99,809.33 | −0.111 | −0.010 | −0.021 | 0.003 |
| May | −4.219 | 96 | 0.000 | −1334.00 | 99,811.33 | −0.293 | −0.021 | −0.030 | −0.012 |
| June | −4.178 | 96 | 0.000 | −1321.00 | 99,810.33 | −0.290 | −0.022 | −0.032 | −0.013 |
| July | −4.697 | 96 | 0.000 | −1485.00 | 99,810.33 | −0.326 | −0.024 | −0.034 | −0.015 |
| August | −4.549 | 96 | 0.000 | −1438.00 | 99,811.33 | −0.326 | −0.026 | −0.037 | −0.016 |
| September | −4.900 | 96 | 0.000 | −1549.00 | 99,810.33 | −0.340 | −0.038 | −0.050 | −0.025 |
| October | −4.783 | 96 | 0.000 | −1512.00 | 99,811.33 | −0.332 | −0.035 | −0.050 | −0.022 |
| November | −4.643 | 96 | 0.000 | −1468.00 | 99,813.33 | −0.322 | −0.047 | −0.067 | −0.029 |
| December | −2.314 | 96 | 0.021 | −732.00 | 99,813.33 | −0.161 | −0.034 | −0.066 | −0.006 |
| Spring | −0.832 | 96 | 0.405 | −264.00 | 99,813.33 | −0.058 | −0.005 | −0.016 | 0.007 |
| Summer | −5.125 | 96 | 0.000 | −1620.00 | 99,813.33 | −0.355 | −0.023 | −0.031 | −0.015 |
| Fall | −5.777 | 96 | 0.000 | −1826.00 | 99,813.33 | −0.400 | −0.038 | −0.050 | −0.027 |
| Winter | −2.580 | 96 | 0.010 | −816.00 | 99,813.33 | −0.179 | −0.030 | −0.053 | −0.008 |
| Annual | −4.017 | 96 | 0.000 | −1270.00 | 99,813.33 | −0.279 | −0.023 | −0.034 | −0.013 |

Table A8.
Results of MK test and ITA for Tmean.
Table A8.
Results of MK test and ITA for Tmean.
| Mann–Kendall Test | ITA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | N | p | S | varS | tau | Sen’s Slope (°C/year) | 95 Percent Confidence Interval | ||
| January | −0.706 | 96 | 0.480 | −224.00 | 99,813.33 | −0.049 | −0.008 | −0.033 | 0.015 |
| February | −0.978 | 96 | 0.328 | −310.00 | 99,813.33 | −0.068 | −0.012 | −0.040 | 0.014 |
| March | 2.450 | 96 | 0.014 | 775.00 | 99,812.33 | 0.170 | 0.032 | 0.006 | 0.055 |
| April | 2.023 | 96 | 0.043 | 640.00 | 99,813.33 | 0.140 | 0.015 | 0.001 | 0.029 |
| May | −0.310 | 96 | 0.756 | −99.00 | 99,812.33 | −0.022 | −0.001 | −0.010 | 0.008 |
| June | 1.019 | 96 | 0.308 | 323.00 | 99,812.33 | 0.071 | 0.005 | −0.005 | 0.014 |
| July | 1.102 | 96 | 0.271 | 349.00 | 99,810.33 | 0.077 | 0.005 | −0.005 | 0.014 |
| August | 0.646 | 96 | 0.519 | 205.00 | 99,810.33 | 0.045 | 0.004 | −0.007 | 0.014 |
| September | −0.801 | 96 | 0.423 | −254.00 | 99,811.33 | −0.056 | −0.005 | −0.017 | 0.006 |
| October | −1.048 | 96 | 0.295 | −332.00 | 99,813.33 | −0.073 | −0.005 | −0.016 | 0.006 |
| November | −1.801 | 96 | 0.072 | −570.00 | 99,811.33 | −0.125 | −0.016 | −0.033 | 0.001 |
| December | −1.168 | 96 | 0.243 | −370.00 | 99,813.33 | −0.081 | −0.017 | −0.045 | 0.012 |
| Spring | 2.314 | 96 | 0.021 | 732.00 | 99,813.33 | 0.161 | 0.014 | 0.002 | 0.026 |
| Summer | 1.352 | 96 | 0.177 | 428.00 | 99,812.33 | 0.094 | 0.005 | −0.002 | 0.012 |
| Fall | −1.567 | 96 | 0.117 | −496.00 | 99,813.33 | −0.109 | 0.007 | −0.017 | 0.002 |
| Winter | −1.345 | 96 | 0.179 | −426.00 | 99,813.33 | −0.093 | −0.012 | −0.031 | 0.005 |
| Annual | −0.193 | 96 | 0.847 | −62.00 | 99,813.33 | −0.014 | −0.001 | −0.009 | 0.008 |

Table A9.
Results of MK test and ITA for PREP.
Table A9.
Results of MK test and ITA for PREP.
| Mann–Kendall Test | ITA | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | N | p | S | varS | tau | Sen’s Slope (mm/year) | 95 Percent Confidence Interval | ||
| January | −2.621 | 96 | 0.009 | −829.00 | 99,800.67 | −0.182 | −0.120 | −0.208 | −0.029 |
| February | −3.697 | 96 | 0.000 | −1169.00 | 99,809.33 | −0.256 | −0.200 | −0.320 | −0.100 |
| March | −2.203 | 96 | 0.028 | −697.00 | 99,804.33 | −0.153 | −0.130 | −0.252 | −0.017 |
| April | −0.541 | 96 | 0.588 | −172.00 | 99,808.33 | −0.038 | −0.058 | −0.260 | 0.144 |
| May | −0.231 | 96 | 0.817 | −74.00 | 99,811.33 | −0.016 | −0.030 | −0.277 | 0.212 |
| June | −2.102 | 96 | 0.036 | −665.00 | 99,801.67 | −0.146 | −0.216 | −0.414 | −0.018 |
| July | −1.231 | 96 | 0.218 | −390.00 | 99,805.33 | −0.086 | −0.088 | −0.232 | 0.046 |
| August | −0.636 | 96 | 0.525 | −202.00 | 99,803.67 | −0.044 | −0.032 | −0.138 | 0.058 |
| September | −1.304 | 96 | 0.192 | −413.00 | 99,800.67 | −0.091 | −0.073 | −0.200 | 0.047 |
| October | −0.684 | 96 | 0.494 | −217.00 | 99,811.33 | −0.048 | −0.079 | −0.343 | 0.150 |
| November | −1.652 | 96 | 0.098 | −523.00 | 99,807.33 | −0.115 | −0.125 | −0.247 | 0.025 |
| December | −1.421 | 96 | 0.155 | −450.00 | 99,801.67 | −0.099 | −0.053 | −0.143 | 0.026 |
| Spring | −0.931 | 96 | 0.352 | −295.00 | 99,812.33 | −0.065 | −0.156 | −0.527 | 0.199 |
| Summer | −1.804 | 96 | 0.071 | −571.00 | 99,812.33 | −0.125 | −0.296 | −0.604 | 0.027 |
| Fall | −2.080 | 96 | 0.038 | −658.00 | 99,804.67 | −0.144 | −0.332 | −0.640 | −0.015 |
| Winter | −3.700 | 96 | 0.000 | −1170.00 | 99,804.67 | −0.257 | −0.378 | −0.580 | −0.182 |
| Annual | −2.899 | 96 | 0.004 | −917.00 | 99,812.33 | −0.201 | −1.156 | −1.882 | −0.416 |
References
- Lee, H.; Romero, J. IPCC, 2023: Climate Change 2023: Synthesis Report, Summary for Policymakers. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Arias, P., Bustamante, M., Elgizouli, I., Flato, G., Howden, M., Méndez-Vallejo, C., Pereira, J.J., Pichs-Madruga, R., Rose, S.K., Saheb, Y., Eds.; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar]
- Cui, L.; Wang, L.; Lai, Z.; Tian, Q.; Liu, W.; Li, J. Innovative Trend Analysis of Annual and Seasonal Air Temperature and Rainfall in the Yangtze River Basin, China during 1960–2015. J. Atmos. Sol. Terr. Phys. 2017, 164, 48–59. [Google Scholar] [CrossRef]
- Khan, A.A.; Zhao, Y.; Khan, J.; Rahman, G.; Rafiq, M.; Moazzam, M.F.U. Spatial and Temporal Analysis of Rainfall and Drought Condition in Southwest Xinjiang in Northwest China, Using Various Climate Indices. Earth Syst. Environ. 2021, 5, 201–216. [Google Scholar] [CrossRef]
- Haldar, S.; Choudhury, M.; Choudhury, S.; Samanta, P. Trend Analysis of Long-Term Meteorological Data of a Growing Metropolitan City in the Era of Global Climate Change. Total Environ. Res. Themes 2023, 7, 100056. [Google Scholar] [CrossRef]
- Gujree, I.; Ahmad, I.; Zhang, F.; Arshad, A. Innovative Trend Analysis of High-Altitude Climatology of Kashmir Valley, North-West Himalayas. Atmosphere 2022, 13, 764. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Meshram, C.; Singh, S.K.; Srivastava, P.K.; Islam, T. Precipitation Trend Analysis of Sindh River Basin, India, from 102-Year Record (1901–2002). Atmos. Sci. Lett. 2016, 17, 71–77. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Karpouzos, D.K.; Kavalieratou, S.; Babajimopoulos, C. Trend Analysis of Precipitation Data in Pieria Region (Greece). Eur. Water 2010, 30, 31–40. [Google Scholar]
- Ceppi, P.; Scherrer, S.C.; Fischer, A.M.; Appenzeller, C. Revisiting Swiss Temperature Trends 1959–2008. Int. J. Climatol. 2012, 32, 203–213. [Google Scholar] [CrossRef]
- Avino, A.; Manfreda, S.; Cimorelli, L.; Pianese, D. Trend of Annual Maximum Rainfall in Campania Region (Southern Italy). Hydrol. Process 2021, 35, e14447. [Google Scholar] [CrossRef]
- Gil-Alana, L.A. Maximum and Minimum Temperatures in the United States: Time Trends and Persistence. Atmos. Sci. Lett. 2018, 19, e810. [Google Scholar] [CrossRef]
- Roca-Flores, E.; Soto-Bernal, J.J.; Rojo-Garibaldi, B.; Fraedrich, K.; Naumis, G.G. Annual Rain Periodicity in the Aguascalientes Region at Central Mexico. J. Hydrol. 2025, 662, 133766. [Google Scholar] [CrossRef]
- Legass, A.M.; Alamirew, T.; Gebrehiwot, S.G.; Haro-Monteagudo, D.; Berhanu, D. Spatiotemporal Climate Change Projection and Trend Analysis Using Selected Downscaled CMIP6 Models for Water Action over Awash River Basin, Ethiopia. Environ. Chall. 2025, 18, 101059. [Google Scholar] [CrossRef]
- Aswad, F.K.; Yousif, A.A.; Ibrahim, S.A. Trend Analysis Using Mann-Kendall and Sen’s Slope Estimator Test for Annual and Monthly Rainfall for Sinjar District, Iraq. J. Duhok Univ. 2020, 23, 501–508. [Google Scholar] [CrossRef]
- Vahdatifar, M.; Mousavi, S.F.; Farzin, S.; Hadiani, M.O. Comprehensive Study of Climate Change Impacts on Temperature and Precipitation in East and West of Mazandaran Province in North of Iran. Water 2025, 17, 1181. [Google Scholar] [CrossRef]
- Türkeş, M. Spatial and Temporal Analysis of Annual Rainfall Variations in Turkey. Int. J. Climatol. 1996, 16, 1057–1076. [Google Scholar] [CrossRef]
- Güner Bacanli, Ü. Trend Analysis of Precipitation and Drought in the Aegean Region, Turkey. Meteorol. Appl. 2017, 24, 239–249. [Google Scholar] [CrossRef]
- Mersin, D.; Tayfur, G.; Vaheddoost, B.; Safari, M.J.S. Historical Trends Associated with Annual Temperature and Precipitation in Aegean Turkey, Where Are We Heading? Sustainability 2022, 14, 13380. [Google Scholar] [CrossRef]
- Koycegiz, C.; Buyukyildiz, M. Analysis of Seasonal Rainfall Variability with Innovative Graphical Methods of Konya Closed Basin, Türkiye. Phys. Chem. Earth 2024, 136, 103767. [Google Scholar] [CrossRef]
- Tongal, H. Spatiotemporal Analysis of Precipitation and Extreme Indices in the Antalya Basin, Turkey. Theor. Appl. Clim. 2019, 138, 1735–1754. [Google Scholar] [CrossRef]
- Ercan, C.; Abu Arra, A.; Şişman, E. Investigation of Precipitation and Temperature Trends Using Classical and Innovative Approaches with Corresponding Frequencies in Antalya Basin, Türkiye. Phys. Chem. Earth 2025, 139, 103958. [Google Scholar] [CrossRef]
- Körük, A.E.; Kankal, M.; Yıldız, M.B.; Akçay, F.; Şan, M.; Nacar, S. Trend Analysis of Precipitation Using Innovative Approaches in Northwestern Turkey. Phys. Chem. Earth 2023, 131, 103416. [Google Scholar] [CrossRef]
- Praveen, B.; Talukdar, S.; Shahfahad; Mahato, S.; Mondal, J.; Sharma, P.; Islam, A.R.M.T.; Rahman, A. Analyzing Trend and Forecasting of Rainfall Changes in India Using Non-Parametrical and Machine Learning Approaches. Sci. Rep. 2020, 10, 10342. [Google Scholar] [CrossRef]
- Pal, A.B.; Khare, D.; Mishra, P.K.; Singh, L. Trend Analysis of Rainfall, Temperature and Runoff Data: A Case Study of Rangoon Watershed in Nepal. Int. J. Stud. Res. Technol. Manag. 2017, 5, 21–38. [Google Scholar] [CrossRef]
- Panda, A.; Sahu, N. Trend Analysis of Seasonal Rainfall and Temperature Pattern in Kalahandi, Bolangir and Koraput Districts of Odisha, India. Atmos. Sci. Lett. 2019, 20, e932. [Google Scholar] [CrossRef]
- Kumar, R.; Gautam, H.R. Climate Change and Its Impact on Agricultural Productivity in India. J. Climatol. Weather Forecast. 2014, 2, 1–3. [Google Scholar] [CrossRef]
- Agbo, E.P.; Offorson, G.C.; Yusuf, A.S.; Bassey, J.O.; Okono, M.A.; Nkajoe, U.; Ushie, P.O. Innovative Trend Analysis of Precipitation Changes over Nigeria: A Case Study of Locations across the Niger and Benue Rivers. J. Niger. Soc. Phys. Sci. 2025, 7, 1868. [Google Scholar] [CrossRef]
- Birpınar, M.E.; Kızılöz, B.; Şişman, E. Classic Trend Analysis Methods’ Paradoxical Results and Innovative Trend Analysis Methodology with Percentile Ranges. Theor. Appl. Clim. 2023, 153, 1–18. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. [Google Scholar] [CrossRef]
- Ahmed, M.; Dars, G.H.; Ahmed, S.; Krakauer, N.Y. Analyzing Drought Trends over Sindh Province, Pakistan. Nat. Hazards 2023, 119, 643–661. [Google Scholar] [CrossRef]
- Mandal, T.; Sarkar, A.; Das, J.; Rahman, A.T.M.S.; Chouhan, P. Comparison of Classical Mann–Kendal Test and Graphical Innovative Trend Analysis for Analyzing Rainfall Changes in India. In India: Climate Change Impacts, Mitigation and Adaptation in Developing Countries; Springer Climate Series; Springer Science and Business Media B.V.: Berlin/Heidelberg, Germany, 2021; pp. 155–183. [Google Scholar]
- Shao, Y.; Dong, Z.; Meng, J.; Wu, S.; Li, Y.; Zhu, S.; Zhang, Q.; Zheng, Z. Analysis of Runoff Variation and Future Trends in a Changing Environment: Case Study for Shiyanghe River Basin, Northwest China. Sustainability 2023, 15, 2173. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Hlaing, P.T. Time Series Trend Analysis and Forecasting of Climate Variability Using Deep Learning in Thailand. Results Eng. 2024, 24, 102997. [Google Scholar] [CrossRef]
- Kopar, İ.; Kaya, G.; Özdemir, M.; Dilek, H.; Çakır, Ç.; Zaman, M.; Birinci, S.; Erhan, K.; Koday, Z.; Sevindi, C.; et al. Geographical Research in Erzurum Province; Birinci, S., Kaymaz, C., Kıvanç Kızılkan, Y., Eds.; Kriter: Istanbul, Turkey, 2022; ISBN 9786256968349. (In Turkish) [Google Scholar]
- Öztürk, M.Z.; Çetinkaya, G.; Aydın, S. Climate Types of Turkey According to Köppen-Geiger Climate Classification. J. Geogr. 2017, 35, 17–27. (In Turkish) [Google Scholar] [CrossRef]
- TSMS. Climate Statistics. Available online: https://www.mgm.gov.tr/veridegerlendirme/il-ve-ilceler-istatistik.aspx?k=undefined&m=ERZURUM (accessed on 18 August 2025).
- Provincial Directorate of Environment, Urbanization and Climate Change. Erzurum Province 2022 Environmental Status Report; Provincial Directorate of Environment, Urbanization and Climate Change: Erzurum, Turkey, 2023. (In Turkish) [Google Scholar]
- TSMS. Mevbis. Available online: https://mevbis.mgm.gov.tr/mevbis/ui/index.html#/Login (accessed on 1 August 2025).
- TSMS Locations of Meteorological Observation Stations. Available online: https://mgm.gov.tr/kurumsal/istasyonlarimiz.aspx?il=Erzurum (accessed on 16 August 2025).
- Iwueze, I.S.; Nwogu, E.C.; Nlebedim, V.U.; Nwosu, U.I.; Chinyem, U.E. Comparison of Methods of Estimating Missing Values in Time Series. Open J. Stat. 2018, 8, 390–399. [Google Scholar] [CrossRef][Green Version]
- Yozgatligil, C.; Aslan, S.; Iyigun, C.; Batmaz, I. Comparison of Missing Value Imputation Methods in Time Series: The Case of Turkish Meteorological Data. Theor. Appl. Clim. 2013, 112, 143–167. [Google Scholar] [CrossRef]
- Wang, K. Sampling Biases in Datasets of Historical Mean Air Temperature over Land. Sci. Rep. 2014, 4, 4637. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Guerschman, J.; Shendryk, Y.; Henry, D.; Harrison, M.T. Estimating Pasture Biomass Using Sentinel-2 Imagery and Machine Learning. Remote Sens. 2021, 13, 603. [Google Scholar] [CrossRef]
- Latrech, B.; Yacoubi, S.; Hermassi, T.; Slatni, A.; Jarray, F.; Pouget, L. Homogeneity and Trend Analysis of Climatic Variables in Cap-Bon Region of Tunisia. Appl. Sci. 2023, 13, 10593. [Google Scholar] [CrossRef]
- Ay, M. Trend and Homogeneity Analysis in Temperature and Rainfall Series in Western Black Sea Region, Turkey. Theor. Appl. Clim. 2020, 139, 837–848. [Google Scholar] [CrossRef]
- Dong, Z.; Jia, W.; Sarukkalige, R.; Fu, G.; Meng, Q.; Wang, Q. Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water 2020, 12, 3293. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Improved Visualization for Trend Analysis by Comparing with Classical Mann-Kendall Test and ITA. J. Hydrol. 2020, 584, 124674. [Google Scholar] [CrossRef]
- Hou, X.; Cao, J.; Yang, H. Characteristics of Spatial and Temporal Distribution of Heavy Rainfall and Surface Runoff Generating Processes in the Mountainous Areas of Northern China. Water 2025, 17, 970. [Google Scholar] [CrossRef]
- Frieda, S. Swed and C. Eisenhart Tables for Testing Randomness of Grouping in a Sequence of Alternatives. Ann. Math. Stat. 1943, 1, 66–87. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods. Biometrika 1957, 44, 298. [Google Scholar] [CrossRef]
- Bayazit, M.; Önöz, B. To Prewhiten or Not to Prewhiten in Trend Analysis? Hydrol. Sci. J. 2007, 52, 611–624. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2011, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Significance Test and Applications. Theor. Appl. Clim. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Dabanlı, İ.; Şen, Z.; Yeleğen, M.Ö.; Şişman, E.; Selek, B.; Güçlü, Y.S. Trend Assessment by the Innovative-Şen Method. Water Resour. Manag. 2016, 30, 5193–5203. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S. Changes of Pan Evaporation in the West of Iran. Water Resour. Manag. 2011, 25, 97–111. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Hrnjica, B.; Bonacci, O.; Torabi Haghighi, A. Innovative and Successive Average Trend Analysis of Temperature and Precipitation in Osijek, Croatia. Theor. Appl. Clim. 2021, 145, 875–890. [Google Scholar] [CrossRef]
- Sensoy, S.; Türkoğlu, N.; Çiçek, İ.; Arabaci, H.; Bölük, E. Urbanization Effect on Trends of Extreme Temperature Indices in Ankara. In Proceedings of the Atmospheric Sciences Symposium with International Participation, Istanbul, Turkey, 28–30 April 2015. [Google Scholar]
- Braganza, K.; Karoly, D.J.; Arblaster, J.M. Diurnal Temperature Range as an Index of Global Climate Change during the Twentieth Century. Geophys. Res. Lett. 2004, 31, 2941–2944. [Google Scholar] [CrossRef]
- Makowski, K.; Wild, M.; Ohmura, A. Diurnal Temperature Range over Europe between 1950 and 2005. Atmos. Chem. Phys. 2008, 8, 6483–6498. [Google Scholar] [CrossRef]
- Qu, M.; Wan, J.; Hao, X. Analysis of Diurnal Air Temperature Range Change in the Continental United States. Weather Clim. Extrem. 2014, 4, 86–95. [Google Scholar] [CrossRef]
- Gallo, K.P.; Easterling, D.R.; Peterson, T.C. The Influence of Land Use/Land Cover on Climatological Values of the Diurnal Temperature Range. J. Clim. Vol. 1996, 9, 2941–2944. [Google Scholar] [CrossRef]
- Karl, T.R.; Diaz, H.F.; Kukla, G. Urbanization: Its Detection and Effect in the United States Climate Record. J. Clim. 1988, 1, 1099–1123. [Google Scholar] [CrossRef]
- Karl, T.R.; Jones, P.D.; Knight, R.W.; Kukla, G.; Plummer, N.; Razuvayev, V.; Gallo, K.P.; Lindseay, J.; Charlson, R.J.; Peterson, T.C. A New Perspective on Recent Global Warming: Asymmetric Trends of Daily Maximum and Minimum Temperature. Bull. Am. Meteorol. Soc. 1993, 74, 1007–1024. [Google Scholar] [CrossRef]
- Wang, K.; Ye, H.; Chen, F.; Xiong, Y.; Wang, C. Urbanization Effect on the Diurnal Temperature Range: Different Roles under Solar Dimming and Brightening. J. Clim. 2012, 25, 1022–1027. [Google Scholar] [CrossRef]
- Duhan, D.; Pandey, A. Statistical Analysis of Long Term Spatial and Temporal Trends of Precipitation during 1901–2002 at Madhya Pradesh, India. Atmos. Res. 2013, 122, 136–149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).