Performance Analysis for Integrated Sensing and Communication Systems in Rainfall Scenarios

Abstract

This paper investigates an integrated sensing and communication (ISAC) system operating in a rainfall scenario, where a base station (BS) simultaneously serves multiple communication users and performs rainfall detection. Specifically, considering the fading characteristics of the millimeter-wave (mmWave) channel and the impact of rainfall on the signal propagation link, we adopt the Weibull distribution as the channel model between the nodes. Based on the above, the received signal-to-noise ratio (SNR), channel capacity, bit error rate (BER), and outage probability of the users within the system are analyzed to characterize the communication performance. Furthermore, the sensing capability of the BS is demonstrated through the analysis of the probability of rainfall. Simulation results reveal that increasing the distance between the BS and users significantly degrades their communication performance. Furthermore, the performance is highly sensitive to the rainfall intensity. Specifically, compared to storm conditions, light rain yields an improvement of 16.9 dB in the average user SNR, a 7.2 bps/Hz increase in channel capacity, and a 40.2% reduction in the outage probability. Additionally, an increase in the complex dielectric constant of raindrops substantially reduces the backscattering coefficient at the ISAC BS.

1. Introduction

Integrated sensing and communication (ISAC), as a core technology for the sixth-generation (6G) networks, aims to endow communication networks with radar-level high-precision sensing capabilities by sharing spectrum, hardware, and algorithmic resources, thereby achieving functional convergence between communication and sensing [1,2,3]. The growing demand for real-time sensing and efficient communication coordination in emerging scenarios such as low-altitude economy, autonomous driving, and smart cities further accelerates the deep convergence of communication and sensing [4,5,6]. The vision of ISAC, however, faces significant practical challenges when deployed in real-world environments, particularly under adverse weather conditions. Emerging application scenarios such as the low-altitude economy and autonomous driving demand persistent and reliable sensing–communication services. For instance, an autonomous vehicle must maintain high-resolution environmental awareness and stable vehicle-to-everything (V2X) links not only in clear weather but also during heavy rain, where road friction changes and visibility drops. Similarly, unmanned aerial vehicles (UAVs) operating in the low-altitude airspace require all-weather capability for navigation and communication. Persistent clear weather can hardly be guaranteed in these operational domains. Therefore, investigating the performance of ISAC systems under practical impairments like rainfall is not merely an academic exercise but a prerequisite for their reliable deployment.

Studies on ISAC

Integrated sensing and communication (ISAC), as a potential key technology for 6G, has garnered significant attention from both industry and academia. In Ref. [7], communication–sensing coexistence and integrated systems were comparatively studied, demonstrating that ISAC delivers substantial performance gains for both communication users and sensing nodes. In Ref. [8], a multi-base-station and multi-carrier coordinated ISAC system in the mmWave band is investigated. By jointly considering communication/sensing requirements, dual-functional radar-communication (DFRC) waveform deployment, and distributions of communication requests/targets, a power allocation scheme is designed to minimize system energy consumption. Reference [9] explored an ISAC model with communication users and sensing targets across different domains. The beamforming design optimizes the received signal-to-noise ratio (SNR) at the sensing end, revealing that near-field/far-field model mismatch, antenna size, and communication channels significantly degrade sensing performance. The authors of [10] proposed a novel ISAC interference cancellation scheme that simultaneously accomplishes dual-functional tasks while mitigating mutual interference, thereby enhancing spectral efficiency. In Ref. [11], a sensing-integrated discrete-Fourier-transform spread orthogonal frequency division multiplexing (DFT-s-OFDM) system for terahertz ISAC was studied. Compared to conventional OFDM, it achieves a lower peak-to-average power ratio (PAPR) and adapts flexibly to terahertz (THz) channel delay spread. Experimental results demonstrated millimeter-level ranging and decimeter-level velocity estimation accuracy without compromising communication performance. Reference [12] designed communication-prioritized, sensing-prioritized, and joint sensing–communication beamforming schemes, respectively, tailored for MIMO-ISAC systems with diverse requirements. In Ref. [13], the authors jointly optimized transceiver beamforming and unmanned aerial vehicle (UAV) trajectory for an ISAC-enhanced UAV system under sensing constraints, maximizing the sum secrecy rate. In Ref. [14], the covert communication performance of ISAC systems was investigated. By jointly optimizing covert communication signals and artificial noise under minimum covert rate constraints, the weighted sum of mean-square error in sensing beam direction and cross-correlation was minimized. Reference [15] studied a NOMA-ISAC system with both uplink and downlink users, characterizing communication and sensing performance through user outage probability, channel capacity, and the probability of detection of the base station (BS). The authors of [16] designed a joint active–passive beamforming scheme assisted by reconfigurable intelligent surfaces (RISs), utilizing dedicated radar signals as artificial noise to maximize the sum secrecy rate while satisfying user QoS requirements, transmit power constraints, and sensing signal strength thresholds. Reference [17] explored cooperative ISAC systems, analyzing user outage performance and diversity gain, and proposes sensing-centric versus communication-centric power allocation schemes to enhance the sensing and communication capabilities, respectively.

The studies cited above [7,8,9,10,11,12,13,14,15,16,17] have undoubtedly propelled the field of ISAC forward, exploring topics from waveform design and beamforming to resource allocation and cooperative networks. A common thread among these works, however, is their underlying assumption of operating under ideal or clear-weather channel conditions. While this simplifies initial analysis and design, it creates a significant gap between theoretical models and practical deployment scenarios. In reality, the performance of wireless channels, especially at the millimeter-wave (mmWave) and terahertz (THz) frequencies central to 6G ISAC, is severely degraded by atmospheric phenomena, with rainfall being a dominant factor [18,19]. The existing literature lacks a systematic performance analysis framework for ISAC that explicitly incorporates the statistical fading characteristics induced by rainfall. This gap is critical, as the simultaneous demands of communication and sensing make ISAC systems uniquely vulnerable to the compound effects of attenuation and scattering caused by raindrops.

Existing studies predominantly focus on ISAC systems under ideal weather conditions, but persistent clear weather can hardly be guaranteed in practical communication scenarios, particularly in adverse environments such as rainfall [18,19]. The impact of rainfall on integrated system performance cannot be overlooked. Fundamentally, it manifests as a physical mapping of high-frequency electromagnetic wave–raindrop interactions onto system performance, characterized by three core effects: performance degradation dominated by signal attenuation, noise–interference coupling, and system-level chain reactions [20,21]. Specifically, surging path loss in millimeter-wave (mmWave) bands causes drastic SNR drops and failure of high-order modulation, while raindrop scattering induces non-Rayleigh fading that significantly increases user outage probability; rain-induced thermal noise elevates system noise figures, and in ISAC scenarios, rain clutter submerges target echoes with reduced signal-to-clutter ratios (SCRs), forcing sensing power to encroach on communication resources; and collapsed channel capacity is due to SNR degradation, with the compressed base station coverage radius to maintain target bit error rate (BER), and safety speed reduction triggered by latency-sensitive service fluctuations [22,23,24]. To address the intrinsic nature of this frequency-selective impairment, resilient communication systems should be constructed through real-time rain intensity monitoring, and dynamic modulation-coding adaptation, as well as joint resource allocation, thereby overcoming the survival challenges of high-frequency wireless networks in severe weather conditions.

It is crucial to clarify the conceptual advancement of ISAC from 5G to 6G systems. While initial 5G standards have begun to explore the coexistence of communication and sensing functionalities, often in a manner where sensing is an auxiliary or secondary feature, 6G ISAC aims for a fundamental, deep integration. The essential improvement lies in the paradigm shift from coexistence to joint optimization. In 6G, sensing and communication are designed as co-primary functions from the ground up, sharing not only the spectrum and hardware but also a unified signal processing framework and joint resource management strategy. This enables mutual performance enhancement, where sensing results can directly inform communication strategies, and communication signals can be leveraged for high-resolution environmental sensing, moving beyond mere interference avoidance.

Given that 6G ISAC is still in its nascent research phase and dedicated testbeds are not yet available, this study establishes a theoretical performance baseline through rigorous analysis and simulation. To ensure the physical fidelity and practical relevance of our work, our channel modeling and performance evaluation are firmly grounded in established international telecommunication standards and empirical meteorological studies. Specifically, the selection of the Weibull distribution For the experts these are probably common knowledge but not so for a somewhat broader audience. for modeling the mmWave channel under rainfall is motivated by its demonstrated accuracy in capturing the right-skewed, heavy-tailed statistics of rain attenuation [25], which has been validated in prior empirical studies of 5G–mmWave links [8]. Furthermore, the critical rain attenuation parameters are sourced directly from the ITU-R P.838-3 recommendation. This recommendation is derived from extensive global measurement campaigns and represents the industry consensus for predicting rain-induced path loss, thereby providing robust, data-backed support for the core calculations in our analysis of a 6G-oriented scenario. The main contributions of this paper are summarized as follows:

• We establish an ISAC system model comprising a dual-functional base station serving multiple communication users while simultaneously performing rainfall detection, a shift from conventional target sensing.
• We conduct a rigorous analytical study from both communication and sensing perspectives. Notably, we derive novel, closed-form expressions for key performance metrics under a Weibull-distributed rainfall channel model, including the following: (1) the average signal-to-interference-plus-noise ratio (SINR) and asymptotic channel capacity of the users; (2) the average bit error rate (BER) for M-QAM modulation and its high-SNR approximation; (3) the exact outage probability of the communication users; and (4) a sensing performance model that links the received echo power to the rainfall reflectivity factor and ultimately to the rainfall rate. Furthermore, to ensure the physical fidelity of our analysis, our channel modeling and performance evaluation are aligned with international telecommunication standards and canonical meteorological studies. The choice of the Weibull distribution for modeling the mmWave channel in rainfall is motivated by its proven ability to accurately capture the right-skewed, heavy-tailed statistics of rain attenuation. Similarly, the sensing analysis is grounded in the standard weather radar equation, ensuring that our derived probability of rainfall is based on physically meaningful parameters.
• We validate our analytical findings through numerical simulations and discuss the non-trivial trade-offs between communication and sensing performance under rainfall-induced impairments. Furthermore, we corroborate our theoretical trends with well-established international standards, such as the ITU-R P.838-3 recommendation for rain attenuation, thereby bridging our novel analysis with established empirical knowledge.

2. System Model

As shown in Figure 1, we consider an ISAC system model in a rainfall scenario, where the BS, S, is in charge of communicating with K users, $D_1,D_2,\dots ,D_K$, and detecting the rainfall probability in the environment. It is assumed that the BS is equipped with $N_t$ and $N_r$ transmitted and received antennas, while all users have single antennas. Regarding the channel model, statistical results indicate that under light rainfall conditions, both the log-normal and Weibull distributions provide good fitting performance. However, under heavy rainfall conditions, the Weibull distribution aligns more closely with the observed statistical results. Furthermore, for millimeter-wave (mmWave) links in the fifth-generation (5G) communications, although the propagation distance is typically short, the high operating frequency means that heavy rainfall exerts a significant impact on signal propagation. Therefore, the Weibull distribution is the preferred choice for modeling rainfall rates in such scenarios. Therefore, the probability density function (PDF) and cumulative distribution function (CDF) of the channel h are, respectively, given by [25]

$$\begin{array}{cc}\hfill f_h\left(h\right)& ={\displaystyle \frac{b}{\alpha lk{R}^{\alpha }}}{\left({\displaystyle \frac{h-C}{k{R}^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}-1}exp\left[-{\left({\displaystyle \frac{h-C}{k{R}^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill F_h\left(h\right)& =1-exp\left[-{\left({\displaystyle \frac{h-C}{k{R}^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right],\hfill \end{array}$$

(2)

where l denotes the distance between the BS and users and $b>0$ denotes the shape parameters. Furthermore, the calculation of rain attenuation is based on the model provided in the ITU-R P.838 recommendation, i.e., $\gamma =k{R}^{\alpha }$, where $\gamma$ is the specific attenuation, measured in decibels per kilometer (dB/km). It quantifies the signal power loss per unit propagation distance (1 km) due to rainfall and serves as a fundamental parameter for the entire communication link budget modeling. R is the rain rate, measured in millimeters per hour (mm/h). It typically refers to the 1-minute average rainfall intensity at a location and is the most critical meteorological parameter for gauging rainfall intensity. k and $\alpha$ are frequency- and polarization-dependent regression coefficients. Their values are entirely determined by the radio wave’s frequency and polarization mode (horizontal or vertical), reflecting the physical mechanistic differences in how electromagnetic waves of different frequencies interact with raindrops of varying sizes.

Figure 1. An illustration of an ISAC network in a rainfall scenario.

ITU-R P.530, entitled “Propagation data and prediction methods required for the design of terrestrial line-of-sight systems”, is a comprehensive international standard recommendation that systematically integrates all major factors influencing line-of-sight radio propagation. These factors include free-space path loss, multipath fading induced by atmospheric refraction, rain attenuation, atmospheric gas absorption, and tropospheric scintillation, among others. In this study, we strictly adhere to the guidelines provided in this recommendation, modeling the total path loss as the summation of multiple loss components, i.e., free-space path loss and rain attenuation as well as some other losses. To focus on the core research problem, and without loss of generality, this paper deliberately neglects other loss factors and concentrates primarily on the two dominant mechanisms: free-space path loss and rain attenuation. The free-space path loss is given by

$$\begin{array}{c}\hfill C=20lgf+20lgl+2.4,\end{array}$$

(3)

where f denotes the carried frequency.

This work investigates a 6G-oriented ISAC scenario characterized by the deep co-design of communication and sensing functions within a single system. The key differentiator from 5G systems lies not in the underlying physical propagation effects, but in the system-level integration density and performance objectives. Specifically, our model considers a BS that simultaneously serves multiple communication users and executes high-precision environmental sensing using the same waveform and hardware resources. This level of functional integration and the requirement for high sensing accuracy alongside communication services represent a 6G target.

To ensure a credible analysis of this advanced scenario, our calculations for the physical layer are grounded in models that have been extensively validated for 5G systems. The propagation channel model, including free-space path loss and the specific rain attenuation based on the Weibull distribution and ITU-R recommendations, is directly applicable to and supported by data from 5G mm Wave links. Therefore, while the system architecture and performance trade-offs we analyze are specific to the 6G vision, the core channel impairments and propagation calculations have been verified in the context of 5G. This approach allows for a reliable performance projection for 6G systems based on well-understood physical phenomena.

The BS intends to transmit signals $\mathbf{x}={\sum }_{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{w}}_0{s}_0$ to communicate with users and detect the rainfall, where ${\mathbf{w}}_k\in {\mathbb{C}}^{N_{\mathrm{t}}\times 1}$ and ${\mathbf{w}}_0\in {\mathbb{C}}^{N_{\mathrm{t}}\times 1}$ denote the transmit beamforming (BF) vectors for $D_k$, $k\in \left\{1,\dots ,K\right\}$, and the sensing signal, while $s_k$ and $s_0$ represent the expected signal for user $D_k$ and the sensing signal, with $\mathbb{E}\left\{{\left|s_k\right|}^2\right\}=\mathbb{E}\left\{{\left|s_0\right|}^2\right\}=1$, respectively. It is further assumed that the communication signal and sensing signal are statistically independent and uncorrelated; the autocorrelation matrix of the transmitted signals can be derived as

$$\begin{array}{c}\hfill {\mathbf{R}}_x=\mathbb{E}\left\{\mathbf{x}{\mathbf{x}}^H\right\}=\sum _{k=1}^K{\mathbf{w}}_k{\mathbf{w}}_k^H+{\mathbf{w}}_0{\mathbf{w}}_0^H,\end{array}$$

(4)

where we further have ${\mathbf{R}}_x\le P_{max}$, and $P_{max}$ is the total budget for the transmitted power of the BS.

2.1. Communication Signal Transmission

According to Equation (4), the received signals at user $D_k$ can be expressed as

$$\begin{array}{cc}\hfill {\mathbf{y}}_k& ={\mathbf{h}}_k\mathbf{x}+{\mathbf{n}}_{\mathrm{c}}\hfill \\ \hfill & ={\mathbf{h}}_k\left(\sum _{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{w}}_0{s}_0\right)+{\mathbf{n}}_k,\hfill \end{array}$$

(5)

where ${\mathbf{n}}_k\sim \mathcal{CN}\left(0,{\sigma }_k^2\mathbf{I}\right)\in {\mathbb{C}}^{K\times 1}$ denotes the additive white Gaussian noise (AWGN) at $D_k$, with mean 0 and noise power ${\sigma }_k^2$, while ${\mathbf{h}}_k^H\in C^{N_{\mathrm{t}}\times K}$ represents the channel between the BS and $D_k$. Therefore, the received signal-to-interference-plus-noise ratio (SINR) of $x_k$ at $D_k$ is given by

$$\begin{array}{cc}\hfill {\gamma }_k& ={\displaystyle \frac{|{\mathbf{h}}_k{\mathbf{w}}_k{|}^2}{{\displaystyle \sum _{i=1,i\ne k}^K}|{\mathbf{h}}_i{\mathbf{w}}_i{|}^2+|{\mathbf{h}}_i{\mathbf{w}}_0{|}^2+{\sigma }_k^2}}\hfill \\ \hfill & ={\displaystyle \frac{\mathrm{tr}\left({\mathbf{H}}_k{\mathbf{W}}_k\right)}{{\displaystyle \sum _{i=1,i\ne k}^K}\mathrm{tr}\left({\mathbf{H}}_k{\mathbf{W}}_i\right)+\mathrm{tr}\left({\mathbf{H}}_k{\mathbf{W}}_0\right)+{\sigma }_k^2}},\hfill \end{array}$$

(6)

where $\mathrm{tr}\left(·\right)$ denotes the trace of a matrix, and ${\mathbf{H}}_k={\mathbf{h}}_k{\mathbf{h}}_k^H$, ${\mathbf{W}}_k={\mathbf{w}}_k{\mathbf{w}}_k^H$, and ${\mathbf{W}}_0={\mathbf{w}}_0{\mathbf{w}}_0^H$, respectively.

2.2. Sensing Signal Transmission

As for sensing, the BS transmits signal $\mathbf{x}$ to detect rainfall, and the echo signal received at the BS can be expressed as [26]

$$\begin{array}{c}\hfill {\mathbf{y}}_S=\mathbf{R}\left(\sum _{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{w}}_0{s}_0\right)+{\mathbf{N}}_S,\end{array}$$

(7)

where ${\mathbf{N}}_S\sim \mathcal{CN}\left(0,{\sigma }_s^2\mathbf{I}\right)\in {\mathbb{C}}^{K\times 1}$ denotes the AWGN at the BS, and $\mathbf{R}$, denoting the response matrix, is expressed as

$$\begin{array}{c}\hfill \mathbf{R}=\beta {\mathbf{a}}_t\left({\theta }_0\right){\mathbf{a}}_r^T\left({\theta }_0\right),\end{array}$$

(8)

where ${\theta }_0$ denotes the direction angle of the rainfall area, $\beta =\sqrt{P_s{G}^2\rho {\lambda }^2/\left[{\left(4\pi \right)}^3{d}_s^4\right]}$ represents the attenuation of the echo for the rainfall area, where $P_s$ denotes the transmitted power of the sensing signal, G is the gain of the transmitted antenna, $\rho$ represents the radar cross-section (RCS) of the raindrop, $\lambda$ is the wavelength of the transmitted signal, and $d_s$ denotes the distance between the BS and the rainfall area. In the context of weather radar, for a spherical raindrop that is small compared to the wavelength, the RCS is given by

$$\begin{array}{c}\hfill \rho ={\displaystyle \frac{{\pi }^5{\left|k_0\right|}^2{D}^6}{{\lambda }^4}}\end{array}$$

(9)

where D denotes the diameter of the raindrop and $|k_0{|}^2=\left|{\displaystyle \frac{m^2-1}{m^2+2}}\right|$, with m representing the complex refraction coefficient of raindrops, which is a function of the operating frequency and temperature. The backscattering coefficient of the rainfall area, which is integral to the received echo power, is directly proportional to the ensemble average of the RCS of the constituent raindrops. Therefore, any change in m directly affects $|k_0{|}^2$, which in turn alters $\rho$ and, ultimately, the backscattering coefficient perceived by the ISAC BS. Furthermore, ${\mathbf{a}}_t\left({\theta }_0\right)\in {\mathbb{C}}^{N_t\times 1}$ and ${\mathbf{a}}_r\left({\theta }_0\right)\in {\mathbb{C}}^{N_r\times 1}$ denote the received and transmitted array steering vectors, which are, respectively, expressed as [27]

$$\begin{array}{cc}\hfill {\mathbf{a}}_t\left({\theta }_0\right)& =\left[1,e^{j{\displaystyle \frac{2\pi d}{\lambda }}sin\left({\theta }_0\right)},\dots ,e^{j{\displaystyle \frac{2\pi d\left(N_t-1\right)}{\lambda }}sin\left({\theta }_0\right)}\right],\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathbf{a}}_r\left({\theta }_0\right)& =\left[1,e^{j{\displaystyle \frac{2\pi d}{\lambda }}sin\left({\theta }_0\right)},\dots ,e^{j{\displaystyle \frac{2\pi d\left(N_r-1\right)}{\lambda }}sin\left({\theta }_0\right)}\right],\hfill \end{array}$$

(11)

where d denotes the spacing of the antenna for the BS. In this paper, we focus on rainfall detection in the context of mmWave rain-attenuated links, utilizing sensing signals transmitted from the ISAC BS. In the process of radar rainfall estimation, the received echo power depends on the scattering properties of the precipitation particles, the transmitted power, the distance between the rainfall area and the ISAC BS, and other physical parameters. The quantitative relationship among these parameters is governed by the weather radar equation.

3. Performance Analysis

In this section, the communication performance of the users for the ISAC system in the rainfall scenario is evaluated by deriving the average SINRs, channel capacity, BER, and outage probability of the users. Furthermore, the sensing performance for the ISAC system in the rainfall scenario is evaluated by deducing the probability of rainfall.

3.1. Average SINRs

The average SINR is a key performance metric that quantifies the reliability of a communication link in the presence of interference and noise, which is defined as

$$\begin{array}{cc}\hfill f_{\gamma }\left(\gamma \right)& =\left|{\displaystyle \frac{dh}{d\gamma }}\right|f_h\left(h\right)\hfill \\ \hfill & =\left|{\displaystyle \frac{d}{d\gamma }}\left(\sqrt{{\displaystyle \frac{\gamma }{{\gamma }_0}}}\right)\right|f_h\left(\sqrt{{\displaystyle \frac{\gamma }{{\gamma }_0}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\sqrt{\gamma {\gamma }_0}}}{f}_h\left(h\right),\hfill \end{array}$$

(12)

where ${\gamma }_0=P_c/\left(P_d+{\sigma }_k^2\right)$, $P_{\mathrm{c}}={\sum }_{k=1}^K{\mathbf{w}}_k{\mathbf{w}}_k^H$ and $P_s={\mathbf{w}}_0{\mathbf{w}}_0^H$ denote the transmitted power of the communication and sensing signals, respectively.

According to the PDF of the channel state for mmWave rain-attenuated channels, the average SINR in slow-fading channels can be derived as

$$\begin{array}{cc}\hfill \overline{\gamma }& ={\int }_0^{\infty }\gamma f_{\gamma }\left(\gamma \right)d\gamma \hfill \\ \hfill & ={\int }_0^{\infty }\gamma f_h\left(h\right)dh.\hfill \end{array}$$

(13)

Substituting Equation (6) into Equation (12) yields the following expression for the average SINRs under the Weibull rainfall channel model:

$$\begin{array}{cc}\hfill \overline{\gamma }& ={\int }_0^{{\gamma }_0{(exp(-C/4.343\left)\right)}^2}{\displaystyle \frac{b}{2\alpha d_{s}k{\lambda }^{\alpha }}}{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }{d}_s}}\right)}^{{\displaystyle \frac{b}{\alpha }}-1}exp\left[-{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }{d}_s}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right]d\gamma \hfill \\ \hfill & ={\int }_0^{{\gamma }_0{(exp(-C/4.343\left)\right)}^2}{\displaystyle \frac{P_c{h}^{2}b}{2\left(P_s{h}^2+{\sigma }_c^2\right)\alpha d_{s}k{\lambda }^{\alpha }}}{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }{d}_s}}\right)}^{{\displaystyle \frac{b}{\alpha }}-1}exp\left[-{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }{d}_s}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right]dh.\hfill \end{array}$$

(14)

3.2. Channel Capacity

The fundamental significance of channel capacity lies in its rigorous definition of the theoretical performance limit of a communication link. It defines the maximum information rate achievable per unit time and per unit bandwidth under ideal error-free transmission conditions, thereby establishing the essential theoretical benchmark for communication system design, selection of modulation and coding schemes, and resource allocation strategies. The channel capacity can be expressed as

$$\begin{array}{c}\hfill C_{ave}={\int }_0^{\infty }\mathrm{lb}(1+\gamma )f_h\left(h\right)dh.\end{array}$$

(15)

Substituting Equation (6) into Equation (15), the channel capacity for the considered ISAC system in the rainfall scenario can be further given by

$$\begin{array}{c}\hfill C_{ave}={\int }_0^{exp(-C/4.343)}\mathrm{lb}(1+{\gamma }_0{h}^2){\displaystyle \frac{b}{\alpha lhk{\lambda }^{\alpha }}}{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}-1}exp\left[-{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right]dh.\end{array}$$

(16)

In the high-SNR regime, the asymptotic channel capacity for the considered ISAC system in the rainfall scenario can be expressed as

$$\begin{array}{c}\hfill C_{ave}^{\mathrm{h}}\approx \mathrm{lb}\left(1+{\displaystyle \frac{P_c}{P_s}}\right).\end{array}$$

(17)

3.3. BER

The core significance of the BER lies in quantitatively assessing the actual transmission reliability of digital communication systems. It directly reflects the level of signal degradation under channel impairments such as noise, interference, and fading by calculating the ratio of erroneous bits to the total transmitted bits at the receiver.

For M-ary Quadrature Amplitude Modulation (M-QAM), the expression for the average BER can be given as [28]

$$\begin{array}{cc}\hfill \stackrel{-}{P_e}& ={\int }_0^{\infty }{f}_h\left(h\right){\displaystyle \frac{4}{\mathrm{lb}M}}(1-{\displaystyle \frac{1}{\sqrt{M}}})Q\left(\sqrt{{\displaystyle \frac{3\mathrm{lb}M}{(M-1)}}{\gamma }_0{h}^2}\right)dh\hfill \\ \hfill & ={\displaystyle \frac{4}{\mathrm{lb}M}}\left(1-{\displaystyle \frac{1}{\sqrt{M}}}\right)\hfill \\ \hfill & \times {\int }_0^{exp(-C/4.343)}{\displaystyle \frac{b}{\alpha lhk{\lambda }^{\alpha }}}{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}-1}exp\left[-{\left({\displaystyle \frac{h-C}{k{\lambda }^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right]Q\left(\sqrt{{\displaystyle \frac{3\mathrm{lb}M}{(M-1)}}{\gamma }_0{h}^2}\right)dh,\hfill \end{array}$$

(18)

where $Q\left(·\right)$ denotes the Gaussian-Q function and can be further expressed as

$$\begin{array}{cc}\hfill Q\left(x\right)& ={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_x^{\infty }exp\left(-{\displaystyle \frac{u^2}{2}}\right)du\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\mathrm{erfc}\left({\displaystyle \frac{x}{\sqrt{2\pi }}}\right),\hfill \end{array}$$

(19)

where $\mathrm{erfc}\left(·\right)$ denotes the complementary error function.

In the high-SNR regime, the asymptotic BER for the considered ISAC system in the rainfall scenario is derived as

$$\begin{array}{c}\hfill \stackrel{-}{P_e}\approx \left(1-{\displaystyle \frac{1}{\sqrt{M}}}\right)Q\left(\sqrt{{\displaystyle \frac{3\mathrm{lb}M{P}_c}{(M-1)P_s}}}\right).\end{array}$$

(20)

3.4. Outage Probability

The core significance of the outage probability lies in quantifying the risk that a communication system fails to meet its minimum quality of service (QoS) requirements under random fading channels. It is defined as the probability that the received SINR falls below the decoding threshold [29]. For the ISAC system under consideration, the outage probability of the user $D_k$ can be expressed as [29]

$$\begin{array}{cc}\hfill P_{\mathrm{out}}& =Pr\left(\gamma \le {\gamma }_{th}^k\right)\hfill \\ \hfill & =Pr\left({\displaystyle \frac{P_k{h}^2}{P_s{h}^2+{\displaystyle \sum _{i=1,i\ne k}^K}{P}_i{h}^2+{\sigma }_c^2}}\le {\gamma }_{th}^k\right)\hfill \\ \hfill & =Pr\left\{{\left|h\right|}^2\le {\displaystyle \frac{{\gamma }_{th}^k{\sigma }_c^2}{P_k-\left(P_s+{\displaystyle \sum _{i=1,i\ne k}^K}{P}_i\right){\gamma }_{th}^k}}\right\},\hfill \end{array}$$

(21)

where ${\gamma }_{th}^k$ denotes the outage threshold of user $D_k$.

By using Equation (2), the exact outage probability of user $D_k$ is derived as

$$\begin{array}{c}\hfill P_{\mathrm{out}}^k=1-exp\left[-{\left({\displaystyle \frac{\frac{{\gamma }_{th}^k{\sigma }_c^2}{P_k-\left(P_s+{\displaystyle \sum _{i=1,i\ne k}^K}{P}_i\right){\gamma }_{th}^k}-C}{k{\lambda }^{\alpha }l}}\right)}^{{\displaystyle \frac{b}{\alpha }}}\right],\end{array}$$

(22)

where we have $P_k>\left(P_s+{\sum }_{i=1,i\ne k}^K{P}_i\right){\gamma }_{th}^k$. Otherwise, $P_{\mathrm{out}}^k=1$.

To provide an intuitive comparison of the impact of rainfall on the communication performance of the system’s users, the average signal-to-noise ratio (SNR), channel capacity, and outage probability under light rain, heavy rain, and storm conditions are analyzed and compared in Table 1.

Table 1. System performance comparison under different rainfall intensities.

Rainfall Intensity (mm/h)	SINR (dB)	Channel Capacity (bps/Hz)	Outage Probability (%)
5 (Light Rain)	15.2	8.7	2.1
25 (Heavy Rain)	5.8	4.2	15.6
50 (Storm)	−2.3	1.5	42.3

3.5. Probability of Rainfall

The core significance of the probability of rainfall lies in providing critical environmental state input for mmWave communication systems and radar sensing. On the communication side, based on the real-time channel state information mapped from the rain rate, the system can adaptively adjust the modulation order. On the sensing side, radar waveform parameters can be optimized according to the rain rate to suppress rain clutter, thereby improving the target detection probability. Furthermore, as a pivotal variable bridging the natural environment and communication/sensing systems, the accurate acquisition and modeling of the rain rate determine the robustness of high-frequency-band wireless systems under complex meteorological conditions.

The received echo power at the BS, which follows the standard form of the weather radar equation [30], is related to the distance between the ISAC BS and rainfall area and can be expressed as

$$\begin{array}{c}\hfill P_r={\displaystyle \frac{c}{1024{\pi }^2\left(ln2\right)d_s^2}}{P}_s\tau {\lambda }^2{G}^2\theta \varphi L_t{L}_{r}f\left(B\right){10}^{-0.2{\int }_0^{d_s}\left(A_g+A_p+A_c\right)dr},\end{array}$$

(23)

where c denotes the velocity of light, G denotes the antenna gain, $d_s$ is the distance between the BS and the rainfall area, $P_s$ is the transmitted power of the sensing signal, $\tau$ denotes the width of the transmitted pulse, $\theta$ and $\varphi$ are the beam width of the main plane of the antenna pattern, respectively, $L_t\le 1$ and $L_r\le 1$ are the loss factor of the transmitter and receiver, respectively, $f\left(B\right)$ is the frequency response loss factor of the receiver, and B denotes the bandwidth of the receiver. Here, Equation (23) represents a form of the weather radar equation tailored for rainfall estimation, where ${10}^{-0.2{\int }_0^{d_s}\left(A_g+A_p+A_c\right)dr}$ is the attenuation term of the signal, and $A_g$, $A_p$, and $A_c$ represent the attenuation coefficients of the atmosphere, sediments, and clouds, respectively.

Based on the echo power derived from Equation (23), we can further estimate the current rainfall reflectivity factor, which satisfies

$$\begin{array}{cc}\hfill Z& ={\int }_0^{D_{max}}N\left(D\right)D^{6}dD\hfill \\ \hfill & ={\displaystyle \frac{P_r{d}_s^2}{\eta }},\hfill \end{array}$$

(24)

where $N\left(D\right)$ is the number of rainfall particles within a unit volume and D is the diameter of the raindrop. Furthermore, $\eta ={\displaystyle \frac{P_s{\lambda }^2{G}^2\theta \varphi h|k_0{|}^2}{1024\pi (ln2)}}$ and $|k_0{|}^2=\left|{\displaystyle \frac{m^2-1}{m^2+2}}\right|$, with m representing the complex refraction coefficient of raindrops.

As a further step, the probability of rainfall is given by

$$\begin{array}{c}\hfill R=6\pi \times {10}^{-4}{\int }_0^{D_{\max }}{D}^3{V}_t\left(D\right)N\left(D\right)dD,\end{array}$$

(25)

where $D_{max}$ represents the maximum diameter of the raindrop and $V_t\left(D\right)$ is the final velocity of the raindrop with a diameter of D, which can be empirically expressed as [31]

$$\begin{array}{c}\hfill V_t\left(D\right)=9.3360-{\displaystyle \frac{24.0650}{1+1.5301exp\left(0.8165D\right)}}.\end{array}$$

(26)

According to the ITU-R P.838 recommendation, for the 78 GHz frequency band under horizontal polarization, the coefficients are taken as $k=0.9552$ and $\alpha =0.7719$. When the 1-minute rain rate $R=25$ mm/h (heavy rain), the calculated specific attenuation is $\gamma =0.9552\times {25}^{0.7719}\approx 14.6$ dB/km. For a link with a length of 2 km, the total rain-induced attenuation amounts to approximately 29.2 dB.

4. Numerical Results

In this section, some numerical results are provided to demonstrate the communication and sensing performance of the ISAC system considered in the rainfall scenario. Unless otherwise stated, the simulation parameters are set as follows: a carried frequency of $f=78\mathrm{GHz}$, a noise power of ${\sigma }_k^2={\sigma }_s^2={10}^{-10}\mathrm{W}$, an order of modulation of $M=64$, a sharp parameter of the Weibull channels of $b=2$ and $\lambda =0.6$, an attenuation index of rainfall of $\alpha =0.71$, and an attenuation coefficient of $K=1.11$.

Model Validation and Trend Analysis

Prior to presenting the detailed numerical analysis of the proposed ISAC system, we address the validity of our theoretical model. Given the absence of operational 6G ISAC testbeds, we validate our approach by comparing the trends of our results with well-established empirical models and published experimental data on rainfall attenuation in mmWave links.

The detrimental impact of rainfall on mmWave signals is a well-documented phenomenon, often quantified by the specific attenuation model provided by the International Telecommunication Union (ITU-R P.838-3 [32]). Applying our system parameters (e.g., a carrier frequency of 78 GHz) to this model confirms that rain-induced path loss increases significantly with both rainfall rate and propagation distance.

The performance trends derived from our simulations exhibit strong qualitative agreement with these established realities. For example, the rapid decay of the average user SNR with increasing path length, as shown later in Figure 2, is a direct consequence of the high path loss captured by our Weibull channel model, which aligns with the attenuation predicted by the ITU-R model [32]. This alignment serves as a critical validation step, demonstrating that our model, despite its analytical novelty, is grounded in established electromagnetic physics. It is through this consistency with foundational standards that we establish confidence in our results in lieu of direct experimental measurements. Therefore, our framework provides a solid theoretical foundation and predictive tool for assessing the performance of future ISAC systems in adverse weather conditions.

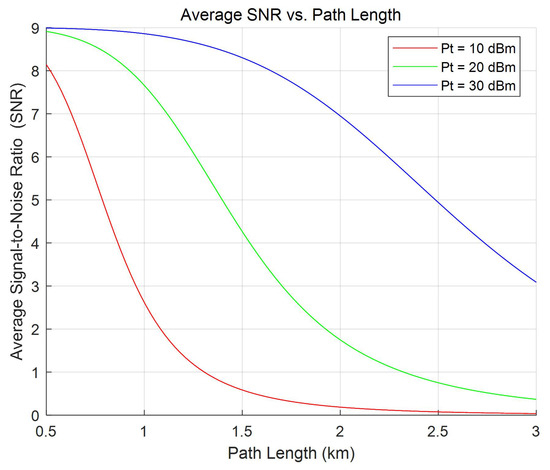
Figure 2. Average user SNR versus path length.

This consistency demonstrates that our analytical framework, though developed for the integrated sensing and communication paradigm, reliably captures the core physical-layer impairments caused by rainfall. Therefore, it provides a solid foundation for assessing the performance of future ISAC systems in adverse weather conditions.

Figure 2 shows a schematic diagram of the average user SNR versus path length. Intuitively, as the path length increases, the received SNR at the user end decreases significantly due to the intensifying path loss over distance. Furthermore, when the transmitted power is 10 dBm and the distance between the BS and the user is 2.5 km, the user’s received SNR approaches zero, whereas increasing the transmit power leads to a noticeable improvement in the SNR at the user.

Figure 3 displays the average received SNR of the users versus the power allocation of the ISAC BS. It can be obtained that as the communication power allocation ratio increases, the received SNR of the users improves significantly. However, in rainfall environments, we observe that even when the ISAC BS allocates full power to communications, distant users achieve negligible SNR improvement due to severe path loss.

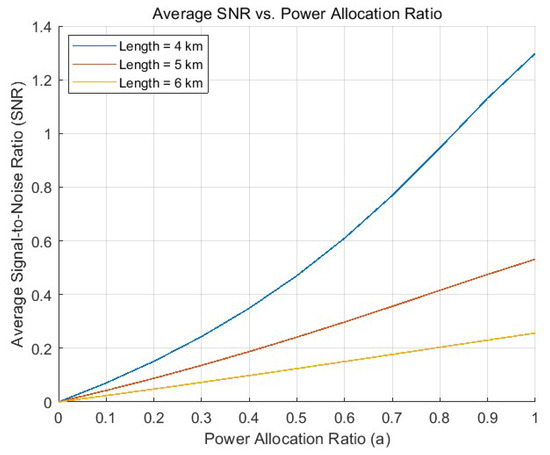
Figure 3. Average user SNR versus the power allocation of the BS.

Figure 4 presents a schematic diagram of the average channel capacity versus the transmitted power of the ISAC BS. As observed from the figure, increasing the transmit power effectively enhances the system channel capacity. Furthermore, a shorter distance between the ISAC BS and the user corresponds to a higher channel capacity. Notably, in the high-transmit-power region, the channel capacity asymptotically approaches saturation. This occurs because, for the communication receiver, the sensing signal transmitted by the ISAC BS constitutes interference.

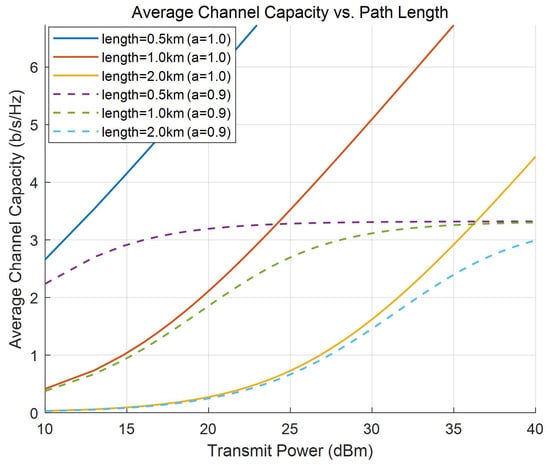
Figure 4. Average channel capacity versus the transmitted power.

Figure 5 depicts the average channel capacity versus the power allocation of the ISAC BS. From Figure 5, we can observe that at low-communication-power ratios, distance has minimal impact on channel capacity. When the power allocation parameter exceeds 0.7, the reduced power allocated to sensing substantially enhances the received SNR of the users, consequently driving significant growth in channel capacity. Notably, in the extreme scenario where all power is allocated to communications, channel capacity exhibits pronounced distance dependency.

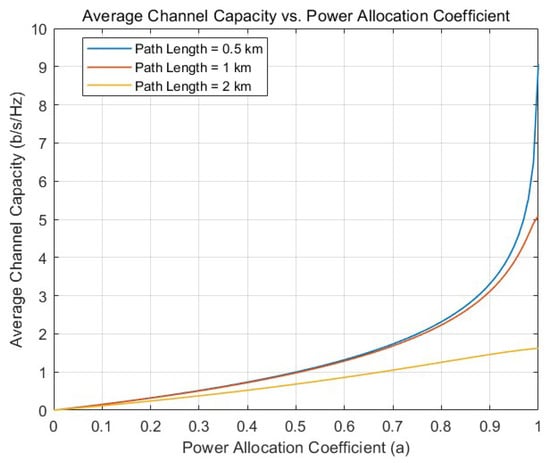
Figure 5. Average channel capacity versus the power allocation of the ISAC BS.

Figure 6 shows a schematic diagram of the user BER versus transmitted power. As seen from the figure, increasing the transmit power continuously improves the BER performance. Furthermore, as expected, increasing the distance between the ISAC BS and the user leads to a degradation in BER performance.

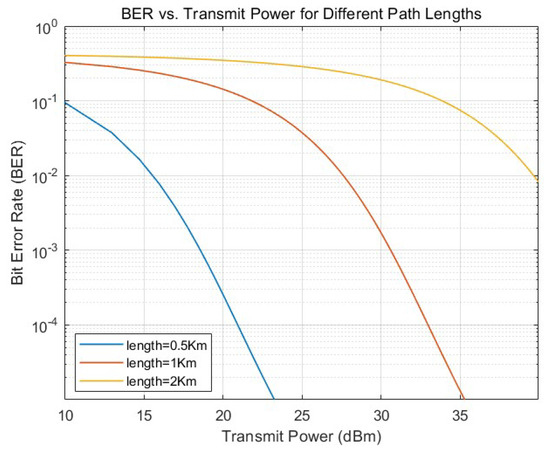
Figure 6. BER of the users versus the transmitted power.

Figure 7 illustrates the user outage probability versus transmitted power. As can be seen from the Figure 7, as the rainfall increases, the outage performance of the users deteriorates. Furthermore, as observed from the figure, a shorter distance between the BS and the user leads to better outage performance. Additionally, comparison with Figure 6 reveals that although increasing the BS–user distance may improve outage performance under certain conditions, it results in a significant rise in the BER. Therefore, in practical ISAC scenarios, it is necessary to optimize the coverage of the ISAC base station to strike a balance between the user outage probability and BER performance. This finding highlights a critical design trade-off that must be considered by system engineers. The theoretical models derived in this paper enable the pre-deployment analysis of such trade-offs without the need for costly and time-consuming field trials in rain.

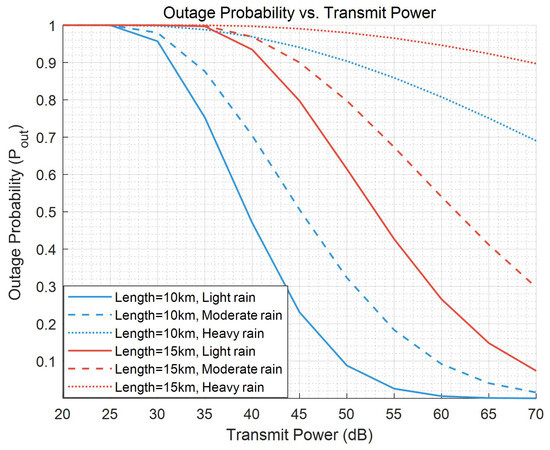
Figure 7. Outage probability of the users versus the transmitted power.

Figure 8 shows the rainfall reflectivity factor versus the received power at the ISAC BS. For comparison, the rainfall reflectivity factor under different frequencies and corresponding polarization-dependent regression parameters is also illustrated. It can be observed from the figure that an increase in either the frequency or the polarization-related regression parameter leads to a reduction in the rainfall reflectivity factor. As shown in the figure, increasing the received power enables more accurate measurement of the radar reflectivity factor, thereby improving rainfall detection accuracy. Additionally, it should be noted that for identical rainfall amounts, a higher reflectivity factor indicates a greater proportion of large droplets. Furthermore, at fixed reflectivity factor levels, rainfall with higher density of small droplets corresponds to greater precipitation. It is also observed that the reflectivity factor Z exhibits a negative correlation with the size parameter m, while coefficient $k_0$ increases monotonically with m. Consequently, increasing $k_0$ reduces the reflectivity factor.

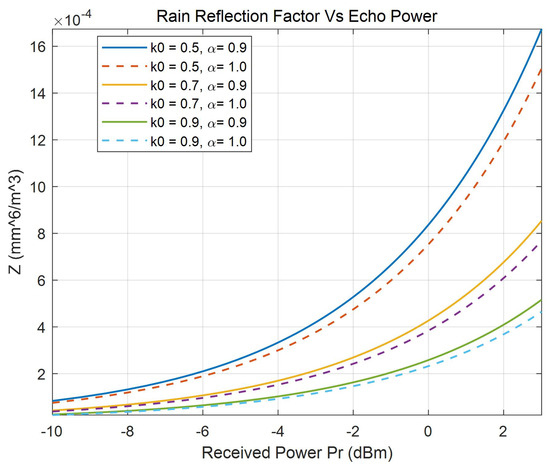
Figure 8. Rainfall reflectivity factor versus the received power.

5. Conclusions

In this paper, we studied an ISAC system in a rainfall scenario, in which the ISAC BS supports communication for multiple users and sensing of the rainfall. Given the isomorphic relationship between raindrop size distribution and the core term of the Weibull distribution, coupled with the natural adaptability of its shape parameter to the right-skewed leptokurtic characteristics of mmWave rain attenuation, we model the channel fading between nodes as Weibull-distributed. The expressions of the received SNRs, channel capacity, BER, and outage probability at the users, as well as the probability of rainfall at the BS, were, respectively, derived to characterize the communication and sensing performance of the ISAC system under consideration. Simulation results demonstrated that increasing the distance between the ISAC BS and users degrades communication performance, while this degradation can be compensated for through jointly optimized communication–sensing power allocation.