Improved Evaluation of Wind Turbine Lightning Exposure: Modeling Upward Leader Effects on Equivalent Collection Area

Abstract

There has been a growing demand for clean energy in recent years, with the advancement of the carbon neutrality vision. Wind power has occupied a significant percentage of clean energy sources. Usually deployed in open fields, on mountaintops, and in offshore areas, wind turbines are particularly vulnerable to lightning strikes due to their unique operational characteristics. Therefore, accurately evaluating the lightning strike risk of wind turbines is an important issue that should be addressed. Current IEC standards lack a physically grounded approach for calculating the equivalent collection area, leading to an overestimation of this value. This paper employs an upward leader initiation model to develop a novel calculation method for the equivalent collection area of wind turbines. By considering the impact of upward leader channel initiation and development, the model demonstrates accuracy through comparison with observational data (0.7761 strikes/year), showing only a −7.1% discrepancy. This study also examines the impact of various blade rotation angles, stepped leader speeds, and peak current of the return stroke on the equivalent collection area. Results indicate that the lightning strike distance specified in IEC standards underestimates the equivalent collection area due to neglecting the upward leader channel, resulting in significant differences compared to our approach, with a maximum deviation of up to 313.12%.

1. Introduction

In recent years, it has become essential to implement measures that reduce carbon emissions and combat global warming. Consequently, countries around the world have widely adopted clean energy sources. Currently, 18% of electricity consumption in the European Union, 20% in the US, 28% in China, and 35.9% in Australia comes from sustainable and renewable sources. Wind energy is among the most crucial of these renewable resources and is becoming more significant in the global energy revolution [1,2,3,4]. The Global Wind Energy Council (GWEC) released the 2025 annual report. According to the report, 117 GW of wind power was installed in 2024, which is a significant turning point in the world’s energy shift. The total global installed wind power capacity has reached 1136 GW, and an additional 981 GW is expected to be deployed by 2030 [5].

Over the past two decades, wind turbines have experienced a significant increase in power generation capacity. The largest single units now reach up to 2500 kW. At the same time, their vertical heights have grown considerably, exceeding 300 m, comparable to those of tall buildings. As wind turbines grow larger and offshore wind farms develop rapidly, observed data indicate that the lightning strike incidents on tall structures increase with their height. Additionally, the probability of upward lightning strikes increases significantly. Direct lightning strikes can cause severe damage to wind turbine blades, electrical equipment, and control systems. This results in extended maintenance downtime, which negatively impacts the efficiency of power generation and the economic benefits of wind farms. Lightning strikes account for 25% of wind energy asset failures worldwide [6]. Wind turbines’ large dimensions make them considerably more likely to be struck by lightning than other objects. Data analysis shows that lightning is the primary cause of unexpected off-grid incidents in wind power generation systems. In Germany, wind turbine incidents are primarily caused by lightning, accounting for 80% of all accidents [7]. A seven-year survey conducted by Rademakers recorded 739 lightning strikes, resulting in 1032 malfunctions, and this highlights that a single lightning strike can damage multiple components of a wind turbine [8]. Therefore, research on predicting and protecting wind turbines against direct lightning strikes has significant scientific and engineering value. Since wind turbines are similar in height to tall buildings, the estimation of the average annual number of lightning flashes can be calculated using the same method for buildings. After statistically analyzing lightning strike events on buildings at altitudes ranging from 20 to 540 m, Eriksson [9] proposed an empirical formula for the annual expected lightning strike frequency ($N_d$) with the lightning ground flash density ($N_g$), expressed as follows:

$$N_d=N_g\times 24\times h^{2.05}\times {10}^{-6}$$

(1)

Due to their height and exposure in open terrains or offshore environments, wind turbines are particularly vulnerable to direct lightning strikes. The equivalent collecting area (ECA) of a wind turbine is a crucial factor in estimating its risk of lightning exposure, as it represents the surface area with which downward lightning leaders interact [10]. However, traditional methods for evaluating lightning risk, such as IEC standards, often have limitations.

The rolling sphere method is the standard technique for determining the protection area of tall structures. According to the IEC 62305 [11], the radius of the rolling sphere used for setting up lightning protection systems on tall structures is defined as follows:

$$\mathrm{S}=10\times I_P^{0.65}$$

(2)

$I_P$ is the peak current of the return stroke. The rolling sphere method estimates that a stepped leader with an expected $I_P$ will be attracted to the structure when its tip approaches it within a critical distance of S. The Electro Geometrical Method uses this geometric concept of striking distance. According to the IEC standard, the variation in striking distance as a function of return stroke peak current is represented by Equation (2). It should be mentioned that the striking distance is unaffected by the structure’s height according to the IEC standard. This indicates that while calculating the critical distance of approach between the tip of the stepped leader and a specific object, the IEC standard does not consider the height of the structure.

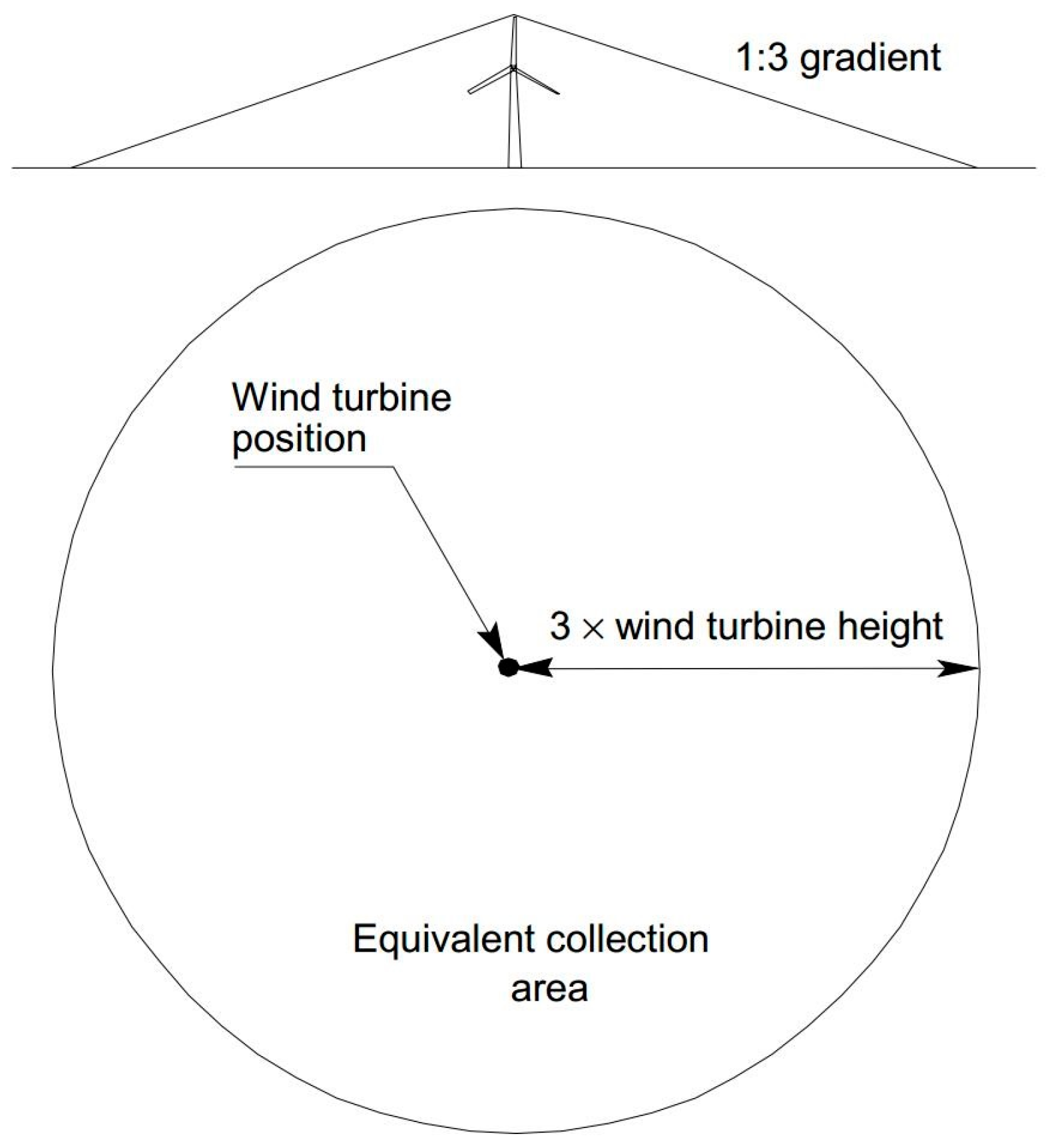
Most lightning protection systems for existing wind turbines are designed in accordance with the technical standard IEC 61400-24 [12]. According to the standard, a structure’s collection area is the ground surface area that experiences the same yearly frequency of lightning strikes as the structure itself. A boundary created by the intersection of the ground surface and a straight line with a 1:3 slope is used to calculate the comparable collection area for isolated constructions. This line encircles and touches the structure after emerging from its upper regions. It is advised that every wind turbine be represented as a tall tower with a height equal to the rotor radius plus the hub height. This is suggested for wind turbines with any kind of blade. The equivalent collection area created by a wind turbine setup on level ground is shown in Figure 1. A circle with a radius three times the turbine’s height is used to represent this region.

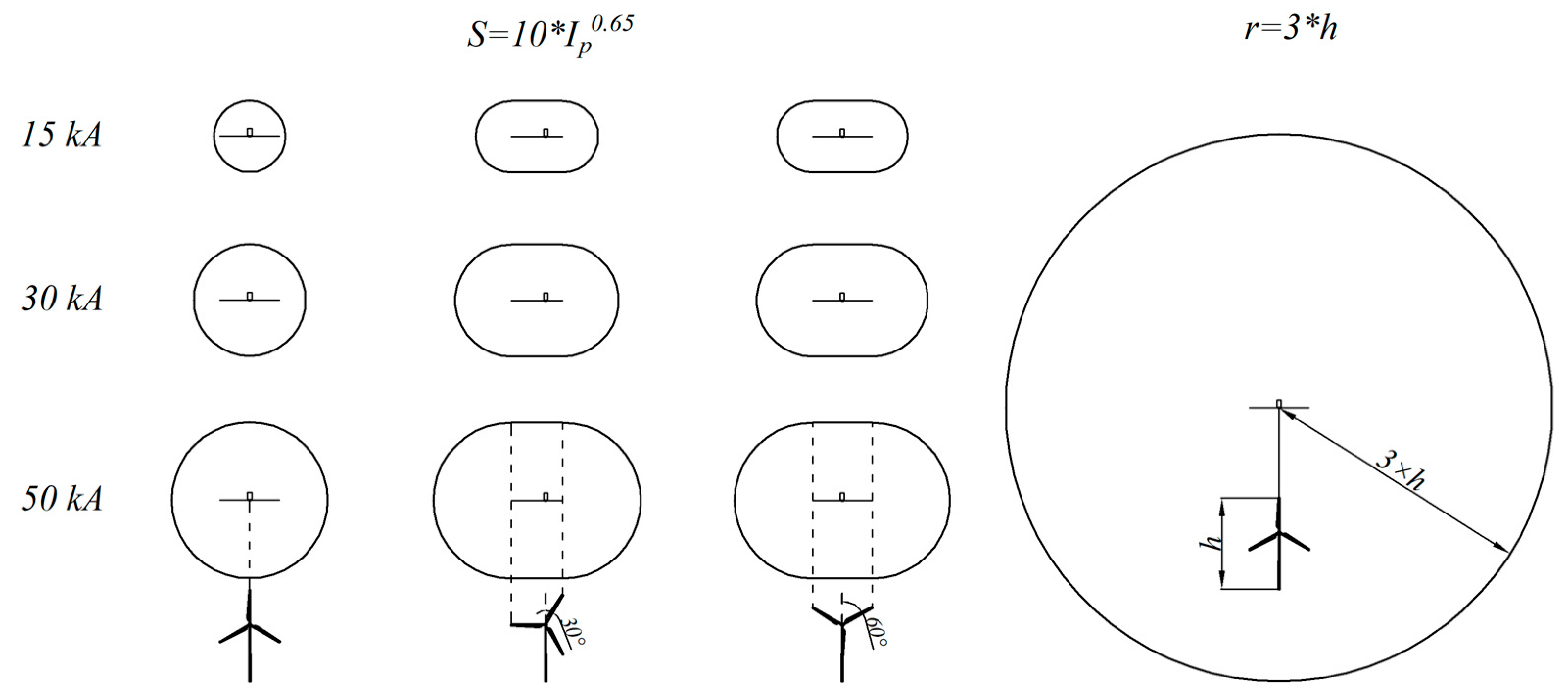
This method lacks physical significance and overestimates the equivalent collection area for tall structures by a large margin. It is merely a designed compromise solution to satisfy the lightning strike risk assessment requirements in the standard. Currently, the calculation of the equivalent collection area for wind turbines can be categorized into two types in engineering. The first type involves calculations without a physical basis. It relies on a simplified method that uses three times the turbine’s height as the equivalent radius. This makes it easier to use in engineering applications. The second type is based on strike distance and offers a calculation method for the equivalent radius depending on the wind turbine blades’ rotation angle. Figure 2 illustrates the equivalent collection areas determined using these two methods:

Table 1. The equivalent collection area was calculated by two methods.

${\mathit{I}}_{\mathit{p}}$	Equivalent Collection Area			IEC 61400 $\mathbf{r}=3\times \mathbf{h}$
	0°	30°	60°
$15 \mathrm{kA}$	10,618 m2	20,389 m2	21,927 m2	653,250 m2
$30 \mathrm{kA}$	26,146 m2	41,478 m2	43,891 m2	653,250 m2
$50 \mathrm{kA}$	50,793 m2	72,164 m2	75,527 m2	653,250 m2

displays the findings of the equivalent collection area determined using the two approaches, showing that the equivalent radius proposed in the IEC 61400 is three times the height of the wind turbine. This calculation ignores the effects of the peak current of the return stroke and the rotation angle of the blades, and remains constant regardless of the conditions, and overestimates the equivalent collection area (about 12.8 to 61.5 times).

In that case, the strike distance method is more objective than the method proposed in IEC 61400 for calculating the equivalent collection area. However, the strike distance calculation method described in IEC 62305 is still limited. The upward leader channel’s existence during the striking process is not taken into account. As a result, it ignores the object’s height and employs only the peak current of the return stroke as the sole variable in its computations. This oversight means that the calculated strike distance remains constant regardless of the object’s height when the peak current of the return stroke is fixed. In reality, both the strike distance and the attraction radius are influenced by the peak current of the return stroke, the height of the object, and the speed of step leader development. These have been confirmed by observed results.

The primary objective of this work is to investigate how the equivalent collection area is affected when a connecting leader is not present, as specified in the IEC standard. To increase the accuracy of the strike distance and attraction radius, the existing approach has to be modified to take into account the upward leader’s development status. The risk of a lightning strike on wind turbines can be evaluated. This study uses the finite element method to create a wind turbine model. By adjusting the position of the stepped leader and considering the initiation and development of the upward leader, the attraction radius of the wind turbine blades at various angles can be simulated and obtained. Additionally, by modifying the charge amount and velocity parameters within the stepped leader channel, the wind turbine’s equivalent collection area can be determined under different conditions.

2. Model and Methods

To determine the stable upward leader inception, the basic inception model of a positive upward connecting leader is employed [13,14].

The electric field causes the free electrons to accelerate. The resulting ionization process increases the number of electrons through collisions with neutral molecules. The coefficient ${\alpha }^{\prime }$ can be represented as follows:

$${\alpha }^{\prime }=\alpha \left(E\right)-\eta \left(E\right)$$

(3)

In the above equation, $\alpha \left(E\right)$ represents the collision ionization coefficient, and $\eta \left(E\right)$ represents the adsorption coefficient. The electron avalanche process is converted into the initial streamer when the transition conditions are met.

$$\left\{\begin{array}{c}{{\displaystyle \int }}_0^l\left(\alpha \left(E\right)-\eta \left(E\right)\right)dl\ge \ln \left(N_{stab}\right)\\ \alpha ={\displaystyle \frac{P_w}{P}}{\alpha }_w+{\displaystyle \frac{P-P_w}{P}}{\alpha }_d\\ \eta ={\displaystyle \frac{P_w}{P}}{\eta }_w+{\displaystyle \frac{P-P_w}{P}}{\eta }_d \\ P_w=\gamma R_{v}T\\ R_v=461.5 \mathrm{J}·\mathrm{Kg}·\mathrm{K}\end{array}\right.$$

(4)

Here, $P_w$ is the partial pressure of water vapor; $\gamma$ represents the absolute humidity; and ${\alpha }_w$ and ${\alpha }_d$ are the ionization coefficients of water vapor under wet and dry conditions, respectively. $l$ is defined as the distance at which the collision ionization coefficient, $\alpha \left(E\right)$, and the adsorption coefficient $\eta \left(E\right)$ are equal. ${\alpha }^{\prime }$ = 0; and $N_{stab}$ is the critical number of ions for self-sustained development, which is generally considered to be 5.5 × 10⁷. Once the number of ions exceeds $N_{stab}$, the initial streamer has begun to develop.

The filaments are formed within the corona zone during the initial stage of streamer initiation. These filaments collect electrons, resulting in the accumulation of a positive charge. As electrons transfer energy to neutral gas molecules through elastic and inelastic collisions, the molecules’ energy increases. This process raises the temperature inside the streamer stem. As the temperature rises to 1500 K, the adsorption capacity of the neutral gas molecules within the streamer stem decreases, and the quantity and density of electrons rise as a result. In essence, the upward leader’s initial procedure is a dynamic conversion to the streamer-leader system. Enough energy is produced by the streamer’s development to form the leader. And the subsequent growth of the leader provides an ideal electric field environment for the head streamer to develop. Once this process reaches dynamic equilibrium, the streamer-to-leader system can develop independently of the surrounding environment. The critical charge required for the transition from the streamer to the leader state is approximately 1 μC. Therefore, it is essential to determine the amount of charge entering the streamer stem to determine the transition between the streamer and leader states.

The average electric field strength within the streamer region is expressed as follows:

$$\begin{array}{c}{E}_{str}=425{\delta }^{1.5}+\left(4+5\delta \right)\gamma \\ P\left(z\right)=P_0\exp \left(-{\displaystyle \frac{z}{z_0}}\right)\\ T=T_0-6H_L\\ \gamma ={\gamma }_0\exp \left(-H_L/z_H\right)\end{array}$$

(5)

$\gamma$ represents absolute humidity, and $\delta$ represents relative air density, which can be expressed as $\delta =\left(P/P_0\right)\left(T_0/T\right)$. $P_0$ is the standard atmospheric pressure, which is 1013.25 hPa. $T_0$ is taken as 293 K. The standard value of $E_{str}$ is approximately 0.52 MV/m ($P$ = P₀, $T$ = $T_0$, and $\gamma$ = 11 g/m³). For stationary objects, $E_{str}$ can be considered a constant value. However, for dynamic systems where surface atmospheric conditions change due to motion, it is necessary to make corresponding corrections to $E_{str}$.

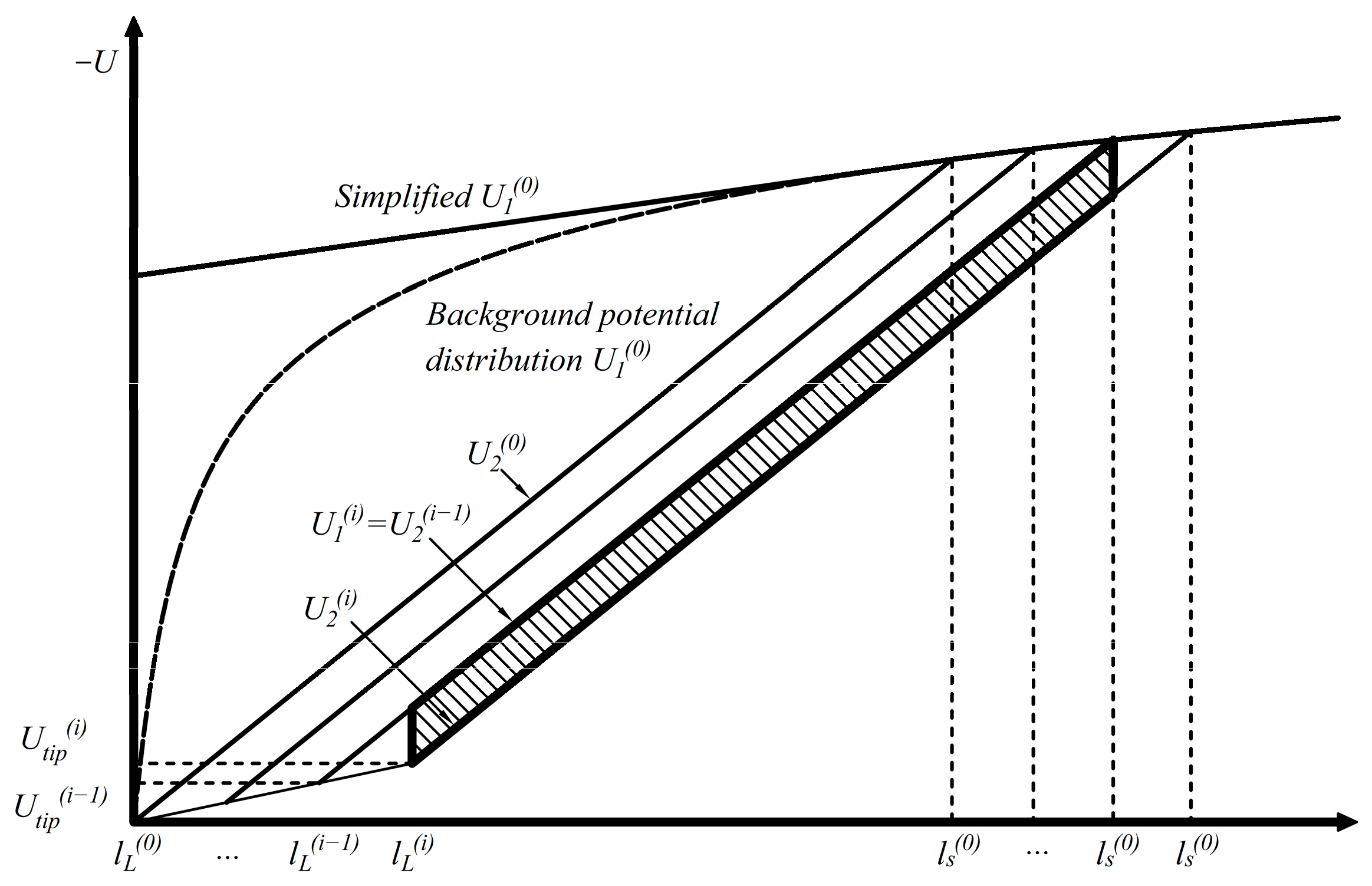
As the stepped leader rapidly approaches the struck object, an upward leader forms on its surface and develops toward the stepped leader. Eventually, the leader breaks through the air and establishes a connection, using this channel to discharge the lightning current. Therefore, identifying where upward leaders are likely to initiate is essential for evaluating lightning areas on wind turbine blades. The difference between the environmental background potential and the potential following the first corona initiation can be used to calculate the corona charge entering the channel. This enables the determination of whether the conditions for stable leader initiation are met, thereby identifying the final point of the lightning strike. The background electric field $U_1^{\left(0\right)}$ can be simplified using linear fitting (Figure 3) and expressed as follows:

$$U_1^{\left(0\right)}\approx E_1·l+U_0^{\prime }$$

(6)

The position $l_s$ of the front of the streamer zone can be obtained as:

$$l_s^{\left(0\right)}=U_0^{\prime }/(E_{str}-E_1)$$

(7)

The amount of charge passing through the streamer zone can be also obtained by the following equation:

$$\Delta Q^0\approx K_Q·{\displaystyle \frac{l_s^2·\left(E_{str}-E_1\right)}{2}}$$

(8)

It can be considered that the temperature inside the channel has reached 1500 K, and the streamer has met the requirements for transitioning into the leader state when the accumulated charge exceeds 1 μC. However, the leader has completed the transition, but it is still in an unstable state. Further analysis is required to determine whether the unstable upward leader can sustain itself in the current electric field environment. The potential at the leader tip can be obtained by the following equation:

$$U_{tip}^i=l_L^i·E_{\infty }+x_0·E_{\infty }·\ln \left({\displaystyle \frac{E_{str}}{E_{\infty }}}-{\displaystyle \frac{E_{str}-E_{\infty }}{E_{\infty }}}·e^{-l_L^i/x_0}\right)$$

(9)

So, the amount of corona charge formed at the front of the leader can be expressed as

$$\Delta Q^{\left(i\right)}\approx K_Q\left[\left(E_{str}·\left(l_L^i-l_L^{i-1}\right)-U_{tip}^i+U_{tip}^{i-1}\right)·\left(l_s^{i-1}-l_L^i\right)\right]$$

(10)

Accordingly, the lengths of the leader and corona zones can also be calculated:

$$l_s^{\left(i\right)}=l_s^{\left(0\right)}+{\displaystyle \frac{E_{str}·l_L^{\left(i\right)}-U_{tip}^{\left(i\right)}}{E_{str}-E_1}}$$

(11)

$$l_L^{\left(i+1\right)}=l_L^{\left(i\right)}+·l_L^{\left(i\right)}=l_L^{\left(i\right)}+{\displaystyle \frac{\Delta \mathrm{Q}}{q_L}}$$

(12)

Through the above series of calculations, it can be concluded that when the conversion length $l_L^{\left(i+1\right)}$ of the leader exceeds the critical distance of 2 m, the condition for stable, upward leader initiation is satisfied. At this point, a stable and continuous upward leader can be considered to have been successfully initiated. The relevant parameters used are listed in

Table 2. Parameters used by the model.

Parameter	Description	Value	Units
IL(1)	Initial leader length	5 × 10−2	m
Estr	Positive streamer gradient	4.5 × 105	V/m
E∞	Final quasi-stationary leader gradient	3 × 104	V/m
x0	Constant given by the ascending positive leader speed and the leader time constant	0.75	m
qL	Charger per unit length necessary for thermal transition	6.5 × 10−7	C/m
KQ	Geometrical constant	4 × 10−11	C/Vm

.

The blades of a wind turbine revolve constantly. Under typical conditions, the blades can rotate at speeds ranging from 10 to 20 revolutions per minute (rpm). The effective collection area for wind power generation varies as the blades rotate. As the sketches in Figure 4, the blades are arranged in a symmetrical pattern, with each blade positioned at a 120° angle relative to the next. This arrangement means that one complete cycle of the wind turbine occurs with each rotation, and this cycle repeats six times.

3. Results and Validation

A wind turbine model with a 95 m hub and 54 m blades was established in the research area, and an upward leader initiation model was used to simulate the initiation and development of upward leaders. By adjusting the geometric position of the stepped leader and considering the effects of the upward leader, we could determine the strike distance and accurately estimate the wind turbine’s equivalent collection area under different conditions.

3.1. Simulation Results

3.1.1. Effect of Different Stepped Leader Development Speeds on Equivalent Collection Area

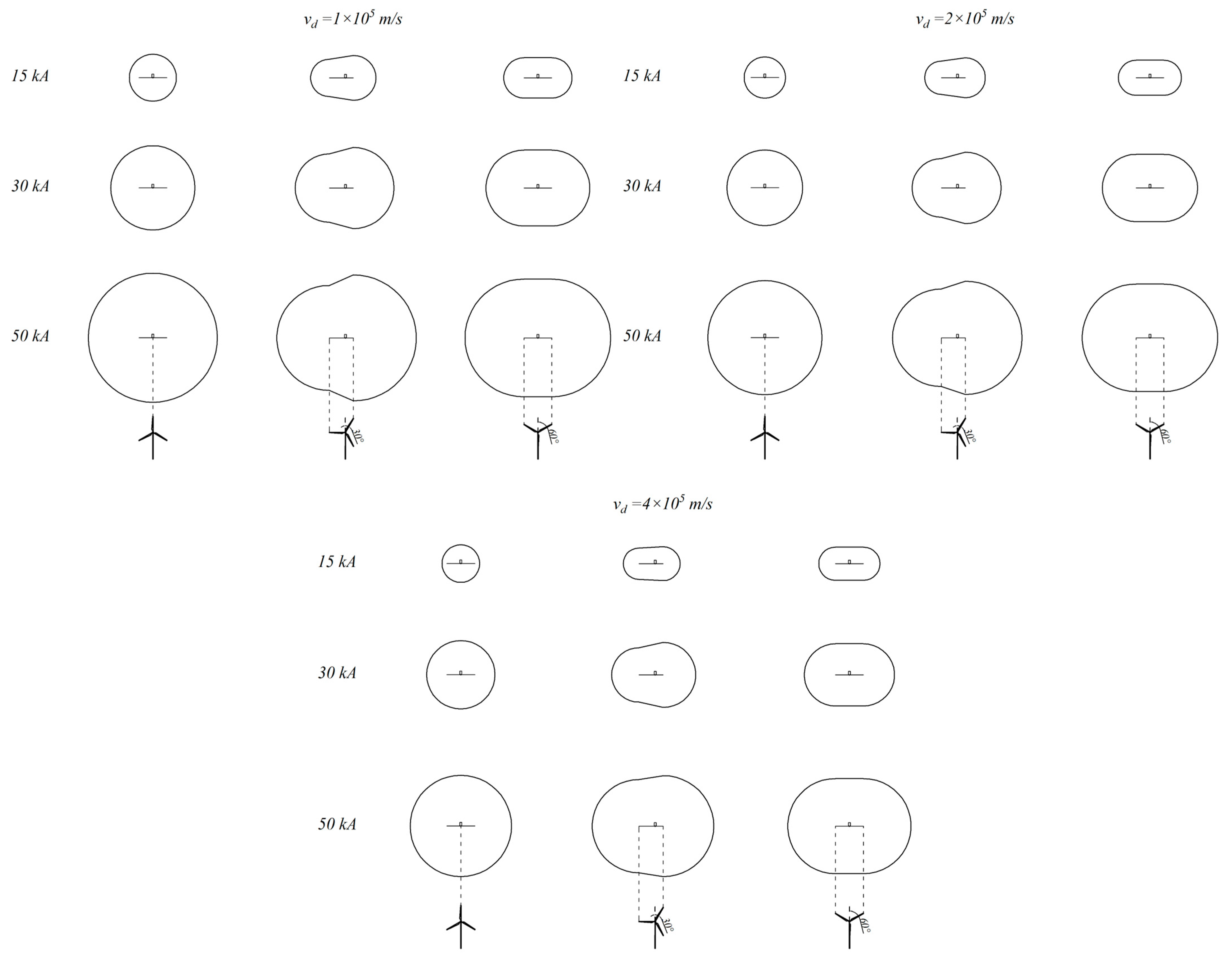
The upward leader’s length and velocity are mostly determined by the stepping leader’s speed. The speed of the stepped leader is negatively correlated with the length of the upward leader channel. According to simulation data, when the average speed of the stepped leader reaches 1 × 10⁵ m/s, the upward leader channel’s final length can extend up to 134.79 m with a wind turbine blade rotation angle of 0°. However, when the stepped leader’s speed increases to 4 × 10⁵ m/s, the channel’s length decreases to 54.98 m. The length of the upward leader channel significantly influences the strike distance and attraction radius. Therefore, the effect of the stepped leader’s development speed on the equivalent collection area of wind turbines should not be underestimated.

Figure 5 shows the simulation results for the wind turbine collection area at different stepped leader development speeds, with a peak current of the return stroke of 15 kA. As the speed of the stepped leader increases, the equivalent collection area of the wind turbine decreases gradually. According to

Table 3. Equivalent collection area of wind turbines at different stepped leader development speeds with current of return stroke intensities of 15 kA, 30 kA, and 50 kA.

Return Stroke Peak Current	Stepped Leader Speeds	Equivalent Collection Area
		0°	30°	60°
$I_p=15 \mathrm{kA}$	$v_d=4\times {10}^5 \mathrm{m}/\mathrm{s}$	13,273 m2	19,409 m2	21,499 m2
	$v_d=2\times {10}^5 \mathrm{m}/\mathrm{s}$	16,286 m2	23,585 m2	23,769 m2
	$v_d=1\times {10}^5 \mathrm{m}/\mathrm{s}$	21,124 m2	28,357 m2	29,245 m2
	IEC	10,618 m2	20,389 m2	21,927 m2
$I_p=30 \mathrm{kA}$	$v_d=4\times {10}^5 \mathrm{m}/\mathrm{s}$	43,743 m2	51,113 m2	57,103 m2
	$v_d=2\times {10}^5 \mathrm{m}/\mathrm{s}$	54,739 m2	59,724 m2	66,108 m2
	$v_d=1\times {10}^5 \mathrm{m}/\mathrm{s}$	67,886 m2	75,586 m2	80,795 m2
	IEC	26,146 m2	41,478 m2	43,891 m2
$I_p=50 \mathrm{kA}$	$v_d=4\times {10}^5 \mathrm{m}/\mathrm{s}$	96,211 m2	116,741 m2	116,851 m2
	$v_d=2\times {10}^5 \mathrm{m}/\mathrm{s}$	124,410 m2	137,549 m2	146,740 m2
	$v_d=1\times {10}^5 \mathrm{m}/\mathrm{s}$	159,043 m2	162,109 m2	172,451 m2
	IEC	50,793 m2	72,164 m2	75,527 m2

, the equivalent collection area derived from the IEC strike distance formula for blade rotation angles of 30° and 60° is slightly higher than the model calculation results in this study at certain stepped leader velocities. However, this is the only instance across all simulations. Furthermore, as the stepped leader development speed decreases, the equivalent collection areas under conditions of upward leader initiation and development exceed the values calculated using the IEC strike distance formula. Specifically, when the stepped leader development speed decreased from 4 × 10⁵ m/s to 2 × 10⁵ m/s and then to 1 × 10⁵ m/s, the average values calculated by the model for the three blade rotation angles were 2.4%, 20.2%, and 48.7% greater than the IEC results, respectively.

As the peak current of the return stroke rises to 30 kA, the equivalent collection area of the wind turbines gradually increases as the blade rotation angle increases. Table 3 shows that the equivalent collection area is largest when the blade is at a 60° angle. Even with a stepped leader velocity of 4 × 10⁵ m/s, the equivalent collection area calculated by the model is 126.70%, 47.26%, and 60.25% larger than the results calculated using the IEC strike distance formula for blades positioned at 0°, 30°, and 60°, respectively. This trend becomes more evident as the intensity of the return current increases. When the peak current of the return stroke reaches 50 kA and the stepped leader develops at $v_d=1\times {10}^5 \mathrm{m}/\mathrm{s}$, the model calculates the equivalent collection area to be 313.12%, 224.64%, and 228.33% of the results obtained from the IEC strike distance for blades positioned at 0°, 30°, and 60°, respectively.

3.1.2. Effect of the Different Peak Current of the Return Stroke on Equivalent Collection Area

The discussion explains how different speeds of stepped leader development impact the equivalent collection area. The peak current of the return stroke has an impact on the equivalent collection area of wind turbine equipment since it has a positive relationship and reflects the total amount of charge in the stepped leader channel.

Literature reviews indicate that the average value of the return stroke current for ground flashes, as measured, is 30 kA via a tower on Monte San Salvatore. Only 5% of peak intensities exceed 80 kA [15]. Other studies have reported an average peak current of the return stroke is 28.4 kA [16]. Based on these findings, the return stroke current intensities in the simulation were set to 15 kA, 30 kA, and 50 kA. However, it is important to note that the strike distance calculation method described in the IEC 62305 standard does not consider the upward leader. Consequently, the strike distance is calculated based only on the final breakdown electric field value. Therefore, the strike distance derived from this method will inevitably be smaller, resulting in a reduced calculated equivalent collection area.

The peak current of the return stroke has a significant impact on the speed of upward leader development. However, this is not factored into the IEC calculation method. Research indicates that with a return stroke current of 15 kA, the maximum speed of upward leader development reaches 7.8 × 10⁴ m/s. When the peak current of the return stroke increases to 50 kA, the speed increases to 1.8 × 10⁵ m/s. The upward leader channel develops faster, the longer it is formed. Figure 6 shows that, when the stepped leader speed remains constant, the equivalent collection area of the wind turbine increases as the peak current of the return stroke increases.

Table 4. Equivalent collection area of wind turbines under different peak current of the return stroke with stepped leader development speeds of 1 × 10⁵ m/s, 2 × 10⁵ m/s, and 4 × 10⁵ m/s, respectively.

Stepped Leader Speeds	Return Stroke Peak Current	Equivalent Collection Area
		0°		30°		60°
		Model	IEC	Model	IEC	Model	IEC
$1\times {10}^5 \mathrm{m}/\mathrm{s}$	$I_p=15 \mathrm{kA}$	21,124 m2	10,618 m2	28,375 m2	20,389 m2	29,245 m2	21,927 m2
	$I_p=30 \mathrm{kA}$	67,886 m2	26,146 m2	75,586 m2	41,478 m2	80,795 m2	43,891 m2
	$I_p=50 \mathrm{kA}$	159,043 m2	50,793 m2	162,109 m2	72,164 m2	172,451 m2	75,527 m2
$2\times {10}^5 \mathrm{m}/\mathrm{s}$	$I_p=15 \mathrm{kA}$	16,286 m2	10,618 m2	23,585 m2	20,389 m2	23,769 m2	21,927 m2
	$I_p=30 \mathrm{kA}$	54,793 m2	26,146 m2	59,724 m2	41,478 m2	66,108 m2	43,891 m2
	$I_p=50 \mathrm{kA}$	124,410 m2	50,793 m2	137,549 m2	72,164 m2	146,740 m2	75,527 m2
$4\times {10}^5 \mathrm{m}/\mathrm{s}$	$I_p=15 \mathrm{kA}$	13,273 m2	10,618 m2	19,410 m2	20,389 m2	21,499 m2	21,927 m2
	$I_p=30 \mathrm{kA}$	43,743 m2	26,146 m2	51,113 m2	41,478 m2	57,103 m2	43,891 m2
	$I_p=50 \mathrm{kA}$	96,211 m2	50,793 m2	116,741 m2	72,164 m2	116,851 m2	75,527 m2

shows that when the velocity of the stepped leader is $v_d=1\times {10}^5 \mathrm{m}/\mathrm{s}$, the equivalent collection area calculated using the leader initiation and development model in this study is 1.33 to 3.13 times larger than the results obtained from the IEC standard for different return current intensities.

As the stepped leader’s speed increases, the equivalent collection area decreases accordingly. This finding contrasts with the method provided by the IEC, which remains unchanged. Despite the downward trend in the equivalent collection area calculated by this model, it is still larger than the results obtained from the IEC standard. For a stepped leader velocity of $v_d=2\times {10}^5 \mathrm{m}/\mathrm{s}$ and return stroke current intensities of 15 kA, 30 kA, and 50 kA, the equivalent collection area obtained from the model is greater than the IEC results by 20.23%, 61.93%, and 105.9%, respectively.

As the velocity of the stepped leader decreases to 4 × 10⁵ m/s, the equivalent collection area under the same return current decreases by 14.86%, 15.84%, and 19.30%, respectively, compared to $v_d=2\times {10}^5 \mathrm{m}/\mathrm{s}$. The small peak current of the return stroke and fast development velocity of the stepped leader result in a shorter upward leader channel. Consequently, the strike distance calculation is similar to the result obtained by ignoring the upward leader. The final development length of the upward leader channel before the return stroke occurs is only 26.93 m when the speed is $2\times {10}^5 \mathrm{m}/\mathrm{s}$ and the return stroke current is 15 kA. This length is relatively small compared to the dimensions of the wind turbine equipment itself. For this reason, the equivalent collection area calculated under these conditions is close to the results found in the IEC standard.

3.2. Validation

The above sections discuss how the velocity of the stepped leader and the peak current of the return stroke impact the equivalent collection area. Table 3 and Table 4 illustrate how different wind turbine blade rotation angles contribute to this equivalent collection area. Comparing these tables reveals that the equivalent collection area is smallest at 0° and largest at 60°. The blades of wind turbines rotate continuously. Because the three sets of blades are symmetrically arranged, the equivalent collection area fluctuates, repeating six times between its greatest and minimum values over the course of a full rotation. Consequently, we can calculate the average equivalent collection area using values obtained at different blade configurations. The number of lightning strike incidents can be estimated annually using these values.

Garolera [17] documented lightning strikes at a wind farm in Kansas from 2009 to 2013. The farm consisted of 67 megawatt-class turbines distributed from east to west. A total of 360 lightning strike events were recorded via devices installed on the turbines over a 4-year period. By comparing the recorded incidents with data from the National Lightning Detection Network (NLDN), considering the NLDN’s detection efficiency and identification capability [18], the annual average lightning strike density is 4.38 km⁻² yr⁻¹ according to NLDN statistical data. These findings suggest an average of 0.7761 lightning strikes per turbine per year.

This paper proposes a model that calculates the expected annual number of lightning strikes to be 0.7207, based on an annual average lightning strike density of 4.38 km⁻² yr⁻¹. This value differs slightly from the statistical value of 0.7761 times per year, as reported by Garolera in 2014, with an error margin of only 7.14%.

Table 5. Differences between the estimated annual lightning strike frequency obtained from different solutions and the observed values.

Solutions	Equivalent Collection Area	Annual Number of Lightning Strikes	Observed Values	Difference
IEC 61400	653,250.2 m2	2.8612	0.7761	268.67%
IEC 62305	66,161.3 m2	0.2898		−62.66%
Eriksson	712,837.6 m2	3.1222		302.30%
This Model	164,534.3 m2	0.7207		−7.14%

summarizes the results obtained using various methods to calculate annual lightning strike frequencies. As the table shows, the frequencies calculated using the IEC 61400 and Eriksson’s method far exceed the statistical values. Both approaches make the assumption that the equivalent collection area is proportionate to three times the height and the height squared, respectively. It does not have any physical meaning; it simply assumes a larger area to broadly cover the equivalent collection area in any situation. The annual expected number of lightning strikes calculated by these two methods is 2.68 and 3.02 times higher than the statistical value, respectively. This is far from the actual condition. However, the IEC strike distance method, which is based on an electrical geometry model, underestimates the annual expected number of lightning strikes because it does not account for upward leaders. This results in a difference of −62.66% between the observed and statistical values. Incorrectly estimating the annual number of lightning strikes on wind turbines will result in an incorrect lightning protection rating. If design and manufacturing processes rely on this flawed rating, wind turbine equipment may lack sufficient protection against lightning. As a result, there is potential for increased vulnerability to damage from lightning strikes.

4. Discussion

An incorrect estimate of the annual number of lightning strikes on wind turbines will directly result in an incorrect lightning protection level. Based on these inappropriate results, the design and manufacturing stages will lack sufficient lightning protection capabilities, making the system more vulnerable to damage. According to the IEC technical report [19], the definition of lightning protection system levels identifies four levels in total, as shown in

Table 6. Lightning protection system levels.

Protection Levels	Interception efficiency ${\mathit{E}}_{\mathit{i}}$	Sizing efficiency ${\mathit{E}}_{\mathit{s}}$	Efficiency $\mathit{E}={\mathit{E}}_{\mathit{i}}\times {\mathit{E}}_{\mathit{s}}$
Ⅰ	0.99	0.99	0.98
Ⅱ	0.97	0.98	0.95
Ⅲ	0.91	0.97	0.90
Ⅳ	0.84	0.97	0.80

.

One minus the lightning protection system efficiency (1 − E) multiplied by the yearly average number of direct strikes to the structure ($N_d$) must be less than or equal to the number of allowed annual critical occurrences ($N_c$).

$$N_c\ge N_d\times \left(1-E\right)$$

(13)

Interception efficiency, which represents the ability to intercept a flash, and scaling efficiency, which represents the capacity to conduct the flash current, are the two key efficiencies that comprise the overall efficiency of a lightning protection system. The following formula can be used to determine the minimum efficiency of a lightning protection system.

$$E\ge 1-{\displaystyle \frac{N_c}{N_d}}$$

(14)

A more efficiency-focused lightning protection system will feature larger conductor sizes and larger earthing systems, which improve the efficiency. To maximize interception efficiency, it will also be designed with more lightning interception points.

Table 7. Maximum values of lightning parameters corresponding to protection levels.

Protection Level	Peak Current (kA)	Specific Energy (kJ/Ω)	Average Rate of Current Rise (kA/μs)	Total Charge Transfer (C)
Ⅰ	200	10000	200	300
Ⅱ	150	5600	150	225
Ⅲ	100	2500	100	150

presents the current, specific energy, rate of current rise, and charge transfer levels required to achieve the various sizing efficiencies of the lightning protection system.

The effectiveness of the lightning protection system must be limited to 1 in 100 significant incidents that occur annually. Equation (14) can be used to determine the required efficiency of the lightning protection system.

$$1-{\displaystyle \frac{0.01}{0.7207}}=0.9861>0.98$$

(15)

When E ≥ 0.98, it should be classified as Protection Level I, as indicated in Table 6. However, when using the IEC 62305 method for calculation, the existence of the upward leader is ignored, resulting in a significant underestimation of the equivalent collection area, which leads to E = 0.9655 < 0.98, and thus it is only classified as a protection level II. According to the descriptions of different protection levels in Table 7, the lightning current parameters corresponding to level II are lower than level I. If an incorrect lightning protection level is adopted, it will certainly increase the probability of lightning strike damage. It is also worth noting that the average annual number of lightning flashes calculated with the IEC 61400 and Eriksson’s method is far greater than the statistical value. The corresponding E values are 0.9965 and 0.9968, respectively, far exceeding the Class I lightning protection level. Of course, increasing the lightning protection level is beneficial for enhancing the equipment’s tolerance to lightning strikes. However, overly overstating the required lightning protection level can lead to overdesign and more complex manufacturing processes.

5. Conclusions

The model proposed in this paper considers the initiation and development of upward positive leaders to calculate a more accurate attraction radius for wind power equipment, which is used to obtain the equivalent collection area of wind turbines. The paper discusses the effects of different rotation angles of blades, stepped leader speeds, and peak current of the return stroke on the equivalent collection area. Furthermore, the equivalent collection area calculated using the model was used to obtain the average annual number of lightning flashes, which was compared with observed data to validate the proposed model in this paper. Then, the lightning protection levels corresponding to different methods were discussed. The main conclusions obtained from the research in this paper are as follows:

The equivalent collection area proposed in the IEC 61400 ignores the impact of the charge amount of the stepped leader channel and the blade rotation angle. The calculation result remains constant in all conditions, and the equivalent collection area is greatly overestimated. However, the strike distance in the IEC 62305 standard does not account for the upward leader channel, resulting in a smaller equivalent collection area.

When the blades of a wind turbine are positioned at 60°, the equivalent collection area is maximized, while it is minimized at 0°. The faster the stepped leader develops, the smaller the equivalent collection area. The maximum difference between the IEC 62305 and calculated results from the proposed model reaches 313.12%, 224.64%, and 228.33% at blade rotation angles of 0°, 30°, and 60°, respectively. The equivalent collection area obtained by this model under different return stroke current intensities is also 1.33 to 3.13 times greater than the IEC standard.

The predicted annual number of lightning strikes can be calculated based on the obtained equivalent collection area. Using this model, the estimated annual number of lightning strikes for a typical megawatt-class wind turbine is 0.7207, which is highly correlated with the observed value of 0.7761, with a difference of only 7.1%.