Collaborative Station Learning for Rainfall Forecasting
Abstract
1. Introduction
- A systematic analysis of four geometric station topologies: linear, triangular, quadrilateral, and circular, to evaluate their impact on prediction accuracy.
- Integration of these topologies with six state-of-the-art deep learning models (LSTM, Bi-LSTM, Stacked-LSTM, GRU, Bi-GRU, and Transformer) for comprehensive benchmarking.
- Demonstration that the linear topology with Bi-GRU configuration achieves the highest predictive performance (R2 = 0.9548, RMSE = 2.2120), surpassing both prior studies and all other tested topologies.
2. Study Area
3. Data and Methods
3.1. Data Sources and Processing
3.2. The Proposed Conceptual Framework
3.3. Experiments
3.4. Cloudburst Event Recorded at ARG Chinchwad Station
3.5. Geometric Station Screening and Topology Design
3.5.1. Selection of Geometrical Configurations
3.5.2. Station Screening Criteria for Cloudburst-Scale Analysis
3.5.3. Screening of AWS/ARG Based on Sensor Type
3.5.4. Data-Quality (QA/QC) Filters
3.5.5. Topology Design for Cloudburst-Scale Prediction
- (i)
- Linear topology: Two configurations were developed (Figure 3a,b) with reversed orientations, but both aligned with the target station (ARG Chinchwad). In Figure 3a, the target lies at the center, with partner stations aligned NNE–SSW within a ±2.5 km band. In Figure 3b, the target is placed at the edge, resulting in distinct partner combinations. Stations beyond a 5 km lateral offset were excluded, as they introduced zigzag rather than linear alignments. Partner stations were required to lie within 3–50 km of the target. Minimum station count: ≥2 partners (3 including target). Linear layouts are well suited for tracking rainfall along orographic channels, valleys, ridges, transport corridors, and river basins where precipitation propagates linearly.
- (ii)
- Triangular topology: Stations were arranged at azimuth separations of ~120° ± 15°. Two designs (Figure 3c,d) with reversed orientations tested variable lengths of 20 km and 35 km. This ensured balanced sampling of inflow variability and convective initiation. Minimum station count: ≥3 partners (4 including target). Triangular configurations are particularly suited for capturing directional inflows from three azimuthal sectors, such as hillslopes and ridge environments.
- (iii)
- Quadrilateral topology: Four stations were positioned at ~90° ± 15° azimuth separations (Figure 3e,f), with reversed orientations tested. This design is effective for resolving rainfall fields across mesoscale domains. Minimum station count: ≥4 partners (5 including target). Quadrilateral arrangements are therefore suited for systems with moderate spatial extent, requiring balanced four-way sampling.
- (iv)
- Circular topology: Circular layouts ensure full 360° sampling of radial precipitation gradients. Six designs were tested (Figure 3g–l), with radii distributed between 15–35 km from the target. Minimum station count: ≥4 partners (5 including target). Circular topologies help capture convergent and centripetal rainfall patterns. Base stations were selected within 15, 20, 30, and 35 km radii around the target ARG Chinchwad. Additionally, extended layouts (Figure 3g–l) were tested with broader coverage (~20%, 30%, 45%, 75%, and up to 100% of the network area). Circular topology is the only configuration that provides flexibility to accommodate the maximum number of stations within the defined radius from the central target station. With this intention, six cases with variations in the number of stations, including the central target station (3, 4, 7, 7, 9, and 9), were considered to examine whether incorporating more spatial information could enhance the model’s ability to learn rainfall trends and patterns. This approach enabled us to investigate how various spatial arrangements affect the model’s performance and its ability to capture underlying rainfall patterns accurately.
3.6. Algorithm Selection
- LSTM—standard memory-cell architecture to capture long short-term dependencies; widely used for meteorological time series [25].
- Stacked-LSTM—deeper LSTM layers to capture hierarchical temporal scales [25].
- Bi-LSTM—processes the sequence forward and backward to exploit context from both directions [25].
- GRU—a simplified recurrent cell with fewer parameters, offering computational efficiency [18].
- Bi-GRU—bidirectional GRU, combining speed with contextual richness (empirically best performer in our experiments) [18].
- Transformer—self-attention architecture for long-range interactions and non-sequential dependency modeling [19].
3.6.1. Model Evaluation and Evaluation Metrics
3.6.2. Model Configuration and Training Setup
4. Results and Discussion
4.1. Performance Evaluation of the DL Models
4.2. Comparison with Literature Results
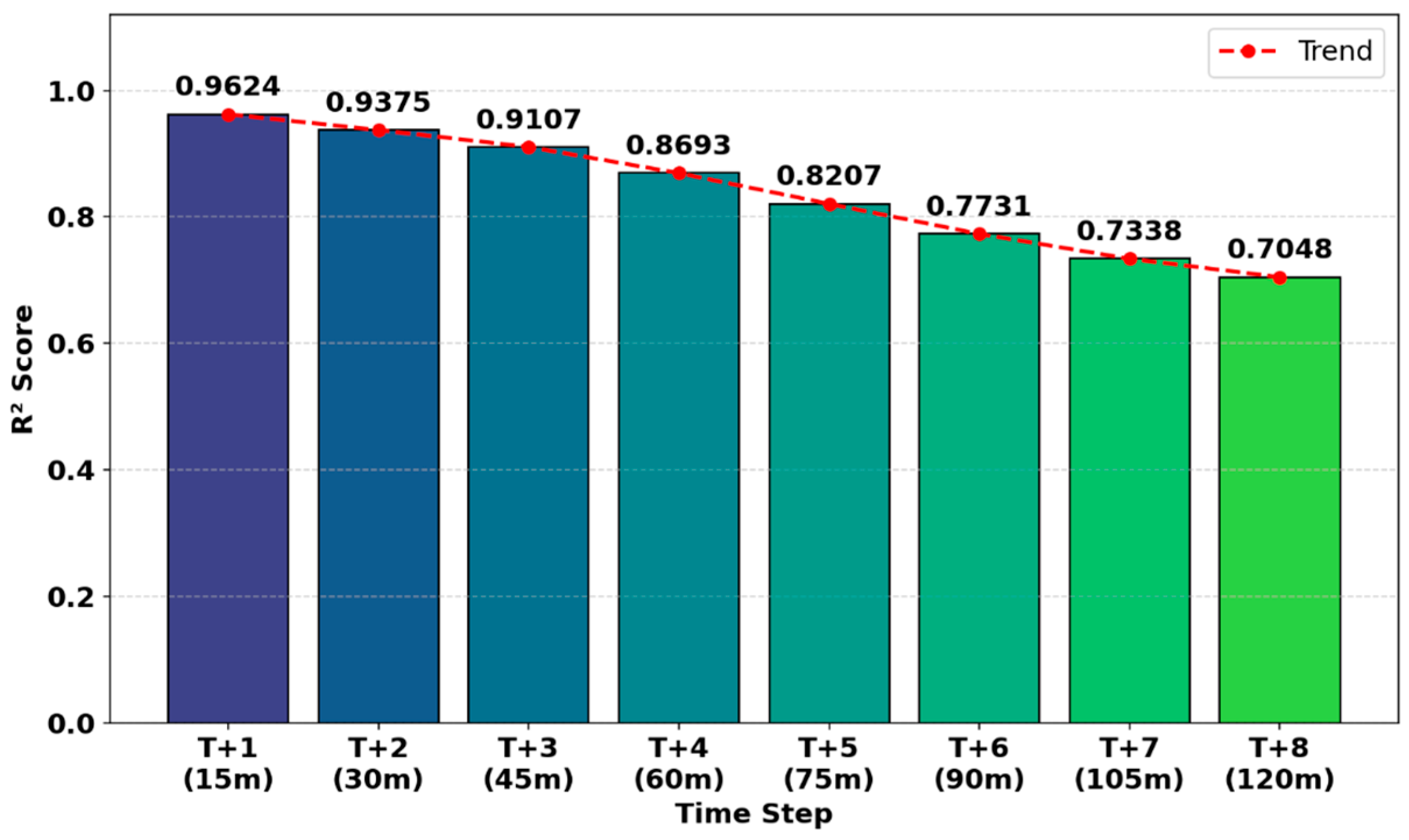
4.3. Dependence on Lead Time
5. Conclusions and Future Work
- This study evaluated the performance of six machine learning models for extreme rainfall prediction using different Automatic Weather Station network topologies. The proposed linear geometry-based approach using the Bi-GRU model emerged as the most consistently accurate model, achieving a greater value of training R2 of 0.9548, validation R2 of 0.9426, and a small RMSE of 2.2120. Comparison shows significant improvements over earlier studies. These enhanced prediction skills can help disaster managers in making timely and informed decisions by providing more accurate forecasting of extreme rainfall events with two hours of lead time.
- The Bi-GRU model with a linear topology achieved the highest predictive performance, surpassing triangular, quadrilateral, and circular station layouts. This result indicates that strategically aligned but fewer stations can outperform larger yet suboptimal placed networks, even at the (15–25 km) spacing required to capture cloudburst signatures. The linear configuration, particularly along the Pavana River basin, effectively represented orographic lifting and wind-channeling effects of the western Deccan Plateau, thereby enhancing precipitation forecasting accuracy.
- Though state-of-the-art in time series modeling, the Transformer model showed inconsistent performance in localized rainfall prediction, with high R2 but elevated MAPE, likely due to redundancy or noise from dense station networks with much additional information. Further investigations are needed to unlock the full capability that requires tailored adaptation to meteorological datasets and data quality and redundancy handling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASL | Above Sea Level |
| CB | Cloudburst |
| COE | Center of Excellence |
| COEP | College of Engineering Pune |
| DL | Deep Learning |
| GPRS | General Pocket Radio Service |
| GRU | Gated Recurrent Unit |
| IMD | India Meteorological Department |
| IOT | Internet of Things |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MCB | Mini-Cloudburst |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| NDC | National Data Centre |
| NWP | Numerical Weather Prediction |
| QA | Quality Analysis |
| QC | Quality Check |
| RNN | Recurrent Neural Network |
| RMSE | Root Mean Squared Error |
| TDMA | Time Division Multiple Access |
| WMO | World Meteorological Organization |
Appendix A. Deep Learning Model Architecture
Appendix A.1. Recurrent Neural Networks (RNNs)
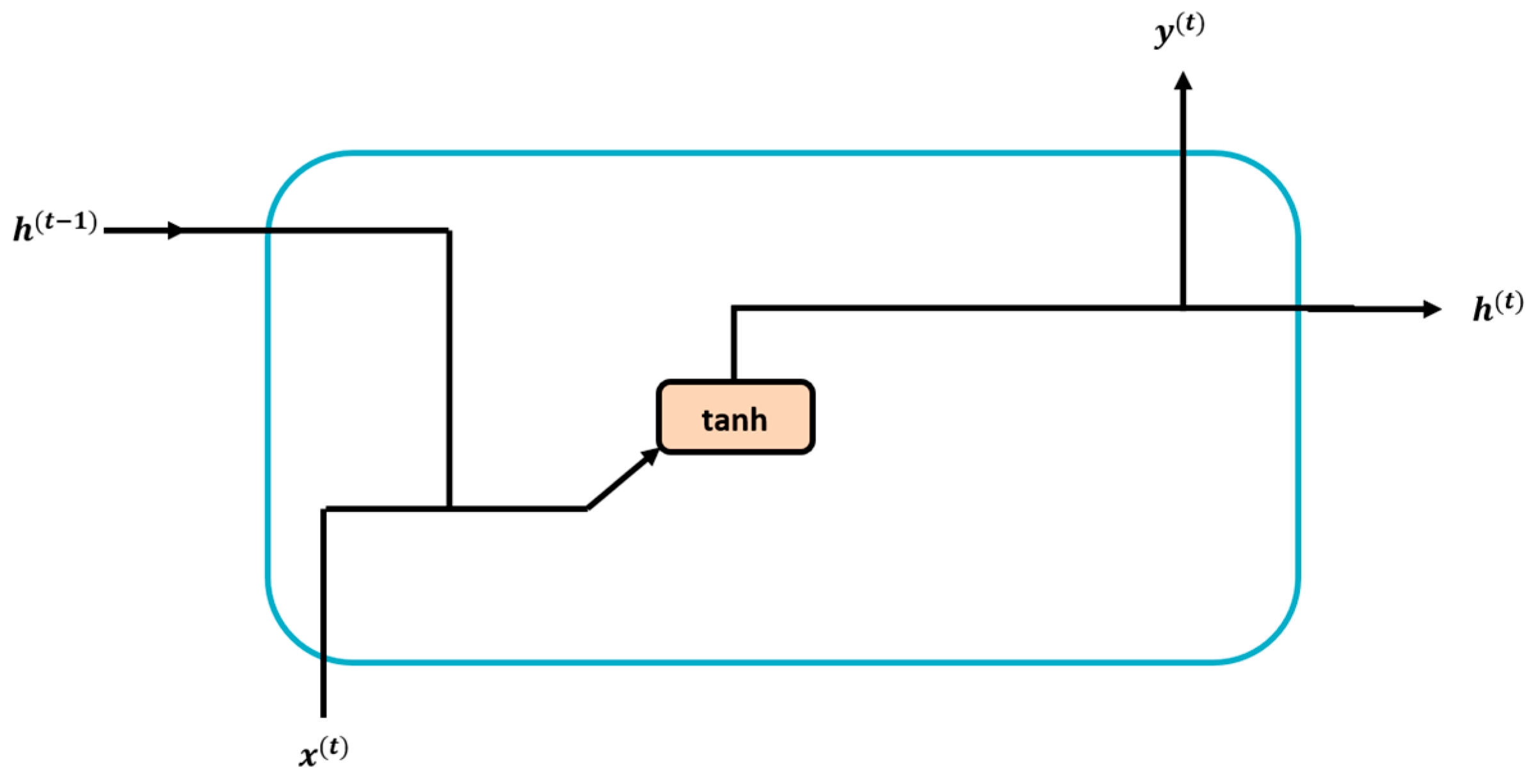
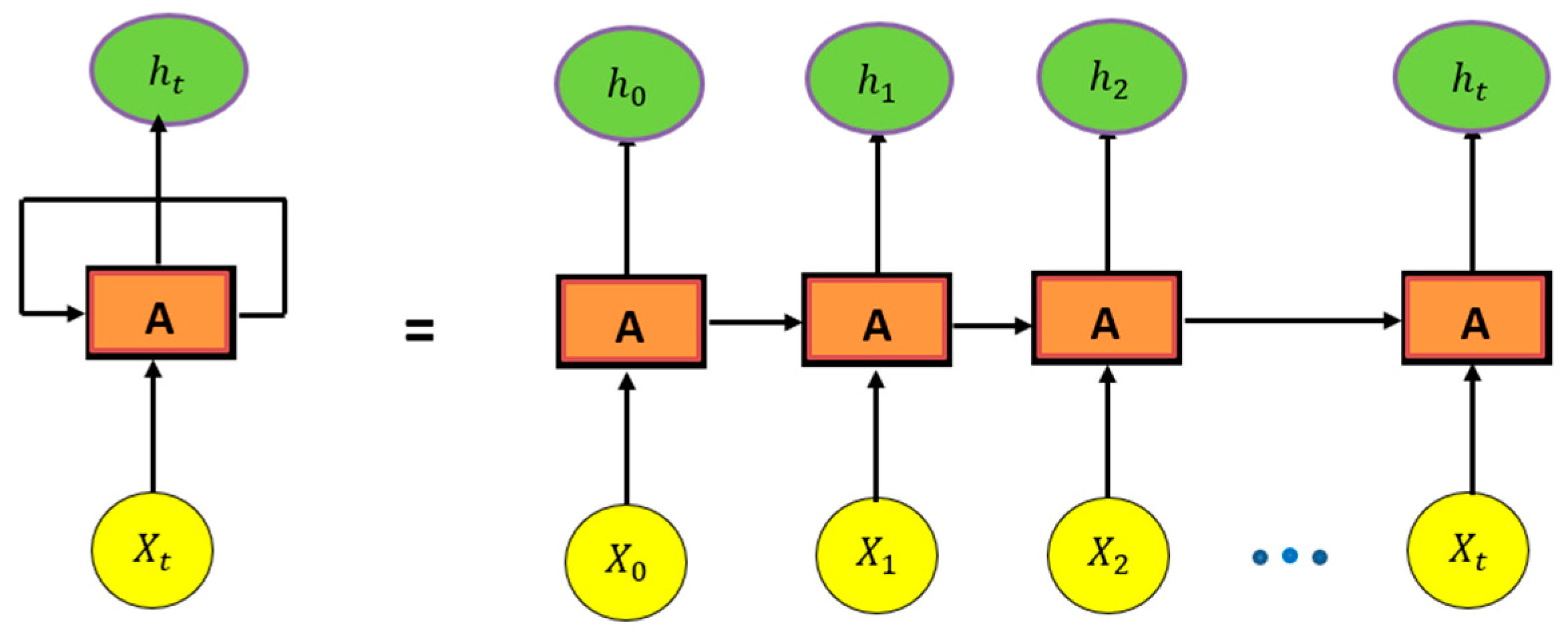
Appendix A.2. Long-Short-Term-Memory (LSTM)
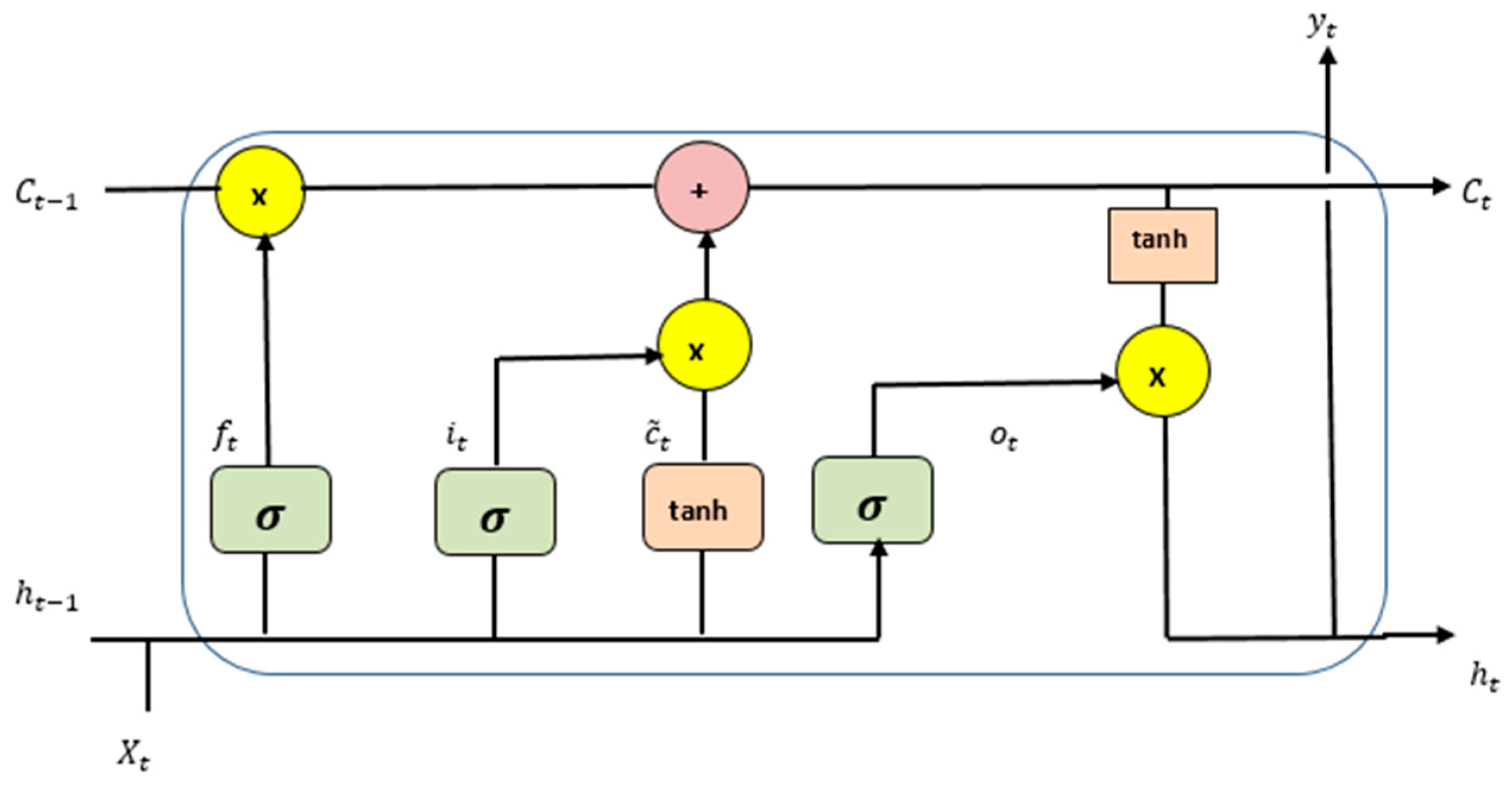
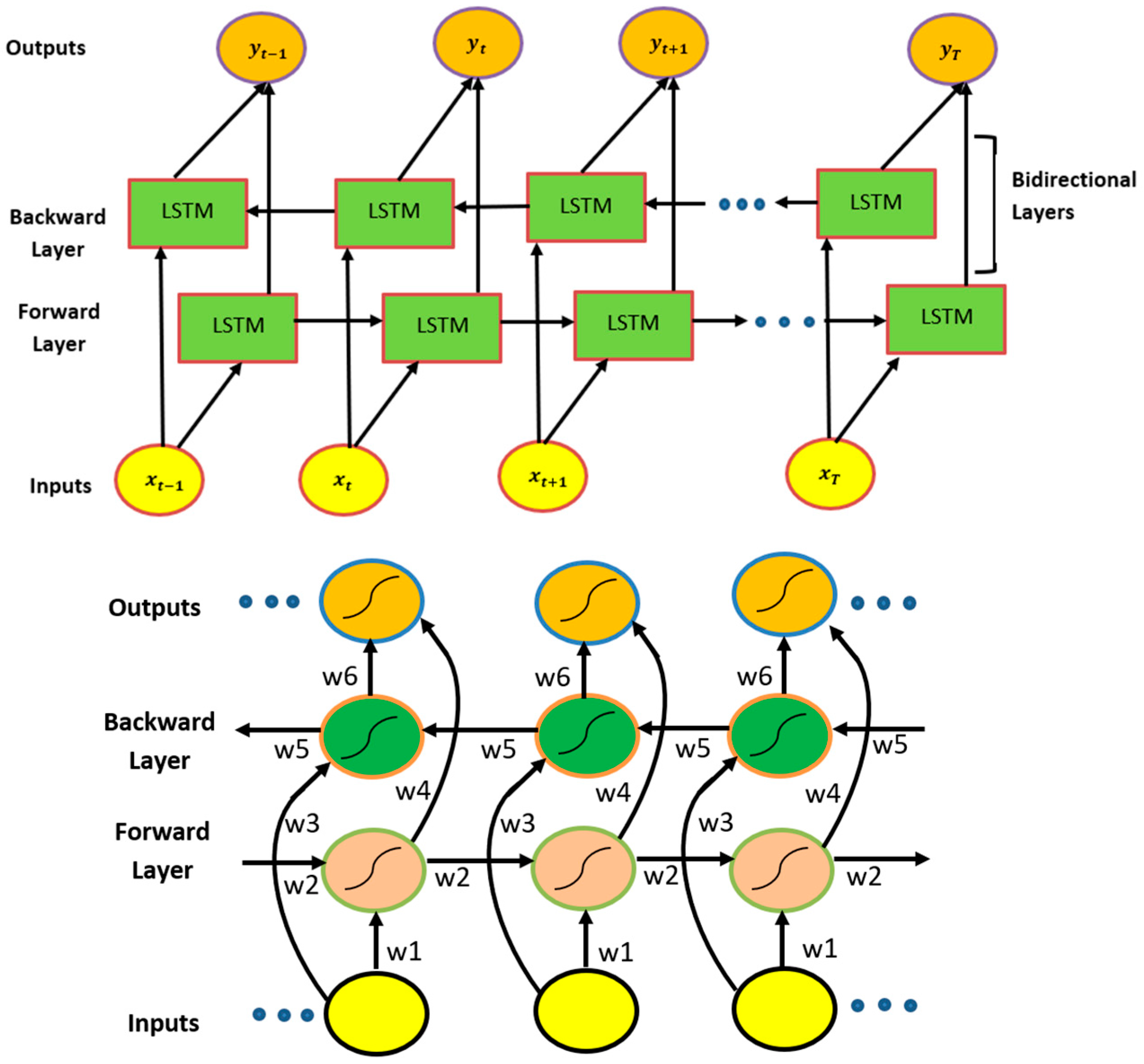
Appendix A.3. Bidirectional-Long-Short-Term-Memory (Bi-LSTM)
Appendix A.4. Gated-Recurrent-Unit (GRU)

Appendix A.5. Bidirectional Gated Recurrent Unit (Bi-GRU)
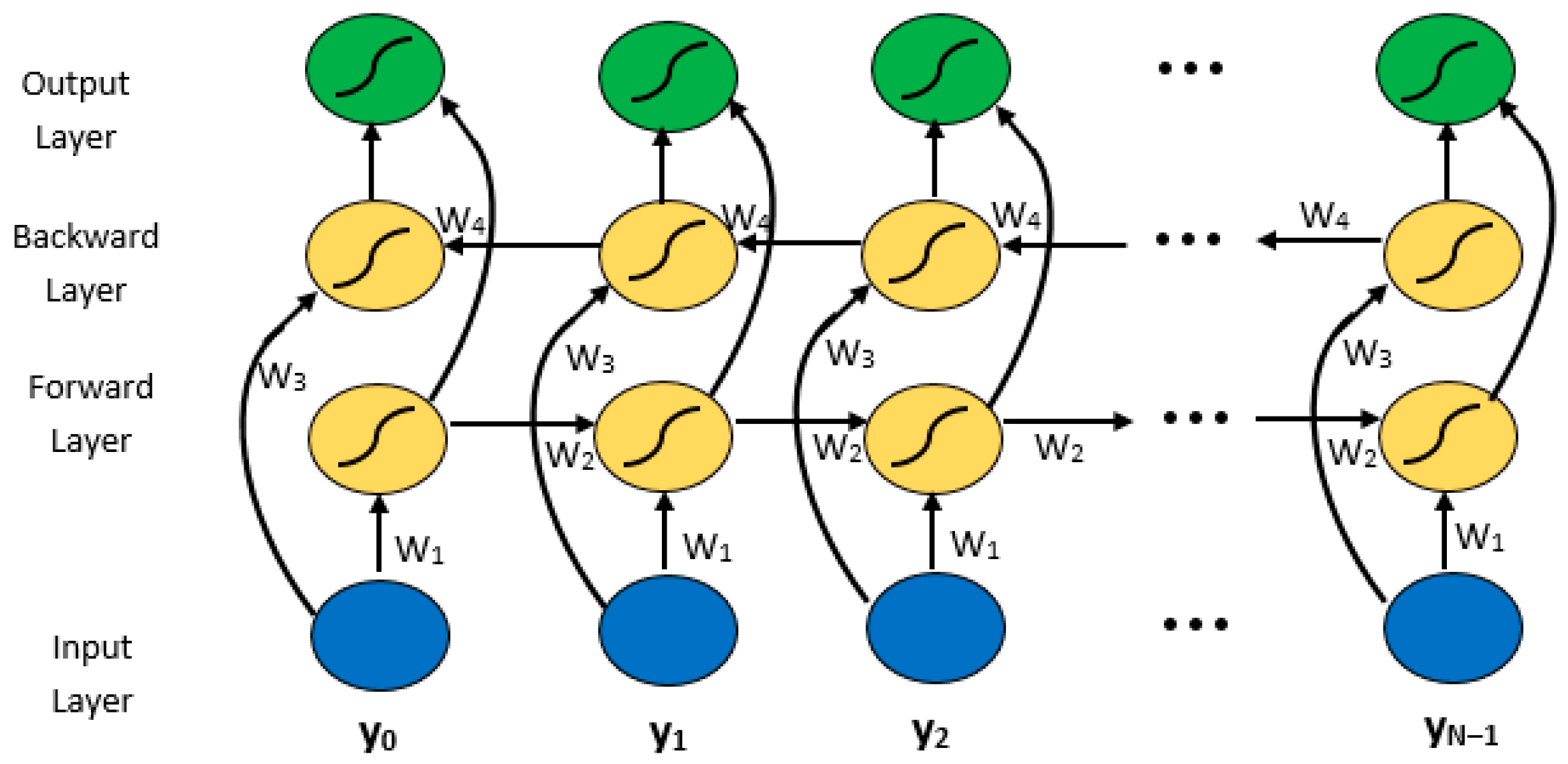
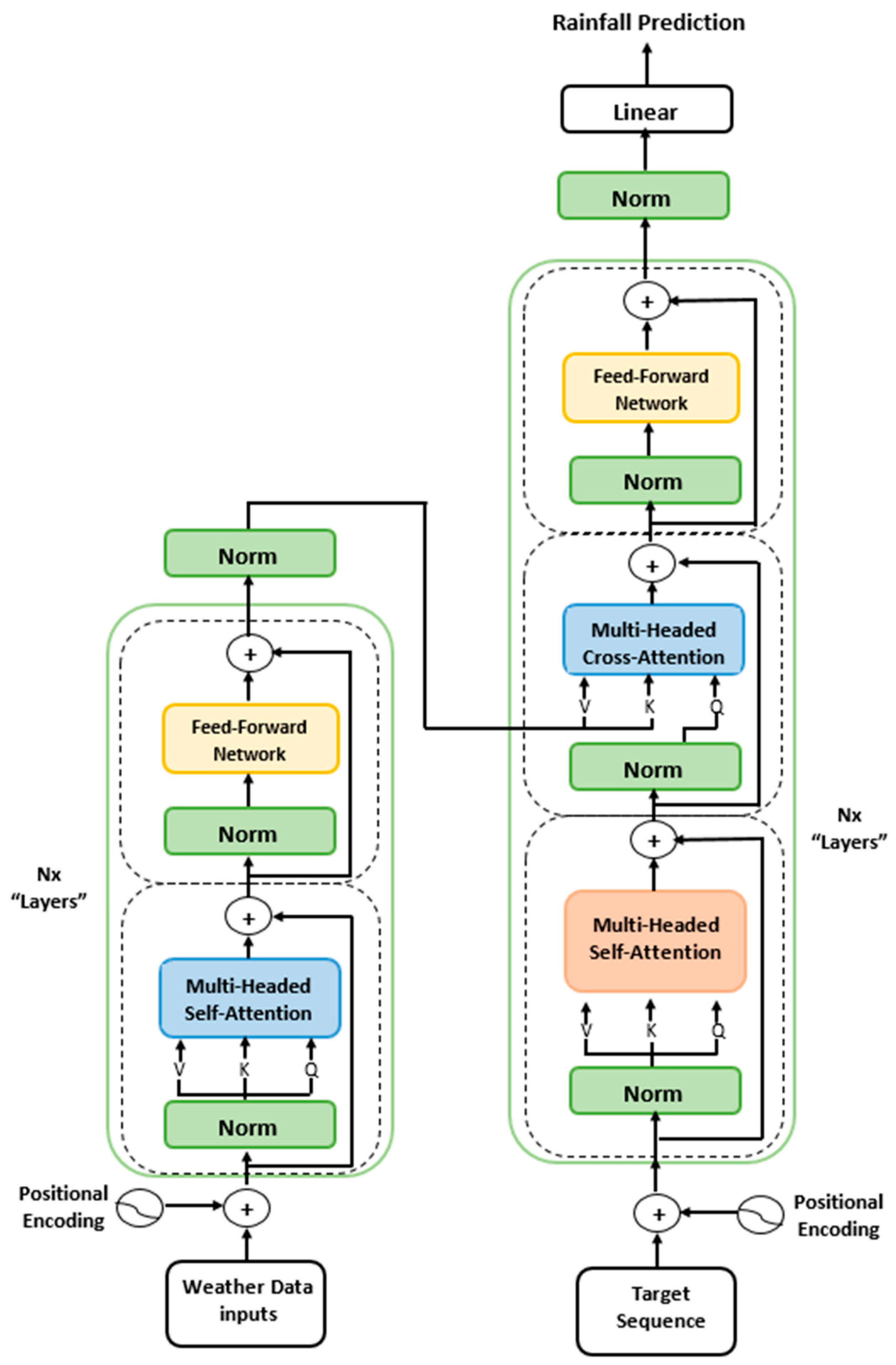
Appendix A.6. Transformer Model
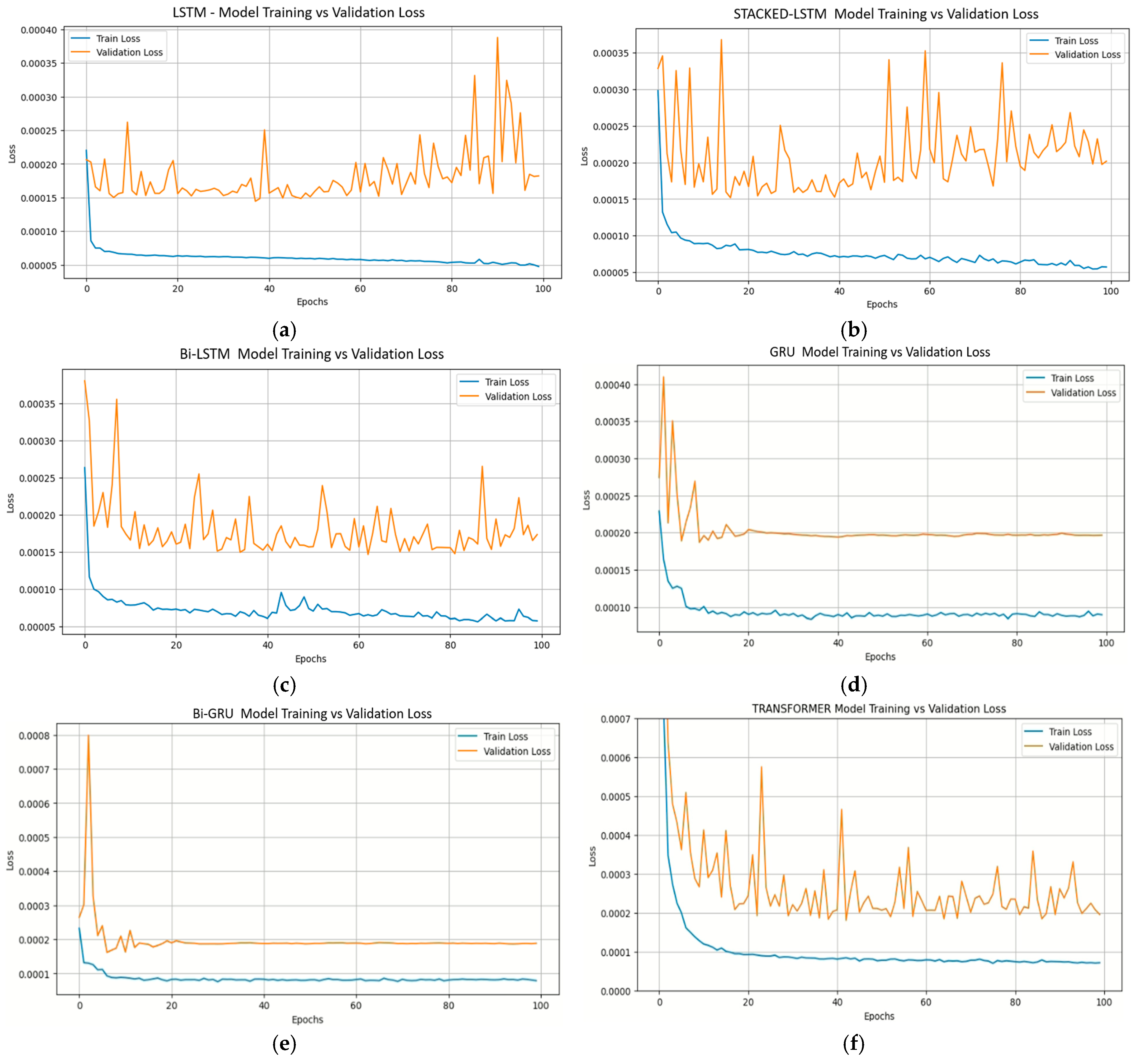
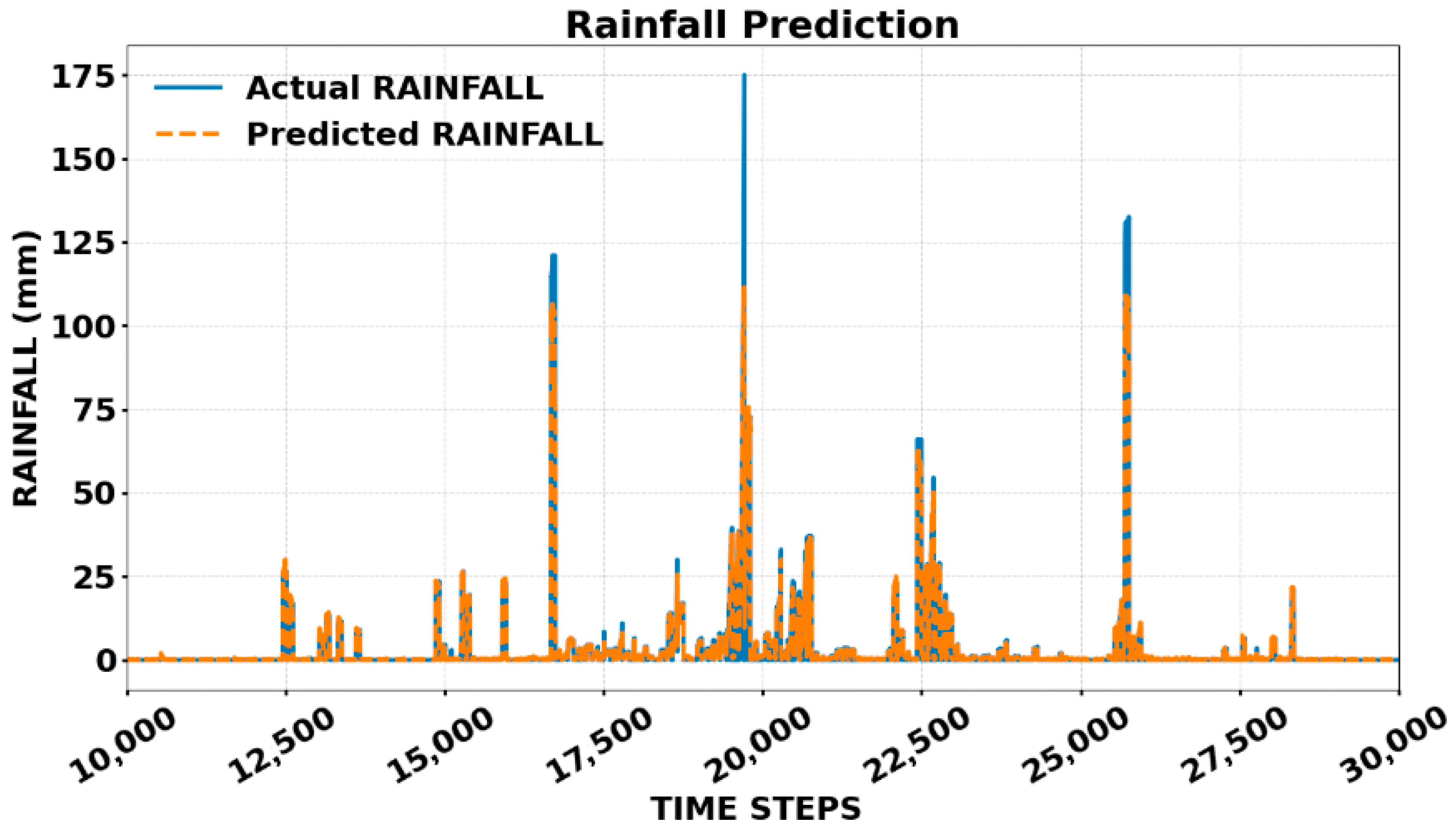
Appendix A.7. Model Training and Validation
| MODEL | PERFORMANCE |
|---|---|
| LSTM | Performs decently but not best-in-class |
| STACKED-LSTM | Inconsistent, often high MAPE |
| Bi-LSTM | High R2, competitive with Bi-GRU, especially in CIRCULAR Topology |
| GRU | Performs well, often just behind Bi-GRU |
| Bi-GRU | Best R2 and lowest RMSE in many cases (especially LINEAR, TRIANGULAR) |
| TRANSFORMER | Most inconsistent: sometimes high R2 but very high MAPE |
| STACKED-LSTM | Inconsistent, often high MAPE |
Appendix B. Performance Comparison for Deep Learning Models Across Different Geometrical Configurations for Rainfall Prediction: MAE vs. Dataset, MAPE% vs. Dataset, MSE vs. Dataset
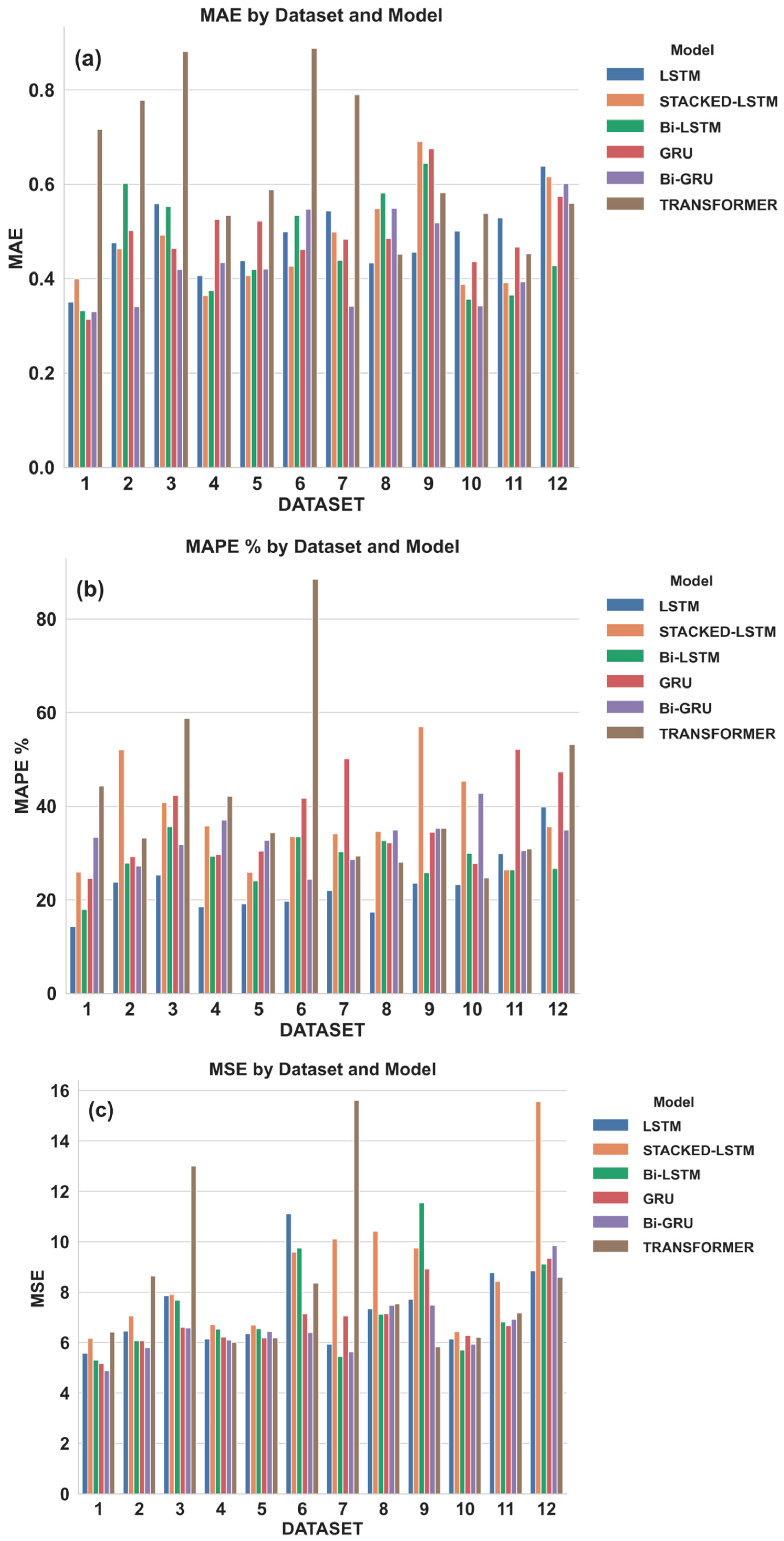
Appendix C. Performance Evaluation Deep Learning Models and Topologies
| S. No. | Geometry | Model | RMSE | MAE | MSE | MAPE% | R2 |
|---|---|---|---|---|---|---|---|
| 1 | Linear | LSTM | 2.3624 | 0.3503 | 5.5808 | 14.27 | 0.9485 |
| STACKED-LSTM | 2.4852 | 0.3995 | 6.1761 | 25.98 | 0.9430 | ||
| Bi-LSTM | 2.3045 | 0.3324 | 5.3108 | 17.94 | 0.9510 | ||
| GRU | 2.2762 | 0.3135 | 5.1812 | 24.60 | 0.9522 | ||
| Bi-GRU | 2.2120 | 0.3300 | 4.8932 | 33.38 | 0.9548 | ||
| TRANSFORMER | 2.5322 | 0.7164 | 6.4121 | 44.28 | 0.9408 | ||
| 2 | Linear | LSTM | 2.5401 | 0.4758 | 6.4520 | 23.82 | 0.9404 |
| STACKED-LSTM | 2.6564 | 0.4632 | 7.0565 | 52.02 | 0.9349 | ||
| Bi-LSTM | 2.4649 | 0.6026 | 6.0759 | 27.88 | 0.9439 | ||
| GRU | 2.4635 | 0.5016 | 6.0688 | 29.24 | 0.9440 | ||
| Bi-GRU | 2.4103 | 0.3403 | 5.8096 | 27.26 | 0.9464 | ||
| TRANSFORMER | 2.9407 | 0.7782 | 8.6478 | 33.20 | 0.9202 | ||
| 3 | Triangular | LSTM | 2.8059 | 0.5586 | 7.8729 | 25.30 | 0.9273 |
| STACKED-LSTM | 2.8131 | 0.4926 | 7.9133 | 40.85 | 0.9269 | ||
| Bi-LSTM | 2.7727 | 0.5528 | 7.6881 | 35.67 | 0.9290 | ||
| GRU | 2.5708 | 0.4644 | 6.6088 | 42.26 | 0.9390 | ||
| Bi-GRU | 2.5666 | 0.4195 | 6.5876 | 31.83 | 0.9392 | ||
| TRANSFORMER | 3.6062 | 0.8816 | 13.005 | 58.80 | 0.8799 | ||
| 4 | Triangular | LSTM | 2.4805 | 0.4067 | 6.1527 | 18.54 | 0.9441 |
| STACKED-LSTM | 2.5922 | 0.3643 | 6.7195 | 35.78 | 0.9390 | ||
| Bi-LSTM | 2.5579 | 0.3748 | 6.5426 | 29.38 | 0.9406 | ||
| GRU | 2.4957 | 0.5252 | 6.2285 | 29.73 | 0.9434 | ||
| Bi-GRU | 2.4719 | 0.4344 | 6.1102 | 37.11 | 0.9445 | ||
| TRANSFORMER | 2.4522 | 0.5343 | 6.0131 | 42.10 | 0.9454 | ||
| 5 | Quadrilateral | LSTM | 2.5216 | 0.4382 | 6.3587 | 19.19 | 0.9413 |
| STACKED-LSTM | 2.5895 | 0.4065 | 6.7053 | 25.91 | 0.9381 | ||
| Bi-LSTM | 2.5614 | 0.4193 | 6.5606 | 24.07 | 0.9394 | ||
| GRU | 2.4889 | 0.5227 | 6.1945 | 30.43 | 0.9428 | ||
| Bi-GRU | 2.5367 | 0.4201 | 6.4346 | 32.78 | 0.9406 | ||
| TRANSFORMER | 2.4884 | 0.5884 | 6.1919 | 34.37 | 0.9428 | ||
| 6 | Quadrilateral | LSTM | 3.3339 | 0.4991 | 11.115 | 19.69 | 0.8974 |
| STACKED-LSTM | 3.0963 | 0.4267 | 9.5868 | 33.52 | 0.9115 | ||
| Bi-LSTM | 3.1238 | 0.5341 | 9.7583 | 33.46 | 0.9099 | ||
| GRU | 2.6731 | 0.4620 | 7.1453 | 41.67 | 0.9340 | ||
| Bi-GRU | 2.5305 | 0.5479 | 6.4034 | 24.44 | 0.9409 | ||
| TRANSFORMER | 2.8931 | 0.8883 | 8.3702 | 88.55 | 0.9227 | ||
| 7 | Circular | LSTM | 2.4360 | 0.5438 | 5.9339 | 22.08 | 0.9452 |
| STACKED-LSTM | 3.1797 | 0.4989 | 10.110 | 34.16 | 0.9067 | ||
| Bi-LSTM | 2.3337 | 0.4390 | 5.4463 | 30.28 | 0.9497 | ||
| GRU | 2.6579 | 0.4835 | 7.0642 | 50.14 | 0.9348 | ||
| Bi-GRU | 2.3738 | 0.3412 | 5.6349 | 28.62 | 0.9480 | ||
| TRANSFORMER | 3.9518 | 0.7899 | 15.617 | 29.39 | 0.8558 | ||
| 8 | Circular | LSTM | 2.7107 | 0.4333 | 7.3482 | 17.37 | 0.9322 |
| STACKED-LSTM | 3.2281 | 0.5484 | 10.420 | 34.69 | 0.9038 | ||
| Bi-LSTM | 2.6706 | 0.5816 | 7.1321 | 32.74 | 0.9342 | ||
| GRU | 2.6742 | 0.4857 | 7.1513 | 32.24 | 0.9340 | ||
| Bi-GRU | 2.7343 | 0.5497 | 7.4764 | 34.98 | 0.9310 | ||
| TRANSFORMER | 2.7447 | 0.4518 | 7.5335 | 28.06 | 0.9305 | ||
| 9 | Circular | LSTM | 2.7794 | 0.4562 | 7.7253 | 23.63 | 0.9287 |
| STACKED-LSTM | 3.1237 | 0.6906 | 9.7573 | 57.03 | 0.9099 | ||
| Bi-LSTM | 3.3988 | 0.6445 | 11.551 | 25.84 | 0.8934 | ||
| GRU | 2.9888 | 0.6755 | 8.9331 | 34.47 | 0.9175 | ||
| Bi-GRU | 2.7356 | 0.5185 | 7.4836 | 35.33 | 0.9309 | ||
| TRANSFORMER | 2.4166 | 0.5821 | 5.8401 | 35.34 | 0.9461 | ||
| 10 | Circular | LSTM | 2.4798 | 0.5006 | 6.1492 | 23.28 | 0.9432 |
| STACKED-LSTM | 2.5361 | 0.3883 | 6.4318 | 45.34 | 0.9406 | ||
| Bi-LSTM | 2.3905 | 0.3566 | 5.7143 | 29.99 | 0.9472 | ||
| GRU | 2.5084 | 0.4362 | 6.2923 | 27.75 | 0.9419 | ||
| Bi-GRU | 2.4359 | 0.3423 | 5.9334 | 42.73 | 0.9452 | ||
| TRANSFORMER | 2.4932 | 0.5385 | 6.2161 | 24.70 | 0.9426 | ||
| 11 | Circular | LSTM | 2.9640 | 0.5287 | 8.7854 | 29.94 | 0.9189 |
| STACKED-LSTM | 2.9042 | 0.3911 | 8.4343 | 26.45 | 0.9221 | ||
| Bi-LSTM | 2.6139 | 0.3651 | 6.8325 | 26.44 | 0.9369 | ||
| GRU | 2.5842 | 0.4671 | 6.6783 | 52.13 | 0.9383 | ||
| Bi-GRU | 2.6316 | 0.3934 | 6.9252 | 30.54 | 0.9361 | ||
| TRANSFORMER | 2.6790 | 0.4525 | 7.1772 | 30.92 | 0.9337 | ||
| 12 | Circular | LSTM | 2.9764 | 0.6382 | 8.8592 | 39.91 | 0.9182 |
| STACKED-LSTM | 3.9451 | 0.6159 | 15.563 | 35.68 | 0.8563 | ||
| Bi-LSTM | 3.0196 | 0.4275 | 9.1182 | 26.74 | 0.9158 | ||
| GRU | 3.0586 | 0.5747 | 9.3549 | 47.31 | 0.9136 | ||
| Bi-GRU | 3.1390 | 0.6020 | 9.8534 | 34.96 | 0.9090 | ||
| TRANSFORMER | 2.9312 | 0.5595 | 8.5919 | 53.18 | 0.9207 |
References
- Chaluvadi, R.; Varikoden, H.; Mujumdar, M.; Ingle, S.T.; Kuttippurath, J. Changes in large-scale circulation over the Indo-Pacific region and its association with the 2018 Kerala extreme rainfall event. Atmos. Res. 2021, 263, 105809. [Google Scholar] [CrossRef]
- Dimri, A.P.; Chevuturi, A.; Niyogi, D.; Thayyen, R.J.; Ray, K.; Tripathi, S.N.; Pandey, A.K.; Mohanty, U.C. Cloudbursts in Indian Himalayas: A Review. Earth-Sci. Rev. 2017, 168, 1–23. [Google Scholar] [CrossRef]
- Deshpande, N.R.; Kothawale, D.R.; Kumar, V.; Kulkarni, J.R. Statistical characteristics of cloudburst and mini-cloudburst events during the monsoon season in India. Int. J. Climatol. 2018, 38, 4172–4188. [Google Scholar] [CrossRef]
- India Meteorological Department (IMD). Standard Operating Procedure—Weather Forecasting and Warning Services; Ministry of Earth Sciences: New Delhi, India, 2021. Available online: https://mausam.imd.gov.in/imd_latest/contents/pdf/forecasting_sop.pdf (accessed on 20 September 2025).
- Endalie, D.; Haile, G.; Taye, W. Deep learning model for daily rainfall prediction: Case study of Jimma, Ethiopia. Water Supply 2022, 22, 3448–3461. [Google Scholar] [CrossRef]
- Aguasca-Colomo, R.; Castellanos-Nieves, D.; Méndez, M. Comparative analysis of rainfall prediction models using machine learning in islands with complex orography: Tenerife Island. Appl. Sci. 2019, 9, 4931. [Google Scholar] [CrossRef]
- Baljon, M.; Sharma, S.K. Rainfall prediction rate in Saudi Arabia using improved machine learning techniques. Water 2023, 15, 826. [Google Scholar] [CrossRef]
- Singh, B.; Thapliyal, R. Cloudburst events observed over Uttarakhand during monsoon season 2017 and their analysis. Mausam 2022, 73, 91–104. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Tripathi, S.; Srivastava, R.; Misra, A. Observation-and numerical-analysis-based dynamics of the Uttarkashi cloudburst. Ann. Geophys. 2015, 33, 671–686. [Google Scholar] [CrossRef]
- Mishra, P.; Al Khatib, A.M.G.; Yadav, S.; Ray, S.; Lama, A.; Kumari, B.; Yadav, R. Modeling and forecasting rainfall patterns in India: A time series analysis with XGBoost algorithm. Environ. Earth Sci. 2024, 83, 163. [Google Scholar] [CrossRef]
- Bouach, A. Artificial neural networks for monthly precipitation prediction in north-west Algeria: A case study in the Oranie-Chott-Chergui basin. J. Water Clim. Change 2024, 15, 582–592. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Zhang, C.; Li, N. Machine Learning Methods for Weather Forecasting: A Survey. Atmosphere 2025, 16, 82. [Google Scholar] [CrossRef]
- Dawoodi, H.H.; Patil, M.P. Rainfall prediction for north Maharashtra, India using advanced machine learning models. Indian J. Sci. Technol. 2023, 16, 956–966. [Google Scholar] [CrossRef]
- Rahman, A.U.; Abbas, S.; Gollapalli, M.; Ahmed, R.; Aftab, S.; Ahmad, M.; Khan, M.A.; Mosavi, A. Rainfall prediction system using machine learning fusion for smart cities. Sensors 2022, 22, 3504. [Google Scholar] [CrossRef] [PubMed]
- Ojo, O.S.; Ogunjo, S.T. Machine learning models for prediction of rainfall over Nigeria. Sci. Afr. 2022, 16, e01246. [Google Scholar] [CrossRef]
- Barrera-Animas, A.Y.; Oyedele, L.O.; Bilal, M.; Akinosho, T.D.; Delgado, J.M.D.; Akanbi, L.A. Rainfall prediction: A comparative analysis of modern machine learning algorithms for time-series forecasting. Mach. Learn. Appl. 2022, 7, 100204. [Google Scholar] [CrossRef]
- Frame, J.M.; Kratzert, F.; Klotz, D.; Gauch, M.; Shalev, G.; Gilon, O.; Qualls, L.M.; Gupta, H.V.; Nearing, G.S. Deep learning rainfall–runoff predictions of extreme events. Hydrol. Earth Syst. Sci. 2022, 26, 3377–3392. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Wangwongchai, A.; Dechpichai, P.; Ahmad, S. Potential of artificial intelligence-based techniques for rainfall forecasting in Thailand: A comprehensive review. Water 2023, 15, 2979. [Google Scholar] [CrossRef]
- Shiri, F.M.; Perumal, T.; Mustapha, N.; Mohamed, R. A Comprehensive Overview and Comparative Analysis on Deep Learning Models. J. Artif. Intell. 2024, 6, 301–360. [Google Scholar] [CrossRef]
- Sarasa-Cabezuelo, A. Prediction of rainfall in Australia using machine learning. Information 2022, 13, 163. [Google Scholar] [CrossRef]
- Shah, N.H.; Priamvada, A.; Shukla, B.P. Validation of satellite-based cloudburst alerts: An assessment of location precision over Uttarakhand, India. J. Earth Syst. Sci. 2023, 132, 161. [Google Scholar] [CrossRef]
- Ranalkar, M.R.; Anjan, A.; Mishra, R.P.; Mali, R.R.; Krishnaiah, S. Development of operational near real-time network monitoring and quality control system for implementation at AWS data receiving earth station. Mausam 2015, 66, 93–106. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668. [Google Scholar] [CrossRef]
- Priatna, M.A.; Esmeralda, C.D. Precipitation prediction using recurrent neural networks and long short-term memory. Telkomnika Telecommun. Comput. Electron. Control 2020, 18, 2525–2532. [Google Scholar] [CrossRef]
- Tuysuzoglu, G.; Birant, K.U.; Birant, D. Rainfall prediction using an ensemble machine learning model based on K-stars. Sustainability 2023, 15, 5889. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guide to the WMO Integrated Processing and Prediction System, (WMO-No. 305); WMO: Geneva, Switzerland, 2023; Available online: https://library.wmo.int/records/item/28978-guide-to-the-wmo-integrated-processing-and-prediction-system?offset=9 (accessed on 20 September 2025).
- Kumar, G.; Chand, S.; Mali, R.R.; Kundu, S.K.; Baxla, A.K. In-situ observational network for extreme weather events in India. Mausam 2016, 67, 67–76. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guide to Instruments and Methods of Observation, (WMO-No. 8); WMO: Geneva, Switzerland, 2021; Available online: https://library.wmo.int/records/item/41650-guide-to-instruments-and-methods-of-observation?language_id=&offset=1 (accessed on 20 September 2025).
- Patro, B.S.; Bartakke, P.P. Quality Control (QC) and Quality Assurance (QA) Procedures for Meteorological Data from Automatic Weather Stations. In Proceedings of the 2025 4th International Conference on Range Technology (ICORT), Chandipur, India, 6–8 March 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Dotse, S.Q. Deep learning–based long short-term memory recurrent neural networks for monthly rainfall forecasting in Ghana, West Africa. Theor. Appl. Climatol. 2024, 155, 4. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Kisi, O.; Alsulamy, S.; Khedher, K.M.; Salem, M.A. A comparative study of machine learning models for daily and weekly rainfall forecasting. Water Resour. Manag. 2025, 39, 271–290. [Google Scholar] [CrossRef]
- Sham, F.A.F.; El-Shafie, A.; Jaafar, W.Z.B.W.; Adarsh, S.; Sherif, M.; Ahmed, A.N. Improving rainfall forecasting using deep learning data fusing model approach for observed and climate change data. Sci. Rep. 2025, 15, 27872. [Google Scholar] [CrossRef]
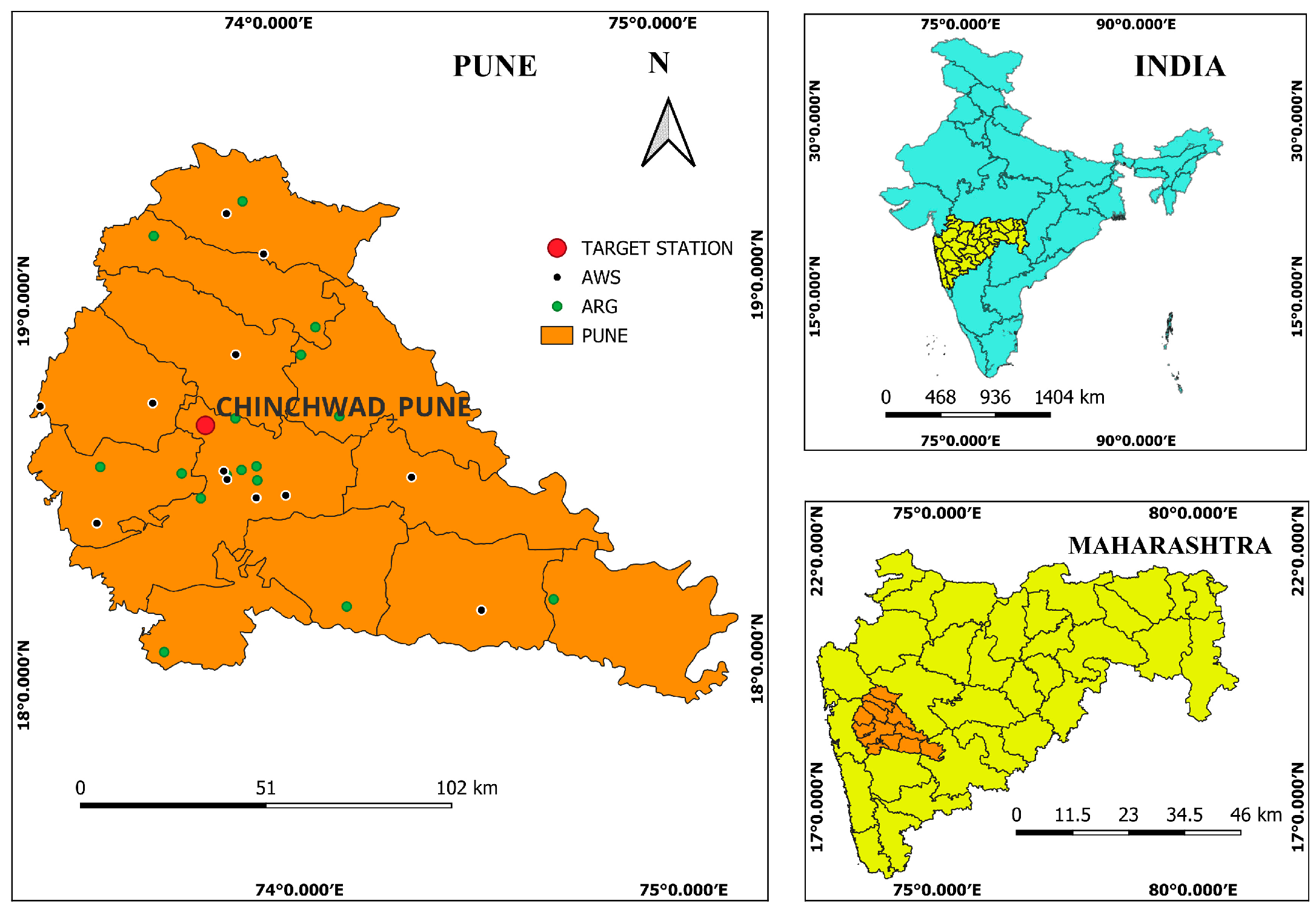








| Station Name | Latitude | Longitude | Elevation | Type |
|---|---|---|---|---|
| NIMGIRI | 19.2092 | 73.8725 | 619.0 | AWS |
| SHIVAJINAGAR1 | 18.5386 | 73.8420 | 559.0 | AWS |
| LAVASA | 18.4144 | 73.5069 | 687.3 | AWS |
| DAPODI | 18.6032 | 73.8541 | 563.2 | AWS |
| HADAPSAR | 18.4659 | 73.9244 | 618.7 | AWS |
| DAUND | 18.5056 | 74.3304 | 554.0 | AWS |
| LONAVALA | 18.7240 | 73.3697 | 620.8 | AWS |
| HAVELI | 18.4697 | 74.0013 | 563.0 | AWS |
| NARAYANGOAN | 19.1003 | 73.9655 | 694.5 | AWS |
| BARAMATI | 18.1530 | 74.5003 | 569.7 | AWS |
| PASHAN1 | 18.5167 | 73.8500 | 577.0 | AWS |
| RAJGURUNAGAR | 18.8410 | 73.8840 | 598.1 | AWS |
| TALEGAON | 18.7220 | 73.6632 | 635.8 | AWS |
| BALLALWADI | 19.2396 | 73.9155 | 719.8 | ARG |
| KOREGOANPARK | 18.5400 | 73.8886 | 546.2 | ARG |
| CHINCHWAD | 18.6595 | 73.7987 | 588.3 | ARG |
| GIRIVAN | 18.5607 | 73.5211 | 750.0 | ARG |
| BHOR | 18.0728 | 73.6706 | 773.0 | ARG |
| JUNNAR | 19.2070 | 73.8679 | 619.0 | ARG |
| KHADAKWADI | 18.9052 | 74.0938 | 585.0 | ARG |
| LAVALE | 18.5363 | 73.7325 | 577.0 | ARG |
| MAGARPATTA | 18.5115 | 73.9285 | 618.7 | ARG |
| AMBEGAON | 19.1574 | 73.6811 | 778.7 | ARG |
| PASHAN2 | 18.5383 | 73.8045 | 586.4 | ARG |
| SHIVANE | 18.4700 | 73.7800 | 586.4 | ARG |
| INDAPUR | 18.1748 | 74.6890 | 386.2 | ARG |
| SHIRUR | 18.8344 | 74.0536 | 667.3 | ARG |
| DUDULGAON | 18.6751 | 73.8772 | 574.7 | ARG |
| SHIVAJINAGAR2 | 18.5286 | 73.8493 | 559.0 | ARG |
| DHAMDHERE | 18.6710 | 74.1480 | 562.4 | ARG |
| KHED | 18.9390 | 73.7744 | 742.7 | ARG |
| WADGAONSHERI | 18.5482 | 73.9278 | 618.7 | ARG |
| WPURANDAR | 18.1748 | 74.1498 | 585.0 | ARG |
| DATASETS | GEOMETRY | AWS/ARG | STATION |
|---|---|---|---|
| 1 | LINEAR | ARG | CHINCHWAD |
| ARG | LAVALE | ||
| AWS | RAJGURUNAGAR | ||
| 2 | LINEAR | ARG | CHINCHWAD |
| AWS | SHIVAJINAGAR1 | ||
| AWS | PASHAN1 | ||
| 3 | TRIANGULAR | ARG | CHINCHWAD |
| AWS | TALEGAN | ||
| ARG | LAVALE | ||
| ARG | DHAMDHERE | ||
| 4 | TRIANGULAR | ARG | CHINCHWAD |
| AWS | SHIVAJINAGAR1 | ||
| AWS | TALEGAON | ||
| AWS | RAJGURUNAGAR | ||
| 5 | QUADRILATERAL | ARG | CHINCHWAD |
| ARG | LAVALE | ||
| ARG | WADGAONSHERI | ||
| AWS | TALEGAON | ||
| AWS | RAJGURUNAGAR | ||
| 6 | QUADRILATERAL | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | GIRIVAN | ||
| AWS | PASHAN1 | ||
| AWS | DHAMDHERE | ||
| 7 | CIRCULAR | ARG | CHINCHWAD |
| ARG | TALEGAON | ||
| ARG | LAVALE | ||
| AWS | SHIVAJINAGAR1 | ||
| 8 | CIRCULAR | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | LAVALE | ||
| AWS | SHIVAJINAGAR1 | ||
| ARG | MAGARPATTA | ||
| ARG | SHIVANE | ||
| AWS | RAJGURUNAGAR | ||
| 9 | CIRCULAR | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | LAVALE | ||
| AWS | SHIVAJINAGAR1 | ||
| ARG | MAGARPATTA | ||
| ARG | SHIVANE | ||
| AWS | RAJGURUNAGAR | ||
| ARG | GIRIVAN | ||
| ARG | DHAMDHERE | ||
| 10 | CIRCULAR | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | LAVALE | ||
| 11 | CIRCULAR | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | LAVALE | ||
| ARG | GIRIVAN | ||
| ARG | SHIVANE | ||
| AWS | PASHAN1 | ||
| ARG | MAGARPATTA | ||
| 12 | CIRCULAR | ARG | CHINCHWAD |
| AWS | TALEGAON | ||
| ARG | LAVALE | ||
| ARG | GIRIVAN | ||
| ARG | SHIVANE | ||
| ARG | MAGARPATTA | ||
| AWS | RAJGURUNAGAR | ||
| AWS | PASHAN1 | ||
| AWS | DHAMDHERE |
| Sr. No. | Terminology | Rainfall Ranges in mm | Number of Events |
|---|---|---|---|
| 1 | Very Light Rainfall | Trace—2.4 | 256 |
| 2 | Light Rainfall | 2.5–15.5 | 166 |
| 3 | Moderate Rainfall | 15.6–64.4 | 147 |
| 4 | Heavy Rainfall | 64.5–115.5 | 11 |
| 5 | Very Heavy Rainfall | 115.6–204.4 | 6 |
| 6 | Extremely Heavy Rainfall | ≥204.5 | 1 |
| 7 | Cloudburst (CB) | ≥100 mm in one hour | 1 |
| 8 | Mini-Cloudburst (MCB) | ≥50 mm in two consecutive hours. | 7 |
| Model | Layers and Units | Activation Function |
|---|---|---|
| LSTM | LSTM (64, 32) | (tanh/relu) |
| STACKED-LSTM | LSTM (128, 64, 32) | relu |
| Bi-LSTM | Bi-LSTM (64, 32) | relu |
| GRU | GRU (64, 64, 32) | relu |
| Bi-GRU | Bi-GRU (64, 64, 32) | relu |
| TRANSFORMER | MultiHeadAttention (4 heads), FFN (128) | relu (FFN), linear (output) |
| Topology | Best Model | R2 | RMSE |
|---|---|---|---|
| Linear | Bi-GRU | 0.9548 | 2.2120 |
| Triangular | Bi-GRU | 0.9445 | 2.4719 |
| Quadrilateral | Bi-GRU | 0.9409 | 2.5305 |
| Circular | Bi-LSTM | 0.9497 | 2.3337 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patro, B.S.; Bartakke, P.P. Collaborative Station Learning for Rainfall Forecasting. Atmosphere 2025, 16, 1197. https://doi.org/10.3390/atmos16101197
Patro BS, Bartakke PP. Collaborative Station Learning for Rainfall Forecasting. Atmosphere. 2025; 16(10):1197. https://doi.org/10.3390/atmos16101197
Chicago/Turabian StylePatro, Bagati Sudarsan, and Prashant P. Bartakke. 2025. "Collaborative Station Learning for Rainfall Forecasting" Atmosphere 16, no. 10: 1197. https://doi.org/10.3390/atmos16101197
APA StylePatro, B. S., & Bartakke, P. P. (2025). Collaborative Station Learning for Rainfall Forecasting. Atmosphere, 16(10), 1197. https://doi.org/10.3390/atmos16101197







