PM2.5 Concentration Prediction Model Utilizing GNSS-PWV and RF-LSTM Fusion Algorithms
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. PWV
- (1)
- GNSS-PWV
- (2)
- RS-PWV
2.2.2. Algorithms
- (1)
- Random Forest
- (2)
- LSTM Neural Network
- (3)
- MLP
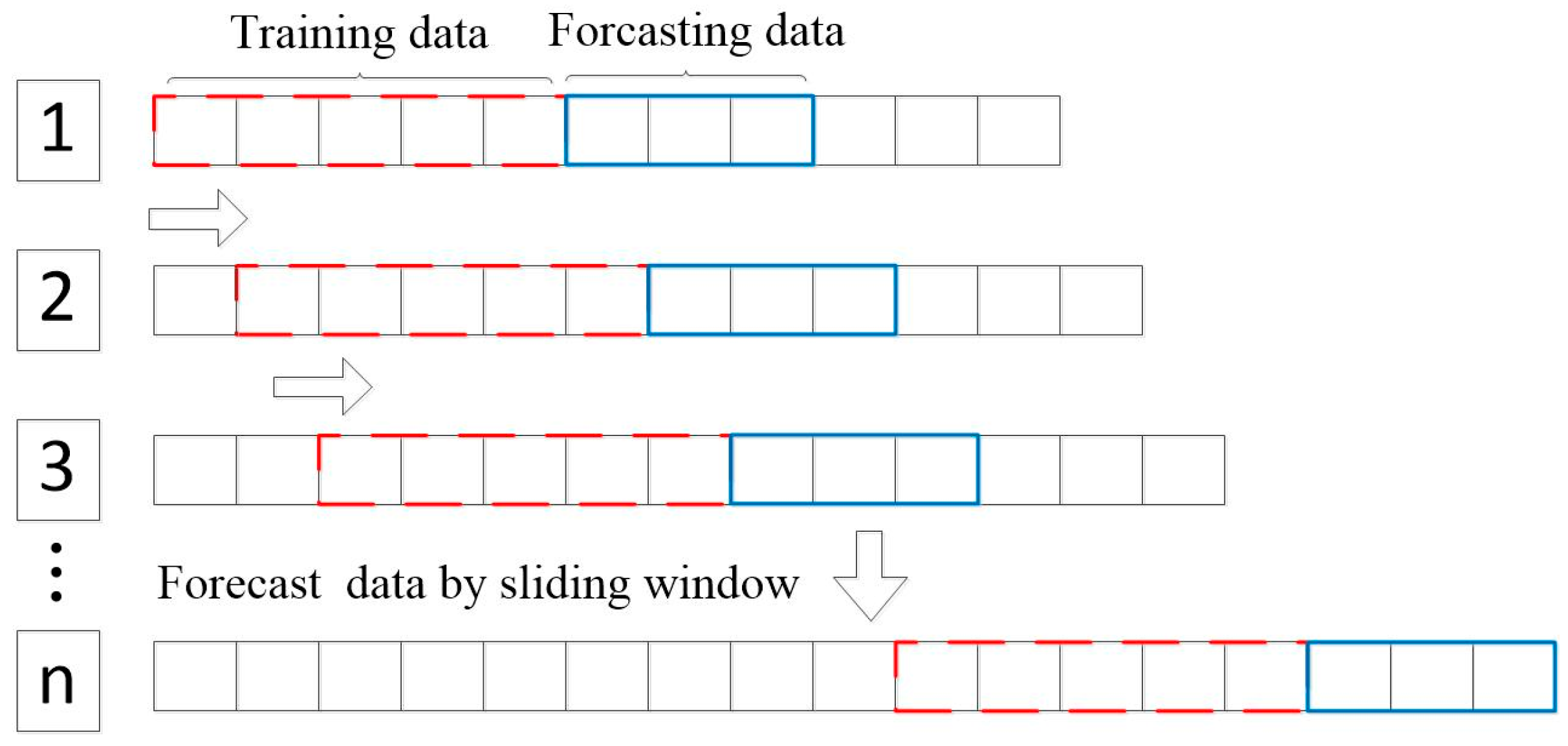
2.2.3. Sliding Window
2.2.4. Accuracy Assessments
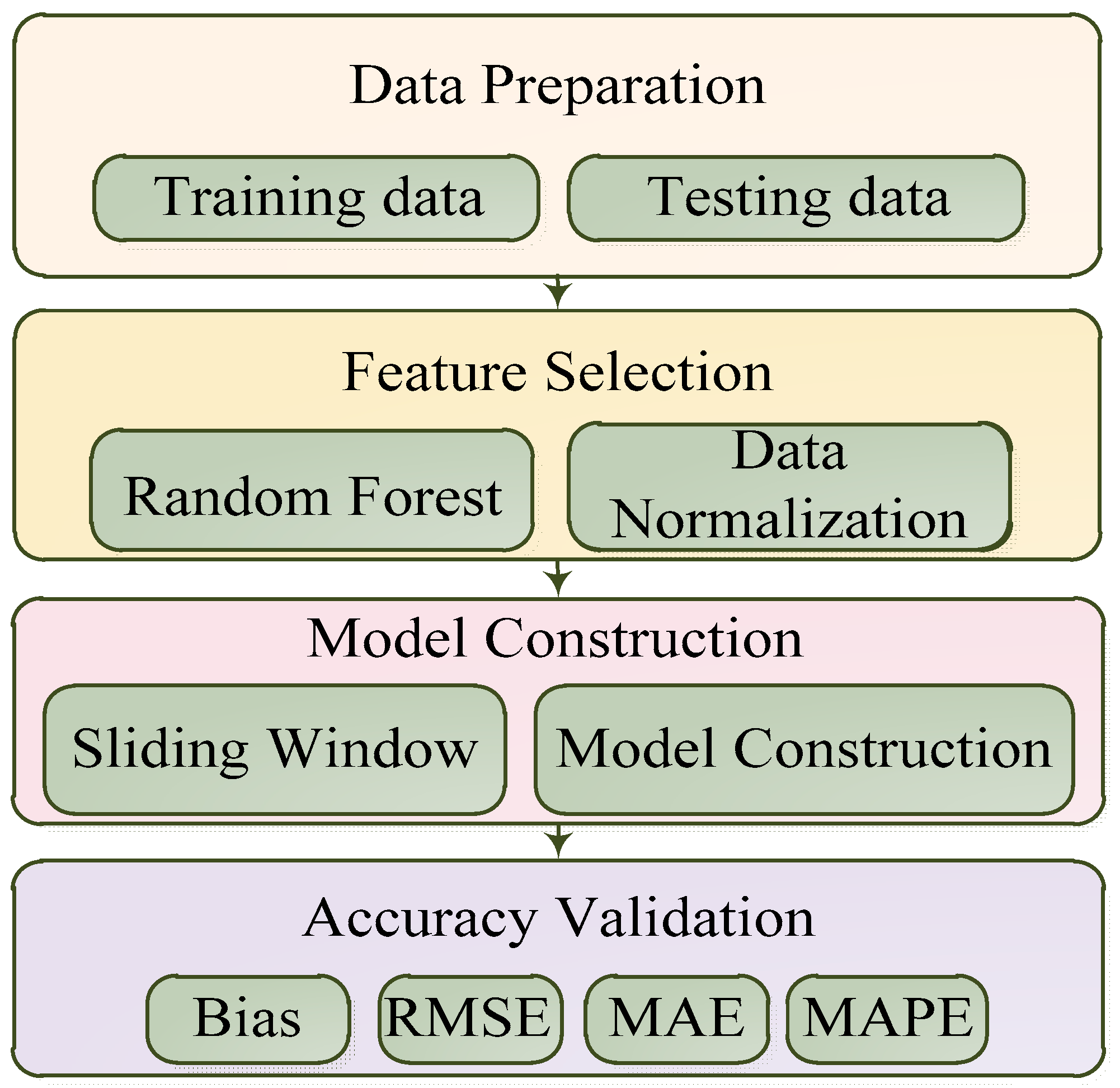
3. Model Construction
3.1. Feature Selection
3.2. Data Normalization
3.3. Selection of Sliding Windows
3.4. Model Construction
4. Result and Analysis
4.1. Accuracy of Models
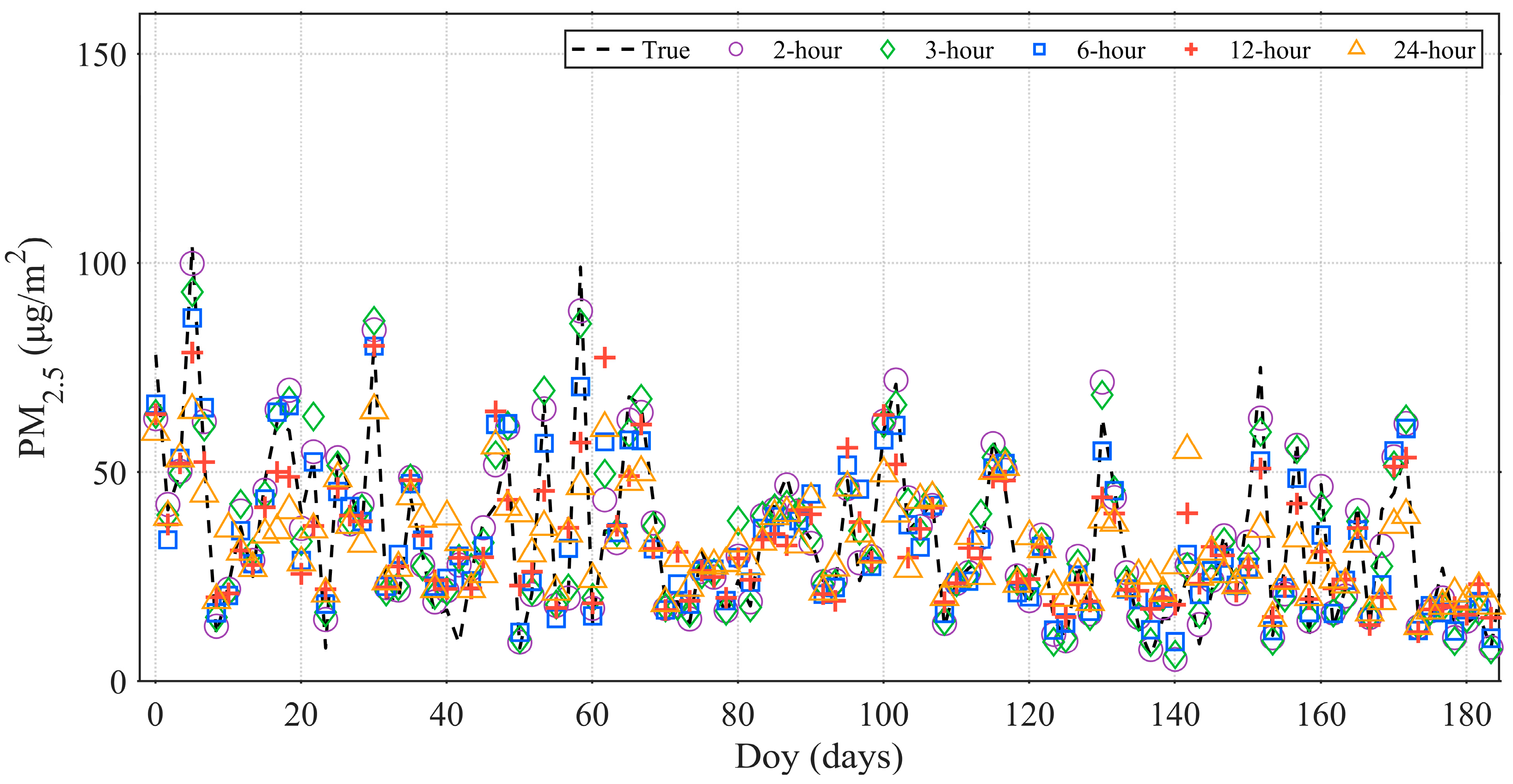
4.2. Prediction Accuracy of the RF-LSTM Model
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsai, F.C.; Smith, K.R.; Vichit-Vadakan, N.; Ostro, B.D.; Chestnut, L.G.; Kungskulniti, N. Indoor/outdoor PM10 and PM2.5 in Bangkok, Thailand. J. Expo. Sci. Environ. Epidemiol. 2000, 10, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Gu, X.; Xue, B.; Zhang, J.; Ren, W. Short period PM2.5 prediction based on multivariate linear regression model. PLoS ONE 2018, 13, e0201011. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, P.; Wang, R.; An, Z.; Qiu, L. Estimation of PM2.5 concentrations with high spatiotemporal resolution in Beijing using the ERA5 dataset and machine learning models. Adv. Space Res. 2023, 71, 3150–3165. [Google Scholar] [CrossRef]
- Wei, P.; Xie, S.; Huang, L.; Zhu, G.; Tang, Y.; Zhang, Y. Prediction of PM2.5 concentration in Guangxi region, China based on MLR-ARIMA. J. Phys. Conf. Ser. 2021, 2006, 23–25. [Google Scholar] [CrossRef]
- Hu, T.; Wang, X.; Liu, T.; Liu, H. A Novel Deep Learning Model for Subway PM2.5 Prediction Using Neighborhood Component Analysis and Convolutional Latent Variables. IEEE Trans. Instrum. Meas. 2025, 74, 2530309. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Karimian, H.; Fan, Q.; Abbasi, R. An Integrated Modeling Framework for PM2.5 Source Apportionment in the Yangtze River Delta Using WRF-CMAQ and ISAM. Atmos. Pollut. Res. 2025, 16, 102637. [Google Scholar] [CrossRef]
- Mohammadi, F.; Teiri, H.; Hajizadeh, Y.; Abdolahnejad, A.; Ebrahimi, A. Prediction of atmospheric PM2.5 level by machine learning techniques in Isfahan, Iran. Sci. Rep. 2024, 14, 2109. [Google Scholar] [CrossRef]
- Garcia, A.; Santa-Helena, E.; De Falco, A.; de Paula Ribeiro, J.; Gioda, A.; Gioda, C.R. Toxicological effects of fine particulate matter (PM2.5): Health risks and associated systemic injuries—Systematic review. Water Air Soil Pollut. 2023, 234, 346. [Google Scholar] [CrossRef]
- Chan, C.K.; Yao, X. Air pollution in mega cities in China. Atmos. Environ. 2008, 42, 1–42. [Google Scholar] [CrossRef]
- Yang, J.; Yan, R.; Nong, M.; Liao, J.; Li, F.; Sun, W. PM2.5 concentrations forecasting in Beijing through deep learning with different inputs, model structures and forecast time. Atmos. Pollut. Res. 2021, 12, 101168. [Google Scholar] [CrossRef]
- Zhou, G.; Xu, J.; Xie, Y.; Chang, L.; Gao, W.; Gu, Y.; Zhou, J. Numerical air quality forecasting over eastern China: An operational application of WRF-Chem. Atmos. Environ. 2017, 153, 94–108. [Google Scholar] [CrossRef]
- Liu, S.-K.; Cai, S.; Chen, Y.; Xiao, B.; Chen, P.; Xiang, X.-D. The effect of pollutional haze on pulmonary function. J. Thorac. Dis. 2016, 8, 41–56. [Google Scholar] [CrossRef]
- Li, W. Modeling Study of Online Public Concern on PM2.5 Pollution in China Based on Baidu index. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2023. [Google Scholar] [CrossRef]
- Lai, X.; Li, H.; Pan, Y. A combined model based on feature selection and support vector machine for PM2.5 prediction. J. Intell. Fuzzy Syst. 2021, 40, 10099–10113. [Google Scholar] [CrossRef]
- Harish Kumar, K.; Gad, I. Time series analysis for prediction of PM2.5 using seasonal autoregressive integrated moving average (SARIMA) model on Taiwan air quality monitoring network data. J. Comput. Theor. Nanosci. 2020, 17, 3964–3969. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, Y.; Huang, L.; Wei, P.; Zhang, J.; Tang, Y. Multi-scale PM2.5 concentration prediction Considering PWV in Guangxi. J. Guilin Univ. Technol. 2024, 44, 90–95. [Google Scholar] [CrossRef]
- Li, R.; Wu, S.; Wang, X.; Sun, K.; Dai, G.; Fan, M.; Ma, L.; Zheng, X.; Long, W.; Meng, F. PM2.5 and PM10 vertical distribution retrieval methods based on coherent Doppler lidar via machine learning: For haze and dust in Qingdao. Atmos. Environ. 2025, 395, 121351. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random forest algorithm overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y. Predictive analysis of PM2.5 in Nanjing under Multiple Machine Learning Models. Environ. Sci. Surv. 2025, 44, 46–52. [Google Scholar] [CrossRef]
- Guo, Q.; Yao, Y.; Zhou, Y. PM2.5 random forest prediction model incorporating GNSS meteorological parameters. Sci. Surv. Mapp. 2021, 46, 37–42+56. [Google Scholar] [CrossRef]
- Wang, W.; Liang, R.; Qi, Y.; Cui, X.; Liu, J. Prediction model of spontaneous combustion risk of extraction borehole based on PSO-BPNN and its application. Sci. Rep. 2024, 14, 5. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Qi, X.; Hu, W.; Si, S. Prediction of flood sensitivity based on Logistic Regression, eXtreme Gradient Boosting, and Random Forest modeling methods. Water Sci. Technol. 2024, 89, 2605–2624. [Google Scholar] [CrossRef]
- Choi, S.W.; Kim, B.H. Applying PCA to deep learning forecasting models for predicting PM2.5. Sustainability 2021, 13, 3726. [Google Scholar] [CrossRef]
- Chang, Y.-S.; Chiao, H.-T.; Abimannan, S.; Huang, Y.-P.; Tsai, Y.-T.; Lin, K.-M. An LSTM-based aggregated model for air pollution forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Kristiani, E.; Lin, H.; Lin, J.-R.; Chuang, Y.-H.; Huang, C.-Y.; Yang, C.-T. Short-Term Prediction of PM2.5 Using LSTM Deep Learning Methods. Sustainability 2022, 14, 2068. [Google Scholar] [CrossRef]
- Yang, X.; Xiao, D.; Bai, H.; Tang, J.; Wang, W. Spatiotemporal distributions of PM2.5 concentrations in the Beijing–Tianjin–Hebei region from 2013 to 2020. Front. Environ. Sci. 2022, 10, 842237. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Z.; Xu, G. Spatial-temporal characteristics of PM2.5 in China: A city-level perspective analysis. J. Geogr. Sci. 2016, 26, 1519–1532. [Google Scholar] [CrossRef]
- Li, T.; Hua, M.; Wu, X. A hybrid CNN-LSTM model for forecasting particulate matter (PM2.5). IEEE Access 2020, 8, 26933–26940. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Liu, L.; Guo, X.; Huang, L.; Hu, M. Application of CNN-LSTM Algorithm for PM2.5 Concentration Forecasting in the Beijing-Tianjin-Hebei Metropolitan Area. Atmosphere 2023, 14, 1392. [Google Scholar] [CrossRef]
- Shang, J.; Zhang, P.; Wang, Y.; Liu, Y.; Wang, H.; Li, S. PM2.5 Concentration Prediction in the Beijing–Tianjin–Hebei Region Based on ERA5 Stratified PWV and Atmospheric Pollutants. Atmosphere 2025, 16, 269. [Google Scholar] [CrossRef]
- Wu, F.; Min, P.; Jin, Y.; Zhang, K.; Liu, H.; Zhao, J.; Li, D. A novel hybrid model for hourly PM2.5 prediction considering air pollution factors, meteorological parameters and GNSS-ZTD. Environ. Model. Softw. 2023, 167, 105780. [Google Scholar] [CrossRef]
- Zhou, X.; Xie, M.; Zhao, M.; Wang, Y.; Luo, J.; Lu, S.; Li, J.; Liu, Q. Pollution characteristics and human health risks of PM2.5-bound heavy metals: A 3-year observation in Suzhou, China. Environ. Geochem. Health 2023, 45, 5145–5162. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; He, Q.; Wang, X. Weighted Mean Temperature Modelling Using Regional Radiosonde Observations for the Yangtze River Delta Region in China. Remote Sens. 2022, 14, 1909. [Google Scholar] [CrossRef]
- Wang, Z.; Chai, H.; Ming, L.; Ye, Y.; Ma, H.; Chen, P. Estimation of PM2.5 concentration in southern China using stacked machine learning models based on GNSS and radiosonde precipitable water vapor. Adv. Space Res. 2025, 76, 1338–1354. [Google Scholar] [CrossRef]
- Li, K.; Li, L.; Tang, J.; Dick, G.; Wickert, J.; Yu, H.; He, Q.; Dong, Z. Research on the PWV prediction model based on the ERA5-PWV calibration and WOA-RNN-BiLSTM-multihead-attention fusion algorithms. Atmos. Res. 2025, 325, 108238. [Google Scholar] [CrossRef]
- Li, K.; Li, L.; Hu, A.; Pan, J.; Ma, Y.; Zhang, M. Research on modeling weighted average temperature based on the machine learning algorithms. Atmosphere 2023, 14, 1251. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New machine learning algorithm: Random forest. In Proceedings of the International Conference on Information Computing and Applications, Chengde, China, 14–16 September 2012; Volume 7473, pp. 246–252. [Google Scholar] [CrossRef]
- Raileanu, L.E.; Stoffel, K. Theoretical comparison between the gini index and information gain criteria. Ann. Math. Artif. Intell. 2004, 41, 77–93. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Jamshidi, S.; Rezvanian, A.; Gheisari, M.; Kumar, A. Advanced fusion of MTM-LSTM and MLP models for time series forecasting: An application for forecasting the solar radiation. Meas. Sens. 2024, 33, 101179. [Google Scholar] [CrossRef]
- Drobnič, F.; Kos, A.; Pustišek, M. On the interpretability of machine learning models and experimental feature selection in case of multicollinear data. Electronics 2020, 9, 761. [Google Scholar] [CrossRef]
- Lakshmi, S.; Krishnamoorthy, A. Effective Multi-Step PM2.5 and PM10 Air Quality Forecasting Using Bidirectional ConvLSTM Encoder-Decoder with STA Mechanism. IEEE Access 2024, 12, 179628–179647. [Google Scholar] [CrossRef]



| Atmospheric Pollutants | SO2 | NO | CO | O3 | PM10 | ||
| 0.317 ** | 0.477 ** | 0.508 ** | −0.145 ** | 0.844 ** | |||
| Meteorological Elements | ZTD | PWV | Temp | Pres | RH | WS | Rain |
| −0.397 ** | −0.395 ** | −0.299 ** | 0.266 ** | −0.039 ** | −0.318 ** | −0.171 ** | |
| Feature | PM10 | Pres | Temp | ZTD | O3 | PWV | WS | RH | NO2 | SO2 | CO | Rain |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Importance | 0.113 | 0.102 | 0.09 | 0.098 | 0.097 | 0.097 | 0.094 | 0.09 | 0.09 | 0.057 | 0.045 | 0.013 |
| Window Length | RMSE | Bias |
|---|---|---|
| 6 h | 8.68 | −0.78 |
| 12 h | 7.30 | 1.04 |
| 24 h | 6.88 | −0.44 |
| 48 h | 6.90 | −0.88 |
| 72 h | 6.85 | 0.36 |
| Parameter Name | Settings (Fusion Algorithm Name) |
|---|---|
| Hidden Layer Dimension | 50 (MLP, RF-MLP and Bi-LSTM) |
| Stacking Layers | 2 (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Activation Function | rule (MLP and RF-MLP) |
| Bidirectional Option | 0.2 (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Loss Function | MSE (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Learning Rate | 0.01 (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Weight Decay Coefficient | 0.001 (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Training Epochs | 100 (MLP, LSTM, Bi-LSTM, RF-MLP, and RF-LSTM) |
| Hidden Layer Dimension | 128 (LSTM, Bi-LSTM and RF-LSTM) |
| Bidirectional Option | False (LSTM and RF-LSTM) |
| Bidirectional Option | True (Bi-LSTM) |
| Random Forest | 100 (RF-MLP and RF-LSTM) |
| Max Depth | 10 (RF-MLP and RF-LSTM) |
| Algorithm | RMSE | Bias | MAE | MAPE (%) |
|---|---|---|---|---|
| LSTM | 6.68 | −0.44 | 4.96 | 17.70 |
| Bi-LSTM | 6.17 | −4.18 | 4.47 | 16.35 |
| MLP | 5.68 | 1.72 | 4.00 | 16.80 |
| RF-MLP | 5.89 | −0.21 | 3.98 | 14.90 |
| RF-LSTM | 4.36 | −0.02 | 2.63 | 9.30 |
| Time | Bias | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|
| 2 h | 0.02 | 5.63 | 3.61 | 13.82 |
| 3 h | −0.02 | 6.87 | 3.66 | 18.28 |
| 6 h | −0.23 | 9.86 | 3.58 | 28.33 |
| 12 h | −0.61 | 12.64 | 8.82 | 38.19 |
| 24 h | −1.26 | 15.33 | 10.76 | 48.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Li, L.; Dick, G.; Wickert, J.; Ma, H.; Meng, Z. PM2.5 Concentration Prediction Model Utilizing GNSS-PWV and RF-LSTM Fusion Algorithms. Atmosphere 2025, 16, 1147. https://doi.org/10.3390/atmos16101147
Zhang M, Li L, Dick G, Wickert J, Ma H, Meng Z. PM2.5 Concentration Prediction Model Utilizing GNSS-PWV and RF-LSTM Fusion Algorithms. Atmosphere. 2025; 16(10):1147. https://doi.org/10.3390/atmos16101147
Chicago/Turabian StyleZhang, Mingsong, Li Li, Galina Dick, Jens Wickert, Huafeng Ma, and Zehua Meng. 2025. "PM2.5 Concentration Prediction Model Utilizing GNSS-PWV and RF-LSTM Fusion Algorithms" Atmosphere 16, no. 10: 1147. https://doi.org/10.3390/atmos16101147
APA StyleZhang, M., Li, L., Dick, G., Wickert, J., Ma, H., & Meng, Z. (2025). PM2.5 Concentration Prediction Model Utilizing GNSS-PWV and RF-LSTM Fusion Algorithms. Atmosphere, 16(10), 1147. https://doi.org/10.3390/atmos16101147







