Analysis of the Ducted Gravity Waves Generated by Elevated Convection over Complex Terrain in China
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
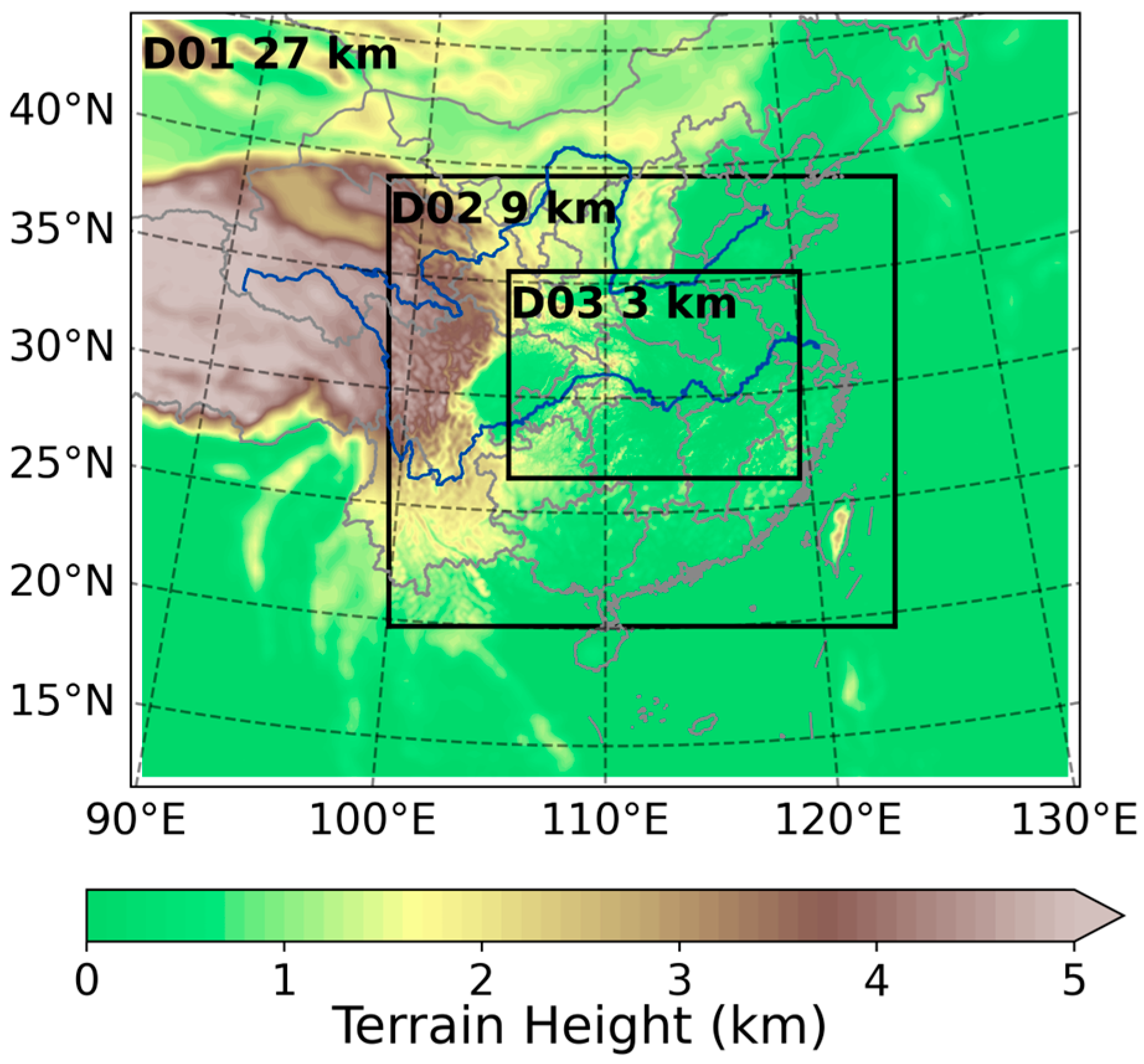
2.2. Model Configuration
3. Results
3.1. Case Overview
3.2. Ducted Gravity Waves
3.3. Terrain Ruggedness Influence
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Wang, X.; Ran, L.; Qi, Y.; Jiang, Z.; Yun, T.; Jiao, B. Analysis of gravity wave characteristics during a hailstone event in the cold vortex of Northeast China. Atmosphere 2023, 14, 412. [Google Scholar] [CrossRef]
- Lane, T.P.; Zhang, F. Coupling between gravity waves and tropical convection at mesoscales. J. Atmos. Sci. 2011, 68, 2582–2598. [Google Scholar] [CrossRef]
- Su, T.; Zhai, G. The role of convectively generated gravity waves on convective initiation: A case study. Mon. Weather Rev. 2017, 145, 335–359. [Google Scholar] [CrossRef]
- Kruse, C.G.; Smith, R.B. Gravity wave diagnostics and characteristics in mesoscale fields. J. Atmos. Sci. 2015, 72, 4372–4392. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, F.; Snyder, C. Generation and propagation of inertia–gravity waves from vortex dipoles and jets. J. Atmos. Sci. 2009, 66, 1294–1314. [Google Scholar] [CrossRef]
- Zhang, F. Generation of mesoscale gravity waves in upper-tropospheric jet–front systems. J. Atmos. Sci. 2004, 61, 440–457. [Google Scholar] [CrossRef]
- Luo, X.; Huang, X.; Fei, J.; Wang, J.; Li, C.; Cheng, X. Role of topography in triggering elevated thunderstorms associated with winter cold fronts over the eastern Yunnan-Guizhou Plateau. J. Geophys. Res. Atmos. 2023, 128, e2023JD038640. [Google Scholar] [CrossRef]
- Luo, X.; Huang, X.; Fei, J.; Wang, J.; Li, C.; Cheng, X. Influence of vortex couplets following cold fronts related to the lateral friction by mountains on elevated thunderstorm initiation. J. Geophys. Res. Atmos. 2025, 130, e2024JD041987. [Google Scholar] [CrossRef]
- Colman, B.R. Thunderstorms above frontal surfaces in environments without positive CAPE. Part I: A climatology. Mon. Weather Rev. 1990, 118, 1103–1121. [Google Scholar] [CrossRef]
- Corfidi, S.F.; Corfidi, S.J.; Schultz, D.M. Elevated convection and castellanus: Ambiguities, significance, and questions. Weather Forecast. 2008, 23, 1280–1303. [Google Scholar] [CrossRef]
- Ma, M.; Huang, X.; Fei, J.; Li, C.; Cheng, X. Characteristics of elevated thunderstorms on the cold side of fronts in China during the period 2017–21. Mon. Weather Rev. 2025, 153, 89–109. [Google Scholar] [CrossRef]
- Knupp, K. Observational analysis of a gust front to bore to solitary wave transition within an evolving nocturnal boundary layer. J. Atmos. Sci. 2006, 63, 2016–2035. [Google Scholar] [CrossRef]
- Marsham, J.H.; Trier, S.B.; Weckwerth, T.M.; Wilson, J.W. Observations of elevated convection initiation leading to a surface-based squall line during 13 June IHOP_2002. Mon. Weather Rev. 2011, 139, 247–271. [Google Scholar] [CrossRef]
- Lindzen, R.S. Wave-CISK in the tropics. J. Atmos. Sci. 1974, 31, 156–179. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, F.; Sun, Y.Q.; Wei, J.; Li, X. Practical and intrinsic predictability of wave-convection coupled bands over Southern China. J. Geophys. Res. Atmos. 2021, 126, e2021JD034882. [Google Scholar] [CrossRef]
- Du, Y.; Fuqing, Z. Banded convective activity associated with mesoscale gravity waves over southern China. J. Geophys. Res. Atmos. 2019, 124, 1912–1930. [Google Scholar] [CrossRef]
- Wu, R.; Li, Y.; Lin, Y. Mesoscale features of a squall line in spring 2013. J. Trop. Meteorol. 2023, 39, 522–535. (In Chinese) [Google Scholar] [CrossRef]
- Smith, R.B. 100 Years of progress on mountain meteorology research. Meteorol. Monogr. 2019, 59, 20.21–20.73. [Google Scholar] [CrossRef]
- Lilly, D.K.; Kennedy, P.J. Observations of a stationary mountain wave and its associated momentum flux and energy dissipation. J. Atmos. Sci. 1973, 30, 1135–1152. [Google Scholar] [CrossRef]
- Chan, K.R.; Pfister, L.; Bui, T.P.; Bowen, S.W.; Dean-Day, J.; Gary, B.L.; Fahey, D.W.; Kelly, K.K.; Webster, C.R.; May, R.D. A case study of the mountain lee wave event of 6 January 1992. Geophys. Res. Lett. 1993, 20, 2551–2554. [Google Scholar] [CrossRef]
- Leutbecher, M.; Volkert, H. The propagation of mountain waves into the stratosphere: Quantitative evaluation of three-dimensional simulations. J. Atmos. Sci. 2000, 57, 3090–3108. [Google Scholar] [CrossRef]
- Smith, R.B. Mountain-induced stagnation points in hydrostatic flow. Tellus A Dyn. Meteorol. Oceanogr. 1989, 41, 270–274. [Google Scholar] [CrossRef]
- Phillips, D.S. Analytical surface pressure and drag for linear hydrostatic flow over three-dimensional elliptical mountains. J. Atmos. Sci. 1984, 41, 1073–1084. [Google Scholar] [CrossRef]
- Wu, Q.; Mei, H.; Qin, M.; Zhang, Y.; Cheng, Y. Study on the orographic gravity wave drag effect during a heavy rainstorm. J. Meteorol. Res. Appl. 2021, 42, 7–12. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Y.; Cui, L.; Yang, C. Application of gravity wave drag scheme in numerical weather prediction of strong wind in Kelamayi. Trans. Atmos. Sci. 2022, 45, 124–134. (In Chinese) [Google Scholar] [CrossRef]
- Eom, J.K. Analysis of the internal gravity wave occurrence of 19 April 1970 in the midwest. Mon. Weather Rev. 1975, 103, 217–226. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Tung, K.K. Banded convective activity and ducted gravity waves. Mon. Weather Rev. 1976, 104, 1602–1617. [Google Scholar] [CrossRef]
- Uccelini, L.W. A case study of apparent gravity wave initiation of severe convective storms. Mon. Weather Rev. 1975, 103, 497–513. [Google Scholar] [CrossRef]
- Zhang, F.; Koch, S.E. Numerical simulations of a gravity wave event over CCOPE. Part II: Waves generated by an orographic density current. Mon. Weather Rev. 2000, 128, 2777–2796. [Google Scholar] [CrossRef]
- Zhou, X.; Du, Y.; Wei, J.; Chen, Z.; Yang, H. Statistical characteristics of wavelike banded convection associated with ducted gravity waves over Southern China. Geophys. Res. Lett. 2024, 51, e2024GL112027. [Google Scholar] [CrossRef]
- Horgan, K.L.; Schultz, D.M.; Hales, J.E., Jr.; Corfidi, S.F.; Johns, R.H. A five-year climatology of elevated severe convective storms in the United States east of the Rocky Mountains. Weather Forecast. 2007, 22, 1031–1044. [Google Scholar] [CrossRef]
- Kastman, J.S.; Market, P.S.; Fox, N.I.; Foscato, A.L.; Lupo, A.R. Lightning and rainfall characteristics in elevated vs. surface based convection in the midwest that produce heavy rainfall. Atmosphere 2017, 8, 36. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on pressure levels from 1940 to present. Clim. Data Store 2023. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Janjić, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Livneh, B.; Restrepo, P.J.; Lettenmaier, D.P. Development of a unified land model for prediction of surface hydrology and land–atmosphere interactions. J. Hydrometeorol. 2011, 6, 1299–1320. [Google Scholar] [CrossRef]
- Kain, J.S. The kain–fritsch convective parameterization: An update. J. Appl. Meteorol. Climatol. 2004, 1, 170–181. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Wang, Y.; Zhang, Y. Influences of the mid-latitude westerly trough on stratospheric gravity waves generated by typhoon lekima (2019). J. Geophys. Res. Atmos. 2021, 126, e2021JD035399. [Google Scholar] [CrossRef]














| Experiment | Domain | Terrain Adjustment | Purposes |
|---|---|---|---|
| Control run | None | None | True terrain control run |
| GF-1 | 27° N−31.5° N 106° E−112.5° E | Gaussian filter (σ = 1) | Exploring the impact of terrain variations |
| GF-3 | Gaussian filter (σ = 3) | ||
| GF-5 | Gaussian filter (σ = 5) | ||
| GF-15 | Gaussian filter (σ = 15) | ||
| Ter-0 | 27° N−31.5° N 106° E−112.5° E | Height × 0 | Exploring whether waves exist in the absence of terrain |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Qin, L. Analysis of the Ducted Gravity Waves Generated by Elevated Convection over Complex Terrain in China. Atmosphere 2025, 16, 1118. https://doi.org/10.3390/atmos16101118
Ma M, Qin L. Analysis of the Ducted Gravity Waves Generated by Elevated Convection over Complex Terrain in China. Atmosphere. 2025; 16(10):1118. https://doi.org/10.3390/atmos16101118
Chicago/Turabian StyleMa, Manman, and Luyao Qin. 2025. "Analysis of the Ducted Gravity Waves Generated by Elevated Convection over Complex Terrain in China" Atmosphere 16, no. 10: 1118. https://doi.org/10.3390/atmos16101118
APA StyleMa, M., & Qin, L. (2025). Analysis of the Ducted Gravity Waves Generated by Elevated Convection over Complex Terrain in China. Atmosphere, 16(10), 1118. https://doi.org/10.3390/atmos16101118






