Investigation of the Influence of Atmospheric Scattering on Photolysis Rates Using the Cloud-J Module

Abstract

This study analyses the wide-band algorithm, Cloud-J v.8.0, from the point of view of the validity of the choice of wide spectral intervals to accelerate the calculations of photolysis rates in the lower and middle atmosphere, considering the features of solar radiation propagation, and to assess the influence of the processes of reflection and scattering on molecules, aerosols, and clouds. The results show that the calculations performed using Cloud-J v.8.0 are in agreement with the data obtained using the high-resolution LibRadtran model. The study also considers the factors influencing the propagation of the solar flux through the atmosphere in Cloud-J v.8.0, which occurs following theoretical concepts. It is shown that the presence of cloud layers can increase photolysis rates by up to 40% in the above-cloud layer and decrease them by up to 20% below the cloud layer. The presence of volcanic aerosol can increase the photolysis rates in the upper part of the layer and above it by up to 75% and decrease them by up to 75% in the underlying atmosphere. Rayleigh scattering can both enhance photolysis rates in the troposphere and reduce them at large zenith angles. Thus, Cloud-J offers a robust method for modelling atmospheric photodissociation processes with high computational efficiency.

1. Introduction

Photodissociation (photolysis) is the process in which air molecules absorb solar photons, leading to the destruction of intramolecular bonds. Photodissociation processes play a key role in atmospheric photochemistry, initiating the most important cycles of the chemical composition change in the middle atmospheric layers; see, for example, [1] and the lower [2] atmospheric layers. The formation and destruction of the stratospheric ozone, which protects the biosphere from harsh ultraviolet solar radiation, are associated with photodissociation processes. In particular, the chain of ozone formation in the stratosphere is initiated from the photolysis of molecular oxygen (1) and continues with the recombination of atomic and molecular oxygen with the participation of any air molecule (M) as a third body (2).

Photolysis of the ozone, which can occur in the stratosphere and troposphere, leads to the formation of both atomic oxygen in the ground O(³P) (3) and excited atomic oxygen O(¹D) (4) states. It does not substantially affect ozone destruction since the recombination reaction (2) quickly restores ozone; however, it is important for the destruction of ozone (5) in chain reactions involving nitrogen, hydrogen, chlorine, and bromine radicals, generally designated as X (e.g., NO, Cl, Br) in (5).

O₂ + hv → O + O; λ < 242 nm

(1)

O + O₂ + M→ O₂ + M

(2)

Photodissociation of chlorofluorocarbons and halons in the stratosphere initiates the formation of chlorine and bromine radicals, which determine the destruction of stratospheric ozone in the chlorine and bromine catalytic cycles. The understanding of the role played by these processes in the global depletion of the ozone layer led to international agreements on phasing out the production and use of CFCs [3].

O₃ + hv → O₂ + O(³P); λ < 850 nm

(3)

O₃ + hv → O₂ + O(¹D); λ < 320 nm

(4)

X + O₃ → XO + O₂
XO + O → X + O₂
O₃ + O → O₂ + O₂

(5)

Photolysis of ozone at wavelengths shorter than 320 nm (4) results in the formation of an excited atomic oxygen atom O(¹D), playing a decisive role in atmospheric chemistry, which leads to the formation of active hydrogen and nitrogen oxides by reactions (6) and (7).

O(¹D) + H₂O → 2OH

(6)

O(¹D) + N₂O → NO + NO

(7)

The formation of ozone holes in the polar regions is also directly related to photolysis processes, which determine the rate of ozone destruction when the Sun returns after the polar night, during which, as a result of chlorine and bromine activation, Cl₂O₂ and Cl₂ molecules, which are sensitive to solar radiation, are formed on polar stratospheric clouds. These molecules quickly disintegrate after sunrise as a result of photodissociation processes (8) and (9), resulting in the formation of free radicals and rapid destruction of ozone in catalytic cycles (5) [4].

Cl₂O₂ + hv → Cl + Cl + O₂; 200 nm < λ < 450 nm

(8)

Cl₂ + hv → Cl + Cl; 270 nm < λ < 400 nm

(9)

Photolysis of nitrogen dioxide (10) plays an important role both in the stratosphere, where it produces active nitrogen oxides participating in the catalytic destruction of ozone, and in the troposphere, where photodissociation of NO₂ is the only channel for the atomic oxygen production since the photodissociation of molecular oxygen (1) does not occur in the troposphere because solar radiation with the wavelengths shorter than 242 nm is completely absorbed in the stratosphere [5]. The Tropospheric ozone is, on the one hand, a greenhouse and toxic gas. It also produces excited atomic oxygen (reaction 3), which promotes the formation of hydroxyl radicals (6) and self-purification of the troposphere.

NO₂ + hv → NO + O; 230 nm < λ < 650 nm

(10)

The photodissociation of nitric acid vapour HNO₃ (11), which is an important reservoir for the nitrogen group, both in the stratosphere and in the troposphere, determines the redistribution of nitrogen-containing gases within the NO_y family. In the stratosphere, as a result of photolysis (11), nitrogen dioxide can return to the catalytic destruction of ozone (5), from which it is extracted as a result of its reaction with hydroxyl radicals, and in the troposphere, after photodissociation of HNO₃, nitrogen dioxide can return to the ozone formation chain through photolysis (10), and recombination (2), which is interrupted during the formation of HNO₃.

HNO₃ + hv → OH + NO₂; 190 nm < λ < 350 nm

(11)

Due to the crucial role of photodissociation processes in atmospheric photochemistry, they are an important part of any chemical transport model (CTM), and any chemical climate model (CCM) used to study the time evolution of atmospheric chemical composition. The quantitative assessment of photodissociation rates used in CTM and CCM is based on the principles of chemical kinetics. According to these principles, the rates of destruction of reactant A, and the formation of products B and C of the photodissociation process (12), are proportional to the concentration of the reactant with a proportionality coefficient, depending on the solar radiation flux and the absorption properties of the atmosphere (13).

$$A+h\nu \to B+C$$

(12)

$${\displaystyle \frac{dB}{dt}}={\displaystyle \frac{dC}{dt}}=-{\displaystyle \frac{dA}{dt}}=J\cdot A$$

(13)

where A is the concentration of reactant and B and C are the concentrations of reaction products, the proportionality coefficient J, called the photolysis rate, is determined by the formula:

$$J_{A,z}={\int }_{\lambda 1}^{\lambda 2}{\sigma }_A\left(\lambda ,\mathrm{T}\right){\mathrm{q}}_A\left(\lambda ,\mathrm{T}\right)I\left(\lambda \right)d\lambda$$

(14)

where σ_A(λ, T) and q_A(λ, T) are the absorption cross sections of gas A and the quantum yield of the reaction, which determine the absorption properties of the gas under consideration at height z and depend on the wavelength (λ) and temperature (T), and I(λ) is the actinic solar radiation flux at wavelength λ at altitude z, λ₁–λ₂ is part of the spectrum in which the molecule can dissociate. The absorption cross sections and quantum yields characterising the absorption properties of gases are based on laboratory measurements and are constantly updated and published in collections that summarise the results of many laboratory measurements, such as JPL [6].

The total solar radiation flux at the height z is determined by the incoming direct, reflected, and scattered radiation of the Sun (15).

$$I_{\lambda }=I_{\lambda }^{direct}+I_{\lambda }^{reflected}+I_{\lambda }^{scattered}$$

(15)

For an accurate calculation of the total solar radiation fluxes, it is necessary to solve the integral radiative transfer equation [7], which can lead to a significant complication of the CTM and CCM code; therefore, the simplified methods are most often used in atmospheric models [8,9,10]. At the same time, the main difficulties in calculating the total radiation are associated with the necessity to consider molecular, aerosol, and cloud scattering. Therefore, simplified methods include a simplified treatment of scattered radiation using two, four, or more stream methods [11,12,13]. However, even the use of simplified methods for calculating scattered radiation with high spectral resolution, such as narrow-band methods, requires substantial computer time, given the need to increase spatial resolution in climate models. A possible solution to the problem is the use of wide-band methods that treat solar radiation fluxes and absorption parameters in rather wide spectral ranges [14,15], or the use of pre-calculated photodissociation rates [16,17,18].

One of the methods using pre-calculated values of photodissociation coefficients is the “Look up table” (LUT), which is used in the SOCOL [19], SLIMCAT/TOMCAT [20], and LMDz-REPROBUS [21] models. The idea of this method is that a high spectral resolution model is used to pre-calculate photolysis rates as a function of several atmospheric parameters. These pre-calculated results are then used to obtain photolysis rates by interpolating tabular values according to current parameters from a global model. Usually, cloud and aerosol effects, which are extremely important in the troposphere, are not considered in LUT calculations, and are added to the photolysis rates obtained by the LUT method only as modification factors. While in the stratosphere, the effect of tropospheric clouds can be reasonably considered by selecting the altitude and albedo of the cloud top, in the troposphere, most of the chemical processes occur within or below the cloud-aerosol layers. Therefore, when developing global models of tropospheric photochemistry, it is necessary to consider both the increase in the rate of photochemical processes above clouds and the upper cloud layers and the decrease in the rate beneath optically thick clouds and absorbing aerosols [22,23,24].

A more accurate accounting of the processes associated with the propagation of solar radiation in the atmosphere became possible thanks to the development of the wide-band Cloud-J algorithm (a modified version of the Fast-J algorithm) [25] for calculating photolysis rates in the presence of cloud and aerosol layers, considering their optical thickness, single scattering albedo, and scattering phase function. Cloud-J enables the modelling of global atmospheric photochemistry by incorporating the physical properties of scattering and absorbing particles directly [26]. This capability enhances the accuracy of photolysis rate calculations by accounting for the complex interactions of solar radiation with various atmospheric components.

The Cloud-J algorithm demonstrates accuracy comparable to many narrow-band methods for calculating photolysis coefficients while its computational efficiency is remarkable. Typically, the time dedicated to its calculations does not exceed 10% of the total computation time needed for the climate model [25]. When employing wide-band methods, special attention should be paid to the accuracy of accounting for the influence of different types of atmospheric scattering and reflection on the photodissociation coefficients in the troposphere and stratosphere. The spectral dependences of the parameters of Rayleigh, aerosol, and cloud scattering exhibit significant differences. In addition, the scattering and reflecting substances reside in distinct altitude layers, which influences their interactions with solar radiation. For example, the influence reflected by surface solar radiation on the photodissociation coefficients depends not only on the reflective properties of the surface but also on the attenuation of downward solar radiation in different spectral regions. Rayleigh scattering, on the one hand, is inversely proportional to the fourth power of the wavelength, which determines its strong dependence on the selected spectral ranges, and, on the other hand, depends on the air density, which decreases exponentially with height. Aerosol and cloud scattering show less variation across the spectrum but occur in narrow altitude layers (cloud in the troposphere, and aerosol in the troposphere and stratosphere) and have a scattering indicatrix strongly elongated along the beam.

Figure 1 illustrates the spectral variability of solar radiation fluxes along with the action spetra (absorption cross sections × quantum yields) of O₂ and O₃ (Figure 1a). Additionally, it shows the action spectra of various gases considered in this study (Figure 1b). The figure highlights the interactions between solar radiation and atmospheric constituents, which are crucial for understanding the photolysis processes discussed in the paper.

All atmospheric gases can be categorised into three distinct groups based on their absorption characteristics: (1) gases with absorption bands only in the hard ultraviolet spectrum, at wavelengths shorter than 250 nm; (2) gases with absorption bands in the entire ultraviolet range (100–410 nm); (3) gases with absorption bands in the ultraviolet and visible ranges. The first group includes molecular oxygen, water vapour, carbon dioxide, nitrous oxide, hydrochloric acid vapour, freons, and other chlorofluorocarbons. Since solar radiation at these wavelengths is entirely absorbed in the stratosphere, the photolysis of these gases occurs at altitudes above the tropopause, where they play a critical role in the photochemistry of the middle atmosphere. Furthermore, because radiation in this ultraviolet range does not reach the Earth’s surface and denser layers of the atmosphere, the photolysis rates of these gases in the troposphere are expected to be largely unaffected by surface reflection and scattering processes.

The second group of gases includes nitric acid vapours and most constituents from nitrogen, hydrogen, chlorine, and bromine groups. These gases exhibit a dependence of photodissociation coefficients on the conditions of solar radiation passage in the 290–320 nm range. In this range, both the solar radiation flux and the absorption by ozone, which determine the absorption properties of the atmosphere, change greatly across the spectrum.

These gases are the most interesting from the point of view of the reflection and scattering effects on the photodissociation rates because the solar radiation in this spectral region reaches the troposphere and the surface. (Figure 1a). A significant aspect of this group is the photodissociation of ozone, which results in the formation of excited oxygen O(¹D), which is formed during the absorption of solar radiation up to 320 nm. Therefore, assessing the effects of tropospheric reflection and scattering on O(¹D) formation rates under varying atmospheric conditions is essential for a comprehensive understanding of photodissociation processes and their implications for atmospheric chemistry.

The primary species in the third category are ozone with the formation of atomic oxygen in the ground state O(³P), nitrogen dioxide NO₂, nitrate trioxide NO₃, as well as chlorine and bromine reservoirs. These gases are essential for understanding the ozone anomalies in the polar regions. It is particularly interesting to analyse the contribution of the visible range of solar radiation to their photodissociation, especially since this spectral range experiences minimal attenuation as it travels through the atmosphere.

Reflection and scattering processes’ in the near ultraviolet and visible spectrum are noteworthy because a significant portion of the incoming solar radiation can penetrate the lower layers of the atmosphere and the surface, where it may subsequently be reflected and scattered upward. The influence of cloud and aerosol layers and other scattering and reflection processes on the photolysis rates were considered in the works [27,28]. Despite the fact that many aspects related to the passage of solar radiation have been clarified, nevertheless, some spectral and altitude features of various gases are not sufficiently understood.

In this study, the Cloud-J algorithm is examined from the point of view of the accuracy of the chosen spectral resolution for the calculations of photodissociation rates in the lower and middle atmosphere. The use of such an algorithm as Cloud-J in CTM or CCM allows for effectively improving the performance in predicting photolysis rates by taking into account the influence of scattering and reflection processes in the presence of cloud and aerosol layers.

This analysis considers the characteristics of solar radiation propagation mentioned earlier and aims to evaluate the impact of reflection and scattering processes on molecules, aerosols, and clouds. At the first stage of the study, the results of calculating the photodissociation coefficients using Cloud-J v.8.0 are compared with those calculated for the same conditions by the LibRadtran method exploiting very high spectral resolution. Then, the Cloud-J algorithm is employed to obtain new estimates of the reflection and scattering processes influence in different spectral ranges on the photodissociation rates of the main gases.

2. Materials and Methods

The photolysis rates of the main gases with absorption bands in different spectral ranges (Figure 1b), which we used as reference data, were calculated using the LibRadtran software (version 2.0.5) package that was designed to calculate radiative transfer in the Earth’s atmosphere. Its main part is the uvspec programme, a widely used tool for UV calculations that has demonstrated good accuracy in a number of validation campaigns, and which can be used to calculate luminosity, illuminance, and actinic fluxes of solar radiation [29]. The data calculated using LibRadtran were used as reference data in article [30], which compared different methods for calculating photolysis rates. The LibRadtran model uses a six-stream discrete ordinate method with a spectral resolution of 0.001 nm in the 121–130 nm range; the Lyman-alpha line (121.6 nm) is in this range, which requires a higher spectral resolution: 0.5 nm in the 130–175 nm range, 0.001–0.002 nm in the 175–205 nm range. This range contains the Schumann–Runge oxygen absorption band(s) (176–192.5 nm), which have a complex structure and also require a high spectral resolution of 0.5 nm in the 205–305 nm range, and 1 nm in the 350–700 nm range (a total of 25,000 spectral intervals, of which 15,000 are in the range from 175 to 700 nm).

The Cloud-J model used to study the effect of scattering and reflectance on photodissociation coefficients is a photolysis rate calculation module based on Fast-J [25]. This new data set (Cloud-J v8.0) includes near-UV cross sections for water vapour absorption that can be used to calculate photolysis rates in atmospheric chemistry models. This code was updated, and improved versions of the last published version 7.6c [31]. It cleans up some minor bugs and now includes the option for water vapour absorption in the ultraviolet region 290–340 nm. The new H2O cross sections are derived from [32].

The radiative transfer calculations in Cloud-J v.8.0 are based on the Feautrier method [33] for solving the radiative transport equations in a plane-parallel atmosphere. The Cloud-J v.8.0 spectral range (177.5–778 nm) is divided into 18 spectral intervals (bins) (see

Table 1. Cloud-J’s v8.0 bins and their spectral ranges (% denotes the proportion of solar flux and the effective absorption cross section).

Bin No.	Wavelength Interval (nm)
Bin 01	177.49–178.30—24.1%, 178.30–179.26—51.1%, 179.26–180.38—39.8%, 180.38–181.65—32.1%, 181.65–183.08—20.4%, 183.08–184.65—55.3%,	184.65–186.37—48.8%, 186.37–188.24—30.4%, 188.24–190.25—15.7%, 190.25–192.42—16.4%, 192.42–194.73—14.8%, 194.73–197.20—7.6%
Bin 02	181.65–183.08—15.3%, 183.08–184.65—19.1%, 184.65–186.37—33.6%, 186.37–188.24—24.3%, 188.24–190.25—36.8%,	190.25–192.42—29.9%, 192.42–194.73—33.3%, 194.73–197.20—19.1%, 197.20–198.50—9.8%
Bin 03	186.37–188.24—22.4%, 188.24–190.25—42.7%, 190.25–192.42—28.7%, 192.42–194.73—28.1%,	194.73–197.20—21.0% 197.20–198.50—19.8%, 198.50–200.00—10.2%, 200.00–202.50—4.7%
Bin 04	192.42–194.73—23.8%, 194.73–197.20—24.7%	197.20–198.50—19.8%, 198.50–200.00—14.2%,
Bin 05	194.73–197.20—27.6% 197.20–198.50—50.6%, 198.50–200.00—75.7%,	200.00–202.50—95.3% 202.5–206.5 nm
Bin 06	206.5–209.5 nm
Bin 07	209.5–212.5 nm
Bin 08	190.25–192.42—15.7%, 212.5–215.5 nm
Bin 09	233.0–275.5 nm
Bin 10	221.5–233.0 nm, 275.5–286.5 nm
Bin 11	215.5–221.5 nm, 286.5–291.0 nm
Bin 12	291.0–298.3 nm
Bin 13	298.3–307.5 nm
Bin 14	307.5–312.5 nm
Bin 15	312.5–320.3 nm
Bin 16	320.3–345.0 nm
Bin 17	345.0–485.0 nm
Bin 18	485.0–778.0 nm

). Photodissociation of molecular oxygen in the 177–215 nm wavelength region plays an important role in the stratosphere leading to the formation of ozone (reactions (1)–(2)). Ozone photolysis and O(¹D) formation contribute to the destruction of long-lived greenhouse and ozone-depleting gases (e.g., N₂O).

The calculation of O₂ photolysis is complicated by the fine structure of the Schumann–Runge oxygen absorption band (176–192.5 nm), which requires a high spectral resolution. Therefore, in Cloud-J v.8.0, the optical depth distribution function in the Schumann–Runge (S–R) bands [34] was used to form the first 11 bins, covering the range of 177.5–291 nm, and spectrally unconnected wavelength ranges with the same optical depth were combined, considering the relative contribution of each bin. The spectral bins are shown in Table 1 from [35].

This separation of each Schumann–Runge band range resulted in a highly accurate accounting of the influence of these bands on the photolysis rates. The influence of the Lyman-alpha line, considered in earlier versions of the code, and which is important for calculating photodissociation in the mesosphere, was excluded in Cloud-J v.8.0. To speed up the calculations, Cloud-J v.8.0 uses a simple attenuation of sunlight by absorption of O₂ and O₃ for wavelengths shorter than 290 nm (bins 1–11). Detailed accounting of scattering and reflection processes is performed only in spectral intervals of 12–18, in which solar radiation can reach the lower atmosphere and surface. Spectral data (absorption cross sections and dissociation quantum yields) are calculated based on laboratory data, in particular, JPL [36] and IUPAC [37].

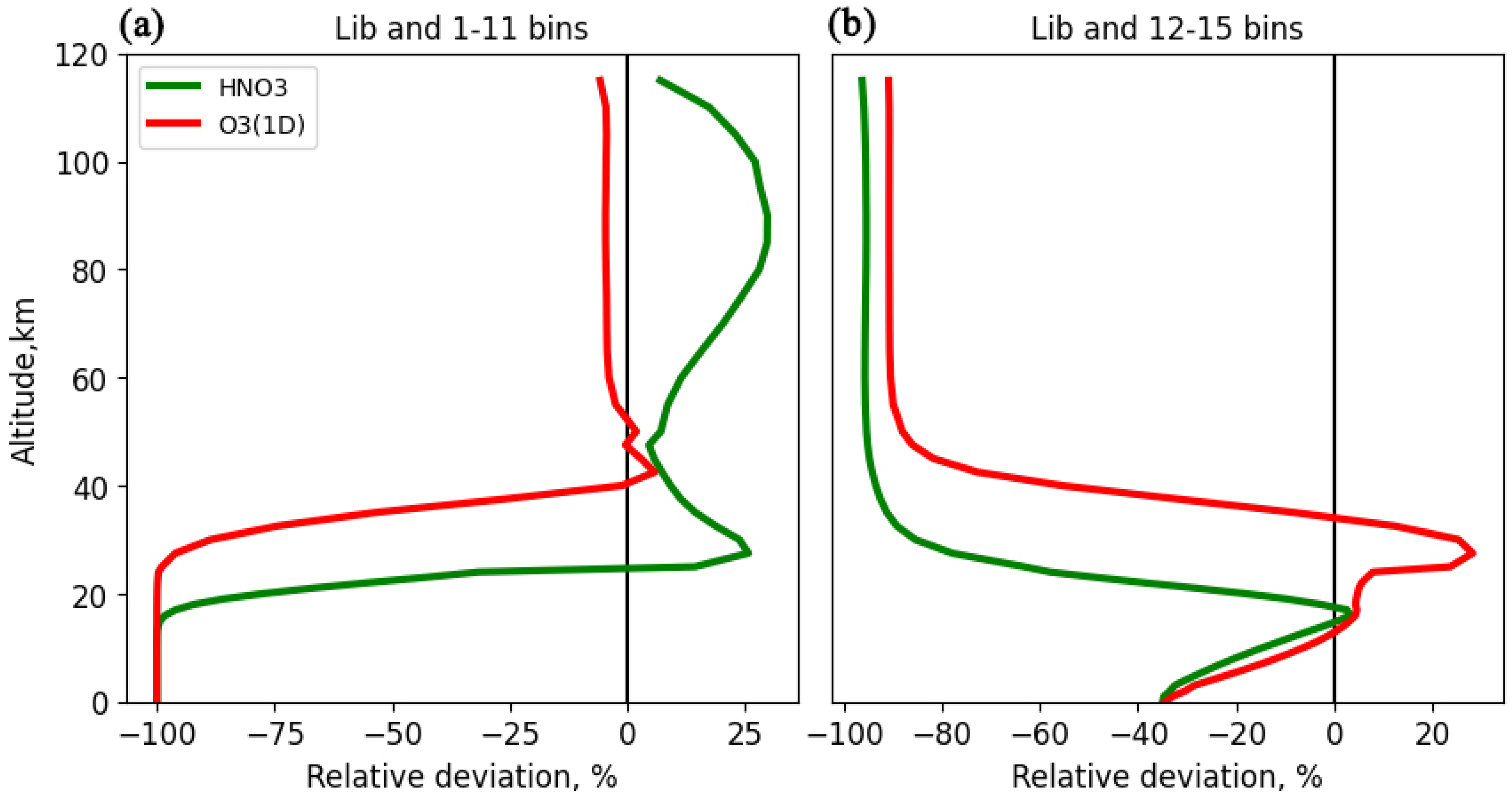
The first 11 bins cover the spectral range of solar radiation up to 290 nm, which does not reach the lower atmosphere and surface; therefore, for gases whose absorption cross sections are located only in this region, reflection from the surface and scattering in the dense layers of the troposphere should not play a significant role in calculating their photolysis coefficients.

Intervals from 12 to 15 cover the spectral range from 290 to 320 nm, in which, on the one hand, with an increase in wavelength, a rapid increase in the solar radiation flux is noted, and, on the other hand, the ozone absorption cross section also quickly decreases, which in this range, determines the transmission of radiation and its passage to the surface and lower troposphere (Figure 1). Rayleigh scattering, which is inversely proportional to the 4th power of the wavelength, is most effective in this spectral range since here, the radiation reaches the dense layers of the atmosphere, and the Rayleigh scattering coefficient remains significant.

In bin 16 (320–345 nm), the maximum sensitivity of the ozone absorption cross sections to wavelength changes is observed, and the solar radiation flux is characterised by an oscillatory change without a general tendency to increase or decrease (Figure 1a). Most of the solar radiation in this range reaches the lower troposphere and the surface, where it is reflected by the surface and scattered by dense layers of the atmosphere near the surface. Reflected and scattered radiation is also slightly attenuated, propagating upward from the surface and lower layers. Thus, due to the short wavelengths in this range, molecular scattering can effectively affect the photodissociation coefficients of gases both in the troposphere and in the stratosphere.

Bin 17 (345–485 nm) is characterised by minimal values of the ozone absorption cross sections, i.e., almost all solar radiation reaches the surface. At the same time, an increase in the intensity of solar radiation is noted (Figure 1a), which increases the significance of Rayleigh scattering in this range; since the scattering coefficient for these wavelengths is still quite high, the attenuation of radiation is small, and the solar radiation fluxes are already quite high. In the 18th bin from (485–778 nm), the solar radiation intensity reaches its maximum values and changes little, and the ozone absorption cross sections also increase slightly and change little, but the wavelength is already large, as a result of which the Rayleigh scattering coefficient is already smaller than in the ranges with shorter wavelengths and the role of this range for Rayleigh scattering becomes small, even though the fact that the radiation fluxes reaching the Earth’s surface reach their maximum values.

Cloud-J v.8.0 calculates photolysis rates in the presence of aerosol layers considering their optical properties: optical attenuation thickness, single scattering albedo, and scattering phase function. Cloud-J v.8.0 includes scattering phase functions for a wide range of atmospheric aerosols. Except for ice clouds, all of these scattering functions are calculated using the Mie theory. To account for the effects of clouds, Cloud-J v.8.0 uses the quadrature method developed by Neu et al. (2007) [38], which is based on the assumption that the calculation of the radiative field from a large number of atmospheric columns can be approximated by selecting a few representative atmospheric columns, each with its cloud distribution in each layer. Up to four independent columns are identified in the model and the photolysis rates calculated for them are averaged to determine the final values for the model cell considered. The inclusion of Rayleigh scattering effects is determined by the pseudo-Rayleigh absorption cross section (% scattering cross section), which considers the loss of radiation in the lower stratosphere due to Rayleigh scattering [35]. The contribution of molecularly scattered radiation to the total radiative field used in Formulas (14) and (15) is considered using an eight-flux approximation with an equal distribution of fluxes over four upward and four downward angles. A complete set of equations, a description of the methods for accounting for processes associated with the passage of solar radiation, and a detailed description of the spectral range can be found in [25,35].

Using LibRadtran v.2.0.5 and Cloud-J v.8.0, the photolysis rates of the most important constituents with absorption bands in different spectral ranges (Figure 1b)—O₂, O₃(O¹D), O₃(O¹D + O³P), HNO₃, Cl₂O₂, and NO₂—were calculated using the spectral solar irradiance (SSI) calculated by the COSI model, which reproduces, with high accuracy, the spectral irradiance measured by the SOLSTICE (up to 320 nm) and SIM (starting from 320 nm) satellites on board the SORCE satellite during the solar minimum of 2008, as well as SOLSPEC during the ATLAS 3 mission in 1994. COSI is used to model the variability of solar irradiance, and also provides SIR with very high spectral resolution. A more detailed description of COSI is given in [39]. In the work of [30], COSI data were used to compare several modules for calculating photolysis rates.

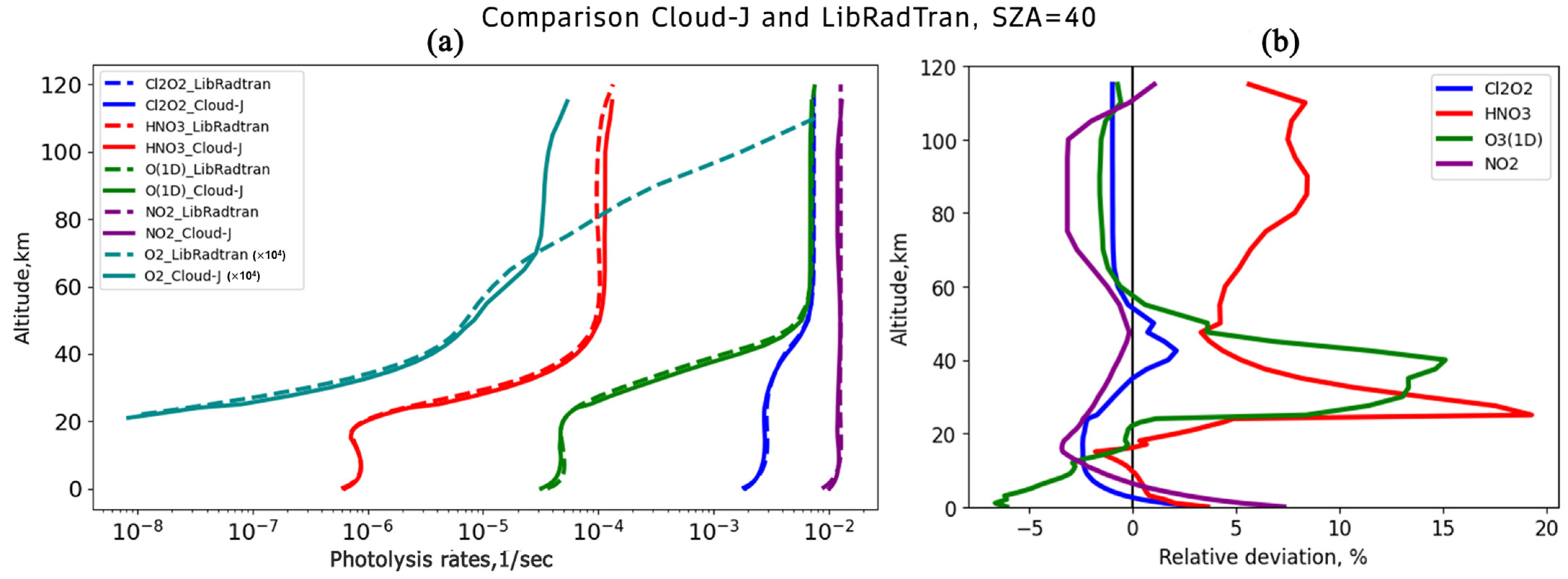
For comparison, Cloud-J v.8.0 and LibRadtran v.2.0.5 were calculated using a tropical standard atmosphere with 50 vertical levels from 0 to 115 km, for cloudless and aerosol-free conditions, for a solar zenith angle of 40° and a surface albedo of 0.1.

To analyse the influence of reflection and scattering processes across different spectral ranges on the photodissociation rates of key atmospheric gases, a series of experiments were conducted. These experiments considered various factors, including the effects of radiation reflection by the surface with different albedo values, Rayleigh molecular scattering, and the scattering of solar radiation by clouds and aerosols. The experimental design allowed these processes to be individually enabled or disabled, providing a clear understanding of their impact. For these experiments, atmospheric parameters were derived from the Cloud-J code. The analysis was performed over 57 vertical levels, extending from the Earth’s surface up to 60 km in altitude. This comprehensive approach aims to elucidate how these scattering and reflection phenomena affect the photodissociation rates at various wavelengths, thereby contributing to a more accurate modelling of atmospheric chemical processes.

3. Results

3.1. Comparison of the Results of Calculating Photolysis Coefficients Using Cloud-J v.8.0 and LibRadtran v.2.0.5

We assess the accuracy of the photodissociation rates calculations with the Cloud-J v.8.0 module by comparing them with the LibRadtran v.2.0.5 results, which is considered as a reference model. Figure 2 shows the Cl₂O₂, HNO₃, O₃(O¹D), NO₂, and O₂ photolysis rates calculated using Cloud-J v.8.0 and LibRadtranv.2.0.5 for a zenith angle of 40° for aerosol and cloud-free atmosphere.

The gases belonging to the first group, with absorption cross sections in the spectral region up to 290 nm (UV-C), are represented in this study by molecular oxygen. Photolysis of molecular oxygen in the middle stratosphere occurs mainly in the Herzberg continuum (200–242 nm), in which the solar flux penetrates to the lower part of the stratosphere. This results in the O₂ photodissociation rate decreasing rapidly below 60 km and becoming negligible below 20 km. In the upper stratosphere and mesosphere, oxygen photolysis in the Lyman-alpha line (121 nm) and in the Schumann–Runge bands (176–192.5 nm) play an important role. The Schumann–Runge continuum (135–176 nm) is only important above 90 km due to the attenuation of radiation in the overlying layers. Since the Lyman-alpha line is absent in the Cloud-J v.8.0, there are significant discrepancies in the oxygen photolysis rates calculated using Cloud-J v.8.0and LibRadtran above about 60 km. Therefore, if photodissociation rates in the upper mesosphere (above 60 km) or thermosphere are necessary, it is advisable to exploit another module or add to Cloud-J v.8.0 additional spectral intervals to account for this process.

Below 60 km, the photodissociation rates calculated with Cloud-J v.8.0 and LibRadtran v.2.0.5 agree well. This indicates that the key process (1) initiating the formation of stratospheric ozone can be successfully reproduced by the Cloud-J module.

Among the gases of the second group, which have main absorption bands only in the shortwave and near-ultraviolet spectral ranges, we analyse the photolysis rates of ozone (channel with O(¹D) formation) and HNO₃. In these specific spectral ranges, radiation is absorbed by oxygen in the Herzberg continuum, and by ozone in the Hartley (200–300 nm) and Higgins (320–360 nm) bands. As a result, the photolysis rates of these species start to decline below 50 km. The photodissociation rates of these gases show minimal variations above 50 km but experienced a rapid decrease from 50 to 20 km, followed by a little variability below 20 km.

To enhance the understanding of how different spectral regions contribute to the photodissociation of gases from the three groups discussed, further calculations of the photodissociation coefficients were carried out. These calculations focused solely on individual spectral ranges, allowing for a clearer assessment of each spectral region’s impact on the overall photodissociation process.

The contribution of different spectral regions for the considered gases and two altitude intervals (0–20 and 20–50 km) are summarised in

Table 2. Contribution of each spectral bin to the total photolysis rate.

Bin No., Wavelength Interval, nm		18 412.5–778.0	17 345.0–412.5	16 320.0–345.0	15 312.5–320.0	14 307.5–312.5	13 298.3–307.5	12 291.0–298.3	1–11 177.5–291.0
Gases	Alti-Tude, km
O3 (total)	0–20	75%	2%	5%	7%	5%	5%	1%	0%
	20–50	18%	1%	1%	2%	2%	6%	10%	60%
O(3P)	0–20	82%	3%	5%	6%	3%	1%	0%	0%
	20–50	60%	2%	4%	5%	3%	2%	3%	21%
O(1D)	0–20	0%	0%	5%	13%	32%	49%	1%	0%
	20–50	0%	0%	0%	0%	3%	7%	12%	78%
NO2	0–20	0%	82%	16%	2%	0%	0%	0%	0%
	20–50	0%	80%	16%	2%	1%	1%	0%	0%
HNO3	0–20	0%	0%	23%	31%	25%	19%	0%	2%
	20–50	0%	0%	0%	1%	1%	2%	2%	94%
Cl2O2	0–20	0%	39%	42%	12%	5%	2%	0%	0%
	20–50	0%	25%	29%	9%	5%	7%	6%	19%

. In this analysis, we combine bins 1 through 11, which span the wavelength range 177–290 nm and do not contribute significantly in the lower stratosphere. The spectral bins from 12 through 18, covering the range 291–778 nm are evaluated separately.

Table 2 indicates that in the 20–50 km layer, the primary contribution to the photolysis of gases from the second group comes from wavelengths shorter than 290 nm. Similarly to molecular oxygen, the photodissociation rates of these gases experience a rapid decline due to the quick attenuation of solar radiation. In contrast to molecular oxygen, these gases also have absorption bands in the near ultraviolet (UV-A and UV-B) (Figure 1b, Table 2). This leads to significant photodissociation rates in the lower stratosphere and troposphere. Additionally, due to weak ozone absorption and the increasing flux of solar radiation in this spectral range (see Figure 1a), the photolysis rates of these gases exhibit minimal changes below 20 km.

The comparison of the photolysis coefficients calculated using Cloud-J v.8.0 and LibRadtran v.2.0.5 for the gases of the second group (Figure 2b) shows that above 50 km, there is a systematic overestimation of the HNO₃ results by Cloud-J, with a difference of 5–7% compared to LibRadtran. In contrast, for O₃(O¹D), Cloud-J shows a slight (1–2%) underestimation. This discrepancy might be attributed to the use of combined intervals in the spectral region of 177–290 nm within Cloud-J v.8.0 (Table 1). In this range, the absorption cross sections of O₃ and HNO₃ vary significantly within the intervals that have been merged into single bins. Additionally, there is a complex variation in the absorption cross sections and solar radiation fluxes in the UV-B region (290–320 nm), which could also contribute to the observed differences in photolysis coefficients. At the same time, for HNO₃, the only one of all the gases considered, the maximum absorption cross sections are in the Schumann–Runge bands, while the ozone absorption maximises at 270–280 nm wavelengths. This may be the reason why HNO₃ is the only gas that systematically overestimates the photodissociation coefficients above 50 km.

In the altitude range of 20–50 km, the deviations of the Cloud-J v.8.0 and LibRadtran v.2.0.5 results become significant and reach 15–18%, with Cloud-J v.8.0 overestimating the photolysis coefficients. As can be seen from Table 2, the main contribution to photolysis at these altitudes is made by the intervals from 177 to 290 nm and from 290 to 320 nm, so the reasons for such a discrepancy may be associated with the same factors as above 50 km, which are superimposed by a rapid decrease in fluxes and, accordingly, photolysis coefficients in this altitude region.

Figure 3 shows the relative difference in the photolysis rates of HNO₃ and O₃(O¹D), calculated for a zenith angle of 40° using Cloud-J v.8.0 and LibRadtran v.2.0.5. The calculation using LibRadtran v.2.0.5 was performed in the entire spectral range, and Cloud-J results were obtained separately for the spectral intervals 177–290 nm and 290–320 nm. For HNO₃, the range from 177 to 290 nm has the main contribution to the overestimation by Cloud-Jv.8.0. For the O₃(O¹D) photolysis, the main role is played by spectral range from 290 to 320 nm. Similar results were obtained by the authors of the article [30].

The gases from the third group, which have absorption bands in the long part of the ultraviolet and visible regions, include ozone (channel with O(³P) formation), nitrogen dioxide, and Cl₂O₂ (see Figure 1b). In this paper, we compare the photolysis rates for Cl₂O₂ and NO₂. The absorption cross sections of Cl₂O₂ are in the wavelength range from 200 to 450 nm, with the interval 177–290 nm accounting for no more than 20% of the contribution to the photodissociation rates at altitudes of 20–50 km, and at altitudes of 0–20 km, about 80% of the contribution comes from the near ultraviolet (UV-A) and the shortwave part of the visible range (Table 2).

For nitrogen dioxide at all altitudes, about 80% of the contribution comes from bin 17 (345–412.5 nm). The attenuation of solar radiation in this spectral region is small (Figure 1a), so the radiation at these wavelengths passes almost freely through the atmosphere both on the direct path from the upper boundary of the atmosphere to the surface and back after reflection by the surface and scattering by dense layers of the lower atmosphere. As a result, the photolysis rate of NO₂ practically does not change with height, and for Cl₂O₂, its changes are small (Figure 2a). The discrepancies in the calculation results between Cloud-J v.8.0 and LibRadtran v.2.0.5 for gases in the third group are within a few percent (Figure 2b), indicating that broadband methods can effectively reproduce the variability of photodissociation coefficients for gases with primary absorption bands in the near ultraviolet and visible region with adequate accuracy for photochemical modelling.

3.2. Estimation of the Sensitivity of Photolysis Rates to Some Atmospheric Parameters

The results from the previous section indicate that the deviations of the photodissociation rates calculated using the Cloud-J v.8.0 broadband method from the LibRadtran v.2.0.5 results are within 20% for both the stratosphere and troposphere. This finding supports the possibility of using Cloud-J v.8.0 in climate models. In this section, we present the results of calculations with Cloud-J v.8.0, in which the processes of surface reflection, molecular, aerosol, and cloud scattering were both turned off and subsequently included. It is performed to further investigate the ability of Cloud-J v.8.0 to reproduce the sensitivity of the photodissociation coefficients to variations in parameters that determine scattering by air molecules, aerosol, and cloud particles, as well as to analyse the features of the influence of scattering parameters in different spectral ranges.

3.2.1. Surface Albedo

To demonstrate the influence of the underlying surface albedo, calculations were performed for a cloudless and aerosol-free atmosphere, but taking into account molecular scattering, for a zenith angle of 40°, with a surface albedo value of 0.0, 0.5, and 1.0. The calculation results are shown in Figure 4. An increase in albedo leads to an increase in the actinic flux due to the reflection and, accordingly, to an increase in the photolysis rate. This increase is reproduced by the Cloud-J model, but the amplitude of the increase depends on the gas under consideration. The main contribution to the photolysis rate of HNO₃ and O₃(O¹D) comes from the first 11 bins, which correspond to radiation with wavelengths shorter than 290 nm. Solar radiation in this spectral range practically does not reach the surface, so the photolysis rate of these trace gases depends weakly on the surface albedo. For such constituents as Cl₂O₂, O₃(O³P), and NO₂, for which photolysis occurs in the range of wavelengths, where the radiation can reach the surface and be reflected, the change in the albedo of the underlying surface plays an important role. An increase in albedo leads to a significant increase in the photolysis rates of all the gases under consideration, especially NO₂. It is interesting to note that above 20 km, the increase in the photolysis rate of NO₂ with increasing albedo is almost linear, whereas, in the troposphere, the increase in photolysis rates with increasing albedo is more intense since at a higher air density, scattering is more intensive. At a high albedo, the photolysis rate in the lower troposphere exceeds its values in the stratosphere and mesosphere, which is not observed at low values of the surface albedo.

At zero albedo (blue curve in Figure 4), a rapid decrease in photodissociation rates is observed for all gases in the lower troposphere, with the fastest decrease for NO₂ and the slowest for O³P. This occurs because, in the troposphere, molecular scattering begins to play the main role in attenuating radiation in bins 14–17 (307–485 nm). For bin 18 (wavelengths greater than 485 nm), the role of molecular scattering is less since it is inversely proportional to the 4th power of the wavelength; therefore, for ozone photodissociation with the formation of O³P, the main role is played by bin 18. The decrease in photodissociation rates down to the surface is weaker than for NO₂ and Cl₂O₂. At non-zero albedo (orange and green curves in Figure 4), most of the reflected radiation remains due to intense scattering in the dense layers of the lower troposphere, which increases the photodissociation coefficients. The greatest effect, again, is observed for NO₂, since about 80% of the contribution to its photodissociation rates is provided by bin 17 (Table 2), where most of the solar radiation reaches the surface and is scattered quite intensively due to the relatively short wavelength. For ozone, the effect is less due to the dominant role of bin 18, where molecular scattering is weak due to the long wavelength. For Cl₂O₂, the largest part of the contribution to the photodissociation rates is coming from the 14–16 intervals, where molecular scattering is more intense; therefore, the growth of the photolysis coefficients with increasing albedo is greater than for O³P, but the ozone absorption cross sections are higher than in bin 17 (Figure 1a); therefore, less radiation reaches the surface and dense layers of the atmosphere than in bin 17, as a result, the growth of the photolysis coefficients of Cl₂O₂ is less than for NO₂.

3.2.2. Molecular (Rayleigh) Scattering

In the denser layers of the atmosphere, solar radiation experiences multiple scattering by various components such as air molecules, aerosol, and cloud particles. The range of sizes of atmospheric scattering centres is quite broad—from gas molecules and density pulsations to large droplets inside convective clouds. This variability in size plays a crucial role in the scattering of light and impacts numerous atmospheric phenomena. The efficiency of light scattering depends on the ratio of the particle size to the wavelength of the incident radiation. When this ratio is small, which is typical for molecular scattering, the scattered light is evenly distributed in both the forward and backward directions, a phenomenon known as Rayleigh scattering. When the particles are larger, most of the radiation is directed forward, which is referred to as a Mie scattering. In this case, the intensity distribution of the scattered radiation becomes quite complex, varying significantly with the scattering angle.

Considering Rayleigh scattering is essential for accurately calculating photolysis rates. Using Cloud-J v.8.0, calculations were conducted with and without Rayleigh scattering in a cloudless and aerosol-free atmosphere, while also accounting for reflection from a surface with an albedo of 0.1. These calculations were performed for a zenith angle of 40 degrees, and the results are presented in Figure 5. It is important to note that the Rayleigh scattering coefficient is inversely proportional to the fourth power of the wavelength and directly proportional to the atmospheric density. As a result, molecular scattering is most intense in the troposphere near the surface for the short wavelengths. However, radiation with wavelengths shorter than 290 nm does not penetrate the lower troposphere, and only a small fraction of radiation in the 290 to 320 nm range reaches this layer, depending on the ozone content (see Figure 1a). Thus, the short-wave portion of solar radiation, which has high scattering cross sections, does not significantly influence the photodissociation of atmospheric gases. For gases of the first two groups, the effect of molecular scattering is insignificant and is not addressed in this paper.

For gases in the third group, the contribution of specific spectral bins to the photolysis coefficients is critical, as also is understanding what fraction of the radiation in these bins reaches the denser layers of the lower troposphere, and how effective molecular scattering in these bins is.

For all three gases of the third group, molecular scattering results in a noticeable increase in the photolysis coefficients in the troposphere. For all gases except NO₂ photolysis rates exhibit only slight changes above the tropopause.

For nitrogen dioxide, bin 17 (345–485 nm) plays a dominant role, as radiation within this range reaches the surface and the lower troposphere with minimal attenuation, allowing for significant scattering and reflection. Without scattering, the NO₂ photolysis rate can be affected by the temperature variations and stays more or less constant in the entire atmosphere. Molecular scattering intensifies upward flux, leading to a fast increase in the NO₂ photolysis in the troposphere, while above the tropopause the shape is not affected.

In the Cl₂O₂ case, the contributions from bins 16 and 17 are almost equal (Table 2), but about 60% of the contribution to the Cl₂O₂ photodissociation rates in the lower atmosphere arises from intervals 13 to 16. However, the radiation in these ranges is significantly attenuated as it travels through the atmosphere. Therefore, although the Rayleigh scattering cross sections in these ranges are larger than in bin 17, the influence of Rayleigh scattering is visible for Cl₂O₂ but is less pronounced than NO₂. The largest contribution to the O₃(O³P) photodissociation rate (about 80%, Table 2) comes from the visible radiation, i.e., from bin 18. Although this radiation reaches the surface, it undergoes minimal scattering due to reduced Rayleigh scattering coefficient at longer wavelengths.

At large zenith angles, the optical path of the Sun’s ray becomes longer, leading to competition between the attenuation of the direct radiation due to scattering and the increase in the scattered radiation. Figure 6 shows the results of comparing the calculations of the effect of molecular scattering for a zenith angle of 80°.

The calculation results show that at large zenith angles, the attenuation of direct radiation dominates in the troposphere leading to less intensive photolysis. As for the angle 40°, the greatest effect of such influence is observed for NO₂, since, as already mentioned above, molecular scattering is most effective in bin 17 due to high atmospheric transmission and sufficiently larger values of scattering cross sections. When scattered radiation propagates upward, it is also significantly diminished at larger zenith angles, primarily due to both scattering processes and absorption by ozone. Consequently, within the 20–50 km layer, the influence of scattered radiation is less pronounced compared to scenarios with smaller zenith angles.

3.2.3. Clouds and Aerosols

Clouds and aerosols play an important role in changing the photolysis rates, either increasing them by reflecting light or decreasing them by absorbing and attenuating them. To assess the degree of influence of cloud and aerosol scattering performed calculations with Cloud-J v.8.0 code with and without taking into account the influence of clouds and aerosol on the photolysis coefficients of some atmospheric gases. The results of these experiments are shown in Figure 7.

To demonstrate the effect of cloudiness, we introduce cloud at the 2–4 km layer with a liquid water content of 2 × 10⁻⁵g/m² and 100% cloud cover. The calculation results show a decrease in the photolysis rates below the cloud layer while an increase is observed within the cloud layer and above it. The reduction in rates is attributed to the attenuation of the actinic flux as it passes through the clouds, while the increase is a consequence of the reflection of radiation upward into the layer above the clouds and the multiple scattering occurring within the cloud layer. Cloud scattering significantly affects the gases in the third group, which possess absorption bands in the visible region. Unlike molecular scattering, which varies with wavelength, cloud scattering has a small wavelength dependency. Thus, the maximum effect is observed for those gases whose absorption bands are located in the most transparent spectral region. The maximum effect is found for ozone, as its primary absorption bands are in the visible region, where solar radiation undergoes little attenuation when passing through the atmosphere. Under the cloud layer, the photolysis rates of all species are reduced by up to 20%.

Some scientific challenges, such as the impact of increasing sulphate aerosol concentrations from volcanic eruptions or anthropogenic sources on ozone, require taking into account their influence on photochemical processes in the atmosphere. Cloud-J v.8.0 contains optical characteristics of various atmospheric aerosol types. To assess the effects of aerosols, we introduce volcanic aerosol at an altitude of 20–23 km (Figure 7b). Despite the difference in the altitudes of the scattering layers for clouds and aerosols, their influence on the photodissociation coefficients appears rather similar. Both clouds and aerosols lead to a decrease in the photolysis rate beneath the aerosol layer while increasing the rate within and above it. Notably, the increase in photolysis rates within the cloud layer begins at the lower boundary, whereas in the aerosol layer, it starts in the centre of the layer. The most pronounced effect on photolysis rates is observed for O₃(total) over 40%, NO₂ over 35%, and Cl₂O₂ around 30%, with a lesser impact (about 20%) for O(¹D) and HNO₃. This is attributed to the different wavelength ranges where these trace gases can dissociate. Furthermore, the influence of both aerosols and clouds, i.e., the increase in actinic flux due to scattering and reflection, persists across all altitudes for NO₂ and Cl₂O₂. For O₃(total), the effect remains significant up to about 40 km due to substantial attenuation in the spectral range of 177–290 nm, which contributes approximately 60% to the O₃(total) photolysis rate at these altitudes, as noted in Table 2. The degree of influence from aerosols remains consistent across different gases, with the greatest effects noted for O₃(total), exceeding 75%, followed by NO₂ at around 60%, Cl₂O₂ at about 50%, and a lesser impact for O(¹D) at around 40% and HNO₃ at about 25%. The presence of volcanic aerosol can significantly reduce photolysis rates in the underlying layers by 50–75%.

3.2.4. Sphericity of the Earth

An important factor in calculating the photolysis rates is consideration of the sphericity of the Earth’s atmosphere, which plays a major role in calculations at large zenith angles of the Sun. In these cases, direct solar radiation experiences substantial attenuation due to a longer optical path. Cloud-J v.8.0 allows for using four variants of spherical corrections defined by the ATM0 parameter, where the value 0 corresponds to a flat model, 1 to a spherical model, 2 to a refractive model, and 3 to a geometric model of the Earth’s atmosphere. To assess the effect of sphericity, photolysis rates were calculated using the ATM0 values of 0 and 2 for zenith angles of 90°, 92°, and 94°. The results of these calculations are presented in Figure 8. The refractive model, which we use in our calculations, implies a spherical model, but also takes into account the processes of atmospheric refraction, an optical phenomenon associated with the refraction of light rays in the Earth’s atmosphere. Due to the change in density, the Sun’s ray is refracted, and a wider altitude range is exposed to illumination.

In the scenario of a flat Earth, the photolysis rate values are 0 for these solar angles. The influence of sphericity becomes relevant in the upper layers of the atmosphere, where solar rays are still able to penetrate at large zenith angles, unlike the troposphere. For all trace gases, an increase in the zenith angle leads to a longer optical path, resulting in a decrease in photolysis rates due to the more significant attenuation of the actinic flux. Due to different spectral ranges, the effect of taking into account sphericity varies with the altitudes. For O(³P), where bin 18 (412.5–778.0 nm) contributes the most to the photolysis rate, the effect of sphericity is evident up to an altitude of 15 km at a zenith angle value of 94°. In contrast, for Cl₂O₂ and NO₂, dominated by bins 16 (320.0–345.0) and 17 bins (345–485 nm), respectively, the influence of sphericity extends up to 30 km.

4. Conclusions

The comparison of the photolysis rates calculated using Cloud-J v.8.0 shows their good agreement with the reference data from the LibRadtran v.2.0.5 model. However, it is important to highlight the peculiarities of calculating the photolysis rates for oxygen. Since the Lyman-Alpha band, crucial for oxygen photodissociation in the mesosphere, is not considered in Cloud-J v.8.0, this process should be treated with other methods.

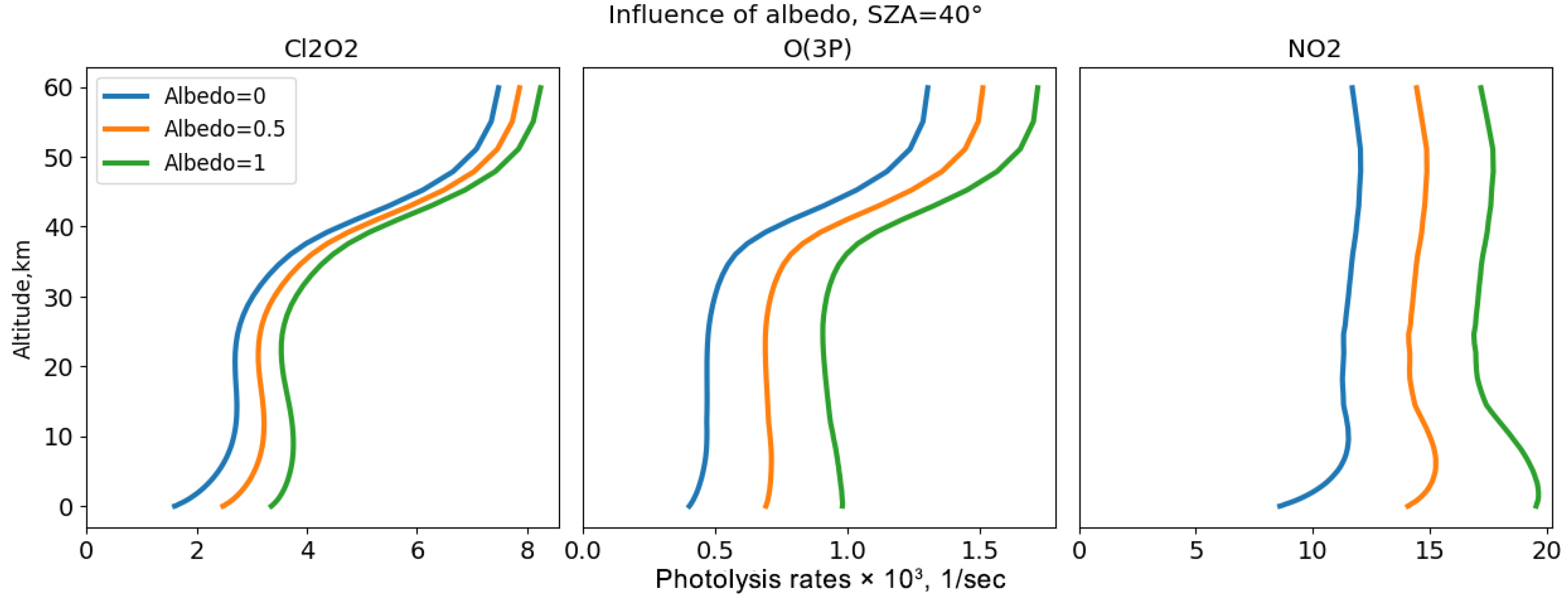
The analysis regarding reflection and scattering effects in different spectral ranges reveals that atmospheric gases respond differently to perturbations of the atmospheric conditions. This variability is associated with the spectral ranges in which these gases have absorption bands and the ability to photodissociate. Gases like NO₂, Cl₂O₂, and O₃(O³P), which absorb in the long-wave UV (greater than 290 nm) and visible regions, are more affected by reflection and scattering processes, as this radiation can penetrate to the dense tropospheric layers and reflective surfaces.

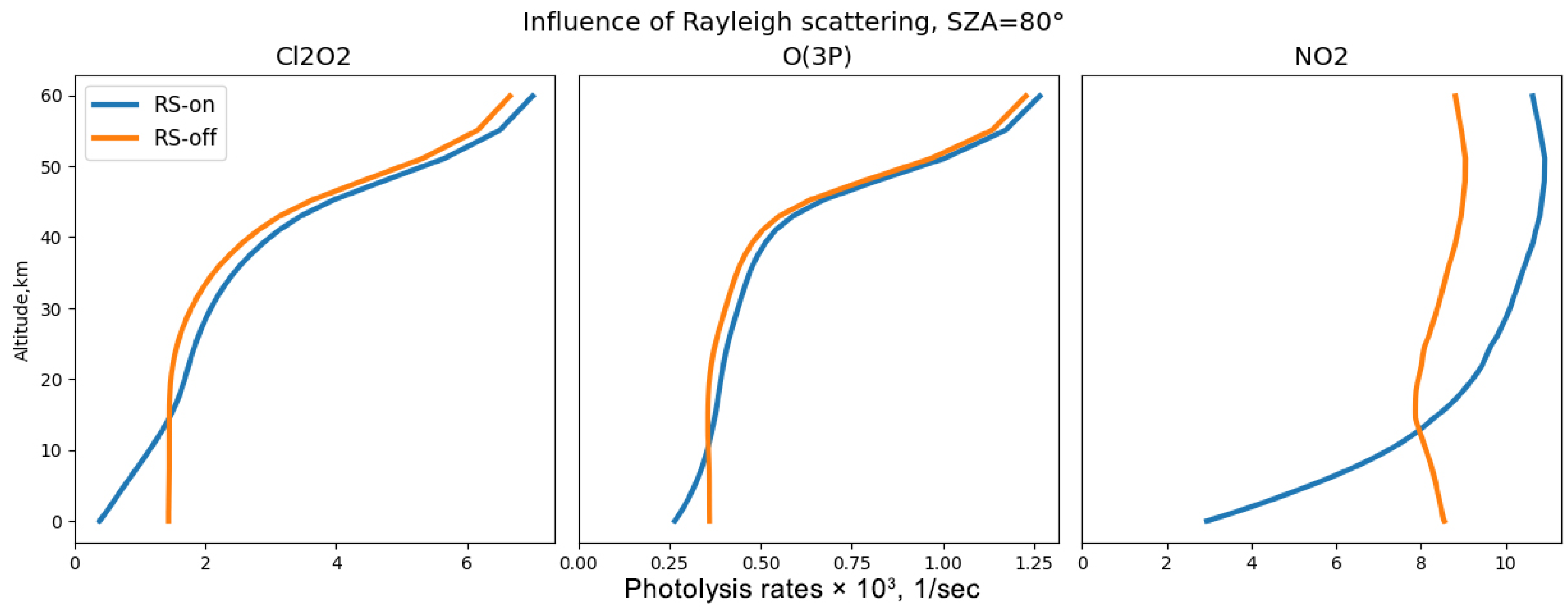
Rayleigh scattering is critically significant in photolysis rate calculations, particularly for gases with an absorption region in the visible spectrum. It can both enhance photolysis rates in the troposphere and reduce them at large zenith angles.

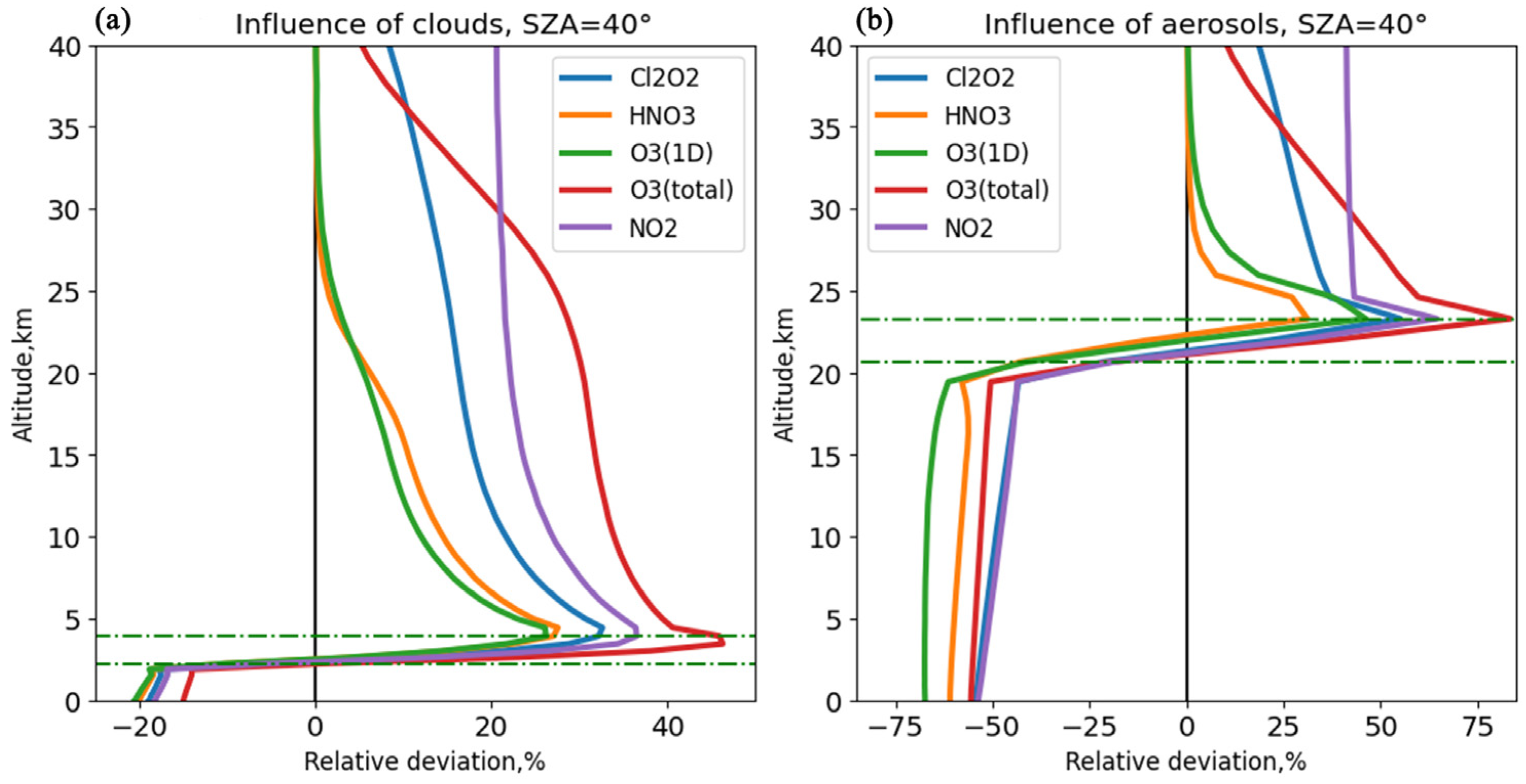
It has been shown that the presence of cloud layers can increase photolysis rates by up to 40% above the cloud layer while decreasing them by up to 20% below the cloud layer. The presence of volcanic aerosol can enhance photolysis rates in the upper parts of the atmosphere and above by up to 75% but may decrease them by the same amount in the lower atmosphere.

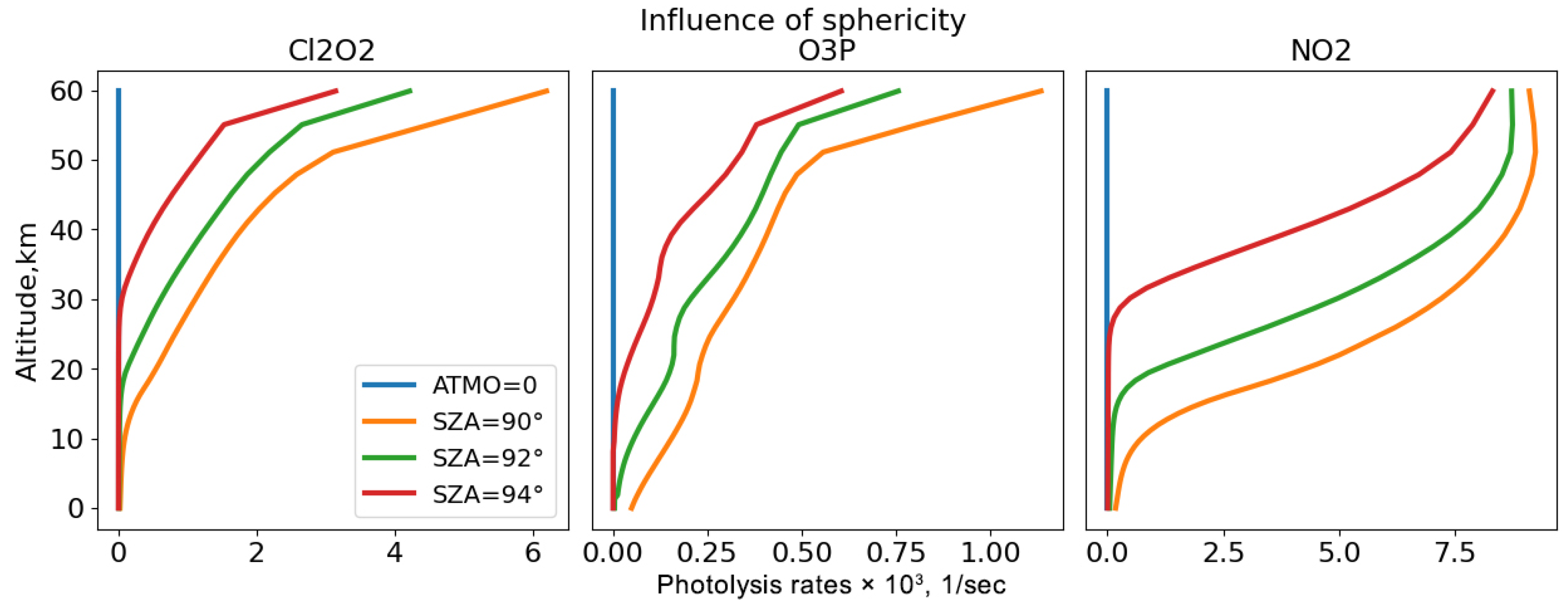
Taking into account the sphericity of the Earth becomes relevant in the upper layers of the atmosphere, where the Sun’s rays are still able to penetrate at large zenith angles. For gases such as O(³P), the influence of sphericity extends to a height of 15 km; for gases such as Cl₂O₂ or NO₂, it extends up to 30 km.

Taking into account the processes of reflection and scattering of solar radiation plays an important role in calculating the rates of photolysis. Thus, the use of Cloud-J v.8.0 will contribute to solving complex geophysical scientific problems, such as the effects of volcanic eruptions and aerosol emissions of geoengineering.

Further research will be devoted to studying the influence of scattering and reflection processes on the concentrations of trace gases in the atmosphere in the framework of 1-D and 3-D chemistry-climate models.